文章信息
- 胡斌, 李忠强, 刘婷婷, 王瀚宇. 2018.
- HU Bin, LI Zhong-qiang, LIU Ting-ting, WANG Han-yu. 2018.
- Huffman与LZW算法在海洋观测浮标通信数据压缩中的应用研究
- Application of Huffman and LZW algorithms in data compression for ocean-observation-buoy communication
- 海洋科学, 42(1): 6-10
- Marine Sciences, 42(1): 6-10.
- http://dx.doi.org/10.11759/hykx20171011002
-
文章历史
- 收稿日期:2017-10-11
- 修回日期:2017-11-20
近年来, 随着中国海洋战略走向深蓝, 我国深远海调查和科考任务越来越多, 使用的科考仪器设备也越来越多。浮标作为一种全天候式的海上观测平台, 能在深远海的海区中连续地、自动地、长期地观测所处海区的海洋气象水文乃至生物化学要素, 是我们了解深海大洋的一个重要设备手段。深远海观测浮标的使用过程中, 离不开数据的通信, 与近岸观测不同, 深远海观测设备保养和回收周期较长, 工作环境更为恶劣和复杂, 因此对浮标通信的可靠性和安全性提出了更高的要求。现阶段深远海海洋观测浮标数据需往往受限制于通信卫星带宽、自容式电池电量有限等问题影响, 发送数据量较小或者效率较低。因此对深远海观测浮标通信数据进行压缩, 对提升通信质量具有很大的必要性。
国内外对数据压缩应用到海洋浮标观测数据领域的研究较少。原因一可能是海洋浮标观测数据量本身较小, 压缩空间不大; 二可能是现阶段大部分海洋观测浮标是作为近海观测浮标应用, 带宽足够, 因此压缩意义不大。随着深远海观测浮标的应用越来越多, 数据量和卫星通信费用的考量越来越重要, 所以对海洋观测数据进行压缩具有必要性。由于海洋科学观测数据要求准确性和科学性, 所以需要对数据进行无损压缩, 能保真地还原原始观测数据, 故有损压缩不在本文讨论范围。无损压缩算法大致分为两类, 一种是基于统计, 一种是基于字典的, 本文分别选取两类中较为具有代表性的Huffman算法和LZW算法, 对海洋观测浮标通信数据进行压缩应用研究。
1 浮标通信数据压缩算法及实现 1.1 Huffman算法及实现Huffman算法是一种基于统计的压缩方法, 并且是一种可变长编码(VLC), 它将数据本身字符的形式拆散, 形成一个以0、1位形式的新的数据串, 其本质是对一段数据中的字符进行重新编码, 出现频率越高的字符, 其对应的编码也越短, 从而达到压缩数据的目的。
对于海洋观测浮标数据来说, 观测数据是一串ASCII码数据, 每个ASCII码占用8个字节大小, 而且数据中的字符往往只使用到ASCII码中的数字和个别标点符号, 故而为Huffman算法提供了可利用的压缩空间。
对于本文Huffman编码来说, 大致需要4个步骤(如图 1所示): (1)对所要压缩的数据进行遍历; (2)对应字符串在数据中的权值(概率); (3)数据中的字符串建立Huffman树, 并建立相应的Huffman码表; (4)通过建立的Huffman树对所要压缩的数据进行重构, 形成压缩数据。
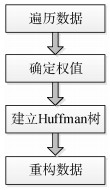 |
| 图 1 Huffman算法步骤 Fig. 1 Huffman algorithm steps |
经过编码后的数据文件, 主要包含2个部分: Huffman码表部分和压缩后的数据内容部分。解压缩的时候, 先把Huffman码表取出来, 然后对压缩内容部分各个字符进行逐一解码, 形成原数据文件。
Huffman编码的核心在于Huffman树的建立并建立与之相应的Huffman码表, Huffman树的建立是通过最优二叉树节点实现, 将其定义为一个指针的结构体, 可以方便地实现节点的遍历和置换。其中部分代码如下:
typedef struct _tagHtNode
{
_tagHtNode(unsigned char byData, unsigned long
dwWeight): Val(byData, dwWeight), pLeft(0),
pRight(0){}
struct _tagDataWW
{
_tagDataWW(unsigned char Data, unsigned
long Weight):byData(Data),
dwWeight(Weight){}
unsigned char byData;
unsigned long dwWeight;
}
_tagHtNode *pLeft;
_tagHtNode *pRight;
}
LZW算法是一种基于字典模型的的压缩算法。最早由Lemple、Ziv、Welch三人共同提出并创造, 故而用他们的名字对算法进行命名。LZW算法的本质是要建立一个字典表, 通过使用较少的字符来表示较长的重复字符来实现对数据的压缩效果。通常对LZW算法来说, 数据是一个数据流的概念, 算法将数据流中每个第一次出现的字符建立一个字典串表(一般用数字表示相应字符), 不断地读取数据流中下一个字符, 如果没有字典中对应字符就在字典中添加新的对应关系串表, 如果在在字典中有对应字符, 就用已知的字典中的对应数字表示, 如此反复, 直到遇到结束标志位字符结束, 最后输出经过字典翻译之后的压缩数据。
对于海洋观测浮标数据来说, 通信数据中主要涉及位置信息、水文气象等数字信息, 大部分是数字信息和标点信息, 并且有大多数观测数据数据格式相同, 这就为LZW算法提供了压缩空间。在LZW算法中, 单字符可以使用ASCII码字典来表示(0至256), 大于等于2个字符的字符串, 可使用的数字范围是256至4 096(LZW算法中, 一般字典中使用12 bit来表示一个字符串), 对于单次通信的浮标观测数据来说已经足够。这样一来, 一个字符(8 bit)需要用12 bit来储存, 而大于等于2个字符的字符串(≥16 bit)也可以用12 bit来存储, 所以在总体上重复率够高的字符串越多, 起到压缩效果越好。经过以上分析, 我们可以使用LZW压缩算法来对海洋观测浮标数据进行压缩, 算法流程如图 2所示, 因为LZW算法在传输过程中不需要携带字典, 故而需要按顺序依次读取字符, 这样在解码时才能不依靠字典无损地解析出原始数据, 其中算法实现部分代码如下:
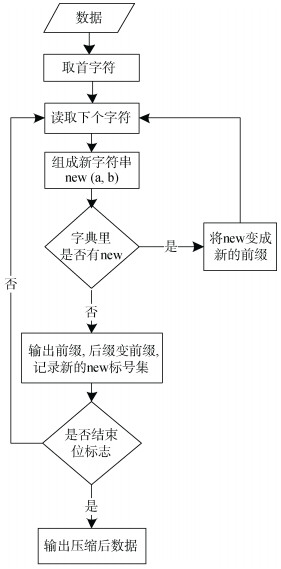 |
| 图 2 LZW算法流程图 Fig. 2 LZW algorithm flow chart |
for (i = 1; i < size; i++)
{
char_type ch = in[i];
string[str_len] = (unsigned char) ch;
str_len++;
if (dict_contains(dictionary, string, str_len))
continue;
else
{
str_len--;
code = *dict_get_code(dictionary, string, str_len);
code_len = code_length(code);
if (code_len > cur_len)
{
write_data(INC_LENGTH, cur_len);
cur_len++;
cur_size = 1
}
write_data(code, cur_len);
if (!dictionary_full)
{
dict_insert(dictionary, string, str_len + 1);
}
*string = (char_type) in[i];
str_len = 1;
if (!dict_allow_insert(dictionary))
dictionary_full = true;
}
}
本文测试数据选取于“全球变化与海气相互作用”专项在西太平洋中南部水体综合调查冬季航次布放的一套深海观测浮标。此套深海观测浮标的单包数据长度是定长(926 bit), 包含信息有:时间、浮标位置(经纬度)、浮标状态标志位、风速风向、温度、湿度、浪高浪向、水流速(ADCP)。数据时间是从2016年1月至3月, 在此时间内随机选取观测浮标数据组(共50组)进行测试, 对每组数据分别使用Huffman和LZW算法测试数据压缩率, 测试结果如图 3所示。
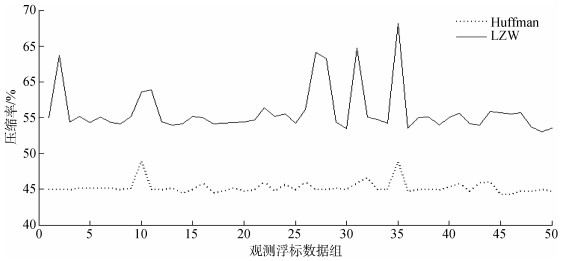 |
| 图 3 Huffman和LZW压缩率对比 Fig. 3 Comparison of Huffman and LZW compression ratios |
通过两种算法的测试结果分析, 可以得出以下几个判断:
(1) Huffman算法对此组观测数据的压缩率大致在45%左右, LZW算法对此组观测数据的压缩率大致在55%。针对本文所使用的海洋观测浮标通信数据而言, 两种方法都能较好地对数据进行压缩。
(2) 从压缩率角度看, Huffman算法要优于LZW算法, 压缩率大致低10%左右。分析可能是因为此包数据的数据格式里面, 重复的字符较高, 而相对重复的长字符串相对较少的原因, 故而从算法来判断Huffman算法压缩率略优。
(3) LZW算法的压缩率浮动较大, 而且最大差值可达15%左右; 而Huffman算法的压缩率曲线浮动较小, 并且最大差值在5%左右。根据数据特点, 数据包中0到9的数字和相应的标点符号等字符出现的概率分布大致是相同的, 故而Huffman算法的稳定性较高一些, 而这些字符出现的排列组合形式可能有较大区别, 对以字符串形式压缩的LZW算法来说稳定就会稍差一些。
(4) 整体看Huffman和LZW算法在压缩率上具有一定的线性相关性。两种算法虽然一个是基于统计的压缩算法, 一个是基于字典的压缩算法, 但本质上都属于使用较少位数来表示数据中较长的位数, 实质上都是针对数据中大量的重复数据除去冗余, 故而存在一定程度上的相线性关性。
(5) 从两种算法复杂度上分析, LZW算法要优于Huffman算法。首先从时间复杂度上分析, Huffman算法至少要遍历两次数据流, 而LZW算法只需要一次遍历数据即可生成压缩数据, 故而在算法结构上LZW算法的时间复杂度要优于Huffman算法; 其次从空间复杂度上分析, 两者在数据压缩重构过程中都产生类似字典性质的数据存储空间, 根据海洋观测浮标数据特点, 两者所需空间复杂度大致相同, 但LZW算法在传输过程中不需要此字典, 而Huffman算法需要通过传输此字典来进行解码, 故LZW算法在空间复杂度要略优于Huffman算法, 因此总体上LZW算法复杂度要优于Huffman算法。
3 结语本文主要通过两种主流无损压缩算法在海洋观测浮标数据压缩中的应用分析, 对两种压缩算法效果进行实验比测。实验结果, 从压缩率角度看, Huffman算法要略优于LZW算法, LZW算法复杂度要略优于Huffman算法。但是两者在压缩效果上, 相较于源数据都能压缩约45%甚至以上, 都基本能满足浮标远程通信需求。
在海洋观测浮标数据通信的实际应用中, 压缩算法的选用还要考虑到通信过程的编码效率的影响, 主要是运算速度、内存及编码时耗等因素的影响。在这些方面, LZW算法相对于Huffman算法有一定的优势, 遍历数据次数少, 需要内存空间也相对较小, 所以运算速度会稍快。所以在实际使用中, 两种算法可以兼顾考虑, 根据具体情况进行选择, 都能较好地达到数据压缩要求, 并提高数据的保密和安全性。
| [1] |
马春生, 潘红, 周洪英, 等. 发展海洋环境监测的意义和作用[J]. 科技创新导报, 2010, 2(2): 122-123. Ma Chunsheng, Pan Hong, Zhou Hongying, et al. Development of the significance and role of marine environment monitoring[J]. News of Science and Technology Innovation, 2010, 2(2): 122-123. |
| [2] |
王波, 李民, 刘世萱, 等. 海域资料浮标观测技术应用现状及发展趋势[J]. 仪器仪表学报, 2014, 35(11): 2401-2414. Wang Bo, Li Min, Liu Shixuan, et al. Application status and development trend of data buoy observation technology in sea area[J]. Journal of Scientific Instrument, 2014, 35(11): 2401-2414. |
| [3] |
孙鑫, 余安萍. VC++深入详解[M]. 北京: 电子工业出版社, 2006. Sun Xin, Yu Anping. VC ++In Depth Detailed[M]. Beijing: Electronic Industry Press, 2006. |
| [4] |
吴乐南. 数据压缩[M]. 南京: 东南大学出版社, 2000. Wu Lenan. Data Compression[M]. Nanjing: Southeast University Press, 2000. |
| [5] |
陈运. 信息理论与编码[M]. 成都: 电子科技大学出版社, 1996. Chen Yun. Information Theory and Coding[M]. Chengdu: University of Electronic Science and Technology Press, 1996. |
| [6] |
黎明, 时海勇. 基于北斗卫星的大型海洋浮标通信机制研究[J]. 海洋技术, 2012, 31(1): 1-5. Li Ming, Shi Haiyong. Research on large ocean buoy communication system based on Beidou satellite[J]. Technology of Marine, 2012, 31(1): 1-5. |
| [7] |
蔡明, 乔文孝, 鞠晓东, 等. 一种新的数据无损压缩编码方法[J]. 电子与信息学报, 2014, 36(4): 1008-1012. Cai Ming, Qiao Wenxiao, Ju Xiaodong, et al. A new lossless compression coding method[J]. Journal of Electronics & Information Technology, 2014, 36(4): 1008-1012. |
| [8] |
郑翠芳. 几种常用无损数据压缩算法研究[J]. 计算机技术与发展, 2011, 21(9): 73-76. Zheng Cuifang. Studies on several commonly used lossless data compression algorithms[J]. Computer Technology and Development, 2011, 21(9): 73-76. |
| [9] |
赵聪蛟, 周燕. 国内海洋浮标监测系统研究概况[J]. 海洋开发与管理, 2013, 30(11): 13-18. Zhao Congjiao, Zhou Yan. A survey of domestic marine buoy monitoring system[J]. Marine Development and Management, 2013, 30(11): 13-18. DOI:10.3969/j.issn.1005-9857.2013.11.004 |
| [10] |
李雷定, 马铁华, 尤文斌. 常用数据无损压缩算法分析[J]. 电子设计工程, 2009, 17(1): 49-51. Li Leiding, Ma Tiehua, You Wenbin. Analysis of lossless compression algorithms for common data[J]. Electronic Design Engineering, 2009, 17(1): 49-51. |
| [11] |
王防修, 周康. 通过哈夫曼编码实现文件的压缩与解压[J]. 武汉轻工大学学报, 2008, 27(4): 46-49. Wang Fangxiu, Zhou Kang. Compression and decompression of files by Huffman coding[J]. Journal of Wuhan Polytechnic University, 2008, 27(4): 46-49. |
| [12] |
杨国为, 涂序焉, 庞杰. 基于虚拟信源的无损压缩方法研究[J]. 电子学报, 2003, 31(5): 728-731. Yang Guowei, Tu Xuyan, Pang Jie. Study on lossless compression based on virtual source[J]. Journal of Electronics, 2003, 31(5): 728-731. |
| [13] |
王文彦, 李文庆, 王晓燕, 等. 数据压缩技术在海洋资料浮标通信系统中的应用[J]. 山东科学, 2015, 28(2): 1-5. Wang Wenyan, Li Wenqing, Wang Xiaoyan, et al. Application of data compression technology in marine data buoy communication system[J]. Science of Shandong, 2015, 28(2): 1-5. DOI:10.3976/j.issn.1002-4026.2015.02.001 |
 2018, Vol. 42
2018, Vol. 42

