文章信息
- 姚鹏, 綦声波, 黎明. 2018.
- YAO Peng, QI Sheng-bo, LI Ming. 2018.
- 基于无人机/无人艇的最优动态覆盖观测技术
- Optimal dynamic coverage for UAV/USV surveillance
- 海洋科学, 42(1): 106-111
- Marine Sciences, 42(1): 106-111.
- http://dx.doi.org/10.11759/hykx20171011015
-
文章历史
- 收稿日期:2017-10-11
- 修回日期:2017-12-22
面向各类智能体如移动机器人、无人机(unmanned aerial vehicle, UAV)、无人艇(unmanned surface vehicle, USV)、自主式水下航行器、传感器的覆盖问题可广泛应用于搜索营救、区域观测、信息采集等任务, 因此近年来得到了国内外学者的广泛研究[1-2]。该类问题主要分为两大类, 即静态覆盖和动态覆盖。静态覆盖的目标是优化各智能体的静态位置分布, 合理有效地分配多智能体资源, 形成最优覆盖配置[3-4]; 而动态覆盖是指通过智能体的不断移动与采样, 直至按指定程度覆盖区域内的所有有价值的任务点[5-6]。本文以UAV/USV对海面任务区域的最优观测为应用背景, 针对动态覆盖问题展开了研究。
根据任务区域内是否存在信息密度, 动态覆盖问题主要有两类求解思路。一方面, 在不存在信息密度或信息密度完全相等的区域(如农田植保等), 可采取各类穷尽策略实现智能体对任务区域的全覆盖。比如, Acar等[7]将区域建模为连接图, 然后采取图搜索策略优化覆盖路径。Choi等[8]利用平行线法获得平行的路径, 解决了基于侧扫声纳的多自主式水下航行器最优覆盖问题, 提高了覆盖网络的观测效率。文献[9]提出一种基于最小二乘法的多水下滑翔机最优覆盖采样方法。另一方面, 当区域内信息密度分布已知且覆盖时间有限时, 上述穷尽策略的效率较低, 因此不再适用, 而启发式策略可较好地解决该类问题。例如, Lanillos等[10]利用滚动时域控制(receding horizon control, RHC)思路规划连续空间的覆盖搜索航路, 通过预估未来时域的观测收益作为代价指标, 然后利用梯度法进行问题求解。基于环境信息密度, 文献[11]采用Voronoi图法对洋流影响下的目标海域进行最优分配, 然后设计针对欠驱动模型的多无人艇控制律, 使得覆盖网络能够从任意初始位置收敛到最优覆盖配置。对多智能体覆盖任务来说, 为避免局部最优、降低优化或控制难度, 一种有效的解决思路就是采用多边形分割、模糊C均值聚类等方法把任务区域分割为多个子区域, 从而将多智能体协同覆盖问题简化为多个单智能体的轨迹优化问题或控制问题[12], 但现有区域分解方法较复杂或缺乏精细的定量描述。
基于上述考虑, 本文针对多无人机/无人艇对海面区域的最优动态覆盖观测问题, 从航路优化的角度进行了问题描述, 提出了基于任务区域精细分解、子区域评估分配、航路规划相结合的分层求解思路:首先, 采用高斯混合模型(Gaussian mixture model, GMM)近似表示任务区域的信息密度分布, 从而量化提取出若干个高价值子区域; 然后, 将子区域进行排序与分配, 从而将复杂的协同优化问题简化为单UAV或USV航路规划问题; 最后, 为满足时间约束, 各UAV或USV在分配的子区域内采用并行RHC算法进行航路规划。仿真结果表明, 本文提出的方法具有较高的覆盖观测收益, 可有效解决无人机/无人艇最优动态覆盖观测问题, 具有重要的应用价值。
1 最优动态覆盖观测问题建模本文研究了面向海面区域最优观测的无人机/无人艇动态覆盖问题, 假设
本文假设无人机的航行速度是无人艇的2倍, 无人机的覆盖范围是无人艇的4倍:在每个采样时刻
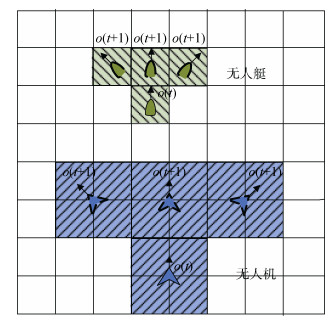 |
| 图 1 无人机/无人艇运动示意图 Fig. 1 Diagram of UAV/USV motion |
定义
| $ G_{}^t(m) = 1-{\left( {1-{g_{\rm{A}}}} \right)^{L_{\rm{A}}^t(m)}}{\left( {1-{g_{\rm{s}}}} \right)^{L_{\rm{s}}^t(m)}} $ | (1) |
其中,
结合信息密度函数
| $ P_{}^t(m) = p(m)G_{}^t(m) $ | (2) |
t时刻所有栅格的历史观测收益可定义为:
| $ P_M^t = \sum\limits_{m = 1}^M {{P^t}(m)} $ | (3) |
定义任务时间为T, 分别定义
| $ P_M^T({\phi _{\rm{A}}}^ *, {\phi _{\rm{s}}}^ * ) \ge P_M^T({\phi _{\rm{A}}}, {\phi _{\rm{s}}}), \forall {\phi _{\rm{A}}} \in {\Phi _{\rm{A}}}, {\phi _{\rm{s}}} \in {\Phi _{\rm{s}}} $ | (4) |
考虑到传统方法存在观测效率低、局部极小等问题, 本文采取基于观测区域分解、子区域排序与分配、航路规划的求解思路:首先, 基于信息密度函数等先验知识, 采取一种基于GMM的观测区域评价与特征提取方法, 将观测区域量化提取出若干个子区域即信息密度的聚类区域; 然后, 以最大化期望观测收益为指标, 将上述子区域排序、分配给各无人机与无人艇, 从而将复杂的协同规划问题简化为单无人机/无人艇规划问题; 最后, 基于观测收益函数, 各无人机或无人艇在分配的各子区域内采用并行RHC算法进行覆盖观测路径规划。采用上述策略, 将优先覆盖信息密度较大的高价值区域, 因此区域观测效率将大大提高, 且有效避免了局部极小问题。
2.2 基于GMM的观测区域特征提取通常来说, 任务区域的信息密度越大, 观测收益越高。为了量化提取任务区域特征, 本项目拟采取GMM来近似表示该区域的信息密度函数。GMM用高斯概率密度函数(正态分布)精确地量化事物, 它通常将事物分解为若干个基于高斯概率密度函数的模型[13-14]。
首先, 定义由
假设用
| $ p(m){\rm{ = }}\sum\limits_{k = 1}^K {{\alpha _k}{G_k}(m)} $ | (5) |
其中,
| $ {G_k}(m){\rm{ = }}\frac{1}{{\sqrt {{{(2\pi )}^2}\left| {{\mathit{\boldsymbol{C}}_k}} \right|} }}{{\rm{e}}^{-\frac{1}{2}{{(\mathit{\boldsymbol{P}}-{\mathit{\boldsymbol{\mu }}_k})}^{\rm{T}}}\mathit{\boldsymbol{C}}_k^{-1}(\mathit{\boldsymbol{P}} - {\mathit{\boldsymbol{\mu }}_k})}} $ | (6) |
其中,
然后, 需对GMM参数如权值
基于上述估计的各高斯模型参数, 即可提取出对应的三个标准差内(概率和99.7%)的椭圆形子区域, 它们代表了信息密度的高价值聚类区域。该子区域以
本文主要考虑了3种分配指标, 即子区域总信息密度、子区域覆盖时间、转场时间等。假设某无人机或无人艇i被分配Ki个子区域, 第k个子区域的总信息密度为:
| $ {R_k} = 0.997{\alpha _k} $ | (7) |
子区域覆盖时间表示无人机或无人艇完全覆盖子区域所需的理想时间:
| $ {{T}_{C,k}}={\text{9 }\!\!\pi\!\!\text{ }{{\sigma }_{{{x}_{k}}}}{{\sigma }_{{{y}_{k}}}}}/{C}\; $ | (8) |
其中, C表示无人机或无人艇搭载的传感器覆盖范围,
转场时间表示由初始点P0到第K个子区域中心(k=1)、或者从第k-1个子区域中心到第k个子区域(k≥2)中心所需的理想飞行或航行时间:
| $ {T_{F, k}} = \left\{ {\begin{array}{*{20}{c}} {\left\| {{\mathit{\boldsymbol{P}}^0}-{\mathit{\boldsymbol{\mu }}_k}} \right\|/V, }&{k{\rm{ = }}1}\\ {\left\| {{\mathit{\boldsymbol{\mu }}_{k-1}}-{\mathit{\boldsymbol{\mu }}_k}} \right\|/V, }&{k \ge 2} \end{array}} \right. $ | (9) |
其中, V表示无人机或无人艇的运动速度。
因此, 无人机或无人艇i对某个子区域k的期望观测收益为:
| $ EP_k^i = \frac{{{R_k}}}{{{T_{C, k}} + {T_{F, k}}}} $ | (10) |
根据上式对Ki个子区域进行迭代排序, 确定最优观测顺序。通常期望观测收益越大, 说明该区域的信息密度越高或理想观测时间越少, 优先级越高。
2.3.2 子区域分配确定各子区域的最优观测顺序后, 可得无人机或无人艇i的期望观测收益:
| $ E{A_i} = \sum\limits_{\bar k = 1}^{{K_i}} {EP_{\bar k}^i} $ | (11) |
其中,
| $ {T_i} = \sum\limits_{\bar k = 1}^{{K_i}} {({T_{C, \bar k}} + {T_{F, \bar k}})} $ | (12) |
则无人机或无人艇的总分配指标为:
| $ EA={{\lambda }_{1}}\sum\limits_{i=1}^{{{N}_{\text{A}}}\text{+}{{N}_{\text{S}}}}{E{{A}_{i}}}\text{+}{{\lambda }_{2}}\sum\limits_{\begin{smallmatrix} i,j=1 \\ i\ne j \end{smallmatrix}}^{{{N}_{\text{A}}}\text{+}{{N}_{\text{S}}}}{\left| {{T}_{i}}-{{T}_{j}} \right|} $ | (13) |
其中, 第一部分表示总期望观测收益, 第二部分用来平衡各无人机或无人艇等各观测力量间的任务执行代价,
| $ A_{{\rm{allocation}}}^* = \arg \max (EA) $ | (14) |
在分配完子区域后, 各无人机或无人艇采取一种以最大化观测收益为目标的并行RHC航路规划方法, 使规划的航路满足任务时间约束。假设无人机或无人艇被分配的子区域中心位置为
首先, 初始化各航路段, 包括从起始点P0到子区域
然后, 如果上述各航路段时间之和小于任务时间T, 则需选择某航路段并添加一个新航点, 具体实现策略如下:采取RHC方法为每条航路段
最后, 将各航路段依次连接起来即
基于并行RHC的覆盖航路规划算法的示意图如图 2所示。
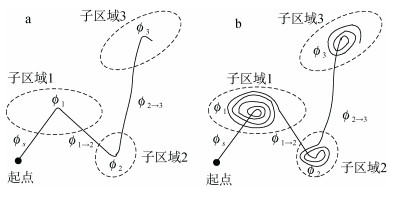 |
| 图 2 基于并行RHC的单机覆盖搜索航路规划示意图 Fig. 2 Search path voverage of single agent by concurrent RHC a.航路初始化; b.覆盖观测航路 a. Initialized path; b surveillance path coverage |
本文采用MATLAB软件进行仿真验证, 每组试验均运行20次, 并对观测收益等统计结果进行分析。假设任务区域为2 500 m×2 500 m, 将该区域平均离散为50个×50个栅格, 信息密度函数由随机产生的10个指数函数组成。其他仿真参数如下:仿真时间T=500s, 无人机数量
假设2架无人艇的初始位置为(100, 100)m, (500, 100)m, 无人机的初始位置为(300, 100)m。任务区域的先验信息密度分布如图 3a所示, 在区域右下角存在一个远离无人机或无人艇初始点和其他子区域的高价值子区域。采取GMM后的近似结果如图 3b所示, 共提取出7个椭圆形的子区域, 它们能较好地近似表示任务区域的信息密度。然后, 采取本文提出的区域评价与分配策略, 排序后的子区域{5, 1}分配给USV1, 子区域{2, 7}分配给USV2, 子区域{6, 4, 3}分配给UAV。基于上述分配结果, 采用并行RHC规划的无人艇与无人机覆盖观测航路如图 3c所示, 它们覆盖了所有高价值子区域, 并且优先监测信息密度较高的区域, 尤其是USV2直接探测右下角的子区域。此外, 由于无人机相比于无人艇具有更大的观测范围与飞行速度, 因此无人机的覆盖航路分布更广泛且更稀疏。
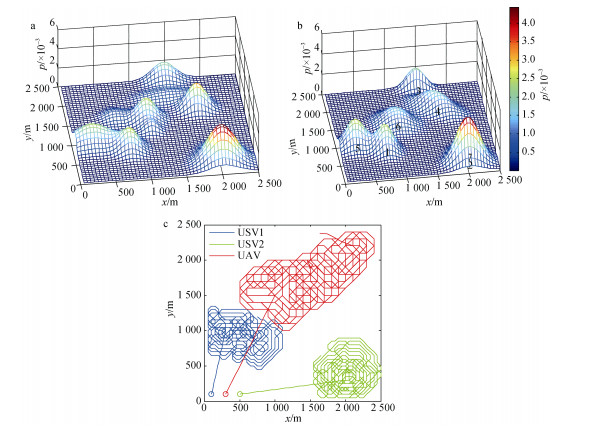 |
| 图 3 基于GMM-RHC的无人机/无人艇覆盖观测示意图 Fig. 3 UAV/USV coverage by GMM-RHC a.信息密度分布图; b. GMM近似结果; c.覆盖航路 a. Information density map; b. GMM results; c. path coverage |
此外, 采取典型的RHC算法进行了仿真对比, 由于未对区域进行评价分配, 传统RHC算法规划的航路会使无人机或无人艇陷入局部区域而无法覆盖右下角区域, 观测效率大大降低, 如图 4所示。我们给出GMM-RHC、RHC、以及广泛应用的平行线法这三种方法的观测收益曲线, 如图 5所示, GMM- RHC具有最优的观测收益, RHC次优, 由于平行线法未有效利用任务区域的信息密度, 因此其观测效率最低。
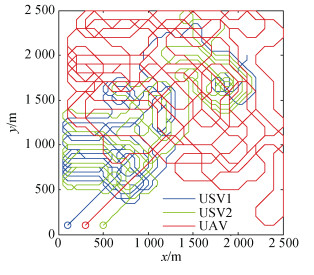 |
| 图 4 基于RHC的无人机/无人艇覆盖观测示意图 Fig. 4 UAV/USV coverage by RHC |
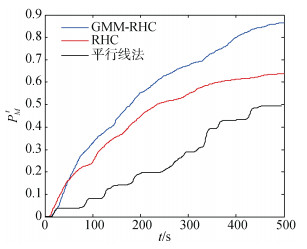 |
| 图 5 采用不同方法的无人机/无人艇覆盖观测收益曲线 Fig. 5 Payoff curve of UAV/USV using different methods |
本文研究了面向动态覆盖观测任务的无人机/无人艇航路优化问题。以最大化观测收益为优化指标, 本文提出一种基于GMM区域分解、子区域分配与并行RHC航路规划相结合的分层求解思路, 从而简化问题求解难度。GMM方法可提取任务区域的特征, 为后续子区域分配提供了量化指标; 子区域分配确定了无人机或无人艇的任务子区域及其观测顺序; 并行RHC方法规划的航路可满足时间约束。仿真结果表明, 本文提出的方法具有较高的覆盖观测效率, 无人机或无人艇优先覆盖观测高价值区域, 有效避免了传统方法中的局部极小问题。
| [1] |
Galceran E, Carreras M. A survey on coverage path planning for robotics[J]. Robotics and Autonomous Systems, 2013, 61(12): 1258-1276. DOI:10.1016/j.robot.2013.09.004 |
| [2] |
Song C, Feng G, Fan Y, et al. Decentralized adaptive awareness coverage control for multi-agent networks[J]. Automatica, 2011, 47(12): 2749-2756. DOI:10.1016/j.automatica.2011.09.006 |
| [3] |
孙昌浩, 段海滨. 基于进化势博弈的多无人机传感器网络K-覆盖[J]. 中国科学:技术科学, 2016, 46(10): 1016-1023. Sun Changhao, Duan Haibin. An evolutionary potential game theoretic approach for the K-COVER problem in multi-UAV sensor networks[J]. Scientia Sinica Technologica, 2016, 46(10): 1016-1023. |
| [4] |
Gupta V, Chung T H, Hassibi B, et al. On a stochastic sensor selection algorithm with applications in sensor scheduling and sensor coverage[J]. Automatica, 2006, 42(2): 251-260. DOI:10.1016/j.automatica.2005.09.016 |
| [5] |
宋程. 移动传感器网络的动态覆盖与聚集[D]. 合肥: 中国科学技术大学, 2012. Song Cheng. Dynamic coverage and rendezvous for mobile sensor networks[D]. Hefei: University of Science and Technology of China, 2012. |
| [6] |
陈海, 何开锋, 钱炜祺. 多无人机协同覆盖路径规划[J]. 航空学报, 2016, 37(3): 928-935. Chen Hai, He Kaifeng, Qian Weiqi. Cooperative coverage path planning for multiple UAVs[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 928-935. |
| [7] |
Acar E U, Choset H, Lee J Y. Sensor-based coverage with extended range detectors[J]. IEEE Transactions on Robotics, 2006, 22(1): 189-198. DOI:10.1109/TRO.2005.861455 |
| [8] |
Choi M H. Optimal underwater coverage of a cellular region by autonomous underwater vehicle using line sweep motion[J]. Journal of Electrical Engineering and Technology, 2012, 7(6): 1023-1033. DOI:10.5370/JEET.2012.7.6.1023 |
| [9] |
朱心科, 俞建成, 王晓辉. 水下滑翔机自适应覆盖采样[J]. 机器人, 2012, 34(5): 566-573. Zhu Xinke, Yu Jiancheng, Wang Xiaohui. Adaptive coverage sampling of underwater glider[J]. Robot, 2012, 34(5): 566-573. |
| [10] |
Lanillos P, Gan S K, Besada-Portas E, et al. Multi-UAV target search using decentralized gradient-based negotiation with expected observation[J]. Information Sciences, 2014, 282: 92-110. DOI:10.1016/j.ins.2014.05.054 |
| [11] |
严卫生, 左磊, 崔荣鑫, 等. 洋流干扰下的多自主水面无人船最优覆盖控制[J]. 西北工业大学学报, 2014, 32(5): 769-774. Yan Weisheng, Zuo Lei, Cui Rongxin, et al. Coverage control of multiple autonomous underwater vehicle with disturbance by ocean currents considered[J]. Journal of Northwestern Polytechnical University, 2014, 32(5): 769-774. |
| [12] |
Li Y, Chen H, Er M J, et al. Coverage path planning for UAVs based on enhanced exact cellular decomposition method[J]. Mechatronics, 2011, 21(5): 876-885. DOI:10.1016/j.mechatronics.2010.10.009 |
| [13] |
Yao P, Wang H, Ji H. Gaussian mixture model and receding horizon control for multiple UAV search in complex environment[J]. Nonlinear Dynamics, 2017, 88(2): 903-919. DOI:10.1007/s11071-016-3284-1 |
| [14] |
Fraley C, Raftery A E. Model-based clustering, discriminant analysis, and density estimation[J]. Journal of the American statistical Association, 2002, 97(458): 611-631. DOI:10.1198/016214502760047131 |
 2018, Vol. 42
2018, Vol. 42

