文章信息
- 赵振华, 赵宜楠, 周志权, 赵占锋, 王晨旭. 2018.
- ZHAO Zhen-hua, ZHAO Yi-nan, ZHOU Zhi-quan, ZHAO Zhan-feng, WANG Chen-xu. 2018.
- 极化X波段雷达海面溢油微波散射模型研究
- Development of microwave scattering model for sea-surface oil spills based on polarimetric X-band radar data
- 海洋科学, 42(1): 128-133
- Marine Sciences, 42(1): 128-133.
- http://dx.doi.org/10.11759/hykx20171011016
-
文章历史
- 收稿日期:2017-10-11
- 修回日期:2017-12-20
2. 山东船舶技术研究院, 山东 威海 264209;
3. 海洋通信与组网观测技术威海市重点实验室, 山东 威海 264209
2. Shandong Institute of Shipbuilding Technology, Weihai 264209, China;
3. Weihai City Key Laboratory of Ocean Communication and Networking Observation Technology, Weihai 264209, China
海洋是人类的摇篮, 其面积约占地球面积的2/3, 并且蕴藏着丰富的资源, 例如生物资源、矿产资源、石油、天然气等能源。但随着对海洋资源的开发以及世界航运业的大发展, 海洋污染日趋严重, 溢油事故的发生屡见不鲜[1-2], 海上石油污染给海洋生态平衡带来严重威胁。
目前对溢油的研究大都集中在对数据的处理上, 而对于溢油的微波散射原理的研究较少, 对溢油的微波散射原理进行深入研究有利于开展快速高效的溢油检测手段, 对于海上溢油污染处理和海洋生态环境的尽快恢复具有重要意义[3]。
1 海面复合微波散射模型对于单站雷达系统, 如果雷达去照射光滑平静的海面, 则会产生镜面反射效应, 几乎没有回波信号会经海面反射回接收器, 在雷达图像上就会显示出一个暗区域, 但是若海面较为粗糙, 通常这种粗糙的海面是由于毛细波(张力波)和重力波组成, 此时雷达的微波信号照射海面之后将会产生各个方向的散射, 形成散射场。其中一部分微波信号会沿原路径返回收发装置, 这部分散射即为后向散射分量, 此时的微波散射系数即为单站雷达系统的微波后向散射系数。
对于粗糙的海面来说, 海浪的形式主要有两种:一种是大尺度海浪, 其海面平均曲率半径远大于波长。第二种是小尺度毛细波, 其海面均方根高度远小于波长, 且均方根斜率较小。真实海浪的形式就是小尺度叠加在大尺度波浪上, 同时大尺度波对小尺度波有调制作用, 这种模型就叫做复合微波散射模型。对大尺度海浪的微波散射建模用几何光学模型, 其后向系数的求解用基尔霍夫近似法。对小尺度波浪的微波散射的建模用小扰动模型, 其后向散射系数的求解我们用微扰法, 求解的过程中需要考虑大尺度波对小尺度波的调制作用, 可以对大尺度波做起伏统计平均处理。
微波的垂直或水平极化方式,
| $ \sigma \left( {{\theta _i}} \right) = {\sigma _{mn}}^0\left( {{\theta _i}} \right) + \sigma _{mn}^1\left( {{\theta _i}} \right) $ | (1) |
式中,
几何光学散射模型[4]后向散射系数表示如下:
| $ {\sigma ^0}_{mn}\left( {{\theta _i}} \right) = \frac{{\rm{ \mathsf{ π} }}}{{{{\cos }^4}({\theta _i})}} \times {\left| {{R_{mn}}} \right|^2}W({\zeta _x}, {\zeta _y}) $ | (2) |
其中,
| ${R_{vv}}(\theta ) = \frac{{ - {\varepsilon _2}\cos \theta + \sqrt {{\varepsilon _2} - {{\sin }^2}\theta } }}{{{\varepsilon _2}{\rm{cos}}\theta + \sqrt {{\varepsilon _2} - {{\sin }^2}\theta } }}$ | (3) |
| ${R_{hh}}(\theta ) = \frac{{\cos \theta - \sqrt {{\varepsilon _2} - {{\sin }^2}\theta } }}{{{\rm{cos}}\theta + \sqrt {{\varepsilon _2} - {{\sin }^2}\theta } }}$ | (4) |
| $\begin{gathered} W({\zeta _x}, {\zeta _y}) = \frac{1}{{2{\pi}{S_x}{S_y}}} \times F\left( {{\zeta _x}, {\zeta _y}} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{}& \times \end{array}\exp \left[{-\frac{1}{2}\left( {\frac{{{\zeta _x}^2}}{{{S_x}^2}} + \frac{{{\zeta _y}^2}}{{{S_y}^2}}} \right)} \right] \hfill \\ \end{gathered} $ | (5) |
其中,
| ${S_x}^2 = 0.005 + 0.78 \times {10^{ - 3}}U{}_{10}$ | (6) |
| ${S_y}^2 = 0.003 + 0.84 \times {10^{ - 3}}U{}_{10}$ | (7) |
其中,
| $\begin{gathered} F({\zeta _x}, {\zeta _y}) = 1 - \frac{1}{2}{D_{21}}\left( {\frac{{{\zeta _y}^2}}{{{S_y}^2}} - 1} \right)\frac{{{\zeta _x}}}{{{S_x}}} \hfill \\ \begin{array}{*{20}{c}} {}{}{} \end{array} + \frac{1}{{24}}{D_{40}}\left( {\frac{{{\zeta _x}^4}}{{{S_x}^4}} - 6\frac{{{\zeta _y}^2}}{{{S_y}^2}} + 3} \right) \hfill \\ \begin{array}{*{20}{c}} {}{}{} \end{array} + \frac{1}{4}{D_{22}}\left( {\frac{{{\zeta _y}^2}}{{{S_y}^2}} - 1} \right)\left( {\frac{{{\zeta _x}^2}}{{{S_x}^2}} - 1} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} + \frac{1}{{24}}{D_{04}}\left( {\frac{{{\zeta _x}^4}}{{{S_x}^4}} - 6\frac{{{\zeta _x}^2}}{{{S_x}^2}} + 3} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} - \frac{1}{6}{D_{03}}\left( {\frac{{{\zeta _x}^3}}{{{S_x}^3}} - 3\frac{{{\zeta _x}}}{{{S_x}}}} \right) \hfill \\ \end{gathered} $ | (8) |
其中, 参数,
| $\begin{gathered} {D_{03}} = (0.04 - 0.034{U_{10}}) \pm 0.12 \hfill \\ {D_{21}} = (0.01 - 0.0088{U_{10}}) \pm 0.03 \hfill \\ {D_{04}} = 0.23 \pm 0.41 \hfill \\ {D_{22}} = 0.23 \pm 0.41 \hfill \\ {D_{40}} = 0.40 \pm 0.23 \hfill \\ \end{gathered} $ | (9) |
小尺度波浪的微波散射系数是利用一阶小扰动近似方法来求的, 后向散射系数如公式(10)和公式(11)所示:
| $\begin{gathered} {\sigma _{mn}}^1\left( {{\theta _i}} \right) = 8{\left| {{k^2}{\sigma _1}\cos \theta \cos {\theta _s}{\alpha _{mn}}} \right|^2}W\left( {{k_x}, {k_y}} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{}&{}&{} \end{array} + 4{\pi}{\left| {{R_{vv}}} \right|^2}\delta \left( {{\theta _s} - {\theta _i}} \right)\delta \left( {{\phi _s} - {\phi _i}} \right) \hfill \\ \end{gathered} $ | (10) |
| $\begin{gathered} W\left( {{k_x}, {k_y}} \right) = \frac{1}{{2\pi }}\int {\int\limits_{ - \infty }^\infty {\rho \left( {u, v} \right)} } \hfill \\ \begin{array}{*{20}{c}} {}&{}&{}& \times \end{array}\exp \left( { - j{k_x}u - j{k_y}v} \right)dudv \hfill \\ \end{gathered} $ | (11) |
其中,
| $\begin{gathered} {\sigma _{mn}}^1\left( {{\theta _i}} \right) = 8{k^4}{\sigma _1}^2{\cos ^4}\theta {\left| {{\alpha _{mn}}} \right|^2}W\left( {2k\sin \theta, 0} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} + 4{\pi}{\left| {{R_{mn}}} \right|^2}\delta \left( {2k\sin \theta } \right) \hfill \\ \end{gathered} $ | (12) |
| ${\alpha _{hh}} = \frac{{\varepsilon - 1}}{{{{\left( {\cos {\theta _i} + \sqrt {\varepsilon - {{\sin }^2}{\theta _i}} } \right)}^2}}}$ | (13) |
| ${\alpha _{vv}} = \frac{{\left( {\varepsilon - 1} \right)\left[{\varepsilon \left( {1 + {{\sin }^2}{\theta _i}} \right)-{{\sin }^2}{\theta _i}} \right]}}{{{{\left( {\varepsilon \cos {\theta _i} + \sqrt {\varepsilon - {{\sin }^2}{\theta _i}} } \right)}^2}}}$ | (14) |
其中,
为解决大尺度波浪对小尺度波的影响, 小扰动的解要对大尺度做平均处理, 求平均后向散射系数如公式(15)所示:
| $\begin{gathered} {\sigma _{mn}}^1\left( {{\theta _i}} \right) = \frac{1}{{2{\pi}}}\int_{{{ - {\pi}} \mathord{\left/ {\vphantom {{ - {\pi}} 2}} \right. } 2}}^{{{\pi} \mathord{\left/ {\vphantom {{\pi} 2}} \right. } 2}} {\left\{ {{\sigma _{mn}}^0\left( {{{\theta '}_i}} \right)\left| {_{{\theta _n} = {{\tan }^{ - 1}}\left( l \right)}} \right.} \right.} \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\left. { + {\sigma _{mn}}^0\left( {{{\theta '}_i}} \right)\left| {_{{\theta _n} = - {{\tan }^{ - 1}}\left( l \right)}} \right.} \right\}d{\phi _n} \hfill \\ \end{gathered} $ | (15) |
其中, m, n代表雷达的垂直或者水平极化形式,
PM谱是由Pierson和Moskowitz在分析了北大西洋充分成长性海浪的一系列资料后, 通过估计、拟合, 获取的一种半经验理论模型, 适用于充分成长型海浪, 如公式(16)所示:
| $S(k) = \frac{\alpha }{{4{{\left| k \right|}^3}}}\exp \left( { - \frac{{\beta {g^2}}}{{{k^2}U_{19.5}^4}}} \right)$ | (16) |
其中,
图 1为PM谱仿真图, 当风速较小时, PM谱的能量比较分散, 此时海浪主要成分是小尺度张力波。当风速逐渐增大, 波谱的峰值向低频移动谱且能量更加集中, 此时海浪主要是以大尺度重力波为主, 也进一步说明PM谱能更好地描述大尺度波浪。
 |
| 图 1 PM海浪谱 Fig. 1 PM wave spectrum |
1997年, Elfouhaily等[6]在PM谱和JW谱的基础上结合实验数据提出了一种新的海浪谱, 称之为Elfouhaily海浪谱, 它适用长波和短波海况, 能更好地描述真实的海浪, 其表达式如公式(17)所示:
| $S(k) = {k^{ - 3}}\left[{{B_l} + {B_h}} \right]$ | (17) |
式中,
长波浪海浪谱
| ${B_l} = \frac{1}{2}{\alpha _p}\frac{{{c_p}}}{c}{F_p}$ | (18) |
| $c = \sqrt {\frac{g}{k}\left( {1 + \frac{{{k^2}}}{{k_m^2}}} \right)} $ | (19) |
| ${F_p} = {L_{PM}}{J_p}\exp \left\{ { - \frac{\Omega }{{\sqrt {10} }}\left[{\sqrt {\frac{k}{{{k_p}}}}-1} \right]} \right\}$ | (20) |
| ${J_p} = {\gamma ^\Gamma }$ | (21) |
| $\Gamma = \exp \left( {\tfrac{{{{\left( {\sqrt {\frac{k}{{{k_p}}}} - 1} \right)}^2}}}{{2{\sigma ^2}}}} \right)$ | (22) |
| $\sigma = 0.08[1 + 4{\Omega ^{-3}}]$ | (23) |
| ${k_p} = {k_0}{\Omega ^2}, {k_0} = g/U_{10}^2$ | (24) |
短波浪海浪谱
| ${B_h} = \frac{1}{2}{\alpha _m}\frac{{{c_m}}}{c}{F_m}$ | (25) |
式中,
| ${F_m} = \exp \left\{ { - \frac{1}{4}{{\left[{\frac{k}{{{k_m}}}-1} \right]}^2}} \right\}$ | (26) |
| ${\alpha _m} = 0.01\left\{ {\begin{array}{*{20}{c}} {1 + \ln ({u^*}/{c_m})} \\ {1 + 3\ln ({u^*}/{c_m})} \end{array}} \right.\begin{array}{*{20}{c}} {{u^*} < {c_m}} \\ {{u^*} > {c_m}} \end{array}$ | (27) |
仿真中, 认为海面是完全发展的, 波龄
图 2为不同风速下的Elfouhaily海浪谱。可以看出, 风速增大时, 谱能量的峰值增大且峰值向低频区移动, 对应着海浪的波长变大, 重力波的作用越来越大。无论风速怎样变化, 谱能量的分布都比较均匀, 说明Elfouhaily谱既能够准确描述大尺度波浪, 也能够准确描述对海面微波散射其主要作用的小尺度的毛细张力波。
 |
| 图 2 Elfouhaily海浪谱 Fig. 2 Elfouhaily wave spectrum |
真实海面的变化情况具有很多的不确定性, 海表面是不规则的, 这种不规则的随机粗糙海面可看作是由相互独立的谐波叠加起来的结果, 由随机函数来表示, 其中蒙特卡罗(Monte Carlo, MC)粗糙海面模拟的方法应用最为广泛。
用蒙特卡罗方法[7]来模拟粗糙海面的主要思想就是采用相互独立、具有高斯分布、零均值等条件的复随机数来对随机粗糙海面进行模拟。先进行频域内的功率谱滤波, 然后再用逆傅里叶变换生成粗糙面的。
长度为L的一维随机粗糙海面:
| $f({x_n}) = \frac{1}{L}\sum\limits_{j = - {\raise0.5ex\hbox{$\scriptstyle N$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}^{{\raise0.5ex\hbox{$\scriptstyle N$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}} - 1} {F({k_j})} {{\rm{e}}^{i{k_j}{x_n}}}$ | (28) |
式中,
| $\begin{gathered} F({k_j}) = {\left[{2{\pi}LS({k_j})} \right]^{\frac{1}{2}}} \hfill \\ \begin{array}{*{20}{c}} {}& \times \end{array}\left\{ {\begin{array}{*{20}{c}} {{\raise0.7ex\hbox{${\left[{N(0, 1) + iN(0, 1)} \right]}$} \!\mathord{\left/ {\vphantom {{\left[{N(0, 1) + iN(0, 1)} \right]} {\sqrt 2 }}}\right.} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} \\ {N(0, 1)} \end{array}} \right.\begin{array}{*{20}{c}} {, j \ne 0, {\raise0.5ex\hbox{$\scriptstyle N$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} \\ {j = 0, {\raise0.5ex\hbox{$\scriptstyle N$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} \end{array} \hfill \\ \end{gathered} $ | (29) |
式中,
图 3利用蒙特卡洛统计模型模拟的清洁粗糙海面, 图中对比分析了PM谱下不同风速的海面粗糙度, 当风速越大时由蒙特卡洛方法模拟的粗糙海面起伏波动越大, 相对于风速较低时变得剧烈, 这与实际情况是相符合的, 风速越大海面越粗糙。
 |
| 图 3 不同风速下清洁海面的粗糙度 Fig. 3 Roughness of clean sea surface at different wind speeds a.风速为15m/s时海面粗糙度; b.风速为8m/s时海面粗糙度 a. Sea surface roughness at wind speed of 15 m/s; b. sea surface roughness at wind speed of 8 m/s |
前面分析了粗糙海面海浪谱的的特征和海面的微波散射模型, 并对清洁海面的粗糙度做了仿真研究。本节将引入溢油衰减模型对清洁海浪谱进行修正得到溢油海浪谱, 用复合微波散射模型和蒙特卡洛统计模型对溢油海面建模, 对比分析溢油对海浪谱和海面后向散射系数值的影响。
3.1 溢油海浪谱研究溢油海浪谱需要引入Lombardini溢油衰减系数[8]。Lombardini建立了海面中带有油膜的海浪谱模型, 实现了从清洁海面到溢油海面的转化, 其表达式为:
| $y(k;{E_0}, {\omega _D}) = \frac{{1 \pm 2\tau + 2{\tau ^2} - X + Y(X + \tau )}}{{1 \pm 2\tau + 2{\tau ^2} - 2X + 2{X^2}}}$ | (30) |
| $\begin{gathered} \tau = {\left( {\frac{{{\omega _D}}}{{2\omega }}} \right)^{\frac{1}{2}}} \hfill \\ X = \frac{{{E_0}{k^2}}}{{\rho {{(2\nu {\omega ^3})}^{\frac{1}{2}}}}} \hfill \\ Y = \frac{{{E_0}k}}{{4\nu \rho \omega }} \hfill \\ f = \frac{\omega }{{2{\pi}}} = \frac{{{{(\varsigma {k^3}/\rho + gk)}^{\frac{1}{2}}}}}{{2{\pi}}} \hfill \\ \end{gathered} $ | (31) |
式中,
溢油海浪谱和清洁海浪谱之间的关系可以用下面的关系式表示:
| ${S_{{\rm{cont}}}}(k;{u_{10}}, {E_0}, {\omega _D}) = \frac{{{S_{clean}}(k;{u_{10}}, \phi )}}{{y(k;{E_0}, {\omega _D})}}$ | (32) |
由公式(32)可看出溢油海浪谱取决于波数、风速、电磁波入射角、油膜的物理参数。
图 4给出了Elfouhaily海浪谱下清洁和溢油海面的海浪谱对比结果。具体参数为:风速为5 m/s、波龄为0.84、溢油特征角频率11 rad/s、表面张力74×10–3 N/m、油膜密度为103 kg/m3、弹性模量为25 N/m、运动黏度系数10–6 m2/s2。横坐标为波数, 纵坐标为海浪谱的幅值。溢油下的海浪谱的幅度有明显的减小, 这个效果跟仿真时所设置的参数有关, 但是总体来说溢油下的海浪谱的幅值是减小的, 溢油下的海浪谱被抑制。
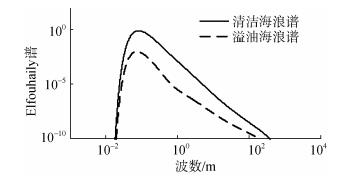 |
| 图 4 清洁和溢油Elfouhaily海浪谱 Fig. 4 Clean and spilled Elfouhaily wave spectrum |
图 5利用蒙特卡洛统计模型分别对清洁和溢油海面做了粗糙度对比分析, 更直观地对比了清洁和溢油海面的粗糙度之间的差别。横坐标为海面各个点距离原点的距离, 纵坐标表示为对应距离的海面高度。通过对比分析图 5a、5b发现溢油海面下的海浪的波峰有明显的下降, 原因是溢油的发生抑制了海面的毛细重力波使海面粗糙度降低。
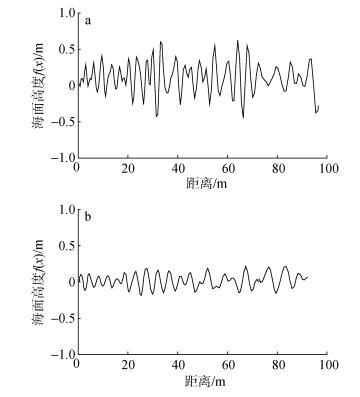 |
| 图 5 清洁和溢油海面粗糙度对比 Fig. 5 Comparison of surface roughness between oil-free and oil–spilled sea surface a.清洁海面的粗糙度; b.溢油海面的粗糙度 a. Roughness of clean sea surface; b. Roughness of oil spill surface |
图 6为清洁海面下几何光学散射模型和复合散射模型下后向散射系数仿真图。在入射角度较小时, 主要是几何光学模型在对后向散射系数做贡献, 系数衰减很快, 当电磁波入射角度接近20°的时候后向散射系数已经衰减到接近–30dB, 在20°之后随着小扰动模型对后向散射系数的贡献, 复合散射模型能更好的模拟海面散射特性。
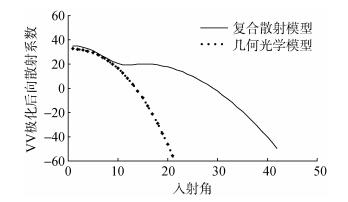 |
| 图 6 X波段VV极化下微波散射系数 Fig. 6 Microwave scattering coefficient under X-band VV polarization |
图 7利用复合散射模型对溢油海面和清洁海面的后向散射系数做对比分析。可以看出, 溢油海面的后向散射系数被明显地抑制, 油膜对海面起到了平滑的作用, 使海面的粗糙度降低, 导致溢油海面所对应的微波散射系数的值降低, X波段雷达在成像时图像上就会就会出现一片暗区域。
 |
| 图 7 无油和溢油海面微波散射系数对比 Fig. 7 Comparison of microwave scattering coefficient between oil-free and oil-spilled sea surface |
基于X波段雷达的溢油的检测时, 只凭借暗区域来检测溢油会造成虚警率高的问题, 也就是有疑似溢油, 这时可以再结合油膜的极化特性, 或者其环境特征结合溢油检测算法来准确的检测溢油。
4 总结海面溢油微波散射模型的研究是掌握溢油微波散射特性的理论基础, 对基于极化X波段雷达溢油信息的提取和识别具有重要的作用和意义。作者通过引入单分子油膜的黏性阻尼系数对经典的海浪谱进行修正, 获得溢油海浪谱。通过运用海面的复合散射模型和蒙特卡洛统计模型理论, 模拟了溢油海面的后向散射系数和海面粗糙度, 定量地分析了油膜对海浪谱和后向散射系数值的影响, 为基于X波段雷达溢油检测提供理论数值资料。在今后的研究中需加强溢油微波散射模型的理论性探索, 同时利用室内陆基等微波散射测量装置在多种海况下用实测数据完善和修正散射模型, 进而提高模型的精确度和适用性。
| [1] |
胡雪春. 海上船舶溢油风险综合评价指标体系研究[D]. 武汉: 武汉理工大学, 2013. Hu Xuechun. Comprehensive evaluation index system for oil spill risk at sea[D]. Wuhan: Wuhan University of Technology, 2013. |
| [2] |
张永宁, 丁倩, 李栖筠. 海上溢油污染遥感监测的研究[J]. 大连海事大学学报, 1993, 25(3): 1-5. Zhang Yongning, Ding Qian, Li Qiyun. Remote sensing monitoring of oil spill pollution at sea[J]. Journal of Dalian Maritime University, 1993, 25(3): 1-5. |
| [3] |
张灯洲, 陈志莉, 胡潭窝, 等. 遥感技术监测海上溢油现状及趋势[J]. 杭州师范大学学报(自然科学版), 2013, 1: 81-88. Zhang Dengzhou, Chen Zhili, Hu Tanwo, et al. Monitoring the present situation and trend of oil spill at sea by remote sensing technology[J]. Journal of Hangzhou Normal University (Natural Science Edition), 2013, 1: 81-88. DOI:10.3969/j.issn.1674-232X.2013.01.016 |
| [4] |
Ghanmi H, Khenchaf A, Comblet F. Numerical mode lingof electromagnetic scattering from sea surface coveredby oil[J]. Journal of Electromant Romagnetic Analysis and Applications, 2014, 6(1): 15-24. DOI:10.4236/jemaa.2014.61003 |
| [5] |
Ulaby F T, Moore R K, Fung A K. Microwave remote sensing: active and passive[M]. USA, Dedham: Artech House Inc, 1986: 1223-1227.
|
| [6] |
Elfouhaily T, Chapron B. A unified directional spectrum for long and short wind-driven wave waves[J]. Journal of Geophysical Research, 1997, 102(C7): 15781-15796. DOI:10.1029/97JC00467 |
| [7] |
梁玉. 粗糙面及其与目标复合电磁散射建模及快速计算研究[D]. 西安: 西安电子科技大学, 2011. Liang Yu. Modeling and fast calculation of rough surface and its composite electromagnetic scattering with target[D]. Xian: Xian University, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1958726 |
| [8] |
Baba-Aissa F, Raeymaekers L. Modulation of the spectra of short gravity waves by sea surface films: Slick detection and characterization with a microwave probe[J]. Journal of Atmospheric & Oceanic Technology, 1989, 6(6): 882-890. |
 2018, Vol. 42
2018, Vol. 42

