
文章信息
- 王瑞英, 肖天贵. 2018.
- WANG Rui-ying, XIAO Tian-gui. 2018.
- 三种基于均生函数的统计模型在厄尔尼诺预测中的应用
- The application of three statistical models based on MGF to El Niño prediction
- 海洋科学, 42(12): 83-93
- Marine Sciences, 42(12): 83-93.
- http://dx.doi.org/10.11759/hykx20180608001
-
文章历史
- 收稿日期:2018-06-08
- 修回日期:2018-08-12
厄尔尼诺是发生在热带太平洋的一种年际异常强信号, 它是大尺度海-气相互作用的产物[1~3]; 而赤道东太平洋海表温度的异常发展, 也会对大气环流产生影响, 进而牵制包括中国在内的全球许多国家和地区的气候变化, 造成旱涝异常和高低温灾害[4]; 因此, 提前预知厄尔尼诺的发生发展对于区域气候预测、防灾减灾都具有重要意义。然而当前由于对厄尔尼诺物理机制认知的局限以及观测资料的不足, 厄尔尼诺的预测仍处于试验阶段[5]: 20世纪80年代以来, 世界各国陆续开展了厄尔尼诺的预报研究, 并在过去的几十年发展出近20种相应的预报模式; 我国于20世纪80年代中期建立了厄尔尼诺监测小组, 20世纪90年代建立了厄尔尼诺监测和预测业务系统, 到今天已发展出了两个厄尔尼诺预报系统:中国科学院大气物理研究所的集合预报版本(IAP Leefs_CDA)和中国科学院海洋研究所的确定性预报版本(IOCAS ICM), 均提供实时的预报结果。目前国际上的近20种厄尔尼诺预报模式, 大部分可以提前6个月给出较为可信的预报, 但由于模式的系统误差, 使得各模式的预报结果间存在较大差距, 同时数值模式对于极端事件的预报效果较差, 难以满足预报需求[6~8]。近年来, 一些学者开始尝试使用统计方法开展厄尔尼诺预报试验, 并取得了一定成果。韦成宁[9]通过对历年厄尔尼诺与与太阳黑子、大气环流的关系分析, 提出了厄尔尼诺的概率统计预报方法; 魏松林[10]提出了一个表征厄尔尼诺/拉尼娜事件的指数——ENI指数, 并在逐月ENI指数谱分析及主周期外推预报的基础上提出了三周期叠加预报方法, 提前6个月成功预报出了1997年的超强厄尔尼诺事件; 冯利华等[11]将最早在天文学领域提出的“可公度性”概念应用于厄尔尼诺的预报研究中, 成功地预测了1997年及2001年的厄尔尼诺事件。尽管学者们在厄尔尼诺预测方面做了一些尝试, 但这还远远不够, 受预报时效、预报准确度的影响, 厄尔尼诺的预测仍然是气候预报中的一个薄弱环节。因此, 本文尝试利用在极值预测方面有较好表现并能进行多步预测的均生函数模型对厄尔尼诺进行预测试验, 并提出了两种改进方案, 以期为厄尔尼诺的预报提供新的思路与方法。
1 资料与方法 1.1 资料本文所用的NINO3指数来源于美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA)气候预测中心, 时间长度为1970年1月~2017年12月; 同时段月平均海温来源于COBE-SST全球海温数据集, 分辨率1°×1°; 月平均高度场、风场来源于NCEP/NCAR再分析资料, 水平分辨率2.5°×2.5°; 向下太阳辐射通量同样为再分析资料, 由逐日数据计算为月平均值, 资料采用高斯格点分布。在应用过程中, 各类数据都进行了距平或标准化处理, 以滤除季节波动。
1.2 方法均生函数[12~14]是本文三种统计预测方法的理论基础, 它是由气候序列按一定时间间隔计算均值而派生出来的。对于长度为n的时间序列:
| $x(t) = \{ x(1), x(2)x(1), \cdots , x(n)\} .$ | (1) |
定义其均值生成函数:
| ${\bar x_l}(i) = \frac{1}{{{n_l}}}\sum\nolimits_{j = 0}^{{n_l} - 1} {x(i + jl)\;\;\;(i = 1, \cdots , l;1 \le l \le m)} , $ | (2) |
其中,
将均生函数定义域延拓到整个数轴上, 即按照公式(3)作周期性延拓:
| ${f_l}(t) = {\bar x_l}\left[ {t - l \times {\rm{INT}}\left( {\frac{{t - 1}}{l}} \right)} \right](t = 1, 2, \cdots , n;l = 1, \cdots , m).$ | (3) |
由此构造均生函数周期延拓序列。简单的均生函数模型就是在这组延拓序列的基础上, 建立与原序列之间的回归, 构建预报方程。
本文在改进均生函数预报模型的过程中, 还用到了小波分析、集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)以及奇异值分解(Singular Value Decomposition, SVD)等方法, 详细介绍可参考文献[15]~文献[19], 这里不再赘述。
1.3 建模步骤 1.3.1 方案1——普通均生函数模型设有长度为n的气候序列, 如公式(1)所示。
(a) 对原序列进行差分计算, 以便拟合序列中的高频部分:
| $ \Delta x\left( t \right) = x\left( {t + 1} \right)-x\left( t \right)(t = 1, 2, \ldots , n-1), $ | (4) |
| $ {\Delta ^2}x\left( t \right) = {\rm{ }}\Delta x\left( {t + 1} \right)-\Delta x\left( t \right)(t = 1, 2, \ldots , n-1). $ | (5) |
得一阶差分序列x(1)(t)和二阶差分序列x(2)(t)。
(b) 对气候序列及其差分序列按照公式(2)分别构造均生函数
(c) 为了拟合时间序列中的增减趋势, 进一步建立累加延拓序列:
| $ f_l^{(3)}(t) = x(1) + \sum\nolimits_{i = 1}^{t - 1} {f_l^{(1)}(i + 1)\;\;\;(t = 2, \cdots , n;l = 1, 2, \cdots , m)} . $ | (6) |
这样共获得4m个均生函数延拓序列:
(d) 建立每一个均生函数延拓序列与预报量的一元回归, 计算双评分准则SCS(couple score criterion)值, 将满足SCS>
(e) 对所有粗选出的预报因子, 计算2p个回归子集, 并依据SCS准则选出其中最优的预报方程。若做q步预报, 则对因子序列做q步外延即可。
均生函数模型自20世纪90年代提出以来, 就在气象、水文、航天等领域得到了广泛应用; 但模型中所用的因变量都是由其自身派生构造出来的, 具有一定的局限性。因此, 本文在均生函数模型的基础上, 还应用了两类改进模型, 尝试提高厄尔尼诺的预报技巧。
1.3.2 方案2——基于EEMD的均生函数模型均生函数模型通过时间序列中隐藏的各种周期和演变趋势进行构造[20]; 因而本文在提取气候变量周期的基础上, 进一步提出了基于EEMD的均生函数模型。EEMD是分析非线性、非平稳信号序列的新方法, 可以将复杂的信号分解为有限个本征模函数IMF和一个趋势项RES, 所分解出的各个IMF分量均包含了原信号不同时间尺度的局部特征。基于EEMD的预报模型相当于普通模型的备选预报因子中, 加入了预报量EEMD分解结果的均生函数序列; EEMD可以将气候序列平稳化处理, 各IMF周期单一且显著, 具有更好的可预报性。具体建模步骤如下:
(a) 对气候序列两端进行延拓, 这是针对端点效应的处理。EEMD的分解过程中信号两端会出现逐渐向内部扩散的失真现象。通常的处理方法是分解后删去部分端点处序列, 但为了不失去预报信息, 本文首先利用镜像延拓方法扩展序列, 实践表明, 镜像延拓能大幅削减端点失真所造成的影响[20]。
(b) 对延拓后的序列进行EEMD分解, 得k个IMF; 分解后删去延拓部分。
(c) 取原序列及k个IMF, 按照公式(4)、公式(5)分别计算它们的一、二阶差分序列, 再根据公式(2)、公式(3)求所有均生函数周期性延拓序列, 最后根据公式(6)建立k+1个累加延拓序列; 最终得4m×(k+1)个均生函数周期性延拓序列作为预报方程的备选因子。
(d) 由于预报因子过多, 采用最优子集回归建立预报方程的计算量过大, 因而采用逐步回归的方法筛选预报因子、建立预报模型。对入选方程的因子做q步外延即可得到q步预报值。
1.3.3 方案3——多变量均生函数模型受普通均生函数模型变量单一的局限, 本文在其基础上, 综合预报量及其影响因子序列, 构建多变量均生函数模型。对模型加入因子变量有两方面的意义[21]:一方面作为备选的自变量数量增加, 可以通过筛选挑选出最佳因子进入预报方程; 另一方面, 气象要素的变化是多种因素共同作用的结果, 模型中加入多种相关的气象因子, 具有更好的物理基础。
设预报量为y(t), 并有k个因子序列: x1(t), x2(t), …, xk(t), t=1, 2, …, n。n为样本长度。
(a) 为消除变量间的差异, 对预报量和所有因子变量进行标准化处理:
其中,
(b) 对标准化后的k+1个变量序列
(c) 通过逐步回归筛选预报因子并建立预报方程, 对入选方程的因子做q步外延即可得到q步预报值。
2 结果与分析2014年底, 海表温度异常增暖率先出现于赤道中太平洋, 伴随赤道西风的增强和暖水东传, 2015年初, NINO3区海温达到厄尔尼诺标准, 同年冬季增温2~3℃以上, 为本世纪以来最强的一次厄尔尼诺。对于此次事件, 国际上近20种厄尔尼诺模式提前6个月, 只有一个成功预测出本次事件强度将超过2℃; 直到2015年6月, 大部分模式才预报出年底可能出现厄尔尼诺[7]。因此本文首先利用三种模型对2015年的超强厄尔尼诺进行预报, 1980~2014年为建模时段, 逐年外推三步, 2015~2017年用于预报检验。在此基础上, 建立滑动的预报模型, 对2001~2017年的NINO3指数进行预测, 并给出整体预报评价; 滑动的样本同样取预报年份之前的35 a, 这是因为:数理统计中通常要求样本序列n不小于30, 但均生函数模型并不作严格限制, 理论上有2个以上数据求平均即可, 但时间序列所能构造生成的均生函数个数与样本量n相关。n越大, 不仅可以为模型提供更多备选因子, 而且可以降低均值序列的随机性; 但n增加到一定程度, 预报技巧的提高将变得缓慢, 还会导致计算量增大。因此, 通过反复试验, 本文将样本量n确定为35 a。
2.1 2015年超强厄尔尼诺的个例预报试验 2.1.1 普通均生函数模型在2015年强厄尔尼诺预报中的应用表 1为普通均生函数模型的预报结果与实测值, 可以看出, 预报效果整体表现一般。外推一步, 前三个月预报与实测值都处在正常值范围内, 4月NINO3指数开始达到0.5℃以上, 而预报值直到8月才达到厄尔尼诺水平; 此外, 二者在数值上也有较大差距, 预报的厄尔尼诺强度偏弱。外推两步, 距平符号与实况基本一致, 但预报的厄尔尼诺结束时间偏早, 仅在8~11月有较好的预报效果。外推三步, 各月距平符号几乎都不一致, 已经失去了预报意义。
| 月份 | 实测值/℃ | 预报值/℃ | |||||
| 2015年 | 2016年 | 2017年 | 2015年 | 2016年 | 2017年 | ||
| 1月 | 0.34 | 2.58 | –0.09 | 0.07 | 0.22 | –1.42 | |
| 2月 | 0.05 | 1.97 | 0.42 | –0.42 | 0.47 | –0.62 | |
| 3月 | 0.14 | 1.58 | 0.39 | –0.35 | 0.05 | –0.56 | |
| 4月 | 0.73 | 0.72 | 0.55 | –0.26 | 0.09 | –0.55 | |
| 5月 | 1.04 | 0.07 | 0.39 | 0.2 | 0.62 | –0.66 | |
| 6月 | 1.57 | –0.02 | 0.18 | 0.24 | 0.56 | –0.67 | |
| 7月 | 1.97 | –0.5 | 0.15 | 0.28 | 0.3 | 0.67 | |
| 8月 | 2.11 | –0.51 | –0.23 | 0.56 | –0.28 | 0.18 | |
| 9月 | 2.47 | –0.29 | –0.75 | 0.72 | –0.63 | 0.13 | |
| 10月 | 2.65 | –0.53 | –0.69 | 1.05 | –0.47 | 0.13 | |
| 11月 | 2.91 | –0.56 | –1.02 | 1.12 | –0.13 | 0.04 | |
| 12月 | 2.87 | –0.44 | –1.2 | 0.03 | –1.44 | –0.39 | |
厄尔尼诺作为强气候信号, 每隔2~7 a出现一次, 但并不遵循严格的周期[22]。近年来厄尔尼诺的发生似乎有愈加频繁的趋势, 其中2002~2010年接连发生四次厄尔尼诺。图 1给出了近38 a年均NINO3指数的小波分析, 可以看出:厄尔尼诺主要表现出两个变化周期:一是2~7 a的年际振荡, 二是9~14 a的年代际振荡; 其中年际振荡更为明显, 为其第一主周期; 值得注意的是, 20世纪90年代后, 年际振荡随时间减弱, 且中心逐渐上移, 但在2~3 a尺度上, 有新的闭合中心发展; 另外, 1982、1998和2015年的强厄尔尼诺事件, 在年际和年代际振荡上表现为一致的正位相(1998年处在更长的年代际振荡正位相上); 不同周期的振荡同位相叠加, 形成强劲的厄尔尼诺, 这可能在某种程度上反映了强厄尔尼诺的特点。
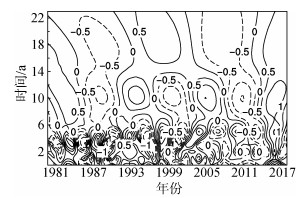 |
| 图 1 NINO3指数的小波变换图 Fig. 1 Wavelet transform of NINO3 index |
进一步对NINO3指数进行EEMD分解, 得到的四个IMF对应的周期依次为: 3~6 a、6~14 a、15~26 a及30 a以上的振荡, 而趋势项表明NINO3区海温经历了先降后增的变化, 近年来海温正处于持续上升阶段, 转折点在20世纪90年代中期。由于前两模态与原序列的相关性较好, 且方差贡献占比较大, 是NINO3指数变化的主要贡献者, 因而图 2主要给出了EEMD分解的前两个模态: IMF1跟原海温序列变化趋势极其接近, 2000年以后, IMF1振幅减小, 振荡周期缩短, 这正体现了21世纪前十年频繁出现的厄尔尼诺。IMF2反映了更长周期的演变特征, 同样在2000年以后振荡频率加快。此外, 两个不同尺度振荡同正位相叠加, 是出现强厄尔尼诺的主要特征。
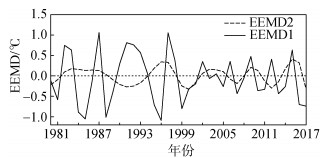 |
| 图 2 NINO3指数EEMD分解的前两模态 Fig. 2 First two modes of EEMD decomposition of NINO3 index |
上述分析表明, 厄尔尼诺具有显著的多时间尺度特征。为建立预报模型, 对建模时段各月NINO3指数同样进行EEMD分解, 各月均得四个IMF和一个RES, 其与年均值分解结果相似, 仅前两模态的相关系数较高; 不同的是分月的IMF1主要表现2~5 a振荡, IMF2反映5~8 a振荡, IMF3体现10~22 a年代际振荡; 各月模态周期基本一致, 少数月份存在一定差异。
在EEMD分解基础上, 通过逐步回归建立分月预报模型; 从各月回归方程入选的预报因子可以看出, 预报量及其EEMD分解前两模态的均生函数延拓序列所占的比例较高, 这也例证了反映预报量“优势周期”的因子序列更容易入选进方程。
表 2给出了基于EEMD的均生函数模型对2015~ 2017年NINO3指数的预报值及实测值, 预报效果较普通均生函数模型有了明显改进。外推一步, 仅4~6月预报效果相对较差; 7月, 模型预报出NINO3指数开始达到厄尔尼诺水平, 期间预报值与实况值较为接近。外推两步, 模型预报出的厄尔尼诺结束时间与实况仅差两个月; 厄尔尼诺结束后紧随而来的海温负距平, 在预测值上也有很好的体现。外推三步, 预报同样失去意义。
| 月份 | 实测值/℃ | 预报值/℃ | |||||
| 2015年 | 2016年 | 2017年 | 2015年 | 2016年 | 2017年 | ||
| 1月 | 0.34 | 2.58 | –0.09 | 1.14 | 2.16 | –1.67 | |
| 2月 | 0.05 | 1.97 | 0.42 | –0.26 | 1.3 | 0.03 | |
| 3月 | 0.14 | 1.58 | 0.39 | –0.08 | 0.32 | –0.39 | |
| 4月 | 0.73 | 0.72 | 0.55 | –0.19 | 0.38 | –0.46 | |
| 5月 | 1.04 | 0.07 | 0.39 | 0.38 | 0.46 | –0.36 | |
| 6月 | 1.57 | –0.02 | 0.18 | 0.33 | 0.04 | –0.25 | |
| 7月 | 1.97 | –0.5 | 0.15 | 1.06 | –0.34 | 0.11 | |
| 8月 | 2.11 | –0.51 | –0.23 | 1.19 | –0.16 | 0.76 | |
| 9月 | 2.47 | –0.29 | –0.75 | 2.63 | –0.16 | 0.05 | |
| 10月 | 2.65 | –0.53 | –0.69 | 2.22 | –0.83 | 0.55 | |
| 11月 | 2.91 | –0.56 | –1.02 | 3.32 | –0.37 | 0.01 | |
| 12月 | 2.87 | –0.44 | –1.2 | 3.15 | –0.79 | –1.28 | |
厄尔尼诺是复杂的海-气相互作用的结果, 为了了解厄尔尼诺与其他因子的相关关系, 本文运用SVD分析技术, 主要从大气环流和太阳辐射的角度, 为厄尔尼诺的预测提供参考。将赤道太平洋海温设为左场, 而右场依次取1 000 hPa高度场、500 hPa高度场、850 hPa纬向风场、850 hPa经向风场、500 hPa垂直速度场以及到达地面的向下太阳辐射通量, 第一模态的方差贡献至少在70%以上(表 3), 远大于其他模态; 同时, 各因子第一模态的左异类相关图表示的海温分布形式相似, 大值中心均位于赤道中、东太平洋; 同时左场时间系数与NINO3指数的相关非常高, 至少在0.94以上, 并全部都通过了99%的显著性检验, 反映了厄尔尼诺的海温分布特征。因此, 在以下分析中仅讨论每种分解结果的第一特征向量。
| 1 000 hPa 高度场 |
500 hPa 高度场 |
850 hPa 纬向风场 |
850 hPa 经向风场 |
500 hPa 垂直速度场 |
向下太阳 辐射通量 |
|
| 第一模态/% | 82.4 | 73.6 | 83.5 | 70.3 | 76.8 | 74.3 |
| 第二模态/% | 6.9 | 13 | 7.5 | 10.3 | 8.5 | 13 |
第一模态的右异类相关图, 即1 000 hPa高度场(图 3a)上, 与厄尔尼诺相关的分布形式表现为明显的东西反相特征, 正负交界处大致在180°附近, 正值中心位于西太平洋的印尼、菲律宾等地, 负值中心位于赤道东太平洋; 这种以日界线为轴的东西高度场符号相反的特征与南方涛动类似。500 hPa高度场(图 3b), 赤道低纬度地区为正值带; 两侧的印度洋及亚洲大陆同为正值区; 但在太平洋上, 正值带两侧为沿纬线分布的负距平带, 这种从北到南的“–, +, –”高度场分布形式, 反映了赤道太平洋西风偏强的特征, 有利于厄尔尼诺的形成。850 hPa纬向风场(图 3c), 太平洋大部分地区盛行西风, 大值中心在赤道中太平洋附近, 有利于西太平洋的暖水向东积聚, 而赤道印度洋仍然为东风距平。850 hPa经向风场(图 3d), 太平洋上, 赤道北侧为负距平, 盛行北风, 而赤道南侧的太平洋中、西部为南风; 经向风应力距平是从两侧向赤道辐合的, 有利于表层暖水在赤道太平洋积聚, 并随西风移向东太平洋。500 hPa垂直速度场(图 3e), 伴随海表温度正值中心的东移, 上升区也移向赤道中、东太平洋, 与厄尔尼诺有很好的对应关系。最后来看到达地表的向下太阳辐射通量(图 3f), 太阳辐射是地气系统能量的总来源, 是气候形成的决定性因子; 众所周知, 由于地气系统吸收太阳辐射的区域不均性, 加之地球自转作用, 产生了三圈环流, 低纬度盛行偏东信风, 当赤道中、东太平洋入射的太阳辐射减弱, 将导致信风减弱, 甚至有可能出现风向翻转, 有利于厄尔尼诺的形成。
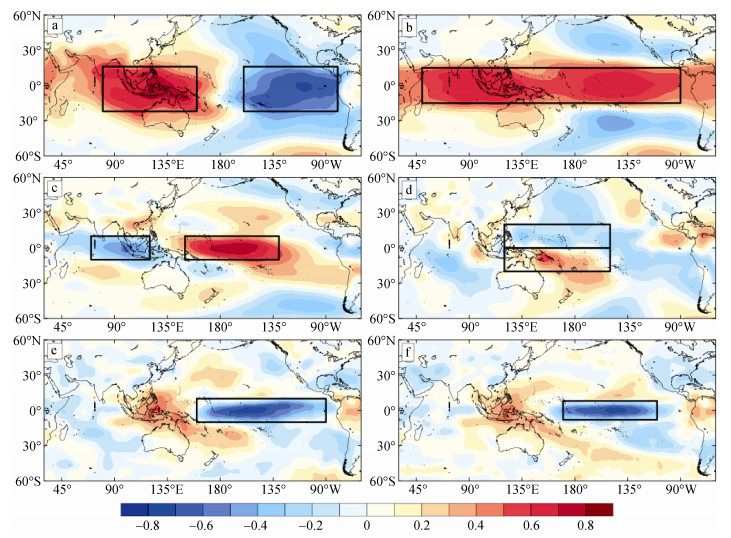 |
| 图 3 海温与气象要素场SVD分解第一右异类空间分布图 Fig. 3 First right heterogeneous correlation map between sea surface temperature and each meteorological field 注: a: 1 000 hPa高度场; b: 500 hPa高度场; c: 850 hPa纬向风; d: 850 hPa经向风; e: 500 hPa垂直速度; f:向下太阳辐射通量 Note: a: hgt-1 000 hPa; b: hgt-500 hPa; c: uwnd-850 hPa; d: vwnd-850 hPa; e: omega-500 hPa; f: Downward solar radiation flux |
再来分析SVD第一模态左、右场时间系数间的时滞相关, 除850 hPa纬向风场为超前海温一月相关系数最大外, 其余各物理因子与海温耦合的相关系数均为同时相关最强。因此, 结合SVD分解的空间型与时间系数, 取各月与厄尔尼诺相关的预报因子(表 4)。
| 序号 | 因子 |
| 1 | 同月80°~160°E, 22°S~16°N, 1000 hPa高度场 |
| 2 | 同月160°~80°W, 22°S~16°N, 1000 hPa高度场 |
| 3 | 同月50°E~90°W, 15°S~15°N, 500 hPa高度场 |
| 4 | 超前一月150°E~130°W, 10°S~10°N, 850 hPa纬向风场 |
| 5 | 超前一月70~120°E, 10°S~10°N, 850 hPa纬向风场 |
| 6 | 同月120°E~150°W, 20°S~0°, 850 hPa经向风场 |
| 7 | 同月120°E~150°W, 0°~20°N, 850 hPa经向风场 |
| 8 | 同月160°E~90°W, 10°S~10°N, 500 hPa垂直速度场 |
| 9 | 同月170°E~110°W, 8°S~8°N, 向下太阳辐射通量场 |
根据多变量均生函数的建模步骤, 建立了各月NINO3指数的预报模型, 并对2015~2017年进行了预报试验, 预报结果如下表:外推一步的预报, 与方案二预报结果类似, 预报与实测值非常接近, 但预报的厄尔尼诺开始时间较晚; 外推两步, 预报与实测值正负演变趋势基本一致, 对厄尔尼诺结束时间以及2016年下半年弱的拉尼娜都有较好的预报; 外推三步, 预报模型失去意义。
2.2 近17年厄尔尼诺的滑动预报试验为了进一步探究均生函数及其两种改进模型在厄尔尼诺预报中的适用性, 本文在2015年强厄尔尼诺个例预报的基础上, 滑动选取35 a预报样本(例如对2006年外推两步的预报, 1970~2004年为建模时段; 2010年外推一步的预报, 则1975~2009年取为样本), 对2001~2017年进行预测, 给出整体预报评价。
| 月份 | 实测值/℃ | 预报值/℃ | |||||
| 2015年 | 2016年 | 2017年 | 2015年 | 2016年 | 2017年 | ||
| 1月 | 0.34 | 2.58 | –0.09 | 0.34 | 1.53 | –0.99 | |
| 2月 | 0.05 | 1.97 | 0.42 | 0.35 | 1.31 | –0.5 | |
| 3月 | 0.14 | 1.58 | 0.39 | –0.3 | 0.5 | –0.72 | |
| 4月 | 0.73 | 0.72 | 0.55 | 0.07 | 0.45 | –0.85 | |
| 5月 | 1.04 | 0.07 | 0.39 | –0.02 | 0.18 | –0.98 | |
| 6月 | 1.57 | –0.02 | 0.18 | 0.48 | 0.1 | –0.95 | |
| 7月 | 1.97 | –0.5 | 0.15 | 1.42 | –0.3 | 0.04 | |
| 8月 | 2.11 | –0.51 | –0.23 | 1.92 | –0.84 | 1.12 | |
| 9月 | 2.47 | –0.29 | –0.75 | 2.44 | –0.53 | 1.04 | |
| 10月 | 2.65 | –0.53 | –0.69 | 2.6 | –0.73 | 1.35 | |
| 11月 | 2.91 | –0.56 | –1.02 | 3.12 | –0.63 | –0.97 | |
| 12月 | 2.87 | –0.44 | –1.2 | 2.77 | –0.22 | –0.31 | |
对于气候预测来说, “趋势”预报正确尤为重要, 业务中往往将预报对象划分若干等级, 预报与实况级别一致即为预报正确。因而本文采用如下评分标准:预报与实况距平符号相同、或符号不同但二者绝对值均小于0.5℃, 则为预报正确, 其余情况为预报错误。表 6、表 7分别给出了三种模型外推一步、外推两步的相对误差及距平准确率, 可以看出:外推一步, 三种方案17 a平均的相对误差最小为1.19%, 最大4.26%, 各月间存在一定差异, 春季预报效果较好, 冬季较差; 整体来看, 两种改进方案不仅多年平均的相对误差有所减小, 而且预报准确率高于普通模型约5个百分点, 预报技巧有一定提升。外推两步, 模型的预报效果略有降低, 但三种方案平均的预报准确率均在65%左右, 仍有一定参考价值。
| 月份 | 相对误差/% | 距平准确率 | |||||
| 方案一 | 方案二 | 方案三 | 方案一 | 方案二 | 方案三 | ||
| 1月 | 3.18 | 2.81 | 3.4 | 0.71 | 0.76 | 0.71 | |
| 2月 | 2.38 | 1.92 | 2.47 | 0.71 | 0.71 | 0.76 | |
| 3月 | 1.92 | 2.48 | 1.63 | 0.82 | 0.76 | 0.82 | |
| 4月 | 1.6 | 1.89 | 1.19 | 0.76 | 0.82 | 0.82 | |
| 5月 | 1.93 | 1.68 | 2.32 | 0.76 | 0.82 | 0.76 | |
| 6月 | 2.59 | 2.7 | 3.18 | 0.71 | 0.71 | 0.65 | |
| 7月 | 3.02 | 2.63 | 2.62 | 0.65 | 0.76 | 0.71 | |
| 8月 | 3.06 | 3.59 | 3.1 | 0.71 | 0.71 | 0.71 | |
| 9月 | 3.58 | 2.73 | 3.07 | 0.59 | 0.82 | 0.76 | |
| 10月 | 3.47 | 2.58 | 3.21 | 0.65 | 0.76 | 0.71 | |
| 11月 | 3.65 | 3.1 | 3.17 | 0.71 | 0.76 | 0.82 | |
| 12月 | 4.26 | 3.85 | 3.19 | 0.65 | 0.71 | 0.76 | |
| 平均 | 2.89 | 2.66 | 2.71 | 0.7 | 0.76 | 0.75 | |
| 月份 | 相对误差/% | 距平准确率 | |||||
| 方案一 | 方案二 | 方案三 | 方案一 | 方案二 | 方案三 | ||
| 1月 | 4.94 | 2.97 | 4.16 | 0.59 | 0.65 | 0.59 | |
| 2月 | 3.19 | 2.45 | 3.64 | 0.71 | 0.71 | 0.65 | |
| 3月 | 2.21 | 2.56 | 1.93 | 0.71 | 0.71 | 0.76 | |
| 4月 | 1.66 | 1.77 | 2.16 | 0.76 | 0.76 | 0.71 | |
| 5月 | 1.92 | 3.09 | 2.65 | 0.71 | 0.65 | 0.71 | |
| 6月 | 2.69 | 2.36 | 2.43 | 0.59 | 0.71 | 0.65 | |
| 7月 | 3.25 | 2.67 | 3.01 | 0.53 | 0.71 | 0.71 | |
| 8月 | 3.08 | 2.96 | 2.68 | 0.71 | 0.65 | 0.65 | |
| 9月 | 3.24 | 3.13 | 3.46 | 0.65 | 0.59 | 0.65 | |
| 10月 | 3.99 | 3.26 | 2.73 | 0.59 | 0.65 | 0.71 | |
| 11月 | 4.02 | 3.51 | 3.62 | 0.65 | 0.65 | 0.59 | |
| 12月 | 4.64 | 4.25 | 4.11 | 0.53 | 0.59 | 0.59 | |
| 平均 | 3.16 | 2.92 | 3.05 | 0.64 | 0.67 | 0.66 | |
对于NINO3指数的预报, 能否正确预报出两类海温异常事件是检验模型优劣的关键。因此, 进一步分析三类模型对2001年以来5次厄尔尼诺和3次拉尼娜的预报情况(表 8、表 9), 表中事件的实际起止日期来源于国家气候中心; 预报值仅给出连续的结果, 中间允许1个月的间断, 非连续值即便达到厄尔尼诺/拉尼娜标准也不计入统计。由表中可以看出:尽管对个别事件的预报效果较差(预报效果欠佳的个例往往是三个模型都有较差的预报结果), 预报的异常事件持续时间明显短于实际持续时间, 甚至出现完全预报失败的情况; 但对于大部分事件, 模型都能给出具有一定参考意义的预报。整体而言两种改进模型的预报结果, 都明显好于普通均生函数模型。此外, 分析发现, 三种方案对中部型海温异常事件的预报效果均欠佳, 尤其是持续时间短、强度弱的个例。例如2004年的中部型厄尔尼诺和2011年的中部型拉尼娜, 三类模型或预报失败或预报的持续时间仅2~3个月, 与实况差别较大; 而2015年的东部型厄尔尼诺及2010年的东部型拉尼娜则有与实况非常接近的预报结果, 其中2015年的厄尔尼诺, 虽然气候中心定义其开始于2014年10月, 但此次事件增温首先出现于赤道中太平洋, NINO3区海温持续大于0.5℃则开始于2015年春季, 预报与实况是接近的。总地来说, 均生函数及其改进模型对厄尔尼诺和拉尼娜的预报是可行的, 两种改进模型也能有效提高模型的预报准确度。
| 事件类型 | 序号 | 实际日期/年.月 | 预报结果/年.月 | ||
| 方案一 | 方案二 | 方案三 | |||
| 厄尔尼诺 | 1 | 2002.05~2003.03 | 2002.09~2002.11 | 2002.07~2002.12 | 2002.07~2003.01 |
| 2 | 2004.07~2005.01 | × | × | × | |
| 3 | 2006.08~2007.01 | × | 2006.11~2007.01 | 2006.10~2006.12 | |
| 4 | 2009.06~2010.04 | 2009.12~2010.03 | 2009.07~2010.02 | 2009.05~2010.02 | |
| 5 | 2014.10~2016.04 | 2015.08~2015.11 | 2015.07~2016.03 | 2015.07~2016.04 | |
| 拉尼娜 | 1 | 2007.08~2008.05 | × | 2007.09~2007.11 | × |
| 2 | 2010.06~2011.05 | 2010.06~2011.03 | 2010.06~2011.01 | 2010.06~2011.02 | |
| 3 | 2011.08~2012.03 | 2011.11~2011.12 | × | 2011.12~2012.02 | |
| 注: ×表示预报失败 Note: ×means failure of prediction |
|||||
| 事件类型 | 序号 | 实际日期/年.月 | 预报结果/年.月 | ||
| 方案一 | 方案二 | 方案三 | |||
| 厄尔尼诺 | 1 | 2002.05~2003.03 | 2002.10~2002.11 | 2002.09~2002.12 | 2002.09~2003.02 |
| 2 | 2004.07~2005.01 | × | × | × | |
| 3 | 2006.08~2007.01 | × | 2006.10~2006.12 | × | |
| 4 | 2009.06~2010.04 | 2009.10~2010.01 | 2009.08~2009.11 | 2009.06~2009.07 | |
| 5 | 2014.10~2016.04 | 2015.09~2015.11 | 2015.07~2016.02 | 2015.05~2016.03 | |
| 拉尼娜 | 1 | 2007.08~2008.05 | × | 2007.09~2007.12 | 2007.11~2007.12 |
| 2 | 2010.06~2011.05 | 2010.06~2011.03 | 2010.05~2011.01 | 2010.06~2010.11 | |
| 3 | 2011.08~2012.03 | × | × | × | |
| 注: ×表示预报失败 Note: ×means failure of prediction |
|||||
本文利用三种基于均生函数的预报方法, 首先对2015年的超强厄尔尼诺进行了预报试验, 为了进一步检验模型的适用性, 还建立了滑动的预报模型对2001~2017年的NINO3区海温指数进行预报, 主要得到以下结论:
(1) 均生函数模型对于极端值的拟合和预测效果较好, 试验表明利用均生函数进行厄尔尼诺/拉尼娜的气候预测是可行的, 模型具有一定实用价值; 基于EEMD的均生函数预测方法和多变量均生函数预测方法相对于普通模型, 预报技巧有了一定的提高, 尤其是外推一步以内, 是改进一般均生函数模型的有效手段。
(2) 研究中发现, 三类模型对于中部型厄尔尼诺/拉尼娜事件的预报效果较差, 尤其是对于持续时间短、强度较弱的个例。这主要是因为文章中仅考虑了NINO3区的海温变化。在今后的分析中, 区分厄尔尼诺类型, 并分别建立预报模型, 是改进厄尔尼诺预报的有效手段。
(3) 一般国际上广泛采用的数值模式, 通常只能提前6个月对厄尔尼诺给出较为正确的预报, 而应用统计预报方法, 外推两年以内的预报具有一定的参考意义, 可以适当延长厄尔尼诺的预报时效; 均生函数模型具有进行多步预测的优点, 可以制作滚动的预报并应用于业务中, 为厄尔尼诺预报提供新的思路与参考。
| [1] |
Aceituno P. El Niño, the Southern Oscillation, and ENSO:Confusing names for a complex ocean atmosphere interaction[J]. Bulletin of the American Meteorological Society, 1992, 73(4): 483-485. DOI:10.1175/1520-0477-73.4.483 |
| [2] |
Trenberth K E. The definition of El Niño[J]. Bulletin of the American Meteorological Society, 1997, 78(12): 2771-2777. DOI:10.1175/1520-0477(1997)078<2771:TDOENO>2.0.CO;2 |
| [3] |
骆高远. 我国对厄尔尼诺, 拉尼娜研究综述[J]. 地理科学, 2000, 20(3): 264-269. Luo Gaoyuan. A general survey of the studies on El Niño and La ña in China[J]. Scientia Geographica Sinica, 2000, 20(3): 264-269. DOI:10.3969/j.issn.1000-0690.2000.03.012 |
| [4] |
莫杰. 全球气候变化及其影响-探索厄尔尼诺之谜[J]. 国土资源科技管理, 2002, 19(6): 63-68. Mo Jie. Global climate change and consequent influences-A probe into the mystery of El Niño[J]. Scientific and Technological Management of Land and Resources, 2002, 19(6): 63-68. DOI:10.3969/j.issn.1009-4210.2002.06.016 |
| [5] |
李崇银, 穆穆, 周广庆, 等. ENSO机理及其预测研究[J]. 大气科学, 2008, 32(4): 761-781. Li Chongyin, Mu Mu, Zhou Guangqing, et al. Mechanism and prediction studies of the ENSO[J]. Chinese Journal of Atmospheric Sciences, 2008, 32(4): 761-781. DOI:10.3878/j.issn.1006-9895.2008.04.06 |
| [6] |
Barnston A G, Tippett M K, L'Heureux M L, et al. Skill of real-time seasonal ENSO model predictions during 2002-11:Is our capability increasing?[J]. Bulletin of the American Meteorological Society, 2012, 93(5): 631-651. DOI:10.1175/BAMS-D-11-00111.1 |
| [7] |
郑飞, 朱江, 张荣华, 等. 2015年超级厄尔尼诺事件的成功预报[J]. 中国科学院院刊, 2016, 2: 251-257. Zheng Fei, Zhu Jiang, Zhang Ronghua, et al. Successful prediction for the super El Niño events in 2015[J]. Bulletin of Chinese Academy of Sciences, 2016, 2: 251-257. |
| [8] |
王会军, 孙建奇, 郎咸梅, 等. 几年来我国气候年际变异和短期气候预测研究的一些新成果[J]. 大气科学, 2008, 32(4): 806-814. Wang Huijun, Sun Jianqi, Lang Xianmei, et al. Some new results in the research of the interannual climate variability and short-term climate prediction[J]. Chinese Journal of Atmospheric Sciences, 2008, 32(4): 806-814. DOI:10.3878/j.issn.1006-9895.2008.04.09 |
| [9] |
韦成宁. 厄尔尼诺与太阳黑子和大气环流的关系及其预报[J]. 广西气象, 2000, 21(1): 28-29. Wei Chengning. Relationships among El Niño, sun spots and atmospheric circulation and its forecast[J]. Journal of Guangxi Meteorology, 2000, 21(1): 28-29. DOI:10.3969/j.issn.1673-8411.2000.01.009 |
| [10] |
魏松林. 1997年强厄尔尼诺事件预报及其检验[J]. 北京大学学报(自然科学版), 2002, 38(1): 77-82. Wei Songlin. Prediction and its verification of strong El Niño event in 1997[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2002, 38(1): 77-82. DOI:10.3321/j.issn:0479-8023.2002.01.014 |
| [11] |
冯利华, 许晓路. 基于可公度性的厄尔尼诺事件预报[J]. 海洋预报, 2000, 17(4): 16-20. Feng Lihua, Xu Xiaolu. Forecast of El Niño event based on commensurability[J]. Marine Forecasts, 2000, 17(4): 16-20. DOI:10.3969/j.issn.1003-0239.2000.04.003 |
| [12] |
魏凤英. 现代气候统计诊断与预测技术[M]. 2版. 北京: 气象出版社, 2007: 214-223. Wei Fengying. Modern Climate Statistical Diagnosis and Prediction Technology[M]. 2th ed. Beijing: China Meteorological Press, 2007: 214-223. |
| [13] |
解明恩, 单巴次仁. 均生函数模型在高原汛期降水预报中的应用[J]. 高原气象, 1998, V17(2): 190-197. Xie Mingen, Danba Ciren. The application of mean generating function model to rainfall forecast over plateau in rainy season[J]. Plateau Meteorology, 1998, V17(2): 190-197. DOI:10.3321/j.issn:1000-0534.1998.02.010 |
| [14] |
Coifman R R. Wavelet analysis and signal processing[J]. Wavelets & Their Applications, 1992, 9(3): 765-780. |
| [15] |
薛小杰, 蒋晓辉, 黄强, 等. 小波分析在水文序列趋势分析中的应用[J]. 应用科学学报, 2002, 20(4): 426-428. Guo Xiaojie, Jiang Xiaohui, Huang Qiang, et al. The application of wavelet analysis in hydrological sequence trend analysis[J]. Journal of Applied Sciences, 2002, 20(4): 426-428. DOI:10.3969/j.issn.0255-8297.2002.04.023 |
| [16] |
Wang T, Zhang M, Yu Q, et al. Comparing the application of EMD and EEMD on time-frequency analysis of seimic signal[J]. Journal of Applied Geophysics, 2012, 83(6): 29-34. |
| [17] |
Wang W C, Xu D M, Chau K W, et al. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD[J]. Journal of Hydroinformatics, 2013, 15(4): 1377-1390. DOI:10.2166/hydro.2013.134 |
| [18] |
魏凤英, 曹鸿兴. 奇异值分解及其在北美陆地气温与我国降水遥相关中的应用[J]. 高原气象, 1997, V16(2): 174-182. Wei Fengying, Cao Hongxing. Singular value decomposition and its application to teleconnection between land air temperature in North America and rainfall in China[J]. Plateau Meteorology, 1997, V16(2): 174-182. DOI:10.3321/j.issn:1000-0534.1997.02.007 |
| [19] |
张德宽, 杨贤为, 邹旭恺. 均生函数-最优子集回归在高温极值预测中的应用[J]. 气象, 2003, 29(4): 44-47. Zhang Dekuan, Yang Xianwei, Zou Xukai. Application of mean generating function-optimal subset regression to the prediction of high temperature extremes[J]. Meteorological Monthly, 2003, 29(4): 44-47. |
| [20] |
徐力彬, 宋余庆, 刘毅. 基于镜像延拓和窗函数的端点效应抑制方法[J]. 计算机工程, 2015, 41(4): 112-116. Xu Libin, Song Yuqing, Liu Yi. Restraining method for end effect based on mirror extension and window function[J]. Computer Engineering, 2015, 41(4): 112-116. DOI:10.3969/j.issn.1000-3428.2015.04.021 |
| [21] |
林爱兰. 多元均生函数模型及其在短期气候预测中的应用[J]. 热带气象学报, 2001, 17(3): 287-292. Lin Ailan. The multiple mean generational function model and its application in short-range climatic forecast[J]. Journal of Tropical Meteorology, 2001, 17(3): 287-292. DOI:10.3969/j.issn.1004-4965.2001.03.012 |
| [22] |
任福民, 郭艳君, 周琴芳, 等. 小波变换及其对厄尔尼诺研究的初步应用[J]. 数理统计与管理, 1998, 3: 21-25. Ren Fumin, Guo Yanjun, Zhou Qinfang, et al. Wavelet transform and its preliminary application in El Niño study[J]. Journal of Applied Statistics and Management, 1998, 3: 21-25. |
 2018, Vol. 42
2018, Vol. 42


