
文章信息
- 李成凤, 刘润, 彭碧瑶, 王秀妍. 2018.
- LI Cheng-feng, LIU Run, PENG Bi-yao, WANG Xiu-yan. 2018.
- 土体约束对海底管道整体屈曲的影响机理研究
- Influence of soil constraint on global buckling of submarine pipelines
- 海洋科学, 42(2): 56-63
- Marine Sciences, 42(2): 56-63.
- http://dx.doi.org/10.11759/hykx20170605001
-
文章历史
- 收稿日期:2017-06-05
- 修回日期:2017-08-26
海底管道被广泛应用于海上油气资源开发中, 主要起着储运介质的作用。为满足工艺要求, 介质通常在高温高压下运输。温压联合作用使管道产生膨胀变形趋势, 但管道受到地基土体的约束力作用无法自由变形释放应力, 应力的累积造成管道出现不可控的整体屈曲, 整体屈曲是海底管道失效的重要形式之一。因此国内外学者对海底管道整体屈曲的机理以及影响因素进行了大量研究。
在海底管道的整体屈曲研究中, 管道的长度对其整体屈曲特性影响十分显著, 1984年, Hobbs[1]基于管道无限长的假设, 推导了理想海底管道发生竖直向和水平向整体屈曲的经典解析解。1986年, Taylor等[2]在Hobbs[1]基础上推导了具有单拱和双拱几何初始缺陷的无限长管道整体屈曲的解析解。2005年, Christensen[3]提出了“短管”的概念, 认为采用建立在管道无限长假设基础上的Hobbs[1]经典解析解计算短管整体屈曲时结果偏保守。2011年, Le等[4]提出管道整体屈曲问题除了Hobbs[1]经典解所假设的无限长管道外, 还应考虑中长管和短管的情况。2016年, 刘润等[5]以含单拱对称几何初始缺陷管道发生三阶模态的整体屈曲为例, 运用能量法推导了管道屈曲段长度与滑动段长度总和的计算表达式, 揭示了管道计算长度与整体屈曲幅值的关系。
由此可见, 将研究对象划分为长管和短管是深入研究海底管道整体屈曲的重要基础。由于管道铺设在海床上, 管道与地基土之间存在复杂的相互作用, 土体对管道约束力的大小, 直接影响长管与短管的界定和管道的整体屈曲规律。2005年, Bruton等[6]在JIP(JointIndustry Project)项目的研究中指出管道整体屈曲的发生受到管道中轴力、管道的初始几何缺陷与土体约束力三个变量的控制, 其中土体约束力对海管整体屈曲计算结果影响显著, 是管道设计中最难确定的参数[7]。2010年, Walker等[8]利用ABAQUS建立有限元模型, 研究了沿管道不对称分布的摩擦系数对管道整体屈曲最大轴向应变的影响。2013年, Haq等[9]探讨了摩擦力对管道整体屈曲的影响, 认为管道的有效轴向应力及轴向应变随管-土摩擦系数增大而增大。2015年, 刘润等[10]通过其开发的子程序VFRIC引入土体阻力大小与管线位移相关的动态土阻力模型, 较为真实地反映了管线整体屈曲过程中受到的土体阻力变化过程, 提出不同土体阻力模型对管线整体屈曲分析结果影响显著。以上关于土体约束力对管道整体屈曲的影响均未考虑管道计算长度的影响, 然而对于两端自由的管道, 土体约束力对管道整体屈曲的影响受管道计算长度的影响显著。
本文依据临界管长将管道分为“长管”与“短管”, 基于动力显式分析方法对不同长度管道的整体屈曲进行模拟, 揭示了长管与短管在升温过程中的整体屈曲规律; 进而分别在长管或短管条件下改变土体约束力系数, 分析了土体约束力系数影响长管和短管整体屈曲的规律性。
1 长管与短管 1.1 长管与短管的定义研究表明, 在管道的整体屈曲分析中存在临界长度Lt, 如图 1所示。当管道计算长度Lm小于其临界长度时, 管道最大整体屈曲幅值vm随管道计算长度Lm的增长而增长, 此时的管道被称为“短管”; 而当管道的计算长度大于其临界长度时, 管道计算长度的增长对其整体屈曲幅值没有影响, 此时的管道则称为“长管”。
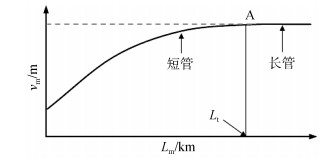 |
| 图 1 管道计算长度与最大屈曲幅值的关系 Fig. 1 Maximum buckling amplitude vs. the length of pipe |
鉴于管道在温度荷载下发生整体屈曲变形的实质是管道内部轴力的释放, 现给出长管、临界管长、短管三种状态管道的轴力p分布图, 以初始缺陷中点为x轴原点, 如图 2所示。
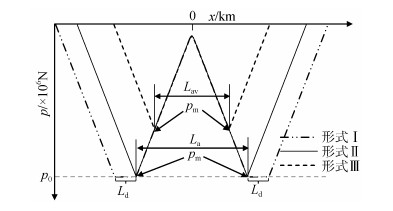 |
| 图 2 不同管长模型的轴力分布 Fig. 2 Axial force distribution along pipes of different lengths |
图 2中pm为管道实受的最大轴力, p0为假定管道处于完全约束状态时的管内最大轴力。当pm < p0时, pm对应位置为虚拟锚固点, 当pm=p0时, pm对应位置为锚固点, 两(虚拟)锚固点之间的距离为(虚拟)锚间距(虚拟锚间距与锚间距分别记为Lav及La)。长管发生整体屈曲变形后的轴力分布如图中形式Ⅰ所示, 完全约束段的长度Ld > 0且pm=p0; 当管道计算长度从长管逐渐变小时, 管道锚间距始终与长管锚间距相等, 完全约束段长度则逐渐减小, 当管道长度减小至等于临界管长时, 管道轴力分布如形式Ⅱ所示, Ld=0且pm=p0; 管道计算长度进一步变小则成为短管, 短管虚拟锚间距小于长管锚间距, 其轴力分布如形式Ⅲ所示, Ld=0且pm < p0。
因此, 对于任意管道模型, 可以根据“Ld=0且pm=p0”的轴力分布特征确定临界管长, 小于临界管长的管道为短管, 反之为长管。
1.2 实际工程中的长管与短管为分析长管与短管的整体屈曲规律, 现以某实际工程的单层保温管为例, 采用通过与经典解析解及室内试验结果对比验证合理的3D-Explicit方法[11]对管道整体屈曲进行模拟。管道采用梁单元, 单元类型为PIPE31, 地基土体采用实体单元, 单元类型为C3D8R;管道的力学行为为线弹性, 材料属性包括管道密度、杨氏弹性模量、泊松比与膨胀系数; 土体的本构模型采用摩尔-库伦模型, 材料属性包括土体容重、弹性模量、泊松比、黏聚力与内摩擦角, 不考虑土体的剪胀性; 在土体的四周约束其水平方向自由度, 底部约束其全方向自由度, 管道的两端为自由约束。管道初始缺陷模态由Taylor[2]初始缺陷表达式确定, 通过CAD建模引入(初始缺陷模态如图 3所示)。管道单位长度的有效重量为1 233.74 N/m, 设计温差为93℃, 具体参数见表 1。
 |
| 图 3 两端自由、初始缺陷左右管长对称的管道铺设形态 Fig. 3 Symmetrical pipe with initial imperfection and free ends |
| 管道外径 D/mm |
管道壁厚 t/mm |
杨氏模量 E/GPa |
有效管重 Q/(N/m) |
管道热膨胀系数Α/℃ | 泊松比 υ |
土体有效容重 γ/(kN/m3) |
土体黏聚力 C/kPa |
土体内摩擦角φ/° |
| 323.9 | 12.7 | 206 | 1233.74 | 1.1×10–5 | 0.3 | 7.8 | 1.8 | 18 |
对于两端自由、左右对称的管道, 假定其初始缺陷幅值为1 m, 得管道铺设模态如图 3所示:
已有的研究表明, 管道的临界长度主要受管道设计温度与土体约束力两个变量控制, 其中土体约束力等于土体约束力系数φ与单位管重的乘积, 现基于不同土体约束力系数下管道整体屈曲结果, 分析土体约束力系数对临界管长的影响。图 4给出了管道的临界长度与土体约束力系数曲线:
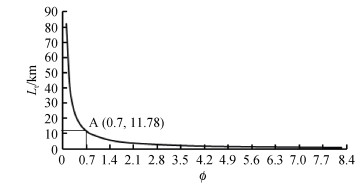 |
| 图 4 临界管长与土体约束力系数关系 Fig. 4 Critical pipe length vs. soil constraint force coefficient |
由图 4知, 当土体约束力系数φ=0.7时, 管道临界长度Lt=11.78 km。说明基于上述参数的管道在土体约束力系数等于0.7时, 长度大于11.78 km的管道属于长管, 小于11.78 km的管道属于短管。图 4显示, 临界管长随土体约束力系数增加而减小, 即在控制其他参数不变的情况下, 临界管长由摩擦系数唯一确定。因此, 在上文所述管道及地基土参数基础上, 仅改变土体约束力系数, 当土体约束力系数小于0.7时, 临界管长是大于11.78 km的某一定值。此时长度等于11.78 km的管道属于短管, 反之在土体约束力系数大于0.7时, 长度等于11.78 km的管道属于长管。因此, 对于长度等于11.78 km的管道, φ=0.7是其属于长管还是短管的界限土体约束力系数。
2 整体屈曲中的长管 2.1 长管在升温过程中的整体屈曲规律根据上文计算结果, 选择土体约束力系数等于0.7时管道计算长度大于11.78 km的长管分析升温过程中的整体屈曲规律。以14 km管长为例, 以其初始缺陷中点为x轴原点, 给出升温过程中管道的水平向位移(v)曲线, 如图 5a所示; 并在此基础上给出管道最大水平向位移(vm)与温度(T)的关系, 如图 5b所示。
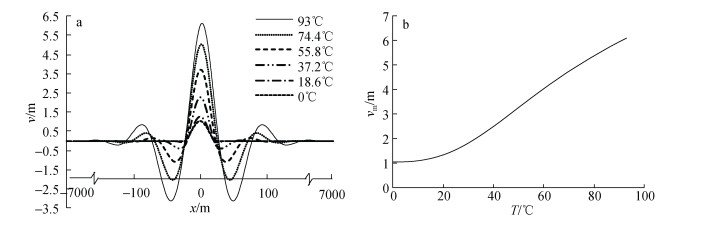 |
| 图 5 升温过程中的水平位移(a)及管道最大水平位移与温度的关系(b) Fig. 5 (a) Lateral displacement during temperatures increase and (b) maximum lateral displacement vs. temperature |
图 5显示, 在温度从0℃升至93℃的过程中, 管道的水平位移幅值持续增大, 增长速度呈现由慢变快然后保持匀速的趋势。管道在温度荷载下发生整体屈曲变形的实质是管道内部轴力的释放, 因此从管道轴向压力、轴向应变、轴向位移三个角度进一步分析长管在升温过程中发生整体屈曲的规律。图 6—图 8分别给出了14 km管道的轴向压力p、轴向位移va、轴向应变ε随温度的变化规律。
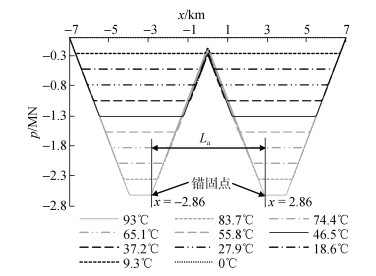 |
| 图 6 管道内部的轴力 Fig. 6 Axial force along pipe |
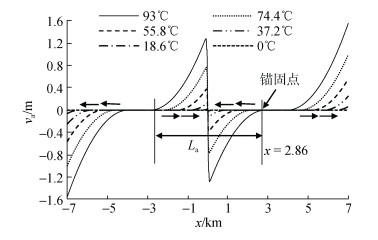 |
| 图 7 管道各点的轴向位移 Fig. 7 Axial displacement along pipe |
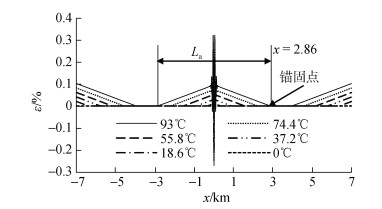 |
| 图 8 管道各点的轴向应变 Fig. 8 Axial strain along pipe |
图 6显示, 开始升温时管道两端通过伸长释放轴力, 而初始缺陷两侧的管道处于静止状态, 无轴力释放; 随着温度的升高管道内部轴力不断累积, 当温度将要达到9.3℃时, 管内轴力达到临界屈曲轴力, 管道发生整体屈曲, 开始释放轴力; 随着温度进一步升高参与轴力释放的管道长度逐渐增长, 当升温至设计温差时, 轴力释放量达到最大值, 此时参与轴力释放的管道长度等于锚间距。在整个升温过程中, 管道完全约束段的长度随着温度的升高而线性减小, 但其轴力始终随着温度增加呈线性增加, 在达到设计温差93℃时, 轴力达到最大值, 等于设计温度对应的完全约束轴力p0, 此时对应的完全约束段在整个升温过程中无轴力释放。
管道上各点的轴向位移如图 7所示, 随着温度从0℃升至93℃, 位于初始缺陷两侧的管段发生朝向管道中点的轴向位移, 如图中箭头所示; 初始缺陷两侧对称存在一段无轴向位移管段, 其长度随温度增加而减小, 且始终与轴力图中对应温度下的完全约束段位置一致, 长度相等; 完全约束段与管道两端点之间的管道产生背离中点的轴向位移。
图 8显示, 管道轴向应变曲线关于初始缺陷对称, 屈曲段轴向应变波动剧烈, 拉、压应变的最大值均出现在屈曲段; 在非屈曲段, 存在轴向应变为0的管段, 对比图 6、图 7可知, 该管段就是管道的完全约束段; 完全约束段与管道两端点之间管段的轴向应变从两端点开始, 呈线性发展。
综上所述, 长管模型在完全约束段无轴力释放、轴向应变和轴向位移, 说明管道的整体屈曲变形量由两锚固点之间管道的膨胀量决定, 管道的屈曲特性仅与锚间距的长度相关。因此管道长度在“长管”范围内变化时, 屈曲段的变形与力学特征不会发生改变。
2.2 土体约束力对长管整体屈曲的影响规律由图 4可知任何长度管道在土体约束力系数大于其界限土体约束力系数时属于长管, 长度Lm=12 km、Lm=14 km及Lm=16 km的管道的界限土体约束力系数依次为φ=0.687、φ=0.589、φ=0.515;因此, 分别以土体约束力系数范围在0.687~2.1、0.589~2.1及0.515~2.1的12、14及16 km管道为例, 分析土体约束力对长管整体屈曲的影响规律, 图 9给出了各长管最大屈曲幅值随土体约束力系数的变化。
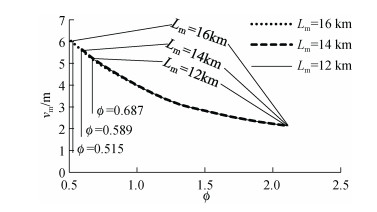 |
| 图 9 长管最大屈曲幅值随土体约束力系数的变化 Fig. 9 Maximum buckling amplitude vs. soil constraint force coefficient for the long pipe |
图 9显示, 各长管的最大屈曲幅值均随土体约束力系数增大而减小, 在0.687~2.1的土体约束力系数范围内, 不同长度管道的最大屈曲幅值-土体约束力系数关系曲线完全重合, 即任意长度的管道的屈曲幅值相等, 遵循长管的屈曲特征。
3 整体屈曲中的短管 3.1 短管在升温过程中的整体屈曲规律根据上文计算结果, 土体约束力系数为0.7时管长小于11.78 km的管道为短管。因此以管长为6 km的管道为例分析短管在升温过程中的整体屈曲规律。以管道初始缺陷中点为x轴原点, 给出升温过程中管道的水平位移(v)曲线, 如图 10a所示; 图 10b给出了管道最大水平位移(vm)与温度(T)的关系。
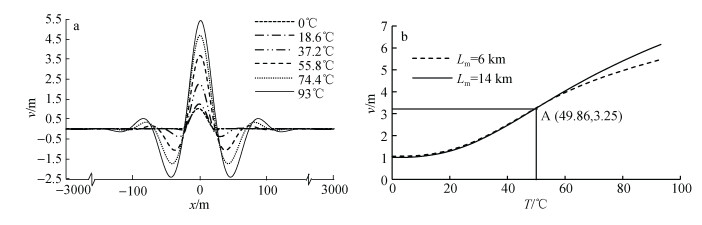 |
| 图 10 升温过程中的水平位移(a)以及6 km和14 km管道最大水平位移与温度的关系(b) Fig. 10 (a) Lateral displacement along pipe and (b) maximum lateral displacement of pipes with 16 km and 14 km vs. temperature |
图 10a显示, 6 km管道水平位移幅值随温度升高持续增长, 但其增长速度与图 5所示14 km管道有明显差异, 如图 10b所示, A点所示温度49.86℃是6 km管道与14 km管道屈曲幅值增长速率产生差异的分界值, 小于该值时, 6 km管道与14 km管道水平位移随温度变化的关系曲线重合, 二者屈曲幅值增长速率一致, 当温度大于49.86℃时, 6 km管道的屈曲幅值的增长速率降低, 而14 km管道屈曲幅值仍随温度匀速增长。以上规律说明, 对于6 km管道, 当温度小于49.86℃时, 遵循长管的整体屈曲规律, 而当温度大于49.86℃时, 遵循短管整体屈曲规律。因此, 49.86℃是该6 km短管整体屈曲规律发生改变的临界温度。为进一步分析各长度短管的临界温度的特征, 现对1 km至16 km管道的整体屈曲进行模拟, 各管道水平位移与温度的关系如图 11所示:
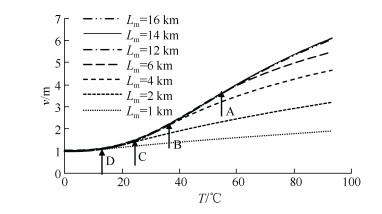 |
| 图 11 不同长度管道模型水平位移与温度的关系 Fig. 11 Lateral displacement vs. temperature |
分析图 11发现, 在设计温度内, 12 km、14 km及16 km长管不存在临界温度, 三者的水平位移与温度的关系曲线重合。各短管均存在临界温度, 且越长的短管临界温度越高。在小于临界温度范围内, 各管道水平位移曲线与长管水平位移曲线重合, 在大于临界温度范围内, 越长的短管的整体屈曲幅值越大, 但均小于长管对应的屈曲幅值。
为进一步分析临界温度对短管整体屈曲的影响规律。以6 km短管为例分析在升温过程中轴向压力、轴向位移及轴向应变的变化规律, 如图 12~图 14所示:
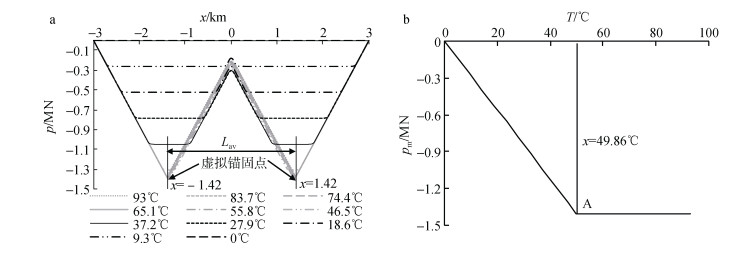 |
| 图 12 管道轴力(a)及完全约束段轴力与温度的关系(b) Fig. 12 (a) Axial force along pipe and (b) axial force at fully constrained section vs. temperature |
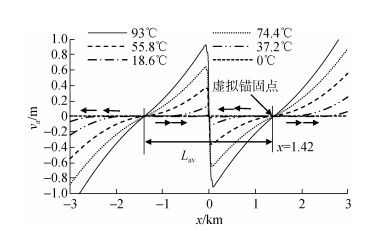 |
| 图 13 管道各点的轴向位移 Fig. 13 Axial displacement along pipe |
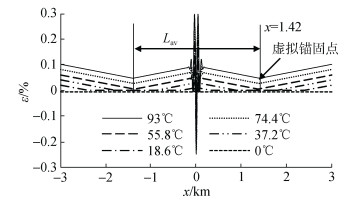 |
| 图 14 管道各点的轴向应变 Fig. 14 Axial strain along pipe |
分析图 12a, 在温度从0℃升至93℃过程中, 管道发生整体屈曲释放轴力, 参与轴力释放的管道长度先随着温度升高逐渐增长而后恒等于虚拟锚间距, 管道完全约束段长度先随温度的升高减小至0而后不再发生变化, 同时完全约束段轴力先随着温度的升高不断累积而后保持定值, 由图 12b可知, 完全约束段轴力不再随温度升高而增加的点对应的温度为49.86℃, 等于上文所述6 km管道的临界温度。在达到临界温度之前, 管道的轴力分布形式与图 2中轴力分布形式Ⅰ相同, 即短管在达到临界温度之前, 与长管变化规律相同; 达到临界温度后再继续升温, 管道轴向压力曲线基本不再发生变化, 即升温所产生的轴力不再沿管道累积, 而是通过轴向变形的方式全部释放, 此时管道相当于无约束的自由伸缩杆。
管道各点的轴向位移如图 13所示, 随着温度从0℃升至93℃, 位于初始缺陷两侧的管段发生朝向管道中点的轴向位移, 轴向位移的幅值以及发生轴向位移的管道长度随着温度的升高而增加; 在达到临界温度之前, 初始缺陷两侧对称存在一段无轴向位移管段, 其长度随温度的升高而减少, 在温度达到临界温度时, 无轴向位移管段长度减小至0, 成为管道虚拟锚固点, 虚拟锚固点的轴向位移始终为0;完全约束段或虚拟锚固点与管道两端点之间的管道产生背离中点的轴向位移。
图 14显示, 管道轴向应变曲线关于初始缺陷对称, 屈曲段轴向应变波动剧烈, 拉、压应变的最大值均出现在屈曲段; 在温度从0℃升至临界温度过程中, 管道的屈曲段与管道两端点之间存在无轴向应变段, 其长度随温度的增加而减小, 当温度升至临界温度时, 无轴向应变段长度减小至0, 成为虚拟锚固点, 当温度继续升高时, 虚拟锚固点开始发生轴向应变, 且随温度的升高而增长。
由以上分析得知, 短管在发生整体屈曲时, 存在临界温度, 在达到临界温度前, 管道的整体屈曲规律与长管整体屈曲规律一致, 存在完全约束段, 在完全约束段无轴力释放、轴向应变和轴向位移; 在临界温度后, 管道的整体屈曲规律发生变化, 完全约束段变为虚拟锚固点, 在虚拟锚固点无轴向位移, 但发生轴力释放和轴向应变。说明管道的整体屈曲变形不仅与两虚拟锚固点之间管道的膨胀量有关, 还与管道计算长度相关。因此管道长度在“短管”范围内变化时, 屈曲段的变形与力学特征会相应发生改变。
3.2 土体约束力对短管整体屈曲的影响由图 4可知不同长度的管道存在不同的界限土体约束力系数, 任何长度管道在土体约束力系数小于其界限土体约束力系数时属于短管。管道长度Lm=1 km、Lm=2 km、Lm=4 km及Lm=6 km的界限土体约束力系数依次为φ=8.245、φ=4.123、φ=2.062、φ=1.374, 因此, 分别以土体约束力系数小于其界限土体约束力系数的1 km、2 km、4 km及6 km管道为例, 分析土体约束力对短管整体屈曲的影响规律, 图 15给出了各短管最大屈曲幅值随土体约束力系数的变化。
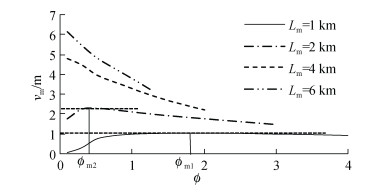 |
| 图 15 短管最大屈曲幅值与土体约束力系数的关系 Fig. 15 Maximum buckling amplitude vs. soil constraint force coefficient for the short pipe |
图 15显示, 在任意土体约束力系数下, 短管越长, 其最大屈曲幅值越大。4 km与6 km管道的最大屈曲幅值随土体约束力系数的增大而减小, 1 km及2 km管道的最大屈曲幅值先随土体约束力系数增大而增大, 在某点达到峰值, 再随土体约束力系数增大而减小, 最大屈曲幅值与土体约束力系数的关系曲线呈山峰形, 将屈曲幅值最大点对应的土体约束力系数命名为峰值土体约束力系数, 记为φm, 则1 km和2 km管道的峰值土体约束力系数分别为图 15所示的φm1和φm2。
现从管土约束力影响管道整体屈曲的两种极端情况来理解φm, 当管土约束力为零的时候, 管道在升温过程中可以自由伸缩, 不会发生屈曲; 当土体对管道为完全约束时, 管道完全受限, 不能通过变形达到轴力释放, 不会发生整体屈曲。因此土体约束力系数对管道整体屈曲的影响规律体现在:土体约束力系数从0增加至某值时, 管道的整体屈曲幅值随之增大, 当土体约束力系数进一步增大, 管道整体屈曲幅值减小。因此, 对于任何长度的管道, 在土体约束力系数从0至无穷大的范围内都存在φm, 且φm随管长增大而减小, 图 13中4 km与6 km管道的φm取值范围在0~0.1之间。较长管道的φm < 0.1, 对于实际工程来说, 可以不考虑峰值土体约束力系数的影响; 较短管道的φm取值范围较大, 对管道整体屈曲规律影响显著, 在实际工程应用中, 应该引起重视, 合理的控制土体约束力。
为了进一步对比土体约束力系数对长、短管整体屈曲影响规律的异同点, 现提取1~16 km管道在土体约束力系数从0.1~3范围内的最大水平位移, 如图 16所示:
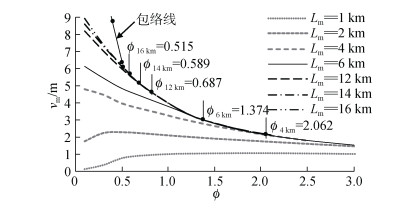 |
| 图 16 各长度管道最大屈曲幅值随土体约束力系数的变化 Fig. 16 Maximum buckling amplitude vs. soil constraint force coefficient |
由图 4可知4 km、6 km、12 km、14 km、16 km管道的界限土体约束力系数分别为2.062、1.374、0.687、0.589和0.515。图 16显示, 4 km、6 km、12 km、14 km、16 km管道的整体屈曲幅值曲线均在土体约束力系数等于其界限土体约束力系数时, 与所有计算长度比它大的管道的整体屈曲幅值曲线重合。随着土体约束力系数增大, 不同长度管道的最大屈曲幅值曲线逐渐趋于同一曲线, 即不同土体约束力系数下管道最大屈曲幅值的包络线。对于任意长度管道, 在土体约束力系数小于界限土体约束力系数时, 管道属于短管, 其最大屈曲幅值小于包络线, 且越长的短管对应屈曲幅值越大, 越接近包络线; 在土体约束力系数大于等于界限土体约束力系数范围内, 管道属于长管, 各长度长管的最大屈曲幅值曲线与包络线完全重合。
4 结论本文基于动力显式分析方法, 揭示了长管与短管在发生整体屈曲过程中, 屈曲幅值与波长、管壁轴向压力、轴向应变及轴向位移的变化规律; 研究了土体约束力影响管道临界长度的规律性, 分析了土体约束力系数对长管与短管整体屈曲变形的影响。具体结论如下:
1) 管道长度在“长管”范围内变化时, 屈曲段的变形与力学特征不会发生改变; 管道长度在“短管”范围内变化时, 屈曲段的变形与力学特征会相应发生改变。短管在发生整体屈曲时存在临界温度并在升温至临界温度后成为不受土体约束的自由伸缩杆。
2) 对于任意长度的两端自由管道, 都存在界限土体约束力系数, 在管道所受土体约束力系数小于界限土体约束力系数时, 管道为短管, 反之为长管。对于长管, 土体约束力系数越大, 管道的最大屈曲幅值越小。对于短管, 存在峰值土体约束力系数φm, 当土体约束力系数小于φm时, 土体约束力系数越大, 管道整体屈曲幅值越大, 当管土约束力系数大于φm时, 管道整体屈曲幅值随土体约束力系数增大而减小。
3) 在其他参数不变的情况下, 管道越短, φm值越大。对于φm < 0.1的短管, 实际工程中可以不考虑土体约束力系数的影响; 对于φm > 0.1的短管, 土体约束力系数对管道整体屈曲规律影响显著, 在实际工程应用中应该引起重视。
| [1] |
Hobbs R E. In-service buckling of heated pipelines[J]. Journal of Transportation Engineering, 1984, 110(2): 175-189. DOI:10.1061/(ASCE)0733-947X(1984)110:2(175) |
| [2] |
Taylor N, Gan A B. Submarine pipeline buckling— imperfection studies[J]. Thin-Walled Structures, 1986, 4(4): 295-323. DOI:10.1016/0263-8231(86)90035-2 |
| [3] |
Christensen L. Analytical linear elastic analysis of lateral buckling of "short" pipelines[C]//International Society of Offshore and Polar Engineers. The Fifteenth International Society of Offshore and Polar Engineering Conference. Seoul, 2005: 93-102.
|
| [4] |
Mao t Y L, Brunet P. Susceptibility to Lateral Buckling: What Hobbs Equations for What Flowlines[C]// American Society of Mechanical Engineers. ASME 2011, Interna tional Conference on Ocean, Offshore and Arctic Engi neering. Rotterdam, 2011: 413-420.
|
| [5] |
Liu R, Liu W, Yan S, et al. Finite-element study of methods for triggering pipeline global buckling based on the concept of the perfect VAS length[J]. Journal of Pipeline Systems Engineering & Practice, 2016, 7(2): 04015027. |
| [6] |
Bruton D, Carr M, Crawford M, et al. The safe design of hot on-bottom pipelines with lateral buckling using the design guideline developed by the SAFEBUCK joint industry project[C]//Deep Offshore Technology Conference. Deep Offshore Technology Conference. Vitoria, 2005: 1-26.
|
| [7] |
Bruton D, Bolton M, Carr M, et al. Pipe-Soil Interaction with Flowlines during Lateral Buckling and Pipeline Walking-The SAFEBUCK JIP[C]// Offshore Technology Conference. Offshore Technology Conference. Houston, 2008: 1-20.
|
| [8] |
Walker A C, Chee K Y, Cooper P. Particular Aspects Regarding the Lateral Buckling Analysis of Flowlines[C]//American Society of Mechanical Engineers. ASME 2010, International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, 2010: 49-56.
|
| [9] |
Haq M M, Kenny S. Lateral Buckling Response of Subsea HTHP Pipelines Using Finite Element Methods[C]//American Society of Mechanical Engineers. ASME 2013, International Conference on Ocean, Offshore and Arctic Engineering. Nantes, 2013: V04AT04A045.
|
| [10] |
刘润, 刘文彬, 洪兆徽, 等. 海底管线整体屈曲过程中土体水平向阻力模型研究[J]. 岩土力学, 2015, 36(9): 2433-2441. Liu Run, Liu Wenbin, Hong Zhaohui, et al. A soil resistance model for subsea pipeline global lateral buckling analysis[J]. Rock and Soil Mechanics, 2015, 36(9): 2433-2441. |
| [11] |
刘润, 刘文彬, 洪兆徽, 等. 双拱初始缺陷海底管线水平向整体屈曲数值模拟分析[J]. 海洋科学, 2015, 39(8): 86-94. Liu Run, Liu Wenbin, Hong Zhaohui, et al. Numerical solution of pipeline global buckling with double arch imperfections[J]. Marine Sciences, 2015, 39(8): 86-94. DOI:10.11759/hykx20140818002 |
 2018, Vol. 42
2018, Vol. 42


