文章信息
- 翟振峰, 黄华, 詹杰民, 张敖. 2018.
- ZHAI Zhen-feng, HUANG Hua, ZHAN Jie-min, ZHANG Ao. 2018.
- 双层直立圆弧型防波堤上绕射波浪力的解析计算
- Analysis of diffracted wave force on a double-layered vertical arc-shaped breakwater
- 海洋科学, 42(8): 62-70
- Marine Sciences, 42(8): 62-70.
- http://dx.doi.org/10.11759/hykx20171228001
-
文章历史
- 收稿日期:2017-12-28
- 修回日期:2018-03-27
防波堤是用于抵抗波浪作用以保护海工设施和近岸作业水域的重要水工结构之一, 其中圆弧形防波堤为常见的设计与建造形式。Wiegel[1]研究了半无限长薄壁直立防波堤的波浪绕射的相关问题。黄培基等[2]给出了波浪与直立堤的作用下的立波压力的计算方法。Losada等[3]解析研究了波浪与位于有限水深中的垂直薄板的相互作用问题。Abul-azm等[4]以及Mciver[5]分别应用解析法和积分方程法计算了无限长分段式等距直立防波堤的波浪绕射作用。李雪艳等[6]研究了斜防波堤典型胸墙波浪力的影响因素。程建生等[7]和楚玉川等[8]对单层圆弧型贯底式薄壁防波堤的防浪效果和绕射波浪力进行了解析研究。张敖等[9-10]分别引入椭圆余弦波模型和孤立波模型推导了浅水波对单层圆弧型防波堤绕射问题的解析解。
研究表明, 对防波堤表面布孔可以降低波浪对防波堤的荷载作用。Chwang[11]研究了透空造波机的理论, 给出了波浪与透空薄板的相互作用关系。Yu[12]计算了波浪对半无限长直线型薄壁防波堤的绕射作用。Darwiche等[13]与Williams等[14]分别解析求解了部分透空圆柱型防波堤对波浪绕射的波势解。Duan等[15]对单层圆弧型浮式透空防波堤的防浪效果进行了解析研究。林皋和刘俊[16]应用比例边界有限元法对双层圆弧型贯底式开孔介质防波堤的水波绕射进行了计算。
基于微幅波的水波绕射理论, 运用特征函数展开法, 本文给出了波浪对双层直立圆弧型透空防波堤绕射问题的解析解, 从而将现有的双层堤比例边界有限元法以及现有的单层堤波浪绕射解析法同时加以了拓展。此外, 双层圆弧堤的波浪绕射解是对仅有的双圆筒(即圆环柱)波浪绕射解的重要拓展, 其所涉及的问题和解法更为复杂, 适用的结构类型更为广泛。
1 双层防波堤的绕射波浪场求解如图 1所示, 在水深为d的均匀海中, 设置有外径和内径分别为a和b且具有同圆心角的双层直立圆弧型透空防波堤。外层堤透空系数为G1, 内层堤透空系数为G2。建立坐标系Oxyz (即坐标系Orθz), 令Oxy平面位于水底, 原点位于圆弧型防波堤的圆心处, 设置Ox轴使内外层防波堤对称位于θ=α至θ=2π–α间, 外层和内层防波堤相应的圆心角为γ= 2π–2α, Oz轴竖直向上。设入射波为Airy微幅波, 波高为H, 入射角(与Ox轴正向夹角)为β, 频率为ω。分别以a和b为半径划一同心圆环柱面, 将流场划分为圆柱外流区Ω0和圆柱内流区Ω1与Ω2。
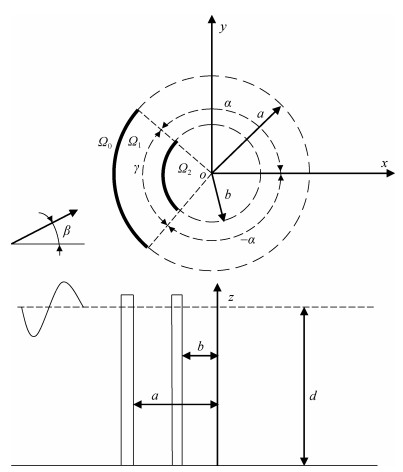 |
| 图 1 双层圆弧型透空防波堤 Fig. 1 Double-layered arc-shaped porous breakwater |
对于大尺度海工结构, 海水可视为无粘性的不可压缩流体且运动无旋。设对应流域Ωj的Airy微幅波波总波势为
| $ {\nabla ^2}{\varphi ^{(j)}} = {\nabla ^2}\varphi _s^{(j)} = 0\, \, \, \, (j = 0, 1, 2) $ | (1) |
| $\frac{{\partial {\varphi ^{(j)}}}}{{\partial z}} = \frac{{\partial \varphi _s^{(j)}}}{{\partial z}} = 0\, \, \, \, \, (z = 0)$ | (2) |
| $ g\frac{{\partial {\varphi ^{(j)}}}}{{\partial z}} - {\omega ^2}{\varphi ^{(j)}} = g\frac{{\partial \varphi _s^{(j)}}}{{\partial z}} - {\omega ^2}\varphi _s^{(j)} = 0\, \, \, \, \, (z = d) $ | (3) |
| $ \mathop {\lim }\limits_{r \to \infty } {r^{\frac{1}{2}}}\left( {\frac{{\partial \varphi _s^{(0)}}}{{\partial r}} - ik\varphi _s^{(0)}} \right) = 0 $ | (4) |
式中,
线性平面入射波势可表示为:
| $ \begin{array}{l} {\varPhi _i} = {\mathop{\rm Re}\nolimits} ({\varphi _i}), \\ \begin{array}{*{20}{c}} {{\varphi _i} = } \end{array} - \frac{{igH}}{{2\omega }}{{\rm{e}}^{ - i\omega t}}\frac{{\cosh kz}}{{\cosh kd}}[\sum\limits_{n = 0}^\infty {{\beta _n}} {J_n}(kr)\cos n\theta \cos n\beta \\ \, \, \, \, \, \, \, \, \, + \sum\limits_{n = 0}^\infty {{\beta _n}} {J_n}(kr)\sin n\theta \sin n\beta ] \end{array} $ | (5) |
基于波浪绕射理论, 应用特征函数展开法, 可取:
| $ {\varphi ^{(1)}} = - \frac{{igH}}{{2\omega }}\frac{{\cosh kz}}{{\cosh kd}}{e^{ - i\omega t}} $ | (6) |
| $ \begin{array}{c} \times \sum\limits_{n = 0}^\infty {\{ [A_n^{(1)}} \cos n\theta + B_n^{(1)}\sin n\theta ]{J_n}(kr)\\ \;\; + [C_n^{(1)}\cos n\theta + D_n^{(1)}\sin n\theta ]H_n^{(1)}(kr)\} \end{array} $ | (7) |
| $ \begin{array}{l} {\varphi ^{(2)}} = - \frac{{igH}}{{2\omega }}\frac{{\cosh kz}}{{\cosh kd}}{e^{ - i\omega t}}\\ \, \, \, \, \, \, \, \, \, \, \;\;\; \times \sum\limits_{n = 0}^\infty {[A_n^{(2)}} \cos n\theta + B_n^{(2)}\sin n\theta ]{J_n}(kr) \end{array} $ | (8) |
式中,
首先考虑外层堤物面和界面条件的应用。外层堤前后侧两流域径向分界面条件以及透空物面条件为:
| $ {\varphi ^{(0)}} = {\varphi ^{(1)}}\, \, \, \, \, \, \, \, \, \, (r = a, 0 \le \theta \le \alpha , 2{\rm{ \mathit{ π} }} - \alpha \le \theta \le 2{\rm{ \mathit{ π} }}) $ | (9) |
| $ \frac{{\partial {\varphi ^{(0)}}}}{{\partial r}} = \frac{{\partial {\varphi ^{(1)}}}}{{\partial r}}\, \, \, \, \, \, \, \, \, \, (r = a, 0 \le \theta \le 2{\rm{ \mathit{ π} }}) $ | (10) |
| $ \begin{array}{l} \frac{{\partial \varphi _{}^{(0)}}}{{\partial r}} = \frac{{\partial \varphi _{}^{(1)}}}{{\partial r}} = \frac{{{\gamma _1}\rho }}{\mu }\left( {\frac{{\partial \varphi _{}^{(0)}}}{{\partial t}} - \frac{{\partial \varphi _{}^{(1)}}}{{\partial t}}} \right){\kern 1pt} \, \\ \, \, \, \, \, \, \, \, (r = a, \alpha \le \theta \le 2{\rm{ \mathit{ π} }} - \alpha ) \end{array} $ | (11) |
式中, ρ、γ1及μ分别为海水密度、具有长度量纲的外层防波堤材料系数及粘性系数。由公式(10)可得:
| $ \begin{align} & {{\beta }_{m}}\cos m\beta {{{{J}'}}_{m}}(ka)+A_{m}^{(0)}H{{_{m}^{(1)}}^{\prime }}(ka) \\ & =A_{m}^{(1)}{{{{J}'}}_{m}}(ka)+C_{m}^{(1)}H{{_{m}^{(1)}}^{\prime }}(ka)\,\,\,\,\,\,\,\,\,\,(m=0,1,\cdots ) \\ \end{align} $ | (12) |
| $ \begin{align} & {{\beta }_{m}}\sin m\beta {{{{J}'}}_{m}}(ka)+B_{m}^{(0)}H{{_{m}^{(1)}}^{\prime }}(ka) \\ & =B_{m}^{(1)}{{{{J}'}}_{m}}(ka)+D_{m}^{(1)}H{{_{m}^{(1)}}^{\prime }}(ka)\,\,\,\,\,\,\,\,\,\,(m=1,2,\cdots ) \\ \end{align} $ | (13) |
定义函数:
| $ f(\theta ) = \left\{ \begin{array}{l} {f_1}(\theta ), 0 \le \theta < \alpha , 2{\rm{ \mathit{ π} }} - \alpha < \theta \le 2{\rm{ \mathit{ π} }}\\ {f_2}(\theta ), \alpha \le \theta \le 2{\rm{ \mathit{ π} }} - \alpha \end{array} \right. = 0 $ | (14) |
其中, 由式(9)和式(11)分别得到:
| $ \begin{array}{c} {f_1}(\theta ) = \sum\limits_{n = 0}^\infty {\{ [{\beta _n}\cos n\beta {J_n}(ka) + A_n^{(0)}H_n^{(1)}(ka)]\cos n\theta } \\ + [{\beta _n}\sin n\beta {J_n}(ka) + B_n^{(0)}H_n^{(1)}(ka)]\sin n\theta \} \\ - \sum\limits_{n = 0}^\infty {\{ [A_n^{(1)}} \cos n\theta + B_n^{(1)}\sin n\theta ]{J_n}(ka)\\ + [C_n^{(1)}\cos n\theta + D_n^{(1)}\sin n\theta ]H_n^{(1)}(ka)\} \\ = 0\, \, \, \, \, \, \, \, \, \, (0 \le \theta \le \alpha , 2{\rm{ \mathit{ π} }} - \alpha \le \theta \le 2{\rm{ \mathit{ π} }}) \end{array} $ | (15) |
| $ \begin{align} & {{f}_{2}}(\theta )=\sum\limits_{n=0}^{\infty }{\{[A_{n}^{(1)}}\cos n\theta +B_{n}^{(1)}\sin n\theta ]k{{{{J}'}}_{n}}(ka) \\ & \,\,\,\,\,\,\,\,\,\,\,\,+[C_{n}^{(1)}\cos n\theta +D_{n}^{(1)}\sin n\theta ]kH{{_{n}^{(1)}}^{\prime }}(ka)\} \\ & \,\,\,\,\,\,\,\,\,\,\,\,-i\begin{matrix} {{G}_{1}} \\ \end{matrix}\sum\limits_{n=0}^{\infty }{\{[A_{n}^{(1)}}\cos n\theta +B_{n}^{(1)}\sin n\theta ]k{{J}_{n}}(ka) \\ & \,\,\,\,\,\,\,\,\,\,\,\,+[C_{n}^{(1)}\cos n\theta +D_{n}^{(1)}\sin n\theta ]kH_{n}^{(1)}(ka)\} \\ & \,\,\,\,\,\,\,\,\,\,\,\,+i\begin{matrix} {{G}_{1}} \\ \end{matrix}\sum\limits_{n=0}^{\infty }{\{[{{\beta }_{n}}\cos n\beta k{{J}_{n}}(ka)+A_{n}^{(0)}kH_{n}^{(1)}(ka)]\cos n\theta } \\ & \,\,\,\,\,\,\,\,\,\,\,\,+[{{\beta }_{n}}\sin n\beta k{{J}_{n}}(ka)+B_{n}^{(0)}kH_{n}^{(1)}(ka)]\sin n\theta \} \\ & \,\,\,\,\,\,\,\,\,\,\,\,=0\,\,\,\,\,\,\,\,\,\,(\alpha \le \theta \le 2\text{ }\!\!\pi\!\!\text{ }-\alpha ) \\ \end{align} $ | (16) |
其中,
将
| $ f(\theta ) = \frac{{{a_0}}}{2} + \sum\limits_{m = 1}^\infty {({a_m}\cos m\theta + {b_m}\sin m\theta ) = 0} $ | (17) |
由
| $ \begin{array}{l} \int_{\;0}^{\;\alpha } {{f_1}(\theta )\cos m\theta d\theta + \int_{\;2{\rm{ \mathit{ π} }} - \alpha }^{\;2{\rm{ \mathit{ π} }}} {{f_1}(\theta )\cos m\theta } } d\theta + \\ \int_{\;\alpha }^{\;2{\rm{ \mathit{ π} }} - \alpha } {{f_2}} (\theta )\cos m\theta d\theta = 0\;\;(m = 0, 1, \cdots ) \end{array} $ | (18) |
| $ \begin{array}{l} \int_{\;0}^{\;\alpha } {{f_1}(\theta )\sin m\theta d\theta + \int_{\;2{\rm{ \mathit{ π} }} - \alpha }^{\;2{\rm{ \mathit{ π} }}} {{f_1}(\theta )\sin m\theta } } d\theta + \\ \int_{\;\alpha }^{\;2{\rm{ \mathit{ π} }} - \alpha } {{f_2}} (\theta )\sin m\theta d\theta = 0\;\;(m = 1, 2, \cdots ) \end{array} $ | (19) |
相应有:
| $ \begin{align} & \sum\limits_{n=0}^{\infty }{{{\beta }_{n}}\cos n\beta {{J}_{n}}(ka)[I_{nm}^{(1)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(2)}]} \\ & +\sum\limits_{n=0}^{\infty }{A_{n}^{(0)}}H_{n}^{(1)}(ka)[I_{nm}^{(1)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(2)}] \\ & +\sum\limits_{n=0}^{\infty }{A_{n}^{(1)}}[k{{{{J}'}}_{n}}(ka)I_{nm}^{(2)}-{{J}_{n}}(ka)(I_{nm}^{(1)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(2)})] \\ & +\sum\limits_{n=0}^{\infty }{C_{n}^{(1)}}[kH{{_{n}^{(1)}}^{\prime }}(ka)I_{nm}^{(2)} \\ & -H_{n}^{(1)}(ka)(I_{nm}^{(1)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(2)})]=0\,\,\,\,\,\,\,\,\,\,(m=0,1,\cdots ) \\ \end{align} $ | (20) |
| $ \begin{align} & \sum\limits_{n=1}^{\infty }{{{\beta }_{n}}\sin n\beta {{J}_{n}}(ka)[I_{nm}^{(3)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(4)}]} \\ & +\sum\limits_{n=1}^{\infty }{B_{n}^{(0)}}H_{n}^{(1)}(ka)[I_{nm}^{(3)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(4)}] \\ & +\sum\limits_{n=1}^{\infty }{B_{n}^{(1)}}[k{{{{J}'}}_{n}}(ka)I_{nm}^{(4)}-{{J}_{n}}(ka)(I_{nm}^{(3)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(4)})] \\ & +\sum\limits_{n=0}^{\infty }{D_{n}^{(1)}}[kH{{_{n}^{(1)}}^{\prime }}(ka)I_{nm}^{(4)} \\ & -H_{n}^{(1)}(ka)(I_{nm}^{(3)}+i\begin{matrix} {{G}_{1}} \\ \end{matrix}kI_{nm}^{(4)})]=0\,\,\,\,\,\,\,\,\,\,(m=1,2,\cdots ) \\ \end{align} $ | (21) |
其中:
| $ \left\{ \begin{array}{l} I_{nm}^{(1)} = \int_{\; - \alpha }^{\;\alpha } {\cos m\theta } \cos n\theta d\theta , I_{nm}^{(2)} = \int_{\;\alpha }^{\;2{\rm{ \mathit{ π} }} - \alpha } {\cos m\theta } \cos n\theta d\theta \\ I_{nm}^{(3)} = \int_{\; - \alpha }^{\;\alpha } {\sin m\theta \sin n\theta d\theta } , I_{nm}^{(4)} = \int_{\;\alpha }^{\;2{\rm{ \mathit{ π} }} - \alpha } {\sin m\theta \sin n\theta d\theta } \end{array} \right. $ | (22) |
公式(12)、(13)、(20)和(21)为待定系数完备代数方程组的组成部分, 其中取
再考虑内层堤物面和界面条件的应用。内层堤前后侧两流域径向分界面以及透空物面条件为:
| $ {\varphi ^{(1)}} = {\varphi ^{(2)}}\, \, \, \, \, \, \, \, \, \, (r = b, 0 \le \theta \le \alpha , 2{\rm{ \mathit{ π} }} - \alpha \le \theta \le 2{\rm{ \mathit{ π} }}) $ | (23) |
| $ \frac{{\partial {\varphi ^{(1)}}}}{{\partial r}} = \frac{{\partial {\varphi ^{(2)}}}}{{\partial r}}\, \, \, \, \, \, \, \, \, \, (r = b, 0 \le \theta \le 2{\rm{ \mathit{ π} }}) $ | (24) |
| $ \begin{array}{l} \frac{{\partial \varphi _{}^{(1)}}}{{\partial r}} = \frac{{\partial \varphi _{}^{(2)}}}{{\partial r}} = \frac{{{\gamma _2}\rho }}{\mu }(\frac{{\partial \varphi _{}^{(1)}}}{{\partial t}} - \frac{{\partial \varphi _{}^{(2)}}}{{\partial t}}){\kern 1pt} \\ \, \, \, \, \, \, \, \, \, \, (r = b, \alpha \le \theta \le 2{\rm{ \mathit{ π} }} - \alpha ) \end{array} $ | (25) |
式中,
| $ \begin{align} & A_{m}^{(1)}{{{{J}'}}_{m}}(kb)+C_{m}^{(1)}H{{_{m}^{(1)}}^{\prime }}(kb)=\,A_{m}^{(2)}{{{{J}'}}_{m}}(kb) \\ & \,\,\,\,\,\,\,\,\,\,(m=0,1,\cdots ) \\ \end{align} $ | (26) |
| $ \begin{align} & B_{m}^{(1)}{{{{J}'}}_{m}}(kb)+D_{m}^{(1)}H{{_{m}^{(1)}}^{\prime }}(kb)=\begin{matrix} B_{m}^{(2)}{{{{J}'}}_{m}}(kb) \\ \end{matrix} \\ & \,\,\,\,\,\,\,\,\,\,(m=1,2,\cdots ) \\ \end{align} $ | (27) |
定义函数:
| $ g(\theta ) = \left\{ \begin{array}{l} {g_1}(\theta ), 0 \le \theta < \alpha , 2{\rm{ \mathit{ π} }} - \alpha < \theta \le 2{\rm{ \mathit{ π} }}\\ {g_2}(\theta ), \alpha \le \theta \le 2{\rm{ \mathit{ π} }} - \alpha \end{array} \right. = 0 $ | (28) |
其中, 由公式(23)和公式(25)得到:
| $ \begin{array}{c} {g_1}(\theta ) = \sum\limits_{n = 0}^\infty {\{ [A_n^{(1)}} \cos n\theta + B_n^{(1)}\sin n\theta ]{J_n}(kb)\\ + [C_n^{(1)}\cos n\theta + D_n^{(1)}\sin n\theta ]H_n^{(1)}(kb)\} \\ - \sum\limits_{n = 0}^\infty {[A_n^{(2)}} \cos n\theta + B_n^{(2)}\sin n\theta ]{J_n}(kb)\\ = 0\, \, \, \, \, \, \, \, \, \, (0 \le \theta \le \alpha , 2{\rm{ \mathit{ π} }} - \alpha \le \theta \le 2{\rm{ \mathit{ π} }}) \end{array} $ | (29) |
| $ \begin{array}{c} {g_2}(\theta ) = \sum\limits_{n = 0}^\infty {[A_n^{(2)}} \cos n\theta + B_n^{(2)}\sin n\theta ]k{{J'}_n}(kb)\\ - i{G_2}\sum\limits_{n = 0}^\infty {[A_n^{(2)}} \cos n\theta + B_n^{(2)}\sin n\theta ]k{J_n}(kb)\\ + i{G_2}\sum\limits_{n = 0}^\infty {\{ [A_n^{(1)}} \cos n\theta + B_n^{(1)}\sin n\theta ]k{J_n}(kb)\\ + [C_n^{(1)}\cos n\theta + D_n^{(1)}\sin n\theta ]kH_n^{(1)}(kb)\} \\ = 0\, \, \, \, \, \, \, \, \, \, (\alpha \le \theta \le 2{\rm{ \mathit{ π} }} - \alpha ) \end{array} $ | (30) |
其中,
将g(θ)在0~2π上展开为傅氏级数, 即有:
| $ g(\theta ) = \frac{{{A_0}}}{2} + \sum\limits_{m = 1}^\infty {({A_m}\cos m\theta + {B_m}\sin m\theta ) = 0} $ | (31) |
由Am=Bm=0可得:
| $ \begin{array}{l} \int_{\;0}^{\;\alpha } {{g_1}(\theta )\cos m\theta d\theta + \int_{\;2{\rm{ \mathit{ π} }} - \alpha }^{\;2{\rm{ \mathit{ π} }}} {{g_1}(\theta )\cos m\theta } } d\theta + \\ \int_{\;\alpha }^{\;2{\rm{ \mathit{ π} }} - \alpha } {{g_2}} (\theta )\cos m\theta d\theta = 0\;\;(m = 0, 1, \cdots ) \end{array} $ | (32) |
| $ \begin{array}{l} \int_{\;0}^{\;\alpha } {{g_1}(\theta )\sin m\theta d\theta + \int_{\;2{\rm{ \mathit{ π} }} - \alpha }^{\;2{\rm{ \mathit{ π} }}} {{g_1}(\theta )\sin m\theta } } d\theta + \\ \int_{\;\alpha }^{\;2{\rm{ \mathit{ π} }} - \alpha } {{g_2}} (\theta )\sin m\theta d\theta = 0\;\;(m = 1, 2, \cdots ) \end{array} $ | (33) |
相应有:
| $ \begin{array}{l} \sum\limits_{n = 0}^\infty {A_n^{(1)}[{J_n}(kb)I_{nm}^{(1)} + i{G_2}k{J_n}(kb)I_{nm}^{(2)}]} \\ + \sum\limits_{n = 0}^\infty {A_n^{(2)}} \{ [k{{J'}_n}(kb) - i{G_2}k{J_n}(kb)]I_{nm}^{(2)} - {J_n}(kb)I_{nm}^{(1)}\} \\ + \sum\limits_{n = 0}^\infty {C_n^{(1)}[H_n^{(1)}(kb)I_{nm}^{(1)} + i{G_2}kH_n^{(1)}(kb)I_{nm}^{(2)}} ] = 0\, \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}(m = 0, 1, \cdots ) \end{array} $ | (34) |
| $ \begin{array}{l} \sum\limits_{n = 0}^\infty {B_n^{(1)}[{J_n}(kb)I_{nm}^{(3)} + i{G_2}k{J_n}(kb)I_{nm}^{(4)}]} \\ + \sum\limits_{n = 0}^\infty {B_n^{(2)}} \{ [k{{J'}_n}(kb) - i{G_2}k{J_n}(kb)]I_{nm}^{(4)} - {J_n}(kb)I_{nm}^{(3)}\} \\ + \sum\limits_{n = 0}^\infty {D_n^{(1)}[} H_n^{(1)}(kb)I_{nm}^{(3)} + i{G_2}kH_n^{(1)}(kb)I_{nm}^{(4)}] = 0\\ \, \begin{array}{*{20}{c}} {}&{}&{} \end{array}(m = 1, 2, \cdots ) \end{array} $ | (35) |
公式(26)、(27)、(34)和(35)为待定系数完备代数方程组的另一组成部分, 其中取
进一步由下式可计算绕射波浪场压力分布:
| $ {P^{(j)}} = - \rho \frac{{\partial {\varPhi ^{(j)}}}}{{\partial t}} = Re({p^{(j)}}), (j = 0, 1, 2) $ | (36) |
令
| $ \left\{ \begin{array}{l} {F_{x1}} = - \int_{\;0}^{\;d} {{\rm{d}}z} \int_{\;\alpha }^{\;2\pi - \alpha } {[{P^{(0)}} - {P^{(1)}}]\left| {_{r = a}} \right.a\cos \theta {\rm{d}}\theta } \\ {F_{y1}} = - \int_{\;0}^{\;d} {{\rm{d}}z} \int_{\;\alpha }^{\;2\pi - \alpha } {[{P^{(0)}} - {P^{(1)}}]\left| {_{r = a}} \right.a\sin \theta {\rm{d}}\theta } \end{array} \right. $ | (37) |
| $ \left\{ \begin{array}{l} {F_{x2}} = - \int_0^d {dz} \int_\alpha ^{2\pi - \alpha } {[{P^{(1)}} - {P^{(2)}}]\left| {_{r = b}} \right.b\cos \theta d\theta } \\ {F_{y2}} = - \int_0^d {dz} \int_\alpha ^{2\pi - \alpha } {[{P^{(1)}} - {P^{(2)}}]\left| {_{r = b}} \right.b\sin \theta d\theta } \end{array} \right. $ | (38) |
相应作用于外、内层防波堤的总波浪力为:
| $ {F_1} = \sqrt {{F_{1x}} + {F_{1y}}} , {F_2} = \sqrt {{F_{2x}} + {F_{2y}}} $ | (39) |
为方便计, 以符号
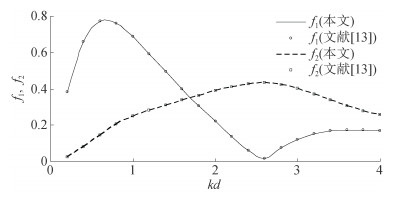 |
|
图 2 双圆筒柱的最大无量纲波浪力随kd的变化( |
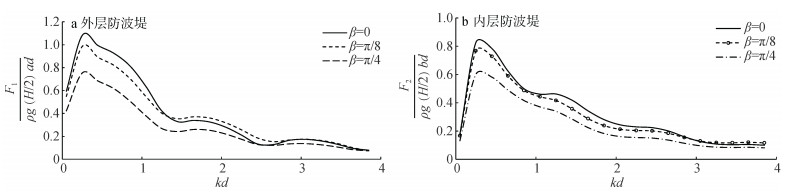
图 3为不同波浪入射角β下双层透空防波堤的最大无量纲总波浪力随参数kd的变化趋势。由计算结果可知:内外层防波堤最大波浪力均随kd先增大后减小。对于外层堤, 当kd < 1时, 波浪力随入射角的增大而减小, 当kd > 1时波浪力呈交错变化趋势, 而对于内层堤波浪力保持随入射角的增大而减小的趋势。其中平均而言, 波浪正入射(β=0)情形对应最大无量纲波浪力幅值。
 |
|
图 3 不同入射角下最大无量纲波浪力 |
图 4为波浪正入射情况下, 单层圆弧型透空防波堤与双层圆弧透空防波堤之内层堤所受最大无量纲波浪力的比较。选取单层堤与内层堤在相同位置, 其他相关参数取值相同。计算结果表明:双层堤中内层堤的最大无量纲波浪力幅值明显低于相同位置上单层堤的对应值。由此可知, 外层堤的构建大为减弱了波浪对内层堤的直接作用, 而外层堤表面透空又可同时减弱波浪对外堤的直接作用。
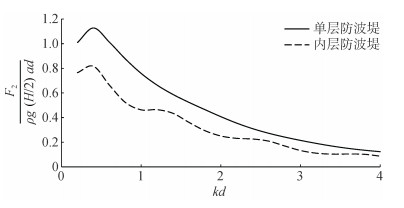 |
| 图 4 单层堤和内层堤无量纲波浪力的比较 Fig. 4 Comparison of the maximum dimensionless wave force on single breakwater and internal breakwater of double-layered breakwater |
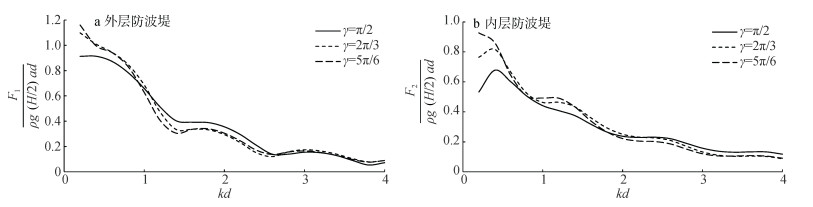
图 5为不同防波堤张角下双层堤的最大无量纲波浪力随
 |
|
图 5 不同防波堤张角下最大无量纲波浪力 |
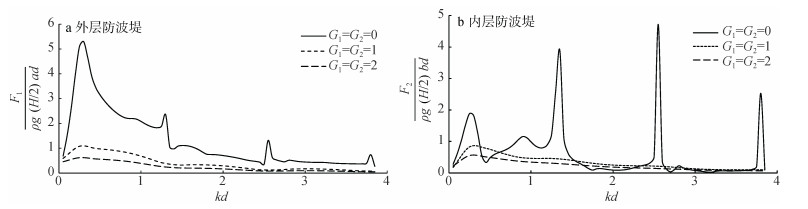
图 6为不同透空系数下双层防波堤的最大无量纲波浪力随kd的变化趋势, 其中内外层堤取相同透空系数, 即取G1=G2。由图可知:内外层防波堤表面同时布孔可明显减小外层堤的波浪承载, 且有效降低内外层堤波浪力幅值的振荡变化, 尤其可避免内层防波堤在特定kd取值下波浪力幅值出现的较为急剧的峰值突增现象。此外, 当防波堤透空系数增大到一定值时, 波浪力幅值下降现象不再明显, 说明对防波堤表面的透空适度进行即可, 防波堤表面过大的透空度对结构的稳定可能产生负面影响。
 |
|
图 6 相同透空系数下的最大无量纲波浪力 |
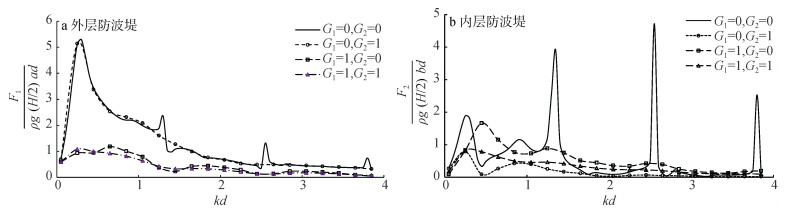
图 7为四种不同透空形式下双层防波堤的最大无量纲波浪力随kd的变化趋势。其中透空形式包括内外层堤均密实(G1=G2=0)、外层堤密实内层堤透空(G1=0, G2=1)、外层堤透空内层堤密实(G1=1, G2=0)以及内外层堤均透空(G1=G2=1)四种。图 7a表明:外层堤表面透空能有效降低外层堤的无量纲波浪力幅值。当内外层堤表面均密实时, 外层堤在特定的kd取值处可能出现陡增的波浪力峰值, 而内层堤表面透空可以有效避免这些陡增峰值的出现。此外, 内层堤表面透空与否基本不影响外层堤波浪力幅值的大小。图 7b表明:当内外层堤均密实时, 内层堤在特定的kd取值处也会出现陡增的波浪力峰值, 且较外层堤陡增现象更为急剧。当外层堤表面透空时可以避免这些峰值的出现, 当然会略为增加内层堤的波浪力幅值, 此时可让内层堤表面同时透空以减弱内层堤的波浪承载。综合而言, 采用内外层堤均透空的结构形式既可避免内外层堤最大波载陡增峰值的出现, 又可同时降低双层堤的波浪力幅值大小, 因而为均衡考虑后相对合理的优化方案。内外层堤均密实所引起的波浪力幅值的陡增现象可以归结为波浪在内外层堤间径向方向的透射受到限制, 导致波浪力幅值整体大幅提高, 该处波浪呈现多重反射的复杂作用机制。
 |
|
图 7 不同透空形式下的最大无量纲波浪力 |
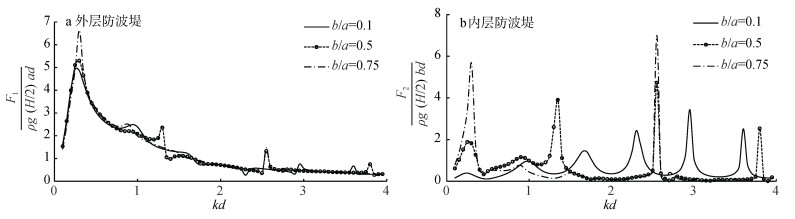
图 8为不同内外半径比下双层密实防波堤的最大无量纲波浪力随kd的变化趋势。结果表明:外层堤的无量纲波浪力幅值整体随内外半径比的变化不大, 当b/a较小时外堤波浪力峰值陡增现象明显趋弱, 说明较小的密实内堤结构对波浪在内域径向方向传播的影响趋弱。内外半径比b/a的变化对密实内层堤的最大无量纲波浪力变化具有一定影响。在内外层堤均密实的情形, 内层堤的无量纲波浪力幅值的陡增现象始终存在, 当b/a较小时(即内外层堤间距增大), 陡增的峰值有所降低。
 |
|
图 8 不同内外半径比下的最大无量纲波浪力 |
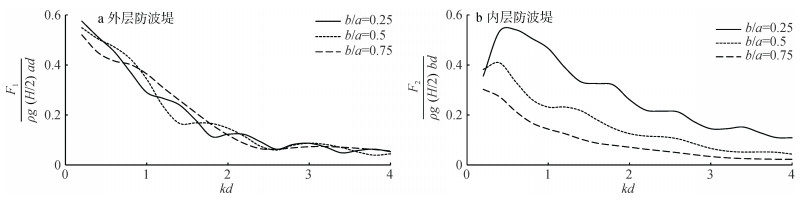
图 9为不同内外半径比下双层透空防波堤的最大无量纲波浪力随
 |
|
图 9 不同内外半径比下的最大无量纲波浪力 |
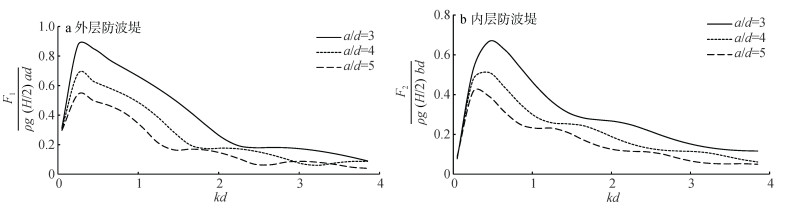
图 10为不同外径水深比下(因为b/a为定值, a/d等价于b/d)双层防波堤的最大无量纲波浪力随kd的变化趋势。由图可见, 整体而言内外层堤的无量纲波浪力幅值均随着外径水深比的增大而减小。
 |
|
图 10 不同外径水深比下的最大无量纲波浪力 |
基于Airy微幅波绕射理论, 推导了双层直立圆弧型透空防波堤波浪绕射问题的解析解, 从而将原有的单层堤问题的解析解进行了拓展, 同时将原有的双圆筒波浪绕射问题的理论解进行了拓展。按本文方法取双层圆弧防波堤圆心角γ=360°, 使结构化为圆环透空柱体(即双圆筒), 对其所受到的最大无量纲波浪力进行计算, 所算结果与已有的双圆筒解析解结果完全吻合, 说明本文方法正确可靠。与单层堤波浪力幅值计算结果的对比说明, 双层堤因外层堤的引入将明显减小内堤承受的波浪荷载。此外, 内层堤表面透空与否虽对外层堤的波浪力幅值大小影响不大, 但内层堤透空可以有效避免外层堤密实时可能出现的波浪力峰值陡增的现象。同样外层堤表面透空可以避免内层堤密实时可能出现的更为急剧的波浪力峰值陡增现象。综合考虑采用内外层堤均透空的结构形式既可避免内外堤波载峰值陡增现象的出现, 又可分别各自降低内外堤的波浪力大小, 因而为相对优化的结构透空形式, 当然外堤的透空将略为增加内堤的波浪承载。进一步波浪的入射角、防波堤张角与半径以及水深等因素的相对变化均一定程度地影响双层堤的绕射波浪作用力。
| [1] |
Wiegel R L. Diffraction of Waves by Semi-Infinite Breakwater[J]. Journal of the hydraulics division, 88(1): 27-44.
|
| [2] |
黄培基, 杨克奇, 吕常五, 等. 海浪对直立堤作用力的研究[J]. 海洋学报, 1979, 1(2): 311-322. Hang Peiji, Yang Keji, Lü Changwu, et al. A study on the force of ocean waves upon a vertical breakwater[J]. Acta Oceanologia Sinica, 1979, 1(2): 311-322. |
| [3] |
Losada I J, Losada M A, Roldán A J. Propagation of oblique incident waves past rigid vertical thin barriers[J]. Applied Ocean Research, 1992, 14(3): 191-199. DOI:10.1016/0141-1187(92)90014-B |
| [4] |
Abul-Azm A G, Williams A N. Oblique Wave Diffraction by Segmented Offshore Breakwaters[J]. Ocean Engineering, 1997, 24(1): 63-82. DOI:10.1016/0029-8018(95)00065-8 |
| [5] |
Mciver P. Diffraction of water waves by a segmented permeable breakwater[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2005, 131(2): 69-76. DOI:10.1061/(ASCE)0733-950X(2005)131:2(69) |
| [6] |
李雪艳, 付聪, 范庆来, 等. 斜坡堤典型胸墙波浪力的影响因素[J]. 海洋科学, 2015, 39(12): 118-129. Li Xueyan, Fu Cong, Fan Qinglai, et al. Factors influencing wave load on typical crest walls of sioping breakwaters[J]. Marine Sciences, 2015, 39(12): 118-129. DOI:10.11759/hykx20150122001 |
| [7] |
程建生, 缪国平, 王景全, 等. 圆弧型贯底式防波堤防浪效果的解析研究[J]. 船舶力学, 2008, 39(1): 12-17. Cheng Jiansheng, Miao Guoping, Wang Jingquan, et al. Analytical research on the sheltering effect on arc- shaped bottom-mounted breakwaters[J]. Journal of Ship Mechanics, 2008, 39(12): 12-17. |
| [8] |
楚玉川, 程建生, 赵鑫, 等. 圆弧型贯底式防波堤上波浪作用力的解析研究[J]. 水动力学研究与进展, A辑, 2014, 29(2): 212-217. Chu Yuchuan, Cheng Jiansheng, Zhao Xin, et al. Analytical study on the wave force of arc-shaped bottom- mounted breakwaters[J]. Chinese Journal of Hydrodnamics, 2014, 29(2): 212-217. |
| [9] |
张敖, 黄华, 詹杰民, 等. 椭圆余弦波对圆弧型固立防波堤的绕射波浪力[J]. 水运工程, 2017, 3: 28-33. Zhang Ao, Huang Hua, Zhan Jiemin, et al. Diffracted wave forces caused by cnoidal wave on arc-shaped bottom-mounted breakwater[J]. Port and Waterway Engineering, 2017, 3: 31-36. |
| [10] |
张敖, 黄华, 詹杰民, 等. 圆弧型贯底式透空防波堤对孤立波的绕射[J]. 中山大学学报(自然科学版), 2017, 56(3): 1-9. Zhang Ao, Huang Hua, Zhan Jiemin, et al. Diffraction of solitary wave by arc-shaped bottom-mounted porous breakwater[J]. Acta Scientiarum Naturalium Universitatis SunYatseni, 2017, 56(3): 1-9. |
| [11] |
Chwang A T. A Porous-wavemaker theory[J]. Journal of Fluid Mechanics, 1983, 132(7): 395-406. |
| [12] |
Yu X. Diffraction of water waves by porous breakwaters[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1995, 121(6): 275-282. DOI:10.1061/(ASCE)0733-950X(1995)121:6(275) |
| [13] |
Darwiche M K M, Williams A N, Wang K H. Wave interaction with Semi-porous cylindrical breakwater[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1994, 120(4): 382-403. DOI:10.1061/(ASCE)0733-950X(1994)120:4(382) |
| [14] |
Williams A N, Li W. Wave Interaction with a Semi- porous Cylindrical Breakwater Mounted on a Storage Tank[J]. Ocean Engineering, 1998, 25(2-3): 195-219. DOI:10.1016/S0029-8018(97)00006-1 |
| [15] |
Duan J, Cheng J, Wang J, et al. Wave diffraction on arc-shaped floating perforated breakwaters[J]. China Ocean Engineering, 2012, 26(2): 305-316. DOI:10.1007/s13344-012-0023-3 |
| [16] |
林皋, 刘俊. 波浪对双层圆弧型贯底式开孔介质防波堤的绕射[J]. 哈尔滨工程大学学报, 2012, 33(5): 539-546. Lin Gao, Liu Jun. Wave diffraction from a double-layered arc-shaped bottom-mounted porous breakwater[J]. Journal of Harbin Engineering University, 2012, 33(5): 539-546. DOI:10.3969/j.issn.1006-7043.201201012 |
 2018, Vol. 42
2018, Vol. 42


