文章信息
- 王元战, 戈浩波, 吴林键. 2018.
- WANG Yuan-zhan, GE Hao-bo, WU Lin-jian. 2018.
- 考虑软土蠕变对强度影响的高桩码头岸坡时变可靠度分析
- Time-variant reliability analysis of bank slope of open type wharf on piles considering the effect of soft soil creep on strength
- 海洋科学, 42(9): 88-97
- Marine Sciences, 42(9): 88-97.
- http://dx.doi.org/10.11759/hykx20171218001
-
文章历史
- 收稿日期:2017-12-18
- 修回日期:2018-06-09
高桩码头岸坡是港口工程中常见的一种岩土结构物。在长期使用荷载作用下, 岸坡土体会产生明显的蠕变, 土的流变学理论认为蠕变会导致土体抗剪强度参数的衰减效应[1]。因此, 研究岸坡土体蠕变对强度的影响, 开发考虑土体物理力学性质时变特性的高桩码头岸坡时变可靠度评估方法具有重要意义。
现阶段, 国内外学者以可靠度分析方法[2]对边坡的稳定性问题进行了大量的研究。陈欣等[3]在有限差分强度折减法中融合蒙特卡罗思想对一简单边坡进行了时不变可靠性分析, 传统蒙特卡罗法是边坡可靠度分析中一种相对精确的方法, 受问题影响的限制小, 但其收敛速度慢, 计算量大, 工程应用具有一定困难。Xu等[4]、Jiang等[5]采用一次二阶矩法和随机响应面法等方法分析边坡可靠度问题, 但在该过程中均未考虑边坡系统中岩土力学性能参数的时变特性。王贺等[6]针对边坡的时变可靠度问题进行了分析, 但其研究的是在强降雨条件下, 边坡饱和层位置随时间变化对边坡稳定性的影响。周世良等[7]基于时变可靠度理论分析了泥岩库岸的稳定性问题, 考虑了水-岩相互作用下岸坡岩土体力学参数随时间的劣化, 但没有考虑岸坡长期蠕变对土体强度的影响。Chen等[8]将支持向量机法和Morgenstern-Price法(MP法)二者结合, 分析了一个三维天然边坡的时变可靠度。其所采用的MP法是基于极限平衡法的基本原理, 采用对土体条分的手段来计算得到边坡的安全系数。
综上所述, 土体抗剪强度指标c和
本文考虑土体蠕变对抗剪强度的影响, 基于Singh- Mitchell蠕变模型建立了岸坡软土的长期强度模型, 用以量化由于土体蠕变导致的土体抗剪强度参数随时间的变化规律。以此为依托, 将可靠度分析与有限元强度折减法相结合, 提出了高桩码头岸坡时变可靠度算法。在可靠度分析过程中采用拉丁超立方抽样方法(LHS法)来改进传统蒙特卡罗法(MC法)的随机抽样过程, 提高计算效率。针对某一岸坡实例, 将采用本文算法计算得到的岸坡失效概率和可靠指标与文献中其他算法评估的结果进行对比分析, 用以验证本文算法的正确性、合理性和可行性。最后以我国沿海某高桩码头岸坡为例, 得到了岸坡土体抗剪强度参数与时间的函数关系, 基于本文算法评估了该岸坡的时变可靠度, 分析了岸坡稳定性的时变规律。文中提出的时变可靠度分析方法不仅可以为在役高桩码头岸坡的安全评估提供强有力的技术支撑, 同时也能为一些新建工程项目提供一定的参考应用价值。
1 土体长期强度模型土的流变学理论认为土体强度参数会随时间的发展而发生变化, 即具有时变特性[9]。引起软土抗剪强度参数时间效应的主要原因是土体结构面上的蠕变[1]。相关学者认为土的流变性质会使土体的抗剪强度参数c(黏聚力)、φ(内摩擦角)不断衰减, 即土的长期强度是降低的。目前, 长期强度的确定方法有很多, 但并没有一个统一意见。王在泉等[10]基于非等间距灰色模型求得泥化夹层的长期抗剪强度。刘晶辉等[11]根据土体流动曲线(剪切速率和剪应力关系)上的拐点确定软弱夹层的长期强度。董卫军[12]利用蠕变模型参数来预测软土的长期强度指标。韩爱果等[13]采用不同正应力下剪应力-剪位移双对数曲线上的拐点来确定大型滑坡滑带土的长期强度。然而, 上述方法依旧存在一些值得进一步探讨的问题, 如:蠕变试验时间短, 得到的长期强度精度会难以保证; 或只能求得土体的长期强度的极限, 无法获得土体抗剪强度参数随时间的衰减函数。本文主要关注由于土体长时间蠕变而引起其抗剪强度参数随时间的衰减效应, 选取蠕变变形达到某常数作为土体长期强度破坏准则, 在已有蠕变实验结果基础上推求软土的长期强度模型。求取软土长期强度模型的步骤如下。
1) Singh-Mitchell蠕变模型可以很好地描述土体在长期流变过程中的应力、应变与时间三者之间的关系, 取蠕变变形ε=15%, Singh-Mitchell蠕变模型可表示成偏应力水平Dr与时间t的关系:
| $ {D_{\rm{r}}} = \left[ {\ln \frac{\varepsilon }{B} - \lambda \ln \left( {t/{t_{\rm{r}}}} \right)} \right]/\beta $ | (1) |
式中, t为试样加载时间; Dr=(σ1–σ3)/(σ1–σ3)f为偏应力水平, (σ1–σ3)f为破坏偏应力, B、β、λ、tr是Singh- Mitchell蠕变模型相关参数, 可由蠕变实验确定。当t=tr时, 式(1)可以写为:
| $ {\varepsilon _{\rm{r}}} = B{{\rm{e}}^{\beta {D_{\rm{r}}}}} $ | (2) |
| $ \ln {\varepsilon _{\rm{r}}} = \beta {D_{\rm{r}}} + \ln B $ | (3) |
由此, 根据式(2)和式(3), β和B可根据tr=1 d(也可以取别的时刻)时刻的
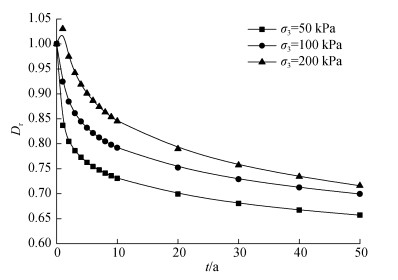 |
| 图 1 Dr与时间t关系图 Fig. 1 Relation diagram of Dr, t |
2) 根据Dr=(σ1–σ3)/(σ1–σ3)f可求得不同时间t对应的剪应力σ1–σ3, 通过三个围压下的剪应力σ1–σ3确定两种软土在不同时刻t下的抗剪强度指标c和φ的值。
3) 本文根据文献[8], 将土体抗剪强度参数c和φ随时间的变化关系表示为:
| $ {S_i}(t) = {\alpha _s}(t){S_i}(0) $ | (4) |
式中, Si(t)为时刻t土体抗剪强度参数c或φ值; Si(0)为初始时刻(t=0)土体抗剪强度参数c或φ值; αS(t)为土体抗剪强度随时间衰减或增长因子。
由该文献提供的某种软土长期抗剪强度数据回归分析可知, c, φ的αS(t)用下式拟合效果较好:
| ${\alpha _s}(t) = {b_1}\exp \left( {{b_2}t} \right) + {b_3}\exp \left( {{b_4}t} \right) $ | (5) |
式中, b1, b2, b3, b4为时间效应参数, 由试验数据确定。采用式(4)和式(5)对c、φ与t的变化关系进行拟合, 最终可求得软土的长期强度模型。
2 岸坡稳定有限元分析的强度折减法有限元强度折减法通过将码头岸坡土体抗剪强度参数逐渐折减直至岸坡失稳破坏, 以临界失稳破坏状态的抗剪强度折减系数作为岸坡安全系数[15]。高桩码头岸坡比一般边坡更为复杂, 且受桩土相互作用和上部结构的影响, 因此有限元强度折减法在高桩码头岸坡稳定性分析中存在着诸多优势[15]。此方法保持了有限元在模拟复杂问题上的优点, 而且思路明确, 结果直观, 易于接受。为简化分析, 土体材料本构模型采用理想弹塑性模型, 屈服准则釆用摩尔-库伦(Mohr-Coulomb)强度准则, 抗剪强度参数采用单强度折减系数, 即岩土体黏聚力和摩擦系数以相同的幅度进行折减:
| $ \left\{ {\begin{array}{*{20}{l}} {{c_F} = c/F}\\ {\tan {\varphi _F} = \tan \varphi /F} \end{array}} \right. $ | (6) |
式中, c和φ分别为岸坡岩土体的黏聚力和内摩擦角; cF和φF分别为折减后的黏聚力和内摩擦角; F为强度折减系数。
计算中先假定初始的强度折减系数F(一般取F=1), 根据土体强度参数折减后的值进行有限元分析, 在整个有限元计算过程中不断增加强度折减系数F, 达到临界破坏时的F就是岸坡稳定安全系数。目前应用较为广泛的岸坡失稳判据有以下3种[16]: (1)以特征点位移拐点作为评价标准; (2)以有限元数值计算不收敛作为评价标准; (3)以形成连续的塑性贯通区作为评价标准。判据(1)中特征点的选取和特征点位移拐点的确定具有主观性; 判据(3)则被相关学者认为是岸坡失稳的必要不充分条件[17], 且形成连续的塑性贯通区与否常需要通过主观经验判断。由于本文在进行可靠度分析的过程中, 需进行大量数值模拟, 并考虑到结果文件的处理方法, 故本文釆用判据(2)作为岸坡失稳判据。
3 基于拉丁超立方抽样和强度折减法评估高桩码头岸坡时变可靠度 3.1 时变可靠度结构时变可靠度的计算方法主要有3类:第一类即动态可靠指标方法[18], 采用功能函数随机过程在某一时刻的时点均值和标准差所计算得到的Cornell可靠指标β(t)作为衡量结构动态可靠度的指标; 第二类方法可被称为时间离散-综合法[19], 该方法是将计算周期T等分为N个时间区段, 把时变可靠度问题转变成一系列不同时段的时不变的串联系统的可靠度问题; 第三类方法则被称为首次超越概率法[20], 这是利用在计算周期内作用效应随机过程超越抗力随机过程概率的概念来计算结构的时变可靠度。若采用第二类方法, 可靠指标的最终结果将在很大程度上依赖于对基准期内各时间段的划分精度。而第三类方法应用随机过程理论研究时变可靠度问题, 其计算过程相对复杂, 应用尚不成熟[21]。相比较而言, 结合已有的相关研究成果[6-8, 22], 可认为采用第一类动态可靠指标分析方法能够高效地计算边坡的时变可靠度。综上所述, 本文基于第一类方法的动态可靠指标的思想, 将结构的时变可靠度表征为其在设计基准期T内, 在正常设计、使用和维护条件下, 考虑环境等因素的影响, 在任意时刻完成预定功能的概率。即:计算设计基准期内不同时刻的岸坡可靠指标, 其功能函数计算表达式为:
| $Z(t) = g\left( {{x_1}, {x_2}, \cdots , {x_n}, t} \right), t \in [0, T] $ | (7) |
对于码头岸坡可靠度分析, 可令g(x1, x2, …, xn, t)=F–1, F为岸坡的安全系数。则岸坡的失效概率为:
| $ {P_f}(t) = P\left[ {g\left( {{x_1}, {x_2}, \cdots , {x_n}, t} \right) < 0} \right] = P[F < 1] $ | (8) |
岸坡的时变可靠指标为:
| $ \beta (t) = {\mathit{\Phi} ^{ - 1}}\left[ {1 - {P_f}(t)} \right] $ | (9) |
式中,
蒙特卡罗法是通过随机模拟和统计试验来求解结构可靠度的一种数值方法[23]。它在目前的可靠度分析中被认为是一种相对准确的方法。但其精度受随机抽样的可靠性和模拟次数制约, 收敛速度较慢, 影响了实际使用[24]。为提高抽样效率和精度发展出了许多抽样方法, 如分层抽样法、重要抽样法、匕首抽样法等。
拉丁超立方抽样方法是分层抽样法的一种, 它首先确定模拟次数N, 然后将变量的概率分布函数等分成N个互不重叠的子区间, 在每个子区间内分别进行独立抽样, 可以避免传统蒙特卡罗法大量反复的抽样工作。以独立标准正态分布为例, 拉丁超立方抽样法的实现步骤如下。
1) 将每个变量的累积概率分布值分成N个不重叠的等概率区间, 在每个子区间内分别进行等概率抽样, 这时, 第i个子区间内的随机数Vi应满足以下关系:
| $ {V_i} = \frac{V}{N} + \frac{{i - 1}}{N} $ | (10) |
式中, i =1, 2, …, N; V为区间[0, 1]内均匀分布的随机数; Vi为第i个子区间内的随机数。
2) 虽然在每个子区间内由每个变量累积概率分布值产生样本点的过程是确定的, 但是样本的排序却是随机的。通常先用一个维度为N×Np的随机产生的标准正态样本矩阵R来表征所抽取样本点的排序, 然后定义一个同维度的整数矩阵Z来记录所抽取样本点的排序信息, 其中Zij=z表示第j变量第i次抽样所抽取的样本在该变量所有N个样本点中由小到大的次序为z, 例如以4个随机变量(Np=4)生成5组样本点(N=5)为例, 随机产生的标准正态分布样本矩阵R与相对应的排序矩阵Z的一种可能形式如下:
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{r}} { - 0.38}&{ - 0.58}&{ - 1.18}&{0.72}\\ {1.25}&{1.28}&{0.23}&{ - 1.52}\\ { - 0.23}&{0.25}&{ - 3.25}&{0.78}\\ {0.18}&{1.05}&{ - 1.02}&{1.45}\\ { - 0.87}&{ - 0.26}&{0.75}&{1.25} \end{array}} \right]与\mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{l}} 2&5&2&2\\ 5&1&4&1\\ 3&3&1&3\\ 4&2&3&5\\ 1&4&5&4 \end{array}} \right] $ | (11) |
3) 根据序号Zij通过下式得到第j个变量的所有拉丁超立方样本点在各个区间中的累积分布函数值为:
| $ {F_{{X_j}}}\left( {{X_{ij}}} \right) \approx \frac{{{Z_{ij}} - V}}{N}, i = 1, \cdots N, j = 1, \cdots , {N_p} $ | (12) |
采用等概率变换方法得到第j个变量独立标准正态空间的拉丁超立方样本点
| $ {\xi _{ij}} = {\mathit{\Phi} ^{ - 1}}\left[ {{F_{{X_j}}}\left( {{X_{ij}}} \right)} \right] $ | (13) |
式中, Φ–1(.)为标准正态变量累积分布函数的反函数, 进而可获得N组维度为Np的独立标准正态空间拉丁超立方样本点。综上, 拉丁超立方抽样是分层抽样法的一种, 具有估值稳定的优点, 避免了重复抽样, 能以较小的样本量得到较理想的结果, 而传统蒙特卡罗法中的随机抽样方法则需要大量的抽样。所以拉丁超立方抽样法可有效地改进抽样效率。另外拉丁超立方抽样对均值和方差的估计和传统蒙特卡罗法相比, 在效果上也有显著改善。
3.3 高桩码头岸坡时变可靠度计算程序的开发本文在建立的岸坡软土长期强度模型的基础上, 将拉丁超立方抽样法结合基于强度折减法的有限元分析, 提出高桩码头岸坡时变可靠度算法。具体分析步骤如下。
1) 建立功能函数
2) 对每组抽样结果进行基于强度折减法的岸坡稳定有限元计算然后处理结果文件。值得注意的是, 这一步是通过编写有限元计算的批处理程序进行自动化计算, 无需打开ABAQUS软件界面, 可避免对有限元的重复操作, 提高了计算效率。
3) 重复1)、2)步进行下一个时刻的岸坡可靠度分析, 直到设计基准期结束。根据极限状态方程, 可得到岸坡的时变可靠度和失效概率。具体流程图见图 2。
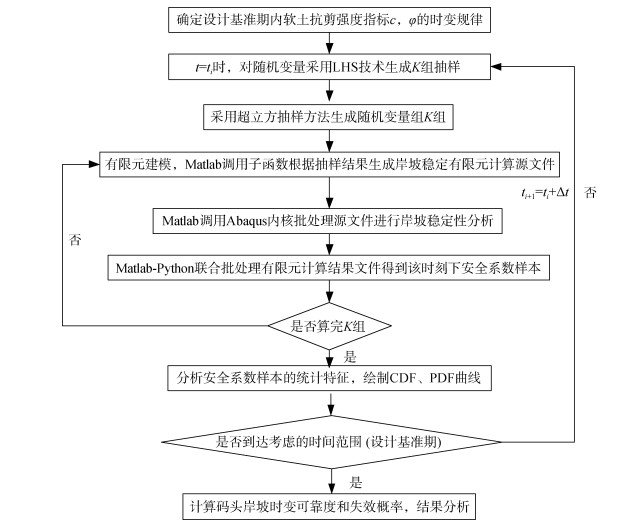 |
| 图 2 计算流程框图 Fig. 2 Block diagram of calculation flow |
现以一经典均质边坡为例, 暂时不考虑时变因素, 仅验证本文所提方法分析边坡可靠度问题的有效性。算例取自文献[25], 坡高10 m, 坡比1︰1, 强度参数c、φ视作随机变量, 并假定服从正态分布, c均值取18 kPa, 变异系数取0.2, φ取30°, 变异系数取0.1。
采用有限元强度折减法计算边坡的安全系数, 分别用拉丁超立方抽样法模拟5 000次和传统蒙特卡罗法模拟15 000次。文献[25]基于一次二阶矩法求得可靠指标和对应失效概率。各方法计算结果比较如表 1所示, 结果表明:基于本文方法(拉丁超立方抽样法)计算得到的岸坡失效概率和可靠指标与文献[24]的结果十分接近, 可靠指标的相对误差在±2%以内, 充分验证了采用本文算法的计算结果的正确性。此外可以发现, 采用蒙特卡罗法模拟15 000次的计算精度与拉丁超立方抽样方法模拟5 000次的计算精度相同, 而同样5 000次模拟, 传统蒙特卡罗法计算得到的可靠指标的相对误差达到±8%, 说明在同样模拟次数下, 拉丁超立方抽样方法比传统蒙特卡罗法计算精度更高。表 2为两种方法计算时间对比, 在得到相同精度结果的前提下, 拉丁超立方抽样法计算时间比传统蒙特卡罗法降低64%, 大大提高了计算效率。
| 计算方法 | 模拟次数 | 计算时间/min |
| 本文方法 | 5 000 | 15 770 |
| 传统MC法 | 15 000 | 44 082 |
根据上述分析, 以我国沿海地区某高桩码头岸坡为例, 基于本文算法评估该码头岸坡的时变可靠度。图 3为我国沿海地区某一高桩码头岸坡, 码头横向排架间距7.0 m, 承台宽度为13.5 m, 桩长30 m, 斜坡坡度为1︰3, 坡高8 m。在有限元模型中, 坡脚到左侧边界距离为20 m, 坡顶到右侧边界距离为55 m, 坡脚下部取32 m, 码头结构相关参数见图 3。土体参数如表 3所示, 其中ρ表示土体密度, E为弹性模量, ν为泊松比。将作为随机变量的软土强度指标的概率分布取为正态分布。根据前文所述, 软土地基长时间蠕变会引起土体抗剪强度参数的衰减效应, 根据文献[25]中针对淤泥质粘土和粉质黏土的蠕变模型实验结果, 拟合回归得到两种软土抗剪强度参数随时间衰减函数如下。
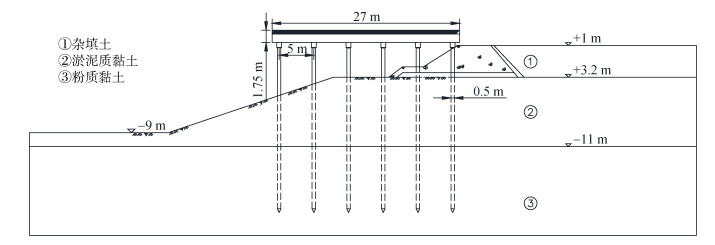 |
| 图 3 高桩码头岸坡断面图 Fig. 3 Section of slope open type wharf on piles |
| 土层名称 | ρ/103kg·m–3 | E/MPa | ν | c/kPa | Φ/(°) | |||
| 均值 | 标准差 | 均值 | 标准差 | |||||
| 杂填土 | 1.80 | 25 | 0.25 | 22 | 6.6 | 26 | 7.8 | |
| 淤泥质黏土 | 1.88 | 15 | 0.30 | 16 | 4.8 | 26 | 7.8 | |
| 粉质黏土 | 1.86 | 58 | 0.25 | 20 | 6.0 | 21 | 6.3 | |
淤泥质黏土:
| $ \begin{array}{l} \;{c_i}(t) = {c_0}\left( {0.6271{{\rm{e}}^{ - 0.00216t}} + 0.3729{{\rm{e}}^{ - 0.6884t}}} \right),\\ {\varphi _i}(t) = {\varphi _0}\left( {0.7687{{\rm{e}}^{ - 0.00536t}} + 0.2313{{\rm{e}}^{ - 0.2622t}}} \right) \end{array} $ | (14) |
粉质黏土:
| $ \begin{array}{l} {c_i}(t) = {c_0}\left( {0.6284{{\rm{e}}^{ - 0.00175t}} + 0.3716{{\rm{e}}^{ - 0.7023t}}} \right),\\ {\varphi _i}(t) = {\varphi _0}\left( {0.8206{{\rm{e}}^{ - 0.00358t}} + 0.1794{{\rm{e}}^{ - 0.2609t}}} \right) \end{array} $ | (15) |
有限元计算中采用理想弹塑性模型和Mohr- Coulomb准则, 基于强度折减法求得岸坡稳定安全系数。为对比拉丁超立方抽样方法和传统蒙特卡罗法, 先分析初始时刻的计算结果。为保证收敛, 分别用拉丁超立方抽样法和传统蒙特卡罗法对初始时刻进行10 000次模拟。由图 4模拟次数-失效概率曲线可知, 拉丁超立方抽样法3 000次模拟后, 失效概率就已经收敛, 而传统蒙特卡罗法则在6 000次收敛, 说明采用拉丁超立方抽样方法可有效减少随机模拟次数, 提高计算效率。相对传统蒙特卡罗法模拟次数可减少50%左右, 且本文计算结果也与文献[26]中采用拉丁超立方抽样方法的有效模拟次数的结论相近。综上所述, 本文在后续基于拉丁超立方抽样方法的可靠度分析中, 模拟次数均取为3 000次。
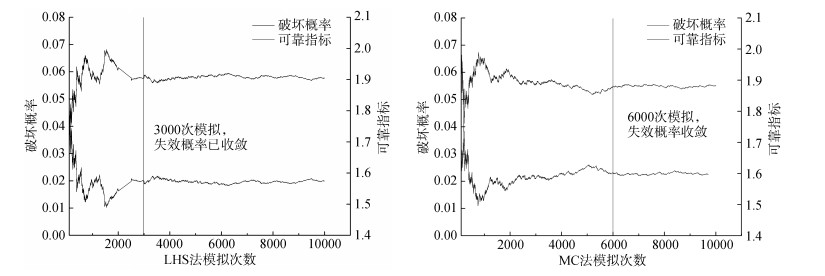 |
| 图 4 失效概率-模拟次数曲线 Fig. 4 Probability of failure vs. simulation times |
图 5给出了基于拉丁超立方抽样方法和有限元强度折减法得到的高桩码头岸坡安全系数样本的统计结果。由图中概率密度函数(PDF)曲线和累积分布函数(CDF)曲线可知:安全系数样本较符合正态分布, 但是安全系数样本值右偏, 其概率分布左边有一段尾部。为了深入研究两种抽样方法得到的安全系数样本的概率分布类型, 图 6给出了两个样本的正态分布概率纸检验结果。概率纸是一种特殊刻度的坐标纸, 用来直观判断所检验的样本是否符合某些常见的概率分布类型。由概率纸检验图可知, 两种方法计算得到的岸坡安全系数样本与正态分布都较为吻合, 但基于传统蒙特卡罗法得到的样本值在左右端尾部与正态分布偏离更大。分别用正态分布拟合两种方法得到的岸坡安全系数样本可得到相关系数, R2(拉丁超立方抽样)=0.9814 > R2(蒙特卡罗)=0.9657。这也间接论证了上述从概率纸检验图所得的结论。
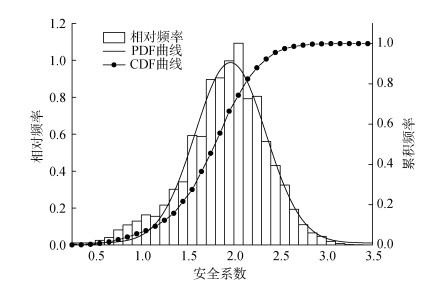 |
| 图 5 安全系数样本统计图 Fig. 5 Statistical chart of safety factor |
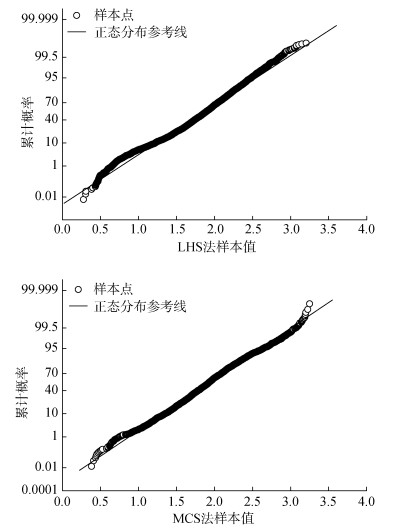 |
| 图 6 正态分布概率纸检验图 Fig. 6 Probability paper of normal distribution |
土的蠕变性质会使土体抗剪强度参数c、φ随着时间的增加不断衰减, 即土的长期强度是降低的, 这也会影响到码头岸坡的稳定性, 使岸坡稳定安全系数的概率分布同样具有时变性。本文在设计基准期t=50 a内取15个时间点, 根据抗剪强度参数c、φ的时变规律, 在每个时间点都用拉丁超立方抽样法进行3 000次模拟。在计算过程中, 假定土体抗剪强度参数变异系数不变, 均取0.3。图 7给出了安全系数中值和均值随着时间的变化规律, 两者差别不是很大(最大相对误差为7.6%, t=50 a)。另外, 随着时间的增加, 由于土体强度的衰减, 安全系数中值和均值都有不同程度的降低, 在设计基准期的前期(前5 a左右), 安全系数降低迅速, 随后衰减速度减缓, 其值逐渐趋于稳定。
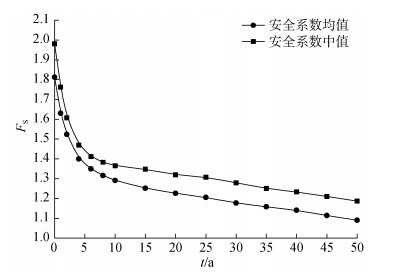 |
| 图 7 岸坡安全系数对比图 Fig. 7 The comparison chart of slope safety factors |
采用本文算法评估该码头岸坡的时变可靠度, 计算结果见图 8。随着时间的发展, 岸坡的失效概率一直增大, 可靠指标不断降低, 说明岸坡可靠度具有明显的时变特性, 在可靠度分析中考虑时间效应是十分必要的。岸坡可靠指标的变化规律表现为前期(前5 a左右)变化特别迅速而后逐渐相对减缓, 所以在码头投入使用的前期是岸坡稳定性衰减最剧烈的时段, 应对码头岸坡进行必要的监测和加固以保证码头的正常使用。在设计基准期内, 高桩码头岸坡的失效概率由初始时刻的5.5%增加到第50年时刻的33.1%, 可靠指标由初始时刻的1.60降低到第50年时刻的0.41, 表明土体蠕变影响下岸坡稳定性降低明显。
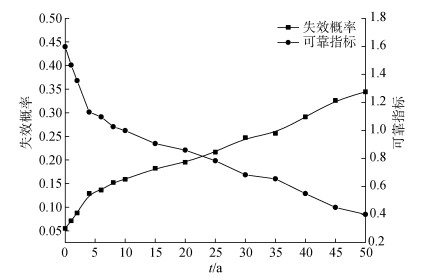 |
| 图 8 岸坡时变可靠性曲线 Fig. 8 The time-varying reliability curves of bank |
1) 软土地基长时间蠕变会引起土体抗剪强度参数的衰减效应, 本文基于Singh-Mitchell蠕变模型建立了岸坡软土的长期强度模型, 用以量化土体的抗剪强度参数随时间的变化规律, 并应用于高桩码头岸坡时变可靠度分析。
2) 将可靠度分析与有限元批处理计算相结合, 提出了高桩码头岸坡时变可靠度算法, 该算法中考虑了对高桩码头岸坡稳定性起控制因素的土体力学性质随时间的变化特性。通过算例验证, 表明该方法可用于岸坡可靠度分析。
3) 拉丁超立方抽样作为一种分层抽样技术, 可避免重复抽样, 能以较少的样本量反映总体的变异规律, 提高计算效率。结果表明拉丁超立方抽样用于岸坡可靠度分析时, 模拟次数相比于传统蒙特卡罗法可减少50%左右。
4) 岸坡土体蠕变影响下, 土体强度随时间不断衰减, 码头岸坡的安全系数和可靠度具有明显的时变特性。随着时间的发展, 码头岸坡的可靠指标和安全系数不断降低, 并且前期衰减特别迅速而后逐渐相对减缓。在设计基准期内, 高桩码头岸坡的可靠指标由初始时刻的1.60降低到第50年时刻的0.41, 码头岸坡的失效概率也具有同样显著的时变性。
| [1] |
张先伟, 王常明. 漳州软土直接剪切蠕变特性及蠕变参数的研究[J]. 四川大学学报(工程科学版), 2011, 43(4): 71-76. Zhang Xianwei, Wang Changming. Study on direct shearing creep characteristics of changzhou soft clay and creep parameters[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(4): 71-76. |
| [2] |
Li Y, Lence B J. Numerical approximations of design points in reliability analysis under parametric changes[J]. Journal of Engineering Mechanics, 2007, 133(11): 1213-1221. DOI:10.1061/(ASCE)0733-9399(2007)133:11(1213) |
| [3] |
陈欣, 付建军, 赵海斌, 等. 有限差分强度折减法中融合蒙特卡罗思想的边坡可靠性分析[J]. 长江科学院院报, 2011, 28(4): 36-40. Chen Xin, Fu Jianjun, Zhao Haibin, et al. Analysis of slope reliability by finite-difference strength-reduction method considering the thought of Monte Carlo Method[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(4): 36-40. DOI:10.3969/j.issn.1001-5485.2011.04.009 |
| [4] |
Xu B, Low B K. Probabilistic stability analyses of embankments based on finite element method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(11): 1444-1454. DOI:10.1061/(ASCE)1090-0241(2006)132:11(1444) |
| [5] |
Jiang S H, Li D Q, Zhou C N, et al. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method[J]. Engineering Geology, 2014, 168: 120-128. DOI:10.1016/j.enggeo.2013.11.006 |
| [6] |
王贺, 张洁, 陈飞扬. 强降雨条件下花岗岩残积土边坡的时变可靠度[J]. 武汉大学学报(工学版), 2016, 49(5): 763-767. Wang He, Zhang Jie, Chen Feiyang. Time-dependent reliability of slopes made of completely decomposed granite under intense rainfall[J]. Engineering Journal of Wuhan University, 2016, 49(5): 763-767. |
| [7] |
周世良, 刘小强, 尚明芳, 等. 基于水-岩相互作用的泥岩库岸时变稳定性分析[J]. 岩土力学, 2012, 33(7): 1933-1939. Zhou Shiliang, Liu Xiaoqiang, Shang Mingfang, et al. Time-varying stability analysis of mudstone reservoir bank based on water-rock interaction[J]. Rock and Soil Mechanics, 2012, 33(7): 1933-1939. DOI:10.3969/j.issn.1000-7598.2012.07.003 |
| [8] |
Chen C F, Xiao Z Y, Zhang G B. Time-variant reliability analysis of three-dimensional slopes based on Support Vector Machine method[J]. J. Cent. South Univ. Technol, 2011, 18: 2108-2114. DOI:10.1007/s11771-011-0950-9 |
| [9] |
陈昌富, 秦海军. 考虑强度参数时间和深度效应边坡稳定性分析[J]. 湖南大学学报(自然科学版), 2009, 36(10): 1-6. Chen Changfu, Qin Haijun. Stability analysis of slopes considering the time and depth effect of strength parameters[J]. Journal of Hunan University (Natural Sciences), 2009, 36(10): 1-6. |
| [10] |
王在泉. 泥化夹层长期强度的灰色预测[J]. 金属矿山, 1998, 2: 16-20. Wang Zaiquan. Grey prediction of the long term strength of mudded intercalation[J]. Metal Mine, 1998, 2: 16-20. |
| [11] |
刘晶辉, 王山长, 杨洪海. 软弱夹层流变试验长期强度确定方法[J]. 勘察科学技术, 1996, 5: 3-7. Liu Jinghui, Wang Shanchang, Yang Honghai. Method to determine the rheological test long-term strength for soft intercalations[J]. Investigation Science and Technology, 1996, 5: 3-7. |
| [12] |
董卫军.软土流变特性室内试验研究及长期强度的确定[D].南京: 河海大学, 2007. Dong Weijun. Laboratory study on rheological properties of soft soil and determination of long-term strength[D]. Nanjing: HoHai University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10294-2007167679.htm |
| [13] |
韩爱果, 聂德新, 任光明, 等. 大型滑坡滑带土剪切流变特性研究[J]. 工程地质学报, 2001, 9(4): 345-348. Han Aiguo, Nie Dexin, Ren Guangming, et al. Study on shear rheologic behaviors of soil in slip zone of alarge- scale landslide[J]. Journal of Engineering Geology, 2001, 9(4): 345-348. DOI:10.3969/j.issn.1004-9665.2001.04.002 |
| [14] |
王元战, 黄东旭, 肖忠. 天津滨海地区两种典型软黏土蠕变特性试验研究[J]. 岩土工程学报, 2012, 34(2): 379-384. Wang Yuanzhan, Huang Dongxu, Xiao Zhong. Experimental research on creep properties of two typical soft clays in coastal region of Tianjin[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 379-384. |
| [15] |
费康. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2010: 393-394. Fei Kang. Application of ABAQUS in Geotechnical Engineering[M]. Beijing: China Water Power Press, 2010: 393-394. |
| [16] |
余神光, 别社安, 李伟, 等. 高桩码头岸坡滑弧模式研究与变形稳定性分析[J]. 岩土力学, 2013, 34(1): 227-234. Yu Shenguang, Bie Shean, Li Wei, et al. Research on slip arc mode and deformation stability of bank slope on high-piled wharf[J]. Rock and Soil Mechanics, 2013, 34(1): 227-234. |
| [17] |
蒋水华.水电工程边坡可靠度非侵入式随机分析方法[D].武汉: 武汉大学, 2014. Jiang Shuihua. Non invasive stochastic analysis method for slope reliability of hydropower projects[D]. Wuhan: Wuhan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015550337.htm |
| [18] |
谢桂华, 李继祥, 耿树勇, 等. 时变结构可靠度预测方法探讨[J]. 武汉工业学院学报, 2004, 23(3): 51-54. Xie Guihua, Li Jixiang, Geng Shuyong, et al. A method discussion on predicting reliability of time-variant structure[J]. Journal of Wuhan Polytechnic University, 2004, 23(3): 51-54. DOI:10.3969/j.issn.1009-4881.2004.03.016 |
| [19] |
Bhargava K, Mori Y, Ghosh A K. Time-dependent reliability of corrosion-affected RC beams. Part 2: estimation of time-dependent failure probability[J]. Nuclear Engineering and Design, 2011, 241(5): 1385-1394. DOI:10.1016/j.nucengdes.2010.03.027 |
| [20] |
Van Noortwijk J M, Van der Weideb J A M, Kallen M J, et al. Gamma processes and peaks-over-threshold distributions for time-dependent reliability[J]. Reliability Engineering and System Safety, 2007, 92: 1651-1658. DOI:10.1016/j.ress.2006.11.003 |
| [21] |
李青美.海港桩基码头耐久性及整体可靠度分析方法[D].天津: 天津大学, 2016. Li Qingmei. Analysis method for durability and overall reliability of harbor pile wharf[D]. Tianjin: TianJin University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10056-1017131102.htm |
| [22] |
Tan X H, Hu N, Li D, et al. Time-variant reliability analysis of unsaturated soil slopes under rainfall[J]. Geotechnical & Geological Engineering, 2013, 31(1): 319-327. |
| [23] |
贡金鑫. 工程结构可靠性设计原理[M]. 北京: 机械工业出版社, 2007: 103-111. Gong Jinxin. Principle of Reliability Design for Engineering Structure[M]. Beijing: Machinery Industry Press, 2007: 103-111. |
| [24] |
伍国军, 陈卫忠, 谭贤君, 等. 基于拉丁超立方抽样的有限元可靠度程序开发及应用[J]. 岩土力学, 2015, 34(2): 550-554. Wu Guojun, Chen Weizhong, Tan Xianjun, et al. Program development of finite element reliability method and its application based on Latin hypercube sampling[J]. Rock and Soil Mechanics, 2015, 34(2): 550-554. |
| [25] |
Hassan A M, Wolff T F. Search algorithm for minimum reliability index of earth slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(4): 301-308. |
| [26] |
吴振君, 王水林, 葛修润. LHS方法在边坡可靠度分析中的应用[J]. 岩土力学, 2010, 31(4): 1047-1054. Wu Zhenjun, Wang Shuilin, Ge Xiurun. Application of Latin hypercube sampling technique to slope reliability analysis[J]. Rock and Soil Mechanics, 2010, 31(4): 1047-1054. DOI:10.3969/j.issn.1000-7598.2010.04.007 |
 2018, Vol. 42
2018, Vol. 42

