文章信息
- 仇颖, 阳德华, 李爽. 2019.
- QIU Ying, YANG De-hua, LI Shuang. 2019.
- Langmuir环流在雷诺平均型模式中的参数化研究进展
- Progress in parameterization of Langmuir circulation in Rey-nolds Average Navier-Stokes(RANS) model
- 海洋科学, 43(11): 103-110
- Marine Sciences, 43(11): 103-110.
- http://dx.doi.org/10.11759/hykx20190114001
-
文章历史
- 收稿日期:2019-01-14
- 修回日期:2019-03-11
上层海洋的动力主要源于与大气边界层中风的相互作用[1], 风和波浪共同作用下产生了Langmuir环流(简称LC)现象, Langmuir环流以一系列交替的水平滚动涡旋的形式出现, 其轴线与风大致对齐, 其在湍流的动量、热量和质量转移中发挥着关键性的作用, 是波流相互作用的主要表现形式之一, 因此Langmuir环流是上层海洋湍流的重要特征之一。Craik和Leibovich进行了一系列关于Langmuir环流基本机制的理论研究[2-5], 指出Stokes漂流和风驱水平流的相互作用, 是引起Langmuir环流的核心机制, 他们之间的相互作用力, 称为“Stokes-Vortex力”。McWilliams等[6]在上述Craik和Leibovich(CL)理论的基础上提出了“Langmuir环流”的理论, 认为上层湍流需要考虑由Langmuir环流导致的湍动能增加项, LC是引起湍流混合的一个重要机制。
近年来, 对于Langmuir环流影响下的上层海洋动力混合的研究大多采用大涡模式。LES能够直接解析大于模拟网格尺度的流动, 仅对次网格部分进行参数化, 大大提高了求解精度, 已成为Langmuir环流模拟的有效工具[7-9]。McWilliams等[6]对平均动量方程中科里奥利和压力项的修正作出了改进, 提出了Langmuir湍流的概念。Skyllingstad和Denbo[7]使用LES对有无对流驱动的和有无Stokes漂流的混合进行模拟, 垂向速度方差和热通量的增加显示了Langmuir环流对海洋上层混合的重要性。一系列研究结果表明在混合层内, LC极大地增强了垂直混合, 导致温度和速度的均匀分布[10-14], 但是研究表明, 关于LC对于混合层加深的作用仍然不是很清晰, 在某些情况下, LC似乎有助于增强混合层的加深[15-16], 但是Skyllingstad[17]使用海表边界层的大涡模拟(LES)湍流模型进行敏感性实验, 结果表明LC的影响主要局限于混合层生长的初始阶段。
为了更好地研究LC对于上层海洋混合的影响, 尽管其在垂直混合中的作用存在不确定性, 越来越多的学者将Langmuir环流因素加入到三维海洋环流模式中进行研究。现有的湍流数值模拟方法有3种:直接数值模拟、大涡数值模拟和雷诺平均模拟。直接数值模拟方法是通过对湍流进行直接计算, 不需要简化和近似, 理论上能得到相对准确的计算结果, 但是直接数值模拟方法对计算机内存空间和计算速度的要求非常高, 目前只能应用于简单流场。雷诺平均模拟方法稳定性相对较好, 需要的计算工作量小, 是应用较广的湍流数值模拟方法, 目前海洋学界常用的雷诺平均模型有POM、HYCOM、ROMS等。但是雷诺平均方法只能给出湍流的平均运动和相应的平均物理量, 而需要通过模型刻画雷诺应力, 且不同的雷诺平均模式缺乏统一性。而由于大涡模拟通过空间平均将湍流分为可解尺度和不可解尺度, 在可解尺度上能直接数值求解计算出雷诺应力项, 用亚格子尺度模型模拟不可解尺度湍流对可解尺度湍流的影响, 因此LES结果被用于提供改进现有参数化的思路, 以改进这些雷诺平均模型中使用的现有参数化方案。
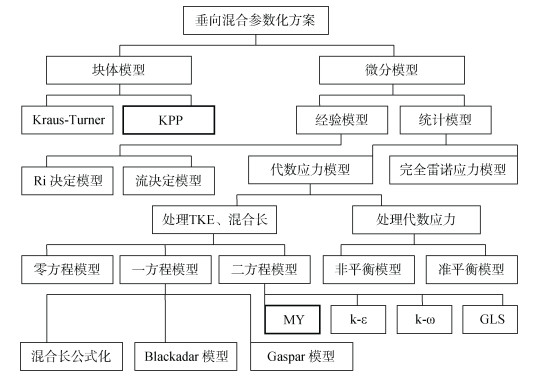
1 雷诺平均模式中现有的垂向混合参数化方案海洋混合的参数化方案在海洋数值模式中起至关重要作用, 不同的参数化方案选取将直接影响数值模拟结果的可靠性, 不适用的混合参数化方案将导致混合强度、温盐分布、水平流动等出现失真的情况。海洋湍流研究的核心目标是开发用于大规模模型的高效、精确的垂直混合参数化方案。现有的湍流垂向参数化方案只是在大尺度运动中模拟了湍流和小尺度的混合效应。在这之中, 按照处理TKE和长度尺度的方程个数, 我们可以将垂向混合参化化方案分为零方程模型、一方程模型、二方程模型。目前比较常用的参数化方案包括Mellor-Yamada模型[19], 基于K理论和湍封闭方法的连续混合层方案例如K-剖面参数化(KPP, K-profile parameterization)方案等。
2 关于在雷诺平均模式中添加Langmuir环流作用的模式改进 2.1 K-剖面参数化(KPP)一种广泛使用的参数化方案是K-剖面参数化(KPP), 它以一维垂直剖面的形式模拟涡流黏度和涡流扩散系数。标准KPP模型是针对纯风致剪切湍流而开发的, 不包括Langmuir环流的影响[20]。
在标准KPP模型中, 涡黏性系数参数化为:
| $ K(z)=z_{\mathrm{m}} W(\sigma) G(\sigma), $ | (1) |
| $ \sigma=-z / z_{\mathrm{m}}, $ | (2) |
| $ K_{\mathrm{c}}(z)=z_{\mathrm{m}} W_{\mathrm{c}}(\sigma) G(\sigma), $ | (3) |
其中K和Kc分别表示动量和标量传输, 这里G是形状函数:
| $ G(\sigma)=\sigma(1-\sigma)^{2}, $ | (4) |
zm是混合层深度, W和Wc是湍流速度尺度传输的动量和标量:
| $ W(\sigma)=\frac{\kappa u_{*}}{\varphi_{\mathrm{m}}(\sigma)}, \quad W_{\mathrm{c}}(\sigma)=\frac{\kappa u_{*}}{\varphi_{\mathrm{c}}(\sigma)}, $ | (5) |
热稳定性函数
K-剖面参数化中的Langmuir混合作用涉及两个要点:第一, Langmuir环流作用在海表边界层内增强的垂直湍流动能(VKE), 第二, 对于更深层混合带来的影响。最近, 一些学者在KPP模型中加入Langmuir环流作用进行研究, 提出了不同的LC参数化方案[10, 21-23], 下面将对这些参数化方案进行描述。
2.1.1 McWilliams和Sullivan[10]参数化方案在McWilliams和Sullivan[10]参数方案中, 基于实验数据发现, 当LC现象明显时, 近表面横向速度(即垂直于风和波方向的水平分量)与表层斯托克斯漂流成正比变化[24-25]。虽然存在两者比例系数值不确定的问题, 但是为简单修改KPP模型添加LC效应提供了相关的思路。因此McWilliam等[10]通过增强的湍流速度标度, 通过增强因子来添加Langmuir环流的作用, 增强因子从湍流Langmuir数中参数化:
| $ W\left(\sigma, L a_{t}\right)=\frac{\kappa u_{*}}{\varphi_{\mathrm{m}}(\sigma)} \cdot \varepsilon\left(L a_{t}\right), $ | (6) |
| $ \varepsilon\left(L a_{t}\right)=\left(1+\frac{C_{w}}{L a_{t}^{2 \alpha_{e}}}\right)^{1 / \alpha_{e}}, $ | (7) |
其中
这些修改使得KPP湍流通量曲线与LES模拟的存在LC的情况相当匹配, 尤其是密度和边界标量表现出很好的一致性。对KPP方案的这种调整导致在Langmuir环流活跃的区域, 即湍流速度与小Lat的区域中的表面斯托克斯漂移成比例。McWilliams[10]表明, 这种改进使参数化的KPP通量曲线与LES相同情况下的模拟结果相当。
2.1.2 Smyth (2002)参数化方案Skyllingstad等[26]使用大涡模拟(LES)描述了在风暴期间24小时内上层海洋混合的情况, 其利用观察到的剖面初始化并由观察到的表面通量驱动模式, 统计量化比较了LES模型中产生的湍流通量与定点测量出的湍流通量之间的关系。这些比较确定了LES对于用来描述上层海洋湍流的的准确性及其限制, 比观测所能提供的要更加全面。因此, 为了改进KPP参数化方案, 将KPP结合到上层海洋的一维模型中, Smyth[21]通过与赤道太平洋西风暴期间上层海洋结构的观测和大涡模拟(LES)的比较来进一步推进了改进KPP模式的工作。Smyth等人利用由TOGA- COARE提供的详细而全面的观察数据库[25], 然后以与LES相同的方式使用观察对其进行初始化和强迫, 在McWilliams(2000)参数方案中, 基于拟静态, 弱对流Langmuir环流的大涡模拟, 恒定Cw的值为0.08。这个值的选取可能需要在强对流或强风的情况下进行修改, 因此, Smyth[21]将Cw乘以一个额外的因子增强Langmuir细胞在稳定(强制)条件下的作用, 并在对流条件下降低它:通过用取决于热稳定性的函数替换常数Cw, 进一步推广了增强因子:
| $ C_{\mathrm{w}}=C_{\mathrm{w} 0}\left(\frac{u_{*}^{3}}{u_{*}^{3}+0.6 w_{*}^{3}}\right)^{l}, $ | (8) |
其中Cw0=0.15, l=2, w*=(–κBfzm)1/3是对流速度刻度, Bf是表面浮力通量。Bf负值对应表面冷却, 这增强了热对流。这种改进增强了Langmuir环流在正浮力强迫下的影响, 并在对流条件下降低了负浮力强迫, 有助于解释风力驱动条件下的Langmuir环流效应, 同时在热对流占主导地位时减少效应产生, 使得修改后的KPP结果与LES之间达成更好的一致性。
2.1.3 Van Roekel(2012)参数化方案在上述两种参数化方案中, 风诱导剪切和斯托克斯强迫的相对重要性由Lat表示。两项研究均假设斯托克斯漂移与表面风应力一致, 而真实海洋中的情况往往并非如此。假设风和波浪方向存在夹角, 摩擦力和斯托克斯漂移速度都必须投射到位于其间的LC轴方向, 以代表风致剪切和Stokes强迫的重要部分, 它通常会降低Langmuir环流的影响。Van Roekel等[22]考虑了斯托克斯漂流方向与风向偏差对LC的影响, 结合斯托克斯漂移穿透深度的影响, 提出了新的Langmuir数:
| $ L a_{\mathrm{SL}, \mathrm{proj}}=\sqrt{\frac{u^{*} \cos (\alpha)}{\left|\left\langle u_{\mathrm{s}}\right\rangle_{\mathrm{SL}}\right| \cos \left(\theta_{\mathrm{ww}}-\alpha\right)}}, $ | (9) |
这里α是风和Langmuir细胞之间的角度, θWW是斯托克斯漂移和风之间的角度。下标SL表示表层的平均值, 表层被定义为混合层的上部20%[9]。
Van Roekel等[22]提出了一个新的增强因子的公式:
| $ \varepsilon=|\cos \alpha| \sqrt{+\left(c_{1} L a_{\mathrm{SL}, \mathrm{proj}}\right)^{-2}+\left(c_{2} L a_{\mathrm{SL}, \mathrm{proj}}\right)^{-4}}, $ | (10) |
其中常数c1=1.5, c2=5.4。
2.1.4 Yang(2015)参数化方案Yang等[23]使用LES数据评估KPP改进模型涡流黏度的垂直剖面。比较了前文中AB两个Langmuir增强型KPP模型与LES的K剖面结果, 对Lat=0.36具有的强Langmuir循环情况, KPP中的Langmuir增强因子ε有助于将涡黏性系数K的峰值增加到更接近从LES获得的峰值, 但是模拟K峰值仍然小于LES的结果。此外, KPP模型的K剖面峰值深度低于LES的K剖面峰值深度。这些观察结果与McWilliams和Sullivan[10]的结论一致, 在此基础上, Yang等[23]提出当αe=4的情况下, KPP模式的结果在不同的Lat情况下与LES结果取得更好的一致性。而且引入了一个新的因子D(Lat)来修正当Lat=∞情况下的KPP-Langmuir增强型模式, 在新的Langmuir增强型KPP模型中, Langmuir循环增强的涡流黏度湍流速度参数化为:
| $ W\left(\sigma, L a_{t}\right)=D\left(L a_{t}\right) \varepsilon\left(L a_{t}\right) \frac{\kappa u_{*}}{\varphi_{\mathrm{m}}(\sigma)}, $ | (11) |
| $ \varepsilon\left(L a_{t}\right)=\left(1+\frac{C_{\mathrm{w}}}{L a_{t}^{8}}\right)^{1 / 4}, $ | (12) |
| $ D\left(L a_{t}\right)=D_{\mathrm{S}}+\frac{D_{\mathrm{LC}}-D_{\mathrm{S}}}{2}\left[1-\tanh \left(\zeta\left(L a_{t}-L a_{\mathrm{c}}\right)\right)\right], $ | (13) |
其中DS=0.62, DLC=1.45, Lac=0.5, ξ=10。使用新的KPP模式与LES结果进行比较显示与先前KPP模型相比, 在新的KPP模型中, 使用增强因子ε改善了小Lat情况下涡黏度K与LES结果的一致性; 将附加的因子D引入KPP模型改善了大的Lat情况下的一致性。
MY2.5模式全称Mellor-Yamada2.5阶模型, 是多数海洋模型中常用的混合参数化方案, 例如普林斯顿海洋模型(POM)、普通海洋湍流模型(GOTM)等。
Kantha和Clayson[27]将产生Langmuir环流的涡力项
| $ \frac{\partial U}{\partial t}-f\left(V+V_{\mathrm{S}}\right)=\frac{\partial}{\partial Z}\left[K_{\mathrm{m}} \frac{\partial U}{\partial Z}\right] $ | (14) |
| $ \frac{\partial V}{\partial t}-f\left(U+U_{\mathrm{S}}\right)=\frac{\partial}{\partial Z}\left[K_{\mathrm{m}} \frac{\partial V}{\partial Z}\right], $ | (15) |
同时将湍动能方程和混合长方程改为:
| $\begin{array}{l} \frac{D}{{{D_t}}}({q^2}) - \frac{\partial }{{\partial z}}\left[ {ql{S_q}\frac{\partial }{{\partial z}}({q^2})} \right] = - 2\overline {uw} \left( {\frac{{\partial U}}{{\partial z}} + \frac{{\partial {u_{\rm{s}}}}}{{\partial z}}} \right) - \\ 2\overline {vw} \left( {\frac{{\partial V}}{{\partial z}} + \frac{{\partial {v_{\rm{s}}}}}{{\partial z}}} \right) + 2\beta g\overline {w\theta } - 2\frac{{{q^3}}}{{{B_1}l}} \end{array}, $ | (16) |
| $\begin{array}{l} \frac{D}{{{D_t}}}({q^2}l) - \frac{\partial }{{\partial z}}\left[ {ql{S_1}\frac{\partial }{{\partial z}}({q^2}l)} \right] = {E_1}l\left( { - \overline {uw} \frac{{\partial U}}{{\partial z}} - \overline {vw} \frac{{\partial V}}{{\partial z}}} \right) + \\ {E_6}l\left( { - \overline {uw} \frac{{\partial {u_{\rm{s}}}}}{{\partial z}} - \overline {vw} \frac{{\partial {v_{\rm{s}}}}}{{\partial z}}} \right) + {E_3}(\beta g\overline {w\theta } ) - \\ {E_2}\frac{{{q^3}}}{{{B_1}}}\left[ {1 + {E_4}{{\left( {\frac{l}{{\kappa {l_{\rm{w}}}}}} \right)}^2}} \right] + {E_5}(2\Omega ){q^2}l \end{array}, $ | (17) |
其中us和vs斯托克斯漂移速度Vs的分量, 表层的stokes漂流的值由Vs0=11.8u*给出, 将修改后的模型结果与McWilliams[6]中LES的结果进行对比, 结果显示加入Langmuir项后在整个混合层中TKE和耗散率升高, 混合增强从而加深了混合层, 海表面温度下降。
2.3 Noh (2016)参数化方案OMLM是通过对Noh模型的修改而开发的, 该模型已被证明可以很好地再现真实的上层海洋结构[28-29]。该模型是使用涡流扩散系数和黏度的湍流闭合模型, 类似于Mellor-Yamada模型, 但是再现了一个均匀的混合层, 已应用于各种海洋模型中进行研究, 并且模型中使用的参数化已经通过LES结果证实。对于模型的详细描述, 可以参考Noh和Kim[28]。在该模型中, 涡流黏度计算方法为:
| $ K_{\mathrm{m}}=S_{\mathrm{m}} q l, $ | (18) |
| $ K_{\mathrm{h}}=S_{\mathrm{h}} q l, $ | (19) |
其中Sm和Sh为经验常数, 和MY2.5模型一样, 在没有分层的情况下, 模式中的混合长为
| $ \frac{1}{l_{0}}=\frac{1}{\kappa\left(z+z_{0}\right)}+\frac{1}{h}. $ | (20) |
Noh等[30]最近通过对LES结果的分析发现, 只有当MLD较浅且分层较弱时, LC才能增强垂直混合, 使得Km和Kh增加。根据公式,
| $\frac{1}{{{l_0}}} = \frac{1}{{\kappa \Gamma (z + {z_0})}} + \frac{1}{h}.$ | (21) |
Γ在不存在LC (Lat=∞)的情况下等于1, 并且随着Lat的减少而增加; 例如, 在Lat =0.32处, Γ可以增大到10。Noh将新的OMLM应用于OGCM模式, 通过简单修改混合长方程再现了与LES结果良好一致的增强垂直混合效果, 纠正了高纬度海洋中夏季混合层过浅的现象, 而不会影响热带海洋中的温跃层。
3 改进的参数化应用及问题讨论Fan和Griffies[31]将McWilliams和Sullivan以及Smyth等人提出的两种改进的KPP模型应用于全球气候模拟。结果表明, 在MOM全球海洋环流模型中使用这种增强的湍流速度尺度参数化方案对某些地区的温度和混合层深度的演变具有显著影响, Smyth2002参数化方案能有效改善MLD和海面温度(SST)。然而, 当在NCAR地球系统模型CESM1.2中实施时, 两种方案都产生了过度混合的现象。Li等[32]将前两种参数化方案以及新的Langmuir数应用到CESM1.2气候模型中, 发现在模拟结果中前两种方案都会出现过度混合的现象, 但新的Langmuir数使得南大洋MLD的浅层偏差在夏季减少了27%, 在冬季减少了9%, 通过Langmuir混合参数化方案改进了气候模式。D’Alessio等[33]在类似MY2.5的2阶湍封闭模型中加入Langmuir环流因素, 通过修改对流速度尺度以及将CL涡度力加入到TKE方程和动量方程, 模拟结果表明混合层加深。Li等[34]修改MY2.5模型, 参数化斯托克斯力探究其对上层海洋混合的影响, 结果表明斯托克斯漂流提高了上层海洋混合的耗散率和湍流能量。Uchiyama等[35]在区域海洋模型ROMS中加入斯托克斯涡度力, 在海洋环流数值模拟中加入波流相互作用。张学峰等[36]基于三维MITgcm海洋模式, 使用包含Langmuir混合作用的KPP方案, 改进了黄海夏季上混合层的模拟效果。Li等[37]利用区域海洋浪流耦合模式(ROMS-SWAN), 在考虑Langmuir环流和波浪破碎机制下, 模拟了2008年9月南海混合层深度, 研究揭示Langmuir环流使南海混合层深度加深。Allard等[38]介绍了由近岸波浪模型(SWAN)和海军海岸海洋模型(NCOM)组成的耦合海洋-大气中尺度预报系统(COAMPS), 对海洋模型进行了修正, 考虑了斯托克斯漂流的影响, 结果表明Langmuir环流增强了垂向混合。Wang等[39]利用普林斯顿海洋模型(POM)对全球海洋环流进行了模拟, 结果表明斯托克斯漂流的大小与欧拉平均流相当, 将斯托克斯漂流因素加入海洋模型既影响欧拉流又影响拉格朗日漂流, 使垂直混合系数增大。
上述研究在大尺度海洋环流模型中考虑了Langmuir环流效应, 在一定程度上改善了对于海洋上混合层非破碎波致应力的影响模拟结果, 但是依然存在有许多不足, 在现有的KPP垂直混合参数化方案中, 对于湍流特征速度增强因子的选取和应用条件需要考虑风诱导剪切和斯托克斯强迫的相对重要性, 以及表层斯托克斯漂流与风向偏差产生的影响, 而添加斯托克斯剪切效应项的方法对于斯托克斯漂流计算方法准确度的依赖度较高, 在复杂的波浪场条件下, 斯托克斯漂流剖面的估算的误差将对结果造成很大影响[40]。
4 小结与展望Langmuir环流将海洋上混合层的热量, 物质和动量带入海洋深层, 增强了海洋混合并影响着海气界面的物质能量交换, 对混合层内湍动能和垂向混合产生重要影响。尽管通过LES方法中可以直接模拟Langmuir效应, 由于LES模型的性质使得难以将它们结合到复杂的海洋环流和海浪耦合模型中, 因此必须在雷诺平均模型中对Langmuir环流进行参数化, 方法大致可以分为三类, 一种是在KPP垂向混合参数化方案中引入湍流特征速度增强因子, 一种是在Mellor-Yamada2.5湍流闭合模型中增加斯托克斯漂流剪切效应项, 对Stokes漂流计算采用单频简谐波假设, 还有一种是修改混合长方程来添加LC效应, 但是由于这些方案都对于Stokes漂流的垂向结构及其方向与风向的偏差造成的影响估计不足, 导致现有的LC海洋混合参数化方案会在模拟上混合层混合过程中产生明显的误差, 尤其是在风况复杂的条件下, 因此, 需要进一步改进stokes漂流的计算方案, 更加优化Langmuir环流参数化方案, 使得其在复杂海况下的适用性更强。
| [1] |
Sullivan P P, Mcwilliams J C. Dynamics of winds and currents coupled to surface waves[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 19-42. |
| [2] |
Craik A D D. The generation of Langmuir circulations by an instability mechanism[J]. Journal of Fluid Mechanics Digital Archive, 1977, 81(2): 15. |
| [3] |
Craik A D D, Leibovich S. A rational model for Langmuir circulations[J]. Journal of Fluid Mechanics Digital Archive, 1976, 73(3): 26. |
| [4] |
Leibovich S. On the evolution of the system of wind drift currents and Langmuir circulations in the ocean. Part 1. Theory and averaged current[J]. Journal of Fluid Mechanics Digital Archive, 1977, 79(4): 29. |
| [5] |
Leibovich S. Convective instability of stably stratified water in the ocean[J]. Journal of Fluid Mechanics Digital Archive, 1977, 82(3): 21. |
| [6] |
Mcwilliams C, Sullivan P, Moeng C. Langmuir turbulence in the ocean[J]. Journal of Fluid Mechanics, 2000, 334(334): 1-30. |
| [7] |
Skyllingstad E D, Denbo D W. An ocean large-eddy simulation of Langmuir circulations and convection in the surface mixed layer[J]. Journal of Geophysical Research Oceans, 1995, 100(C5): 8501-8522. DOI:10.1029/94JC03202 |
| [8] |
Thorpe S A. Langmuir circulation[J]. Annual Review of Fluid Mechanics, 2004, 36(36): 55-79. |
| [9] |
Harcourt R R, D'Asaro, Eric A. Large-Eddy simulation of Langmuir turbulence in pure wind seas[J]. Journal of Physical Oceanography, 2008, 38(7): 1542-1562. DOI:10.1175/2007JPO3842.1 |
| [10] |
Mcwilliams J C, Sullivan P P. Vertical mixing by Langmuir circulations[J]. Spill Science & Technology Bulletin, 2000, 6(3): 225-237. |
| [11] |
Li M, Garrett C, Skyllingstad E. A regime diagram for classifying turbulent large eddies in the upper ocean[J]. Deep-Sea Research, Part Ⅰ (Oceanographic Research Papers), 2005, 52(2): 0-278. |
| [12] |
Noh Y, Min H S, Raasch S. Large eddy simulation of the ocean mixed layer:The effects of wave breaking and Langmuir circulation[J]. Journal of Physical Oceanography, 2004, 34: 720-735. DOI:10.1175/1520-0485(2004)034<0720:LESOTO>2.0.CO;2 |
| [13] |
Noh Y, Kang I S, Herold M, et al. Large eddy simulation of particle settling in the ocean mixed layer[J]. Physics of Fluids, 2006, 18(8): 085109. DOI:10.1063/1.2337098 |
| [14] |
Grant A L M, Belcher S E. Characteristics of Langmuir Turbulence in the ocean mixed layer[J]. Journal of Physical Oceanography, 2009, 39(8): 1871-1887. |
| [15] |
Kukulka T, Plueddemann A J, Trowbridge J H, et al. Significance of Langmuir circulation in upper ocean mixing:comparison of observations and simulations[J]. Geophysical Research Letters, 2009, 36(10): 92-103. |
| [16] |
李爽. Langmuir环流和波浪破碎对上层海洋混合影响的数值研究[D].青岛: 中国科学院海洋研究所, 2010. Li Shuang. Numerical study of the effects of Langmuir circulation and wave breaking on upper ocean mixing[D]. Qingdao: Institute of Oceanology, Chinese Academy of Sciences, 2010. http://cdmd.cnki.com.cn/Article/CDMD-80068-2010147143.htm |
| [17] |
Skyllingstad E D. Scales of Langmuir circulation generated using a large-eddy simulation model[J]. Spill Science & Technology Bulletin, 2000, 6(3): 239-246. |
| [18] |
Burchard H, Craig P D, Gemmrich J R, et al. Observational and numerical modeling methods for quantifying coastal ocean turbulence and mixing[J]. Progress in Oceanography, 2008, 76(4): 399-442. |
| [19] |
Mellor G L, Yamada T. Development of a turbulence closure model for geophysical fluid problems[J]. Reviews of Geophysics and Space Physics, 1982, 20(4): 851-0. DOI:10.1029/RG020i004p00851 |
| [20] |
Large W G, Mcwilliams J C, Doney S C. Oceanic vertical mixing-a review and a model with a nonlocal boundary-layer parameterization[J]. Reviews of Geophysics, 1994, 32(4): 363-403. |
| [21] |
Smyth W D, Skyllingstad E D, Crawford G B, et al. Nonlocal fluxes and Stokes drift effects in the K-profile parameterization[J]. Ocean Dynamics, 2002, 52(3): 104-115. DOI:10.1007/s10236-002-0012-9 |
| [22] |
Van Roekel L P, Fox-Kemper B, Sullivan P P, et al. The form and orientation of Langmuir cells for misaligned winds and waves[J]. Journal of Geophysical Research, 2012, 117(C5). |
| [23] |
Yang D, Chen B, Chamecki M, et al. Oil plumes and dispersion in Langmuir, upper-ocean turbulence:Largeeddy simulations and K-profile parameterization[J]. Journal of Geophysical Research:Oceans, 2015, 120(7): 4729-4759. DOI:10.1002/2014JC010542 |
| [24] |
Smith J A. Evolution of Langmuir circulation during a storm[J]. Journal of Geophysical Research (Oceans), 1998, 103(C6). |
| [25] |
Smith J. A. Observations of wind, waves, and the mixed layer: The Scaling of Surface Motion[M]. Banner M L. Wind-Driven Air-Sea Interface: Electromagnetic and Acoustic Sensing, Wave Dynamics, and Turbulent Fluxes. Sydney: University of New South Wales, 1999: 231-238.
|
| [26] |
Skyllingstad E D, Smyth W D, Moum J N, et al. Upper-Ocean Turbulence during a Westerly Wind Burst:A Comparison of Large-Eddy Simulation Results and Microstructure Measurements[J]. Journal of Physical Oceanography, 1999, 29(1): 5-28. |
| [27] |
Kantha L H, Clayson C A. An improved mixed layer model for geophysical applications[J]. Journal of Geophysical Research Oceans, 1994, 99(C12): 25235-25266. DOI:10.1029/94JC02257 |
| [28] |
Noh Y, Kim H J. Simulations of temperature and turbulence structure of the oceanic boundary layer with the improved near-surface process[J]. Journal of Geophysical Research (Oceans), 1999, 104(C7). |
| [29] |
Noh Y, Jang C J, Yamagata T. Simulation of more realistic upper-ocean processes from an OGCM with a new ocean mixed layer model[J]. Journal of Physical Oceanography, 2002, 32(5): 1284-1307. DOI:10.1175/1520-0485(2002)032<1284:SOMRUO>2.0.CO;2 |
| [30] |
Noh Y, Goh G, Raasch S. Influence of Langmuir Circulation on the Deepening of the Wind-Mixed Layer[J]. Journal of Physical Oceanography, 2011, 41(3): 472-484. DOI:10.1175/2010JPO4494.1 |
| [31] |
Fan Y, Griffies S M. Impacts of parameterized Langmuir turbulence and nonbreaking wave mixing in global climate simulations[J]. Journal of Climate, 2014, 27(12): 4752-4775. DOI:10.1175/JCLI-D-13-00583.1 |
| [32] |
Li Q, Webb A, Foxkemper B, et al. Langmuir mixing effects on global climate:WAVEWATCH Ⅲ in CESM[J]. Ocean Modelling, 2016, 103: 145-160. DOI:10.1016/j.ocemod.2015.07.020 |
| [33] |
D'Alessio S J D, Abdella K, Mcfarlane N A. A new second-order turbulence closure scheme for modeling the oceanic mixed layer[J]. Journal of Physical Oceanography, 1998, 28(8): 1624-1641. DOI:10.1175/1520-0485(1998)028<1624:ANSOTC>2.0.CO;2 |
| [34] |
Li S, Song J, Sun Q. Effect of Stokes drift on upper ocean mixing[J]. Acta Oceanologica Sinica, 2008, 27(2): 11-20. |
| [35] |
Uchiyama Y, Mcwilliams J C, Shchepetkin A F. Wave-current interaction in an oceanic circulation model with a vortex-force formalism:Application to the surf zone[J]. Ocean Modelling, 2010, 34(1): 16-35. |
| [36] |
张学峰.波浪破碎和Langmuir环流对黄海夏季上层混合影响的数值研究[D].北京: 中国科学院大学, 2011. Zhang Xuefeng. Numerical investigation of the effexts of surface wave breaking and Langmuir circulation on the upper mixing during summer in the Yellow Sea[D]. Beijing: Graduate School of Chinese Academy of Sciences, 2011. http://ir.scsio.ac.cn/handle/344004/14091?mode=full&submit_simple=Show+full+item+record |
| [37] |
Li S, Song J, Fan W. Effect of Langmuir circulation on upper ocean mixing in the South China Sea[J]. Acta Oceanologica Sinica, 2013, 32(3): 28-33. DOI:10.1007/s13131-013-0285-5 |
| [38] |
Allard R, Rogers E, Martin P, et al. The US Navy coupled ocean-wave prediction system[J]. Oceanography, 2014, 27(3): 92-103. DOI:10.5670/oceanog.2014.71 |
| [39] |
Wang Z, Wu K, Dong S, et al. Effect of wave-induced Stokes drift on the dynamics of ocean mixed layer[J]. Chinese Journal of Oceanology and Limnology, 2015, 33(1): 233-242. DOI:10.1007/s00343-015-4036-7 |
| [40] |
Webb A, Fox-Kemper B. Impacts of wave spreading and multidirectional waves on estimating Stokes drift[J]. Ocean Modelling, 2015, 96: 49-64. DOI:10.1016/j.ocemod.2014.12.007 |
 2019, Vol. 43
2019, Vol. 43