文章信息
- 郑好, 李晓春, 王道胜, 蒋浩宇, 赵恩金. 2019.
- ZHENG Hao, LI Xiao-chun, WANG Dao-sheng, JIANG Hao-yu, ZHAO En-jin. 2019.
- 基于T/P和Jason-1/2卫星高度计海面高度数据获取南海同潮图的研究
- Extraction of cotidal charts in the South China Sea from sat-ellite altimeter sea surface height data
- 海洋科学, 43(7): 61-71
- Marine Sciences, 43(7): 61-71.
- http://dx.doi.org/10.11759/hykx20190102002
-
文章历史
- 收稿日期:2019-01-02
- 修回日期:2019-03-31
2. 中国地质大学深圳研究院, 广东 深圳 518057
2. Shenzhen Research Institute, China University of Geosciences, Shenzhen 518057, China
南海是一个半封闭海, 其与外界水体交换的主要通道是吕宋海峡[1], 南海北部具有宽广的大陆架和大陆坡, 陆架区潮汐现象显著[2]。因此, 针对南海潮汐的研究一直在国内外颇受重视。TOPEX/ POSEIDON(T/P)卫星是由美国国家航空航天局和法国空间局联合于1992年8月10日发射的世界上第一颗专门为研究世界大洋环流而设计的高度计卫星。T/P卫星在2002年9月变轨, 原轨道的任务由2001年12月发射的Jason-1卫星执行。Jason-1卫星于2009年2月变轨到T/P卫星变轨后的轨道上继续运行。原有轨道测量任务随后交给2008年6月发射的Jason-2卫星。T/P、Jason-1和Jason-2三颗卫星高度计系统的定轨精度和测高精度较以前有显著提高, 其测量精度约为5 cm, 为潮汐的研究提供了重要的数据源。鉴于T/P和Jason卫星高度计观测海面高度精度高的特性, 国内外很多学者将其应用到潮汐研究中。Yanagi等[3]基于3年的卫星高度计资料及沿岸验潮站的调和分析结果, 以指数函数为插值系数插值得到了中国东海和黄海八个主要分潮的调和常数。Fang等[4]利用卫星高度计资料及验潮站数据进行二次多项式拟合, 得到了渤、黄、东海网格点的调和常数, 进而得到了渤、黄、东海五个主要分潮的调和常数。范丽丽[5]基于物理量在空间上的连续性, 提出一种通过轨道上的调和常数拟合轨道间任意点调和常数的方法, 并将该方法应用于夏威夷海域。
本文数据采用1992~2016年T/P和Jason卫星高度计海面高度资料, 对南海海域(2°~25°N, 99°~ 122°E, 图 1)的潮汐信号进行了提取。然后, 采用以格林函数为基础的双调和样条插值法对所提取的M2、S2、K1和O1四个主要分潮调和常数进行了空间二维插值, 得到了南海四个主要分潮的同潮图, 并利用全球潮汐模型TPXO7.2、验潮站数据和前人研究中无潮点位置对插值结果进行了评估。
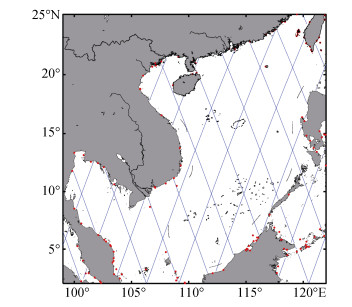 |
| 图 1 4309个星下观测点(蓝点)以及141个验潮站(红点)分布 Fig. 1 Distribution of 4309 T/P satellite tracking points (blue points) and 141 tidal stations (red points) |
变轨前的T/P卫星轨道高度达1 336 km, 倾角为66°, 覆盖面大, 轨道的交点周期(绕地球一圈的时间)为6 745.8 s, 轨道运行127圈以后精确重复, 重复周期为9.915 6 d。本文高度计数据来自南海海域(2°~ 25°N, 99°~122°E)变轨前T/P卫星轨道上1992~2016年多卫星数据, 包含: 1992~2002年未变轨的T/P卫星高度计数据、2002~2008年未变轨的Jason-1卫星高度计数据和2008~2016年Jason-2卫星高度计数据(下载地址: ftp://avisoftp.cnes.fr/AVISO/pub/), 共有4 300多个星下观测点, 每个星下观测点都对应一个海面高度的时间序列。
1.2 验潮站数据本文中的141个验潮站(验潮站分布情况见图 1)数据来自于中国近海及周边海域验潮站的资料和国际上公开的验潮站资料, 包括M2、S2、K1和O1四个主要分潮的潮汐调和常数。
1.3 调和分析方法实际水位可以看作是很多个分潮所致水位迭加的结果, 但是在实际分析中只能选取有限个主要分潮。假设我们选取J个分潮, 任意一点的潮位h的表达式为:
| $ h = {S_{\rm{0}}} + \sum\limits_{j = 1}^J {{f_j}{H_j}\cos ({\sigma _j}t + {V_{{\rm{0}}j}} + {u_j} - {g_j})}, $ | (1) |
其中, S0为余水位, fj为第j个分潮的交点因子, uj为第j个分潮的交点订正角, Hj、gj分别为第j个分潮的振幅和迟角, 统称为调和常数, σj为第j个分潮的分潮角速度, V0j为第j个分潮的初相位, t为时间。
某一分潮所引起的水位变化为:
| $ {f_j}{H_j}\cos ({\sigma _j}t + {V_{{\rm{0}}j}} + {u_j} - {g_j}). $ | (2) |
式(2)可化为式(3):
| $ \begin{array}{l} {f_j}\cos ({\sigma _j}t + {V_{{\rm{0}}j}} + {u_j}){H_j}\cos {g_j} + \\ {f_j}\sin ({\sigma _j}t + {V_{{\rm{0}}j}} + {u_j}){H_j}\sin {g_j} \end{array}, $ | (3) |
其中, 时间t和分潮角速度σj均为已知, 交点因子交点fj、交点订正角uj和分潮初相位V0j可根据Doodson数和时间t计算得出[6]。对应J个分潮, 则有:
| $ \begin{array}{l} h = {S_{\rm{0}}} + \sum\limits_{j = 1}^J {{f_j}\cos ({\sigma _j}t + {V_{{\rm{0}}j}} + {u_j})} {H_j}\cos {g_j} + \\ \sum\limits_{j = 1}^J {{f_j}\sin ({\sigma _j}t + {V_{{\rm{0}}j}} + {u_j})} {H_j}\sin {g_j} \end{array}. $ | (4) |
如果在n个时刻
| $ \left\{ {\begin{array}{*{20}{c}} {{S_{\rm{0}}} + \sum\limits_{j = 1}^J {{x_j}{f_j}\cos ({\sigma _j}{t_1} + {V_{\rm{0}}} + {u_j}) + \sum\limits_{j = 1}^J {{y_j}{f_j}\sin ({\sigma _j}{t_1} + {V_{\rm{0}}} + {u_j}) = {h_{\rm{1}}}} } }\\ {{S_{\rm{0}}} + \sum\limits_{j = 1}^J {{x_j}{f_j}\cos ({\sigma _j}{t_2} + {V_{\rm{0}}} + {u_j}) + \sum\limits_{j = 1}^J {{y_j}{f_j}\sin ({\sigma _j}{t_2} + {V_{\rm{0}}} + {u_j}) = {h_{\rm{2}}}} } }\\ \vdots \\ {{S_{\rm{0}}} + \sum\limits_{j = 1}^J {{x_j}{f_j}\cos ({\sigma _j}{t_n} + {V_{\rm{0}}} + {u_j}) + \sum\limits_{j = 1}^J {{y_j}{f_j}\sin ({\sigma _j}{t_n} + {V_{\rm{0}}} + {u_j}) = {h_n}} } } \end{array}} \right.. $ | (5) |
方程(5)中xj对应
双调和样条插值法是以格林函数为基础的内插法, 通过插值计算, 找到通过空间数据点的曲率最小的曲线或曲面。在二维空间中, 满足平面上N个点的双调和方程为:
| $ \begin{array}{*{20}{c}} {{\nabla ^4}\zeta (x) = \sum\limits_{j = 1}^N {{\alpha _j}\delta (x - {x_j})} }\\ {\zeta ({x_j}) = {\zeta _j}, } \end{array} $ | (6) |
其中,
| $ \delta (x - {x_j}) = \left\{ \begin{array}{l} 0, x \ne {x_j}\\ \infty , x = {x_j} \end{array} \right.且\int_{\; - \infty }^{\; + \infty } {\delta (x){\rm{d}}x} = 1.$ | (7) |
双调和方程的通解为
| $ \zeta (x) = \sum\limits_{j = 1}^N {{\alpha _j}\Phi (x - {x_j})} . $ | (8) |
加权系数αj可以通过求解线性方程
双调和样条插值综合利用数据值和斜率确定插值曲面, 比样条插值更为灵活, 此外, 即使是带噪声的数据, 也能在最小二乘意义下实现有效插值, 特别适合对不规则的卫星高度计数据进行插值[7-8]。
1.5 评估方法本文采用振幅差ΔH和迟角差Δg分别评估振幅和迟角的误差, 采用矢量差Δ综合评估振幅和迟角的误差[4]。矢量差Δ表达式如下:
| $ \Delta {\rm{ = [(}}{H_{\rm{a}}}\cos {g_{\rm{a}}} - {H_{\rm{b}}}{\rm{cos}}{g_{\rm{b}}}{{\rm{)}}^2}{\rm{ + (}}{H_{\rm{a}}}{\rm{sin}}{g_{\rm{a}}} - {H_{\rm{b}}}{\rm{sin}}{g_{\rm{b}}}{{\rm{)}}^2}{{\rm{]}}^{1/2}}, $ | (9) |
其中, Ha和ga为卫星高度计数据或者插值所得的振幅和迟角, Hb和gb为验潮站资料提取的振幅和迟角或者全球潮汐TPXO7.2模式的振幅和迟角。矢量差Δ、振幅差ΔH和迟角差Δg的平均值分别用
参照Fang等[4]和暴景阳[9]中所述方法, 计算了M2、S2、K1和O1四个主要分潮的混淆周期, 结果见表 1。然后根据Rayleigh准则, 计算得到了分离四个主要分潮所需的最短资料长度为2.97 a(表 2)。剔除观测时间小于2.97 a的星下点数据, 得到了可以分离出四个主要分潮调和常数的4309个星下点(图 1)。
| 分潮 | 周期/h | 潮汐混淆周期/d |
| M2 | 12.42 | 62.11 |
| S2 | 12.42 | 58.74 |
| K1 | 23.93 | 173.19 |
| O1 | 25.82 | 45.71 |
| K1 | S2 | M2 | |
| O1 | 0.17 | 0.56 | 0.47 |
| K1 | 0.24 | 0.27 | |
| S2 | 2.97 |
利用调和分析方法得到了4 309个星下观测点处M2、S2、K1和O1四个主要分潮的调和常数(注:下文的迟角都为东8区迟角)。以15 km的空间窗口对4 309个星下观测点与南海141个验潮站的位置在空间上进行了匹配, 其中有40个验潮站符合要求。
对比星下观测点处调和分析的结果和验潮站处观测结果(表 3)可知, 利用卫星高度计数据所得星下点处的四个主要分潮调和常数结果与验潮站处观测结果误差较小, 半日分潮的振幅绝均差整体大于全日分潮的振幅绝均差。其中, M2分潮的振幅绝均差和矢量均差均最大, 分别为3.16 cm和4.99 cm; K1分潮与验潮站处观测结果的振幅绝均差最小, 为1.75 cm; S2分潮与验潮站处观测结果的矢量均差最小, 为3.43 cm。
| 验潮站位置/ (°E/°N) | 星下点位置/ (°E/°N) | 距离/km | ΔH/cm | Δ/cm | |||||||
| M2 | S2 | K1 | O1 | M2 | S2 | K1 | O1 | ||||
| 114.03/22.10 | 114.03/22.08 | 2.70 | 2.40 | 0.04 | 0.66 | 0.14 | 2.52 | 3.77 | 4.16 | 3.20 | |
| 114.03/22.10 | 114.05/22.13 | 3.29 | 1.28 | 2.03 | 0.18 | 0.89 | 2.66 | 4.38 | 1.01 | 4.43 | |
| 101.00/2.88 | 100.97/2.90 | 4.17 | 7.72 | 0.56 | 0.65 | 0.34 | 11.78 | 1.67 | 0.68 | 0.88 | |
| 110.68/20.17 | 110.73/20.21 | 6.77 | 1.75 | 6.82 | 6.79 | 1.08 | 5.40 | 8.70 | 12.32 | 11.96 | |
| 101.00/2.88 | 100.95/2.85 | 7.04 | 8.47 | 1.20 | 0.92 | 0.18 | 10.21 | 2.31 | 2.24 | 0.47 | |
| 101.00/2.88 | 100.98/2.95 | 7.41 | 7.50 | 1.02 | 1.41 | 0.35 | 12.17 | 2.65 | 2.34 | 0.52 | |
| 108.95/10.50 | 108.91/10.45 | 7.61 | 0.09 | 2.20 | 1.15 | 12.41 | 1.77 | 2.59 | 7.70 | 12.41 | |
| 114.03/22.10 | 114.01/22.03 | 8.56 | 2.74 | 0.86 | 0.94 | 1.74 | 3.27 | 1.08 | 2.67 | 2.44 | |
| 108.70/11.17 | 108.67/11.09 | 9.02 | 1.39 | 0.73 | 0.77 | 0.24 | 2.86 | 1.85 | 7.91 | 0.41 | |
| 108.95/10.50 | 108.87/10.54 | 9.93 | 3.96 | 3.17 | 0.39 | 10.40 | 4.91 | 3.22 | 9.91 | 10.41 | |
| 108.85/3.05 | 108.76/3.07 | 10.36 | 6.69 | 0.12 | 2.02 | 1.24 | 8.10 | 3.83 | 2.26 | 2.96 | |
| 113.98/4.58 | 113.89/4.57 | 10.38 | 0.07 | 1.91 | 0.41 | 0.69 | 2.47 | 4.61 | 0.77 | 2.57 | |
| 110.68/20.17 | 110.71/20.26 | 10.43 | 1.02 | 8.34 | 6.80 | 0.80 | 5.58 | 10.43 | 10.85 | 10.39 | |
| 113.98/4.58 | 113.91/4.52 | 10.90 | 1.88 | 1.84 | 0.27 | 2.78 | 2.63 | 2.76 | 1.01 | 3.54 | |
| 110.60/20.95 | 110.71/20.94 | 11.02 | 8.96 | 2.59 | 0.98 | 6.12 | 11.44 | 5.96 | 6.96 | 6.95 | |
| 121.28/18.87 | 121.19/18.92 | 11.07 | 3.11 | 0.16 | 4.35 | 2.33 | 4.10 | 0.17 | 4.81 | 2.53 | |
| 111.62/16.55 | 111.71/16.50 | 11.15 | 0.87 | 2.75 | 1.06 | 0.50 | 2.69 | 4.74 | 3.61 | 1.78 | |
| 121.10/18.62 | 121.11/18.72 | 11.50 | 2.71 | 3.79 | 0.96 | 2.55 | 4.89 | 4.04 | 2.15 | 2.90 | |
| 99.82/11.80 | 99.91/11.75 | 11.62 | 0.31 | 0.26 | 2.08 | 0.76 | 0.91 | 2.00 | 2.37 | 1.44 | |
| 111.62/16.55 | 111.73/16.55 | 11.67 | 2.26 | 3.25 | 1.05 | 1.53 | 2.35 | 3.58 | 4.24 | 2.40 | |
| 121.28/18.87 | 121.17/18.87 | 11.69 | 2.33 | 1.47 | 4.16 | 0.55 | 2.96 | 1.51 | 4.35 | 1.76 | |
| 108.95/10.50 | 108.93/10.40 | 11.92 | 0.64 | 2.14 | 0.85 | 13.07 | 2.09 | 2.68 | 7.43 | 13.07 | |
| 101.00/2.88 | 100.93/2.80 | 12.30 | 9.14 | 0.79 | 0.99 | 1.35 | 10.60 | 2.17 | 2.34 | 1.35 | |
| 103.00/11.42 | 102.89/11.38 | 12.67 | 2.19 | 0.68 | 3.53 | 4.41 | 4.58 | 1.03 | 3.54 | 8.03 | |
| 120.30/16.62 | 120.22/16.53 | 12.71 | 1.60 | 0.71 | 1.36 | 1.04 | 2.09 | 1.30 | 1.37 | 1.21 | |
| 101.00/2.88 | 101.00/3.00 | 12.73 | 7.72 | 1.53 | 0.21 | 0.48 | 13.88 | 3.38 | 3.29 | 0.57 | |
| 113.98/4.58 | 113.87/4.62 | 12.90 | 1.83 | 0.70 | 2.12 | 11.67 | 3.46 | 1.72 | 2.27 | 11.67 | |
| 114.00/22.23 | 114.05/22.13 | 13.00 | 1.48 | 1.53 | 0.42 | 0.29 | 2.76 | 5.39 | 0.56 | 3.81 | |
| 121.28/18.87 | 121.21/18.97 | 13.34 | 6.33 | 3.06 | 3.54 | 0.57 | 6.44 | 3.67 | 5.31 | 2.49 | |
| 120.15/23.00 | 120.06/22.91 | 13.76 | 1.64 | 0.80 | 0.71 | 1.10 | 1.90 | 3.19 | 7.60 | 2.34 | |
| 108.70/11.17 | 108.69/11.04 | 13.87 | 1.80 | 2.17 | 0.65 | 0.40 | 2.91 | 2.19 | 10.10 | 0.65 | |
| 103.00/11.42 | 102.87/11.43 | 13.91 | 0.47 | 0.23 | 3.28 | 5.10 | 4.28 | 0.52 | 3.32 | 8.51 | |
| 110.60/20.95 | 110.73/20.99 | 14.04 | 7.99 | 3.62 | 0.39 | 7.06 | 11.55 | 8.21 | 5.17 | 7.54 | |
| 103.00/11.42 | 102.91/11.33 | 14.06 | 2.89 | 1.30 | 4.71 | 5.33 | 3.96 | 3.27 | 4.84 | 8.41 | |
| 108.85/3.05 | 108.74/3.12 | 14.31 | 7.51 | 0.02 | 1.39 | 2.21 | 7.78 | 2.30 | 1.77 | 2.71 | |
| 114.03/22.10 | 113.99/21.98 | 14.45 | 1.27 | 2.03 | 0.03 | 0.79 | 2.59 | 2.12 | 2.63 | 2.06 | |
| 109.53/18.22 | 109.51/18.09 | 14.56 | 0.27 | 10.10 | 0.92 | 1.56 | 5.03 | 11.06 | 4.83 | 4.91 | |
| 111.62/16.55 | 111.75/16.60 | 14.76 | 0.10 | 2.23 | 1.01 | 0.91 | 0.54 | 3.13 | 3.60 | 0.95 | |
| 121.28/18.87 | 121.15/18.82 | 14.84 | 1.79 | 1.07 | 4.08 | 0.93 | 3.68 | 1.09 | 4.17 | 2.21 | |
| 108.95/10.50 | 108.85/10.59 | 14.95 | 2.34 | 2.68 | 1.92 | 12.61 | 3.76 | 2.88 | 8.37 | 12.61 | |
| 均值 | 3.16 | 2.06 | 1.75 | 2.96 | 4.99 | 3.43 | 4.42 | 4.54 | |||
通过与前人结果进行对比(表 4)可知:相对于李培良等[10], 本文调和分析所得星下观测点处K1分潮的振幅和迟角与验潮站处观测结果的误差均相对较小; M2、S2和O1分潮振幅和迟角拟合效果与前人结果相当, 其中S2分潮迟角绝均差相对较大, 但仍与暴景阳等[9]、王延强等[11]和Fang等[12]在南海的误差结果相近。
| 结果来源 | ∆H/cm | ∆g/° | |||||||
| M2 | S2 | K1 | O1 | M2 | S2 | K1 | O1 | ||
| 本文 | 3.16 | 2.06 | 1.75 | 2.96 | 6.87 | 13.64 | 8.50 | 6.72 | |
| 赵云霞等[13] | 2.00 | — | 2.60 | — | 3.70 | — | 7.10 | — | |
| 暴景阳等[9] | 1.61 | 0.51 | 0.85 | 0.75 | 3.20 | 22.20 | 3.60 | 3.90 | |
| 王延强等[11] | 4.40 | 2.40 | 3.10 | 3.30 | 7.70 | 13.20 | 7.20 | 7.80 | |
| Fang等[12] | 6.50 | 2.50 | 4.50 | 2.70 | 9.40 | 14.00 | 7.10 | 9.90 | |
| 李培良等[10] | 11.91 | — | 4.73 | — | 28.43 | — | 11.60 | — | |
| 注: —表示论文中未涉及此分潮误差的分析 | |||||||||
总的来看, 调和分析所得星下观测点处K1分潮的误差相对最小, M2、S2和O1分潮结果总体偏差与前人研究相当, 上述结果表明:利用1992~2016年的卫星高度计数据进行调和分析所得结果是可信的。
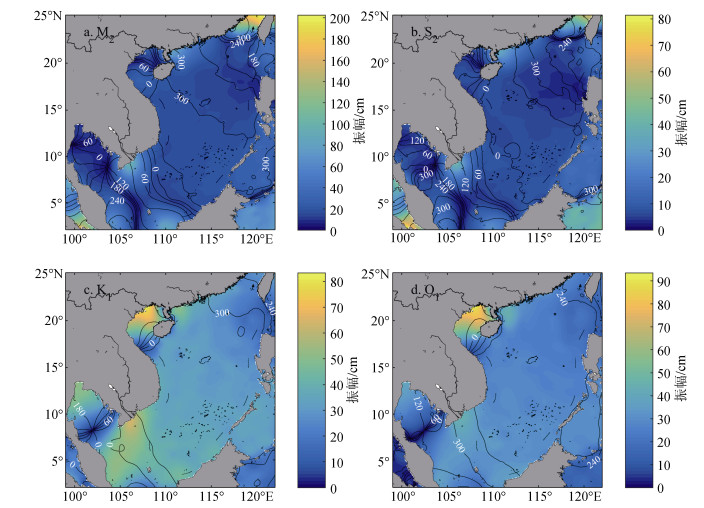
2.2 南海同潮图 2.2.1 双调和样条插值所得同潮图以美国国家海洋大气局发布的水深数据ETOPO5为参考, 制作了分辨率为5′×5′的插值参考点。将调和分析所得M2、S2、K1和O1四个主要分潮的振幅H和迟角g转化为Hsing和Hcosg, 然后采用双调和样条插值法对其进行插值, 再将插值所得网格点处的Hsing和Hcosg转化为振幅H和迟角g, 进而绘制了四个主要分潮的同潮图(图 2)。
TPXO7.2是由俄勒冈大学开发的全球海洋潮汐模型, 该模式以拉普拉斯潮汐方程组为基础, 同化了T/P、Jason卫星高度计和验潮站数据[14]。高秀敏等[14]采用南海60个验潮站的调和常数资料对TPXO7.2模式结果进行了评估, M2、S2、K1和O1四个主要分潮的拟合程度均大于83%。此外, TPXO7.2模式结果与本文141个验潮站处M2、S2、K1和O1四个主要分潮的矢量均差分别为: 12.68、6.32、9.32和7.23 cm。上述结果表明: TPXO7.2模式结果在南海有较高的准确度, 可用于评估双调和样条插值方法所得南海同潮图。
利用TPXO7.2模式结果绘制了南海四个主要分潮的同潮图(图 3), 并将其作为基准, 与插值所得同潮图进行了对比。从同潮图整体分布来看, 双调和样条插值所得四个分潮的同潮图在南海中部、南海南部和泰国湾等绝大部分研究区域与TPXO7.2模式所得同潮图的等振幅线和等迟角线的变化趋势较为接近; 在雷州半岛附近海域、台湾海峡和泰国湾湾顶等少数浅水海域与TPXO7.2模式的同潮图存在一定的误差。
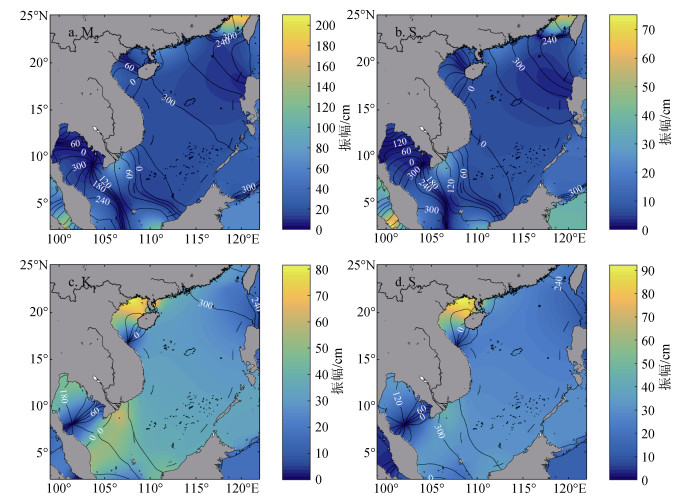 |
| 图 3 TPXO7.2模式得到的南海同潮图 Fig. 3 Cotidal charts obtained from TPXO7.2 model in the South China Sea |
为了定量计算插值结果和TPXO7.2模式结果之间的误差, 将南海48 500个网格点处双调和样条插值所得调和常数和TPXO7.2模式结果进行了比较, 四个主要分潮的矢量差在南海的分布见图 4, 整体误差统计结果见表 5。可以看出, 四个分潮的矢量差在远离陆地的开阔海域都小于4 cm, 矢量差大于10 cm的网格点大多分布在雷州半岛附近海域和台湾海峡等少数近岸浅水海域, 这可能与TPXO7.2模式在我国近海海域精度较差有关[15]。车贝雪夫多项式广泛应用于气象要素插值[16], 车贝雪夫多项式插值所得的O1分潮的同潮图与TPXO7.2模式结果误差最小, 振幅绝均差和迟角绝均差分别为: 4.49 cm和17.58°, 而双调和样条插值所得O1分潮的同潮图与TPXO7.2模式结果振幅绝均差和迟角绝均差分别为: 1.43 cm和6.06°, 双调和样条插值所得结果明显优于车贝雪夫多项式插值结果。此外, 双调和样条插值所得M2分潮的同潮图与TPXO7.2模式结果误差最大, 振幅绝均差和迟角绝均差分别为: 3.06 cm和7.37°, 但也在合理范围之内。以上结果表明:双调和样条插值结果和TPXO7.2模式结果之间整体误差较小。
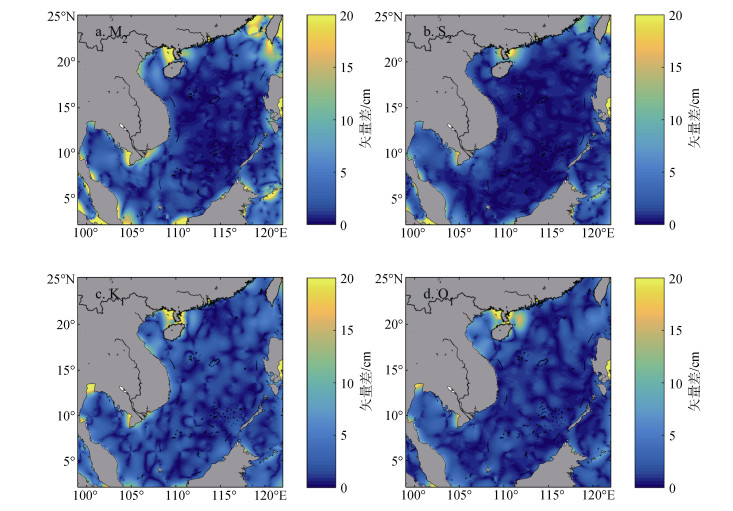 |
| 图 4 双调和样条插值结果和TPXO7.2模式结果之间矢量差分布 Fig. 4 Distribution of vector difference between the result of the interpolation method and that of TPXO7.2 model |
| 分潮类型 | ∆H/cm | ∆g/° | ∆/cm |
| M2 | 3.06 | 7.37 | 4.69 |
| S2 | 1.63 | 9.55 | 2.46 |
| K1 | 1.94 | 4.80 | 3.13 |
| O1 | 1.43 | 6.06 | 2.42 |
为了进一步验证利用双调和样条插值法所得同潮图的精度, 比较了141个验潮站处双调和样条插值所得四个主要分潮调和常数和验潮站观测结果, 四个主要分潮振幅插值结果与验潮站观测结果的对比见图 5, 振幅绝均差、迟角绝均差和矢量均差结果见表 6。可以看出, M2、S2、K1和O1四个主要分潮的矢量均差分别为22.59、10.26、10.24和8.51 cm, 平均相对误差均小于36%。车贝雪夫多项式插值所得M2、S2、K1和O1分潮的矢量均差分别为46.15、14.93、16.60和14.83 cm, 均大于双调和样条插值方法所得误差, 进一步说明双调和样条插值所得结果优于车贝雪夫多项式插值结果。以上结果说明利用双调和样条插值所得结果与利用验潮站观测资料提取的调和常数误差较小, 能够较好地刻画四个主要分潮的特征。
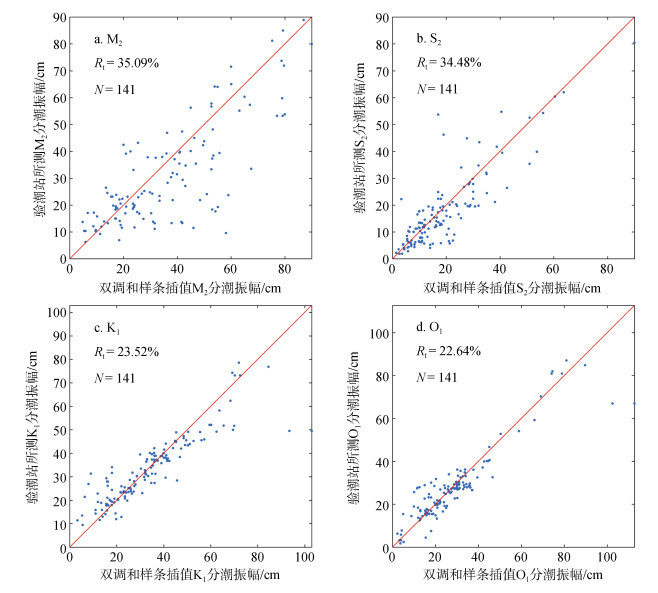 |
| 图 5 双调和样条插值振幅和验潮站处观测振幅的比较 Fig. 5 Comparison of amplitude between the result of the interpolation method and the observations of tidal stations 注: Rt:振幅插值结果相对于验潮站的平均相对误差; N:匹配对数量 Note: Rt: average relative error of the interpolation results relative to that of tidal stations; N: the number of matching pairs |
| 分潮类型 | ∆H/cm | ∆g/° | ∆/cm |
| M2 | 12.83 | 23.87 | 22.59 |
| S2 | 5.05 | 32.13 | 10.26 |
| K1 | 5.33 | 16.48 | 10.24 |
| O1 | 4.53 | 16.50 | 8.51 |
李培良等[10]利用正交潮响应法对南海T/P高度计资料进行了潮波分析, 并按照潮汐在海洋内部的变化向岸边插值, 与53个验潮站处的主要分潮数据进行了对比, 结果表明: K1分潮振幅和迟角的平均绝对误差分别是4.73 cm和11.6°, M2分潮振幅和迟角的平均绝对误差分别是11.91 cm和28.4°。高秀敏等[17]利用一个考虑内潮耗散的二维潮波模型模拟了南海M2、S2、K1和O1四个主要分潮, 并与南海63个验潮站和24个T/P卫星高度计轨道交叉点处的调和常数进行了对比, M2、S2、K1和O1四个主要分潮的振幅绝均差分别为: 13.57、3.09、12.23和3.81 cm, 迟角绝均差分别为: 17.41°、13.92°、24.97°和19.27°。可以看出, 利用双样条调和插值方法所得南海四个主要分潮的误差与前人利用正交潮响应法或者数值模拟方法得到的误差相近, 但本文所采用的双调和样条插值方法计算量更小、更易实施, 是一种有效获取南海同潮图的方法。
2.2.4 无潮点位置的对比本文得到的M2、S2、K1和O1四个主要分潮的无潮点均分布在泰国湾(具体位置见表 7), M2分潮在泰国湾有两个旋转潮波系统, 湾口的无潮点呈顺时针旋转, 潮波系统特征和无潮点位置与Fang等[18]在泰国湾的潮汐数值拟合结果相近, 湾顶的逆时针无潮点离陆地很近, 位置与曹德明等[19]的结果最接近(见表 7), S2、K1和O1分潮均在泰国湾有一个无潮点, S2分潮的潮波系统呈顺时针旋转, K1和O1分潮的潮波系统都是逆时针方向旋转, 三者的无潮点位置均与前人的研究结果基本一致。M2、S2、K1和O1四个主要分潮无潮点位置的比较结果表明:双调和样条插值所得结果不仅能够在整体上刻画南海四个主要分潮的特征, 还能较为准确地再现无潮点位置这一局部特征。
| 分潮类型 | 沈育疆等[20] | 曹德明等[19] | Fang等[18] | 高秀敏[17] | 本文 |
| M2 | 105°00′E, 7°36′N 100°30′E, 11°12′N | 103°30′E, 8°25′N 99°40′E, 11°10′N | 103°20′E, 8°35′N 100°00E′, 11°20′N | 103°30′E, 8°05′N 100°15′E, 10°00′N | 103°50′E, 8°45′N 99°50′E, 11°10′N |
| S2 | 105°00′E, 7°36′N 100°30′E, 11°12′N | —— | 104°40′E, 9°25′N | —— | 104°27′E, 8°50′N |
| K1 | 102°03′E, 8°37′N | 102°12′E, 8°18′N | 102°20′E, 8°10′N | 102°05′E, 8°10′N | 102°30′E, 8°20′N |
| O1 | 102°03′E, 8°37′N | —— | 102°10′E, 8°30′N | 102°00′E, 8°10′N | 102°35′E, 8°35′N |
| 注: —表示论文中未涉及此分潮无潮点位置的分析 | |||||
基于1992年至2016年卫星高度计海面高度资料, 运用调和分析方法得到了南海区域卫星星下观测点处M2、S2、K1和O1四个主要分潮的调和常数, 并通过和验潮站观测数据以及前人研究结果的对比验证了调和分析结果的准确性。
利用双调和样条插值方法对星下观测点处四个主要分潮的调和常数进行插值, 进而绘制了南海M2、S2、K1和O1四个主要分潮的同潮图。插值结果在在雷州半岛附近海域和台湾海峡等少数近岸浅水区域与TPXO7.2模式结果误差较大, 在其他海域均与TPXO7.2模式结果误差较小; 与141个验潮站处观测结果的矢量均差分别为22.59、10.26、10.24和8.51 cm; 所得四个主要分潮的无潮点数量和位置与前人研究结果基本一致。此外, 利用双样条调和插值方法所得南海四个主要分潮的误差与前人利用正交潮响应法或者数值模拟方法得到的误差相近。上述结果表明:双调和样条插值方法是一种有效的插值方法, 能够通过对卫星高度计所得调和常数数据进行插值获取较为准确的南海同潮图。
| [1] |
刘昆.吕宋海峡内潮生成与传播的数值模拟研究[D].青岛: 中国科学院海洋研究所, 2016. Liu Kun. Numerical study on the generation and propagation of internal tides in the Luzon Strait[D]. Qingdao: Institute of Oceanology, CAS, 2016. http://cdmd.cnki.com.cn/Article/CDMD-80068-1016206090.htm |
| [2] |
李明杰.南海北部内潮的三维模拟与研究[D].青岛: 中国科学院海洋研究所, 2012. Li Mingjie. Three-dimensional Numerical Simulation and Analysis of Internal Tides in the Northern South China Sea[D]. Qingdao: Institute of Oceanology, CAS, 2012. http://d.wanfangdata.com.cn/Thesis_Y2186957.aspx |
| [3] |
Yangi T, A Morimoto, K lchikawa. Co-tidal and Co-range Charts for the East China Sea and the Yellow Sea Derived from Satellite Altimetric Data[J]. Journal of Oceanography, 1997, 53: 303-309. |
| [4] |
Fang G, Wang Y, Wei Z, et al. Empirical cotidal charts of the Bohai, Yellow, and East China Seas from 10 years of TOPEX/Poseidon altimetry[J]. Journal of Geophysical Research, 2004, 109(C11). |
| [5] |
范丽丽.风暴潮数值同化研究和高度计资料拟合方法研究[D].青岛: 中国海洋大学, 2011. Fan Lili. Research on simulation of storm surges and application of altimeter data[D]. Qingdao: Ocean University of China, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011230104.htm |
| [6] |
陈宗镛. 潮汐学[M]. 北京: 北京科学出版社, 1980: 127-168. Chen Zongyong. Tidalogy[M]. Beijing: Beijing Science and Technology Press, 1980: 127-168. |
| [7] |
夏吉庄. 双调和样条内插方法在测井和地震资料整合中的应用[J]. 石油与天然气地质, 2010, 31(02): 244-249. Xia Jizhuang. An application of biharmonic spline interpolation to integration of logging and seismic data[J]. OIL and GASGEOLOGY, 2010, 31(02): 244-249. |
| [8] |
Sandwell D. Biharmonic spline interpolation of GEOS-3 and SEASAT altimeter data[J]. Geophysical Research Letter, 1987, 14(2): 139-142. DOI:10.1029/GL014i002p00139 |
| [9] |
暴景阳, 晁定波, 李建成. 南中国海TOPEX/POSEIDON轨迹交叉点测高数据的潮汐调和分析[J]. 测绘学报, 2000, 1: 19-25. Bao Jingyang, Chao Dingbo, Li Jiancheng. Tidal Harmonic Analysis near Crossovers of TOPEX/POSEIDON Ground Track in South China Sea[J]. Acta Geodaetica et Cartographica Sinica|Acta Geod Cartogr Sin, 2000, 1: 19-25. |
| [10] |
李培良, 左军成, 李磊, 等. 南海TOPEX/POSEIDON高度计资料的正交响应法潮汐分析[J]. 海洋与湖沼, 2002, 3: 287-295. Li Peiliang, Zuo Juncheng, Li Lei, et al. Orthogonalized convolution method for analysis of South China Sea tidal data from TOPEX/Poseidon[J]. Oceanologia et Limnologia Sinica, 2002, 3: 287-295. DOI:10.3321/j.issn:0029-814X.2002.03.009 |
| [11] |
王延强, 仉天宇, 朱学明. 基于18.6年卫星高度计资料对南海潮汐的分析与研究[J]. 海洋预报, 2014, 2: 35-40. Wang Yanqiang, Zhang Tianyu, Zhu Xueming. Tidal characteristics analysis in the South China sea by 18.6 years satellite altimetry data[J]. Marine Forecasts, 2014, 2: 35-40. DOI:10.11737/j.issn.1003-0239.2014.02.006 |
| [12] |
Fang G, Kwok Y, Yu K, et al. Numerical simulation of principal tidal constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand[J]. Continental Shelf Research, 1999, 19(7): 845-869. DOI:10.1016/S0278-4343(99)00002-3 |
| [13] |
赵云霞, 魏泽勋, 王新怡. 利用T/P卫星高度计资料调和分析南海潮汐信息[J]. 海洋科学, 2012(05): 10-17. Zhao Yunxia, Wei Zexun, Wang Xinyi. The South China Sea tides analysis based on TOPEX/Poseidon altimetry[J]. Marine Sciences, 2012(05): 10-17. |
| [14] |
高秀敏, 魏泽勋, 吕咸青, 等. 全球大洋潮汐模式在南海的准确度评估[J]. 海洋科学进展, 2014(01): 1-14. Gao Xiumin, Wei Zexun, Lv Xianqin, et al. Accuracy assessment of Global Ocean Tide Models in the South China Sea[J]. Advances in Marine Science, 2014(01): 1-14. DOI:10.3969/j.issn.1671-6647.2014.01.001 |
| [15] |
付延光, 周兴华, 周东旭, 等. 利用验潮站资料的中国近岸海潮模型精度评估[J]. 测绘科学, 2017, 42(08): 28-32. Fu Yanguang, Zhou Xinghua, Zhou Dongxu, et al. Accuracy analysis of ocean tidal model over China seas based on the gauge data[J]. Science of Surveying and Mapping, 2017, 42(08): 28-32. |
| [16] |
王冰, 海云莎. 用车贝雪夫多项式作中国西南雨季降水场预报[J]. 云南大学学报(自然科学版), 2001(04): 294-296+302. Wang Bing, Hai Yunsha. Forecasting the Precipitation Distribution of Southwest of China with Chebyshev Polynomials[J]. Journal of Yunnan University, 2001(04): 294-296+302. DOI:10.3321/j.issn:0258-7971.2001.04.012 |
| [17] |
高秀敏.考虑内潮耗散的南海潮波伴随同化研究[D].青岛: 中国海洋大学, 2013. Gao Xiumin. Data assimilation tides in the South China Sea using adjoint method considering the internal tide dissipation[D]. Qingdao: Ocean University of China, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10423-1013348199.htm |
| [18] |
Fang G, Kwok Y, Yu K, et al. Numerical simulation of principal tidal constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand[J]. Continental Shelf Research, 1999, 19(7): 845-869. DOI:10.1016/S0278-4343(99)00002-3 |
| [19] |
曹德明, 方国洪, 黄企洲, 等. 南沙及其西南海域的潮波系统[J]. 海洋与湖沼, 1997(02): 198-208. Cao Demin, Fang Guohong, Huang Qizhou, et al. Tidal regime in the Nansha sea area and its adjacent southwest waters[J]. Oceanologia et Limnologia Sinica, 1997(02): 198-208. DOI:10.3321/j.issn:0029-814X.1997.02.013 |
| [20] |
沈育疆, 胡定明, 梅丽明, 等. 南海潮汐数值计算[J]. 海洋湖沼通报, 1985(01): 1-11. Shen Yujiang, Hu Singming, Mei Liming, et al. Numerical computation of the tides in the South China Sea[J]. Transactions of Oceanology and Limnology, 1985(01): 1-11. |
 2019, Vol. 43
2019, Vol. 43