
文章信息
- 李海涛, 刘泰麟, 邵泽东, 黄海广. 2019.
- LI Hai-tao, LIU Tai-lin, SHAO Ze-dong, HUANG Hai-guang. 2019.
- 基于决策树与二分分割算法的BP神经网络在赤潮等级预测中的应用研究
- Application of a BP neural network based on decision tree and two partition algorithm in prediction of red tide severity
- 海洋科学, 43(9): 34-40
- Marine Sciences, 43(9): 34-40.
- http://dx.doi.org/10.11759/hykx20181130001
-
文章历史
- 收稿日期:2018-11-30
- 修回日期:2019-02-18
2. 温州科技职业学院, 浙江 温州 325000
2. Wenzhou Vocational College of Science and Technology, Wenzhou 325000, China
近年来, 赤潮频繁暴发, 破坏了正常海洋生态系统的平衡, 严重危害海洋渔业资源、海洋捕捞、海水养殖和人类健康, 造成巨大的经济损失。因此, 开展赤潮等级预测研究有重要意义和实际应用价值[1-4]。经调研, 目前在赤潮方面科学的预测方法有多元回归、相关分析、时间序列、SVM[5]、神经网络模型[6]、灰色模型[7]等, 包括:采用定量化的赤潮生态动力学模型、基于IOWA算子的赤潮预测模型[8]、基于融合分层凝聚的赤潮预报模型等[9]。相对于其他预测模型, BP神经网络是最高效和适用的方法之一。并且, 利用现有的各种算法结合数据构建相应的算法模型, 是当今赤潮研究主要方向[10]。传统的BP神经网络模型在输入层神经元选择和隐含层节点数量确定方面存在不足, 导致神经网络在对于非平稳序列、非线性和相关关系复杂、预测精度要求高的赤潮灾害等级预测中, 容易出现网络训练时间长、学习效率低、易陷入局部极小、预测精度低的问题, 从而使其应用和扩展存在一定的局限性。
为了解决上述问题, 本文提出了基于C4.5决策树[11]与二分分割算法[12]优化的BP神经网络赤潮等级预测模型。探索利用优化后的BP神经网络模型来预测赤潮发生的等级, 并提高赤潮灾害等级预测的精确度, 辅助决策。
1 数据与方法 1.1 数据来源与赤潮等级划分鉴于海洋气象预报数据监测准确、采集方便、时效性强的特点, 本研究收集了青岛浮山湾海域和胶州湾海域等赤潮易发海域2000—2017年共计31个赤潮案例有效数据。每个样本包括赤潮发生的时间、地点、持续时间、面积、优势藻种、等级以及当时的气象数据, 统计数据来自国家海洋局北海环境监测中心。在赤潮发生海域的水文条件、化学条件、生物条件等已具备的情况下, 本文利用气象因素数据的变化对赤潮等级进行预测。影响赤潮发生的气象因素包括气温、气压、降水、风速、日照和湿度[13], 赤潮样本收集其发生海域前七天内的六个气象因子数据, 分别计算各因子数据七天的平均值作为神经网络模型学习与训练的输入值(Xk)。
根据《青岛市海洋赤潮灾害应急预案》和国家海洋局2008年发布的《赤潮灾害应急预案》以及模型的具体情况, 对赤潮预报结果划分等级并赋值。现将赤潮发生分为5个等级:特别重大、重大、较大、一般和轻微, 并对应赋值为0.9、0.7、0.5、0.3、0.1。
1.2 数据预处理采用归一化方法对模型输入数据进行数据预处理, 在训练集的选取上涵盖最大最小特征值, 避免测试集的数据发生越界。将各要素统一到[0, 1]区间, 减少不同要素取值范围差异过大而导致小数值数据价值被忽略的情况[14]。线性归一化公式和还原公式如下:
| $ \hat{x}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}, $ | (1) |
| $ x=\hat{x}\left(x_{\max }-x_{\min }\right)+x_{\min }, $ | (2) |
上述两式中, x和
C4.5决策树算法具有良好的分类和预测能力, 被广泛应用于数据挖掘中。它能够克服数据要求高、参数复杂、计算繁琐等困难, 可以根据既定规则完成基本的决策任务[15]。本研究将利用决策树理论在保证不影响网络效率的前提下, 约简输入条件属性以降低神经元的输入维度, 从而实现加快网络收敛速度、提高预测精度和抑制噪声的目的[16]。C4.5决策树算法的原理如下:
设S是类样本的数据训练集, m是训练集中的类别数量, Si为S中第i类样本的数量, i = 1, 2, …, m, 即:
| $ S=\sum\limits_{i=1}^{m} S_{i}, $ | (3) |
此时训练集S的信息熵H(S)为:
| $ H(S)=-\sum\limits_{i=1}^{m} \frac{\left|S_{i}\right|}{|S|} \log _{2} \frac{\left|S_{i}\right|}{|S|}, $ | (4) |
式中, 训练集S被属性A的属性值划分为m个子集, i = 1, 2, …, m, |Si|表示第i个子集中的样本数量, |S|表示划分前数据集中样本的总数量。
根据属性A, 令S={S1, S2, …, Sn}, 其中n为属性A包含不同值的数目。于是, 训练集在属性A上的信息熵为:
| $ H(S)=-\sum\limits_{i=1}^{n} \frac{S_{i}}{S} H(S), $ | (5) |
对应的信息增益为:
| $R(S, A)=\frac{H(S)-H(S, A)}{H(S, A)}, $ | (6) |
信息增益率为:
| $R_{\mathrm{G}}(S, A)=\frac{R(S, A)}{H(S)}. $ | (7) |
“二分分割算法”是使区间的两个端点逐渐向零点逼近, 来得到零点近似值的方法。基本思想如下:
(1) 首先, 确定隐含层节点数的近似范围, 假设范围是[1, 10]。
(2) 将s1=1、s2=10、s3=(s1+s2)/2=6(四舍五入)分别带入训练网络, 用同一组样本数据、同样的转移函数、训练函数进行训练, 分别比较不同的隐含层节点数在神经网络训练下的输出均方误差(MSE)。
(3) 计算3个不同节点数输出的均方误差的大小, 假设s1输出误差为E(s1), s2的输出误差为E(s2), s3的输出误差为E(s3)。如果E(s1) > E(s2), 则将隐含层节点数范围压缩至[s3, s2]。如果E(s1) < E(s2), 则将隐含层节点数范围压缩至[s1, s3]。连续压缩区间范围, 直至均方误差最小的那个节点数即为本文所需要的隐含层节点数。
1.4 BP神经网络BP神经网络是模拟人类大脑神经网络的结构和特性构建的网络模型。具有良好的学习和归纳能力, 在各类预测模型中被广泛应用[17]。神经网络可以很好地代替人脑来模拟赤潮灾害气象要素之间的关系, 把输入、输出问题转化为非线性映射, 解决由于缺乏精确计算公式而导致的赤潮等级预测精度低的问题[18]。BP神经网络的建立包括3个过程:网络初始化、正向传递和反向传递[19-20]。算法具体步骤如下:
(1) 输入学习样本(Xi, Yi)(i=1, 2, …, n), Xi和Yi分别是学习样本的输入参数和输出结果;
(2) 确定各层的神经元数量并随机在两层神经元之间建立连接权重矩阵
(3) 计算各节点的输出
(4) 比较各输出节点的均方根误差:
(5) 判断RMSE是否符合原定误差ε, 如果满足要求, 则结束, 否则进入步骤6;
(6) 修改第1层到第L+1层的连接权重矩阵:
转至步骤4, 直到结果的均方根误差在允许的误差范围之内。
2 赤潮等级预测模型构建在BP神经网络模型基础上, 根据已知样本数据, 通过决策树的分类选择方法过滤多余输入气象要素, 取最简属性集合作为神经网络输入节点构建神经网络, 隐含层节点数量通过“二分分割算法”来确定, 并在赤潮等级和气象因子之间建模, 如图 1所示。
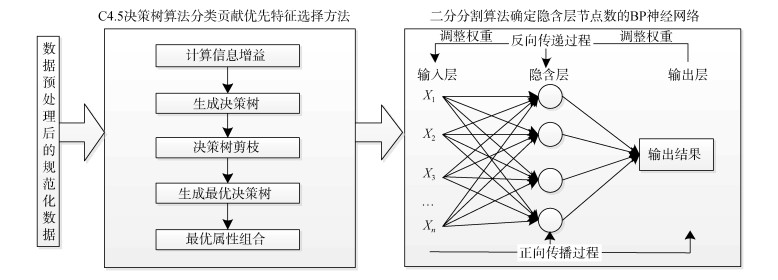 |
| 图 1 赤潮等级预测模型建立过程 Fig. 1 Establishment of red tide grade prediction model |
通过样本数据训练, 获得预测网络, 经测试、调整, 便可用于赤潮等级预测。具体实施步骤如下:
(1) 对网络的权重、阈值、收敛精度和最大迭代次数进行初始化;
(2) 通过决策树依次获取信息增益率最高的属性并结合模型情况, 确定网络最佳条件属性集合;
(3) 通过二分分割算法快速计算确定隐含层节点数量;
(4) 确定优化的BP神经网络结构, 并进行网络训练;
(5) 进行网络测试, 检查训练是否达到预期精度, 若达到预期精度或达到最大迭代次数, 停止并获取网络的输出结果。
3 神经网络预测模型应用分析 3.1 输入神经元优化在输入BP神经网络进行训练的数据中通常包含很多属性, 其中有些属性与目标能力无关或影响很小。当输入属性太多时, 神经网络收敛速度会降低, 还会增加过度拟合的可能性。因此在将属性数据输入神经网络进行训练前, 需要根据目标能力对属性进行约简, 选择合适的输入属性, 确定BP神经网络的最优输入属性集合。C4.5决策树分类选择最佳输入属性方法是对训练数据进行计算后比较各个属性的信息增益率的大小, 选择信息增益率大的属性或者属性集合来确定网络的初始输入[21]。经研究, 气象条件中的气温、气压、降水、风速、湿度、日照等气象要素与赤潮的发生、发展和消亡存在十分密切的关系[22-24]。本研究收集的2000—2017年青岛胶州湾海域和浮山湾海域赤潮案例与相应的气象因素数据共31个样本, 见表 1。
| 样本编号 | 发生地点 | 平均气温/ ℃ |
平均降水/ mm |
平均风速/ (m/s) |
平均相对湿度/ % |
平均气压/ hPa |
平均日照/ h |
等级赋值 |
| 1 | 浮山湾海域 | 20.600 0 | 1.900 0 | 1.000 0 | 71 | 1008.900 0 | 2.7 | 0.300 0 |
| 2 | 浮山湾海域 | 21.400 0 | 11.000 0 | 1.000 0 | 75 | 1007.800 0 | 3.5 | 0.500 0 |
| 3 | 胶州湾海域 | 20.800 0 | 6.700 0 | 1.650 0 | 72 | 1005.400 0 | 5.7 | 0.100 0 |
| 4 | 浮山湾海域 | 23.000 0 | 12.800 0 | 1.200 0 | 69 | 1005.500 0 | 4.8 | 0.300 0 |
| 5 | 浮山湾海域 | 23.500 0 | 11.700 0 | 1.500 0 | 86 | 1005.800 0 | 9.9 | 0.500 0 |
| 6 | 胶州湾海域 | 21.500 0 | 2.200 0 | 1.500 0 | 59 | 1006.600 0 | 3.4 | 0.300 0 |
| … | … | … | … | … | … | … | … | … |
| 27 | 浮山湾海域 | 17.900 0 | 6.900 0 | 1.960 0 | 64 | 1013.700 0 | 7.2 | 0.100 0 |
| 28 | 胶州湾海域 | 27.600 0 | 13.700 0 | 2.320 0 | 79 | 1019.400 0 | 8.3 | 0.500 0 |
| 29 | 胶州湾海域 | 21.300 0 | 2.400 0 | 1.600 0 | 74 | 1006.700 0 | 3.4 | 0.500 0 |
| 30 | 浮山湾海域 | 24.600 0 | 12.600 0 | 1.500 0 | 81 | 1005.900 0 | 9.9 | 0.700 0 |
| 31 | 胶州湾海域 | 19.200 0 | 10.800 0 | 1.750 0 | 70 | 1011.200 0 | 8.6 | 0.300 0 |
经C4.5决策树算法理论计算相关气象因子的信息增益率, 计算结果见表 2。
| 气象因子 | 信息增益率/% |
| 平均气温 | 37.85 |
| 平均降水 | 28.47 |
| 平均风速 | 1.73 |
| 平均相对湿度 | 0.22 |
| 平均气压 | 0.31 |
| 平均日照 | 36.11 |
气象因子属性的信息增益率与赤潮发生的等级成正相关。根据实际需要, 选择信息增益率大于1%的平均气温(x1)、平均降水(x2)、平均风速(x3)、平均日照(x4)4个气象属性作为最优特征组合。输入属性由原先的6个降至4个, 降低了输入神经元的维度, 并且由之后的预测模型可知, 这些选出的属性将作为神经网络的输入变量。
3.2 BP神经网络设计BP神经网络输入层神经元即经决策树分类优先特征选择算法约简后的气温、降水、风速、日照4个影响赤潮的气象因子数据, 网络转移函数采用Sigmoid函数, 即:
| $ f(x)=\frac{1}{1+\mathrm{e}^{-x}}, x \in(0, 1). $ | (8) |
为提高模型收敛速度和减少误差, 避免陷入局部极小, 本模型采用Delta学习规则使误差信号的目标函数达到最小:
| $ \Delta W_{i j}(n)=\eta\left(y_{i}(n)-O_{j}(n)\right) O_{i}(n), $ | (9) |
上述公式中, ΔWij(n)表示当输入向量为xn时神经元i和j之间的连接权值, η和yi分别表示学习效率和神经元i的期望输出值, Oi和Oj分别表示神经元i和神经元j的激活值。经试验, 取η为0.48, 误差容量为0.000 1, 最大迭代次数为2 000。
经调研, 目前, 在隐含层节点数量精确确定的问题上还没有成熟的理论依据来支持。很多专家和学者都是根据以往的经验公式得到一个确定的值[25]。常见的经验公式如下:
| $ C=\sqrt{m n}, $ | (10) |
| $ C=\sqrt{m+n}+a, $ | (11) |
| $ C=\log _{2} n, $ | (12) |
上述3个公式中, C、m和n分别表示隐含层节点数、输出层神经元数和输入层神经元数, a∈[1, 10]。
根据经验公式, 可以得到隐含层节点的数量, 但是它的经验性太强, 误差太大, 预测结果不够准确。本文经过经验公式粗略计算, 再结合“二分分割算法”后, 确定本文神经网络模型的最佳隐含层节点数为5。隐含层节点数有无限个的单隐层BP神经网络能够实现任意的非线性映射[26]。所以, 本文网络模型中隐含层层数为1。最终, BP神经网络预测模型的拓扑结构为4-5-1。拓扑结构如图 2所示。
 |
| 图 2 BP神经网络预测模型拓扑 Fig. 2 Topology of BP neural network prediction model |
为检验优化后的神经网络赤潮等级预测模型的性能, 实验采用表 1中的样本数据, 选择2015—2017年共5组(序号为27、28、29、30、31)数据进行模型预测验证, 其余年份的26组数据用于模型训练, 并与优化前传统BP神经网络模型的预测结果进行比较, 对比结果见表 3。
| 样本编号 | 赤潮实际等级赋值 | 赤潮等级预测结果 | |
| 本文模型 | 传统BP模型 | ||
| 27 | 0.100 0 | 0.100 9 | 0.111 4 |
| 28 | 0.500 0 | 0.510 7 | 0.462 2 |
| 29 | 0.500 0 | 0.488 1 | 0.536 7 |
| 30 | 0.700 0 | 0.720 4 | 0.749 3 |
| 31 | 0.300 0 | 0.276 8 | 0.357 1 |
采用均方根误差(RMSE)来评估优化的BP神经网络赤潮等级预测模型和传统的BP神经网络预测模型的性能。RMSE的值与模型的预测精度成反比。公式如下:
| $\operatorname{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(O_{i}-P_{i}\right)^{2}}, $ | (13) |
本文模型与传统BP神经网络预测模型在RMSE和学习速率(平均耗时时间)上的差异对比结果见表 4。
| 模型 | RMSE | 平均耗时时间/ms |
| 本文模型 | 0.12 | 8 |
| 传统BP模型 | 0.23 | 13 |
由表 3可知, 在2015—2017年发生的赤潮案例等级预测中, 使用本文模型的预测结果相比较传统BP神经网络模型的预测结果, 预测结果准确率分别提高了1.05%、2.71%、2.48%、2.89%、3.39%, 并且, 由表 4可知, 预测模型的均方根误差相比较传统BP神经网络模型减少了0.11, 均方误差更小。由实验结果可知, 本文的赤潮等级预测模型能在较短时间内获得较高精度的预测结果, 预测结果准确性更高, 可以应用到实际的赤潮等级预测中去。
4 结论利用BP神经网络结合C4.5决策树算法以及二分分割算法对历史赤潮案例气象因子数据进行训练, 形成的网络模型用于赤潮等级预测, 预测结果误差相对变小、平均耗时时间相对缩短, 可以满足赤潮等级预测的基本要求。同时, 基于神经网络的数据训练分析模型可以应用到渔获量预测、水产养殖产量预测、水质分析与评价、养殖病害诊断等研究中去, 具有一定的扩展性和推广价值。
| [1] |
丛丕福, 张丰收, 曲丽梅. 赤潮灾害监测预报研究综述[J]. 灾害学, 2008, 23(2): 2-3. Cong Pifu, Zhang Fengshou, Qu Limei. Review of red tide disaster monitoring and forecasting[J]. Disaster Science, 2008, 23(2): 2-3. |
| [2] |
黄良民, 黄小平, 宋星宇, 等. 我国赤潮多发海域及其生态学特征[J]. 生态科学, 2003, 22(3): 1-3. Huang Liangmin, Huang Xiaoping, Song Xingyu, et al. Red tide-prone sea areas in china and their ecological characteristics[J]. Ecological Science, 2003, 22(3): 1-3. |
| [3] |
Wang Hongli, Feng Jianfeng, Li Shengpeng. Statistical analysis and prediction of the concentration of harmful algae in Bohai Bay[J]. Transactions of Tianjin University, 2005, 308-312. |
| [4] |
He Dongmei, Duan Shunshan. Revieurrence of marine ecosystem and harmful red tides in offshore[J]. Ecological Science, 2011, 30(4): 1-4. |
| [5] |
陈作聪, 宋武. 基于改进粒子群SVM的海洋赤潮监测算法设计[J]. 青岛大学学报(自然科学版), 2016, 29(4): 1-3. Chen Zuocong, Song Wu. Design of ocean red tide monitoring algorithms based on improved particle swarm optimization SVM[J]. Journal of Qingdao University (Natural Science Edition), 2016, 29(4): 1-3. |
| [6] |
何恩业, 李海, 任湘湘, 等. BP人工神经网络在渤海湾叶绿素预测中的应用[J]. 海洋预报, 2008, 25(2): 3-9. He Enye, Li Hai, Ren Xiangxiang, et al. Application of BP artificial neural network in prediction of chlorophyll in bohai bay[J]. Marine Prediction, 2008, 25(2): 3-9. |
| [7] |
杜小伟.灰色预测模型在青岛市水产养殖产量预测中的应用[D].青岛: 中国海洋大学, 2011. Du Xiaowei. Application of grey prediction model in forecasting aquaculture yield in qingdao city[D]. Qingdao: Ocean University of China, 2011. http://cdmd.cnki.com.cn/article/cdmd-10423-1011229301.htm |
| [8] |
张承慧, 钱振松, 孙文星, 等. 基于IOWA算子的赤潮LMBP神经网络组合预测模型[J]. 天津大学学报, 2011, 44(2): 2-6. Zhang Chenghui, Qian Zhensong, Sun Wenxing, et al. Combination forecasting model of red tide LMBP neural network based on IOWA operator[J]. Journal of Tianjin University, 2011, 44(2): 2-6. |
| [9] |
彭模, 赵爱博. 基于融合分层凝聚和TS模糊推理集成的赤潮预测模型[J]. 科技通报, 2016, 32(5): 2-5. Peng Mo, Zhao Aibo. Red tide prediction model based on integration of hierarchical condensation and TS fuzzy reasoning[J]. Bulletin of Science and Technology, 2016, 32(5): 2-5. |
| [10] |
苏新红, 金丰军, 杨奇志, 等. 基于BP神经网络模型的福建海域赤潮预报方法研究[J]. 水产学报, 2017, 44(11): 2-4. Su Xinhong, Jin Fengjun, Yang Qizhi, et al. Research on red tide forecasting method in fujian sea area based on BP neural network model[J]. Journal of Fisheries of China, 2017, 44(11): 2-4. |
| [11] |
陈凯, 徐国庆, 熊焘, 等. 基于C4.5决策树的道路结冰预报模型构建与应用[J]. 交通运输研究, 2018, 4(1): 1-5. Chen Kai, Xu Guoqing, Xiong Tao, et al. Construction and application of road ice prediction model based on c4.5 decision tree[J]. Transportation Research, 2018, 4(1): 1-5. |
| [12] |
阮翔.基于改进的BP神经网络库存预测模型及其应用研究[D].南昌: 南昌大学, 2016. Ruan Xiang. Research on inventory forecasting model based on improved BP neural network and its application[D]. Nanchang: Nanchang University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10406-1016720801.htm |
| [13] |
符生辉. 2007—2012年浙南洞头沿海赤潮与气象关系研究[D].兰州: 兰州大学, 2015. Fu Shenghui. Study on the relationship between red tide and meteorology in dongtou coastal area of southern zhejiang province from 2007 to 2012[D]. Lanzhou: Lanzhou University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10730-1015354925.htm |
| [14] |
邵旻晖. 决策树典型算法研究综述[J]. 电脑知识与技术, 2018, 14(8): 1-2. Shao Minhui. Review of typical decision tree algorithms[J]. Computer Knowledge and Technology, 2018, 14(8): 1-2. |
| [15] |
Steinberg D, Colla P. CART: Classification and regression trees[J]. The Top Ten Algorithms in Data Mining, 2009, 13(2): 177-179. |
| [16] |
邵旻晖, 张琳, 周凡. 基于决策树的最佳通信渔船选择方法[J]. 渔业现代化, 2018, 45(3): 3-5. Shao Minhui, Zhang Lin, Zhou Fan. Optimal selection method of communication fishing vessel based on decision tree[J]. Fishery Modernization, 2018, 45(3): 3-5. |
| [17] |
王洪礼, 沈菲, 冯剑丰, 等. 基于人工神经网络的浮游植物密度预测模型研究[J]. 气象水文海洋仪器, 2004, 3(4): 1-3. Wang Hongli, Shen Fei, Feng Jiangfeng, et al. Prediction model of phytoplankton density based on artificial neural network[J]. Meteorological, Hydrological and Oceanographic Instruments, 2004, 3(4): 1-3. |
| [18] |
孙晓慧.基于人工神经网络的赤潮预测方法研究[D].舟山: 浙江海洋学院, 2012. Sun Xiaohui. Research on red tide prediction method based on artificial neural network[D]. Zhoushan: Zhejiang Ocean University, 2012: 29-51. |
| [19] |
Dai Zhengmei, Tian Jianyan. Summary of neural network predictive control[J]. Scientific and Technological Information Development and Economy, 2007, 17(15): 2-3. |
| [20] |
Louis E, Yan Xiaohai. A neural network model for estimating sea surface chlorophyll and sediments from thematic mapper imagery[J]. Remote Sensing of Environment, 1998, 66: 153-165. DOI:10.1016/S0034-4257(98)00054-6 |
| [21] |
董明明, 蒋涛, 晏婉晨, 等. 数据挖掘中神经网络与决策树技术的应用研究[J]. 经济研究导刊, 2018, 20(4): 1-5. Dong Mingming, Jiang Tao, Yan Wanchen, et al. Application of neural network and decision tree in data mining[J]. Economic Research Guide, 2018, 20(4): 1-5. DOI:10.3969/j.issn.1673-291X.2018.04.001 |
| [22] |
刘东君, 邹志红. 最优加权组合预测法在水质预测中的应用研究[J]. 环境科学学报, 2012, 32(12): 3128-3132. Liu Dongjun, Zou Zhihong. Application of optimal weighted combination forecasting method in water quality forecasting[J]. Journal of Environmental Science, 2012, 32(12): 3128-3132. |
| [23] |
刘霜, 张继民, 张洪亮, 等. 青岛近海赤潮灾害分级与时空分布及赤潮生物的变化[J]. 水生态学杂志, 2014, 35(4): 1-5. Liu Shuang, Zhang Jimin, Zhang Hongliang, et al. Classification and spatial-temporal distribution of red tide disasters and changes of red tide organisms in qingdao offshore[J]. Journal of Aquatic Ecology, 2014, 35(4): 1-5. DOI:10.3969/j.issn.1674-3075.2014.04.001 |
| [24] |
Steven S. C4.5: Programs for machine learning by J.Ross Quinlan[J]. Machine Learning, 1994, 16(3): 235-240. |
| [25] |
Seni G, Elder J F. Ensemble methods in data mining: Improving accuracy through combining predictions[J]. Synthesis Lec-tures on Data Mining and Knowledge Discovery, 2010, 2(1): 1-126. |
| [26] |
胡月. BP算法并行化及在数据挖掘中的应用研究[D].重庆: 重庆大学, 2003. Hu Yue. Parallelization of BP algorithm and its application in data mining[D]. Chongqing: Chongqing University, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10611-2004051041.htm |
 2019, Vol. 43
2019, Vol. 43


