文章信息
- 尹超, 黄海军, 王道儒, 谢琳. 2020.
- YIN Chao, HUANG Hai-jun, WANG Dao-ru, XIE Lin. 2020.
- 海南岛近岸养殖区台风浪预报技术研究
- Storm wave forecasting technique for the nearshore aquaculture area of Hainan Island
- 海洋科学, 44(1): 1-7
- Marine Sciences, 44(1): 1-7.
- http://dx.doi.org/10.11759/hykx20190330002
-
文章历史
- 收稿日期:2019-03-30
- 修回日期:2019-05-23
2. 中国科学院大学, 北京 100049;
3. 海南省海洋与渔业科学院, 海南 海口 571126
2. University of the Chinese Academy of Sciences, Beijing 100049, China;
3. Hainan Academy of Ocean and Fisheries Sciences, Haikou 571126, China
台风是对海南影响较大的气象灾害, 特别是水产养殖行业。海南临高县后水湾网箱养殖密度和产值均较高, 是临高县支柱产业, 占全县GDP一半以上。2011年, 遭受台风“纳沙”(NESAT)和“尼格” (NALGAE)袭击, 受损2050口网箱, 占全省的78.8%, 直接经济损失7.63亿元; 2014年, 遭受台风“威马逊”(RAMMASUN)及“海鸥”(KALMAEGI)袭击, 受损1 383口网箱, 占全省的45%。到了2018年, 海南省开始推进渔业产业结构调整, 在陵水县新建3个大型智能化养殖网箱, 从水深20米以浅近岸区域拓展到50米以深的深远海区域, 从养殖装备直径20~ 30米量级拓展到近100米量级。随着养殖产业升级, 为了维护生命和财产安全, 需要加强近岸海域的海浪预报系统的建设以提供科学依据, 提高海洋防灾减灾的能力。
影响海浪预报的最重要因素是风场预报的准确性[1]。目前主要的两大气象业务预报系统分别是欧洲中期天气预报中心的全球模式ECMWF(European Centre for Medium-range Weather Forecasts), 和美国全球预报系统GFS(Global Forecast System)。GFS是由美国国家海洋和大气管理局NOAA(National Oceanic and Atmospheric Administration)推出的全球数值天气预报计算模式, 该模式每天分别于世界时00时、06时、12时和18时发布四次预报结果, 预报时效长达16天。从2015年开始空间分辨率已经提高到了0.25°, 时间分辨率随着预报时效增加而降低, 5天内分辨率为1小时, 5天至10天分辨率为3小时, 10天至16天分辨率降为12小时。
目前国内外的业务化海浪数值预报主要基于第3代海浪模式, 广泛应用的主要有WAM(Wave Modeling), WAVEWATCH Ⅲ和SWAN(Simulating Waves Nearshore)等。美国气象局采用WAVEWATCH Ⅲ, 欧洲气象中心采用WAM, 英国气象局采用WAM和SWAN等。我国的国家海洋环境预报中心用WAM和WAVEWATCH Ⅲ模型进行大洋的海浪预报, 用WAVEWATCH Ⅲ和SWAN嵌套模型进行中国海的海浪预报[2]。通常, WAVEWATCH Ⅲ模式适用于深水大洋波浪计算, SWAN模式更适和近岸波浪计算, WAVEWATCH Ⅲ和SWAN模式的嵌套常用于跨尺度的波浪计算[3]。
台风浪往往伴有风暴潮, 风暴潮会引起海岸增水[4, 5], 水位的变化直接影响近岸波高的大小[6], 而波浪的辐射应力的又会引起水位的改变[7]。潮汐引起的水位变化也会影响风暴潮和海浪的增长。网箱养殖区往往设置在半封闭海湾中, 以躲避强风浪的直接作用。但其几何特征有利于风暴潮增水, 以至于增大了台风浪风险。所以, 近岸的风浪潮流动力过程存在着强相互作用, 而浪潮流耦合模型适用于近岸动力环境问题的解决[8]。Dietrich耦合了ADCIRC(Advanced circulation model)和SWAN模式研究了飓风Gustav (2008)过程的台风浪和风暴潮特征[9]; 冯兴如等基于ADCIRC+SWAN模型研究了浙江和福建海域台风浪变化特征[10]。
本研究通过海南岛近岸养殖区台风浪精细化预报系统的建设, 提高网箱养殖环境监测预警水平。为渔业工作者投喂作业和维护设备提供合理的时间窗口, 并降低其劳动风险; 为养殖企业的生产决策和地方政府的应急管理服务提供科学合理的依据。
1 近岸养殖区台风浪数值预报系统 1.1 耦合模型的建立ADCIRC模式由Luettich和Westerink于1992年开发并不断完善发展[11]。该模式采用了有限元方法, 在二维条件下应用了深度平均正压和浅水方程, 通过求解广义波连续性方程(Generalized Wave Continuity Equation, GWCE), 水深和动量方程可以表述为:
| $ \frac{{{\partial ^2}\zeta }}{{\partial {t^2}}} + {\tau _0}\frac{{\partial \zeta }}{{\partial t}} + \frac{{\partial {{\tilde J}_x}}}{{\partial x}} + \frac{{\partial {{\tilde J}_y}}}{{\partial y}} - UH\frac{{\partial {\tau _0}}}{{\partial x}} - VH\frac{{\partial {\tau _0}}}{{\partial y}} = 0, $ | (1) |
| $ \begin{array}{l} \frac{{\partial U}}{{\partial t}} + U\frac{{\partial U}}{{\partial x}} + V\frac{{\partial U}}{{\partial y}} - fV = \\ - {\rm{g}}\frac{{\partial \left[ {\zeta + {P_{\rm{s}}}/{{\rm{ \mathsf{ ρ} }}_{\rm{0}}}{\rm{g}} - \alpha \eta } \right]}}{{\partial x}} + \frac{{{\tau _{{\rm{s}},x}} - {\tau _{b,x}}}}{{{{\rm{ \mathsf{ ρ} }}_0}H}} + \frac{{{M_x} - {D_x} - {B_x}}}{H}, \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{\partial V}}{{\partial t}} + U\frac{{\partial V}}{{\partial x}} + V\frac{{\partial V}}{{\partial y}} - fU = \\ - {\rm{g}}\frac{{\partial \left[ {\zeta + {P_{\rm{s}}}/{{\rm{ \mathsf{ ρ} }}_{\rm{0}}}{\rm{g}} - \alpha \eta } \right]}}{{\partial y}} + \frac{{{\tau _{{\rm{s}},y}} - {\tau _{b,y}}}}{{{{\rm{ \mathsf{ ρ} }}_0}H}} + \frac{{{M_y} - {D_y} - {B_y}}}{H}, \end{array} $ | (3) |
式中: U和V是垂向积分平均流速; f为科氏力参数; ζ为海表面自由高度; Ps为海水自由表面大气压; ρ0是海水密度; η为牛顿引潮势; τs, x, τs, y为海表面应力; H=ζ+h为水深加自由表面高度; τb, x, τb, y为底切应力; g为重力加速度; M, D和B分别代表了侧向应力梯度、动量耗散和斜压梯度。为了满足CFL条件, 时间步长取为1 s。ADCIRC模式带有干湿网格判断, 最小水深设为0.1 m。
SWAN模式包含了较多的近岸波浪物理过程, 例如折绕射、浅化、白冠破碎、底摩擦、波-波相互作用等。笛卡儿坐标下控制方程表述为:
| $ \frac{{\partial N}}{{\partial t}} + {\nabla _{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }} \cdot \left[ {\left( {{{\vec c}_{\rm{g}}} + \vec U} \right)N} \right] + \frac{{\partial {c_\theta }N}}{{\partial \theta }} + \frac{{\partial {c_\sigma }N}}{{\partial \sigma }} = \frac{{{S_{{\rm{tot}}}}}}{\sigma }, $ | (4) |
N(
在耦合过程中, ADCIRC和SWAN使用同一套非结构网格。所以在数据传递过程中不需要再调用计算资源进行插值和数据分配, 保证了计算效率和稳定性。因为SWAN模式的有更大的时间步长, SWAN和ADCIRC模式的数据交换时间间隔设定为SWAN时间步长[9]。由ADCIRC模式计算的风速、海表面水位和流速每10分钟传递给SWAN模式, 而SWAN模式将辐射应力梯度传回给ADCIRC模式。
1.2 水深岸线及边界条件设定水深地形采用美国国家海洋大气管理局NOAA提供的ETOPO1数据集, 该数据为栅格化数据, 分辨率为1′×1′。由于ETOPO1对近岸水深的观测误差较大, 近岸水深数据采用中华人民共和国海军航海保证司令部出版的海图, 分辨率从1︰150 000加密到1︰50 000再到重点海湾的1︰25 000(见图 1)。
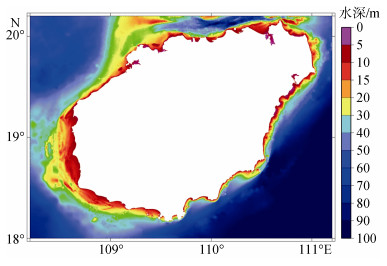 |
| 图 1 海南岛近岸地形分布图 Fig. 1 Topography around Hainan Island |
近岸养殖区台风浪耦合数值预报模型计算区域范围是105.5°—119.7°E和10.8°—24.7°N, 包括海南岛和南海大部分的海域。由于海南岛海岸岛屿众多, 为了精确描述岸线特征, 达到精细化预报要求, 我们从Google Earth提取了整个海南岛的岸线, 使沿岸区域分辨率达到了100 m。网格分辨率从南海深海到陆架到近岸再到重点海湾逐渐提高(见图 2)。模型在开边界处加入了俄勒冈州立大学开发的TPXO模型(http://volkov.oce.orst.edu/tides/)的8个主要天文分潮(P1、Q1、K1、O1、K2、N2、M2和S2)。
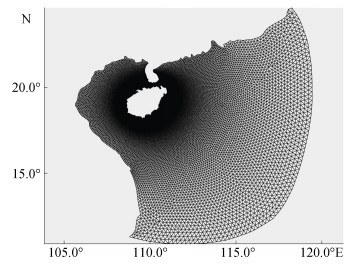 |
| 图 2 模式计算域网格 Fig. 2 Unstructured grid of the model domain |
2014年09号台风“威马逊”生成于西北太平洋, 2014年7月11日由热带低压升级为热带风暴, 7月14日升级为强热带风暴, 并于下午5时升级为台风。7月15日“威马逊”在菲律宾阿尔拜省拉普拉普登陆, 7月16日台风向西北偏西移动, 进入南海海域。17日, 进入南海北部, 形成为强台风, 其路径见图 3。台风“威马逊”于7月18日15时30分在海南省文昌市翁田镇登陆, 中心最大风力达到了60 m/s, 中心气压为910 hPa, 10级风圈半径180 km, 7级风圈半径300 km。于19日7时10分在广西防城港市再次登陆, 之后强度逐渐减弱, 于20日5时进入云南境内, 并减弱为热带低压[13]。超强台风“威马逊”对海南、广东和广西沿海地区造成的直接经济损失达265.5亿元。
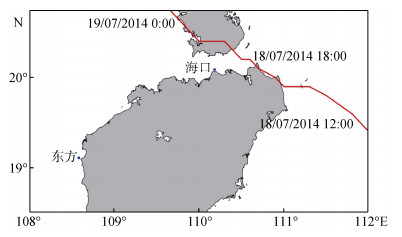 |
| 图 3 海洋观测站(蓝点)和台风“威马逊”路径(红色实线) Fig. 3 Oceanographic stations (blue dots) and track of the RAMMASUN cyclone (red line) |
潮位和波浪观测数据由国家海洋局南海分局海口中心站提供, 站位如图 3所示。潮位数据每小时一次, 波浪数据每3小时一次, 当台风强度增强则加密到1小时一次。海口站波浪数据因为仪器原因, 在接近波高最大值时停止工作, 缺失数据。
强迫场方面使用CFSv2(Climate Forecast System Version 2)再分析数据, 包括海面10 m风场和海表面气压场。CFSv2系统由美国环境预报中心NCEP(National Centers for Environmental Prediction)开发, 它是全耦合模型包括了大气、海洋、陆地和海冰模块, 于2011年投入业务化运行。该强迫场时间分辨率为1小时, 空间分辨率为0.2°×0.2°。
2.3 结果分析模型计算时间从2014年7月9日18时至20日6时。模式的输出变量设定含有效波高、谱峰周期、平均周期、波向, 输出频率为每小时一次。为检验模式的结果, 将计算的潮位和有效波高结果与台风“威马逊”期间观测波高进行对比, 对比结果见图 4。由近岸观测站潮位对比(图 4a和b)可知, 模拟的潮位在东方站和实测值基本一致, 海口站略低且峰值提前, 原因可能是再分析风圈结构和实际风圈有差别。由近岸观测站有效波高对比图(图 4c和d)可知, 有效波高增长趋势一致性较好, 最高值基本在同一时刻。海口站和东方站模拟有效波高值均略大于实测值。
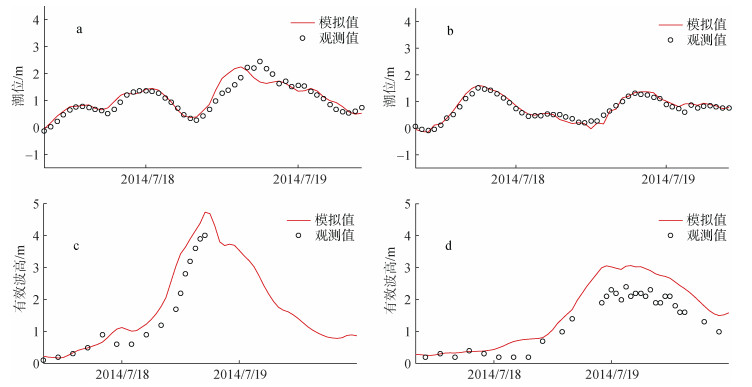 |
| 图 4 1409号台风“威马逊”期间沿岸各站潮位及有效波高观测值和模拟值 Fig. 4 Computed results of sea surface elevations and significant wave heights (red lines) vs. observations (black dots) during Typhoon RAMMASUN 注: a:海口站; b:东方站; c:海口站; d:东方站 |
2018年7月19日在海南岛近岸生成了热带风暴, 其过程持续到7月25日。图 5给出的是GFS预报的热带风暴过程的风速场和气压场分布图, 预报时间均为2018年7月22日18时(UTC)。左图为2018年7月21日0时(UTC)发布的预报数据, 该组数据的预报时效约48小时。右图为2018年7月22日0时(UTC)的发布数据, 该组数据的预报时效约24小时。图 5a和c显示, 热带风暴中心大体位于琼州海峡中部, 海南岛东部风速较大, 能达到18 m/s。图 5b和d显示, 预报的热带风暴中心向西偏移, 大体位于海南岛西北部海域, 海南岛南部风速较大, 达到了16 m/s, 比21日0时发布的预报数据极值偏小。
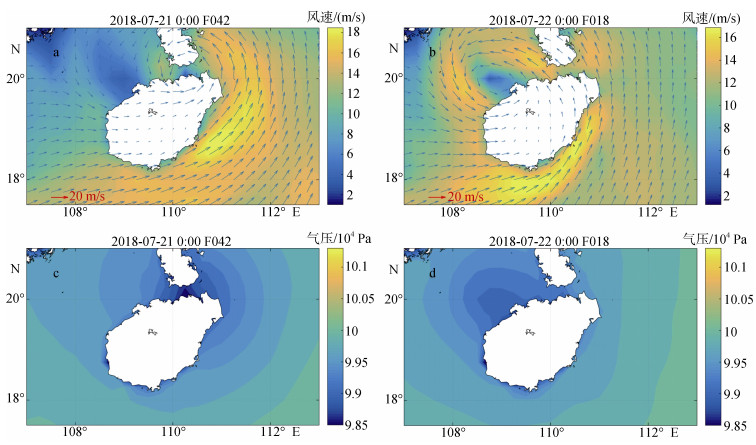 |
| 图 5 GFS预报的2018年7月22日18时(UTC)海南岛附近风速场和气压场 Fig. 5 Wind and surface air pressure fields predicted by GFS at 18: 00 UTC on July 22, 2018 near Hainan Island 注: a: 2018年7月21日0时(UTC)发布的预报风速场; b: 2018年7月22日0时(UTC)发布的预报风速场; c: 2018年7月21日0时(UTC)发布的预报气压场; d: 2018年7月22日0时(UTC)发布的预报气压场 |
图 6显示的是模拟的2018年7月22日18时(UTC)海南岛附近波浪场, 图 6a采用2018年7月21日0时(UTC)发布的预报风速场和气压场, 而图 6b采用2018年7月22日0时(UTC)发布的预报风速场和气压场。有效波高的分布与图 5风速强度分布基本吻合。图 6a波浪高值区域在海南岛东部海域, 最大值达到了5 m。图 6b高值区域在海南岛南部海域, 相比于图 6a最大值减少了大概1 m。
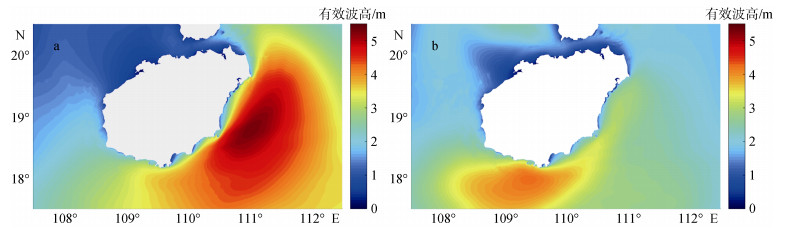 |
| 图 6 模拟的2018年7月22日18时(UTC)海南岛附近波浪场 Fig. 6 Simulated significant wave heights at 18: 00 UTC on July 22, 2018 near Hainan Island 注: a: 48小时预报的有效波高; b: 24小时预报的有效波高 |
将48小时、24小时预报值和海南陵水湾波浪观测数据进行对比(见图 7)。时间范围选取7月20日16时-24日2时, 其中红线代表 48小时预报值、蓝线代表 24小时预报值、黑色点代表实测值。48小时预报最大有效波高为3.2 m左右, 24小时预报最大有效波高为2.15 m左右, 二者在近岸的最大有效波高差值接近1.0 m。在7月23日4时之前, 48小时预报的有效波高较24小时预报值偏大, 之后较24小时预报值偏小且和实测值更为吻合。48小时预报结果存在极值偏高的现象, 且波高增长时间及区间提前。24小时预报有效波高在波浪增长、整体趋势上和实测值更为吻合, 7月23日9时之后的数值较实测值偏大。对比图 5可以看出, 48小时预报最大风速中心区域在海南岛东海岸, 陵水波浪观测站受其影响较大, 风速比24小时预报值偏大, 导致波浪计算结果也较大。
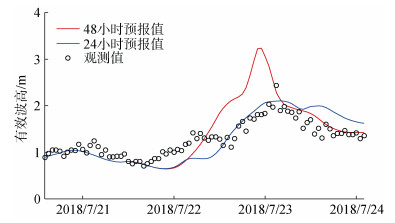 |
| 图 7 热带风暴期间48小时和24小时预报的有效波高 Fig. 7 The 48 h and 24 h forecasts of significant wave heights during the tropical storm 注:黑色空心圆代表实测值, 蓝线代表 24小时预报值, 红线代表 48小时预报值 |
最后对有效波高进行定量检验评估, 评估参数包括平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)和皮尔逊相关系数(R)[14-16]。其中, 平均绝对误差、平均相对误差和均方根误差体现了观测值同实测值的平均偏离情况, 皮尔逊相关系数则能反映观测值同实测值变化趋势的密切程度。检验评估的计算公式如下所示:
| $ 平均绝对误差\;\;\;\;\;\;\;\; {\rm{MAE}} = \frac{1}{N}\mathop \sum\limits_{i = 1}^N {\left| {{{X'}_I} - {X_i}} \right|} , $ | (5) |
| $ 平均相对误差\;\;\;\;\;\;\;\; {\rm{MRE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N \frac{{{\left| {{{X'}_i} - {X_i}} \right|}}}{{{X_i}}}, $ | (6) |
| $ 均方根误差{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{X_i} - \bar X} \right)}^2}} } , $ | (7) |
| $ 相关系数{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{R = }}\frac{{\sum\limits_{i = 1}^N {\left( {{X_i} - \bar X} \right)\left( {{Y_i} - \bar Y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^N {{{\left( {{X_i} - \bar X} \right)}^2}} \sum\limits_{i = 1}^N {{{\left( {{Y_i} - \bar Y} \right)}^2}} } }}. $ | (8) |
有效波高的预报值与观测值的检验统计结果如表 1所示。24小时和48小时预报的MAE均小于0.3 m, 24小时的MAE为0.22 m, 相对于48小时预报值提高了23%。48小时预报值MRE为20.75%, 而24小时预报值MRE为17.0%。48小时预报值RMSE为0.439 m, 24小时预报值的RMSE提高到了0.272 m, 提高幅度较大。24小时和48小时的相关系数R均大于0.8, 24小时预报值略有提高达到了0.87。四项统计指标24小时预报值均好于48小时的结果, 其中RMSE和MAE指标提高较大。
| 预报时效 | MAE/m | MRE/% | RMSE/m | R |
| 24 h | 0.220 | 17.0 | 0.272 | 0.871 |
| 48 h | 0.284 | 20.75 | 0.439 | 0.837 |
本文根据近岸网箱养殖区台风浪精细化预报的工作需求, 基于非结构网格的ADCIRC+SWAN耦合模型, 采用GFS风场和气压场数据, 建立了适用于海南近岸的海浪预报系统。利用近岸观测资料对2014年7月“威马逊”台风过程进行后报验证, 在此基础上对2018年7月海南岛近岸海域热带风暴过程进行海浪预报及结果统计分析检验。主要结论如下:
(1) 采用高分辨率CFSv2风场和气压场作为模式输入, 在最大波高与波浪增长衰减过程两个方面, 计算的结果和近岸观测一致性较好。模拟的有效波高值略大于实测值。
(2) GFS预报的风场与气压场每6小时不断更新, 热带气旋的路径、中心气压和中心强度均不断变化。预报时效对海浪预报有直接影响。
(3) 热带风暴过程的预报结果对比发现, 48小时预报的最大波高比实测偏大较多, 24小时预报的波浪增长衰减过程和实测值更为吻合。24小时预报的平均相对误差达到了17%, 均方根误差为0.272 m, 24小时和48小时预报的相关系数均大于0.8。
通过对预报结果的统计检验, 该模型的预报精度可以满足近岸养殖区台风浪预报业务的需求。可以为养殖企业的生产决策和地方政府的应急管理服务提供科学合理的依据。
| [1] |
李本霞, 王德帅. 集合海浪预报的发展与应用回顾[J]. 海洋预报, 2014, 31(6): 79-85. Li Benxia, Wang Deshuai. Review on the ensemble wave forecast[J]. Marine Forecasts, 2014, 31(6): 79-85. |
| [2] |
周水华, 俞胜宾, 梁昌霞, 等. 南海海浪业务化数值预报系统检验[J]. 海洋预报, 2012, 29(6): 30-36. Zhou Shuihua, Yu Shengbin, Liang Changxia, et al. The verification of operational surface wave forecast system in the South China Sea[J]. Marine Forecasts, 2012, 29(6): 30-36. |
| [3] |
徐丽丽, 肖文军, 石少华, 等. WaveWatch Ⅲ和SWAN模型嵌套技术在业务化海浪预报系统中的应用及检验[J]. 海洋通报, 2015, 34(3): 283-294. Xu Lili, Xiao Wenjun, Shi Shaohua, et al. Application and validation of an operational wave forecast model system based on the nesting use of WaveWatch Ⅲ and SWAN model[J]. Marine Science Bulletin, 2015, 34(3): 283-294. |
| [4] |
傅赐福, 于福江, 王培涛, 等. 滨海新区温带风暴潮灾害风险评估研究[J]. 海洋学报, 2013, 35(1): 55-62. Fu Cifu, Yu Fujiang, Wang Peitao, et al. A study on extratropical storm surge disaster risk assessment at Binhai New Area[J]. Acta Oceanologica Sinica, 2013, 35(1): 55-62. |
| [5] |
付元冲, 丁平兴, 葛建忠, 等. 长江河口沿海区域温带风暴潮预报模式的建立与应用[J]. 华东师范大学学报(自然科学版), 2017(2): 116-125. Fu Yuanchong, Ding Pingxing, Ge Jianzhong, et al. Development and application of the forecasting model for extratropical storm surges around the Changjiang estuary[J]. Journal of East China Normal University (Natural Science), 2017(2): 116-125. DOI:10.3969/j.issn.1000-5641.2017.02.015 |
| [6] |
赵昊辰, 尹宝树, 冯兴如, 等. 台湾附近海域超强台风南玛都期间风暴潮对海浪影响的数值研究[J]. 海洋科学, 2015, 39(3): 127-134. Zhao Haochen, Yin Baoshu, Feng Xingru, et al. Numerical study of influence of surge and wave interaction on waves in waters surrounding Taiwan[J]. Marine Sciences, 2015, 39(3): 127-134. |
| [7] |
Dietrich J C, Bunya S, Westerink J J, et al. A highresolution coupled riverine flow, tide, wind, wind wave, and storm surge model for southern Louisiana and Mississippi. Part Ⅱ:synoptic description and analyses of Hurricanes Katrina and Rita[J]. Monthly Weather Review, 2020, 138(2): 378-404. |
| [8] |
龚文平, 汪亚平, 王道儒, 等. 海南新村港潮汐汊道波流联合作用下的动力特征及其沉积动力学意义[J]. 海洋学研究, 2008(2): 1-12. Gong Wenping, Wang Yaping, Wang Daoru, et al. Hydrodynamics under combined action of wave and tide and its implication for the sediment dynamics in Xincun Tidal Inlet, Hainan[J]. Journal of Marine Sciences, 2008(2): 1-12. DOI:10.3969/j.issn.1001-909X.2008.02.001 |
| [9] |
Dietrich J C, Westerink J J, Kennedy A B, et al. Hurricane Gustav (2008) waves and storm surge:hindcast, synoptic analysis, and validation in Southern Louisiana[J]. Monthly Weather Review, 2011, 139(8): 2488-2522. DOI:10.1175/2011MWR3611.1 |
| [10] |
冯兴如, 杨德周, 尹宝树, 等. 中国浙江和福建海域台风浪变化特征和趋势[J]. 海洋与湖沼, 2018, 49(2): 233-241. Feng Xingru, Yang Dezhou, Yin Baoshu, et al. The change and trend of the typhoon waves in Zhejiang and Fujian coastal areas of China[J]. Oceanologia et Limnologia Sinica, 2018, 49(2): 233-241. |
| [11] |
Luettich R A, Westerink J J, 2004. Formulation and numerical implementation of the 2D/3D ADCIRC finite element model version 44. XX[R]. Chapel Hill: University of north Carolina.
|
| [12] |
Garratt J R. Review of drag coefficients over oceans and continents[J]. Monthly Weather Review, 1977, 105(7): 915-929. DOI:10.1175/1520-0493(1977)105<0915:RODCOO>2.0.CO;2 |
| [13] |
杨万康, 杨青莹, 尹宝树, 等. 1409号"威马逊"台风对铁山港海域的风暴潮增水研究[J]. 海洋预报, 2016, 33(1): 80-85. Yang Wankang, Yang Qingying, Yin Baoshu, et al. Study on the storm surge characteristics of No[J]. Marine Forecasts, 2016, 33(1): 80-85. |
| [14] |
吴欢, 汪一航, 滕涌, 等. 浙江海域MASNUM海浪模式在台风"达维""海葵"及"布拉万"过程的波浪数值模拟[J]. 应用海洋学学报, 2017, 36(2): 249-259. Wu Huan, Wang Yihang, Teng Yong, et al. Numerical simulation for waves of Typhoon "David" "Anemone" and "Bolaven" by MASNUM wave model[J]. Journal of Applied Oceanography, 2017, 36(2): 249-259. DOI:10.3969/J.ISSN.2095-4972.2017.02.012 |
| [15] |
张露, 傅赐福, 董剑希, 等. 台风"妮妲"风暴潮与近岸浪的数值模拟与预报[J]. 海洋预报, 2018, 35(2): 27-35. Zhang Lu, Fu Cifu, Dong Jianxi, et al. Numerical simulation and forecasting on storm surge and offshore wave of Typhoon "Nida"[J]. Marine Forecasts, 2018, 35(2): 27-35. |
| [16] |
李毅能, 彭世球, 周峰华, 等. 东印度洋天气和风暴潮预报系统的初步评估[J]. 南京信息工程大学学报(自然科学版), 2018, 10(3): 361-369. Li Yingneng, Peng Shiqiu, Zhou Fenghua, et al. Preliminary assessment of a real-time forecasting system for atmosphere and storm surge in eastern Indian Ocean[J]. Journal of Nanjing University of Information Science and Technology (Natural Science Edition), 2018, 10(3): 361-369. |
 2020, Vol. 44
2020, Vol. 44


