
文章信息
- 李嘉, 郑向阳, 张华, 姜德娟, 王玉琳, 蔡永兵. 2020.
- LI Jia, ZHENG Xiang-yang, ZHANG Hua, JIANG De-juan, WANG Yu-lin, CAI Yong-bing. 2020.
- 基于Delft 3D模型的感潮河口示踪模拟
- Simulation of tracer experiment in the tidal estuary based on the Delft 3D model
- 海洋科学, 44(10): 23-32
- Marine Sciences, 44(10): 23-32.
- http://dx.doi.org/10.11759/hykx20191112002
-
文章历史
- 收稿日期:2019-11-12
- 修回日期:2019-12-26
2. 山东省海岸带环境过程重点实验室, 山东 烟台 264003;
3. 中国科学院烟台海岸带研究所, 山东 烟台 264003;
4. 安徽科技学院 资源与环境学院, 安徽 凤阳 233100
2. Shandong Key Laboratory of Coastal Environmental Processes, Yantai 264003, China;
3. Yantai Institute of Coastal Zone Research, Chinese Academy of Sciences, Yantai 264003, China;
4. College of Resource and Environment, Anhui Science and Technology University, Anhui 233100, China
扩散是控制水体中污染物行为和分布的关键过程,研究污染物扩散过程是评估其在水环境中迁移的重要前提。扩散系数与研究区的水力条件、研究区范围和地形等因素有关。不同水域的扩散系数通常存在较大的差异,即使同一水域不同区段的扩散系数也可能具有较大的变化范围。例如,梅江的纵向扩散系数为18.2 m2/s[1]; 黄河不同河段的纵向扩散系数为31~89 m2/s[2-4]; 逛荡河不同河段的纵向扩散系数为0.027 4~0.127 0 m2/s[5]。目前,扩散系数的获取方式包括理论计算、经验公式和示踪实验[6]。顾莉和华祖林[6]总结发现,理论计算和经验公式具有较大的局限性和较差的适用性; 相比之下,通过示踪实验可以较为准确的获取研究区的扩散系数,同时,示踪结果也可以为模型验证提供数据支撑[1]。
示踪实验是研究水体动力学特征,定量获取示踪剂弥散/扩散系数的实验。其实验方法通常是在研究区上游通过特定的投放方式释放示踪剂,根据现场情况在下游设置相应的观测站点,定时取样,分析示踪剂浓度; 根据示踪剂的迁移情况估算研究区的扩散系数[5]。示踪剂的投放方式可以分为单点源、多点源、连续释放、瞬时释放和有限时段释放等[7]。示踪剂分为反应型示踪剂和保守型示踪剂,前者在研究体系中会发生衰减; 后者在研究体系中较为稳定。示踪剂的选择通常需满足以下几个条件: (1) 示踪剂在研究水域中的背景浓度极低; (2) 示踪剂在水体中的半衰期足够长,能保证在示踪实验期间保持稳定; (3) 生态毒性低; (4) 检测限低,易于分析,分析成本低。目前常用的几类示踪剂包括: 放射性物质(如镭、氡等同位素)、荧光染色剂(如罗丹明WT、罗丹明B、荧光素钠和荧光黄等)、无机离子(如氯离子、溴离子和锂离子等)。各类示踪剂的优缺点明显,常根据具体的实验条件进行选择。例如,放射性物质的环境背景值低,但对实验条件要求高(实验人员需经过专门培训),且成本较高,导致其应用受限; 无机离子成本低、易操作,但只适用于内陆淡水水域,且投加量较大; 相对而言,荧光染色剂具有检测限低、毒性弱、操作简单、不受研究水体限制等优点,是示踪实验中常用的一类示踪剂。其中,罗丹明类物质(罗丹明WT、罗丹明B、磺酰罗丹明B等)是最常用的一类荧光示踪剂。目前,国内外不少学者利用罗丹明类荧光染色剂在不同研究水域开展了示踪实验研究[8-13]。
Delft 3D模型是一套具有强大功能的水动力-水质模拟系统,主要由网格、水动力、水质、波浪、粒子示踪、泥沙输运和生态7个模块构成。其自带的Quickplot工具可以处理三维模拟结果,可以将一维时间序列数据和二维空间数据进行动态显示; Delft 3D模型配备网格编辑和生成功能,可快速生成正交网格且灵活度高; 水动力计算采用基于有限差分法中的显、隐式交替数值积分求解,稳定性高,计算速度较快; 此外,模型的后处理能力较强,可以与ArcGIS和Matlab等软件配套使用。Delft 3D模型已成为目前最先进的水动力数值模型之一,被广泛应用于我国长江口、海南岛、鄱阳湖、三峡库区和天津近海等地区[14-18]。
研究表明,超过90%的天然和人类活动产生的物质将随河流输送进入海洋[19],处于陆海交汇位置的河口区域作为陆源物质向海输送的必经通道[20],在陆源污染物向海输运过程中扮演着重要角色。由于受径流和潮汐的双重影响,河口的水动力条件特殊且复杂,直接影响污染物在河口水体中的迁移和分布。在河口区域开展示踪实验,不仅能揭示河口水动力变化特征及其稀释扩散能力,对于揭示污染物的迁移行为及其向海传输也具有重要意义。小清河是一条典型的陆源入海河流,是莱州湾主要的污染来源[21-23],其水质好坏直接影响莱州湾区域经济的可持续发展和海洋资源的合理利用。因此,本文选取小清河口作为研究区,通过释放示踪剂罗丹明B开展现场示踪实验,采用多站位连续观测的方式获取示踪剂的时空分布特征; 通过Delft 3D水动力学模块和粒子示踪模块耦合模拟示踪剂的扩散规律,获取实验期间小清河口的水平湍流扩散系数。本研究有助于揭示小清河口的水动力特征,同时为污染物在该河口的迁移模拟提供了数据支撑。
1 实验与方法 1.1 研究区概况小清河下游自石村至入海口为感潮河段,全长约70 km。石村下游20 km处建有王道闸,具有调水挡潮的功能。本研究选取王道闸至入海口作为研究区(图 1),研究区全长约43.6 km。小清河口河道宽度从王道闸至入海口逐渐增加,河口呈喇叭状向海扩展。王道闸下游河道宽约100 m,河口中游河道宽约150 m,河口下游河道宽约250 m; 河道平均水深约为3 m。小清河口潮汐类型为不规则半日潮,潮差约2 m,受潮汐和径流的双重影响,示踪河段纵向流速季节性变化明显,丰水期河流径流流速大于潮汐流速,枯水期潮汐流速大于河流径流流速[24]。
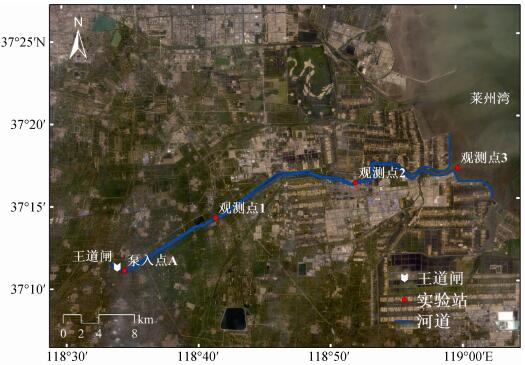 |
| 图 1 研究区示意图及观测点分布 Fig. 1 Schematic of the Xiaoqing River estuary and distribution of observation sites |
2017年5月3—18日在小清河口开展现场示踪实验。本文将示踪剂泵入点设置在王道闸下游约1 000 m处,5月4日上午9: 10(满潮),在河道中央利用蠕动泵持续、匀速地释放罗丹明B (RhB)溶液(浓度为20 g/L),泵入速度约为1.6 L/min,连续泵入总时间为5 h 10 min,RhB总投加量为10 kg。为了监测示踪剂的扩散情况,本文分别在泵入点下游11.5 km(观测点1)、30.1 km(观测点2)和43.6 km(观测点3)处设置连续观测站点,监测频率为1 h。
实验开始前,分别在3个观测站位取背景河水,用于配制标准曲线,以去除河水基质干扰。实验期间,利用不锈钢采水器在3个观测站的河道中央定时采集表层水,具体采样情况如表 1所示。水样经0.45 μm针式过滤器过滤后装入15 mL塑料离心管,拧紧瓶盖,置于加冰的保温箱内避光保存。样品运回实验室后,立即用荧光光谱仪(F-7000,Hitachi,Japan)进行分析。分析条件为: 激发波长550 nm,发射波长580 nm。采用外标法定量,河水中RhB的检出限为0.01 μg/L。
| 站位 | 布放仪器 | 布放时间 | 采样周期 | 采样频率/h | 样品量/个 |
| 泵入点 | 电磁海流计(AEM,ALEC) 水位计(RBRdute TD wave,RBR) 水质仪(GL-500,Global Water) |
5月3—17日 | — | — | — |
| 观测点1 | 电磁海流计(AEM,ALEC) YSI (V2-6600,YSI) |
5月3—17日 | 5月4日9: 30—5月17日7: 30 | 1 | 310 |
| 观测点2 | 电磁海流计(AEM,ALEC) 水位计 (RBRdute TD wave,RBR) YSI (V2-6600,YSI) |
5月3—17日 | 5月4日19: 00—5月18日10: 00 | 1 | 326 |
| 观测点3 | ADCP (瑞江1 200 kHz,RDI) 温盐深仪 (XR-420,RBR) |
5月3—17日 | 5月5日19: 00—5月17日10: 00 | 1 | 278 |
| 注: “—”表示无采样计划 | |||||
为了获取研究区的水文参数,以便为后续的模型模拟和验证工作提供基础数据,本文在泵入点及3个观测站位分别布放了相应的观测仪器,各站位仪器布放情况如表 1所示。
1.3 示踪模型构建 1.3.1 模型简介本文利用Delft 3D模型的FLOW模块和PART模块对示踪实验结果进行模拟。Delft 3D-FLOW是一个三维河流、海洋水动力模型。由FLOW模块计算得到的水动力条件(流速、水位、密度、盐度、垂直涡流和粘度等)可作为Delft3D其他模块的输入文件。FLOW模块基于Boussinesq假定和静水压假定,在垂向动量方程中不考虑垂直加速度,求解不可压缩流体的纳维-斯托克斯方程,控制方程建立在正交曲线坐标系(ξ, η)下[25]。其中,二维水动力数值模拟的连续性方程(1)和动量方程(2)—(4)如下。
垂向平均的连续性方程:
| $ \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{{\sqrt {{G_{\zeta \zeta }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \left[ {(d + \zeta)U\sqrt {{G_{\eta \eta }}} } \right]}}{{\partial \xi }} + \\ \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \left[ {(d + \zeta)V\sqrt {{G_{\xi \xi }}} } \right]}}{{\partial \eta }} = Q, $ | (1) |
ζ为参考参照平面以上的水深值,d是参照平面以下的水深值;
| $ Q = H\int_{ - 1}^0 {\left({{q_{{\rm{in}}}} - {q_{{\rm{out}}}}} \right)} {\rm{d}}\sigma + P - E, $ | (2) |
H为总水深; qin和qout分别为源和汇; P为降水量; E为蒸发量。
垂向平均的动量方程:
ξ方向:
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial u}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial u}}{{\partial \eta }} + \frac{w}{{d + \zeta }}\frac{{\partial u}}{{\partial \sigma }} - \\ \frac{{{v^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\sqrt {{G_{\eta \eta }}} }}{{\partial \xi }} + \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\sqrt {{G_{\xi \xi }}} }}{{\partial \eta }} - fv\\ = - \frac{1}{{{\rho _0}\sqrt {{G_{\xi \xi }}} }}{P_\xi } + {F_\xi } + \frac{1}{{{{\left({d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left({vV\frac{{\partial u}}{{\partial \sigma }}} \right) + {M_\xi }, \end{array} $ | (3) |
η方向:
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial v}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial v}}{{\partial \eta }} + \frac{w}{{d + \zeta }}\frac{{\partial v}}{{\partial \sigma }} + \\ \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \xi }} - \frac{{{u^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\xi \xi }}} }}{{\partial \eta }} - fu\\ = - \frac{1}{{{\rho _0}\sqrt {{G_{\eta \eta }}} }}{P_\eta } + {F_\eta } + \frac{1}{{{{\left({d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left({vV\frac{{\partial u}}{{\partial \sigma }}} \right) + {M_\eta }, \end{array} $ | (4) |
u,v,w分别为ξ,η,σ方向上的速度。
Delft 3D-PART模块通过粒子追踪的方法模拟物质输运和简单的水质过程。粒子追踪方法基于随机游走理论或蒙特卡罗理论,可以在复杂的空间模式中描述水质过程,解决子网格浓度分布[26]。PART模块假设粒子扩散由湍流引起,水平方向的扩散系数与时间相关。根据气体动力学理论和布朗运动理论,分子扩散系数可表示为
| $ {D_{\xi, \eta }} = a{t^b}, $ | (5) |
t代表粒子的迁移时间(单位: s),粒子被释放时,t=0; 系数a和b(0<b<1)由模型校准所得。
1.3.2 模型构建 1.3.2.1 构建网格和地形数据在RGFGRID模块中选择笛卡尔坐标系,导入边界文件,分别在与边界平行和垂直的方向手动添加样条曲线(spline),生成粗略的网格; 然后在每个网格内生成等数量的加密网格(图 2),检验网格正交性后,保存为网格文件(.grd)。研究区的总网格数为12×1 472。小清河口的水深散点数据来自两部分: 王道闸至羊口港段的水深为实测值,羊口港以下河段的水深值取自海图。利用Arcgis对散点水深数据进行数字化处理,导出坐标值与深度值,保存成水深文件(.xyz文件); 使用三角插值选项进行插值,然后进行内部扩散和平滑处理,将插值处理后的文件保存成地形文件(.dep)。结果如图 2所示。
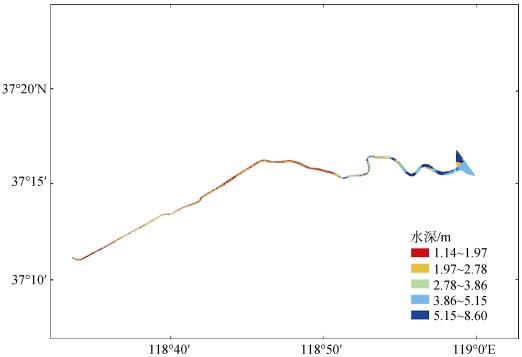 |
| 图 2 小清河口水深地形图 Fig. 2 Topographic map of the Xiaoqing River estuary |
将生成的边界文件、网格文件和地形文件导入FLOW模块,设置模拟时间段为2017年3月20日— 2017年5月19日,参照时间为2017年3月1日,时间步长设置为30 min; 其他模型参数均采用默认值。由于缺乏模拟区上边界的实测流量数据,本文基于泵入点的实测流速(5月3日至5月17日)与河道横截面积估算河流的径流量; 其他时段的河流径流量取平均值8.3 m3/s。模型的开边界位于观测站3,使用该站实测水深数据作为开边界条件。
1.3.2.3 构建粒子示踪模型将FLOW模块生成的水动力文件导入PART模块。将模拟目标设置为示踪剂(Tracer),设置粒子数量为10 000。释放方式为连续释放,同时设置释放点位置、释放时间(5月4日09: 10: 00—14: 10: 00)与示踪剂浓度(20 g/L); 调整扩散系数和示踪剂衰减常数; 设置观测站位; 最后设置输出文件的时间范围和步长。
1.4 模型验证利用示踪实验期间在各观测站位获取的水文数据进行流速、流向和水深的验证,利用示踪剂实测浓度验证示踪模拟结果。分别采用相关性系数(R2)和均方根误差(RMSE)评估模型模拟结果。
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{\left({i = 1} \right)}^N {{{\left[ {{{\left({{C_{{\rm{sim}}}}} \right)}_i} - {{\left({{C_{{\rm{obs}}}}} \right)}_i}} \right]}^2}} }, $ | (6) |
其中,Csim为示踪剂的模拟浓度值; Cobs为示踪剂的实测浓度值; N为数据量。
2 结果与讨论 2.1 基于实测水文参数的小清河口水动力特征分析河口水体受河水径流和潮汐的双重影响,其水深和电导率呈现周期性变化。因此,电导率和水深是反映河口水体运动的重要水文参数。由于海水的电导率远大于河水,海水上溯可引起河口水体电导率增大,同时伴随水深升高。如图 3所示,泵入点处的电导率总体呈现上升的趋势,最大值为16 mS/cm; 且此处的电导率与水深变化无关,水深降低时电导率缓慢增大,水深增加时电导率急剧增加。这表明潮汐不是控制此处水体电导率的单一因素。RhB分子中含有氯离子,当其溶于水后,会电离出氯离子,引起周围水体电导率增加。在RhB释放期间(09: 10—14: 10),尽管时处落潮,河水电导率仍随RhB的泵入缓慢增加; 释放结束后,涨潮时(16: 10—19: 10),高电导率的RhB水团被推回泵入点,加之海水上溯,导致此时水体电导率急剧增加。此外,同样是涨潮,当潮能较大时(03: 10—07: 10),更多的RhB水团被推回泵入点以及更多的海水上溯,导致此时电导率增加的更明显。这表明非汛期时潮汐对小清河口上游的水动力也有较强的影响。
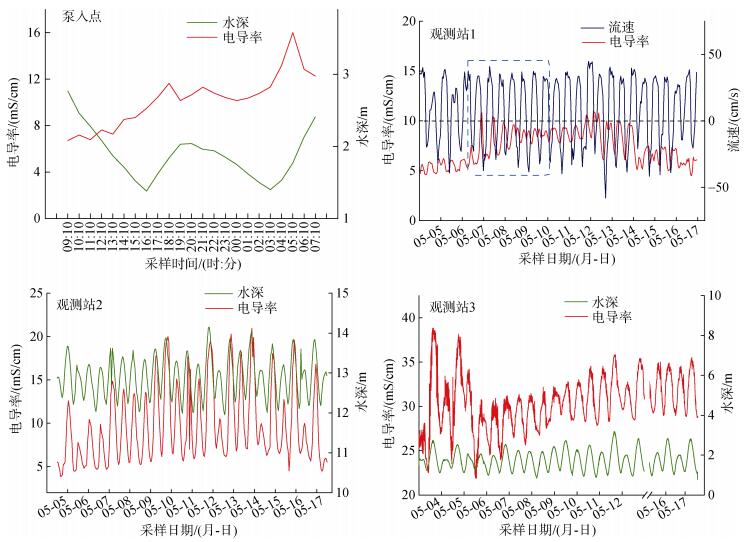 |
| 图 3 不同站位的水文参数 Fig. 3 Conductivity and depth/flow rate for different sites |
由于观测站1没有布放水位计,无法获取水深实测值,因此本文使用流速方向指示潮汐变化规律。沿河方向的流速有正负之分,其中正值代表流向向海,即落潮; 负值表示流向向岸,即涨潮。当流速值由正值逐渐变为0时,水深值最小; 当流速值由负值逐渐变为0时,水深最大。如图 3所示,该处的电导率与流速方向之间的关系并不固定。5月6日至5月10日,落潮时(流速为正),电导率增加; 涨潮时(流速为负),电导率降低。表明此时该处的电导率主要受上游高电导率的河水(RhB电离)控制。5月10日后,RhB水团迁移至观测站1的下游,涨潮时(流速为负)电导率增加。如图 3所示,观测站2和3的电导率与其水深变化规律一致,受潮能变化的影响两个站位电导率的峰值呈现高低起伏的变化趋势,表明这两个站位的电导率完全由潮汐所控制。因为这两个站位距离泵入点足够远(>30 km),RhB水团在迁移过程中不断被稀释,当其到达观测站2和3时,并没有对此处水体的电导率构成影响。此外,观测站3处水体的电导率明显高于观测站2,表明越接近河口下游,潮汐的作用越明显。结合4个站位水文参数的变化规律可发现,非汛期时小清河口的水动力主要受潮汐控制,尤其是河口下游区域。
2.2 示踪剂在小清河口的扩散规律分析观测站1相距泵入点11.5 km,示踪剂的质量浓度峰值出现在5月6日至5月7日,随后RhB的浓度维持在一定水平波动,5月12日RhB的浓度明显降低(图 4)。观测站2距离泵入点约30 km,RhB到达此处的时间大约为5月10日; 5月15日观测站2的RhB浓度达到最大值; 5月18日,即实验结束时仍能在观测站2检测到RhB(图 4)。因此实验期间,示踪剂并没有到达观测站3。总体上,示踪剂在小清河口向海传输的速度较慢,释放14 d后,RhB仍在距释放点约30 km的区域回荡。这主要是因为示踪实验期间小清河正值枯水期,河流径流量较小,在潮汐作用下,示踪剂向海扩散受阻。由此可推断出,非汛期时,来自河流输入的污染物容易在小清河口滞留,对河口生态系统构成巨大威胁。
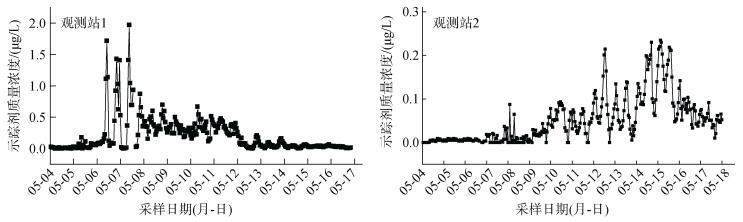 |
| 图 4 示踪剂的时空分布规律 Fig. 4 Spatial and temporal distribution of tracer |
小清河口水动力模拟时段为2017年3月20日0点至2017年5月19日0点。为了验证小清河口二维水动力模型的准确性,本文分别对各站位的水深和流速的实测值与模拟值进行了相关性分析。
泵入点的水深实测值与模拟值如图 5所示,二者的变化趋势一致(P<0.01),相关系数(R2)为0.878,且水深实测值与模拟值在数量级上也较为接近。5月11日,大潮引起水深明显增加,二维动力学模型很好地模拟出这一过程。由于观测站1缺少水深实测值,故无法进行对比。如图 5所示,观测站2的水深实测值与模拟值也呈现高度一致性(R2=0.955,P<0.01); 对于5月4日至5月7日观测站2水深的不规则波动,该模型也能很好的模拟。D站位的水深观测值作为模型的开边界条件,因此模拟值与实测值也基本重合。
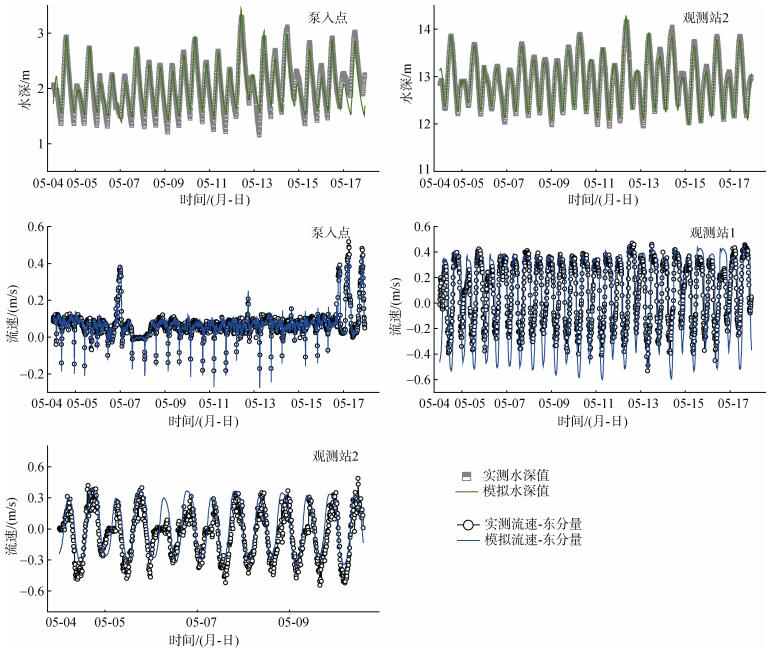 |
| 图 5 各站位水深与流速的实测值和模拟值 Fig. 5 Measured and simulated water depth and flow rate for different sites |
如图 5所示,泵入点处的流速在东-西方向上以正值为主,即为向海方向(东方向),表明此处流向主要受河流径流控制。泵入点处东-西向的流速实测值与模拟值呈高度一致性(R2=0.956,P<0.01)。观测站1处的流速实测值与模拟值如图 5所示,二维水动力模型可以较好地模拟该站东-西方向的流速(R2=0.668,P<0.01)。观测站2处的海流计发生故障,仅记录了5月4日至10日之间的流速数据(图 5)。结果表明,观测站2处的东-西向流速模拟值与实测值拟合度较高(R2=0.667,P<0.01)。
总体上,水深和流速的模拟结果与实测值拟合度较好。表明本文基于Delft 3D-FLOW模块构建的二维动力学模型能够提供较准确的动力场,该动力学模型可以与独立的示踪模块或水质模块进行耦合,进而实现小清河口目标物质的迁移和归趋模拟。
2.4 小清河口示踪模拟分析由于采样期间,示踪剂未迁移至观测站3。所以本文仅选取观测站1和观测站2的示踪剂实测值来验证示踪模型的模拟结果。两个观测站位的示踪剂实测值与模拟值如图 6所示。观测站1的示踪剂模拟值与实测值较为接近,优化后的模型可以很好地再现5月6日至5月8日的浓度峰; 5月8日至5月15日的低浓度峰,该模型也能较好地拟合。相关性分析结果表明,观测站1的示踪剂模拟值与实测值之间呈显著正相关(P<0.01),相关系数(R2)为0.717(图 6),均方根误差(RMSE)为0.176。如图 6所示,优化后的模型也能很好地拟合观测站2的示踪剂浓度变化规律。该示踪模型可以很好地再现示踪剂峰值出现的时间,模拟值在量级上与实测值也较为接近。相关性分析结果表明,观测站2的示踪剂模拟值与实测值之间呈显著正相关(P<0.01),二者之间的相关系数R2=0.707(图 6),均方根误差(RMSE)为0.036。
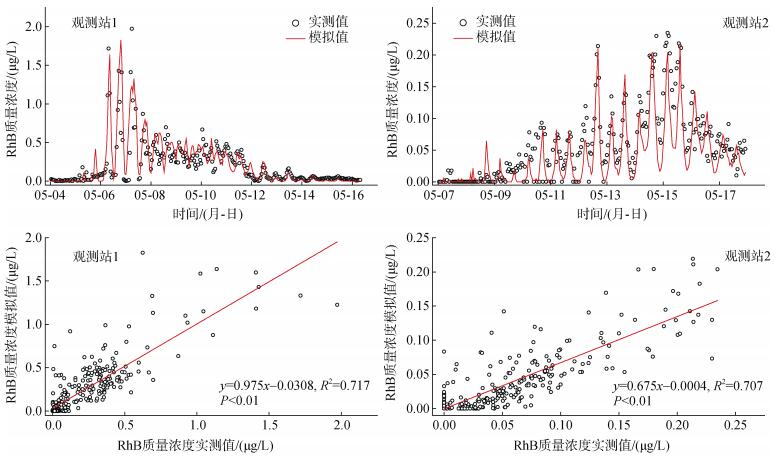 |
| 图 6 各站位示踪剂的实测值和模拟值及相关性分析 Fig. 6 Measured and simulated concentration of tracer for different sites,and correlation analysis between simulated and observed values of tracer |
经过模型参数调试,小清河口示踪剂的水平扩散系数被确定为
RhB被释放后导致周围水体电导率增加,因此会干扰感潮河口部分区域水体的电导率变化规律。非汛期时,潮汐是控制小清河口水力特征的关键因素; 且越接近河口下游,潮汐的作用越明显,表现为河口下游东-西向流速的绝对值较为接近。河口上游水体的流向以向海方向为主,表明此处河流径流的作用强于潮汐。由于非汛期河流径流较弱,示踪剂在小清河口向海传输的速度较慢。在潮汐的作用下,释放14 d后,RhB仍在距离释放点下游30 km的区域回荡。模型验证结果表明,本文基于Delft 3D-FLOW模块构建的二维动力学模型能够准确地模拟小清河口的动力场,为后续的示踪模拟提供了可靠的动力学文件。通过Delft 3D-FLOW模块和Delft 3D-PART模块耦合,本文成功模拟了不同观测站位示踪剂浓度的变化规律。示踪剂模拟值与实测值呈显著正相关(P<0.01),相关系数大于0.7。经过模型参数调整,小清河口水平湍流扩散系数确定为
| [1] |
吴群河. 梅江染料示踪实验[J]. 中山大学学报, 1990, 9(1): 25-29. Wu Qunhe. A tracing experiment in Meijiang River[J]. Journal of Sun Yatsen University, 1990, 9(1): 25-29. |
| [2] |
吕巍, 张建军, 闫莉, 等. 黄河潼关河段污染物示踪扩散研究[J]. 人民黄河, 2016, 38(9): 59-63. Lv Wei, Zhang Jianjun, Yan Li, et al. Research of the pollutants tracer experiment in the Tongguan reach of the Yellow River[J]. Yellow River, 2016, 38(9): 59-63. |
| [3] |
肖翔群, 连煜, 胡国华, 等. 黄河孟津段扩散系数的确定[J]. 水资源保护, 1996, 12(1): 38-40. Xiao Xiangqun, Lian Yu, Hu Guohua, et al. Determination of diffusion coefficient in Mengjin reach of the Yellow River[J]. Water Resources Protection, 1996, 12(1): 38-40. |
| [4] |
邵庆山, 张红军. 多沙大河的扩散示踪研究[J]. 环境科学进展, 1994, 2(3): 65-70. Shao Qingshan, Zhang Hongjun. Study on diffusion tracer of sandy river[J]. Progress in Environmental Science, 1994, 2(3): 65-70. |
| [5] |
于靖, 张华. 城市小型河流水动力弥散和潜流交换过程[J]. 水科学进展, 2015, 26(5): 714-721. Yu Jing, Zhang Hua. Hydrodynamic dispersion and hyporheic exchange in a small urban stream[J]. Advances in Water Science, 2015, 26(5): 714-721. |
| [6] |
顾莉, 华组林. 天然河流纵向离散系数确定方法的研究进展[J]. 水利水电科技进展, 2007, 27(2): 85-89. Gu Li, Hua Zulin. Advances in determination of longitudinal dispersion coefficient of natural rivers[J]. Advances in Science and Technology of Water Resources, 2007, 27(2): 85-89. |
| [7] |
周世良. 水扩散示踪实验在环评中的应用[J]. 海峡科学, 2009(6): 3-4, 8. Zhou Shiliang. Application of water diffusion tracer test in environmental impact assessment[J]. Straits Science, 2009(6): 3-4, 8. |
| [8] |
Hiatt M, Passalacqua P. Hydrological connectivity in river deltas:The first-order importance of channel-island exchange[J]. Water Resources Research, 2015, 51(4): 2264-2282. |
| [9] |
Williams C F, Nelson S D. Comparison of Rhodamine-WT and bromide as a tracer for elucidating internal wetland flow dynamics[J]. Ecological Engineering, 2011, 37(10): 1492-1498. |
| [10] |
Wolkersdorfer C. Tracer test in a settling pond:The passive mine water treatment plant of the 1 B mine pool, Nova Scotia, Canada[J]. Mine Water and the Environment, 2011, 30(2): 105-112. |
| [11] |
李培泉. 应用罗丹明-B作示踪剂研究海水的稀释扩散规律[J]. 海洋科学, 1981, 5(2): 38. Li Peiquan. Study on the dilution and diffusion of seawater using Rhodamine B[J]. Marine Sciences, 1981, 5(2): 38. |
| [12] |
梁健. 污染扩散的示踪剂罗丹明-B的试验[J]. 重庆环境科学, 1990, 12(6): 41-44. Liang Jian. Test of contamination diffusion using tracer rhodamine B[J]. Chongqing Environmental Science, 1990, 12(6): 41-44. |
| [13] |
聂艳华, 段文刚, 树锦. 示踪法定量分析水流连通问题[J]. 长江科学院院报, 2013, 30(2): 16-19. Nie Yanhua, Duan Wengang, Shu Jin. Quantitative analysis of flow connectivity by tracing method[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(2): 16-19. |
| [14] |
范翻平. 基于Delft3D模型的鄱阳湖水动力模拟研究[D]. 南昌:江西师范大学, 2010. Fan Fanping. The study of hydrodynamic simulation of Poyang Lake based on Delft 3D model[D]. Nanchang:Jiangxi Normal University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10414-1011031299.htm |
| [15] |
龚文平, 李昌宇, 林国尧, 等. Delft 3D在离岸人工岛建设中的应用:以海南岛万宁日月湾人工岛为例[J]. 海洋工程, 2012, 30(3): 35-44. Gong Wenping, Li Changyu, Lin Guoyao, et al. Application of Delft 3D model for plan design of an artificial island:A case study for the artificial island construction in the Riyue Bay, Wanning City, Hainan Island[J]. The Ocean Engineering, 2012, 30(3): 35-44. |
| [16] |
李林娟, 童朝锋. 基于Delft3D-Flow模型的长江口盐度扩散规律模拟[J]. 人民长江, 2016, 47(23): 107-111. Li Linjuan, Tong Chaofeng. Simulation of salinity diffusion of Yangtze River estuary based on Delft3D-flow model[J]. Yangtze River, 2016, 47(23): 107-111. |
| [17] |
陆仁强, 何璐珂. 基于Delft3D模型的近海水环境质量数值模拟研究[J]. 海洋环境科学, 2012, 31(6): 877-880. Lu Renqiang, He Luke. Study on numerical simulation of environmental quality in coastal water based on Delft 3D model[J]. Marine Environmental Science, 2012, 31(6): 877-880. |
| [18] |
黄庆超, 石巍方, 刘广龙, 等. 基于Delft3D的三峡水库不同工况下香溪河水动力水质模拟[J]. 水资源与工程学报, 2017, 28(2): 33-39. Huang Qingchao, Shi Weifang, Liu Guanglong, et al. Modeling the hydrodynamics and water quality of Xiangxi River under different working conditions of Three Gorges Reservoir based on Delft 3D[J]. Journal of Water Resources & Water Engineering, 2017, 28(2): 33-39. |
| [19] |
Abdel-moati A R. Behaviour and fluxes of copper and lead in the Nile River estuary[J]. Estuarine Coastal and Shelf Science, 1990, 30(2): 153-165. |
| [20] |
Simpson J H, Vennell R, Souza A J. The salt fluxes in a tidally-energetic estuary[J]. Estuarine Coastal and Shelf Science, 2001, 52(1): 131-142. |
| [21] |
李嘉, 张瑞杰, 王润梅, 等. 小清河流域抗生素污染分布特征与生态风险评估[J]. 农业环境科学学报, 2016, 35(7): 1384-1391. Li Jia, Zhang Ruijie, Wang Runmei, et al. Distribution characteristics and ecological risk assessment of antibiotic pollution in Xiaoqing River watershed[J]. Journal of Agro-Environment Science, 2016, 35(7): 1384-1391. |
| [22] |
Shen J Y, Luo X X, Zheng H, et al. Pollution and ecological risk characteristics of heavy metals in surface sediments in Xiaoqing River Estuary and adjacent sea areas[J]. Environmental Chemistry, 2017, 36(7): 1516-1524. |
| [23] |
Shi Y L, Vestergren R, Xu L, et al. Characterizing direct emissions of perfluoroalkyl substances from ongoing fluoropolymer production sources:A spatial trend study of Xiaoqing River, China[J]. Environmental Pollution, 2015, 206: 104-112. |
| [24] |
Zou T, Zhang H, Meng Q J, et al. Seasonal hydrodynamics and salt exchange of a shallow estuary in northern China[J]. Journal of Coastal Research, 2016, 74: 95-103. |
| [25] |
Deltares. Delft3D-FLOW user manual version 3[J]. Netherlands:Delft, 2009. |
| [26] |
Deltares. Delft3D-PART user manual version 2[J]. Netherlands:Delft, 2009. |
| [27] |
罗家海. 河口及海湾地区水平扩散系数确定研究[J]. 海洋环境科学, 1989, 8(3): 36-40. Luo Jiahai. Study on determination of horizontal diffusion coefficient in estuary and bay[J]. Marine Environmental Science, 1989, 8(3): 36-40. |
| [28] |
匡国瑞, 俞光耀, 张淮, 等. 现场海域水平、铅直扩散系数的推算[J]. 海洋学报, 1994, 16(4): 23-34. Kuang Guorui, Yu Guangyao, Zhang Huai, et al. Estimation of horizontal and vertical diffusion coefficient in Bohai sea[J]. Acta Oceanologica Sinica, 1994, 16(4): 23-34. |
 2020, Vol. 44
2020, Vol. 44


