
文章信息
- 李海涛, 袁森. 2020.
- LI Hai-tao, YUAN Sen. 2020.
- 基于遗传算法和BP神经网络的海洋工程材料腐蚀预测研究
- Corrosion prediction of marine engineering materials based on genetic algorithm and BP neural network
- 海洋科学, 44(10): 33-38
- Marine Sciences, 44(10): 33-38.
- http://dx.doi.org/10.11759/hykx20191118003
-
文章历史
- 收稿日期:2019-11-18
- 修回日期:2020-02-13
海洋工程材料在海洋环境中各种物理因素、化学因素以及生物因素的共同作用下,极易发生腐蚀破坏,海洋工程材料腐蚀在经济上和安全上容易引发较大危害。研究海洋工程材料在海洋环境下的腐蚀规律,对海洋开发利用,海洋环保以及海洋装备的制造等具有重要意义[1]。在海洋环境中,引起海洋工程材料进行腐蚀的影响因素较多,其影响因素与海洋工程材料的相关反应皆为非线性相关,因此传统的数学函数无法适用于该相关反应,因此目前多采用神经网络模型、灰关联分析、SWM等[2]科学算法对海洋工程材料在海洋环境中的腐蚀速率进行预测,如宋诗哲等[3]建立了海水影响因素、碳钢合成元素以及碳钢的腐蚀反应的人工神经网络的腐蚀预测模型; 朱相荣等[4]将灰关联分析应用到海水腐蚀相关性的研究; 邓志安等[5]建立由模糊算法优化神经网络的模型进行腐蚀速率预测的研究; 胡松青等[6]采用采用反向传播(Back Propagation,BP)神经网络模型进行研究输油管线内的腐蚀反应等。
与其他预测模型相比,BP神经网络具有高效性和适应性,尤其是对于非线性的、无规律的海洋工程材料腐蚀数据,在海洋工程材料的腐蚀速率研究工作中利用BP神经网络模型,能够获取到比较准确的预测结果。但是,应用传统的BP神经网络模型容易出现网络模型训练周期较长、常常导致局部过小、误差较实际值偏大等问题[7]。为了使上述问题得到合理性的解决,本文研究提出将遗传算法(GA)优化BP神经网络的模型应用到海洋工程材料腐蚀速率的预测中。遗传算法的特点是全局寻优,能够将BP神经网络的阈值和权值进行优化,避免了传统BP网络模型在数据训练上易出现陷入局部极小值等问题。GA-BP网络模型具有相对稳定,迭代次数较少,与传统BP神经网络相比误差较小等优点。BP神经网络和遗传算法在人工智能方向发展已经成熟,现如今使BP神经网络和遗传算法彼此相融合,互补长短,使其不仅仅具有理论上的优势,在实践中也可有长远的应用[8]。
1 基本理论 1.1 BP神经网络BP神经网络[9]是由Rumelhard和McCelland于1986年提出,该网络模型的构建是基于人类大脑神经网络特征和构造的基础,具有自我学习和归纳等特点,应用于各个领域中的预测研究工作中。BP神经网络模型可以很好地模拟海洋工程材料的腐蚀速率以及与其相关的各环境要素之间的关系, 将简单的条件输入和结果输出的线性相关替换为非线性相关的映射,在计算海洋工程材料腐蚀的速率工作中,缺少与之相匹配的计算公式并且常常困于经验主义导致精度较低,该模型的提出能够很好的解决该问题。BP神经网络模型的构建主要有三个部分: 一是BP神经网络模型的网络初始化,二是前向传播信号,三是反向传播误差。BP神经网络能够通过训练试验数据对BP神经网络结构中的阈值和权值继续调节,可以使BP神经网络模型的误差平方和达到最小。然在实际的应用中,网络模型训练时间较长、易陷入局部较小、误差较实际值偏大等问题在BP神经网络常常出现。BP神经网络计算流程如图 1所示。
 |
| 图 1 BP神经网络计算流程图 Fig. 1 BP neural network calculation flow chart |
遗传算法(GA)是一种以“适者生存”为基础的优化算法,具有普遍随机性、适用性强和并行度高等优点,利用复制、交叉、变异等操作步骤,能够将问题解编码表示的“染色体”群一代代不断进化, 从而群体收敛到最合适,并最终获取到目标问题的最优解[10]。遗传算法有着理论及实操简易、适应性强以及限制条件约束弱等优点,且具有隐含并行性以及在全局寻优的过程中有着突出优势,遗传算法能够与其他智能算法进行融合,该方式已在各个领域得到了全面的实际应用。遗传算法能够在搜索全局方面达到最优是基于模仿自然界生物进化机制实现的。遗传算法使用适者生存的原则可对所有试验数据进行逐次操作,通过搜索全局可得到一个与实际误差最小的最优方案。遗传算法的流程如图 2所示。
 |
| 图 2 遗传算法模型 Fig. 2 Genetic algorithm model |
本文的研究内容为海洋工程材料在海洋环境中的腐蚀速率预测,特选取2Cr1312不锈钢,Q235B碳钢和6082铝合金三种代表性的海洋工程材料作为本次研究的实验对象,该数据皆来源于中国腐蚀与防护网。对海洋工程材料的腐蚀影响因素进行研究,以收集的环境影响因素数据为基础,经遗传算法理论计算相关影响因素的影响率,由表 1影响因素的影响率表可以看出,海洋环境中的水温、溶解氧、盐度、电导率、pH值和氧化还原电位等六种海洋环境影响因素在海洋工程材料腐蚀过程中与该材料的腐蚀速率有着密切联系。
| 影响因素 | 水温 | 溶解氧 | 风速 | pH值 | 相对湿度 | 降雨量 | ORP值 | 盐度 | 电导率 | 气温 |
| 影响率/% | 21.78 | 28.65 | 7.83 | 27.41 | 13.29 | 14.76 | 23.18 | 25.46 | 24.91 | 5.76 |
特从中国腐蚀与防护网上面选取三种基本海洋工程材料的六种基本海洋环境因素数据,共计1 350组数据,每组数据有2Cr1312不锈钢,Q235B碳钢和6082铝合金三种材料,共计4 050条数据,通过数据清洗,去除错误以及冗余数据23条,剩余4 027条数据。其中选择4 024条数据作为模型的训练数据,剩余数据作为2Cr1312不锈钢,Q235B碳钢和6082铝合金的测试数据。2Cr1312不锈钢环境影响因素以及相应腐蚀速率部分数据如下表 2所示。将该数据输入GA-BP网络模型进行训练,与实际腐蚀速率进行相比较且与传统BP神经网络模型进行预测结果和训练时间上进行对比。
| 影响因素 | 水温/℃ | 溶解氧/(mg/L) | 盐度/% | 电导率/(mS/cm) | pH 值 | 氧化还原电位/mV | 腐蚀速率/(mm/a) |
| 1 | 14.68 | 7.73 | 30.38 | 36.15 | 8.09 | 197.63 | 0.013 1 |
| 2 | 26.89 | 7.7 | 30.88 | 49.2 | 8.25 | 106.72 | 0.004 4 |
| 3 | 17.4 | 5.6 | 32 | 38.42 | 8.16 | 153.29 | 0.009 5 |
| 4 | 20.9 | 5.3 | 27 | 31.26 | 8.17 | 193.25 | 0.013 4 |
| 5 | 26.7 | 4.5 | 34 | 40.39 | 8.30 | 113.76 | 0.007 4 |
| 6 | …… | …… | …… | …… | …… | …… | …… |
在海洋工程材料腐蚀速率预测的研究工作之中, 能够首先得知BP神经网络的输入层和输出层的节点个数,输入层为海洋工程材料腐蚀影响因素,影响因素包含水温、溶解氧、盐度、电导率、pH值和氧化还原电位共6个影响因素,输入层节点个数为6, 输出层节点个数为1(腐蚀速率)。因此,如何确定隐含层的个数成为BP神经网络模型优化的关键。可由下式获取隐含层节点个数:
| $ L = \sqrt {m + n} + a, $ | (1) |
上式中, L为隐含层节点个数, m,n为输入层及输出层节点个数, a为[0-10]之间的常数。
经研究表明, 在BP神经网络模型中的隐含层节点个数确定方面,目前未有成熟的理论支撑,多数从事BP神经网络的研究人员确定隐含层的个数皆是根据以往的经验公式获取。
根据上述公式, 本文经过式(1)计算, 得出隐含层结点的区间范围为[4,11], 但由于公式具有经验性,导致误差过大,预测结果不够准确。通过对模型进行反复试验,当隐含层节点个数为8时,最终算法得到完美的收敛,该神经网络模型的预测精度最高,所以最终确定隐含层节点数为8。因此构建的BP神经网络拓扑结构为6-8-1,BP神经网络模型构建后的结构图如图 3所示。
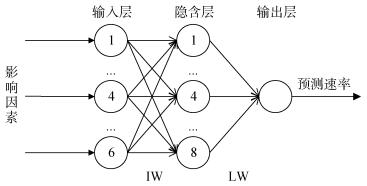 |
| 图 3 BP神经网络模型结构图 Fig. 3 Structure of BP neural network model |
图 3中,影响因素为水温、溶解氧、盐度、电导率、pH值和氧化还原电位,IW和LW表示各层中的连接权值,预测速率为输出结果。
BP神经网络模型的输入层神经元, 通过研究选择pH值、电导率、水温、溶解氧、盐度和氧化还原电位六个影响海洋工程材料腐蚀速率的环境数据, 利用Sigmoid函数作为BP神经网络模型的转移函数,即:
| $ {\rm{f}}\left(x \right) = \frac{1}{{1 + {e^{ - x}}}}, x \in \left({0, 1} \right). $ | (2) |
BP神经网络模型由于具有陷入局部最小的问题,因此,为提高模型的精准度和收敛速率, 利用Delta学习规则应用于BP神经网络,从而使误差信号的目标函数达到最小:
| $ \Delta {W_{ij}}\left(n \right) = \eta \left({{y_i}\left(n \right) - {O_j}\left(n \right)} \right){O_i}\left(n \right). $ | (3) |
上述公式中, ΔWij(n)为当输入为n时的权值(i与j之间),yi为i的期望输出值, η为学习效率,Oi和Oj为神经元i和j的激活值。
通过试验研究工作,设定训练次数为10 000,学习效率η为0.50,误差容量为0.000 01。
2.3 基于GA优化BP模型的构建采用遗传算法对BP神经网络进行优化,主要有两个方面表现: 一遗传算法具有全局寻优的特征,能够优化BP神经网络模型的权阈值; 二是优化网络的拓扑结构[11]。
在对BP神经网络模型进行训练之前,首先引入遗传算法对BP神经网络进行阈值和权值的优化。对参数进行初始设定: 交叉概率为0.6, 变异概率为0.05, 种群规模为50, 进化代数为100。下面讲述具体的优化步骤:
1)BP神经网络模型的阈值和权值的编码过程是选取实数编码方式,网络模型的各层神经元个数决定着编码长度y。设定BP神经网络共三层,输入层、隐含层和输出层,通过计算得出隐含层的个数,确定6-8-1为模型的结构,则权值的个数为6×8+8×1=56个,阈值的个数为8+1=9, 最终通过计算得到65为编码长度y。
2) 本次研究将种群规模设定为50。
3)BP神经网络模型得出的实际值和结果输出值的越接近,那么染色体则有着优秀的体现,所以染色体的适用值E计算公式为:
| $ E = \sum\limits_{k = 1}^N {{{\left({{T_k} - {Y_k}} \right)}^2}}, $ | (4) |
式中N表示样本数量;T为期望值;Y为模型输出值。其中个体的适用度值是染色体适用值的倒数。
4)将实验数据进行归一化处理是网络模型进行训练的前提条件,使相关数据能够转化为[0,1]之间的数是此步骤的目的,能够将归一化处理的数据更好的应用于BP神经网络模型的训练,最终能够使得模型程序在进行训练时运行时耗时减少,提高模型的预测准确率。该步骤的公式如下所示:
| $ {{\rm{X}}^*} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}, $ | (5) |
上式中, Xmax和Xmin分别是该样品数据的最大值和最小值。
5)在Matlab中,选取其中的遗传算法工具箱,利用该工具箱进行优化操作,通过工具箱解码获取到的种群最优个体的最优解,优化后的BP神经网络模型的初始阈值和权值能够通过此步骤得到,目的为优化BP神经网络模型。
6)多次训练网络模型获得最优解,获取最优BP神经网络模型的阈值和权值。
2.4 网络模型构建在BP神经网络模型基础上, 应用Matlab数学建模工具,建立实现GA-BP网络模型的实现程序,将相关输入条件从已知的样本数据中提取,并将其整合为最简属性集合, 从而构建神经网络并将该集合作为神经网络输入节点,并在环境影响因素和材料腐蚀速率之间建模, 并对数据进行训练。构建后的GA-BP网络预测模型流程图如图 4所示。
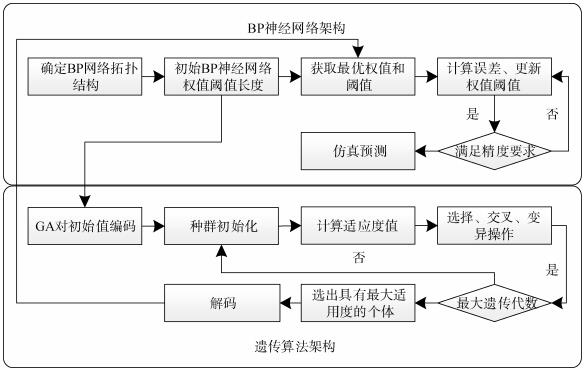 |
| 图 4 网络预测模型流程图 Fig. 4 Network prediction model flow chart |
将海洋工程材料2Cr1312不锈钢、Q235B碳钢和6082铝合金共计4 027条数据作为训练数据输入GA-BP网络模型进行训练。将2Cr1312不锈钢、Q235B碳钢和6082铝合金的水温、溶解氧、盐度、电导率、pH值和氧化还原电位作为输入数据,输入的阈值和权值由遗传算法优化获得,利用Matlab分别编写传统BP神经网络模型和GA-BP网络模型函数,输入层与隐含层之间的传输函数选用Matlab中的Sigmod函数,隐含层与输出层之间的传输函数选用Matlab中purelin函数,学习函数采用“trainbr”进行训练。
神经网络学习效率为0.50,误差容量为0.000 01,训练次数为10 000; 遗传算法(GA)的染色体编码长度y=6×8+8×1+8+1=65,种群规模设定为50, 交叉概率设定为0.6, 变异概率设为设定为0.05, 经过多次试验迭代次数设定为100, 确保能通过遗传算法(GA)寻找到最优的初始化参数。
在Matlab环境下将构建完成的GA-BP神经网络模型进行训练,模型经过90余次训练,神经网络模型误差可达到0.000 01精度要求; 而传统的BP神经网络却经过4 000余次才达到0.000 01的精度要求。因此可以看出,GA-BP神经网络模型可以很好的拟合海洋工程材料腐蚀相关数据,预测效果较好。
3.2 实例分析将2Cr1312不锈钢,Q235B碳钢和6082铝合金的测试数据输入训练好的传统BP神经网络模型和GA-BP模型,可得出下表 3中的2Cr1312不锈钢,Q235B碳钢和6082铝合金的预测值,由表 3可以看出,与2Cr1312不锈钢,Q235B碳钢和6082铝合金实际腐蚀速率相比较,和实际腐蚀速率数值相吻合,同时可以看出利用GA-BP网络模型比传统BP神经网络模型相对误差较小,且训练时间相对较短。
| 材料牌号 | 真实值/(mm/a) | 传统BP神经网络模型 | GA-BP模型 | |||||
| 预测值/(mm/a) | 相对误差/% | 平均耗时时间/ms | 预测值/(mm/a) | 相对误差/% | 平均耗时时间/ms | |||
| 2Cr1312 不锈钢 | 0.004 | 0.003 14 | 21.5% | 9 | 0.003 76 | 6.0 | 5 | |
| Q235B 碳钢 | 0.028 3 | 0.018 62 | 34.204% | 15 | 0.026 57 | 6.11% | 8 | |
| 6082 铝合金 | 0.015 3 | 0.017 80 | 14.04% | 11 | 0.016 23 | 5.56% | 6 | |
本文通过将遗传算法和BP神经网络相融合,使两种算法优势互补进行的可行性研究。利用BP神经网络结合遗传算法对2Cr1312不锈钢,Q235B碳钢和6082铝合金海洋工程材料环境数据进行训练, 形成的网络模型在应用于海洋工程材料在海水环境中的腐蚀速率预测中,可使预测结果误差相对变小、平均耗时时间相对缩短, 同时海洋工程材料海水腐蚀速率预测使用该模型可大大提高实际的预测准确率。在海洋工程材料处于海洋环境中的腐蚀速率预测等研究工作中,使用基于遗传算法优化后的BP神经网络模型,能够减少危害性, 具有一定的扩展性、应用性以及推广价值。
| [1] |
刘学庆. 海洋环境工程钢材腐蚀行为与预测模型的研究[D]. 青岛:中国科学院海洋研究所, 2004. Liu Xueqing. Study on Corrosion Behavior and Prediction Model of Steel for Marine Environmental Engineering[D]. Qingdao:Institute of Oceanology, Chinese Academy of Sciences, 2004. http://cdmd.cnki.com.cn/Article/CDMD-80068-2004121261.htm |
| [2] |
李响, 余建星, 苗春生, 等. 基于遗传算法SVM的海洋环境腐蚀速率预测[J]. 中国海洋平台, 2018, 33(5): 56-62. Li Xiang, Yu Jianxing, Miao Chunsheng, et al. Corrosion rate prediction of marine environment based ongenetic algorithm SVM[J]. China Offshore Platform, 2018, 33(5): 56-62. |
| [3] |
宋来洲, 高志明, 宋诗哲. 人工神经网络优化碳钢表面TiO_2修饰膜制备工艺[J]. 中国腐蚀与防护学报, 2001, 2: 38-42. Song Laizhou, Gao Zhiming, Song Shizhe. Optimization of preparation process of TiO_2 mod-ified film on carbon scteel surface by artificial neural network[J]. Journal of Chinese Society for Corrosion and protection, 2001, 2: 38-42. |
| [4] |
朱相荣, 张启富. 海水中钢铁腐蚀与环境因素的灰关联分析[J]. 海洋科学, 2000, 24(5): 37-40. Zhu Xiangrong, Zhang Qifu. Grey correlation analysis of steel corrosion and environmental factors in seawater[J]. Marine Sciences, 2000, 24(5): 37-40. |
| [5] |
邓志安, 李姝仪, 李晓坤, 等. 基于模糊神经网络的海洋管线腐蚀速率预测新方法[J]. 中国腐蚀与防护学报, 2015, 35(6): 571-576. Deng Zhian, Li Shuyi, Li Xiaokun, et al. A new method for predicting corrosion rate of marine pipelines based on fuzzy neural network[J]. Journal of Chinese Society for Corrosion and protection, 2015, 35(6): 571-576. |
| [6] |
胡松青, 石鑫, 胡建春, 等. 基于BP神经网络的输油管道内腐蚀速率预测模型[J]. 油气储运, 2010, 29(6): 1-3. Hu Songqing, Shi Xin, Hu Jianchun, et al. Prediction model of corrosion rate in oil pipelines based on BP neural network[J]. Oil & Gas Storage and Transportation, 2010, 29(6): 1-3. |
| [7] |
宋伟伟, 董彩常, 张波. 人工神经网络在我国海水腐蚀中的应用[J]. 腐蚀与防护, 2012, 33(8): 668-671, 694. Song Weiwei, Dong Caichang, Zhang Bo. Application of artificial neural network in seawater corrosion in China[J]. Corrosion and Protection, 2012, 33(8): 668-671, 694. |
| [8] |
李昕, 王原嵩, 陈严飞. GA-BP人工神经网络应用于海底腐蚀管道极限承载力的研究[J]. 中国海洋平台, 2009, 24(4): 43-49. Li Xin, Wang Yuansong, Chen Yanfei. Application of GA-BP artificial neural network to ultimate bearing capacity of submarine corrosion pipelines[J]. China Offshore Platform, 2009, 24(4): 43-49. |
| [9] | |
| [10] |
Steinberg D, Colla P. CART:Classification and regression trees[J]. The Top Ten Algorithms in Data Mining, 2009, 13(2): 177-179. |
| [11] |
向乃瑞, 闫海, 王炜, 等. GA-BP神经网络预测金属腐蚀速率[J]. 电力学报, 2018, 33(1): 1-6. Xiang Nairui, Yan Hai, Wang Wei, et al. GA-BP neural network predicts metal corrosion rate[J]. Journal of Electric Power, 2018, 33(1): 1-6. |
 2020, Vol. 44
2020, Vol. 44


