
文章信息
- 刘培学, 闫东, 董丽, 陈玉杰. 2020.
- LIU Pei-xue, YAN Dong, DONG Li, CHEN Yu-jie. 2020.
- 近海海洋信息实时采集传输系统设计与实现
- Design and implementation of offshore marine forecast information acquisition system
- 海洋科学, 44(11): 87-93
- Marine Sciences, 44(11): 87-93.
- http://dx.doi.org/10.11759/hykx20191225001
-
文章历史
- 收稿日期:2019-12-25
- 修回日期:2020-07-04
2. 烟台大学, 山东 烟台 264005
2. Yantai University, Yantai 264005, China
我国是一个海洋大国, 大陆海岸线长达18 000多公里, 近海海洋环境是海洋最易受污染区域, 近海岸海洋环境与人民生活息息相关[1]。对近海海洋信息进行实时采集监测, 对近海海洋养殖、海洋旅游产业等具有十分重要的意义[2]。目前, 近海海域的海洋环境参数测量主要采用人工测量、浮标测量两种方式。人工测量时测量仪器需要挂到测量船只上, 测量员驾驶船只在近海岸巡航测量, 测量完一片海域后返航, 到岸后整理数据; 浮标测量是将测量装置放置在浮标上, 利用GPRS网络将数据传输到指定服务器, 服务器接收数据, 电源部分由电池和光伏板共同供电。两种方式各有各的缺点, 人工测量不能长期连续测量、数据有间断、测量周期长, 浮标测量耗电量大、传输速率慢、成本高, 同时, 近海较复杂的电磁环境也容易对浮标测量的无线传输产生干扰。上述问题导致了近海海洋信息监控系统发展缓慢[3-5]。因此, 设计一款实时海洋信息采集传输系统具有十分重要的意义。
1 系统架构系统主要由两部分组成, 分别是终端数据采集模块和岸基协调器模块。终端数据采集模块对近海海洋信息环境参数进行实时采集, 采用星型链路网络对终端节点进行组网设计形成433M网络, 通过该网络将数据发送给岸基协调器模块[6-7]。岸基协调器包含数据显示模块、4G网络传输模块等, 能够接收终端数据采集模块上报的信息、分类存储及完成数据上报工作。岸基协调器接收收据后, 首先对数据进行融合, 对参数真实值进行最优估计, 消除电磁干扰等各种干扰信号导致的错误数据及传感器本身测量不准确度带来的采集误差, 随后把数据按照溶解氧、温度、pH值以及数据采集终端节点编号进行分类存储, 同时通过4G网络将信息上传至云平台, 供用户查看, 系统整体结构如图 1所示。
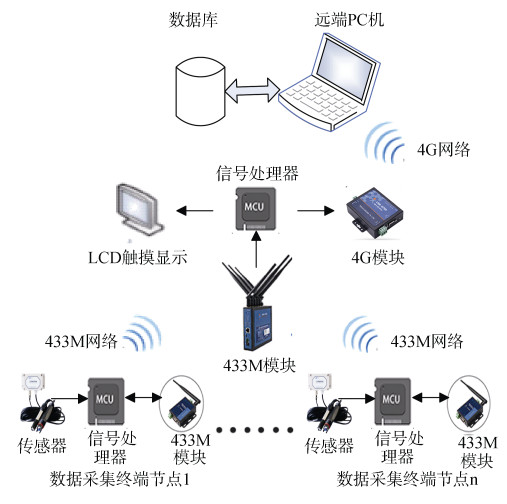 |
| 图 1 系统整体结构图 Fig. 1 Overall structure of the system |
硬件设备是实现海洋信息实时采集监测的关键, 系统由岸基协调器和终端采集器两部分构成, 其中, 终端采集器工作在海洋中, 供电是重点需要解决的问题, 因此, 硬件系统的低功耗设计方案, 是本文介绍的重点。
2.1 岸基协调器设计岸基协调器系统结构如图 2所示, 协调器由STM32控制器、4G模块、433M模块、显示模块、时钟模块和电源模块等部分组成。STM32控制器为整个岸基协调器的控制芯片, 4G模块负责信息远程通信; 433M模块实现多节点和433M网关之间的有机结合, 实现端到云的一步传输; 显示模块采用液晶触摸屏来显示相关数据信息和采集触摸按键信息, 实现客户端的人机交互功能, 时钟模块和电源模块分别提供时钟频率和电源。
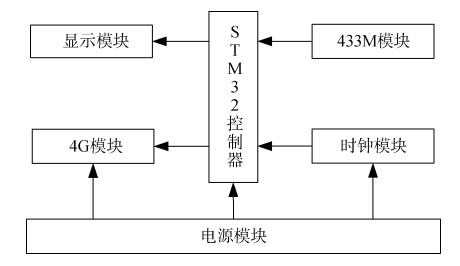 |
| 图 2 岸基协调器系统结构图 Fig. 2 Structure of shore based coordinator system |
控制器选择ARM微控制器STM32F103VGT6, 该处理器是一种32位处理器, 具有1 024 kB的程序存储器、96 kB的数据存储器, 自带模拟/数字转换器(ADC), 功能强大, 能够满足本次设计需要。4G模块采用USR-G780 V2, 支持5模13频移动、联通、电信4G高速接入。USR-G780 V2软件功能完善、使用方便, 通过简单的设置即可实现串口到网络的双向数据透明传输。该模块具有高速率、低延时、极速响应快速透传的特点, 并且支持TCP Client, TCP Server和UDP Client, UDP Server, 支持串口AT指令。433M模块选用SX1278, 和采集数据终端模块的SX1278进行组网, 一步到位实现端到云的无线数据传输。显示模块选用翼盟4.3寸电容触摸液晶屏LCD模块, 该模块屏幕分辨率为800×480, 16位真彩显示, 采用NT35510驱动, 自带GRAM, 无需外加驱动器, 方便单片机的驱动。模块采用电容触摸屏, 支持5点同时触摸, 操控效果非常好, 本次设计中, 4G模块、433M模块通信串口分别连接于控制器的第一、第二串口。
2.2 终端采集器设计信息采集终端设计重点为低功耗设计及各种传感器校准设计。本次设计中MCU选择为低功耗STM8S105K4T6芯片, 供电电路如图 3所示。S1是贴片开关, C3为滤波电容, C4为退耦电容, TPS78230的5号引脚是稳压后3.0 V输出引脚, 3号脚为使能引脚, 与单片机的PC6引脚相连, 高电平使能打开, 低电平使能关闭, 关闭时切断除MCU外的所有电源, 即只有MCU供电且为休眠状态。从而实现低功耗设计。在本设计中, 将MCU的AD转换基准电压设定为2.5 V, 2.5 V数字电源由电源管理电路输出的3 V电源通过TL431稳压输出(采用TL431直接输出2.5 V电路)。数字2.5 V通过10UH的电感转换为2.5 V的模拟电源, 数字地与模拟地通过0欧电阻相连, 降低相互干扰。
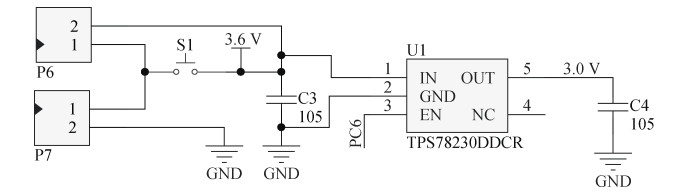 |
| 图 3 供电电路图 Fig. 3 Power supply circuit diagram |
温度采集模块采用KTR-DS18B20[8], 该传感器采用不锈钢管封装, 防水密闭, 适合在海洋环境中使用。溶解氧传感器采用GC-11型传感器, 输出信号电压范围为0~10 mV, 测量范围为0~30 mg/L, 输出阻抗约为20 kΩ。pH值传感器选用了pH复合电极, 输出为电压信号, 零电位为7 pH, 误差为0.5 pH, 内阻≤250 MΩ, 在pH 0~14内输出信号电压为线性电压, 输出稳定, 适用于近海浪涌环境下工作。
3 软件设计 3.1 岸基协调器软件设计岸基协调器是上位机和433M局域网之间联系的桥梁, 一方面, 接受上位机的指令进行相应操作; 另一方面, 接收采集终端上传的终端数据并进行滤波、显示和上传处理。岸基协调器软件流程如图 4所示, 系统上电后, 进行4G、433M通信模块初始化、显示模块初始化及中断初始化。通信模块初始化主要是串口初始化, 进行串口波特率的设置, 建立起串口通信连接。显示初始化主要是触摸显示屏的初始化。中断初始化主要完成定时中断、串口中断的配置, 方便上位机对协调器及下位机的控制命令下达。初始化工作完成后, 循环检测是否正确接收无线节点发来的数据, 如果是, 就进行线性预测滤波处理并暂时存储, 线性预测采用二次卡尔曼滤波方式, 参数超标则进行报警。然后进入实时数据显示界面, 进行实时数据及预警信息的显示。如果发生中断, 分为两种情况。一种是上位机发来的中断, 需要协调器进行相关指令的执行; 另一种是定时中断, 用户没有特殊需求的情况下, 协调器通过4G网络定时向上位机进行数据上报。
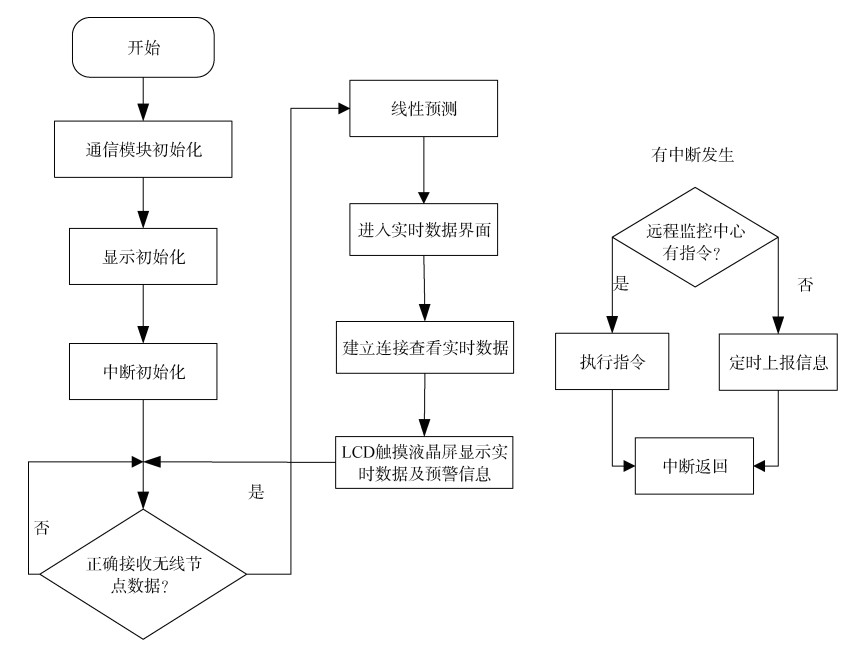 |
| 图 4 岸基协调器软件流程图 Fig. 4 Software flow chart of shore-based coordinator |
近海环境复杂, 电磁干扰严重, 容易出现数据误传及丢失情况, 提出了一种二次卡尔曼滤波方法提高数据采集精度, 下面以溶解氧浓度为例分析该方法, 首先分别建立溶解氧浓度的状态方程和量测方程:
| $ X\left( {k + 1} \right) = FX\left( k \right) + w\left( k \right), $ | (1) |
| $ Z\left( {k + 1} \right) = HX\left( {k + 1} \right) + v\left( {k + 1} \right), $ | (2) |
其中, X(k + 1)和X(k)分别为k + 1时刻溶解氧的浓度值和k时刻的浓度值, F表示状态转移矩阵, 它表示k + 1时刻浓度值和k时刻浓度值之间的关系, 海水中溶解氧浓度不能突变, 此处F取值1, H为系统量测矩阵, 表示目标状态变量对测量变量的增益, 此处取值为1。w(k), v(k + 1)分别为过程噪声和量测噪声, 一般假设它们都为均值为零、互不相关的高斯白噪声, 方差分别为Q和R, 卡尔曼滤波过程包括状态预测与状态更新两个递推环节, 描述如下:
状态预测:
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k + 1\left| k \right.} \right) = F\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k\left| k \right.} \right), $ | (3) |
求出基于上次滤波值的预测值。
预测误差协方差为:
| $ P\left( {k + 1\left| k \right.} \right) = FP\left( {k\left| k \right.} \right){F^T} + \mathit{\boldsymbol{Q}}\left( k \right), $ | (4) |
求出预测的误差协方差。
状态更新:
| $ k\left( {k + 1} \right) = P\left( {k + 1\left| k \right.} \right){\rm{\cdot}}{H^T}{\left[ {HP\left( {k + 1\left| k \right.} \right){H^T} + \mathit{\boldsymbol{R}}} \right]^{ - 1}}, $ | (5) |
k(k + 1)为卡尔曼增益,
| $ \begin{array}{l} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k + 1\left| {k + 1} \right.} \right) = \\ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k + 1\left| k \right.} \right) + \;k\left( {k + 1} \right)\left[ {Z\left( {k + 1} \right) - H\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k + 1\left| k \right.} \right)} \right], \end{array} $ | (6) |
求出k+1时刻的滤波值, 此值即为输出值, 使量测和预测的均方误差最小, 其中,
| $ \begin{array}{l} P\left( {k + 1\left| {k + 1} \right.} \right) = \\ \left( {I - KH} \right)P\left( {k + 1\left| k \right.} \right){\left( {I - KH} \right)^T} + KR{K^T}, \end{array} $ | (7) |
求出滤波误差协方差, 根据上述公式, 即可完成滤波的递归。
公式中的量测噪声方差通常是测量传感器引起, 相对比较固定, 因此量测噪声方差R我们采用固定值, 但是过程噪声是随机的, 采用固定值会引起滤波不够精准或滤波发散, 因此采用自适应方式。
定义转换坐标Kalman滤波中的新息、残差如下所示:
| $ \begin{array}{l} d\left( {k + 1} \right) = Z\left( {k + 1} \right) - H\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k + 1\left| k \right.} \right) = \\ Hx\left( {k + 1} \right) - H\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k + 1\left| k \right.} \right) + v\left( {k + 1} \right) = \\ He\left( {k + 1\left| k \right.} \right) + v\left( {k + 1} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;, \end{array} $ | (8) |
| $ \begin{array}{l} \varepsilon \left( {k + 1} \right) = Z\left( {k + 1} \right) - H\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( {k + 1\left| {k + 1} \right.} \right) = \\ Hx\left( {k + 1} \right) - H\hat x\left( {k + 1\left| {k + 1} \right.} \right) + v\left( {k = 1} \right) = \\ He\left( {k + 1\left| {k + 1} \right.} \right) + v\left( {k + 1} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;. \end{array} $ | (9) |
由公式(8)和公式(9)可以得到
根据新息和残差正交原理有:
| $ \begin{array}{l} E\left[ {\left( {d\left( {k + 1} \right) - \varepsilon \left( {k + 1} \right)} \right){{\left( {d\left( {k + 1} \right) - \varepsilon \left( {k + 1} \right)} \right)}^T}} \right]\\ = H\left( {e\left( {k + 1\left| {k + 1} \right.} \right) - e\left( {k + 1\left| k \right.} \right)} \right)\\ {\left( {e\left( {k + 1\left| {k + 1} \right.} \right) - e\left( {k + 1\left| k \right.} \right)} \right)^T}{H^T}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;. \end{array} $ | (10) |
根据新息序列和残差序列的不相关性, 公式(10)可以化简为:
| $ \begin{array}{l} E\left( {d\left( {k + 1} \right)d{{\left( {k + 1} \right)}^T}} \right) + E\left( {\varepsilon \left( {k + 1} \right)\varepsilon {{\left( {k + 1} \right)}^T}} \right) = \\ HE\left( {e\left( {k + 1\left| {k + 1} \right.} \right)e{{\left( {k + 1\left| {k + 1} \right.} \right)}^T}} \right){H^T} + \\ HE\left( {e\left( {k + 1\left| k \right.} \right)e{{\left( {k + 1\left| k \right.} \right)}^T}} \right){H^T}\\ = H\left( {P\left( {k + 1\left| {k + 1} \right.} \right)} \right){H^T} + H\left( {P\left( {k + 1\left| k \right.} \right)} \right){H^T}. \end{array} $ | (11) |
我们可以在滤波的过程中得到新息序列和残差序列, 因此可以通过统计方法得到两者实际的方差, 即:
| $ E\left( {\varepsilon \left( {k + 1} \right)\varepsilon \left( {k + 1} \right)} \right) = \frac{1}{M}\sum\limits_{i = k - M + 2}^{k + 1} {\varepsilon \left( i \right)\varepsilon {{\left( i \right)}^T}} , $ | (12) |
| $ E\left( {d\left( {k + 1} \right)d\left( {k + 1} \right)} \right) = \frac{1}{M}\sum\limits_{i = k - M + 2}^{k + 1} {d\left( i \right)d{{\left( i \right)}^T}} , $ | (13) |
其中, M为统计计算时估计窗口的宽度。则由公式(4)、(11)、(12)、(13)可以得到过程噪声方差的估计值为:
| $ \begin{array}{c} H\hat Q{H^T} = \frac{1}{M}\sum\limits_{i = k - M + 2}^{k + 1} {\varepsilon \left( i \right)\varepsilon {{\left( i \right)}^T}} + \frac{1}{M}\sum\limits_{i = k - M + 2}^{k + 1} {d\left( i \right)d{{\left( i \right)}^T}} - \\ \;\;HP\left( {k + 1} \right){H^T} - HFP\left( k \right){F^T}{H^T}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;, \end{array} $ | (14) |
在本文中H为单位矩阵, 因此可以化简为:
| $ \begin{array}{c} \hat Q\left( k \right) = \frac{1}{M}\sum\limits_{i = k - M + 2}^{k + 1} {\varepsilon \left( i \right)\varepsilon {{\left( i \right)}^T}} + \frac{1}{M}\sum\limits_{i = k - M + 2}^{k + 1} {d\left( i \right)d{{\left( i \right)}^T}} - \\ \;\;HP\left( {k + 1} \right){H^T} - HFP\left( k \right){F^T}{H^T} \end{array} $ | (15) |
由此得出, 过程方差Q的估计值, 此值为K时刻应该采取的过程方差, 故需利用公式1-4, 采用估计的Q跟传感器的方差R进行二次滤波, 得到较准确的线性预测值, 温度、pH值采用类似方法处理。
3.2 采集终端软件流程本系统中, 采集终端需要完成对无线模块组网状态检测、校准状态检测、校准值存储、温度数据读取、pH值、溶解氧传感器输出的电压值的识别、转化、计算、分析、数据处理、数据无线发送以及休眠唤醒等功能。模块化的软件设计使得系统更稳定、分工明确。软件总体设计流程如图 5所示。
 |
| 图 5 软件总体设计流程 Fig. 5 Overall software design process |
系统上电后首先进行系统初始化, 初始化完毕后进入main函数, 初始化变量; 主频时钟配置为16 MHz, 等待主频时钟稳定后开始初始化串口、EEPROM及I/O口, 读取EEPROM中存储的pH值和溶解氧传感器的校准值, 读取成功后关闭EEPROM, 开始检测无线模块是否组网成功(当无线模块的状态引脚变为低电平后表示组网成功); 接下来检测校准功能引脚电平是否为低电平, 如果为低电平则执行校准功能程序, 否则直接执行下一步, 将运行模式标志位置位(开机运行一次后进入休眠模式), 进入运行模式; MCU提高运行主频, 打开电源管理芯片使能, 给温度传感器、pH值、溶解氧信号放大电路供电, 唤醒无线模块, 让无线模块处于发送状态; 接下来初始化DS18B20, 读取温度, 初始化ADC模块, 开始AD转化, 数字滤波, 数值量化, 量化完毕后关闭ADC, 关闭电源管理芯片使能; 再给无线模块发送数据包, 发送完毕后运行标志位清除, 初始化唤醒I/O口, 配置为外部中断下降沿触发模式, 降低MCU工作主频, 同时MCU进入休眠模式, 等待外部中断将其唤醒进行一下次信息采集。
4 系统测试在系统完成软硬件设计后, 对系统进行测试, 系统测试分为室外功耗测试及室内误差测试两部分, 首先进行室外功耗测试, 在某近海海域布设6个采集终端、1个岸基协调器进行测试, 采样深度0.5 m, 采样速率1次/min, 采集终端分布于该海域养殖工作平台上, 采集终端与离岸基协调器直线距离范围为200~600 m, 针对采集终端的电流进行实验测定, 结果如表 1所示。从表中可以看出, 所设计的系统待机工作电流约为200个UA, 工作电流约为10 MA, 较之现有设备几十至几百的工作电流有较大幅度的下降。
| 编号 | 参数 | 测量误差 | 参数 | 测量误差/℃ | 参数 | 测量误差/ (mg/L) |
| 1 | pH | 0.02 | 温度 | 0.2 | 溶氧 | 0.02 |
| 2 | 0.01 | 0.1 | 0.02 | |||
| 3 | 0.02 | 0.1 | 0.03 | |||
| 4 | 0.01 | 0.1 | 0.04 | |||
| 5 | 0.02 | 0.3 | 0.04 | |||
| 6 | 0.03 | 0.2 | 0.02 |
室内误差测试由专业测试机构青岛华测计量有限公司检测给出, 采集误差结果如表 2所示。
| 编号 | 参数 | 测量值/mA | 参数 | 测量值/MA |
| 1 | 待机电流 | 0.227 | 工作电流 | 10.25 |
| 2 | 0.225 | 10.35 | ||
| 3 | 0.229 | 10.29 | ||
| 4 | 0.225 | 10.29 | ||
| 5 | 0.230 | 10.31 | ||
| 6 | 0.225 | 10.32 |
从表 2数据可以看出, pH值误差在0.02左右, 温度误差不高于0.2, 溶解氧误差不超过0.04 mg/L, 量测值与计量公司标准仪器具有较高的一致性, 其中温度参数误差偏差最大, 误差满足海洋观测规范(GB/T14914.2-2019)中规定的表层海水温度二级误差允许规范, pH值、溶解氧误差较小, 满足一级误差允许规范。对于每个采集终端采集误差, 可采用软件修正方式进行修正, 使显示值与真实值更接近。
5 结束语基于二次卡尔曼滤波方法, 设计了一种近海海洋信息实时采集传输系统, 该系统能够实现近海海洋参数的多点、大范围监测和无线传输, 无需复杂布线, 大大提高了近海海洋信息实时采集效率。同时, 系统具有超低功耗特点, 适合海上长期工作, 能够为近海海洋养殖业、近海旅游业、近海环保提供数据支撑, 具有较好的应用前景。
| [1] |
李浩, 任宇辉, 刘凤娇. 量子无线通信技术在海洋环境监测中的应用[J]. 海洋科学, 2018, 42(2): 94-98. Li Hao, Ren Yuhui, Liu Fengjiao. Application of quantum wireless communication technology in marine environmental monitoring[J]. Marine science, 2018, 42(2): 94-98. |
| [2] |
谢先伟, 毛红. 海洋环境监测数据自动分析系统的设计与实现[J]. 舰船科学技术, 2016, 38(12): 121-123. Xie Xianwei, Mao Hong. Design and implementation of automatic analysis system for marine environmental monitoring data[J]. Ship science and technology, 2016, 38(12): 121-123. |
| [3] |
李颖, 杨光松, 郭文静, 等. 一种基于ZigBee的海洋环境监控系统设计与实现[J]. 重庆理工大学学报(自然科学), 2018, 32(9): 149-156. Li Ying, Yang Guangsong, Guo Wenjing, et al. Design and implementation of a marine environment monitoring system based on ZigBee[J]. Journal of Chongqing University of Technology (NATURAL SCIENCE), 2018, 32(9): 149156. |
| [4] |
温玉波. 海洋环境污染信息智能图像监测技术研究[J]. 现代电子技术, 2018, 41(6): 109-111, 116. Wen Yubo. Research on intelligent image monitoring technology of marine environmental pollution information[J]. Modern electronic technology, 2018, 41(6): 109-111, 116. |
| [5] |
Daniel O B Jones, Andrew R. Gates, Veerle A I, et al. Autonomous marine environmental monitoring:Application in decommissioned oil fields[J]. Science of the Total Environment, 2019, 668. |
| [6] |
王荣.基于433MHz无线自组传感器网络系统的研究与设计[D].天津: 天津理工大学, 2018. Wang Rong. Research and design of wireless ad hoc sensor network system based on 433MHz[D]. Tianjin: Tianjin University of Technology, 2018. |
| [7] |
靳熙芳, 王硕. 海洋环境数据智能化监控的现状与关键技术[J]. 海洋预报, 2009, 26(2): 95-102. Jin Xifang, Wang Shuo. Status quo and key technologies of intelligent monitoring of marine environmental data[J]. Ocean forecast, 2009, 26(2): 95-102. |
| [8] |
Huimin Lu, Yujie Li, Shenglin Mu, et al. Motor anomaly detection for unmanned aerial vehicles using reinforcement learning[J]. IEEE Internet of Things Journal, 2017, 99: 1-2. |
| [9] |
Wang T, Zhang Y, Yan T C, et al. Physics-based coastal current tomographic tracking using a Kalman filter[J]. The Journal of the Acoustical Society of America, 2018, 143(5): 2938-2953. DOI:10.1121/1.5036755 |
| [10] |
Nonomura T, Shibata H, Takaki R. Dynamic mode decomposition using a Kalman filter for parameter estimation[J]. AIP Advances, 2018, 8(10): 105-106. |
 2020, Vol. 44
2020, Vol. 44

