文章信息
- 陈俊池, 刘祚时, 陈俊华, 陈炫光. 2020.
- CHEN Jun-chi, LIU Zuo-shi, CHEN Jun-hua, CHEN Xuan-guang. 2020.
- 基于CFD模拟的单点系泊船型网箱浮架结构分析与设计
- Structural analysis and design of single point mooring cage floating frame based on CFD simulation
- 海洋科学, 44(4): 116-123
- Marine Sciences, 44(4): 116-123.
- http://dx.doi.org/10.11759/hykx20190715003
-
文章历史
- 收稿日期:2019-07-15
- 修回日期:2019-08-29
2. 浙江大学宁波理工学院机电与能源工程学院, 浙江 宁波 315100;
3. 宁波大学 机械工程与力学学院, 浙江 宁波 315211
2. College of Mechatronics and Energy Engineering, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China;
3. School of Mechanical Engineering and Mechanics, Ningbo University, Ningbo 315211, China
随着海洋渔业资源的不断减少, 以及近海养殖日益严重的环境污染, 现阶段我国提出了“发展外海, 拓展远洋”的渔业养殖发展方针, 海洋养殖业正向着深远海发展[1]。深远海域渔业资源丰富, 水体交换强, 有利于海水养殖, 但也存在着海流强、风浪大的特点。因此, 提高养殖网箱在外海恶劣环境下的安全性和可靠性正成为现在养殖网箱研究的热点问题之一[2-3]。程晖等[4]对投放于黄海冷水团的“钻石型”单点系泊网箱的箱体结构进行了数值模拟, 用于改进其水动力特性。徐为兵等[5]建立了碟形网箱的数值计算模型, 对其多海况下的水动力特性进行了研究。Drach等[6]通过有限元软件设计分析了一种用于外海养殖的“金字塔”型单点系泊铜合金网衣网箱。Shainee等[7]设计了一种自潜式单点系泊笼式网箱, 并进行了数值模拟以分析其浸没特性和浮力变化。
目前我国在深水网箱养殖领域普遍采用圆形重力式深水网箱, 锚泊方式为多点固定并与海底桩柱连接。这种固定式养殖网箱的养殖残渣沉积在一块养殖区域, 会对当地海洋环境造成一定污染[8]。若采用单点系泊方式锚泊网箱, 则可有效改善这一状况。单点系泊(SPM)网箱系统可以随着潮流改变方向而在锚点周围移动。这种流动性有助于在相对较大的区域内散布未吃的食物和鱼粪, 从而减轻当地海洋环境的恶化[9], SPM笼系统可以将固定鱼笼下废物的底栖积累减少2~70倍。此外, 与当前的多点系泊系统相比, SPM系统的使用将锚固安装成本降低了50%以上[10]。然而, 由于SPM网箱系泊力远大于传统的圆形网箱, 离岸环境承受风浪时SPM网箱系统的风险极高。
针对这一问题设计了船型浮架结构的网箱。浮架的结构参数对网箱的抗风浪能力有着至关重要的影响, 因此选择较优的浮架结构参数组合十分重要。影响网箱水动力性能的因素很多, 若使用全面设计方案, 水动力数值计算及结果处理很庞大。笔者采用了正交设计理论, 通过计算机流体力学数值模拟(CFD)技术, 运用极差分析法处理计算结果, 选出较优的浮架结构设计参数。
1 单点系泊船型网箱简介船型网箱属于重力式网箱, 依靠上部结构(网箱浮架)提供浮力和下部结构(沉子或底圈)重量的组合来维持鱼类养殖体积, 图 1为船型网箱结构图。在单点系泊的条件下, 船型结构物在受到方向不同的波流力时可以很快调整自身位置, 使浮架与来流方向形成一定角度, 以减小波流力, 降低网箱在台风大浪时的失效风险。
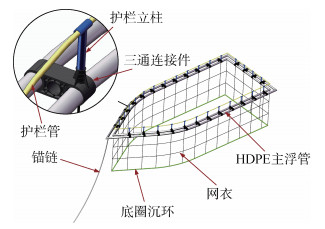 |
| 图 1 船型网箱结构图 Fig. 1 Structural chart of the ship-type cage |
本文研究的船型网箱除了浮架结构外其余部分均与传统圆形中重力式网箱相同, 所以本文只研究船型网箱的浮架结构部分, 对锚泊, 沉子和网衣系统不作讨论。表 1为浮架各结构的部件参数。
| 结构部件 | 材料 | 管径/ mm |
壁厚/ mm |
单位长度 质量/(kg/m) |
| 内浮管 | HDPE | 250 | 15 | 10.52 |
| 外浮管 | HDPE | 250 | 15 | 10.52 |
| 护栏 | HDPE | 110 | 8 | 3.44 |
| 护栏立柱 | HDPE | 125 | 10 | 2.44 |
| 连接件 | HDPE | 250 | 无 | 8* |
| 注: “*”单位为kg/个 | ||||
我国目前使用中的圆形重力式深水网箱浮架周长大多在50~80 m。本文设计的船型网箱浮架结构周长也与之相仿。
2 试验方案设计影响船型浮架抗风浪性能的因素有很多, 包括组成浮架的HDPE管的规格和连接方式、浮架头部角度、框架的长度和宽度以及波浪的波高和波频等。由于影响因素众多, 且各种因素之间还会有交互作用, 若采用传统的全面试验则需要进行大量计算, 在试验时, 无论是数据量的计算规模, 还是人工修改计算参数等都十分繁杂, 需要耗费大量人力物力, 在实际应用中无法实现。
正交试验设计是多因素多水平的优化设计, 通过对各试验参数的合理安排, 科学分析各试验因素, 从众多试验条件中找到最具代表性的参数组合, 科学安排试验, 使花费尽可能少的试验次数就能得到较优的方案。本文采用正交设计方法, 解决船型浮架结构的参数设计问题。
2.1 试验目的及考察指标的确定本文通过数值模拟试验方法, 探讨船型浮架不同结构参数对网箱所受波流力的影响, 并选取较优的参数组合方案, 从而达到减小网箱所受波流力的效果, 得到较优的船型浮架结构设计方案。
网箱在台风大浪中的失效原因主要是承受的波流力超过了本身的极限。作用在网箱浮架上的力难以测量, 锚绳受力可以比较清晰地反应浮架所受的波流力。但网箱越大, 所受波流力越大, 为了从数据上衡量船型网箱的性能优劣, 引入了网箱系数这一考察指标, 这里定义:网箱系数=网箱锚绳力×浮架周长/浮架面积。
网箱锚绳力为望小特性, 越小说明网箱越不容易失效; 浮架周长指浮架内浮环所用HDPE管材的总长度, 越小说明网箱成本越低; 浮架面积指网箱内浮环所围成的面积, 网箱的养殖体积=浮架面积×网深, 这里假设网箱网深相同, 则浮架面积越大, 网箱养殖体积越大, 故浮架面积为望大特性。由上可知, 网箱系数越小, 说明该组设计参数越优秀。
2.2 试验因素及水平的确定波浪的波高、波频以及海水流速等波浪海流条件可以根据铺设地实际条件来选定, 网箱的锚碇系统采用单点系泊的方式。
考虑到控制成本和浮力配给, 以及以往重力式网箱浮管的连接方式, 船型浮架采用内外两根HDPE管组成双浮管结构, 浮管间距为0.5 m, 每隔2 m设置一个三通连接支架。HDPE管外直径选择250 mm, 壁厚15 mm。
在排除上述条件后, 剩余还有船型网箱的浮架头部角度, 浮架长度和浮架宽度3个因素。
1) 浮架长度
浮架主体受到的波流阻力可分为摩擦阻力和剩余阻力。摩擦阻力RF与黏性水和浮架湿表面的关系为[11]:
| $ {R_{\rm{F}}} = \frac{1}{2}{C_{\rm{F}}}pS{V^2}, $ | (1) |
式中, CF为摩擦阻力系数; ρ为水的密度; S为船体湿表面积; V为浮架相对海流速度。
由此可知, 当浮架长度增加时, 湿表面积增加, 浮架主体所受波流力也随之增加。对剩余阻力来说, 长度增加, 则长度与宽度的比值增加, 船型浮架相对更加瘦长, 网箱所受波流力也随之减小。故需要设计优化一个较为合理的浮架长度。
2) 浮架宽度
对于海上漂浮物, 浮体的宽度是影响横摇的主要因素。网箱的横摇周期T指完成一次完整横摇的时间, 公式如下[12]:
| $ T = 0.58B\sqrt {1 + {{(2{{\rm{Z}}_{\rm{G}}}/B)}^2}} {H_{\rm{M}}}^{ - 0.5}, $ | (2) |
式中, B为浮架宽度; ZG为浮架重心距水面高度; HM为浮架重心到稳心的高度。
改变浮架宽度时, 浮架距水面高度不变, 且ZG/B很小, 对横摇周期影响不大。故由式(2)可知当浮架宽度增加时, 横摇周期T将迅速缩短。此外, 横摇的角速度、角加速度也会随着浮架宽度的增加而增大。总之, 过长的浮架宽度会引起剧烈的横摇。而网箱的稳定性是网箱设计中十分重要的一点, 过大的横摇会带动浮架两侧挂网随水晃动, 压缩养殖水体, 造成网内养殖鱼受挤压死亡。
从公式(1)可知, 由于网箱浮架为宽短纵长的船型, 浮架宽度的增加对摩擦阻力影响不大。但对剩余阻力而言, 浮架宽度增加时, 会加大兴波阻力及漩涡阻力, 同时, 浮架过宽会使迎浪面增大, 风浪中的附加阻力也会增加。
3) 浮架头部角度
浮架头部角度指船型浮架两侧HDPE管弯折所形成的角度。船型浮架的头部角度也是影响浮架所受波流力的重要因素。对剩余阻力来说, 浮架头部角度的减小, 会使浮架头部兴波区域的型线变的平缓, 兴波作用相对减小, 网箱所受波流力也随之减小。同时角度减小使浮架框架曲度变化缓和, 能够减小漩涡的产生, 降低形状阻力。
综合考虑浮架长度A、宽度B和头部角度C对网箱所受波流力的影响后, 对上述3个因素各安排3个水平, 图 2为各因素示意图, 具体因素水平安排如表 2所示。
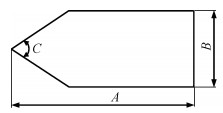 |
| 图 2 船型浮架设计尺寸 Fig. 2 Design dimensions of the ship floating frame |
| 因素 | A/m | B/m | C/(°) |
| 1 | 18 | 6 | 60 |
| 2 | 24 | 9 | 75 |
| 3 | 30 | 12 | 90 |
本试验有3个因子, 每个因子有3个水平, 所以选用L9(34)的正交表。由于本试验不考虑各因子之间的交互作用, 可以把因子放在任意的列上, 一个因子占一列。
3 数值计算方法由于网箱的浮架结构只有两根主浮管和连接支架直接与海面接触, 故可将上部结构包括扶手管、三通、立柱等的质量简化到主浮管上, 忽略其余部分的影响。浮架结构每个部件的尺寸与海浪的波长和波高相比较小, 采用小尺度波浪结构物的计算方法, 用改进的Morison方程[13]计算浮架受力F。
| $ F = \frac{1}{2}p{C_{\rm{D}}}A{V_{\rm{R}}}\left| {{V_{\rm{R}}}} \right| + p\nabla {K_{\rm{M}}}\frac{{\partial {V_{\rm{R}}}}}{{\partial t}} + p\nabla \frac{{\partial V}}{{\partial t}}, $ | (3) |
其中ρ是海水的密度, CD是阻力系数, A是投影面积, VR=V–R是水粒子与结构间的相对速度, KM是增加的质量系数, 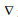
| $ \left( {m + p\nabla {K_{\rm{M}}}} \right)\frac{{{\partial ^2}R}}{{\partial {t^2}}} = {F_{\rm{D}}} + {F_1} + {F_{\rm{B}}} + {F_{\rm{W}}} + {F_{\rm{T}}}, $ | (4) |
其中FD和FI分别代表阻力和惯性力, 它们都与流体的运动状态有关。因为水流和波浪对运动流体的水动力影响最大[15], 可以引入表示均匀流和满足拉普拉斯方程的渐进波的线性波速势:
| $ \phi \left( {x, y, z, t} \right) = \left( {{V_x}x + {V_y}y} \right) +\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{Hg\cosh K\left( {h + z} \right)}}{{2{\omega_e}\cosh Kh}}\cos \left( {{k_x}x + {k_y}y - \omega t} \right), $ | (5) |
其中Vx和Vy是x和y方向均匀流的分量, (x, y, z)是位置坐标, H是相互作用后的波高, g是重力加速度, ωe=ω–kxvx–kyvy是表观角频率, ω是波浪角频率, T是波浪周期,
| $ \eta = \frac{H}{2}{\rm{sin}}\left( {{k_x}x + {k_y}y - \omega t} \right), $ | (6) |
| $ {\omega _e}^2 = gK\tanh Kh, $ | (7) |
利用式(5)对(x, y, z)和t求导, 分别得到了三维速度场和加速度场。利用线性波理论进一步简化水深, 可以得到波峰下的水平流速为:
| $ u = {V_X} + \omega {\zeta _a}{\rm{exp}}kz, $ | (8) |
其中ζa是一个波周期的振幅。接下来, 如果我们只考虑等式(5)的黏性阻力部分, 并将其应用于等式(8), 我们得到以下表达式:
| $ {F_{\rm{D}}} = 0.5p{C_{\rm{D}}}\left( {{V^2} + 2{V_X}\omega {\zeta _{\rm{a}}}{{\rm{e}}^{kz}} + {\omega ^2}{\zeta _{\rm{a}}}{{\rm{e}}^{2kz}}}, \right) $ | (9) |
建立数值分析模型需要模拟波浪周期、频率和波高。网箱的铺设地位于浙江省象山县, 根据当地水文环境的调查研究[16], 网箱试验的波浪条件可以基本确定。选取当地平均波高3 m, 波频选择6 s。根据实际铺设地海况设计仿真环境条件, 水深为20 m, 锚绳长度为50 m, 采用悬链线锚绳, 波浪和水流均沿x轴正方向入射, 水流速度为1 m/s。为了便于分析, 考虑到以后开展模型试验时造波类型的局限性, 将波浪视为规则波。
4 计算结果及分析 4.1 网箱水动力数值计算基于以上的表头设计, 采用了CFD方法, 开展了网箱船型浮架的数值计算。图 3为9组试验的网箱浮架外形图, 并将浮架进行了无系泊条件下的水动力分析, 并得到浮架在波浪下的框架应力图。进而进行浮架水动力的时域系泊分析, 得到单点系泊船型网箱在给定海况下的运动情况与锚绳力随时间的变化曲线。将锚绳力在每个周期下的变化取最大值, 计算结果如下表 3所示。
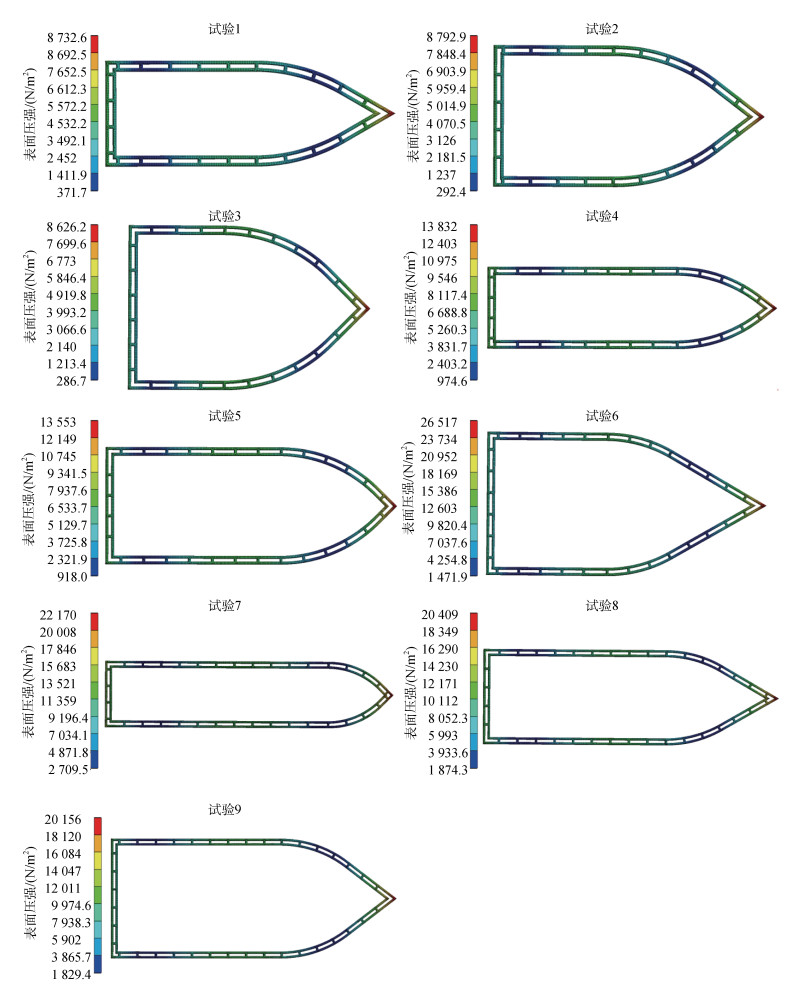 |
| 图 3 各因子水平下的网箱浮架结构及其受力分析 Fig. 3 Cage floating frame structure and its force analysis under the level of each factor |
| 序号 | 浮架长度/ m |
浮架宽度/ m |
头部角度/° | 浮架周长/ m |
浮架面积/ m2 |
受力峰值/ N |
网箱横摇/° | 网箱系数 |
| 1 | (1)18 | (1)6 | (1)60 | 43.4 | 90.6 | 5 840 | 13.2 | 2 798 |
| 2 | (1)18 | (2)9 | (2)75 | 48.0 | 132.2 | 6 668 | 11.1 | 2 421 |
| 3 | (1)18 | (3)12 | (3)90 | 52.0 | 173.8 | 9 190 | 14.8 | 2 750 |
| 4 | (2)24 | (1)6 | (2)75 | 55.5 | 128.8 | 6 110 | 10.1 | 2 633 |
| 5 | (2)24 | (2)9 | (3)90 | 60.0 | 189.6 | 6 023 | 8.5 | 1 906 |
| 6 | (2)24 | (3)12 | (1)60 | 62.9 | 223.9 | 7 058 | 8.7 | 1 983 |
| 7 | (3)30 | (1)6 | (3)90 | 67.8 | 168.2 | 6 238 | 14.0 | 2 514 |
| 8 | (3)30 | (2)9 | (1)60 | 71.1 | 233.2 | 7 540 | 7.1 | 2 299 |
| 9 | (3)30 | (3)12 | (2)75 | 75.5 | 310.1 | 8 564 | 8.2 | 2 085 |
| 注:表中(1) (2) (3)分别为正交试验的试验条件, 网箱系数=浮架周长/浮架面积 | ||||||||
在所用浮管同规格的情况下, 浮架周长能代表网箱成本, 浮架面积能代表网箱养殖容量, 周长除以面积就代表了单位养殖体积网箱所花造价, 将其命名为成本系数, 并将计算获得的锚绳受力峰值乘成本系数得到本试验的考察指标网箱系数, 网箱系数综合考虑了养殖网箱的抗风浪性能和养殖成本, 能一定程度上代表船型网箱的性能优越性。
从表 3的试验结果可以直观看到, 随着浮架周长和面积的增大, 网箱在周期下的受力峰值并不一直增大, 而是呈现波动。直接分析试验结果比较困难, 采用极差分析对结果进行判断。船型浮架各因子对网箱优劣的影响程度大小可从各个因子的“极差”来判别。极差指该因子各水平下的平均值的最大值与最小值之差, 该值越大, 改变这一因子水平对指标造成的影响也就越大, 反之亦然。对同一因子不同水平下的试验结果之和取平均值, 可代表该因子对结果的影响。
图 4为船型浮架长、宽、头部角度在不同水平下的试验均值变化, 图中A1, A2, A3为浮架长度的3个水平; B1, B2, B3为宽度的3个水平; C1, C2, C3为浮架头部角度的3个水平。
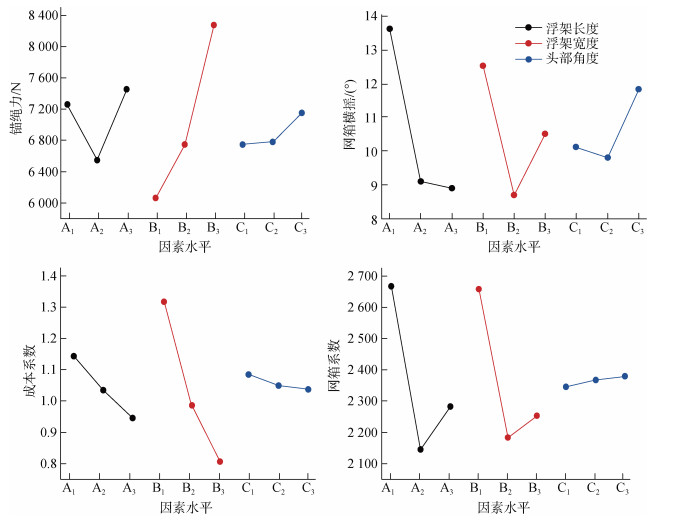 |
| 图 4 浮架各因素极差变化图 Fig. 4 Line graphs of the change of the factors' range |
从图 4中可看出浮架各因素水平情况下网箱锚绳力的变化情况, 该变化反应了网箱所受波流力的变化。观察折线A的水平变化可得, 当浮架长度增加时网箱受力先减小后增大。这可能是因为浮架长度增加时, 湿表面积增加, 摩擦阻力随之增大。同时长度的增加使船形浮架型线更加平缓, 兴波作用缓和, 兴波阻力随之变小, 并且船型浮架的去流段增长使船体曲度变化缓和, 减少漩涡的产生, 降低形状阻力。故锚绳力在浮架长度增加时呈现先减小后增大的趋势。从B因素变化折线可知锚绳力随浮架宽度的增加而增加。从C因素变化曲线得浮架头部角度从60°变化为75°时锚绳力增加值很小, 但增大为90°时锚绳力增加较多。
4.3 各因素对网箱横摇的影响网箱的横摇是衡量网箱优劣的重要条件之一, 如图 4可知, 当浮架长度由18 m增加到24 m时网箱横摇减小较多, 从24 m增加为30 m时横摇降低较少; 浮架宽度增加时, 网箱横摇先减小后增大; 浮架头部角度增大时, 网箱横摇先减小后增大。
4.4 各因素对网箱成本系数的影响网箱成本系数为周长/面积所获得的值, 可以代表养殖一个单位鱼类所需要的网箱造价成本。从图 4可以看出, 随着浮架长度、宽度、头部角度的增加, 网箱成本系数逐渐降低, 但减小成本的同时浮架面积的增大也增加了深水网箱在受到风浪时受损的风险。
4.5 各因素对网箱系数的影响从对图 4的极差分析可看出, 船型浮架的长度与宽度对网箱系数的影响较大。随着网箱船型浮架长度和宽度以及头部角度的增加, 网箱整体受力会随之增加, 但同时网箱的养殖面积也会增大, 所以需要综合考虑养殖风险与经济效益之间的平衡关系。由图 4可知, 浮架长度和宽度的变化对网箱系数影响较大, 而浮架的头部角度则对其影响较小。在浮架长度取24 m, 浮架宽度取9 m, 浮架头部角度为60°时网箱系数最小, 即此参数的网箱具有较好的经济性与安全性。
4.6 结论的合理性验证在铺设地象山港水深20 m, 承受波高6 m, 周期6.8 s大浪的工况下, 通过仿真计算得到本设计的网箱浮架所受应力最大值为6 MPa左右, 小于同工况条件下同周长圆形HDPE网箱所受7 MPa的应力。同时本设计所选用直径250 mm, 壁厚15 mm的HDPE浮管屈服强度为24.1 MPa, 大于其在6 m大浪时所受应力。初步验证本设计的网箱浮架在恶劣海况下失效概率较低, 能较好地完成设计任务。
5 结语目前人们对海产品日益增长的需求, 很大程度上可以通过水产养殖来满足。当近岸养殖达到饱和并引发日益严重的养殖污染时, 离岸养殖便成了唯一的解决方案。在相对恶劣的离岸环境下进行网箱设计是一项挑战, 也是一项不断发展的技术, 为此世界各地的研究人员提出了各种符合当地海洋环境的离岸式网箱解决方案。本研究通过CFD数值模拟仿真的方法, 在模拟海洋环境下对不同结构参数的船型浮架进行了分析, 发现船型网箱受力并不是随着浮架长度的增加而一直增加, 而是存在一个较优长度, 并结合制造成本对网箱参数进行了选择, 得出了一个较为合理的方案。本研究提出的船型网箱丰富了在单点系泊网箱领域的研究, 为我国的养殖网箱深水化发展提供了一定的理论参考依据。
| [1] |
陈志明, 毛沛盛, 严谨, 等. 现代海水网箱、海洋牧场技术进展及研究方法[J]. 广东造船, 2018, 37(2): 46-49. Chen Zhiming, Mao Peisheng, Yan Jin, et al. The technology progress and design method of modern marine cage and ranching[J]. Guangdong Shipbuilding, 2018, 37(2): 46-49. |
| [2] |
张起信, 张启胜, 刘光穆, 等. 浅谈深海抗风浪网箱养鱼业[J]. 海洋科学, 2007, 31(3): 82-83. Zhang Qixin, Zhang Qisheng, Liu Guangmu, et al. An elementary introduction to culturing fish in anti-wave cages[J]. Marine Sciences, 2007, 31(3): 82-83. |
| [3] |
林德芳, 关长涛, 黄滨, 等. 海水养殖网箱抗风浪措施的探讨[J]. 海洋水产研究, 2005, 26(6): 55-60. Lin Defang, Guan Changtao, Huang Bin, et al. Discussion on anti-wave measures of mairculture cage[J]. Marine Fisheries Research, 2005, 26(6): 55-60. |
| [4] |
程晖, 黄六一, 倪益, 等. 水流条件下单点系泊不同结构"钻石型"重力式网箱的水动力特性数值模拟[J]. 中国海洋大学学报(自然科学版), 2019, 49(3): 161-170. Cheng Hui, Huang Liuyi, Ni Yi, et al. Numerical study on hydrodynamics of single-point mooring different structural net of "diamond shape" gravity fish cage in current[J]. Periodical of Ocean University of China, 2019, 49(3): 161-170. |
| [5] |
徐为兵, 朱克强, 张大朋, 等. 网格锚定单体碟形网箱的水动力特性研究[J]. 海洋科学, 2015, 39(10): 68-72. Xu Weibing, Zhu Keqiang, Zhang Dapeng, et al. Hydrodynamic characteristics of single grid mooring ocean spar sea station[J]. Marine Sciences, 2015, 39(10): 68-72. |
| [6] |
Drach A, Tsukrov I, Decew J, et al. Engineering procedures for design and analysis of submersible fish cages with copper netting for exposed marine environment[J]. Aquacultural Engineering, 2016, 70: 1-14. |
| [7] |
Shainee M, Leira B J, Ellingsen H, et al. Investigation of a self-submersible SPM cage system in random waves[J]. Aquacultural Engineering, 2014, 58: 35-44. |
| [8] |
郭芳, 黄小平. 海水网箱养殖对近岸环境影响的研究进展[J]. 水产科学, 2006, 25(1): 37-41. Guo Fang, Huang Xiaoping. Advances of studies on impacts of net-cage mariculture on coastal environment[J]. Fisheries Science, 2006, 25(1): 37-41. |
| [9] |
Huang C C, Pan J Y. Mooring line fatigue:A risk analysis for an SPM cage system[J]. Aquacultural Engineering, 2010, 42(1): 8-16. |
| [10] |
Goudey C A, Loverich G, Kite P H, et al. Mitigating the environmental effects of mariculture through single point moorings (SPMs) and drifting cages[J]. ICES Journal of Marine Science, 2001, 58(2): 497-503. |
| [11] |
Boualem K. The Governing Equations and Dry Dynamics[M]. Berlin: Springer International Publishing, 2019: 78-82.
|
| [12] |
朱仁庆, 杨松林, 王志东. 船舶流体力学[M]. 北京: 国防工业出版社, 2015: 39-42. Zhu Renqing, Yang Songlin, Wang Zhidong. Ship Hydrodynamics[M]. Beijing: National Defence Industrial Press, 2015: 39-42. |
| [13] |
Brebbia C A, Walker S. Dynamic analysis of offshore structures[J]. Applied Ocean Research, 1987, 3(4): 205. |
| [14] |
Huang C C, Tang H J, Pan J Y. Numerical modeling of a single-point mooring cage with a frontal rigid frame[J]. IEEE Journal of Oceanic Engineering, 2009, 34(2): 113-122. |
| [15] |
Dean R G, Dalrymple R A. Water Wave Mechanics for Engineers and Scientists[M]. New Jersey: Prentice Hall, 1984: 70-75.
|
| [16] |
杨忠良, 叶钦, 施伟勇.基于AWAC观测在象山海域自然海况条件下波浪特征及波浪能统计分析[C]//国家海洋技术中心.中国海洋可再生能源发展年会暨论坛.北京: 海洋出版社, 2013: 567-573. Yang Zhongliang, Ye Qin, Shi Weiyong. Statistical analysis of wave characteristics and wave energy under natural sea conditions in Xiangshan sea area based on AWAC observation[C]//National Marine Technology Center. Annual Meeting and Forum on Marine Renewable Energy Development in China.Beijing: Ocean Press, 2013: 567-573. |
 2020, Vol. 44
2020, Vol. 44


