文章信息
- 张源源, 庞华基, 刘钊, 宋琳, 邓猛. 2020.
- ZHANG Yuan-yuan, PANG Hua-ji, LIU Zhao, SONG Lin, DENG Meng. 2020.
- 起伏海面的雷电电磁场传播特征及其对闪电定位精度的影响
- Propagation characteristics of the lightning electromagnetic fields along rough sea surface and the effects on the accuracy of ToA-based lightning location
- 海洋科学, 44(5): 34-41
- Marine Sciences, 44(5): 34-41.
- http://dx.doi.org/10.11759/hykx20190726001
-
文章历史
- 收稿日期:2019-07-26
- 修回日期:2019-11-01
2. 青岛市气象灾害防御工程技术研究中心, 山东 青岛 266003;
3. 山东省气象局气象灾害防御技术中心, 山东 济南 250000
2. Qingdao Technology Research Center for Meteorological Disaster Prevention, Qingdao 266003, China;
3. Shandong Engineering Technology Research Center for Meteorological Disaster Prevention, Jinan 250000, China
目前, 对闪电的定位主要采用时差法, 即利用闪电电磁场波峰到达多个测站的时间来计算闪电发生的位置, 我国气象和电力系统建设的闪电定位网均是采用这种定位方法[1-3]。多人[4-10]研究揭示, 当雷电电磁场沿地表传播时, 地表的起伏和下垫面电导率的不同, 均会对雷电波传输产生影响。Weidman等[11-12]和Willett[13]等观测表明, 随着观测距离的增大, 海面对雷电电磁波谱具有低通滤波功能, 超过1 MHz的高频分量按照频率平方的倒数迅速衰减, 超过20 MHz的则几乎观测不到。Ming和Cooray等[14]和张其林等[15]利用数值模式从理论上验证了海面对雷电电磁场传播的影响。李东帅等[16-18]利用时域有限差分算法(FDTD)分析起伏地表的雷电电磁场传播特性及其对闪电定位系统的影响, 指出由起伏地表引起的雷电电磁波上升沿时间的延迟, 会对基于时差法的闪电定位系统产生影响。
综上, 前人对陆地对雷电电磁场的传输影响以及其对闪电定位误差的影响进行了卓有成效的研究, 但对海面对雷电电磁场的传输影响及其对闪电定位误差的影响的研究较少, 本文拟在前人的基础上, 利用Wait近似算法分析海浪对雷电波传输的影响, 并进一步分析这种影响对基于时差法定位闪电带来的误差。
近海的闪电探测和定位对港口作业、船舶的航行及经济活动十分重要, 因此研究近海起伏海面对闪电定位系统的影响具有重要意义。本文选取一次雷暴天气过程, 将实测的浮标站风场数据输入模式算法中, 有针对性地研究海面对雷电电磁传播的影响, 为近海雷电探测及定位误差修订提供参考。
1 起伏海面的雷电垂直电场近似算法 1.1 计算起伏海面的雷电垂直电场假定地面的电导率无限大, 闪电通道垂直于地面, 则地表任意一点处的垂直电场的时域表达式为[19-20]:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{E_{v, \infty }}(0, r, t) = \\ \frac{1}{{2\pi {\varepsilon _0}}}\int_{\;0}^{\;L'(t)} {\frac{{2 - 3{{\sin }^2}\theta (z')}}{{{R^3}(z')}}} \int_{\;{t_b}(z')}^{\;t} {i\left[ {z', t - R(z')/{\rm{c}}} \right]\;} {\rm{d}}t{\rm{d}}z'\\ + \frac{1}{{2\pi {\varepsilon _0}}}\int_{\;0}^{\;L'(t)} {\frac{{2 - 3{{\sin }^2}\theta (z')}}{{{\rm{c}}{R^2}(z')}}} i\left[ {z', t - R(z')/{\rm{c}}} \right]{\rm{d}}z'\\ - \frac{1}{{2\pi {\varepsilon _0}}}\int_{\;0}^{\;L'(t)} {\frac{{{{\sin }^2}\theta (z')}}{{{{\rm{c}}^2}R(z')}}} \frac{{\partial i\left[ {z', t - R(z')/{\rm{c}}} \right]}}{{\partial t}}{\rm{d}}z', \end{array} $ | (1) |
其中,
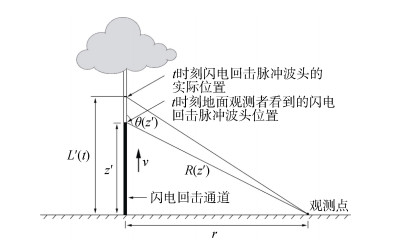 |
| 图 1 雷电回击过程示意图 Fig. 1 Geometry of lightning return stroke |
根据Wait算法, 雷电回击过程产生的垂直电场沿起伏海面传播时, 距雷电回击通道水平距离r处的垂直电场为[14]:
| $ {E_{\nu , \sigma }}(0, r, t) = \int_0^t {{E_{v, \infty }}(0, r, t - \tau )w(0, r, \tau ){\rm{d}}\tau , } $ | (2) |
其中,
| $ W(0, r, j\omega ) = 1 - j\sqrt {\pi q} \exp ( - q){\rm{erfc}}(j\sqrt q ), $ | (3) |
| $ q = - \frac{{{\rm{j \mathsf{ ω} r}}}}{{{\rm{2c}}}}\Delta _{{\rm{eff}}}^2, $ | (4) |
其中,
为了研究Wait近似算法的准确性, Shoory等人[24]分析了混合传输路径雷电电磁传播的Wait算法, 指出在距离闪电通道10 km时, Wait近似算法的计算得到的峰值电场最大观测误差为4.8%, 峰值上升时间的最大误差为18%。张其林等人[25]又进一步验证了距离闪电通道200~1 000 m范围内Wait近似算法的精确度, 认为在距离闪电通道几百米的近距离范围内, Wait近似算法的精确度也可以接受。
按照Barrick等效表面阻抗理论[26-27], 起伏海面的等效表面阻抗Δeff可表示为:
| $ {\Delta _{{\rm{eff}}}} = \Delta + \Delta \prime . $ | (5) |
其中, Δ为平静海面的等效表面阻抗, Δ′为起伏海面引起的表面阻抗的增量。
| $\Delta = \frac{{{k_0}}}{k}{\left( {1 - \frac{{k_0^2}}{{{k^2}}}} \right)^{1/2}}, $ | (6) |
| $k = {k_0}{({\varepsilon _r} - j60\sigma {\lambda _0})^{1/2}}, $ | (7) |
| $ {k_0} = \omega {({\mu _0}{\varepsilon _0})^{1/2}}, $ | (8) |
| ${\lambda _0} = {\mathop{\rm c}\nolimits} /(\omega /2\pi ), $ | (9) |
| $ \Delta ' = \frac{1}{4}\int_{ - \infty }^{ + \infty } {{\rm{d}}\gamma } \int_{ - \infty }^{ + \infty } {G(\gamma , \eta )V(\gamma , \eta ){\rm{d}}\eta } , $ | (10) |
| $ \begin{array}{l} G(\gamma , \eta ) = \frac{{{\gamma ^2} + b \cdot \Delta \cdot ({\gamma ^2} + {\eta ^2} - \omega \gamma /{\rm{c}})}}{{b + \Delta \cdot ({b^2} + 1)}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\Delta \cdot ({\gamma ^2} - {\eta ^2})}}{2} + \Delta \cdot \omega \cdot \gamma /{\rm{c}}, \end{array} $ | (11) |
| $ b = \frac{{\rm{c}}}{\omega }{\left[ {{{\left( {\frac{\omega }{{\rm{c}}}} \right)}^2} - {{\left( {{\gamma ^2} + \frac{\omega }{{\rm{c}}}} \right)}^2} - {\gamma ^2}} \right]^{1/2}}, $ | (12) |
其中, γ和η分别为x和y方向的波数(或空间频数)。V(γ, η)是不规则起伏地表的高度谱密度函数。如果已知V(γ, η), 根据公式(6)—(12)可以计算起伏海面的归一化等效表面阻抗Δeff。
1.2 模拟起伏海面的模型在模拟海面的雷电电磁传播过程中, 选取合适的海面模型非常关键, 近年来人们发现海浪既具有规律性又具有随机性, 利用二维分形模型能够更为贴切地描述真实海面。本文采用王运华[28]提出的一种改进二维分形海面模型, 这种改进模型同时考虑了空间波数大于和小于基波波数的两种波浪对海面表面轮廓的影响, 海面谱的表达式为:
| $ V(\gamma , \eta ) = S(\gamma , \eta )D(\gamma , \eta , \phi ), $ | (13) |
其中S(γ, η)为谱密度, D(γ, η, ϕ)为方向分布函数。
| $ S(\gamma , \eta ) = \left\{ \begin{array}{l} - \frac{{{\tau ^2}{\chi ^2}}}{{2\ln a}}k_0^{2(d - \xi )}{\left( {\sqrt {{\gamma ^2} + {\eta ^2}} } \right)^{[ - 2(d - \xi ) - 1]}}, \sqrt {{\gamma ^2} + {\eta ^2}} < {k_0}\\ \frac{{{\tau ^2}{\chi ^2}}}{{2\ln b}}k_0^{2(d - 3)}{\left( {\sqrt {{\gamma ^2} + {\eta ^2}} } \right)^{[ - 2(d - 3) - 1]}}, \sqrt {{\gamma ^2} + {\eta ^2}} \ge {k_0} \end{array} \right., $ | (14) |
| $ D(\gamma , \eta , \phi ) = 1 + \frac{{4\pi }}{{\sqrt {{\gamma ^2} + {\eta ^2}} }}\sum\limits_{l = 1}^\infty {U(\sqrt {{\gamma ^2} + {\eta ^2}} , 2l)\cos [2l(\phi - {\beta _0})]} , $ | (15) |
其中ϕ为海浪和风向之间的角度, β0为雷电电磁场和风向之间的角度。
| $ U(\sqrt {{\gamma ^2} + {\eta ^2}} , 2l) = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {{\alpha _0}\sec {h^2}({\alpha _0}\varphi )\exp ( - j2l\varphi ){\rm{d}}\varphi } , $ | (16) |
| $ \left\{ \begin{array}{l} {\alpha _0}{\rm{ = }}2.61{({{\sqrt {{\gamma ^2} + {\eta ^2}} } \mathord{\left/ {\vphantom {{\sqrt {{\gamma ^2} + {\eta ^2}} } {{k_0}}}} \right. } {{k_0}}})^{1.3}}, 0.65 \le {{\sqrt {{\gamma ^2} + {\eta ^2}} } \mathord{\left/ {\vphantom {{\sqrt {{\gamma ^2} + {\eta ^2}} } {{k_0}}}} \right. } {{k_0}}} \le 0.95\\ {\alpha _0}{\rm{ = }}2.61{({{\sqrt {{\gamma ^2} + {\eta ^2}} } \mathord{\left/ {\vphantom {{\sqrt {{\gamma ^2} + {\eta ^2}} } {{k_0}}}} \right. } {{k_0}}})^{ - 1.3}}, 0.956 {{\sqrt {{\gamma ^2} + {\eta ^2}} } \mathord{\left/ {\vphantom {{\sqrt {{\gamma ^2} + {\eta ^2}} } {{k_0}}}} \right. } {{k_0}}} < 1.6\\ {\alpha _0}{\rm{ = }}1.24, 其他 \end{array} \right.. $ | (17) |
本文选取2015年4月2日这次雷暴过程, 将青岛长门岩浮标站的风速数据输入到以上的模式中, 分析此次雷暴过程青岛近海起伏海浪对雷电电磁场的影响。
青岛长门岩浮标站位于距青岛海岸线23.3 km的长门岩岛。这里采用的是10分钟的风速平均值, 也就是十分风速。图 2给出了2015年4月2日雷暴天气过程时的十分风速, 可以看出, 此次雷暴过程不同时刻风速的变化非常大, 十分风速的最大值达到13.4 m/s, 最小值为2.5 m/s。
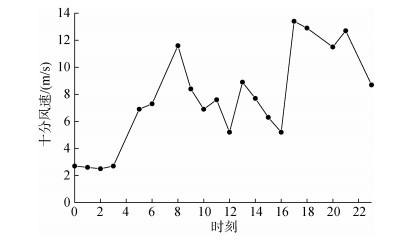 |
| 图 2 2015年4月2日雷暴天气过程时的十分风速 Fig. 2 Ten minute-mean wind speed data of Qingdao buoy station on April 2, 2015 |
回击通道底部电流即基电流, 基电流中的击穿电流和电晕电流都采用双Heilder指数表达式计算[29], 其表达式如下
| $ i(0, t) = \frac{{{I_{01}}}}{{{\eta _1}}}\frac{{{{(t/{\tau _{11}})}^{{n_1}}}}}{{\left[ {{{(t/{\tau _{11}})}^{{n_1}}} + 1)} \right]}}{{\rm{e}}^{ - t/{\tau _{12}}}} + \frac{{{I_{02}}}}{{{\eta _2}}}\frac{{{{(t/{\tau _{21}})}^{{n_2}}}}}{{\left[ {{{(t/{\tau _{21}})}^{{n_2}}} + 1)} \right]}}{{\rm{e}}^{ - t/{\tau _{22}}}}, $ | (18) |
| $ {\eta _1} = \exp \left[ { - \frac{{{\tau _{11}}}}{{{\tau _{12}}}} \cdot {{\left( {{n_1}\frac{{{\tau _{12}}}}{{{\tau _{11}}}}} \right)}^{1/{n_1}}}} \right], $ | (19) |
| $ {\eta _2} = \exp \left[ { - \frac{{{\tau _{21}}}}{{{\tau _{22}}}} \cdot {{\left( {{n_2}\frac{{{\tau _{22}}}}{{{\tau _{21}}}}} \right)}^{1/{n_2}}}} \right], $ | (20) |
其中, I01、I02分别表示击穿电流和电晕电流最大值, η1、η2为修正因子, τ11、τ12、τ21、τ22分别表示用来确定电流上升时间、衰减时间以及峰值的时间常量, n1、n2为电流陡度因子。这些参数具体取值见表 1, 则闪电回击通道底部基电流的波形如图 3所示。
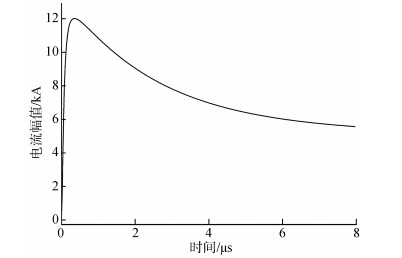 |
| 图 3 闪电通道底部采用的基电流波形 Fig. 3 Channel-based current waveform corresponding to a typical subsequent return stroke |
闪电回击模型选取MTLL(the modified transmission- line model with linear current decay with height)模型[31], 即回击电流波形随高度呈线性衰减, 其表达式为:
| $ i\left( {z',t - {{z'} \mathord{\left/ {\vphantom {{z'} v}} \right. } v}} \right) = i\left( {0,t} \right)\left( {1 - {{z'} \mathord{\left/ {\vphantom {{z'} H}} \right. } H}} \right), $ | (21) |
其中,
图 4给出了起伏海面对地闪回击垂直电场的影响, 观测点距闪电通道的水平观测距离d分别为1、30、100、200 km。假定电磁场传播方向与风向垂直。曲线1表示电导率无限大的理想海面, 曲线2、3、4、5分别表示风速为2.5、5.2、8.7、13.4 m/s的海面垂直电场强度。
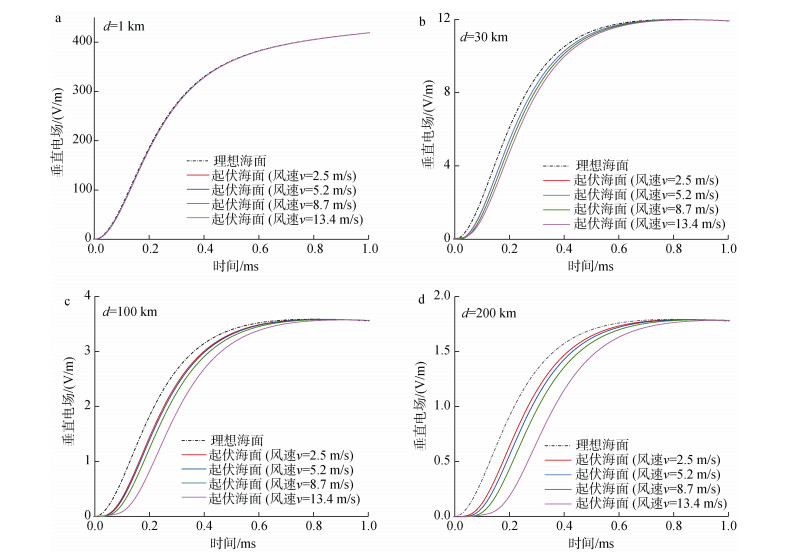 |
| 图 4 起伏海面对时域垂直电场的影响 Fig. 4 Propagation effect of sea surface on the lightning vertical electric field in the time domain at distances of 1 km (a, b), 30 km (c, d), 100 km (e, f), and 200 km (g, h) from the lightning channel 注:黑色虚线表示电导率无限大的理想海面, 彩色实曲线分别表示风速为2.5、5.2、8.7和13.4 m/s的起伏海面。观测点距闪电通道的距离为: a: 1 km; b: 30 km; c: 100 km; d: 200 km |
由图 4可以看出, 观测距离相同时, 海面的起伏对垂直电场峰值的影响不显著, 但对波形的上升时间的影响较为明显。风速越大, 即海面的起伏程度越大, 上升时间越长; 当观测距离变化时, 垂直电场达到半峰值的时间随着距离而增大。
为了具体分析风速对上升沿时间影响的原因, 图 5给出了图 4对应的垂直电场频谱。可以看出, 随着观测距离的增加, 地闪回击电磁波谱的高频成分优先衰减, 观测距离小于100 km时, 频率超过10 MHz以上的部分按照1/f2的速度快速衰减(f为频率)。超过100 km时, 电磁波谱的中低频段也逐渐开始衰减。
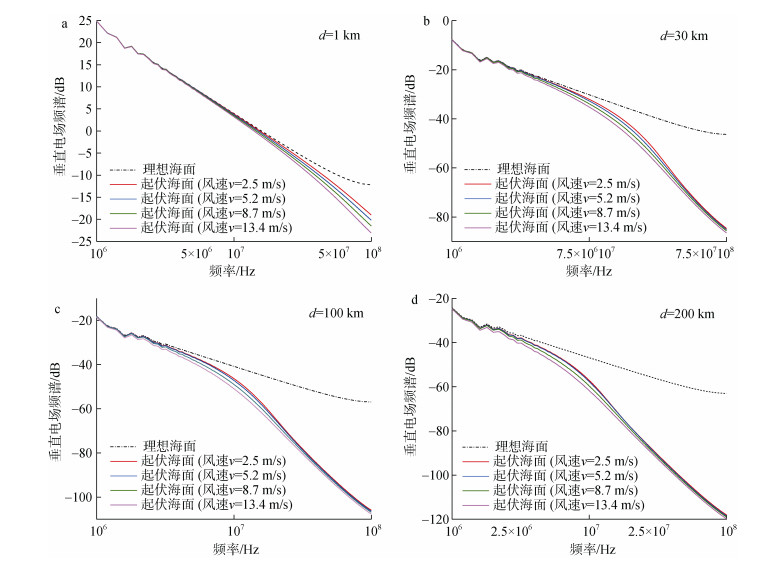 |
| 图 5 起伏海面对垂直电场频谱的影响 Fig. 5 Propagation characteristics of sea surface on the lightning vertical electric field in the frequency domain at distances of 1 km (a, b), 30 km (c, d), 100 km (e, f), and 200 km (g, h) from the lightning channel 注:观测点距闪电通道的距离为a: 1 km; b: 30 km; c: 100 km; d: 200 km |
同样的, 我们对水平磁场进行分析研究, 发现海面的起伏对水平磁场的影响与垂直电场类似。差别在于, 二者到达半峰值的时间不同, 相同的海表情况和相同的观测距离, 水平磁场到达半峰值的时间滞后要短一些。
因此, 当观测距离很远且风速较大时, 无论是利用垂直电场还是水平磁场, 进行雷电放电参数的反演, 海面起伏的影响都不容忽视。
2.4 海浪对闪电定位精度的影响根据以上对雷电电磁波沿起伏海面传播特性的研究揭示, 海面的起伏会导致地闪回击电磁波上升沿时间的有不同程度的滞后, 这会引起基于时差法的闪电定位系统在定位时产生误差, 从而影响闪电定位的精度。
2.4.1 山东省闪电定位系统介绍山东省闪电定位系统于2006年6月布设完成, 由中国华云技术开发公司研制生产。系统主要由采用了时差法(TOA)进行闪电定位, 由13个闪电定位仪组成, 分别在章丘、龙口、荣成、即墨、日照、东明、东平、沾化、夏津、鱼台、蒙阴、郯城和昌邑, 位置如图 6所示。山东省内大部分地区闪电探测效率理论值为95%(图 6)。
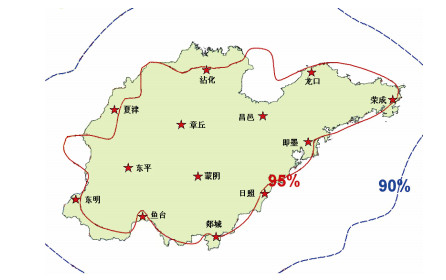 |
| 图 6 山东省LD-II闪电定位系统探测效率图 Fig. 6 Detection efficiency of LLS in Shandong Province |
对于时差法的闪电定位系统, 为了减小下垫面的影响, Cooray、Honma等人[32-33]提出了几种确定与测量波形相关的到达时间的方法。在本文中, 我们将考虑两种方法: (1)对应于电场峰值的波头时间, (2)对应于电场的半峰值时间。
表 2和表 4分别给出了此次天气过程中不同风速下电场峰值对应的波头时间和半峰值时间。表 3和表 5分别对应于表 2和表 4的延迟时间。值得注意的是, 当观测距离较近时, 风速对电场峰值的波头时间影响很小。电场的延迟时间随风速以及观测距离的增大而增大。当距离可达100 km以上时, 风速对峰值场的时间有显著影响。当风速达到13.4 m/s, 观测距离为200 km时, 波头时间为0.575 μs, 对应的延迟时间为0.075 μs, 半峰值时间为0.35 μs, 对应的延迟时间为0.165 μs。
| 观测点距 闪电通道 的距离d |
风速v | ||||
| 0 m/s | 2.5 m/s | 5.2 m/s | 8.7 m/s | 13.4 m/s | |
| 1 km | 1.45 | 1.45 | 1.45 | 1.45 | 1.475 |
| 30 km | 0.45 | 0.455 | 0.46 | 0.47 | 0.49 |
| 100 km | 0.44 | 0.45 | 0.46 | 0.49 | 0.53 |
| 200 km | 0.44 | 0.45 | 0.48 | 0.52 | 0.575 |
| 观测点距闪电通道的距离d | 风速v | ||||
| 0 m/s | 2.5 m/s | 5.2 m/s | 8.7 m/s | 13.4 m/s | |
| 1 km | 0.25 | 0.26 | 0.27 | 0.27 | 0.27 |
| 30 km | 0.185 | 0.205 | 0.205 | 0.23 | 0.245 |
| 100 km | 0.185 | 0.215 | 0.23 | 0.24 | 0.315 |
| 200 km | 0.185 | 0.22 | 0.24 | 0.265 | 0.35 |
为了进一步讨论海面起伏对时差法闪电定位探测精度的影响, 我们选取了2015年4月2日天气过程中发生的两次闪电(图 7)。这两次雷击共利用了四个测站进行定位, 分别为即墨站(36.392°N, 120.469°E)、日照站(35.432°N, 119.539°E)、荣成站(37.17°N, 122.493°E)和龙口站(37.64°N, 120.341°E)。表 6给出了输入参数和结果。计算得出, 当风速达到13.4 km/s时, 海面起伏对闪电定位精度有显著影响, 由海面的起伏引起的定位误差分别为12 662 m和3 944 m。第一次闪电定位误差较大的原因是由于第一次闪击点更靠近闪电定位系统组网探测的外围区域, 产生了较大的布站误差, 该误差是由站点之间布放的位置形状产生的。
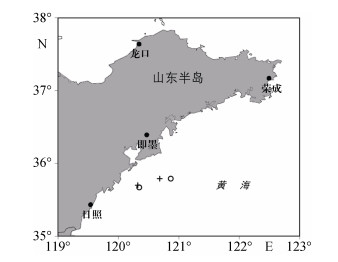 |
| 图 7 海面起伏对闪电定位的影响 Fig. 7 Effect of rough sea surface on lightning location 注: “+”为闪电定位系统探测的闪击点位置, “○”为起伏海面模型修订后闪击点位置。右侧一组为第一次闪击的位置, 左侧一组为第二次闪击的位置 |
| 闪电定位系统探测的闪击点位置 | 风速, v/(km/s) | 闪击点距各测站间的延迟时间/μs | 起伏海面模型修订后闪击点位置 | 定位误差/m | |||
| 即墨站 | 龙口站 | 日照站 | 荣成站 | ||||
| 35.79°N, 120.683°E | 13.4 | 0.04 | 0.061 | 0.087 | 0.049 | 35.78°N, 120.84°E | 12 662 |
| 35.7°N, 120.32°E | 11 | 0.08 | 0.08 | 0.08 | 0.15 | 35.67°N, 120.344°E | 3 944 |
本文分析了海面起伏对雷电垂直电场的影响, 并选取2015年4月2日雷暴天气过程, 将青岛浮标站测量的风速数据输入计算模型。结果表明, 海面起伏对垂直电场的峰值影响较小, 但会引起波形的上升时间的延迟, 风速越大, 即海面的起伏程度越大, 影响越明显。随着观测距离的增加, 雷电垂直电场波形的上升时间逐渐变长。分析垂直电场频谱发现, 随着观测距离的增加, 地闪回击电磁波谱的高频成分优先衰减, 观测距离小于100 km时, 频率超过10 MHz以上的部分快速衰减。当观测距离超过100 km时, 电磁波谱也逐渐由中低频段开始衰减。
雷电电磁场沿起伏海面引起的上升时间的延迟, 将会影响基于时差法闪电定位系统的定位精度, 通过个例验证, 定位误差可达几至十几公里。由于闪击点位置的不同, 定位误差的差异可能很大。这其中也包括了闪电定位仪组网形状产生的系统误差。
| [1] |
Cummins K, Murphy M, Bardo E, et al. A combined ToA/MDF technology upgrade of the US National Lightning Detection Network[J]. J Geophys Res, 1998, 103(D8): 9035-9044. |
| [2] |
Cummins K, Murphy M, Tuel J. Lightning detection methods and meteorological applications[C]//IV International Symposium on Military Meteorology, Polland, 2000, Sep 26-28.
|
| [3] |
Lewis E, Harvey R, Rasmussen J. Hyperbolic direction finding with sferics of transatlantic origin[J]. J Geophys Res, 1960, 65(7): 1879-1905. |
| [4] |
Rubinstein M. An approximate formula for the calculation of the horizontal electric field from lightning at close, intermediate, and long range[J]. IEEE Trans Electro Compat, 1996, 38(3): 531-535. |
| [5] |
Cooray V. Propagation effects due to finitely conducting ground on lightning-generated magnetic fields evaluated using Sommerfeld's integrals[J]. IEEE Trans Electro Compat, 2009, 51(3): 526-531. |
| [6] |
Cooray V, Fernando M, Sorensen T, et al. Propagation of lightning generated transient electromagnetic fields over finitely conducting ground[J]. J Atmospheric Sol-Terrestrial Phys, 2000, 62(7): 583-600. |
| [7] |
Delfino F, Procopio R, Rossi M. Lightning return stroke current radiation in presence of a conducting ground:1. Theory and numerical evaluation of the electromagnetic fields[J]. J Geophys Res:Atmospheres, 2008, 113(D5): 79-88. |
| [8] |
Delfino F, Procopio R, Rossi M, et al. Lightning return stroke current radiation in presence of a conducting ground:2. Validity assessment of simplified approaches[J]. J Geophys Res:Atmospheres, 2008, 113(D05111). |
| [9] |
Cooray V. On the accuracy of several approximate theories used in quantifying the propagation effects on lightning generated electromagnetic fields[J]. IEEE Trans Antennas Propag, 2008, 56(7): 1960-1967. |
| [10] |
Shoory A, Mimouni A, Rachidi F, et al. Validity of simplified approaches for the evaluation of lightning electromagnetic fields above a horizontally stratified ground[J]. IEEE Trans Electromagn Comp, 2010, 52(3): 657-663. |
| [11] |
Weidman C, Krider E, Uman M. Lightning amplitude spectrum in the interval from 100 kHz to 20 MHz[J]. Geophys Res Lett, 1981, 8(8): 931-934. |
| [12] |
Weidman C, Krider E, Uman M. Lightning amplitude spectra in the interval from 100 kHz to 20 MHz[J]. Geophys Res Lett, 1981, 8(8): 931-934. |
| [13] |
Willett J, Bailey J, Leteinturier C, et al. Lightning electromagnetic radiation field spectrum in the interval from 0.2 to 20 MHz[J]. J Geophys Res, 1990, 95(D12): 20367-20387. |
| [14] |
Ming Y, Cooray V. Propagation effects caused by a rough ocean surface on the electromagnetic fields generated by lightning returns strokes[J]. Radio Sci, 1994, 29(1): 73-85. |
| [15] |
Zhang Q, Yang J, Li D, et al. Propagation effects of a fractal rough ocean surface on the vertical electric field generated by lightning return strokes[J]. Journal of Electrostatics, 2012, 70(1): 54-59. |
| [16] |
Li D, Paknahad J, Rachidi F, et al. Propagation effects on lightning magnetic fields over hilly and mountainous terrain[C]//2015 IEEE International Symposium on Electromagnetic Compatibility (EMC). IEEE, 2015: 1436-1440.
|
| [17] |
Li D, Azadifar M, Rachidi F, et al. Analysis of lightning electromagnetic field propagation in mountainous terrain and its effects on ToA-based lightning location systems[J]. J Geophys Res Atmos, 2016, 121(2): 895-911. |
| [18] |
Li D, Azadifar M, Rachidi F, et al. On lightning electromagnetic field propagation along an irregular terrain[J]. IEEE Trans on Electromagn Comp, 2015, 58(1): 161-171. |
| [19] |
Thottappillil R, Rakov V, Uman M. Distribution of charge along the lightning channel:Relation to remote electric and magnetic fields and to return-stroke models[J]. J Geophys Res, 1997, 102(D6): 6987-7006. |
| [20] |
Thottappillil R, Rakov V. On different approaches to calculating lightning electric fields[J]. J Geophys Res, 2001, 106(D13): 14191-14205. |
| [21] |
Wait J. Transient fields of a vertical dipole over a homogeneous curved ground[J]. Canadian Journal of Physics, 1956, 34(1): 27-35. |
| [22] |
Wait J. Recent analytical investigations of electromagnetic ground wave propagation over inhomogeneous earth models[J]. Proceedings of the IEEE, 1974, 62(8): 1061-1072. |
| [23] |
Wait J. The ancient and modern history of EM ground-wave propagation[J]. IEEE Antennas and Propagation Magazine, 1998, 40(5): 7-24. |
| [24] |
Shoory A, Mimouni A, Rachidi F, et al. On the accuracy of approximate techniques for the evaluation of lightning electromagnetic fields along a mixed propagation path[J]. Radio Science, 2011, 46(2): 1-8. |
| [25] |
Zhang Q, Li D, Fan Y, et al. Examination of the Cooray-Rubinstein (C-R) formula for a mixed propagation path by using FDTD[J]. Journal of Geophysical Research:Atmospheres, 2012, 117(D15). |
| [26] |
Barrick D. Theory of HF and VHF propagation across the rough sea, 1, the effective surface impedance for a slightly rough highly conducting medium at grazing incidence[J]. Radio Science, 1971, 6(5): 517-526. |
| [27] |
Barrick D. Theory of HF and VHF propagation across the rough sea, 2, application to HF and VHF propagation above the sea[J]. Radio Sci, 1971, 6(5): 527-533. |
| [28] |
王运华, 郭立新, 吴振森. 改进的二维分形模型在海面电磁散射中的应用[J]. 物理学报, 2006, 55(10): 5191-5199. Wang Yunhua, Guo Lixin, Wu Zhensen. Application of an improved 2D fractal model for electromagnetic scattering from the sea surface[J]. Acta Physica Sinica, 2006, 55(10): 5191-5199. |
| [29] |
Heidler F. Traveling current source model for LEMP calculation[C]//Proc. 6th Int. Zurich Symp. Electromagnetic Compatibility, Zurich, Switzerland, 1985: 157-162.
|
| [30] |
Caligaris C, Delfino F, Procopio R. Cooray-Rubinstein formula for the evaluation of lightning radial electric fields:Derivation and implementation in the time domain[J]. IEEE Transactions on Electromagnetic Compatibility, 2008, 50(1): 194-197. |
| [31] |
Caligaris C, Delfino F, Procopio R. A modified transmission line model for lightning return stroke field calculations[C]//Proc. 9th Int Symp Electromagn Compat, 1991: 229-235.
|
| [32] |
Cooray V. Effects of propagation on the return stroke radiation fields[J]. Radio science, 1987, 22(5): 757-768. |
| [33] |
Honma N, Suzuki F, Miyake Y, et al. Propagation effect on field waveforms in relation to time-of-arrival technique in lightning location[J]. Journal of Geophysical Research:Atmospheres, 1998, 103(D12): 14141-14145. |
 2020, Vol. 44
2020, Vol. 44

