文章信息
- 才瀚涛, 黄华, 苏炜. 2020.
- CAI Han-tao, HUANG Hua, SU Wei. 2020.
- V形防波堤与圆弧型防波堤之浅水波绕射作用的比较
- Comparison of shallow water wave diffracted effects caused by a V-shaped breakwater and arc-shaped breakwater
- 海洋科学, 44(6): 91-100
- Marine Sciences, 44(6): 91-100.
- http://dx.doi.org/10.11759/hykx20190521001
-
文章历史
- 收稿日期:2019-05-21
- 修回日期:2019-12-27
防波堤被广泛应用于近岸工程以抵抗波浪作用, 从而对离岸海工设施和近岸作业水域实施保护。防波堤具有各种常见类型, 包括直立直墙式防波堤、岛式防波堤、梳式防波堤、斜坡式防波堤、T形防波堤、圆弧型防波堤以及V形防波堤等等。Stokes[1]给出了半无限长薄壁单突堤的波浪绕射解析解形式。Losada等[2]应用特征函数展开法研究了有限水深中微幅波对垂直薄板的波浪作用。Lick[3]研究了楔形堤的微幅波绕射问题。洪广文[4]对不完全反射边界楔形堤和隅角堤的波浪绕射问题进行了解析研究。朱梦华等[5-6]分别对正入射与斜入射下椭圆余弦波对无限长直立堤的波浪反射与透射作用以及波浪渗流作用进行了解析研究。楚玉川等[7]解析计算了单层圆弧型薄壁防波堤的绕射波浪力。张敖等[8-9]分别应用椭圆余弦波和孤立波模型解析研究了浅水波对圆弧型防波堤的绕射问题。此外, 波浪对其他类型防波堤作用的理论研究也十分广泛, 例如何军等[10]对T型防波堤与波浪的相互作用展开了数值计算。李雪艳等[11]研究了斜防波堤典型胸墙波浪力的影响因素问题。为设计可临时快速构建和撤收的结构系统, V形防波堤在美国首次提出并构建。该类防波堤通过V形尖角迎浪, 其内部形成防浪掩护区, 具有建造和使用便捷且防浪效果良好等特点。Kao等[12]对微幅波作用下的V形防波堤的防浪效应展开数值研究。陆志妹等[13]和程建生等[14]采用特征函数展开法解析了微幅波作用于V形防波堤的波浪力并分析了绕射效应。丁宁等[15]计算了V形浮式防波堤的动压分布。
本文基于椭圆余弦波的浅水波模型, 推导了任意张角下V形防波堤的波浪绕射解析解, 从而将Airy微幅波理论模型加以了有效拓展。本文方法可用于张角180°有限长薄壁直立堤的浅水波绕射计算, 从而将现有的无限长直墙堤对应的浅水波反射理论加以了拓展。本文选取两种几何形状相近的V形防波堤与圆弧防波堤进行防浪效应比较, 取得了具有实际应用和理论意义的比较结果。
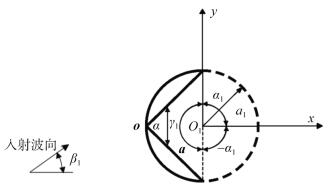
1 椭圆余弦波对V形防波堤绕射的波浪场解析解与波浪力算式设在均匀水深为d的海域中设置有两臂长均为a的V形固立防波堤(如图 1所示)。取坐标系oxyz (即坐标系orθz), oxy平面位于水底, 原点位于堤的两臂相交点, ox正轴与下臂重合, 两臂张角(即夹角)为α, 其中0 < α≤π, oz轴垂直向上。入射波为浅水波中的椭圆余弦波一阶分量, 入射角(与ox轴正向夹角)为β。以a为半径划一圆柱面, 将流场划分为圆柱外流区Ω0和圆柱内流区Ω1与Ω2 (如图 1所示)。
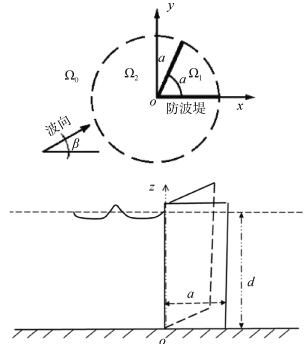 |
| 图 1 椭圆余弦波作用下的V形固立防波堤 Fig. 1 V-shaped breakwater in cnoidal waves |
设水波总速度Φ=Φ1+Φs=Re(φ)=Re(φ1+φs), 其中φ1为入射波势, φs为散射波势。另φ须满足V形堤物面条件, φs须满足径向无穷远处的辐射条件。入射角为β的一阶入射椭圆余弦波的波势可表达为[7, 13]
| $ \begin{array}{c} {\varphi _{\rm{i}}} = \frac{{H\sqrt {gd} }}{{kd}}\sum\limits_{n = 1}^\infty {\frac{{{A_n}}}{{{\rm{i}}n}}} {{\rm{e}}^{{\rm{i}}nkr\cos (\theta - \beta )}}{{\rm{e}}^{ - {\rm{i}}n\omega t}}\\ = \frac{{H\sqrt {gd} }}{{kd}}\sum\limits_{n = 1}^\infty {\frac{{{A_n}}}{{{\rm{i}}n}}{{\rm{e}}^{ - {\rm{i}}n\omega t}}} \sum\limits_{m = 0}^\infty {{\beta _m}{J_m}(nkr)} \\ \;\;\left( {\cos m\theta \cos m\beta + \sin m\theta \sin m\beta } \right){\rm{e, }}\\ \begin{array}{*{20}{c}} {\;\;{\beta _0} = 1, {\beta _m} = 2{i^m}, m = 1, 2, \cdots }&{\rm{, }} \end{array} \end{array} $ | (1) |
其中,
| $ \mathop {\lim }\limits_{r \to \infty } {r^{\frac{1}{2}}}\left[ {\frac{{\partial \varphi _{{\rm{s}}n}^{(0)}}}{{\partial r}} - i{k_n}\varphi _{{\rm{s}}n}^{(0)}} \right] = 0, $ | (2) |
由此若取对应流域Ω(j)的椭圆余弦波总波势为
| $ \begin{array}{c} {\varphi ^{(0)}} = {\varphi _{\rm{i}}} + \varphi _{\rm{s}}^{(0)} = \frac{{H\sqrt {gd} }}{{kd}}\sum\limits_{n = 1}^\infty {\frac{{{A_n}}}{{{\rm{i}}n}}} {{\rm{e}}^{ - {\rm{i}}n\omega t}}\sum\limits_{m = 0}^\infty {\left[ {{\beta _m}{J_m}(nkr)} \right.} \left( {\cos m\theta \cos m\beta + \sin m\theta \sin m\beta } \right) + \\ \left. {\;H_m^{(1)}(nkr)\left( {A_{nm}^{(0)}\cos m\theta + B_{nm}^{(0)}\sin m\theta } \right)} \right], \end{array} $ | (3) |
| $ {\varphi ^{(1)}} = \frac{{H\sqrt {gd} }}{{kd}}\sum\limits_{n = 1}^\infty {\frac{{{A_n}}}{{{\rm{i}}n}}} {{\rm{e}}^{ - {\rm{i}}n\omega t}}\sum\limits_{m = 0}^\infty {A_{nm}^{(1)}{J_{\frac{{m{\rm{ \mathsf{ π} }}}}{\alpha }}}(nkr)\cos \frac{{m{\rm{ \mathsf{ π} }}}}{\alpha }\theta } \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{, 0 \le \theta \le \alpha } \end{array}} \end{array} $ | (4) |
| $ {\varphi ^{(2)}} = \frac{{H\sqrt {gd} }}{{kd}}\sum\limits_{n = 1}^\infty {\frac{{{A_n}}}{{{\rm{i}}n}}} {{\rm{e}}^{ - {\rm{i}}n\omega t}}\sum\limits_{m = 0}^\infty {A_{nm}^{(2)}{J_{\frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}}}(nkr)\cos \frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}(\theta - \alpha )} \begin{array}{*{20}{c}} {}&{, \alpha \le \theta \le 2{\rm{ \mathsf{ π} }}} \end{array} $ | (5) |
式中,Hm(1)(nkr)为m阶第一类汉克耳函数; Anm(0)、Anm(1)、Anm(2)和Bnm(0)均为待定系数且取Bn0(0)。可以验证, 所取波势解已满足方程、海底条件、无穷远处辐射条件和防波堤V形两臂侧表面法向速度为零的物面条件。
将各区圆柱交界面径向质点速度和压强连续条件统一写为
| $ \frac{{\partial {\varphi ^{(0)}}}}{{\partial r}} = \frac{{\partial {\varphi ^{(1)}}}}{{\partial r}}\begin{array}{*{20}{c}} {} \end{array}, r = a, 0 \le \theta \le \alpha $ | (6) |
| $ \frac{{\partial {\varphi ^{(0)}}}}{{\partial r}} = \frac{{\partial {\varphi ^{(2)}}}}{{\partial r}}\begin{array}{*{20}{c}} {} \end{array}, r = a, \alpha \le \theta \le 2\pi $ | (7) |
| $ {\varphi ^{(0)}} = {\varphi ^{(1)}}\begin{array}{*{20}{c}} {} \end{array}, r = a, 0 \le \theta \le \alpha $ | (8) |
| $ {\varphi ^{(0)}} = {\varphi ^{(2)}}\begin{array}{*{20}{c}} {} \end{array}, r = a, \alpha \le \theta \le 2\pi $ | (9) |
由式(6)和(7), 可设并可得:
| $ \begin{align} & {{f}_{1}}(\theta )=\sum\limits_{m=0}^{\infty }{\{[nk{{\beta }_{m}}{{{{J}'}}_{m}}(nka)}\cos m\beta \text{ }+A_{nm}^{(0)}nkH{{_{m}^{(1)}}^{\prime }}(nka)]\cos m\theta +[nk{{\beta }_{m}}{{{{J}'}}_{m}}(nka)\sin m\beta + \\ & \text{ }\ \ \ B_{nm}^{(0)}nkH{{_{n}^{(1)}}^{\prime }}(nka)]\sin m\theta \}-\sum\limits_{m=0}^{\infty }{A_{nm}^{(1)}}nk{{{{J}'}}_{\frac{m\text{ }\!\!\pi\!\!\text{ }}{\alpha }}}(nka)\cos \frac{m\text{ }\!\!\pi\!\!\text{ }}{\alpha }\theta =0\begin{matrix} \ , & {} & 0\le \theta \le \alpha \\ \end{matrix}, \\ \end{align} $ | (10) |
| $ \begin{align} & {{f}_{2}}(\theta )=\sum\limits_{m=0}^{\infty }{\{[nk{{\beta }_{m}}{{{{J}'}}_{m}}(nka)}\cos m\beta +A_{nm}^{(0)}nkH{{_{m}^{(1)}}^{\prime }}(nka)]\cos m\theta +[nk{{\beta }_{m}}{{{{J}'}}_{m}}(nka)\sin m\beta +B_{nm}^{(0)}nkH{{_{m}^{(1)}}^{\prime }}(nka)]\sin m\theta \}- \\ & \text{ }\sum\limits_{m=0}^{\infty }{A_{nm}^{(2)}}nk{{{{J}'}}_{\frac{m\text{ }\!\!\pi\!\!\text{ }}{2\text{ }\!\!\pi\!\!\text{ }-\alpha }}}(nka)\cos \frac{m\text{ }\!\!\pi\!\!\text{ }}{2\text{ }\!\!\pi\!\!\text{ }-\alpha }(\theta -\alpha )=0\text{, }\alpha \le \theta \le 2\text{ }\!\!\pi\!\!\text{ ,} \\ \end{align} $ | (11) |
式中, 取Bn0(0)=0。进一步可设
| $ f(\theta ) = \left\{ \begin{array}{l} {f_1}(\theta ){\rm{ = }}0, 0 \le \theta < \alpha \\ {f_2}(\theta ){\rm{ = }}0, \alpha \le \theta \le 2\pi \end{array} \right., $ | (12) |
将f(θ)在0~2π上展开为傅氏级数, 即
| $ f(\theta ) = \frac{{{a_0}}}{2} + \sum\limits_{l = 1}^\infty {({a_l}\cos l\theta + {b_l}\sin l\theta ) = 0} {\rm{ }} $ | (13) |
由a0 = al = bl = 0 (l = 1, 2, …), 相应有:
| $ \left\{ \begin{array}{l} \int_0^\alpha {{f_1}} (\theta )\cos l\theta {\rm{d}}\theta + \int_\alpha ^{2\pi } {{f_2}} (\theta )\cos l\theta {\rm{d}}\theta = 0, \;l = 0, 1, \cdots \\ \int_0^\alpha {{f_1}} (\theta )\sin l\theta {\rm{d}}\theta + \int_\alpha ^{2\pi } {{f_2}} (\theta )\sin l\theta {\rm{d}}\theta = 0, \;l = 1, 2, \cdots \end{array} \right., $ | (14) |
代入f1(θ)和f2(θ), 分别可得系数方程为:
| $ \begin{align} & nk{{\beta }_{l}}{{{{J}'}}_{l}}(nka)(1+{{\delta }_{l0}})\text{ }\!\!\pi\!\!\text{ }\cos l\beta +A_{nl}^{(0)}nkH{{_{l}^{(1)}}^{\prime }}(nka)(1+{{\delta }_{l0}})\text{ }\!\!\pi\!\!\text{ }-\sum\limits_{m=0}^{\infty }{A_{nm}^{(1)}}k{{{{J}'}}_{\frac{m\text{ }\!\!\pi\!\!\text{ }}{\alpha }}}(nka)T_{ml}^{(1)}- \\ & \sum\limits_{m=0}^{\infty }{A_{nm}^{(2)}n}k{{{{J}'}}_{\frac{m\text{ }\!\!\pi\!\!\text{ }}{2\text{ }\!\!\pi\!\!\text{ }-\alpha }}}(nka)T_{ml}^{(2)}=0,\begin{matrix} \text{ }l=0,1,2,\cdots \text{,} & \text{ } \\ \end{matrix} \\ \end{align} $ | (15) |
| $ \begin{align} & nk{{\beta }_{l}}{{{{J}'}}_{l}}(nka)\text{ }\!\!\pi\!\!\text{ }\sin l\beta +nkB_{nl}^{(0)}H{{_{l}^{(1)}}^{\prime }}(nka)\text{ }\!\!\pi\!\!\text{ }-\sum\limits_{m=0}^{\infty }{A_{nm}^{(1)}n}k{{{{J}'}}_{\frac{m\text{ }\!\!\pi\!\!\text{ }}{\alpha }}}(nka)T_{ml}^{(3)}- \\ & \sum\limits_{m=0}^{\infty }{A_{nm}^{(2)}}nk{{{{J}'}}_{\frac{m\text{ }\!\!\pi\!\!\text{ }}{2\text{ }\!\!\pi\!\!\text{ }-\alpha }}}(nka)T_{ml}^{(4)}=0,\text{ }l=1,2,\cdots , \\ \end{align} $ | (16) |
其中,
| $ \begin{array}{l} \left\{ \begin{array}{l} T_{ml}^{(1)} = \int_0^\alpha {\cos l\theta } \cos \frac{{m{\rm{ \mathsf{ π} }}}}{\alpha }\theta {\rm{d}}\theta \\ T_{ml}^{(2)} = \int_\alpha ^{2{\rm{ \mathsf{ π} }}} {\cos l\theta } \cos \frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}(\theta - \alpha ){\rm{d}}\theta , \;\;m = 0, 1, 2, \ldots ;l = 0, 1, \cdots , \; \end{array} \right.\\ \left\{ \begin{array}{l} T_{ml}^{(3)} = \int_0^\alpha {\sin l\theta \cos \frac{{m{\rm{ \mathsf{ π} }}}}{\alpha }\theta {\rm{d}}\theta } \\ T_{ml}^{(4)} = \int_\alpha ^{2{\rm{ \mathsf{ π} }}} {\sin l\theta \cos \frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}(\theta - \alpha ){\rm{d}}\theta , \;\;\;m = 0, 1, \ldots ;l = 1, 2, \cdots } , \end{array} \right. \end{array} $ | (17) |
进一步应用边界条件式(8)和式(9), 分别可得:
| $ \begin{array}{l} \sum\limits_{m = 0}^\infty {A_{nm}^{(1)}} {J_{\frac{{m{\rm{ \mathsf{ π} }}}}{\alpha }}}(nka)\cos \frac{{m{\rm{ \mathsf{ π} }}}}{\alpha }\theta - \sum\limits_{m = 0}^\infty {\{ [{\beta _m}{J_m}(nka)} \cos m\beta + A_{nm}^{(0)}H_m^{(1)}(nka)]\cos m\theta {\rm{ + }}\\ [{\beta _m}{J_m}(nka)\sin m\beta + B_{nm}^{(0)}H_m^{(1)}(nka)]\sin m\theta \} = 0, 0 \le \theta \le \alpha , {\rm{ }} \end{array} $ | (18) |
| $ \begin{array}{l} \sum\limits_{m = 0}^\infty {A_{nm}^{(2)}} {J_{\frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}}}(nka)\cos \frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}(\theta - \alpha ) - \sum\limits_{m = 0}^\infty {\{ [{\beta _m}{J_m}(nka)} \cos m\beta + A_{nm}^{(0)}H_m^{(1)}(nka)]\cos m\theta + \\ [{\beta _m}{J_m}(nka)\sin m\beta + B_{nm}^{(0)}H_m^{(1)}(nka)]\sin m\theta \} = 0, \;\alpha \le \theta \le 2{\rm{ \mathsf{ π} }}, \end{array} $ | (19) |
再分别利用函数系
| $ \begin{array}{l} A_{nl}^{(1)}{J_{\frac{{l{\rm{ \mathsf{ π} }}}}{\alpha }}}(ka)(1 + {\delta _{l0}})\frac{\alpha }{2} - \sum\limits_{m = 0}^\infty {{\beta _m}{J_m}(nka)T_{lm}^{(1)}\cos m\beta } - \sum\limits_{m = 1}^\infty {{\beta _m}} {J_m}(nka)T_{lm}^{(3)}\sin m\beta - \\ \begin{array}{*{20}{c}} {} \end{array}\sum\limits_{m = 0}^\infty {A_{nm}^{(0)}H_m^{(1)}(nka)} T_{lm}^{(1)} - \sum\limits_{m = 1}^\infty {B_{nm}^{(0)}} H_m^{(1)}(nka)T_{lm}^{(3)} = 0, \;\;l = 0, 1, 2, \cdots , {\rm{ }} \end{array} $ | (20) |
| $ \begin{array}{l} A_{nl}^{(2)}{J_{\frac{{l{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}}}(nka)(1 + {\delta _{l0}})\frac{{2{\rm{ \mathsf{ π} }} - \alpha }}{2} - \sum\limits_{m = 0}^\infty {{\beta _m}{J_m}(nka)T_{lm}^{(2)}\cos m\beta } - \sum\limits_{m = 1}^\infty {{\beta _m}} {J_m}(nka)T_{lm}^{(4)}\sin m\beta \begin{array}{*{20}{c}} - \end{array}\\ \sum\limits_{m = 0}^\infty {A_{nm}^{(0)}H_m^{(1)}(nka)} T_{lm}^{(2)} - \sum\limits_{m = 1}^\infty {B_{nm}^{(0)}} H_m^{(1)}(nka)T_{lm}^{(4)} = 0, \;\;l = 0, 1, 2, \cdots , \end{array} $ | (21) |
方程(15)、(16)、(20)和(21)构成了未知系数Anm(0)、Anm(1)、Anm(2)和Bnm(0)的无限维完备代数联立方程组, 其中取Bn0(0)=0。实算中进行适度有限维运算即可满足计算精度要求。
对应浅水波一阶近似绕射波浪场流域Ωj的绕射波面以及最大无量纲绕射波面为:
| $ {\eta ^{(j)}} = - \frac{1}{g}\frac{{\partial {\mathit{\Phi }^{(j)}}}}{{\partial t}}\left| {_{z = d}} \right. = {\rm{Re}}(\eta _0^{(j)}),(j = 0,1,2),\frac{{{\eta _{{{\max }^{(j)}}}}}}{H} = \max \{ {\rm{Re}}(\frac{{\eta _0^{(j)}}}{H})\} ,$ | (22) |
对应浅水波一阶近似绕射波浪场流域Ωj的压力分布公式为:
| $ {P^{(j)}} = - \rho \frac{{\partial {\mathit{\Phi }^{(j)}}}}{{\partial t}} = {\rm{Re}}({p^{(j)}})\begin{array}{*{20}{c}} , \end{array}j = 0,1,2,$ | (23) |
据此, 可得作用于防波堤上臂的波浪力分量积分公式:
| $ \begin{array}{l} {F_{1x}} = \int_0^d {{\rm{d}}z} \int_0^a {[{P^{(2)}} - {P^{(1)}}]\left| {_{\theta = \alpha }} \right.\sin \alpha {\rm{d}}r} {\rm{, }}\\ {F_{1y}} = - \int_0^d {{\rm{d}}z} \int_0^a {[{P^{(2)}} - {P^{(1)}}]\left| {_{\theta = \alpha }} \right.\cos \alpha {\rm{d}}r} {\rm{, }} \end{array} $ | (24) |
以及防波堤下臂的波浪力分量积分公式:
| $ {F_{2x}} = 0{\rm{, }}{F_{2y}} = \int_0^d {{\rm{d}}z} \int_0^a {[{P^{(2)}}\left| {_{\theta = 2\pi }} \right. - {P^{(1)}}\left| {_{\theta = 0}} \right.]{\rm{d}}r} {\rm{, }} $ | (25) |
上臂和下臂的总波浪力分量为:
| $ \left\{ \begin{array}{c} {F_x} = {F_{1x}} + {F_{2x}} = {\mathop{\rm Re}\nolimits} ({f_x}), {F_y} = {F_{1y}} + {F_{2y}} = {\mathop{\rm Re}\nolimits} ({f_y}), \\ {f_x} = \frac{{\rho gHad\sin \alpha }}{{ka}}\sum\limits_{n = 1}^\infty {\frac{{{A_n}{{\rm{e}}^{ - {\rm{i}}n\omega t}}}}{n}} \sum\limits_{m = 0}^\infty {[A_{nm}^{(2)}\int_0^{nka} {{J_{\frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}}}(x)} } {\rm{d}}x - {( - 1)^m}A_{nm}^{(1)}\int_0^{nka} {{J_{\frac{{m{\rm{ \mathsf{ π} }}}}{\alpha }}}(x)} {\rm{d}}x], \\ {f_y} = \frac{{\rho gHad}}{{ka}}\sum\limits_{n = 1}^\infty {\frac{{{A_n}{{\rm{e}}^{ - {\rm{i}}n\omega t}}}}{n}} \sum\limits_{m = 0}^\infty {\{ [{{( - 1)}^m} - \cos \alpha ]A_{nm}^{(2)}} \int_0^{nka} {{J_{\frac{{m{\rm{ \mathsf{ π} }}}}{{2{\rm{ \mathsf{ π} }} - \alpha }}}}(x)} {\rm{d}}x - [1 - {( - 1)^m}\cos \alpha ]A_{nm}^{(1)}\\ \begin{array}{*{20}{c}} {}&{\int_0^{nka} {{J_{\frac{{m\pi }}{\alpha }}}(x)} {\rm{d}}x\} , } \end{array} \end{array} \right. $ | (26) |
总波浪力公式为:
| $ F = \sqrt {F_x^2 + F_y^2} $ | (27) |
进一步可给出V形堤总波浪力矩公式:
| $ \left\{ \begin{array}{c} {M_x} = {M_{1x}} = \frac{d}{2}{F_x}, {M_y} = {M_{1y}} + {M_{2y}}\\ = \frac{d}{2}({F_{1y}} + {F_{2y}}) = \frac{d}{2}{F_y}, \\ M = \sqrt {M_x^2 + M_y^2} = \frac{d}{2}F, \end{array} \right. $ | (28) |
其中, 下标x和y分别表示绕Oy轴和Ox轴的水平波浪力矩分量。
2 算例与分析在实算中, 符号F/ρg(H/2)ad表示V形防波堤的无量纲总波浪力幅值, 符号η/H表示浅水波对V形波堤绕射的最大无量纲波面。由波浪力矩公式(28)可知, 椭圆余弦波无量纲波浪力矩值为无量纲波浪力值的一半, 因而仅需针对无量纲波浪力进行计算即可。在计算中将引入浅水特征参数λ= 4к2K(к)/3π2 = H/k2d3, 它能够反映浅水波波浪参数与水深相对变化对波浪作用的综合影响效应。
为了验证本文所建立的V形防波堤之椭圆余弦波一阶绕射理论的正确性, 在本文公式中取V形堤张角为180°, 结构化为有限长直墙薄壁密实防波堤。进一步取堤长足够大, 与文献[5]的无限长直立直墙有限厚度密实防波堤(密实直墙薄壁堤与密实直墙有限厚度堤之堤前波面分布相同)在水波正入射条件下的椭圆余弦波一阶近似最大波面分布中心轴线剖面图进行对比(图 2a), 两者计算结果完全吻合, 相应的最大波面分布立体图对比(图 2b和c)也基本吻合, 从而验证了本文方法的正确性。其中比对部分为张角180°V形堤中心轴线邻域最大波面分布。图中为沿中心轴线的无量纲长度。文献[5]的最大波面依据椭圆余弦波一阶近似分量对无限长直墙堤的反射波理论进行计算, 这与本文的V形薄壁堤绕射波理论在解析解结构与形式上存在明显差别。在防波堤临波侧面几何形状相似以及波型和相关参数完全相同的情况下, 两种不同方法的剖面结果吻合, 说明本文方法是合理可靠的。图 2条件如下: λ= 1, a = 1 000, d = 2, α = 180°, β = 90°。
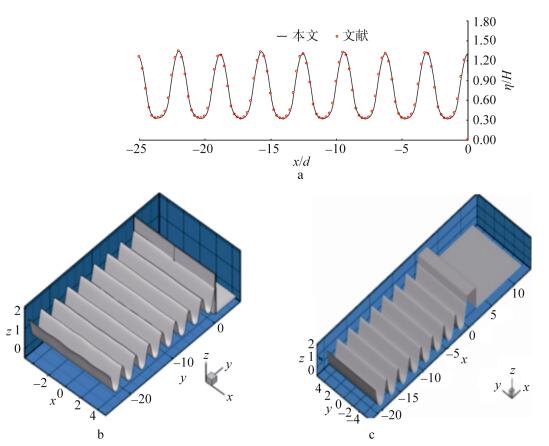 |
| 图 2 与无限长密实直墙堤的最大波面分布以及分布图中心线剖面的比较 Fig. 2 Comparison between the maximum wave surface distribution and center profile of infinite long solid breakwater 注: a:为最大波面分布中心线剖面的比较; b:为足够长180°V形堤最大波面分布; c:为无限长直墙堤最大波面分布 |
图 3为相同浅水条件下椭圆余弦波与Airy微幅波对张角120°V型防波堤的最大无量纲波浪力的比较。由图可见, 椭圆余弦波模型和Airy波模型分别计算的防波堤最大无量纲波浪力随参数kd(0)(kd为水深与波长的相对比例参数)的变化趋势大致相同。由解析公式(26)和(27)可见, 波浪力计算涉及贝塞尔函数积分的多重求和运算, 而kd = ka(d/a), 当d/a一定时, 振荡变化的贝塞尔函数随ka变化与随kd变化等价, 因而最大无量纲波浪力随kd呈现出一定的振荡态势且在相对较小Anm(0)处出现峰值, 它表明:在相对较浅的特定水域中, 波浪参数变化对波浪力可能具有明显影响。由图 3, 椭圆余弦波一阶近似分量理论所算结果明显高于Airy波理论的对应值, 说明在一定浅水条件下采用椭圆余弦波模型更为合理可靠。条件为: β = π/3, λ=3, d/a = 1/5, α = 2π/3。
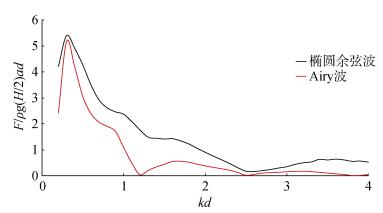 |
| 图 3 椭圆余弦波与Airy波所对应的最大无量纲波浪力的比较 Fig. 3 Comparison of the maximum dimensionless wave force between the cnoidal wave and Airy wave |
图 4为张角120°V形堤在相同参数下椭圆余弦波一阶近似分量与Airy正入射波之最大无量纲绕射波面分布中心线剖面的比较, 其中沿来波正入射中心线设立剖面图的横坐标, 坐标取值为无量纲水平距离。由图可见, 椭圆余弦波一阶分量的防波堤前壁最大波浪爬高可高于Airy对应值约100%, 堤后最大波面分布趋于相近。条件如下: β = π/3, λ= 3, d/a = 1/5,
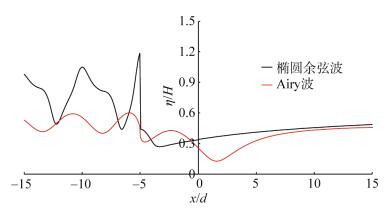 |
| 图 4 椭圆余弦波与Airy波所对应的最大绕射波面分布之剖面比较 Fig. 4 Comparison of the profile for the maximum diffraction wave surface between the cnoidal wave and Airy wave |
如图 5所示, 取来波正入射下防波堤两端相连、张角均为120°的V形防波堤与单层圆弧密实防波堤进行波浪作用的比较, 即取α = γ1 = 120° (α为V形防波堤两臂的夹角, 即V形堤张角, γ1为圆弧型防波堤的圆心角, 即圆弧堤张角), 圆弧堤来波正入射角β1 = 0 (等价于张角120°V形防波堤中正入射角β = 60°), 相应有V形堤臂长等于圆弧堤半径, 即a = a1, 其他海况条件等相关参数选取相同。其中V形防波堤堤长为l1 = 2a, 圆弧密实防波堤堤长为
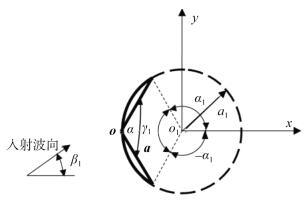 |
| 图 5 V形防波堤与圆弧型密实防波堤波浪作用对比的结构示意图 Fig. 5 Structure for the V-shaped breakwater and solid arc- shaped breakwater |
首先进行两种防波堤的同因子无量纲波浪力幅值的比较。由图 6可见:圆弧堤所受最大无量纲波浪力和V形堤的对应值随kd的变化趋势基本趋于一致, 当kd < 0.7时。圆弧堤的总无量纲波浪力幅值略高于V形堤的对应值, 两者十分接近。当kd > 0.7时, 圆弧堤的无量纲波浪力幅值明显高于V形堤的对应值。条件如下: λ= 3, G = 0, d/a = 1/5, a =1/5, α = γ1 = 2π/3, β1 = 0。
 |
| 图 6 V形堤与圆弧堤的最大无量纲波浪力的比较 Fig. 6 Comparison of the maximum dimensionless wave force between V-shaped breakwater and Arc-shaped breakwater |
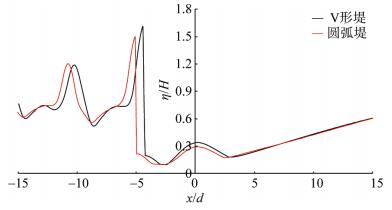
下面进行两种防波堤在来波正入射下的最大无量纲波面分布的比较。图 7和图 8为相同参数下圆弧堤与V形堤的椭圆余弦波一阶分量最大无量纲波面分布等高线图。图 9与图 10分别为两者的椭圆余弦波一阶分量最大无量纲波面分布中心线和斜射线(与x正轴夹角150°的斜射线, 该线与V形堤壁垂直)的剖面图。图中结果表明:相同条件下, 张角均为120°的V形堤与圆弧堤的堤后最大波面分布十分接近, 其中V形堤堤后的无量纲最大波面值仅略高于或完全等于圆弧堤的对应值。此外, 圆弧堤后的最大波面低值区面积值以及整体防护水域均略大于V形堤的对应值。两种堤堤前最大波面分布存在一定差异, 其中圆弧堤中心线前壁处的最大波面值(即最大波浪爬高)明显高于V形堤的对应值。而斜射线剖面中的V形堤壁与圆弧堤堤壁仅存在一个很小的距离差, 堤后最大波面值几乎相等。
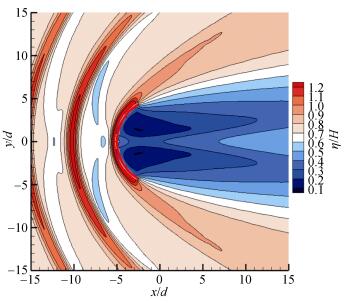 |
| 图 7 圆弧堤最大无量纲波面分布 Fig. 7 Distribution of maximum dimensionless wave surface for Arc-shaped breakwater |
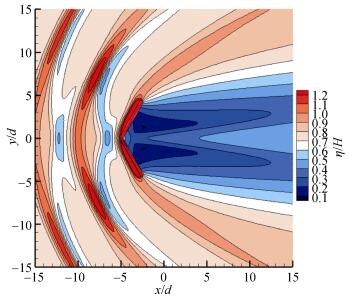 |
| 图 8 V形堤最大无量纲波面分布 Fig. 8 Distribution of maximum dimensionless wave surface for V-shaped breakwater |
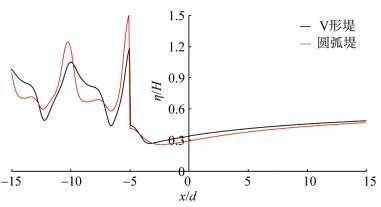 |
| 图 9 V形堤与圆弧堤的最大无量纲波面分布中心线剖面比较 Fig. 9 Comparison of the profile for the maximum wave surface diffracted using V-shaped breakwater and Arc-shaped breakwater |
 |
| 图 10 V形堤与圆弧堤的最大无量纲波面分布斜射线剖面比较(与x正轴夹角150°) Fig. 10 Comparison of the profile for the maximum wave surface diffracted using V-shaped breakwater and Arc-shaped breakwater(The angle between the incident direction and x-axis is 150°) |
综合考虑两种堤的波浪力与波面分布的比较结果, 可知: V形堤相对圆弧密实堤略占优势。其一圆弧堤施工难度相对较大, 且堤身略长从而增加用料; 其二, 圆弧堤总波浪力承载略高, x而堤后防浪效果相近。条件如下: λ= 3, G = 0, d/a = 1/5, α = 2π/3, kd = 0.6, β1 = 0。
图 9条件如下:综合考虑两种堤的波浪力与波面分布的比较结果, 可知: V形堤相对圆弧密实堤略占优势。其一圆弧堤施工难度相对较大, 且堤身略长从而增加用料; 其二, 圆弧堤总波浪力承载略高, x而堤后防浪效果相近。条件如下: λ= 3, G = 0, d/a = 1/5, a= a1, α = γ1 = 2π/3, kd = 0.6, β1 = 0, y = 0。
图 10条件如下: λ= 3, G = 0, d/a = 1/5, a= a1, α = γ1 = 2π/3, kd = 0.6, β1 = 0, y = 0
2.2 张角90°的V形防波堤与张角180°的圆弧防波堤结果的比较如图 11所示, 取来波正入射下防波堤两端相连、张角为90°的V形防波堤与张角为180°的单层圆弧密实防波堤进行波浪作用的比较, 即取α = 90°, γ1 = 180° (α为V形防波堤两臂的夹角, 即V形堤张角;
γ1为圆弧型防波堤的圆心角, 即圆弧堤张角), 圆弧堤来波正入射角β1 = 0 (等价于张角90°V形防波堤中正入射角β = 45 °), 相应有V形堤臂长等于
 |
| 图 11 V形防波堤与圆弧型密实防波堤波浪作用对比的结构示意图 Fig. 11 Structure for the V-shaped breakwater and solid arc- shaped breakwater |
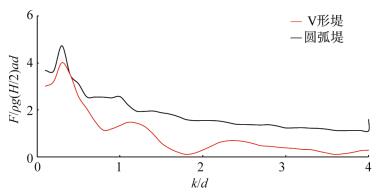
首先进行两种防波堤的无量纲波浪力幅值的比较。由图 12可见:圆弧堤所受最大无量纲波浪力和V形堤对应值随kd的变化趋势大致一样, 其中圆弧堤受力明显高于V形堤对应值。与张角120°两堤无量纲波浪力幅值比较的对应结果相比, 此处比较结果中圆弧堤总波浪力高于V形堤对应值的幅度明显更大。条件如下: λ= 3, G = 0, d/a = 1/5,
 |
| 图 12 V形堤与圆弧堤的最大无量纲波浪力的比较 Fig. 12 Comparison of maximum dimensionless wave force between the V-shaped breakwater and Arc-shaped breakwater |
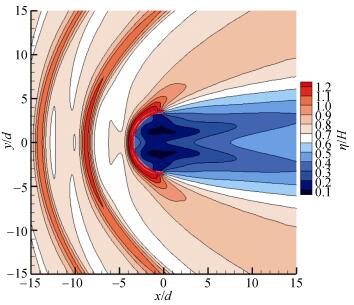
图 13和图 14为相同参数下圆弧堤与V形堤的椭圆余弦波一阶分量最大无量纲波面分布等高线图。图 15与图 16分别为两者最大无量纲波面分布中心线和斜射线(与x正轴夹角135°的斜射线, 该线与V形堤壁垂直)的剖面图。图中结果表明:相同条件下, 张角为90°的V形堤与张角为180°圆弧堤的堤后最大波面分布存在一定差异, 其中V形堤堤后的无量纲最大波面值略高于或明显高于圆弧堤的对应值。圆弧堤后的最大波面低值区面积值以及整体防护水域均明显大于V形堤的对应值。此外, 圆弧堤中心线前壁处的最大波面值(即最大波浪爬高)明显高于V形堤的对应值, 而斜射线剖面中的V形堤壁与圆弧堤堤壁存在一定的距离差, 堤前最大波面分布相近, 但堤后相同位置处V形堤最大波面值明显高于圆弧堤。
 |
| 图 13 圆弧堤最大无量纲波面分布 Fig. 13 Distribution of maximum dimensionless wave surface for Arc-shaped breakwater |
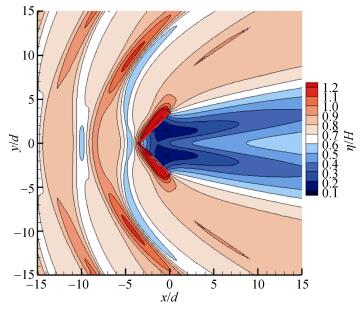 |
| 图 14 V形堤最大无量纲波面分布 Fig. 14 Distribution of maximum dimensionless wave surface for V-shaped breakwater |
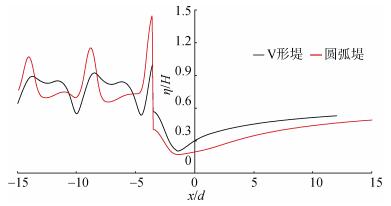 |
| 图 15 V形堤与圆弧堤的最大无量纲波面分布中心线剖面比较 Fig. 15 Comparison of the profile for the maximum wave surface diffracted using V-shaped breakwater and Arc-shaped breakwater |
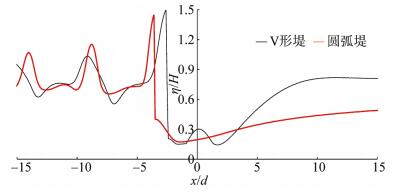 |
| 图 16 V形堤与圆弧堤的最大无量纲波面分布斜射线剖面比较(与x正轴夹角135°) Fig. 16 Comparison of the profile for the maximum wave surface diffracted using V-shaped breakwater and Arc-shaped breakwater(The angle between the incident direction and x-axis is 135°) |
综合考虑两种堤的波浪力与波面分布的比较结果, 可知: V形堤同因子无量纲总波浪力幅值相对较低且堤身短于圆弧堤从而节省用料, 并且施工难度较小。不过圆弧堤堤后防浪区域以及最大波面低值区面积明显大于张角90°V形堤的对应结果。条件如下: λ= 3, G = 0, d/a = 1/5, α = π/2, γ1 = π, β1 = 0, kd = 0.6。
条件如下: λ= 3, G = 0, d/a = 1/5,
件如下: λ= 3, G = 0, d/a = 1/5,
本文引入椭圆余弦波一阶分量模型, 针对V形防波堤的经典结构形式, 应用特征函数展开法, 对浅水波的绕射问题进行了系统的解析研究, 从而将Airy微幅波的对应理论加以了有效拓展。文中推导了椭圆余弦波对V形防波堤绕射的波势精确解, 据此对浅水波作用下的水平波浪力进行了实算与分析。主要结论有:
1) 本文结果首次给出了有限长直立薄壁直墙式防波堤的浅水波绕射模型。通过将本文理论应用于来波正入射下足够长张角180°直墙薄壁密实堤的绕射波面计算, 与已有的无限长有限厚度直墙密实堤的正反射波面对应结果加以比较, 在防波堤临波侧面几何形状相似以及波型和相关参数完全相同的情况下, 两种不同方法的最大波面剖面结果吻合, 说明本文方法是合理可靠的。
2) 利用本文椭圆余弦波一阶分量理论计算所得的V形防波堤的最大无量纲波浪力(矩)明显大于相同浅水条件下Airy微幅波波理论的对应结果, 说明在一定的浅水条件, 采用本文的V形堤浅水波绕射理论更为合理可靠的。
3) 本文选取了几何形状相近的单层密实圆弧堤与V形防波堤的特例进行了防浪效应与承载的特别比较。其中张角120°V形堤与张角120°圆弧密实堤几何形状最为接近, 且V形堤略占优势。圆弧堤施工难度较大, 并且堤身略长从而增加用料, 其同因子无量纲总波浪力幅值略高, 而两种类型堤后防浪效果相近。此外, 张角90°V形堤的同因子无量纲总波浪力幅值低于张角180°单层密实圆弧堤, 且堤身明显短于圆弧堤从而节省用料, 并且施工难度小。但圆弧堤堤后防浪区域以及最大波面低值区面积却明显大于张角90°V形堤的对应值。因此, 两种类型结构各有优劣势。
| [1] |
Stokes J J. Water Waves[M]. New York: Inter-science Publishers, 1957: 69-147.
|
| [2] |
Losada I J, Losada M A, Roldan A J. Propagation of oblique incident waves past rigid vertical thin barriers[J]. Applied Ocean Research, 1992, 14(3): 191-199. DOI:10.1016/0141-1187(92)90014-B |
| [3] |
Lick W. Diffraction of waves by a wedge[J]. Journal of the Waterway, Port, Coastal and Ocean Division, 1978, 104(2): 119-133. |
| [4] |
洪广文. 不完全反射边界楔形堤和隅角堤波浪绕射理论解析解[J]. 海洋学报, 1990, 12(4): 487-504. Hong Guangwen. Analytical solutions of wave diffraction theory for wedge dike and corner dike with incomplete reflection boundary[J]. Acta of Oceanologica Sinica, 1990, 12(4): 487-504. |
| [5] |
朱梦华, 黄华, 詹杰民, 等. 椭圆余弦波对透空直立防波堤波浪力解析计算[J]. 人民黄河, 2015, 37(11): 36-39. Zhu Menghua, Huang Hua, Zhan Jiemin, et al. Analytical Calculation of Cnoidal Wave forces on the Porous Vertical Breakwater[J]. Yellow River, 2015, 37(11): 36-39. DOI:10.3969/j.issn.1000-1379.2015.11.010 |
| [6] |
朱梦华, 黄华, 詹杰民, 等. 斜入射椭圆余弦波对直立防波堤的波浪渗流作用[J]. 中山大学学报(自然科学版), 2016, 55(4): 39-46. Zhu Menghua, Huang Hua, Zhan Jiemin, et al. Oblique incidence cnoidal water wave-induced seepage effects on vertical breakwater[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(4): 39-46. |
| [7] |
楚玉川, 程建生, 赵鑫, 等. 圆弧型贯底式防波堤上波浪作用力的解析研究[J]. 水动力学研究与进展, A辑, 2014, 29(2): 212-217. Chu Yuchuan, Cheng Jiansheng, Zhao Xin, et al. Analytic study on Arc-shaped bottom-mounted breakwaters[J]. Journal of Hydrodynamics, A, 2014, 29(2): 212-217. |
| [8] |
张敖, 黄华, 詹杰民, 等. 椭圆余弦波对圆弧型固立防波堤的绕射波浪力[J]. 水运工程, 2017(3): 28-33. Zhang Ao, Huang Hua, Zhan Jiemin, et al. Diffracted wave forces caused by cnoidal wave on arc-shaped bottom-mounted breakwater[J]. Port & Waterway Engineering, 2017(3): 28-33. DOI:10.3969/j.issn.1002-4972.2017.03.006 |
| [9] |
张敖, 黄华, 詹杰民, 等. 圆弧型贯底式透空防波堤对孤立波的绕射[J]. 中山大学学报(自然科学版), 2017, 56(3): 1-9. Zhang Ao, Huang Hua, Zhan Jiemin, et al. Diffraction of solitary wave by arc-shaped bottom-mounted porous breakwater[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2017, 56(3): 1-9. |
| [10] |
何军, 蒋昌波, 李冬, 等. T型防波堤与波浪相互作用数值研究[J]. 海洋工程, 2010, 28(1): 50-57. He Jun, Jiang Changbo, Li Dong, et al. Numerical study on T-type breakwaters interaction with wave[J]. The Ocean Engineering, 2010, 28(1): 50-57. DOI:10.3969/j.issn.1005-9865.2010.01.008 |
| [11] |
李雪艳, 付聪, 范庆来, 等. 斜坡堤典型胸墙波浪力的影响因[J]. 海洋科学, 2015, 39(12): 118-129. Li Xueyan, Fu Cong, Fan Qinglai, et al. Factors influencing wave load on typical crest walls of sloping breakwaters[J]. Marine Sciences, 2015, 39(12): 118-129. DOI:10.11759/hykx20150122001 |
| [12] |
Kao H C, Deng H T, Liang H H. Accurate solution to diffraction around a modified V-shaped breakwater[J]. Coastal Engineering, 2012, 68: 56-66. DOI:10.1016/j.coastaleng.2012.05.002 |
| [13] |
陆志妹, 缪国平, 朱仁传, 等. V形贯底式防波堤上波浪作用力的解析研究[J]. 水动力学研究与进展, 2007, 22(1): 136-141. Lu Zhimei, Liao Guoping, Zhu Renchuan, et al. Analytical research on wave force exerted on V-shaped bottom-mounted breakwaters[J]. Journal of Hydrodynamics, 2007, 22(1): 136-141. |
| [14] |
丁宁, 于建星, 侯佳佳. V形浮式防波堤的动压力特性[J]. 排灌机械工程学报, 2014, 32(1): 29-32. Ding Ning, Yu Jianxing, Hou Jiajia. Characteristics of dynamic pressure on floating V-shaped breakwater[J]. Journal of Drainage and Irrigation Machinery Engineering, 2014, 32(1): 29-32. |
| [15] |
程建生, 缪国平, 尤云祥, 等. 波浪在V形贯底式防波堤上绕射的解析研究[J]. 上海交通大学学报, 2005, 9(5): 813-817. Cheng Jiansheng, Liao Guoping, You Yunxiang, et al. Analytical research on the wave diffraction on V-type bottom-mounted breakwaters[J]. Journal of Shanghai Jiaotong University, 2005, 9(5): 813-817. DOI:10.3321/j.issn:1006-2467.2005.05.033 |
| [16] |
Isaacson M D S Q. Shallow wave diffraction around large cylinder[J]. Journal of the Waterway, Port, Coastal and Ocean Division, 1977, 103(1): 69-82. |
 2020, Vol. 44
2020, Vol. 44


