文章信息
- 杨雪雪, 刘强. 2021.
- YANG Xue-xue, LIU Qiang. 2021.
- 基于KPCA-RBF模型的风暴潮灾害经济损失预测
- Economic loss assessment of storm-surge disasters based on the KPCA-RBF model
- 海洋科学, 45(10): 32-39
- Marine Sciences, 45(10): 32-39.
- http://dx.doi.org/10.11759/hykx20200322001
-
文章历史
- 收稿日期:2020-03-22
- 修回日期:2020-06-27
风暴潮灾害是迄今为止最具破坏性的海洋灾害, 世界上大多数重大沿海灾害都是由风暴潮造成的[1-2]。在我国的海洋灾害影响清单中, 风暴潮灾害一直占据着主导地位, 几乎每年都会给沿海地区造成巨大的经济损失。为减轻风暴潮灾害对沿海地区经济社会发展的影响, 运用科学的手段提高灾害损失预测的能力, 对于指导沿海地区的防灾减灾工作十分重要。
近年来, 国内外学者在风暴潮灾害损失预测方面做了大量研究工作。Wood等[3]利用巨灾损失模型对英格兰东部沿海平原的潜在风暴潮洪水事件进行了概率量化, 根据洪水深度和洪水流速与财产损失量之间的脆弱性函数来预测风暴潮洪水损失; Jin等[4]提出了一种经济计量模型组方法来精化风暴潮损失的评估, 并利用支持向量机模型验证了模型组方程能较详细地反映风暴潮灾害与其他相关变量的关系; Yang等[5-6]采用扩展卡尔曼滤波和极限理论来预测风暴潮灾害经济损失和伤亡人口; 潘艳艳等[7]基于时间序列预测法, 运用傅里叶级数扩展模型模拟了风暴潮灾害直接经济损失的时间路径; 殷克东等[8]以近年来东南沿海风暴潮灾害损失的历史数据为基础, 利用主成分分析法对样本风暴潮进行了聚类分析并证明了其在风暴潮灾害损失评估中的有效性, 上述研究为科学预测风暴潮灾害损失提供了理论指导。由于风暴潮灾害损失预测是较复杂的系统[9-10], 为提高预测精度并丰富现有风暴潮灾害损失预测方法, 本文采用核主成分分析对风暴潮灾害数据进行降维优化, 在此基础上, 利用径向基函数神经网络对优化后的数据进行训练, 结果表明该方法具有较好的非线性拟合能力, 可实现对风暴潮灾害直接经济损失的预测。
1 风暴潮灾害经济损失评估指标 1.1 数据来源本文以广东省风暴潮灾害为研究对象, 收集了广东省1996—2018年间记录相对完整的32个风暴潮灾害的相关数据进行分析研究, 数据主要来源于《中国海洋灾害公报》[11]《广东省海洋灾害公报》[12]《广东统计年鉴》[13]等。
广东省位于我国南部沿海, 是我国受风暴潮影响最严重的省份之一。由于广东沿海地区人口稠密、经济发达, 台风风暴潮每年造成的直接经济损失十分巨大[14]。近10 a来, 全国因风暴潮灾害造成的直接经济损失中, 广东省累计占比接近50%, 如图 1所示。随着海洋经济的快速发展, 广东沿海地区的风暴潮灾害风险日益突出, 防灾减灾形势也愈发严峻, 因此, 采取科学的手段对风暴潮灾害损失进行合理预测对广东省经济社会的可持续发展具有重要意义。
 |
| 图 1 风暴潮灾害直接经济损失值 Fig. 1 Direct economic loss value because of storm surge disasters |
为了对风暴潮灾害直接经济损失进行科学准确的预测, 我们需要建立相对完善的评估指标体系[9-10]。风暴潮灾害损失的大小取决于自身的危险性程度以及当地的经济社会发展状况[15], 本文基于自然灾害风险分析理论, 结合风暴潮的成灾特点以及指标数据的易取性和全面性, 建立了风暴潮灾害直接经济损失评估指标体系, 包括致灾因子危险性、承载体易损性、孕灾环境三个方面, 如图 2所示。
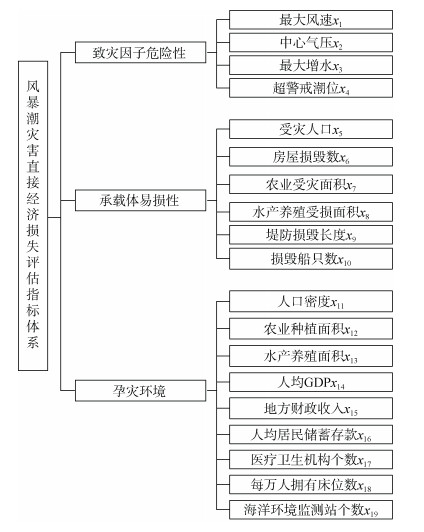 |
| 图 2 风暴潮灾害直接经济损失评估指标体系 Fig. 2 Indicator system for evaluating direct economic losses because of storm surge disasters |
(1) 致灾因子危险性。风暴潮的致灾能力主要体现在台风引起的风暴增水方面, 台风强度越大, 中心气压越低, 则风暴增水越大, 造成的损失往往越严重[15]。本文选取台风登陆时的最大风速、中心气压、最大增水和超警戒潮位4个指标来描述风暴潮致灾因子危险性。
(2) 承载体易损性。承灾体是风暴潮灾害的直接作用物, 主要包括风暴潮过境地域的社会经济因素, 如人口、农业、堤防设施等。风暴潮灾害承载体的易损性可用致灾因子对承载体造成的可能损失大小表示, 本文选取受灾人口、房屋损毁、农业受灾面积、堤防损毁等6个指标来反映承载体的易损性。
(3) 孕灾环境。这里主要指当地的经济社会发展状况及应灾水平。本文从经济社会发展现状、社会防灾能力、监测预警能力[15-16]等多个方面综合选取了人口密度、农业种植面积、人均GDP、地方财政收入、医疗卫生机构数、海洋环境监测站个数等9个指标作为孕灾环境影响因子。
2 预测模型的建立 2.1 核主成分分析原理核主成分分析(kernel principle component analysis, KPCA)是Schokopf等[17]提出的一种将核函数引入到主成分分析(principle component analysis, PCA)的方法。PCA是一种常用的特征提取和降维的线性方法, 在实际处理数据中, 由于数据之间存在复杂的非线性关系, 使得它难以准确获得数据的高阶特征, 处理高维非线性数据的能力有限。由于风暴潮灾害直接经济损失评估指标数据非线性程度高且指标间存在信息重叠, 为提高运算效率, 本文首先利用KPCA对原始数据进行降维处理。KPCA实现了对PCA的改进, 它可对输入变量进行非线性特征提取, 提取速度快且能够充分保留所有输入变量的非线性信息[18]。
KPCA实质上是通过非线性映射, 将原始数据从原始输入空间Rn映射到高维空间F中, 然后在F中进行主成分分析。其原理: 设
| $\sum\limits_{i = 1}^M {\boldsymbol{\varPhi} ({x_i})} = 0 .$ | (1) |
高维空间F中的协方差矩阵可表示为:
| $C = \frac{1}{M}\sum\limits_{i = 1}^M {\boldsymbol{\varPhi} ({x_i}){\rm{ }}} \boldsymbol{\varPhi} {({x_i})^{\rm{T}}} = \frac{1}{M}\boldsymbol{\varPhi} (X)\boldsymbol{\varPhi} {(X)^{\rm{T}}} .$ | (2) |
对上述协方差矩阵C进行特征矢量分析, 设其特征值为λ, 特征向量为V, 则
| $ \lambda \boldsymbol{V}=\boldsymbol{C V}. $ | (3) |
由于
| $\boldsymbol{V}= \sum\limits_{i = 1}^M {\frac{{{\rm{ }}\boldsymbol{V}\boldsymbol{\varPhi} {{({x_i})}^{\rm{T}}}}}{{M\lambda }}\;} \boldsymbol{\varPhi} ({x_i}) .$ | (4) |
上式可以写成:
| $\lambda \boldsymbol{\varPhi} {(\boldsymbol{X} )^{\rm{T}}}\boldsymbol{\alpha} = \frac{1}{M}\boldsymbol{\varPhi} {(\boldsymbol{X} )^{^{\rm{T}}}}\boldsymbol{\varPhi} (\boldsymbol{X} )\boldsymbol{\varPhi} {(\boldsymbol{X} )^{^{\rm{T}}}}\boldsymbol{\varPhi} (\boldsymbol{X} )\boldsymbol{\alpha} .$ | (5) |
定义M×M维的核矩阵K:
| ${(\boldsymbol{K} )_{i, j}} = \boldsymbol{\varPhi} {({x_i})^{{T}}}\boldsymbol{\varPhi} ({x_j}) = K({x_i}, {x_j}) .$ | (6) |
将式(6)代入式(5)并将结果写成矩阵形式:
| $M\lambda K\alpha = {K^2} \boldsymbol{\alpha} \to M\lambda \boldsymbol{\alpha} = K\boldsymbol{\alpha} .$ | (7) |
对式(7)进行求解可得高维空间中的特征值λ及特征向量V, 原始输入样本X在特征向量V1方向的投影为:
| ${y_1} = \boldsymbol{V} _1^{\rm{T}}\boldsymbol{\varPhi} (\boldsymbol{X} ) = \sum\limits_{i = 1}^M {\alpha _i^1\boldsymbol{\varPhi} {{{\rm{(}}{x_i}{\rm{)}}}^{\rm{T}}}\boldsymbol{\varPhi} (\boldsymbol{X} )} = \sum\limits_{i = 1}^M {\alpha _i^1K({x_i}, \boldsymbol{X} )} .$ | (8) |
径向基函数(radial basis function, RBF)神经网络是一种高效的神经网络形式, 它具有良好的非线性函数拟合和泛化能力, 而且结构简单、学习收敛速度快, 可以保证全局收敛[19], 因此本文采用径向基函数神经网络建立风暴潮灾害直接经济损失预测模型。RBF网络结构如图 3所示, 其中隐含层节点的激活函数采用径向基函数对输入变量进行处理, 再线性映射到输出层。
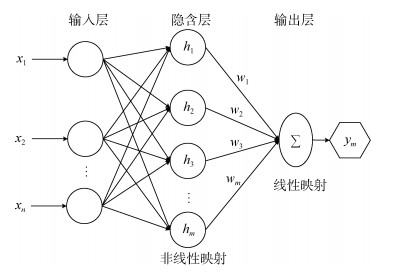 |
| 图 3 RBF神经网络结构 Fig. 3 Diagram of the RBF neural network |
在RBF网络结构中, 令
其中, m为隐含层节点数, h为高斯径向基函数, 则hm可表示为:
| ${h_m} = \exp \left( { - \frac{{{{\left\| {\boldsymbol{X} - {c_m}} \right\|}^2}}}{{2b_m^2}}} \right), $ | (9) |
式中, C = [c1, c2, …, cm]T为隐含层节点的中心参数, B = [b1, b2, …, bm]T为径向基函数的宽度参数, W = [w1, w2, …, wm]T为隐含层到输出层的网络权值参数, 则k时刻RBF网络的输出可表示为:
| $y\left( k \right) = \sum\limits_{j = 1}^m {{h_j}} {w_j} .$ | (10) |
本文模型建立的过程如下:
(1) 采用KPCA对风暴潮灾害直接经济损失评估指标数据进行降维处理, 从而减少RBF神经网络的输入向量数。KPCA的具体步骤如下:
(a) 对初始指标数据进行标准化处理(本文采用标准差归一化法), 计算核矩阵K;
(b) 由于本文收集的风暴潮数据是非中心化的, 需对其进行中心化处理, 中心化的核矩阵表示为:
| ${\boldsymbol{K}^*} = \boldsymbol{K} - \frac{1}{M}j{\rm{ }}j'{\rm{ }}\boldsymbol{K} - \frac{1}{M}\boldsymbol{K}{\rm{ }}j{\rm{ }}j' + \frac{1}{{{M^2}}}{\rm{( }}j'{\rm{ }}\boldsymbol{K}{\rm{ }}j)j{\rm{ }}j', $ | (11) |
式中, j为元素全为1的M维向量;
(c) 计算矩阵K*的特征值V与特征向量λ;
(d) 将特征向量规范化, 即:
| ${\alpha ^j} = \frac{1}{{\sqrt {{\lambda _i}} }}{V^j}, {\rm{ }}j = 1, {\rm{ }}2, \cdots , M.$ | (12) |
(e) 计算特征值 λ1, λ2, …, λm的累计贡献率B1, B2, …, Bm, 根据已设定的主成分累计贡献率p, 当Bk≥p, 则选取k个主成分及对应的主分量α1, α2, …, αk;
(f) 计算原始样本X在α1, α2, …, αk上的投影Y, Y = K*·α, Y即为原始输入数据经过KPCA降维后的结果。
(2) 将原始数据划分成训练样本和测试样本。
(3) 将训练样本作为RBF网络输入向量, 输出为风暴潮灾害直接经济损失预测值, 对RBF网络进行训练。
(4) 将测试样本输入模型进行独立样本检验。
本文以MATLAB 2014b为平台, 采用MATLAB自带的神经网络工具箱newrb函数[20-21]建立RBF网络, 其语法为:
net = newrb (P, T, goal, spread, MN, DF)
式中, P为输入矩阵; T为输出矩阵; goal为均方误差的目标, 取goal = 0.001; spread表示径向基函数的扩散速度[22], 取spread = 20; MN指隐含节点的最大个数, 取MN = 200; DF指两次显示之间所添加的神经元数目, 取DF = 1。
综上所述, 可建立KPCA-RBF预测模型, 如图 4所示。
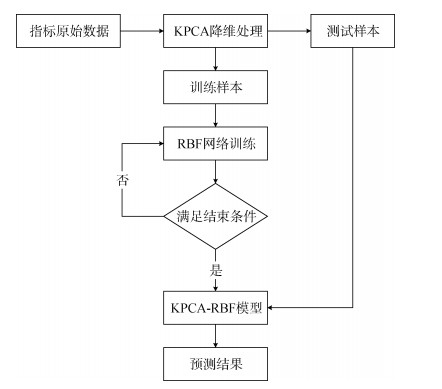 |
| 图 4 KPCA-RBF预测模型流程图 Fig. 4 Flowchart of the KPCA-RBF assessment model |
本文首先将风暴潮灾害直接经济损失评估指标数据进行KPCA降维处理, 其主成分累计贡献率如图 5所示。
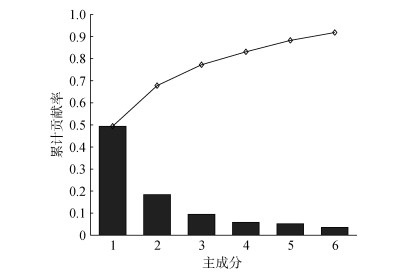 |
| 图 5 KPCA主成分累计贡献率 Fig. 5 Cumulative contribution rate of KPCA |
本文设定的主成分累计贡献率p = 90%, 由图 5可知, 前6个主成分的累计贡献率达到了91.83%, 可以认为前6个主成分包含了全部指标的绝大部分信息, 计算原始数据在α1, α2, …, α6上的投影Y, 从而得到RBF网络的输入向量。
对所收集的广东省32个风暴潮灾害样本进行随机划分, 选取其中29个作为训练样本, 其余3个为测试样本。将训练样本输入RBF网络中, 输出值为风暴潮灾害直接经济损失预测值, 预测结果如图 6所示, 从图中可以看出, 大部分训练样本的预测值逼近实际值, 模型的拟合精度较高。
 |
| 图 6 KPCA-RBF神经网络训练集拟合结果 Fig. 6 Fitting results of training set based on the KPCA- RBF neural network |
现有的BAS-BP模型[9]、SVM-BP模型[10]为科学预测风暴潮灾害损失提供了方法指导, 但仍存在不足, 如: BAS-BP、SVM-BP所采用的降维方法均是通过删除部分评估指标来实现降维, 无法充分保留所有指标的非线性信息; 两者均是对BP神经网络的改进, 较传统BP神经网络有性能方面的提高, 但BP网络隐含层神经元个数的选取尚无理论上的指导, 而是根据经验公式确定, 这使得网络具有较大的冗余性, 无形中增加了学习时间。为客观比较KPCA- RBF模型与现有模型的性能, 本文将KPCA-RBF与BAS-BP、SVM-BP进行对比实验, 分别计算它们的平均相对误差(MRE)、均方误差(MSE)和CPU运行时间, 结果如表 1所示。可以看出, 在处理相同样本时, KPCA-RBF模型的综合表现最好, 训练时间明显少于其他两个模型, 学习收敛速度快, 预测精度较高。这是因为KPCA-RBF在一定程度上克服了现有模型的不足: KPCA可充分考虑每项评估指标包含的信息, 使得神经网络的输入数据比较全面准确, 而且RBF网络的隐含层可以自动增加神经元直到满足精度要求为止, 简化了网络结构, 有效提高学习收敛速度。
| 模型 | MRE | MSE | CPU运行时间/s | |||
| 训练样本 | 测试样本 | 训练样本 | 测试样本 | |||
| KPCA-RBF | 1.338 9 | 0.248 7 | 26.553 3 | 1.393 6 | 1.48 | |
| BAS-BP | 1.296 6 | 0.253 1 | 25.887 3 | 1.411 6 | 25.54 | |
| SVM-BP | 1.533 7 | 0.301 7 | 28.397 2 | 1.676 4 | 16.85 | |
为进一步证明KPCA-RBF模型的有效性, 本文基于上述样本划分方法, 将风暴潮灾害样本随机划分成多组训练样本和测试样本进行试验。选取普通RBF网络模型、KPCA-RBF模型以及PCA-RBF模型对各组训练样本进行处理, 由于三种模型的CPU运行时间均在2 s以内, 学习速度差别不大, 因此本文主要以训练精度作为评价各模型性能优劣的依据, 分别计算每组训练样本在不同模型中的MRE和MSE, 结果如表 2所示, 可以看出基于不同的样本划分情况, RBF和PCA-RBF的两种误差平均值均较大, PCA-RBF略优于RBF, 而KPCA-RBF两种误差均最小, 对训练样本的拟合效果最好, 这表明KPCA-RBF在处理高维非线性数据时具有一定的优越性, 拟合结果精度较高。
| 模型 | 多组训练样本 | 多组的误差平均值 | ||||||||||||
| 1 | 2 | … | n | |||||||||||
| MRE | MSE | MRE | MSE | MRE | MSE | MRE | MSE | MRE | MSE | |||||
| RBF | 1.140 9 | 28.927 2 | 1.662 1 | 28.648 7 | … | … | 1.586 6 | 29.456 3 | 1.472 1 | 29.101 8 | ||||
| KPCA-RBF | 1.338 9 | 26.553 3 | 0.852 2 | 22.157 7 | … | … | 1.326 1 | 27.934 9 | 1.073 5 | 24.456 4 | ||||
| PCA-RBF | 1.644 6 | 28.602 2 | 0.865 3 | 26.181 4 | … | … | 1.589 9 | 28.516 8 | 1.402 1 | 28.522 4 | ||||
本文将上述多组测试样本作为独立样本来检验三种模型在预测精度上的差异, 分别计算三种模型的误差, 结果如表 3所示, 从表 3可以看出, 与RBF和PCA-RBF相比, KPCA-RBF的测试误差值相对更小, 具有更好的预测效果, 这主要是KPCA-RBF模型集成了KPCA和RBF神经网络在处理非线性数据方面的优势, KPCA利用核映射对原始非线性序列进行降维, 用低维数据表示原始数据的信息, 弥补了PCA处理高维非线性数据时存在的不足, 而且RBF神经网络可有效实现对非线性数据序列的拟合和预测。由此可知, KPCA- RBF模型具有较好的非线性拟合能力, 预测结果具有更高的精度, 可有效地用于风暴潮灾害直接经济损失预测。
| 模型 | 测试样本 | 多组测试样本 | 多组的误差平均值 | ||||||||||||||||
| 1 | 2 | … | n | ||||||||||||||||
| RE | MRE | MSE | RE | MRE | MSE | MRE | RE | MSE | RE | MRE | MSE | MRE | MSE | ||||||
| RBF | 1 | 0.115 8 | 0.272 7 | 1.830 2 | 0.119 9 | 0.085 5 | 0.133 5 | … | … | … | 0.320 7 | 0.312 9 | 4.571 6 | 0.346 3 | 2.076 4 | ||||
| 2 | 0.343 8 | 0.067 2 | … | 0.258 1 | |||||||||||||||
| 3 | 0.358 5 | 0.069 3 | … | 0.359 9 | |||||||||||||||
| KPCA-RBF | 1 | 0.281 1 | 0.248 7 | 1.393 6 | 0.117 7 | 0.073 8 | 0.104 9 | … | … | … | 0.186 8 | 0.172 3 | 3.157 3 | 0.234 9 | 1.798 8 | ||||
| 2 | 0.316 5 | 0.057 4 | … | 0.094 8 | |||||||||||||||
| 3 | 0.148 5 | 0.046 4 | … | 0.235 3 | |||||||||||||||
| PCA- RBF | 1 | 0.265 3 | 0.256 0 | 1.424 9 | 0.118 5 | 0.074 2 | 0.106 2 | … | … | … | 0.176 1 | 0.184 0 | 3.413 3 | 0.258 8 | 1.913 2 | ||||
| 2 | 0.317 3 | 0.057 6 | … | 0.170 5 | |||||||||||||||
| 3 | 0.185 4 | 0.046 4 | … | 0.205 4 | |||||||||||||||
本文基于风暴潮灾害的成灾特点建立了风暴潮灾害直接经济损失预评估指标体系, 提出基于KPCA-RBF网络的风暴潮灾害直接经济损失预测模型, 利用KPCA对高度非线性的评估指标数据进行降维优化, 降维后的数据可最大程度保留原始数据信息, 再利用RBF神经网络输出预测值。针对风暴潮灾害数据具有很强的非线性特点, 该模型表现出良好的适用性, 对非线性数据序列有较好的预测效果, 为海洋灾害损失预测提供了模型参考。
| [1] |
BERZ G. Windstorm and storm surges in Europe: loss trends and possible counter-actions from the viewpoint of an international reinsurer[J]. Philosophical Transactions Mathematical Physical & Engineering Sciences, 2005, 363(1831): 1431-1440. |
| [2] |
LE K T. An Analysis of the recent severe storm surge disaster events in China[J]. Natural Hazards, 2000, 21(2): 215-223. |
| [3] |
WOOD R M, DRAYTON M, BERGER A, et al. Catastrophe loss modelling of storm-surge flood risk in eastern England[J]. Philosophical Transactions of The Royal Society A Mathematical Physical and Engineering Sciences, 2005, 363(1831): 1407-1422. DOI:10.1098/rsta.2005.1575 |
| [4] |
JIN X, SHI X, GAO J, et al. Evaluation of loss due to storm surge disasters in China based on econometric model groups[J]. International Journal of Environmental Research and Public Health, 2018, 15(4): 604. DOI:10.3390/ijerph15040604 |
| [5] |
YANG S, LIU X, LIU Q. A storm surge projection and disaster risk assessment model for China coastal areas[J]. Natural Hazards, 2016, 84(1): 649-667. DOI:10.1007/s11069-016-2447-1 |
| [6] |
YANG S, LIU X, LIU Q, et al. A study of storm surge disasters based on extreme value distribution theory[J]. Journal of Coastal Research, 2017, 33(6): 1423-1435. |
| [7] |
潘艳艳, 王涛, 赵昕. 风暴潮灾害损失时间路径模拟与预测[J]. 统计与决策, 2016, 5: 87-89. PAN Yanyan, WANG Tao, ZHAO Xin. Time path simulation and prediction of storm surge disaster loss[J]. Statistics & Decision, 2016, 5: 87-89. |
| [8] |
殷克东, 王辉. 风暴潮灾害损失评估的主成分模型研究[J]. 统计与决策, 2010, 19: 63-64. YIN Kedong, WANG Hui. Study on the principal component model of storm surge disaster loss assessment[J]. Statistics & Decision, 2010, 19: 63-64. |
| [9] |
王甜甜, 刘强. 基于BAS-BP模型的风暴潮灾害损失预测[J]. 海洋环境科学, 2018, 37(3): 457-463. WANG Tiantian, LIU Qiang. The assessment of storm surge disaster loss based on BAS-BP model[J]. Marine Environmental Science, 2018, 37(3): 457-463. |
| [10] |
冯倩, 刘强. 基于SVM-BP神经网络的风暴潮灾害损失预评估[J]. 海洋环境科学, 2017, 36(4): 615-621. FENG Qian, LIU Qiang. Pre-assessment for the loss caused by storm surge based on the SVM-BP neural network[J]. Marine Environmental Science, 2017, 36(4): 615-621. |
| [11] |
中华人民共和国自然资源部. 1996-2018年中国海洋灾害公报[EB/OL]. http://www.mnr.gov.cn/sj/sjfw/hy/gbgg/zghyzhgb/. Ministry of natural resources of the people's Republic of China. 1996-2018 China marine disaster bulletin[EB/OL]. http://www.mnr.gov.cn/sj/sjfw/hy/gbgg/zghyzhgb/. |
| [12] |
广东省自然资源厅. 2018年广东省海洋灾害公报[EB/OL]. http://nr.gd.gov.cn/gdlr_notice/2/content/post_2644380.html. Department of natural resources of Guangdong Province. Guangdong marine disaster bulletin in 2018[EB/OL]. http://nr.gd.gov.cn/gdlr_notice/2/content/post_2644380.html. |
| [13] |
广东省统计局. 广东统计年鉴. http://stats.gd.gov.cn/gdtjnj/. Guangdong provincial bureau of statistics. Guangdong statistical yearbook. http://stats.gd.gov.cn/gdtjnj/. |
| [14] |
余东华, 吴超羽, 吕炳全, 等. 广东沿海地区风暴潮灾害及其防御[J]. 浙江海洋学院学报(自然科学版), 2009, 28(4): 440-444. YU Donghua, WU Chaoyu, LV Bingquan, et al. Disaster of storm surge and the countermeasures in Guangdong coastal areas[J]. Journal of Zhejiang Ocean University (Natural Science), 2009, 28(4): 440-444. DOI:10.3969/j.issn.1008-830X.2009.04.014 |
| [15] |
赵昕, 王保颂, 郑慧. 基于RS-SVM模型的风暴潮灾害损失测度[J]. 海洋环境科学, 2015, 34(4): 596-600. ZHAO Xin, WANG Baosong, ZHENG Hui. The assessment of storm surge disaster loss based on RS-SVM model[J]. Marine Environmental Science, 2015, 34(4): 596-600. |
| [16] |
李莉, 沈琼. 风暴潮灾害防灾减灾能力评价——以山东省沿海城市为例[J]. 中国渔业经济, 2011, 6: 102-110. LI Li, SHEN Qiong. The evaluation of storm surge prevention and mitigation capability: case of costal cities in Shandong Province[J]. Chinese Fisheries Economics, 2011, 6: 102-110. DOI:10.3969/j.issn.1009-590X.2011.01.016 |
| [17] |
SCHOLKOPF B, SMOLA A J, MULLER K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Confutation, 1998, 10: 1299-1319. DOI:10.1162/089976698300017467 |
| [18] |
彭志兰, 孙海, 高惠瑛, 等. 基于KPCA和GA-LSSVR的惠州砖混建筑物震害易损性研究[J]. 地震工程与工程振动, 2018, 38(2): 176-183. PENG Zhilan, SUN Hai, GAO Huiying, et al. Study on seismic damage vulnerability of Huizhou brick masonry building based on KPCA and GA-LSSVR model[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(2): 176-183. |
| [19] |
刘登峰, 王栋, 丁昊, 等. 城市水灾害风险等级的RBF-C评估方法[J]. 人民黄河, 2014, 36(1): 8-10, 14. LIU Dengfeng, WANG Dong, DING Hao, et al. A risk assessment method based on RBF artificial neural network-Cloud model for urban water disaster[J]. Yellow River, 2014, 36(1): 8-10, 14. |
| [20] |
李德根, 刘晓亮, 宋胜伟, 等. 熵权法径向基神经网络的截割粉尘浓度模型与预测[J]. 煤炭技术, 2018, 37(6): 177-179. LI Degen, LIU Xiaoliang, SONG Shengwei, et al. Prediction and model of cutting dust concentration of radial basis neural network with entropy weight[J]. Coal Technology, 2018, 37(6): 177-179. |
| [21] |
闻新, 李新, 张兴旺, 等. 应用MATLAB实现神经网络[M]. 北京: 国防工业出版社, 2015. WEN Xin, LI Xin, ZHANG Xingwang, et al. Using MATLAB to Realize Neural Network[M]. Beijing: National Defense Industry Press, 2015. |
 2021, Vol. 45
2021, Vol. 45


