
文章信息
- 吴云帆, 边旭, 吴宝勤, 朱先德, 王风帆. 2021.
- WU Yun-fan, BIAN Xu, WU Bao-qin, ZHU Xian-de, WANG Feng-fan. 2021.
- 基于WRF模式的一种台风人造涡旋构建方案
- A typhoon Bogus vortex scheme constructed on the Weather Research and Forecasting (WRF) model
- 海洋科学, 45(12): 65-76
- Marine Sciences, 45(12): 65-76.
- http://dx.doi.org/10.11759/hykx20200524001
-
文章历史
- 收稿日期:2020-05-24
- 修回日期:2020-10-25
2. 天津仁爱学院, 天津 301636;
3. 国家海洋信息中心, 天津 300171
2. Tianjin Renai College, Tianjin 301636, China;
3. National Marine Data and Information Service, Tianjin 300171, China
台风是地球上最具毁灭性的自然灾害之一[1]。如何使台风路径的预报更加精确, 一直以来是学者们研究的重要问题。Stuart等[2]从的理论和实践两方面指出, 台风路径的预报不仅需要对以往台风特征的统计分析, 更依赖于客观化的数值预报。
大气是一个对初值敏感、高度非线性的动力系统, 这一特征决定了初始场的质量对数值预报效果有明显作用[3], 同时在弱的环境场中, 台风内部动力和热力结构对自身发展和运动具有重要影响[4-5], 因此如何确定合理的台风初始场结构是台风数值预报最具挑战性的问题之一[6]。初始场包含的大量台风内部结构信息, 可以用于改进台风路径的预报[7]。然而海上观测资料的稀缺, 导致对台风内核和外围结构特征刻画不够准确, 给数值天气预报中初始场模型的构造带来重大的挑战[8]。尤其是初始场中偏弱的台风强度及错误定位[9], 会影响之后内核结构的演变[10], 严重制约了台风的预报水平[11]。因此, 为了给数值预报模式提供一个更接近实际的涡旋初始场, 应重点改进涡旋初始化技术[12]。
基于台风涡旋的观测资料和模式背景场资料, 台风涡旋初始化技术能够形成更符合观测事实的数值模式初始场。Bogus作为涡旋初始化的关键技术, 人为地在模式初始场中加入一个能反映实况的台风涡旋, 是一种重塑台风内部结构的有效方法, 对提高台风数值预报水平至关重要。Bogus的构造包括2步[13]: 1) 背景场涡旋的检测和去除, 修正涡度、地转涡度和散度, 然后分别求解非发散流函数的变化以及位势和速度势, 计算出一个修正的速度场; 2) Bogus涡旋的构造和添加, 首先综合考虑气旋的几个关键因素, 利用梯度风平衡或者经验的台风风廓线分布构造Bogus涡旋模型, 再通过求解动力平衡方程、插值或变分同化方法, 最终将Bogus涡旋植入到模式初始分析场中。研究指出, 台风位置、强度和尺度这些有限的观测资料, 是构造Bogus的关键因素[9]。利用这些观测资料, 构造更接近实际的Bogus涡旋的方法主要有2种。一是通过给定中心气压, 利用梯度风关系从气压中得到Bogus的风场结构[14], 但实际大气中, 相同强度的台风, 可能具有完全不同的切向风廓线; 二是用涡旋的切向风廓线, 直接构造Bogus风场结构[15]。很多研究表明, 台风外围风场结构较其强度对台风路径预报的影响更为显著[16-17]。张红华等[18]通过同化有限的测风塔和风廓线雷达资料, 进一步证明, 台风切向风廓线结构是影响Bogus涡旋的重要因素。因此, 如何利用更多的风圈信息, 构造更接近实况的台风切向风廓线结构, 是构造Bogus模型应考虑的关键问题。
为了更加全面地考虑台风风圈信息, 本文基于Gao等[19]的研究, 参考Low-Nam等[13]和孟智勇等[20]提出的台风Bogus方案, 构造出一种新的台风切向风廓线方程, 实现了两种方案的完整融合。然后将这种新的Bogus涡旋植入到WRF模式中, 并开展了大量的试验以验证该方案的可行性和有效性, 最终选取2011年9号台风“梅花”的模式数据进行分析与讨论。
1 数据本文采用了FNL(final operational global analysis)和CFSR(climate forecast system reanalysis)大气再分析资料, GOOS(global ocean observing system)海温资料、WMO(world meteorological organization)提供的台风最佳路径资料以及GTS(global telecommunications system)数据。具体应用方式如下:
1) WRF(The Weather Research and Forecasting Model)数值模拟采用FNL再分析资料(空间分辨率为1°×1°; 时间间隔为6 h)提供初始背景场与时变侧边界, GOOS海温资料(时间间隔为1 d)提供底边界。
2) 台风Bogus涡旋的构造采用日本气象厅发布的台风观测数据, 包括模拟初始时刻的台风位置最大风速圈、15.4 m/s和25.7 m/s风圈的风速(相当于7级和10级风)及半径信息。
3) 采用WMO最佳路径资料和NCEP(national centers for environmental prediction)的CFSR(coupled forecast system reanalysis)再分析资料(空间分辨率为0.5°×0.5°; 时间间隔为6 h), 反映台风过程实况[21]。
4) 数值试验采用3DVAR(three-dimensional variational data assimilation)方法同化了GTS数据。
2 方法 2.1 数值模式本文选用WRF-Version 3.4.1开展数值试验。WRF是由NCAR(national center for atmospheric research)和NCEP共同开发的, 集数据同化、大气模拟、数值预报为一体, 用来满足业务化预报和气象研究需求的一种完全可压的非静力模式[22]。其水平方向采用Arakawa C网格, 垂直方向采用地形跟随质量坐标, 时间积分方面采用高阶的Runge-Kutta算法, 并采用经过改进的物理过程参数化方案, 是提高不同尺度重要天气特征预报水平的重要工具。
2.2 Bogus方案简介Low-Nam等[13]为NCAR-AFWA(air force weather agency)提出的Bogus方案, 作为WRF模式中原有的Bogus方案, 采用的是较为简单的函数:
| ${V_{\rm low - nam}}(r) = \left\{ \begin{array}{l} {V_{\max }}\frac{r}{{{R_{\max }}}}, r < {R_{\max }}\\ {V_{\max }}{\left( {\frac{r}{{{R_{\max }}}}} \right)^\alpha }, r \ge {R_{\max }} \end{array} \right., $ | (1) |
其中, Vlow-nam(r)是切向风速, r是离台风中心的距离, Vmax与Rmax分别是台风观测报中最大风速与最大风速半径。当Vmax与Rmax给定, 则r=Rmax以外廓线形状由α决定。根据已有研究[23], α值的变动范围在–0.5~–0.75。
根据Corbosiero等[24]定义, 台风内核包括眼区、眼壁区和内螺旋雨带, 通常指距台风中心100 km以内的范围。由于式(1)考虑到了最大风圈的实测值, 该方案在台风内核区域给出的结果较为理想[19]; 然而, 实际中台风的运动与台风的中心强度关系不大, 却对台风外围风廓线结构十分敏感[25], 即中心强度相近的台风可以具有显著不同的外围结构[26], 因此式(1)给出的台风外围风廓线结构可能并不理想。
孟智勇等[20]考虑台风的外围风场结构, 参考Chan等[15]提出的下列切向风廓线形式:
| ${V_{\rm chan}}(r) = {V_{{\mathop{\rm max}\nolimits} '}}\frac{r}{{{R_{{\mathop{\rm max}\nolimits} '}}}}\exp \left\{ {\frac{1}{b}\left[ {{{\left( {1 - \frac{r}{{{R_{{\mathop{\rm max}\nolimits} '}}}}} \right)}^b}} \right]} \right\}, $ | (2) |
其中, b是一个指数因子, 与式(1)中α类似, 其他量和式(1)具有相同定义。
当Rmax′和Vmax′给定后, 因子b决定台风外风廓线结构。如果台风观测值有最大风速圈以外任意2个风速圈的风速和半径信息(孟智勇等[20]采用台风7级和10级风圈风速和半径观测信息), 那么就可以确定参数b的值[20]。由于考虑到了台风外围更多的观测信息, 式(2)对台风外围的风场结构刻画得更加准确。然而, 该方案并没有考虑到Vmax和Rmax的实测值, 解得的最大风圈速度值通常比观测值要小, 记为Vmax′, 解得的最大风圈半径记为Rmax′。然而, 较小的Vmax′值会导致初始场中气旋变弱, 直接影响台风的模拟结果。
| ${V_{\rm gao}}(r) = \left\{ \begin{array}{l} {V_{\rm low - nam}}(r), r < {R_\rm c}\\ \frac{1}{2}\left[ {{V_{\rm low - nam}}(r) + {V_{\rm chan}}(r)} \right], r \ge {R_\rm c} \end{array} \right..$ | (3) |
为了同时考虑到台风内核和外围的风圈信息, Gao等[19]构造了式(3)所示的台风切向风廓线结构, 找到了以上2种切向风廓线的交点, 对应半径为Rc, 在Rc范围以内的台风内核区域, 保留式(1)的台风内核切向风廓线结构, 在Rc范围以外的台风外围区域, 通过计算式(1)和式(2)风速的平均值得到台风外围的切向风廓线结构。该方案融合了式(1)和式(2)两种方案, 构造出更接近实况的风场结构, 数值模拟结果显示对台风路径的预报有明显的改善。虽然该方案使式(1)在交点半径范围以外的外围风廓线向实测结果更加靠近, 但并没有像式(2)直接采用7级和10级风速圈的观测值, 导致该方案外围风廓线与实际测得的7级和10级风速圈的观测值并不完全吻合; 另外该方案也存在少数无法构造的情况, 如图 1(a)所示, 当Vmax > Vmax时, Rc不存在。
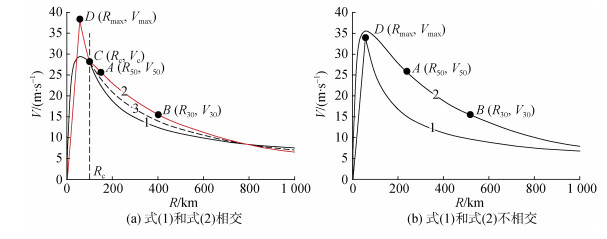 |
| 图 1 台风Bogus方案切向风廓线示意图 Fig. 1 Schematic diagram of the tangential wind profile of the typhoon Bogus scheme 注: 图 1(a)存在方案1和方案2的交点, 修改自Gao等(2005); 图 1(b)交点不存在 |
图 1(a)和图 1(b)分别给出了式(1)和式(2)相交和不相交的两种情况, 其中点D代表最大风圈观测值(Rmax, Vmax), 点A和点B分别代表 10级和7级风圈半径和速度观测值(R50, V50)和(R30, V30)。将式(1)和式(2)交点记为C, 对应半径Rc即为V1(r)–Vchan(r)=0处距台风中心的距离。
图 1中, 式(1)在台风内核经过D点, 台风外围结构由线1给出, 记作方案1; 式(2)在台风内核不经过点D, 在台风外围同时经过点A和点B, 由线2给出, 记作方案2; 式(3)由式(1)和式(2)的切向风廓线相交得到, 在台风内核区域采用方案1, 经过D点, 在台风外围区域采用方案1和方案2的平均, 由线3给出, 记作方案3; 在台风内核区域采用方案1, 经过D点, 台风外围直接采用方案2, 经过点A和点C, 本文将这种新构造的Bogus切向风廓线记作方案4。图 2(a)—(d)分别显示了方案1—4这4种Bogus方案在数值模式中的10 m高度初始风场形态, 其中浅色阴影区域风速在7级和10级风速之间, 深色阴影区域风速大于10级风速。
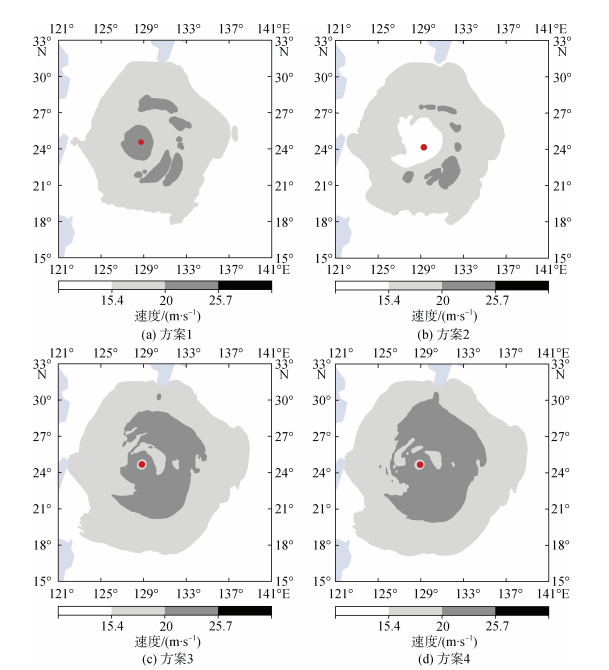 |
| 图 2 4种Bogus方案的10 m高度初始风场结构示意图 Fig. 2 Schematic diagrams of the initial wind field structure of the 4 Bogus schemes |
由图 2可见方案1、3和4中心有深色阴影区, 而方案2的台风中心无阴影, 内核结构显著不同, 可知方案1、3和4的风场强度远大于方案2, 与图 1(a)中各方案在小于Rc区域的切向风廓线构造一致; 方案1、3和4主要区别在台风外围风场结构, 方案4阴影区面积最大, 表示方案4风场最强, 与图 1(a)中各方案在大于Rc区域的切向风廓线构造一致。方案4通过明确变量的取值范围, 解决了方案3中交点Rc可能不存在的问题, 将方案1和方案2完整地融合在一起。首先假设Rc存在, 根据陈联寿等[27]对台风外区以及Gao等[19]对Rc的取值范围, 取Rmax < Rc < 10Rmax。方案4在r < Rc的台风内核采用方案1, 在r≥Rc的台风外围直接采用方案2, 由线2给出。由图 1可知, 方案4所构造的Bogus模型同时经过点A、B和D这3个观测点, 不仅在台风中心附近保留了实际的风场强度, 又在台风外围构造出与实际观测更为一致的风场结构。
为了构造方案4的Bogus模型, 需要式(1)和(2)中各参量具有相同定义, 令
| ${V_{\rm chan'}}(r) = \gamma {V_{\max }}\frac{r}{{d{R_{\max }}}}\exp \left\{ {\frac{1}{b}\left[ {1 - {{\left( {\frac{r}{{{R_{\max }}}}} \right)}^b}} \right]} \right\}, $ | (4) |
同时方案4的函数表达形式为:
| ${V_{\rm new}}(r) = \left\{ \begin{array}{l} {V_{\rm low - nam}}(r), r < {R_\rm c}\\ {V_{\rm chan'}}(r), r \ge {R_\rm c} \end{array} \right..$ | (5) |
综上, 需要对Rc进行讨论。当r≥Rmax时, 根据式(1)和式(4)可得:
| ${V_{\rm max}}{\left( {\frac{{{R_\rm c}}}{{{R_{\rm max}}}}} \right)^\alpha } = \gamma {V_{\rm max }}\frac{{{R_\rm c}}}{{d{R_{\max }}}}\exp \left\{ {\frac{1}{b}\left[ {1 - {{\left( {\frac{{{R_\rm c}}}{{d{R_{\max }}}}} \right)}^b}} \right]} \right\}, $ | (6) |
化简为:
| $\ln \left[ {\frac{d}{\gamma }{{\left( {\frac{{{R_\rm c}}}{{{R_{\rm max}}}}} \right)}^{\alpha - 1}}} \right] = \frac{1}{b}\left[ {1 - {d^{ - b}}{{\left( {\frac{{{R_\rm c}}}{{{R_{\max }}}}} \right)}^b}} \right].$ | (7) |
令
| $(\alpha - 1)\ln y = 1 - b\ln \frac{d}{\gamma } - {d^{ - b}}y, $ | (8) |
式(8)为超越方程, 无法直接获得解的信息。
故我们通过分析讨论得到各个变量的限定条件, 最终得到所需解。经计算可知, 当αb ln d + (α – 1) ln(1 – α)≤α + b ln
| ${R_\rm c} = {F_{{R_\rm c}}}(\alpha , b, \gamma , d),$ | (9) |
即Rc是关于
又因为最大风圈以外, 风速随半径单调递减, 因此限定Rmax < Rc。综上所述,
| $\left\{ \begin{array}{l} \alpha b\ln d + (\alpha - 1)\ln (1 - \alpha ) \le \alpha + b\ln \gamma \\ {F_{{R_\rm c}}}(\alpha , b, \gamma , d) > d{R_{\max }}\\ \alpha < 0\\ \gamma > 0\\ d > 0 \end{array} \right. .$ | (10) |
根据式(10), 由于所涉及参数种类较多, 同时变化范围较大, 故采用粒子群优化(PSO; partical swarm optimization)算法对
因此, 可构造出新的台风Bogus切向风廓线方程(方案4):
| ${V_{\rm new}}(r) = \left\{ \begin{array}{l} {V_{\rm max}}\frac{r}{{{R_{\max }}}}, r < {R_{\max }}\\ {V_{\rm max}}{\left( {\frac{r}{{{R_{\max }}}}} \right)^\alpha }, {R_{\max }} \le r < {F_{{R_\rm c}}}(\alpha , b, g, d)\\ \gamma {V_{\rm max}}\frac{r}{{d{R_{\max }}}}\exp \left\{ {\frac{1}{b}\left[ {1 - {{\left( {\frac{r}{{d{R_{\max }}}}} \right)}^b}} \right]} \right\}, r \ge {F_{{R_\rm c}}}(\alpha , b, g, d) \end{array} \right. .$ | (11) |
2011年9号台风“梅花”生成于菲律宾以东洋面, 8月3日经过黑潮区域并达到超强台风级别, 5日从我国南海逐渐转向西北方向进入东海南部, 并于8月8日18时在朝鲜西北部沿海登陆, 减弱消亡, 期间维持长达97 h。图 3是台风“梅花”8月3日06时刻卫星云图。此时台风螺旋结构完整, 台风中心附近云系紧密, 台风眼清晰可见, 台风中心轴竖直向上。“梅花”自生成以来移速仅为10~15 km/h, 远小于该海域台风的平均移速20 km/h, 由此, 台风涡旋结构对其路径预报的影响更为显著。
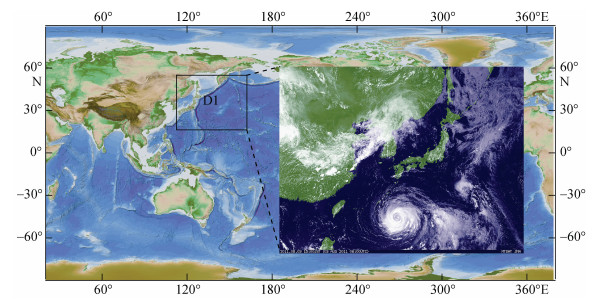 |
| 图 3 WRF模拟区域示意图和2011年8月3日06 UTC的日本MTSAT云图 Fig. 3 WRF domain settings and MTSAT cloud image at August 3, 2011, 06 UTC, Japan 注: 云图资料取自http://weather.is.kochi-u.ac.jp/sat/gms.sea, 背景地形图资料取自https://www.gebco.net/ |
本文针对台风“梅花”, 分别采用4种不同的Bogus方案, 展开数值模拟并讨论。
3.2 试验设置模式区域选取92°E~155°E, 10°N~64°N(图 3), 模拟时间开始于2011年8月3日00 UTC, 结束于7日06 UTC, 共计时长102 h, 模式分辨率为18 km, 具体参数设置见表 1。
试验采用3DVAR方法同化GTS数据, 同时提供了包括模拟时段在内的10 d的CV5背景误差[34], 由NMC(national meteorology center)的SSI(spectral statistical interpretation)方法生成。经多次对比试验, 选取MYNN边界层方案、积云对流KF方案, 水平分辨率18 km、垂直44层, 积分时间步长30 s, 并在数据同化前后分别进行了2次DFI (digital-filter initialization)动力调整。
将初始场的台风位置、最大风圈风速及半径、7级和10级风圈信息代入式(1—11)中进行计算, 可以得到Bogus模型设置的各个重要参数, 如表 2所示。
| Bogus选项 | 具体设置 | |
| 中心位置 | 24.2°N, 132.8°E | |
| 最大风速 | 43.7 m/s | |
| 最大风速半径 | 55 000 m | |
| 10级风速半径 | 166 680 m | |
| 7级风速半径 | 463 000 m | |
| 参数 | α | –0.6 |
| b | 0.536 | |
| γ | 0.597 | |
| d | 2.42 | |
根据表 2提供的参数设置, 图 4给出了本文所采用的台风“梅花”的4种切向风廓线结构。其中, Rc以内经过点D, Rc以外用线1表示, 为方案1; Rc以内不经过点D, Rc以外用线2表示, 为方案2; Rc以内经过点D, Rc以外用线3表示, 为方案3; 用红色实线标出的切向风廓线结构, 为本文新构造的Bogus方案, 即为方案4。
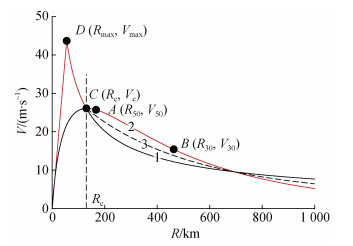 |
| 图 4 台风“梅花”的4种Bogus方案切向风廓线 Fig. 4 Tangential wind profiles of the four Bogus schemes of Typhoon Muifa 注: 方案1: Rc以内经过点D, Rc以外用线1表示; 方案2: Rc以内不经过点D, Rc以外经过点A和点B, 用线2表示; 方案3: Rc以内经过点D, Rc以外取方案1和方案2速度的平均值, 用线3表示; 方案4: Rc以内经过点D, Rc以外与方案2一致, 方案4为新构造的Bogus切向风廓线方案, 用红色实线表示 |
以模拟6 h及模拟30 h的500 hPa等位势高度场为例(图 5), 图 5(a)和图 5(b)为台风实况, 图 5(c)和图 5(d)为加入了新构造的Bogus涡旋后的模拟初始场和结果。
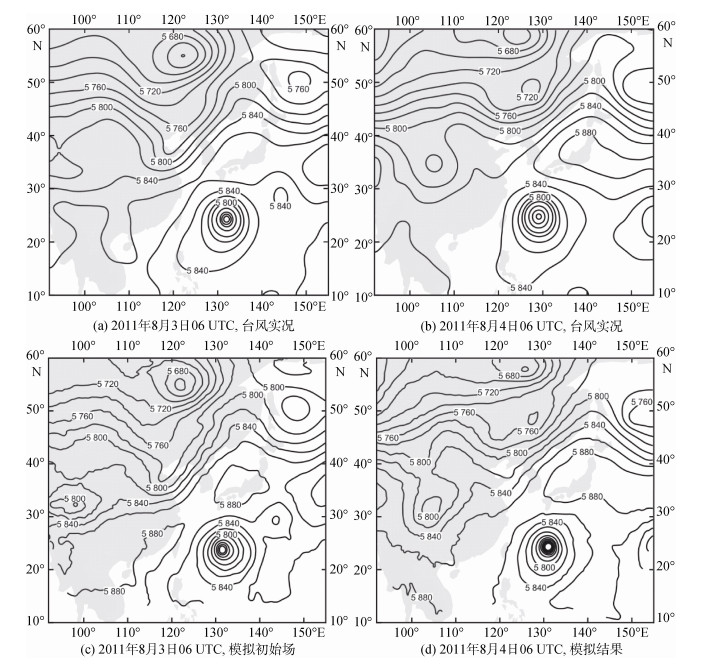 |
| 图 5 500 hPa等位势高度场(单位: gpm) Fig. 5 Geopotential height field (gpm) on 500 hPa 注: 台风实况资料取自NCEP的CFSR数据 |
由图 5可知, 模拟结果的500 hPa高空槽位置与实况一致, 等值线数值相当, 且台风均向槽前移动; 副高5 880 hPa等值线均逐渐西伸, 呈东西向, 导致台风在2011年8月3日06 UTC至2011年8月4日06 UTC共24 h期间以西行为主。由于500 hPa高空引导气流的模拟结果与台风实况一致, 本文模拟结果可信。图 6给出了观测(紫色)及4种Bogus方案的路径模拟结果。
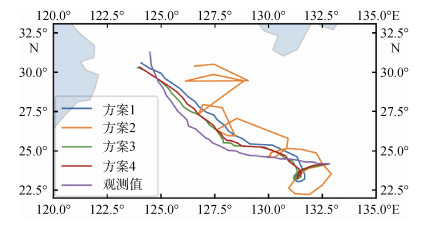 |
| 图 6 4种Bogus方案路径 Fig. 6 Tracks of the four Bogus schemes 注: 紫色为观测路径, 其他颜色为加入了不同Bogus涡旋后的模拟路径 |
图 6给出的模拟结果显示, 方案2的路径并不平滑, 向东北、东南象限摆动前行, 而方案1、3和4的路径较方案2更接近实况, 普遍向西北象限移动, 逐渐加快。由这4种Bogus方案不同的风廓线方程可知, 方案2与方案1、3、4在台风内核的切向风廓线不同, 造成了方案2与方案1、3、4路径的明显差异。因此, 台风路径对台风内核风场结构十分敏感。
利用平均偏差, 对比不同方案对台风路径的模拟结果。用m表示模式输出值, o表示观测值,
| $\overline {D\left( {{x_M}} \right)} = \frac{1}{M}\sum\limits_{t = 0}^M {\left[ {m\left( {{x_t}} \right) - o\left( {{x_t}} \right)} \right]} ,$ | (12) |
其中,
本文分别用台风位置在总体上的偏差[m(s) – o(s)], 来体现台风路径的预报偏差。
为了更直观地反映台风路径的模拟效果, 根据式(12)得到了方案1、3、4的
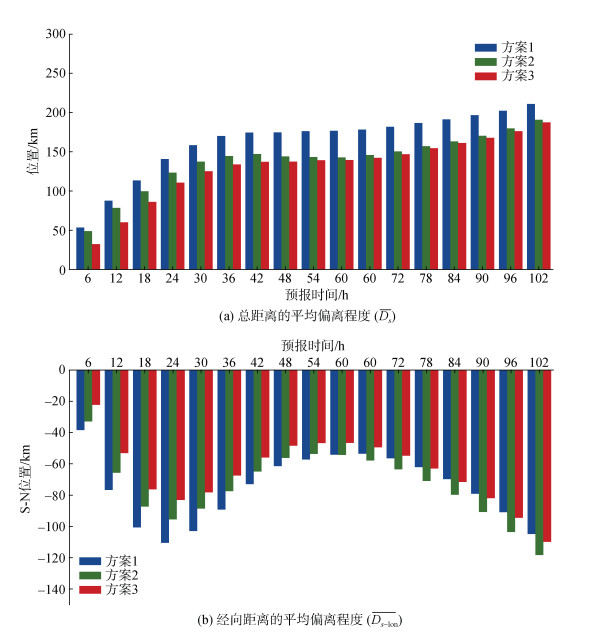 |
| 图 7 总距离(a)和经向距离(b)的平均偏离程度随时间变化 Fig. 7 The average deviation of the total (a) and meridional (b) distance over time 注: 蓝色代表方案1, 绿色代表方案3, 红色代表方案4 |
由图 7(a), 方案4的
为了更清楚地体现方案4的模拟效果, 定义式(13):
| ${P_\rm c}\left( {{x_t}} \right) = \frac{{\overline {{D_{{\rm scheme\;}N}}\left( {{x_t}} \right)} - \overline {{D_{\rm scheme\;4}}\left( {{x_t}} \right)} }}{{\overline {{D_{{\rm scheme\;}N}}\left( {{x_t}} \right)} }} \times 100\% ,$ | (13) |
其中, Pc(xt)是方案4的xt较其他方案(N)提高的百分比。下标schemeN依次代表方案1和3。
当Pc(xt) > 0时, 方案4较其他方案有所改进; 否则反之。且数值越大, 改善效果越好。将各方案
| 预报时长 | Pc(s) | |
| 方案1 | 方案3 | |
| 6 h | 39.64% | 34.04% |
| 12 h | 30.83% | 22.61% |
| 24 h | 21.30% | 10.26% |
| 36 h | 21.03% | 7.02% |
| 48 h | 21.32% | 4.66% |
| 60 h | 21.03% | 2.45% |
| 72 h | 19.03% | 2.23% |
| 84 h | 15.88% | 1.55% |
| 96 h | 12.94% | 1.94% |
| 102 h | 11.24% | 1.74% |
表 3给出了方案4的
在全部模拟时段内(T=102 h), 每3 h输出一组xt, 依据式(13), 可以得到各组xt对应Pc(xt)的平均, 即APc(xT), 表示在全部预报时段上方案4较其他方案提高的平均百分比:
| ${A_{P{\rm{c}}}}({x_T}) = \frac{1}{T}\sum\limits_{t = 0}^T {{P_{\rm{c}}}({x_t})} . $ | (14) |
按照式(12)—(14), 表 4给出了方案4对方案1、3的APc(xT)。其中, APc(s)和APc(v)分别描述了方案4路径的模拟效果。
| 方案1 | 方案3 | |
| APc(s-lon) | 13.72% | 12.53% |
| APc(s-lat) | 26.19% | 0.27% |
| APc(v) | 18.34% | 1.53% |
| APc(s) | 20.86% | 7.47% |
由表 4, 方案1的APc全部为正, 且数值很大, 其APc (s)百分比数值是方案3的近3倍, 由于计算结果全部为正, 方案4预报效果最优。分析可知, 方案4在南北方向上位置的预报比方案1改善13.72%, 比方案3改善12.53%, 在东西方向上位置的预报比方案1改善26.19%, 台风移动速度的模拟效果比方案1改善18.34%。而方案4的台风中心位置在总体上的预报比方案1改善20.86%, 比方案3改善7.47%。由此可见, 模拟结果在南北、东西方向以及移动速度上的改善, 导致了对方案4位置的预报在总体上提高最为明显。
图 8以方案4为例, 给出了初始场的台风结构, 图中等值线表示海平面气压, 阴影区域表示10 m高度风速大于7级风的大风区域, 台风中心附近灰色最深处代表 10 m风速大于10级风的大风区域。台风中心位置指向最大风速位置, 即图 9中气压场圆心位置指向深色阴影区位置所得的方位角(由正北方向顺时针旋转至目标方向的角度), 为最大风速方位, 表示台风的非对称性方位; 以连接台风中心位置和台风中心附近最大风速位置的直线为轴, 在1 000 hPa闭合等高线范围内, 得到轴两侧的平均10 m风场差值, 来衡量台风的非对称程度[17]。图 9给出了方案1、2、3和4模拟初始场中的台风非对称性以及非对称性程度的关系。
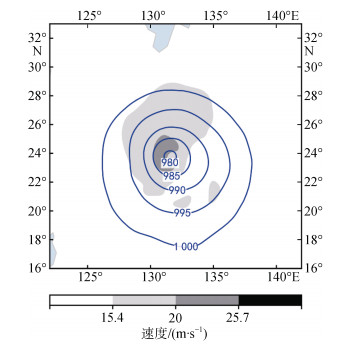 |
| 图 8 2011年8月3日06 UTC, 海平面气压(蓝色等值线, 单位: hPa)和10 m高度风场(色标, 单位: m/s) Fig. 8 The sea level pressure (blue contours, hPa) and the 10 m wind speed field (m/s) |
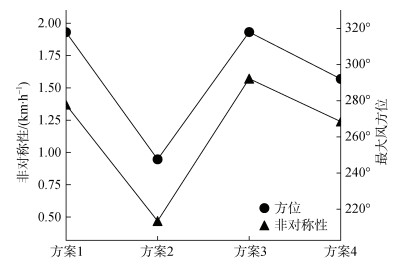 |
| 图 9 4种Bogus方案的非对称性方位及程度 Fig. 9 The direction and degree of asymmetry for the four Bogus schemes |
由于初始场的质量对数值预报效果有明显影响[3], 图 8较为平滑的初始气压场结构, 使得方案4在后期对路径的预报有显著改善。分析图 9可知, 4种Bogus方案的非对称性方位和非对称性程度呈正比。其中, 方案2较其他3个方案, 非对称性方位偏小至80°, 非对称性程度偏小至0.8 km/h; 而方案1、3、4的非对称性方位及变化程度十分接近, 分别只有0.3°和0.2 km/h的差异。分析可知, 不同的台风Bogus的内核风场强度造成方案2与其他3个方案的显著差距, 而不同的台风Bogus的外围风场结构, 导致方案1、3、4的较小差异。由此可知, 台风内核风场强度, 对其非对称结构起到关键的作用。
5 结论本文基于Low-Nam等[13]和孟志勇等[20]提供的台风Bogus方案, 在Gao等[19]的研究基础上, 构造了一种新的Bogus方案, 并将其成功植入WRF模式中。通过对2011年9号台风“梅花”展开一系列数值试验, 对模拟结果进行分析和讨论, 得出如下结论:
1) 新方案融合了Low-Nam等[13]提供的台风内核风廓线结构, 以及Chan等[15]提供的台风外围风廓线结构, 更加真实地反映了台风的风场实况。
2) 这种新构造的台风Bogus涡旋对台风位置的预报, 较Low-Nam等[13]的Bogus方案改善了20.86%, 相对Gao等[19]的Bogus方案改善了7.47%, 对路径模拟效果有明显的改善。因此, 新构造的台风Bogus涡旋更利于台风路径的预报。
3) 台风内核风场强度对其非对称结构起到关键的作用, 其变化直接影响了台风移动路径。
新构造的台风Bogus风廓线方案对台风“梅花”强度的预报效果改善并不明显。未来将采用更多台风个例对该Bogus方案进行验证, 并选择适当的方法, 在初始场中同化台风中心气压的观测值, 进一步改善台风强度的预报效果。
致谢: 感谢中国海洋大学高山红教授提供其代码作为本文研究基础, 并对本文写作提出了宝贵意见。
| [1] |
PEDUZZI P, CHATENOUX B, DAO H, et al. Global trends in tropical cyclone risk[J]. Nature Climate Change, 2012, 2(4): 289-294. DOI:10.1038/nclimate1410 |
| [2] |
STUART N A, MARKET P S, TELFEYAN B, et al. The future of humans in an increasingly automated forecast process[J]. Bulletin of the American Meteorological Society, 2006, 87(11): 1497-1502. DOI:10.1175/BAMS-87-11-1497 |
| [3] |
LORENZ E N, INC E. The essence of chaos[J]. Physics Today, 1993, 48(2): 77-110. |
| [4] |
HUANG Y Y, ZHENG B. Tropical cyclone structure in the South China Sea based on high-resolution reanalysis data and comparison with that of 'bogus' vortices[J]. Dynamics of Atmospheres and Oceans, 2020(89): 1-13. |
| [5] |
CHEN L S, LUO Z X. Some relations between asymmetric structure and motion of typhoons[J]. Acta Meteorologica Sinica, 1995, 9(4): 412-419. |
| [6] |
XIAO Q, KUO H, ZHANG Y, et al. Experiments of a typhoon bogussing scheme in the mm53d-var cycling system[J]. Chinese Journal of Public Health, 2004, 30(2): 178-181. |
| [7] |
GAO Y D, XIAO H, CHAN P W, et al. Application of the multigrid 3D variation method to a combination of aircraft observations and bogus data for Typhoon Nida (2016)[J]. Meteorological Applications, 2019, 26: 312-323. DOI:10.1002/met.1764 |
| [8] |
LIU Y, ZHANG W. Improved hurricane forecasting from a variational bogus and ozone data assimilation (BODA) scheme: case study[J]. Meteorology and Atmospheric Physics, 2016, 128: 715-732. DOI:10.1007/s00703-016-0460-2 |
| [9] |
ZOU X, XIAO Q, LIPTON A E, et al. A numerical study of the effect of GOES sounder cloud-cleared brightness temperatures on the prediction of Hurricane Felix[J]. Journal of Applied Meteorology and Climatology, 1999, 40: 34-55. |
| [10] |
WU C C, LIEN G Y, CHEN J H, et al. Assimilation of tropical cyclone track and structure based on the ensemble Kalman Filter (ENKF)[J]. Journal of the Atmospheric Sciences, 2010, 67(12): 3806-3822. DOI:10.1175/2010JAS3444.1 |
| [11] |
REEVES H, SNYDER C, ROTUNNO R, et al. Prediction of landfalling hurricanes with the advanced hurricane WRF model[J]. Monthly Weather Review, 2008, 136(6): 1990-2005. DOI:10.1175/2007MWR2085.1 |
| [12] |
CHEN L S, LUO Z X. Numerical study on function affecting tropical cyclone structure and motion[J]. Acta Meteorologica Sinica, 1998, 12(4): 504-512. |
| [13] |
LOW-NAM S, DAVIS C. Development of a tropical cyclone bogussing scheme for the MM5 system[C]. In: Eleventh PSU/NCAR Mesoscale Model Users' Workshop, Boulder Colorado: National Center for Atmospheric Research, 2001, 130-134.
|
| [14] |
HOLLAND G J. An analytic model of the wind and pressure profiles in hurricanes[J]. Monthly Weather Review, 1980, 108(8): 1212-1218. DOI:10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 |
| [15] |
CHAN J C L, WILLIAMS R T. Analytical and numerical studies of the beta-effect in tropical cyclone motion. Part I: Zero mean flow[J]. Journal of the Atmospheric Sciences, 1987, 44(9): 1257-1265. DOI:10.1175/1520-0469(1987)044<1257:AANSOT>2.0.CO;2 |
| [16] |
LESLIE L M, HOLLAND G J. On the bogussing of tropical cyclones in numerical models: A comparison of vortex profiles[J]. Meteorology and Atmospheric Physics, 1995, 56(1): 101-110. |
| [17] |
FIORINO M, ELSBERRY L R. Some aspects of vortex structure related to tropical cyclone motion[J]. Journal of the Atmospheric Sciences, 1989, 46(7): 975-990. DOI:10.1175/1520-0469(1989)046<0975:SAOVSR>2.0.CO;2 |
| [18] |
张红华, 王桂臣, 曾明剑, 等. 风廓线与测风塔资料在地面风场预报中的应用研究[J]. 气象科技, 2014, 42(3): 451-459. ZHANG Honghua, WANG Guichen, ZENG Mingjian, et al. Application of wind profile and wind tower data in surface wind field prediction[J]. Meteorological Science and Technology, 2014, 42(3): 451-459. DOI:10.3969/j.issn.1671-6345.2014.03.016 |
| [19] |
GAO S H, YANG B, WU Z M. A tangential wind profile for simulation strong tropical cyclones with MM5[J]. Journal of Ocean University of China, 2005, 4(1): 21-28. DOI:10.1007/s11802-005-0019-1 |
| [20] |
孟智勇, 徐祥德, 陈联寿. 一种适于较强台风的切向风廓线方案及其对异常台风路径的数值模拟研究[J]. 大气科学, 2001, 25(2): 193-199. MENG Zhiyong, XU Xiangde, CHEN Lianshou. A method to study the tangential wind profile for strong tropical cyclone and its contribution to abnormal tropical cyclone track Simulation[J]. Scientia Atmospherica Science, 2001, 25(2): 193-199. DOI:10.3878/j.issn.1006-9895.2001.02.05 |
| [21] |
BARCIKOWSKA M, FESER F, VON S H. Usability of best track data in climate statistics in the Western North Pacific[J]. Monthly Weather Review, 2012, 140(9): 2818-2830. DOI:10.1175/MWR-D-11-00175.1 |
| [22] |
SUN Y, ZHONG Z, LI T, et al. Impact of ocean warming on tropical cyclone size and its destructiveness[J]. Scientific Reports, 2017, 7(8154): 1-10. |
| [23] |
SHEETS R C. Some mean hurricane soundings[J]. Journal of Applied Meterology, 1969, 8(1): 134-146. DOI:10.1175/1520-0450(1969)008<0134:SMHS>2.0.CO;2 |
| [24] |
CORBOSIERO K L, MOLINARI J, BLACK M L. The structure and evolution of Hurricane Elena (1985). Part I: Symmetric intensification[J]. Monthly Weather Review, 2006, 133(10): 2905-2921. |
| [25] |
FIORINO M, ELSBERRY R L. Contributions to tropical cyclone motion by small, medium and large scales in the initial vortex[J]. Monthly Weather Review, 1989, 117(4): 721-727. DOI:10.1175/1520-0493(1989)117<0721:CTTCMB>2.0.CO;2 |
| [26] |
HOLLAND G J, MERRILL R T. On the dynamics of tropical cyclone structural changes[J]. Quarterly Journal of the Royal Meteorological Society, 1984, 110(465): 723-745. DOI:10.1002/qj.49711046510 |
| [27] |
陈联寿, 徐祥德, 解以扬, 等. 台风异常运动及其外区热力不稳定非对称结构的影响效应[J]. 大气科学, 1997, 21(1): 83-90. CHEN Lianshou, XU Xiangde, XIE Yiyang, et al. The effect of tropical cyclone asymmetric thermodynamic structure on its unusual motion[J]. Scientia Atmospherica Sinica, 1997, 21(1): 83-90. DOI:10.3878/j.issn.1006-9895.1997.01.09 |
| [28] |
NAKANISHI M. Improvement of the Mellor-Yamada turbulence closure model based on large-eddy simulation data[J]. Boundary Layer Meteorology, 2001, 99(3): 349-378. DOI:10.1023/A:1018915827400 |
| [29] |
KAIN J S, FRITSCH J M. A one-dimensional entraining detraining plume model and its application in convective parameterization[J]. Journal of the Atmospheric Sciences, 1990, 47(23): 2784-2802. DOI:10.1175/1520-0469(1990)047<2784:AODEPM>2.0.CO;2 |
| [30] |
LIN Y L, FARLEY R D, ORVILLE H D. Bulk parameterization of the snow field in a cloud model[J]. Journal of Climate and Applied Meteorology, 1983, 22(6): 1065-1092. DOI:10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2 |
| [31] |
MLAWER E J, TAUBMAN S J, BROWN P D, et al. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave[J]. Journal of Geophysical Research, 1997, 102(D14): 16663-16682. DOI:10.1029/97JD00237 |
| [32] |
DUDHIA J. A multi-layer soil temperature model for MM5[C]//Sixth Annual PSU/NCAR Mesoscale Model Users' Workshop. Boulder Colorado: National Center for Atmospheric Research, 1996: 49-51.
|
| [33] |
CHEN F, MITCHELL K, SCHAAKE J, et al. Modeling of land surface evaporation by four schemes and comparison with FIFE observations[J]. Journal of Geophysical Research, 1996, 101(D3): 7251-7266. DOI:10.1029/95JD02165 |
| [34] |
PARRISH D F, DERBER J C. The national meteorological center's spectral statistical-interpolation analysis system[J]. Monthly Weather Review, 1992, 120(8): 1747-1763. DOI:10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2 |
 2021, Vol. 45
2021, Vol. 45


