
文章信息
- 王腾, 李树勃, 肖炜杰, 包兴先. 2021.
- WANG Teng, LI Shu-bo, XIAO Wei-jie, BAO Xing-xian. 2021.
- 双浮子点吸收式波能转换装置参数研究
- Parameter study of two-body point absorption wave energy converters
- 海洋科学, 45(4): 31-39
- Marine Sciences, 45(4): 31-39.
- http://dx.doi.org/10.11759/hykx20200806002
-
文章历史
- 收稿日期:2020-08-06
- 修回日期:2020-11-05
国际社会对保障能源安全、保护生态环境、应对气候变化等问题日益重视, 加快开发利用海洋能已成为世界沿海国家和地区的普遍共识和一致行动。波浪能是海洋能的重要组成部分, 各种型式的波浪能开发利用装置已引起广泛研究[1-3]。点吸收式波能转换装置是具有较好应用前景的一种波浪能开发利用装置。深入研究和优化点吸收式波能转换装置的各项参数对提高波浪能资源的采集和转换效率具有重要意义。
目前国内外学者针对如何提高点吸收式波能转换装置的波能转换效率研究做了很多工作。许多学者通过数值模拟对方形、圆柱形浮子结构的水动力特性进行了研究, 从浮子结构所受波浪激励力、结构附加质量、波浪辐射与绕射等多个角度对结构的水动力响应进行了全面的分析与研究。Zheng等[4]采用分离变量法和本征函数匹配展开法研究了有限深度海域矩形长浮子的线性波辐射问题, 并详细讨论了波浪入射角、结构吃水和结构宽度对波浪力和水动力系数的影响。Shen等[5]采用半解析的方法分析了底坎对自由表面上的矩形浮子水动力系数、波浪力以及反射和透射系数的影响, 并将分析结果与边界元法的解析结果进行比较, 证明了辐射势和衍射势的解析表达式的正确性。Vantorre等[6]运用线性波理论计算了点吸收式波能转换装置在具有代表性的几种波浪条件下的发电性能, 将浮子的几何形状、外部阻尼和附加质量作为可变参数来优化波能转换装置, 并通过物理模型试验对数值结果进行了验证。Zhang等[7]研究了一种基于边界离散化的半解析方法, 发现对于具有相同外径、相同位移的波能转换装置, 圆柱型装置在某些给定波浪频率下具有良好的波能俘获能力, 而在随机海浪中, 抛物线型和锥形装置则具有较好的稳定性和适用性。
除了浮子形状, 还有学者对浮子的几何尺寸、系泊缆的布设、浮子质量分布、外负载条件等进行了优化分析。Shadman等[8]提出了一种基于统计分析和频域水动力分析的波能转换装置几何优化方法, 并针对里约热内卢近岸区域的波浪特点给出了最佳的浮子尺寸。Sergiienko等[9, 10]分析了点吸收波能转换装置系泊缆的最佳角度, 同时对比了单缆与三缆系泊的性能。Meng等[11]通过模态分析研究了具有不对称质量分布的球形点吸收装置的工作原理, 结果表明该装置能充分利用纵荡和垂荡运动获得更高的发电效率。杨岑[12]通过物理模型试验对点吸收式波浪能泵的运行特性进行了研究, 结果表明对于尺寸固定的浮子系统, 当入射波频与外负载条件匹配时, 可以获得最优的转换效率。
单浮子式点吸收波能转换装置通常需要较大的质量与尺度, 以降低自身固有频率, 从而尽可能地与波浪频率相吻合以获得更高的俘能功率, 这导致其经济性较低。有学者提出了双浮子结构来解决这一问题, 即在单浮子结构的基础上, 增加一潜入水中的浮子, 从而降低结构频率以获得较高的俘能功率。Candido等[13]分析了仅做垂荡运动的共轴式双浮子式波能转换装置在线性阻尼负载条件下的运行特性, 数值结果表明波浪频率和对运动振幅的约束措施是影响其转换效率的主要因素。Shami等[14]应用Taguchi方法分析了7个不同的参数对仅考虑垂荡运动的直驱式双浮子波能转换装置俘能功率的影响。Liang等[15]研究了频域内双浮子波能转换装置的线性粘性阻尼和流体动力阻尼, 据此提出装置的优化设计以获得最大俘能功率。Muliawan等[16]对松弛式系泊的双浮子波能装置在规则和不规则波浪条件下进行了研究, 发现系泊力对浮子俘能功率的影响很小。
通过文献调研发现, 当前大多数学者只对点吸收波能转换装置的某个或几个参数进行孤立分析研究。但事实上, 在波能采集过程中, 影响点吸收波能转换装置俘能功率的参数有很多, 而且在很多情况下这些参数的影响并不是孤立的。因此, 针对这一问题, 以青岛斋堂岛海域为目标海域, 首先应用单因素敏感性分析法研究分析双浮子直驱式点吸收波能转换装置的浮子尺寸、PTO阻尼、PTO刚度、波流夹角、锚链与铅垂线夹角、锚链与波浪在水平面内夹角等6项参数对装置俘能功率的影响规律; 之后应用稳健设计方法, 分析多项参数对装置俘能功率的综合影响, 明确各参数组合对装置俘能功率的影响程度; 最后根据研究结果提出目标海域优选的装置参数设计方案。
1 目标海域与装置模型 1.1 目标海域介绍本研究的目标海域选为青岛斋堂岛海域。该海域地处黄海北部, 其东向和东南向面临开阔海域。2012年斋堂岛海域建成了中国北方最大的海洋能综合试验基地, 将重点开展多能互补智能化独立能源系统, 波浪能、潮流能发电装置和低成本海洋能输变电设备等海洋可再生能源综合利用技术开发。
斋堂岛海域适合波浪能发电的水域水深约为30 m, 有效波高Hs为0.6 m, 平均周期
JONSWAP谱包含峰升高因子
| ${S_{\left( \omega \right)}} = 2\pi \alpha {\text{g}^2}{\omega ^{ - 5}}\exp \left[ { - \frac{5}{4}{{\left( {\frac{{{\omega _0}}}{\omega }} \right)}^4}} \right]{\gamma ^{\exp \left[ { - \frac{{{{\left( {\omega - {\omega _0}} \right)}^2}}}{{2{\sigma ^2}\omega _0^2}}} \right]}}.$ | (1) |
通过实测谱拟合得到α=0.006 2,
本文研究的双浮子直驱式点吸收波能转换装置原理图如图 1(侧视图)所示。装置的上浮子为圆柱形, 下浮子为球形, 下浮子采用张紧式四锚链形式进行锚固, 上下浮子中间为能量输出系统(PTO), 在波浪作用下上下浮子运动会产生相对位移, 由此带动PTO系统中的直线发电机动子做往复运动, 从而实现把波浪能转化为电能。假设上下浮子半径相同, 作者主要针对上下浮子半径R、PTO阻尼C、PTO刚度K、锚链与铅垂线夹角α、锚链与波浪在水平面内的夹角β、波流夹角
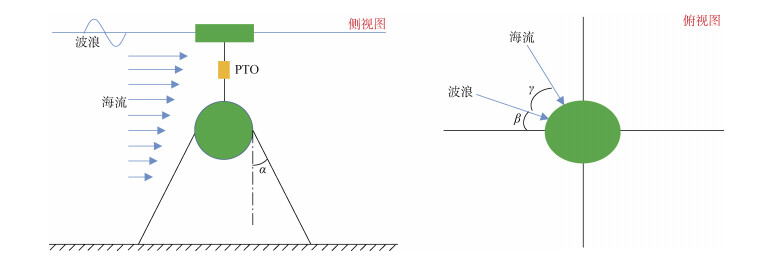 |
| 图 1 双浮子直驱式点吸收波能转换装置基础模型 Fig. 1 Sketch of the two-body wave energy converters system |
由于PTO系统位于上下浮子之间, 根据牛顿第二定律, 考虑波流等环境因素及系泊系统的共同作用, 则分别建立上、下两浮子运动方程, 如式(2)和(3):
| $\left( {{m_1} + {m_\text{a1}}} \right){X''_1} + {c_\text{r1}}{X'_1} + {F_\text{pto}} + {F_\text{s}} + {F_\text{v1}} = {F_\text{e1}} + {F_\text{load1}}, $ | (2) |
| $\left( {{m_2} + {m_\text{a2}}} \right){X''_2} + {c_\text{r2}}{X'_2} - {F_\text{pto}} + {F_\text{v2}} = {F_\text{e2}} + {F_\text{load2}}, $ | (3) |
其中, m1、m2分别为上、下两浮子的质量, ma1、ma2分别为上、下两浮子的附加质量,
PTO作用力可表示为:
| $ F_{\text {pto }}=F_{\mathrm{c}}+F_{\mathrm{k}}, $ | (4) |
式中, Fc为阻尼力, Fk为回复力。
仅考虑线性阻尼与线性刚度系数, 则有
| $ F_{\mathrm{c}}=c_{\mathrm{p}}\left(X_{1}^{\prime}-X_{2}^{\prime}\right), $ | (5) |
式中, cp为PTO阻尼系数。
| $ F_{\mathrm{k}}=k_{\mathrm{p}}\left(X_{1}-X_{2}\right), $ | (6) |
式中, kp为PTO线性刚度系数, X1、X2分别为上、下两浮子在6个自由度方向上的(角)位移量。
波能转换装置在一段时间T内的平均俘能功率为
| ${P_\text{average}} = \frac{1}{T}\int_0^T {{F_\text{c}}\left( {{{X'}_1} - {{X'}_2}} \right)\text{d}t} .$ | (7) |
将式(5)代入式(7)中得到:
| ${P_\text{average}} = \frac{1}{T}\int_0^T {{c_\text{p}}{{\left( {{{X}'_1} - {{X}'_2}} \right)}^2}\text{d}t}. $ | (8) |
因此, 当已知PTO阻尼系数cp和一段时间T内的上下浮子间的相对运动速度
研究过程中应用AQWA软件分析装置在不同工况下的时域运动响应, 考虑波能转换装置横荡、纵荡、垂荡3个自由度的运动, 取装置稳定后1 000 s内的数据进行分析。根据上下浮子坐标位置可以得到3个自由度运动状态下两浮子相对位移随时间变化曲线(图 2), 对曲线求导可以进一步得到两浮子相对运动速度, 根据公式(8)可计算得到波能发电装置的俘能功率。
 |
| 图 2 两浮子相对位移随时间变化曲线 Fig. 2 Relative displacement between two floats over time |
单因素敏感性分析法, 可以用来分析单个不确定因素的变动对方案整体产生的影响, 应用过程中首先要确定分析指标、各个需要分析的不确定因素以及这些因素的变动范围。本节研究中, 应用单因素敏感性分析法主要讨论R、C、K、α、β、
| 工况 | R/m | C/(N·s·m–1) | K/(N·m–1) | α/(°) | β/(°) | 频率/Hz | |
| 1 | 0.9~2.3 | 3 000 | 300 | 40 | 0 | 0 | 0~0.7 |
| 2 | 1.6 | 3 000~18 000 | 300 | 40 | 0 | 0 | 0~0.7 |
| 3 | 1.6 | 3 000 | 100~1 200 | 40 | 0 | 0 | 0~0.7 |
| 4 | 1.6 | 3 000 | 300 | 10~70 | 0 | 0 | 0~0.7 |
| 5 | 1.6 | 3 000 | 300 | 40 | 0~45 | 0 | 0~0.7 |
| 6 | 1.6 | 3 000 | 300 | 40 | 0 | 0~180 | 0~0.7 |
工况1下, 浮子尺寸对装置俘能功率和俘能带宽的影响如图 3所示。可以看出, 随着两浮子半径的增大, 最大俘能功率呈现先增大后减小的趋势, 在半径1.2 m时俘能功率最大, 为448 W; 在浮子半径逐渐增大情况下, 装置达到最大俘能功率时对应的波浪频率则逐渐减小, 这是由于浮子尺寸增大, 装置整体固有频率降低导致的; 另外可以看到装置的俘能带宽随浮子尺寸增大逐渐减小, 装置达到最大俘能功率即浮子半径为1.2 m时俘能带宽为0.275 Hz。
 |
| 图 3 浮子尺寸变化对俘能功率和俘能带宽的影响 Fig. 3 Captured power and bandwidth related to the radius of buoys |
图 4为工况2下PTO阻尼对装置俘能功率和俘能带宽的影响图。装置PTO阻尼的增加会阻碍两浮子的相对运动, 减小其相对运动速度, 但根据公式(8)可知, PTO阻尼又与装置的俘能功率呈正相关。因此可见随着PTO阻尼增大, 装置俘能功率迅速增加, 在11 000 N·s·m–1~15 000 N·s·m–1区间内俘能功率达到最大值700 W并保持稳定, 之后随着PTO阻尼继续增加, 最大俘能功率略有下降; 另外随着PTO阻尼的增大, 装置俘能带宽也随之增加, 当PTO阻尼为18 000 N·s·m–1时, 俘能带宽达到最大, 为0.34 Hz。
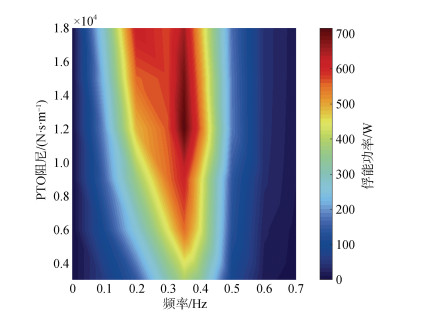 |
| 图 4 PTO阻尼变化对俘能功率和俘能带宽的影响 Fig. 4 Captured power and bandwidth related to PTO damping |
工况3下, PTO刚度对装置俘能功率和俘能带宽的影响如图 5所示。PTO刚度在500 N·m–1~800 N·m–1时, 装置俘能功率较高, 但总体来看, 俘能功率随PTO刚度变化不大; 另外装置俘能带宽也不随PTO刚度变化而产生显著变化。这是由于PTO刚度的变化虽然会影响两浮子的相对运动速度, 但是当刚度在合理区间内变动时对两浮子的相对运动速度影响不会很大, 这也可以说明PTO刚度的变化对装置俘能功率和俘能带宽无明显影响。
 |
| 图 5 PTO刚度变化对俘能功率和俘能带宽的影响 Fig. 5 Captured power and bandwidth related to PTO stiffness |
图 6为工况4下锚链与铅垂线夹角对装置俘能功率和俘能带宽的影响图。可以看出, 锚链与铅垂线夹角约40°时俘能功率最小, 其他角度范围内装置俘能功率变化不明显; 另外随着角度的增加装置的俘能带宽先减小后略微增大, 并在50°~70°时达到稳定。由于锚链与下浮子相连, 其主要作用为固定装置在一定范围内运动, 而且锚链相对较长且存在一定拉伸能力, 因此不会对两浮子相对运动速度产生较大影响, 从而不会大幅度影响俘能功率, 这也与图 6结果较为一致。
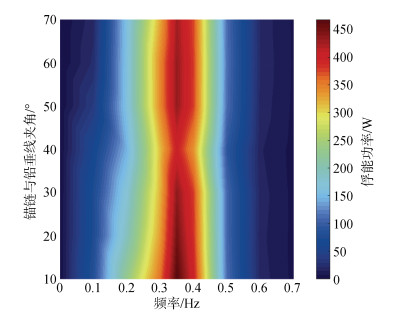 |
| 图 6 锚链与铅垂线夹角变化对俘能功率和俘能带宽的影响 Fig. 6 Captured power and bandwidth related to the angle between the anchor chain and the plumb line |
图 7显示了上浮子的漂移距离随锚链与铅垂线夹角的变化情况。可以发现, 当锚链与铅垂线夹角10°时, 上浮子漂移距离最大, 约为4 m; 当锚链与铅垂线夹角50°时, 上浮子漂移距离最小, 约为2.25 m。实际应用中, 锚链与铅垂线夹角的选择应综合考虑俘能功率与锚固效果两方面的情况。本文锚链与铅垂线夹角取50°时, 俘能功率较大, 而且上浮子漂移距离最小。
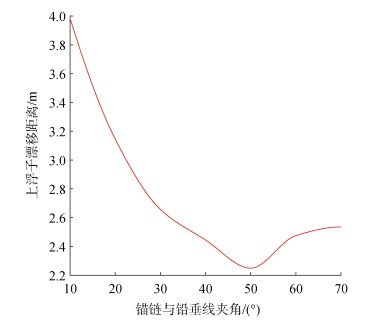 |
| 图 7 锚链与铅垂线夹角变化对浮子漂移距离的影响 Fig. 7 Drift distance of the floater related to the angle between the anchor chain and the plumb line |
图 8为工况5下锚链与波浪在水平面内的夹角对装置俘能功率和俘能带宽的影响图。由于锚固方式采用四锚链形式, 因此锚链与波浪在水平面内的夹角变化范围为0°~45°, 根据前文描述的锚链对装置的作用来看, 可以推测此项参数的变化对俘能功率的影响也会较小, 同时从图中可以看到此夹角的变化对俘能功率的影响很小, 基本可忽略不计, 装置的俘能带宽也基本稳定在0.23 Hz。
 |
| 图 8 锚链与波浪在水平面内夹角变化对俘能功率和俘能带宽的影响 Fig. 8 Captured power and bandwidth related to the angle between the projection of the anchor chain in the horizontal plane and the direction of the wave |
图 9为工况6下波流夹角对装置俘能功率和俘能带宽的影响图。波浪海流都会对装置两浮子的相对运动产生较大影响, 其波流同向更有利于提高俘能功率, 因此可以发现, 当波流夹角在0°~60°时俘能功率较大, 100°~180°时俘能功率较小; 装置的俘能带宽随角度的增大先平稳保持在0.225 Hz, 之后在60°时开始逐渐增加, 在130°时达到最大俘能带宽0.46 Hz, 最后略有下降, 但整体来看波流同向或夹角较小时对装置发电效果更有益。
 |
| 图 9 波流夹角变化对俘能功率和俘能带宽的影响 Fig. 9 Captured power and bandwidth related to the angle between the direction of wave propagation and that of the current |
图 10表示了在表 1所示6种研究工况下, 当相关可变动参数取最优值时的俘能功率。在柱状对比图中可以明显发现仅考虑单参数变化时PTO阻尼取最优值时俘能功率最大, 可达到719 W; 而其他各项参数取最优值时装置所达到的最大俘能功率大致近似, 均为450 W左右。
 |
| 图 10 各工况下相关参数取最优值时俘能功率对比 Fig. 10 Captured power when relevant parameters assume the optimal value under different working conditions |
本节采用单因素敏感性分析法分析了6项参数对俘能功率的孤立影响规律, 得到在不同波频下各参数变化时的装置俘能功率。可以发现浮子尺寸、PTO阻尼、波流夹角3项参数均对俘能功率有显著影响, 而PTO刚度、锚链与铅垂线夹角、锚链与波浪在水平面内夹角3项参数对俘能功率影响较小。
2.2 多参数对装置俘能功率的综合影响考虑到实际情况下, 装置各参数对俘能功率的影响并不是孤立的, 需要考虑各参数的综合影响, 从而确定最优的装置参数组合。因此本节引入稳健设计方法对装置各参数的综合影响进行分析。
稳健设计方法的理论基础是田口玄一博士于1950年—1958年创作的三段式设计, 故又称田口方法[18]。该方法广泛应用于化工领域的工艺优化。它基于统计分析, 研究系统输出对输入变量的敏感性, 从而提高设计产品的质量。该方法可以评估不同参数下系统的响应, 以及各参数影响的程度, 因而也适用于本文各装置参数对俘能功率的综合影响研究。
根据上节单因素敏感性分析结果, 选取每项参数对应3个特征水平的代表数值, 如表 2所示。之后利用稳健设计方法进行综合影响规律分析。在进行各参数综合影响规律分析时, 增加海流流速V参数, 目标海域表层海流流速约为0.1 m·s–1 ~1.0 m·s–1。表 3给出了正交实验的L18矩阵, 共包含18个独立实验, 每个实验中各参数取值代表其特征水平。
| 参数 | 水平1 | 水平2 | 水平3 |
| R/m | 1.2 | 1.6 | 2 |
| C/(N·s·m–1) | 3 000 | 11 000 | 19 000 |
| K/(N·m–1) | 300 | 900 | 1 500 |
| α/(°) | 20 | 40 | 60 |
| 0 | 90 | 180 | |
| β/(°) | 0 | 15 | 45 |
| V/(m·s–1) | 0.1 | 0.5 | 1 |
| 实验编号 | R | C | K | α | β | V | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 | 3 |
| 4 | 2 | 1 | 1 | 2 | 2 | 3 | 3 |
| 5 | 2 | 2 | 2 | 3 | 3 | 1 | 1 |
| 6 | 2 | 3 | 3 | 1 | 1 | 2 | 2 |
| 7 | 3 | 1 | 2 | 1 | 3 | 2 | 3 |
| 8 | 3 | 2 | 3 | 2 | 1 | 3 | 1 |
| 9 | 3 | 3 | 1 | 3 | 2 | 1 | 2 |
| 10 | 1 | 1 | 3 | 3 | 2 | 2 | 1 |
| 11 | 1 | 2 | 1 | 1 | 3 | 3 | 2 |
| 12 | 1 | 3 | 2 | 2 | 1 | 1 | 3 |
| 13 | 2 | 1 | 2 | 3 | 1 | 3 | 2 |
| 14 | 2 | 2 | 3 | 1 | 2 | 1 | 3 |
| 15 | 2 | 3 | 1 | 2 | 3 | 2 | 1 |
| 16 | 3 | 1 | 3 | 2 | 3 | 1 | 2 |
| 17 | 3 | 2 | 1 | 3 | 1 | 2 | 3 |
| 18 | 3 | 3 | 2 | 1 | 2 | 3 | 1 |
通过数值模拟得到18个装置参数组合所对应的俘能功率, 并求得每项参数3个特征水平所对应的俘能功率均值(表 4中第2~4列), 进而求得3个特征水平对应的俘能功率均值最大值与最小值之差, 即极差(表 4中第5列), 最终计算极差占最优水平时俘能功率的百分比(表 4中第6列), 百分比越大说明此项参数对装置俘能功率的影响越显著。
| 参数 | 水平1俘能功率/W | 水平2俘能功率/W | 水平3俘能功率/W | 极差/W | 极差占比/% |
| R | 281.667 | 427.500 | 373.667 | 145.833 | 34 |
| C | 225.667 | 422.833 | 434.333 | 208.666 | 48 |
| K | 382.500 | 342.500 | 357.833 | 40.000 | 10 |
| α | 382.833 | 340.000 | 360.000 | 42.833 | 11 |
| 448.833 | 333.167 | 300.833 | 249.834 | 56 | |
| β | 296.667 | 391.833 | 394.333 | 97.666 | 25 |
| V | 271.667 | 436.500 | 374.167 | 164.833 | 38 |
从表 4可以看出, 当考虑多参数综合影响时PTO阻尼和波流夹角两项参数对俘能功率的影响最为显著, 极差占比分别为48%和56%。根据公式(8), 装置在一段时间内的平均俘能功率与PTO阻尼和两浮子相对运动速度有直接关系, 而波流夹角会对浮子的相对运动速度产生较大影响, 因此这两项参数对俘能功率有显著影响是并不意外的。具体来看, 随着PTO阻尼的增大, 装置的俘能功率也增大。当波流同向时, 装置的俘能功率最大; 波流反向时, 装置的俘能功率最小。其余5项参数中, 浮子尺寸、海流流速、锚链与波浪在水平面内夹角3项参数对俘能功率也有一定影响, 但与PTO阻尼、波流夹角两项参数相比较小, 而PTO刚度、锚链与铅垂线夹角两项参数变化对俘能功率影响不明显。
2.3 参数优化组合根据上述各参数孤立影响规律和多参数综合影响规律研究, 可以确定目标海域双浮子直驱式点吸收波能转换装置的最优参数组合, 以提供最佳的俘能功率。综合实际海况, 重点考虑对俘能功率影响较大的几个参数, 提出以下参数设计方案:
(1) 目标海域波频多集中在0.25 Hz ~0.4 Hz, 此区间内浮子半径为1.2 m时俘能功率最大, 适应的波频宽度也最广, 因此最优浮子半径设置为1.2 m。
(2) 在单参数对装置俘能功率的影响研究中发现, PTO阻尼在11 000 N·s·m–1~15 000 N·s·m–1内俘能功率较高; 而在多参数综合影响研究中, PTO阻尼在11 000 N·s·m–1和19 000 N·s·m–1时俘能功率相差不大, 这是由于多参数相互影响导致的。综合考虑两方面的研究以及目标海域的常见波浪频率, PTO阻尼设置在11 000 N·s·m–1~ 15 000 N·s·m–1内较好。
(3) 锚链与铅垂线夹角变化对装置俘能功率影响不明显, 但却对浮子漂移距离有较大影响, 当锚链与铅垂线夹角为50°时装置俘能功率不会有大的改变, 但却有很好的锚固效果, 因此锚链与铅垂线夹角设置为50°。
(4) 根据研究结果发现波流夹角较小时装置俘能功率较大, 为使装置有总体较高的俘能功率, 装置最好安装于波流夹角约为0°的海域。
(5) 通过多参数对装置俘能功率的综合影响研究发现, 装置在海流流速0.5 m·s–1时俘能功率最大, 而目标海域表层海流流速约为0.1 m·s–1~1.0 m·s–1, 因此装置最好安装于表层海流流速约为0.5 m·s–1的海域。
3 结语作者根据斋堂岛海域具体海况, 建立了双浮子直驱式波能转换装置基础模型, 并通过数值模拟进行了装置的水动力响应分析, 提出了双浮子直驱式点吸收波能转换装置参数研究方法。
(1) 通过稳健设计的极差分析可以看出, 波流夹角、PTO阻尼、海流流速、浮子尺寸4项参数的极差占比分别达到56%、48%、38%和34%, 表明波流夹角、PTO阻尼、海流流速、浮子尺寸对装置俘能功率的影响较大, 其中波流夹角、PTO阻尼影响最为突出, 在针对该类型波能转换装置进行参数优化时, 这几项参数应着重考虑。
(2) PTO刚度、锚链与铅垂线夹角、锚链与波浪在水平面内的夹角对发电效率影响不明显, 其极差占比仅为10%、11%和25%, 与其他几项参数相比有较大差距。另外研究发现当锚链与铅垂线夹角10°时, 上浮子漂移距离最大, 约为4 m; 当锚链与铅垂线夹角50°时, 上浮子漂移距离最小, 约为2.25 m。因此锚固形式的设置应综合考虑装置俘能功率和锚固效果两方面的影响。
(3) 提出的参数研究方法可为其他海域的点吸收式波能转换装置参数设计提供参考。
本文采用数值模拟研究了双浮子直驱式点吸收波能转换装置参数对装置俘能功率的影响, 下一步将采用模型实验进一步验证本文结论。
| [1] |
王世明, 吴帅桥, 田卡, 等. 一种涵道双向泵叶轮浪流发电装置的研究分析[J]. 海洋科学, 2017, 41(2): 29-34. WANG Shiming, WU Shuaiqiao, TIAN Ka, et al. Study of a wave-flow generation device with ducted bidirectional pump impeller[J]. Marine Sciences, 2017, 41(2): 29-34. |
| [2] |
陈永华, 李思忍. 有效吸收和传递波浪能的锚泊系统的设计制作[J]. 海洋科学, 2012, 36(4): 95-98. CHEN Yonghua, LI Siren. Design and development of a mooring system for the absorption and transmission of wave energy[J]. Marine Sciences, 2012, 36(4): 95-98. |
| [3] |
胡聪, 毛海英, 尤再进, 等. 中国海域波浪能资源分布及波浪能发电装置适用性研究[J]. 海洋科学, 2018, 42(3): 142-148. HU Cong, MAO Haiying, YOU Zaijin, et al. Study on the distribution of wave energy resources in China and the applicability of wave energy generation device[J]. Marine Sciences, 2018, 42(3): 142-148. |
| [4] |
ZHENG Y H, SHEN Y M, YOU Y G, et al. Wave radiation by a floating rectangular structure in oblique seas[J]. Ocean Engineering, 2006, 32(1): 59-81. |
| [5] |
SHEN Y M, ZHENG Y H, YOU Y G. On the radiation and diffraction of linear water waves by a rectangular structure over a sill. Part Ⅰ. Infinite domain of finite water depth[J]. Ocean Engineering, 2005, 32(8-9): 1073-1097. DOI:10.1016/j.oceaneng.2004.07.011 |
| [6] |
VANTORRE M, BANASIAK R, VERHOEVEN R. Modelling of hydraulic performance and wave energy extraction by a point absorber in heave[J]. Applied Ocean Research, 2004, 26(1-2): 61-72. DOI:10.1016/j.apor.2004.08.002 |
| [7] |
ZHANG W, LIU H, ZHANG L, et al. Hydrodynamic analysis and shape optimization for vertical axisymmetric wave energy converters[J]. China Ocean Engineering, 2016, 30(6): 954-966. DOI:10.1007/s13344-016-0062-2 |
| [8] |
SHADMAN M, ESTEFEN S F, RODRIGUEZ C A, et al. A geometrical optimization method applied to a heaving point absorber wave energy converter[J]. Renewable Energy, 2018, 115: 533-546. DOI:10.1016/j.renene.2017.08.055 |
| [9] |
SERGIIENKO N Y, RAFIEE A, CAZZOLATO B, et al. Feasibility study of the three-tether axisymmetric wave energy converter[J]. Ocean Engineering, 2018, 150: 221-233. DOI:10.1016/j.oceaneng.2017.12.055 |
| [10] |
SERGIIENKO N Y, CAZZOLATO B S, DING B, et al. An optimal arrangement of mooring lines for the three-tether submerged point-absorbing wave energy converter[J]. Renewable Energy, 2016, 93: 27-37. DOI:10.1016/j.renene.2016.02.048 |
| [11] |
MENG F, DING B, CAZZOLATO B, et al. Modal analysis of a submerged spherical point absorber with asymmetric mass distribution[J]. Renewable Energy, 2019, 130: 223-237. DOI:10.1016/j.renene.2018.06.014 |
| [12] |
杨岑, 张永良. 波浪能压力泵运行特性的试验研究[J]. 水利学报, 2013, 44(9): 1107-1111. YANG Cen, ZHANG Yongliang. Experimental study on operation performance of wave-driven pressure pump[J]. Journal of Hydraulic Engineering, 2013, 44(9): 1107-1111. |
| [13] |
CANDIDO J, JUSTINO P. Modelling, control and pontryagin maximum principle for a two-body wave energy device[J]. Renewable Energy, 2011, 36(5): 1545-1557. DOI:10.1016/j.renene.2010.11.013 |
| [14] |
SHAMI E A, WANG X, ZHANG R, et al. A parameter study and optimization of two body wave energy converters[J]. Renewable Energy, 2019, 131: 1-13. DOI:10.1016/j.renene.2018.06.117 |
| [15] |
LIANG C, ZUO L. On the dynamics and design of a two-body wave energy converter[J]. Renewable Energy, 2017, 101: 265-274. DOI:10.1016/j.renene.2016.08.059 |
| [16] |
MULIAWAN M J, GAO Z, MOAN T, et al. Analysis of a two-body floating wave energy converter with particular focus on the effects of power take-off and mooring systems on energy capture[J]. Journal of Offshore Mechanics & Arctic Engineering, 2013, 135(3): 317-328. |
| [17] |
杨忠良, 叶钦, 欧阳伟, 等. 斋堂岛东南海域波浪特征及海浪谱分析[J]. 海洋学研究, 2017, 35(2): 91-95. YANG Zhongliang, YE Qin, OUYANG Wei, et al. The wave characteristics and the analysis of wave spectrum off the southeastern coast of Zhaitang Island[J]. Journal of Marine Sciences, 2017, 35(2): 91-95. DOI:10.3969/j.issn.1001-909X.2017.02.010 |
| [18] |
ROY R. A primer on the Taguchi method[M]. USA: Van Nostrand Rheinhold, 1990.
|
 2021, Vol. 45
2021, Vol. 45


