
文章信息
- 季智灵, 周晨琦, 赵忠伟, 孔俊. 2021.
- JI Zhi-ling, ZHOU Chen-qi, ZHAO Zhong-wei, KONG Jun. 2021.
- 水库对海岸带海水入侵影响的数值模拟研究
- Numerical study of the influence of coastal reservoir on seawater intrusion
- 海洋科学, 45(4): 75-82
- Marine Sciences, 45(4): 75-82.
- http://dx.doi.org/10.11759/hykx20201013002
-
文章历史
- 收稿日期:2020-10-13
- 修回日期:2021-01-15
近年来, 在滨海地区, 经济的快速发展加剧了水资源短缺的问题, 中国、韩国和新加坡等国家修建了大量海岸水库工程来提供淡水资源[1]。而在滨海地区, 海水入侵问题广泛存在, 并且成为海内外学者研究的重点。海水入侵会导致土壤盐渍化, 地下水水质恶化等问题, 这都是制约滨海地区经济发展的重要因素[2-3], 海水入侵的防治日趋关键, 常见的防治工程有淡水帷幕工程和地下坝工程[4]。海岸水库的建立改变了海岸水文地质环境, 对海水入侵的程度有着一定的影响[5]。为此深入研究海岸水库建设下, 海水入侵的影响方式和程度, 并进行海水入侵的防治尤为必要。
海水入侵的研究聚焦于咸淡水界面的形状、运移机理和规律, 研究海水入侵的方法之一是建立数值模型来讨论, 一种是突变界面模型[6-8], 另一种是过渡带模型[9-11]。Robinson等[12]采用有限元法模拟了地下河口地下水流动和盐分运移过程, 武雅洁等[13]使用OpenGeoSys软件模拟了潮汐波动对海水入侵规律的影响, Nishikawa等[14]使用过渡带模型中的SUTRA模型研究了洛杉矶多明戈斯地区的海水入侵, Mahmoodzadeh等[15]利用SUTRA建立了模型, 对海岛淡水透镜体的海水入侵进行了研究。本文采取的模型咸淡水过渡带较宽且由于过渡带模型能够反映复杂水文地质条件、人为活动条件等诸多因素下的水流流动和溶质迁移, 故采用过渡带模型中的SUTRA模型[16]。
21世纪以来, 许多学者对海岸水库与海水入侵的关系展开了大量的研究, 一方面聚焦于海水入侵对水库水质的影响, Liang等[17]通过同时求解地表水和地下水方程来模拟泻湖的盐度变化, Mao等[18]使用Delft3D在沿海水库中模拟了海水淡化过程; 另一方面也有许多学者研究了海岸水库对海水入侵的影响, Jin等[5]指出当干旱时期水库水位低时, 海水更有可能侵入水库, Mehdizadeh等[19]通过物理模型试验和数值模拟研究了淡水库的建立对咸淡水界面的影响。对于海岸水库对海水入侵的研究大部分没有考虑潮汐作用, 而在潮汐作用下, 海水入侵的程度和方式发生改变, 会形成上混合区[20-23], 加快海水与淡水循环, Xin等[24]指出潮汐减弱了含水层—海洋界面上的水通量相位滞后效应, 加强了盐通量的相位滞后效应。Robinson等[12]指出潮汐形成的上混合区具有环流特征, 增加了入海地下水水量。
本文采用SUTRA模型建立具有代表性的二维海岸剖面模型, 考虑了潮汐作用, 并分不同库区水位进行数值模拟研究, 以找出库区水位和海水入侵的关系, 为修建海岸水库地区的海水入侵防治提供参考。
1 数值模型 1.1 控制方程由美国地质调查局开发出来的饱和带/非饱和带运移模型SUTRA(saturated-unsaturated transport)采用了有限元法和有限差分法, 来求解地下水的两个物理过程, 一是饱和和非饱和地下水流动, 二是能量或者溶质在含水层多孔介质中的运移, 来解决地下环境中水流溶质和盐度的饱和和不饱和运输。
SUTRA模型的二维有限元地下水流动控制方程如式(1)所示:
| $\partial \left( {\rho \phi {S_w}} \right)/\partial t = - \nabla \cdot \left( {\rho {S_\rm w}\mathop q\limits^ \to } \right) + {\rho _ \rm s} , $ | (1) |
| $ \mathop q\limits^ \to = - K\left( \psi \right)\nabla \cdot \left( {\frac{P}{{\rho g}} + z} \right) , $ | (2) |
式中: ρ为流体密度;
SUTRA的溶质运移方程如式(2)所示:
| $ \partial (\rho \phi C{S_\rm w})/\partial t = - \nabla (\rho \mathop {qC}\limits^ \to ) + \nabla \cdot (\rho \phi {S_\rm w}D\nabla C) + {\rho _\rm s}Q{C^ * } , $ | (3) |
式中: D为水动力弥散常量, C为流体盐度, C*为源流体盐度。
根据Van Genuchten[25]提出的经验公式, 非饱和土壤的水力参数由下式确定:
| $ {S_\rm w}(\psi ) = {S_{\rm {wres}}} + \left\{ {\frac{{1 - {S_{\rm {wres}}}}}{{{{\left[ {1 + {{\left( {\alpha \left| \psi \right|} \right)}^n}} \right]}^{\frac{{n - 1}}{n}}}}}} \right\} , $ | (4) |
| $ K(\psi)=K_{\mathrm{s}} S_{\mathrm{w}}^{* 1 / 2}\left\{1-\left[1-S_{\mathrm{w}}^{*\left(\frac{n}{n-1}\right)}\right]^{\frac{n-1}{n}}\right\}^{2} , $ | (5) |
| $ S_{\mathrm{w}}=\frac{S_{\mathrm{w}}-S_{\mathrm{wres}}}{1-S_{\mathrm{wres}}} , $ | (6) |
式中: α和n为形状系数; Ks为饱和系数; Swres为孔隙水残余饱和度。
1.2 概念模型海岸水库指修建在海岸地区的水库, 其主要作用是利用其堤坝抵挡海水, 并蓄积淡水, 为滨海地区提供淡水资源。为研究海岸水库对海水入侵造成的影响, 本文对研究模型进行了概化, 构建了一个概化的海滩剖面进行研究, 在低潮位处设立坝体, 坝后蓄淡, 形成海岸水库。如图 1所示, 建模时将平均海平面与海岸的交点设为O(150, 20), 在F(155, 19)处设置坝体, 坝高4 m, 坝厚1 m, AB=30 m, BE=200 m, AC=100 m, DE=10 m。潮汐振幅A=1 m, 周期T=12 h。
 |
| 图 1 概念模型图 Fig. 1 Conceptual model |
在SUTRA模型中将计算模型分剖分为了24 000个单元, 24 461个节点, 生成四边形网格, 网格最小尺度为0.5 m, 在模型中假定为各向同性介质, 计算所采用的具体参数参照了Xin等[24]在模拟中使用的参数, 见表 1。
| 参数 | 数值 | 符号 |
| 渗透系数 | 10 m/d | K |
| 纵向弥散度 | 0.5 m | αL |
| 横向弥散度 | 0.05 m | αT |
| 分子扩散系数 | 10–9 m2s–1 | Df |
| 孔隙率 | 0.45 | |
| 海水密度 | 1 025 kg/m3 | ρs |
| 淡水密度 | 1 000 kg/m3 | ρ0 |
| 海水浓度 | 33.4 g/L | C* |
| 孔隙水残余饱和度 | 0.1 | Swres |
| 进气参数 | 14.5 | α |
| 指数参数 | 2.68 | n |
如图 1所示, 模型左侧边界为内陆边界, 设为定水位边界, 淡水水位为21 m, 右边界为海向边界, 底部边界BE设为不透水边界, 模型滩面位置的表面边界考虑三种工况:
1) 无水库、无潮汐情况, 我们把表面CD段设为定水头定浓度边界;
2) 无水库, 有潮汐情况, CD段设为潮汐动力边界;
3) 修建海岸水库工况, 坝体为不透水边界, FD为潮汐动力边界, 其中CF段又考虑三种库区水位情况: (a) 库区不蓄水0 m, (b) 库区水位为1 m, (c) 库区水位为2 m, 都设置为定水头零浓度边界。
通过使用SUTRA运行计算模型, 得出每个节点的盐度值, 流速, 绘制盐度流场图, 计算整个模型区域的盐量, 分析计算结果, 总结规律, 分析不同水位的海岸水库对海水入侵的影响。
2 结果与分析 2.1 潮汐对海水入侵的影响首先对比潮汐作用对滨海地区含水层的盐淡水分布情况, 以无潮稳定状态为初始状态, 模拟出有潮汐作用下的地下含水层的时均稳态盐度分布。模型中内陆水位边界为21 m, 以周期平均的方法绘制在一个周期内含水层的盐度分布, 并采用拉格朗日质点法研究含水层物质输移特征, 在滩面和内陆边界分别释放一定数量的粒子, 绘制其运动轨迹, 白线上的数字就是其从释放点到排出点所经历的时间, 结果如图 2、图 3所示, 图 2是无潮汐条件下的稳定状态, 图 3有潮汐条件下的稳定状态。图中红色代表的是海水, 黑线代表 50%海水盐度等值线(17.5)。将咸淡水界面(50%海水盐度等值线即17.5)与底部边界的交点称为海水入侵点, 其与海向边界的水平距离称为海水入侵距离。
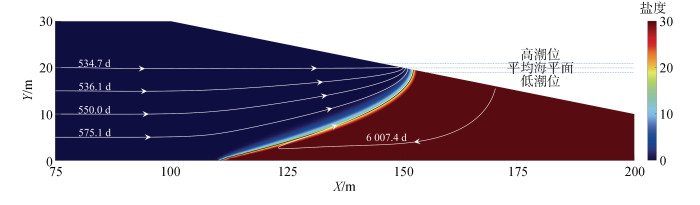 |
| 图 2 无潮汐盐度分布和粒子路径 Fig. 2 Salinity distribution and particle path lines without tide |
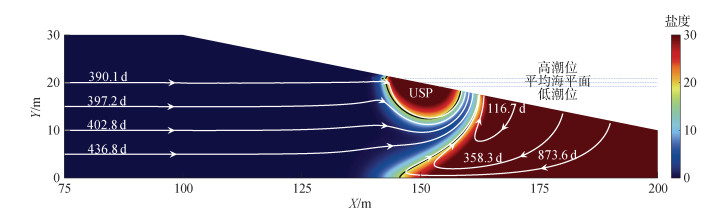 |
| 图 3 有潮汐盐度分布和粒子路径 Fig. 3 Salinity distribution and particle path lines with tide |
从图 3可以看出在潮汐条件下, 在潮间带形成了上部混合区即USP(upper saline plume), 在潮汐作用下, 高潮期海水在滩面入渗, 并在低潮位线附近流出, 形成了较快的海水循环, USP处的土壤和地下水的含盐浓度较高, 在密度流作用下, 内陆淡水出流通道被向下顶托, 从图 2可以看出无潮汐用下, 咸淡水过渡带的宽度为2 m; 从图 3可以看出在潮汐作用下, 咸淡水过渡带的宽度为10 m, 这说明了潮汐让咸淡水混合作用加大。
进一步从图 3可以看出加上潮汐作用, 盐水楔会向海侧移动, 海水入侵距离从88.5 m减小到53.0 m, 即盐水楔后退了35.5 m, 这是因为水流在USP和盐水楔之间形成了较窄的淡水排泄通道, 此处的流速较大, 使得盐分从盐水楔下部加快稀释流出到海洋, 同时形成了向海的水位梯度, 抑制了底层盐水的入侵, 导致底层盐水楔后退。通过计算整个模型的盐量变化, 可以发现在无潮汐作用下的单宽盐量为6.448×104 kg/m, 潮汐作用下含水层的单宽盐量为4.901×104 kg/m, 减少了24.0%, 这也进一步说明了潮汐波动效应降低了海水入侵的程度。
观察粒子运移时间, 可以看出无潮汐作用下, 粒子先水平运动到咸淡水交界面, 然后在垂直坡面方向运动排出, 越靠近底部含水层的粒子所需时间越长。对比图 2和图 3可知, 由于潮汐作用形成了上混合区, 并与盐水楔之间形成了淡水排泄通道, 此处的流速较大, 加快了内陆物质输运, 如从(0, 5)处释放的粒子运移时间从575.1 d减少到436.8 d, 减少了24.0%。而滩面释放的粒子运移时间由于盐水楔的回退而减少。如从(170, 16)释放的粒子运移时间从6 007.4 d减小到116.7 d, 减小了98%, 明显减小, 一方面是因为盐水楔后退, 缩短了质点运移距离, 另一方面是因为潮汐作用促进了底层咸淡水的混合循环过程, 导致海侧物质在潜水层内的输移时间变短。
2.2 潮汐作用下海岸水库工程对海水入侵的影响为了研究海岸水库工程对海水入侵的影响, 在有潮稳定工况的基础上, 考虑建库工程。在低潮位F点设立坝体, 将有潮汐时的稳定状态设为初始状态, 模拟3种水文情况, 分别是坝后蓄水0 m、1 m、2 m, 计算出建库后的盐度分布, 模型模拟的盐度分布和粒子路径如图 4—图 6所示。
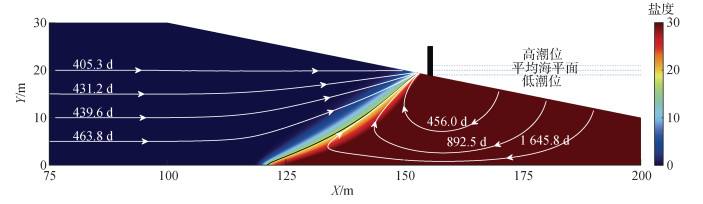 |
| 图 4 加坝蓄水0 m盐度分布和粒子路径 Fig. 4 Salinity distribution and particle path lines with the impounding of the dam (0 m) |
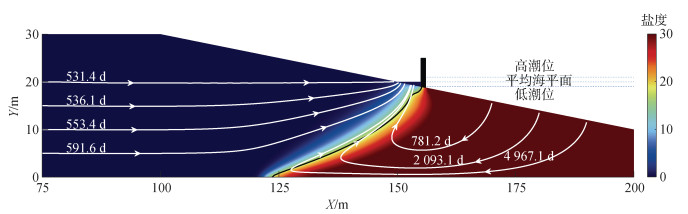 |
| 图 5 加坝蓄水1 m盐度分布和粒子路径 Fig. 5 Salinity distribution and particle path lines with the impounding of the dam (1 m) |
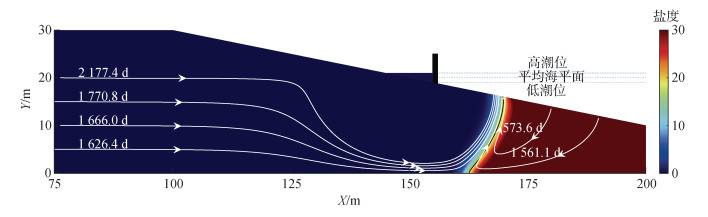 |
| 图 6 加坝蓄水2 m盐度分布和粒子路径 Fig. 6 Salinity distribution and particle path lines with the impounding of the dam (2 m) |
首先对比图 3和图 4, 可以看出, 建坝以后, 盐水楔向内陆移动, 海水入侵距离增大, 这是因为坝体阻隔了海水与滩面, 潮汐无法作用于潮间带, 滩面上层盐水羽逐渐消失, 从稳定后的流场看, 之前在盐水羽和盐水楔之间形成的较窄的淡水排泄通道消失, 流速变小, 淡水对下层盐水楔的挤压作用减弱, 因此盐水楔前进。坝后蓄水0 m工况下的海水入侵距离为80.0 m, 增加了50.9%, 为了进一步说明海水入侵程度的变化, 我们计算建坝后的模型的单宽盐量, 坝后蓄水0 m时, 潜水层内的单宽盐量为6.392×104 kg/m, 增加了30.4%, 此时海水入侵程度较大。
进一步抬高库区水位至1 m, 从图 5看出海水入侵距离基本没变, 单宽盐量为5.871×104 kg/m, 只减少了8.2%, 过渡带变宽; 抬高水位至2 m, 从图 6可以看出海水入侵距离迅速减少到35.6 m, 比库区水位0 m工况下减少了59.1%, 计算模型单宽盐量为2.731×104 kg/m, 比库区水位0 m工况下减少了57.3%。
为了进一步研究不同水位工况下对海水入侵的影响, 设置6种库区水位工况, 分别为0 m、0.5 m、1 m、1.5 m、2 m、2.5 m, 计算出对应的海水入侵距离和模型单宽盐量, 并拟合相关曲线, 如图 7, 图 8所示, 图中×点为数据标记。可以看出库区水位小于平均海平面时, 即库区水位小于1 m, 海水入侵距离和模型单宽盐量变化较小, 这是因为该工况下, 含水层的水力梯度由潮汐波动控制, 潮汐动力因素占主导, 而出现过渡带变宽现象源于库区存在水力梯度, 加强了过渡带间的弥散作用; 当库区水位高于平均海平面, 海水入侵距离和含盐量迅速减少, 水库水位为2.5 m时, 海水入侵距离减少了68.8%, 单宽盐量减少了66.9%, 显著减少, 这是因为此时库区水位高于平均海平面, 在含水层形成了新的水力梯度, 随着水位的抬高导致上层淡水对下层盐水楔的挤压作用加强, 使得盐水楔向海一侧推移, 抑制了海水入侵程度, 海水入侵距离降低, 含水层盐量降低。
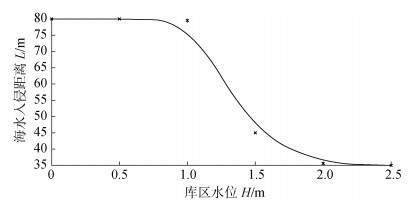 |
| 图 7 库区水位和海水入侵距离关系 Fig. 7 Relationship between the reservoir water level and seawater intrusion distance |
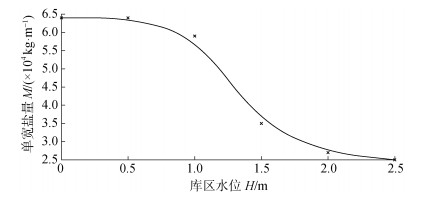 |
| 图 8 库区水位和单宽盐量关系 Fig. 8 Relationship between the reservoir water level and salt content per unit width |
观察粒子运移时间, 库区水位在平均海平面以下时, 随着水位的抬高, 过渡带的弥散作用加强, 海侧释放粒子运移路径延长, 运移时间增加, 如库区水位为1.0 m时, 在(190, 12)释放的粒子运移时间比水位为0 m时增加了66.9%。库区水位在平均海平面以上时, 随着水库水位的抬高, 内陆粒子运移时间增加, 海侧边界粒子运移时间减少, 这是因为库区高水位使得盐水楔向海一侧推移, 内陆粒子运移的路径变长, 海侧边界粒子运移的路径相对变短。不难得出库区高水位会导致陆源污染物运移路径变长, 运移时间变长, 运移区域变广, 高水位抑制了盐水楔的入侵, 过渡带后退变窄, 过渡带是硝化和反硝化的重要区域, 影响到陆源氮类污染物的硝化及随后的反硝化过程, 库区底部氮类污染物大量堆积, 容易对水库水质产生影响。
从图 4可以看出, 在库区水位较低时, 库区底部含水层盐度较高, 此时库区水体易受海水入侵的盐分渗入, 为了进一步说明水位和海水入侵的关系, 设置了库区6种水位, 分别是0 m、0.5 m、1 m、1.5 m、2 m、2.5 m, 算出不同水位工况下模型库底F点(155, 19)处盐度值, 拟合出曲线, 绘制出水位与库区底部盐度关系曲线图, 如图 9所示, 图中×点为数据标记。图 9说明, 水库水位在平均海平面以上时, 底盐度变化较小, 都维持在相对较高的盐度; 当水库水位在平均海平面以上时, 随着水位的抬高, 库区底部边界的盐度迅速降低, 在库区水位2 m时库区底部盐度接近0, 此后水位抬高, 库区底部盐度保持为0, 所以要保证库区水体盐度, 让水库不受盐分渗入, 该模型的库区控制水位应在2 m以上。
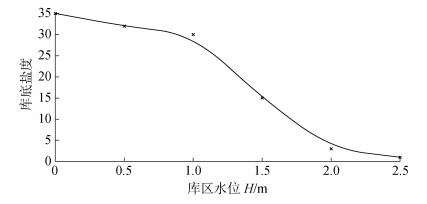 |
| 图 9 库区水位和库底盐度关系 Fig. 9 Curve of relationship between the reservoir water level and reservoir bottom salinity |
从图 6可以观察到海岸水库在高水位时地下含水层淡水储量较多, 而保证地下含水层淡水储量是修建海岸水库需要考虑的重要因素。一般来说将水体盐度在0.5以下的当作淡水, 为了分析库区水位与地下淡水储量关系, 设置了6个水位, 分别是0 m、0.5 m、1 m、1.5 m、2 m、2.5 m, 计算出各个水位工况下的地下含水层单宽淡水储量, 拟合出曲线, 如图 10所示, 图中×点为数据标记。可以看出, 当水库水位在平均海平面以下时, 随着水位的抬高, 含水层单宽淡水储量变化不大; 当水库水位在平均海平面以上时, 随着水库水位的抬高, 单宽淡水储量迅速增加, 水库水位为2 m时含水层单宽淡水储量为3 953 m2, 水库水位增加到2.5 m, 淡水储量只增加了13 m2。因此在考虑淡水储量尽可能保持充足的情况下, 水库控制水位应在2 m以上。
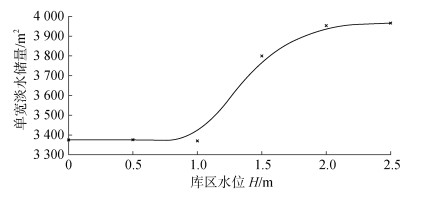 |
| 图 10 库区水位和淡水储量关系 Fig. 10 Relationship between the reservoir water level and freshwater resources |
本文采用SUTRA(saturated-unsaturated transport)模型建立具有代表性的二维海岸模型, 研究潮汐作用下海岸水库工程对海水入侵的影响, 结果表明:
1) 潮汐作用抑制底层盐水楔的入侵, 加快海陆物质交换。
2) 海岸水库坝体的建立加剧了海水入侵, 水库水位在平均海平面以下时, 含水层潮汐动力因素占主导, 海水入侵程度基本保持不变, 海岸水库在旱季时存在水位较低的情况, 应注意海水入侵的防治, 以及对库区水质的监测。
3) 库区水位在平均海平面以上时, 海水入侵程度随着库区水位的抬高而减少, 可以人为地调控水库水位来进行地下水的退咸, 从而进行滨海地区海水入侵防治。
4) 通过研究水位与库底盐度、含水层淡水储量关系, 得出海岸水库在建设中存在一个控制水位, 水库水位在控制水位以上, 库区水体盐度和含水层淡水储量能得到保证。
5) 当库区水位较高时, 内陆物质运移时间较长, 运移区域更广, 需重视相关的滨海污染物的入海防治。库区高水位削弱库区底部陆源氮类污染物在盐淡水混合区的硝化反硝化过程, 影响库区底部含水层的水质。
| [1] |
袁文秀, 杨树滩, 张明. 江苏省如东县沿海平原水库水源论证[J]. 人民长江, 2007, 38(6): 35-37. YUAN Wenxiu, YANG Shutan, ZHANG Ming. Arguments of the coastal reservoir in Ru Dong JiangSu Province Yangtze River[J]. Yangtze River, 2007, 38(6): 35-37. DOI:10.3969/j.issn.1001-4179.2007.06.015 |
| [2] |
李冬顺, 杨劲松, 姚荣江. 生态风险分析用于苏北滩涂土壤盐渍化风险评估研究[J]. 土壤学报, 2010, 47(5): 51-58. LI Dongshun, YANG Jinsong, YAO Rongjiang. Application of ecological risk analysis to soil salinization risk assessment of coastal tidal flat in north Jiangsu Province[J]. Acta Pedologica Sinica, 2010, 47(5): 51-58. |
| [3] |
姚荣江, 杨劲松, 陈小兵, 等. 苏北海滩典型围垦区土壤盐渍化风险评估研究[J]. 中国生态农业学报, 2010, 18(5): 1000-1006. YAO Rongjiang, YANG Jinsong, CHEN Xiaobing, et al. Evaluating soil salinization risk in typical coastal reclaimed regions in North Jiangsu Province[J]. Chinese Journal of Eco-Agriculture, 2010, 18(5): 1000-1006. |
| [4] |
王辉, 许学工. 淡水帷幕防治海水入侵的国际经验[J]. 中国农村水利水电, 2017(4): 62-66. WANG Hui, XU Xuegong. International experience on hydraulic barrier serving as a seawater intrusion countermeasure[J]. China Rural Water and Hydropower, 2017(4): 62-66. DOI:10.3969/j.issn.1007-2284.2017.04.017 |
| [5] |
JIN G Q, MO Y M, LI M D, et al. Desalinization and salinization: A review of major challenges for coastal reservoirs[J]. Journal of Coastal Research, 2019, 35(3): 664-672. DOI:10.2112/JCOASTRES-D-18-00067.1 |
| [6] |
JAKOVOVIC D, WERNER A D, DE LOUW P G B, et al. Saltwater upconing zone of influence[J]. Advances in Water Resources, 2016, 94: 75-86. DOI:10.1016/j.advwatres.2016.05.003 |
| [7] |
KARATZAS G P, DOKOU Z. Optimal management of saltwater intrusion in the coastal aquifer of Malia, Crete (Greece), using particle swarm optimization[J]. Hydrogeology Journal, 2015, 23(6): 1181-1194. DOI:10.1007/s10040-015-1286-6 |
| [8] |
PARK N, SHI L. A comprehensive sharp-interface simulation-optimization model for fresh and saline groundwater management in coastal areas[J]. Hydrogeology Journal, 2015, 23(6): 1195-1204. DOI:10.1007/s10040-015-1268-8 |
| [9] |
COBANER M, YURTAL R, DOGAN A, et al. Three-dimensional simulation of seawater intrusion in coastal aquifers: A case study in the Goksu Deltaic Plain[J]. Journal of Hydrology, 2012, , 464-465: 262-280. DOI:10.1016/j.jhydrol.2012.07.022 |
| [10] |
XIAO H, WANG D, HAGEN S C, et al. Assessing the impacts of sea-level rise and precipitation change on the surficial aquifer in the low-lying coastal alluvial plains and barrier islands, east-central Florida (USA)[J]. Hydrogeology Journal, 2016, 24(7): 1-16. |
| [11] |
薛显武, 陈喜, 魏玲娜, 等. 基于GIS的海水入侵可视化数值模拟系统[J]. 地下水, 2006, 29(5): 35-39. XUE Xianwu, CHEN Xi, WEI Lingna, et al. Visualized numeric simulation system of seawater intrusion based on GIS[J]. Ground Water, 2006, 29(5): 35-39. |
| [12] |
ROBINSON C, LI L, BARRY D A. Effect of tidal forcing on a subterranean estuary[J]. Advances in Water Resources, 2007, 30(4): 851-865. DOI:10.1016/j.advwatres.2006.07.006 |
| [13] |
武雅洁, 杨自良, 程从敏, 等. 潮汐波动对潜水含水层海水入侵规律的影响研究[J]. 中国海洋大学学报(自然科学版), 2020, 50(10): 91-98. WU Yajie, YANG Ziliang, CHENG Congmin. The influence of tidal oscillations on the behaviors of seawater intrusion in unconfined coastal aquifers[J]. Periodical of Ocean University of China, 2020, 50(10): 91-98. |
| [14] |
NISHIKAWA T, SIADE A J, REICHARD E G, et al. Stratigraphic controls on seawater intrusion and implications for groundwater management, Dominguez Gap area of Los Angeles, California, USA[J]. Hydrogeology Journal, 2009, 17(7): 1699-1725. DOI:10.1007/s10040-009-0481-8 |
| [15] |
MAHMOODZADEH D, KETABCHI H, ATAIE-ASHTIANI B, et al. Conceptualization of a fresh groundwater lens influenced by climate change: A modeling study of an arid-region island in the Persian Gulf, Iran[J]. Journal of Hydrology, 2014, 519: 399-413. DOI:10.1016/j.jhydrol.2014.07.010 |
| [16] |
VOSS C I, PROVOST A M. SUTRA: A model for 2D or 3D saturated-unsaturated, variable-density ground-water flow with solute or energy transport[R]. U.S. Geological Survey Water-Resources Investigations Report 2002-4231, 2002. https://doi.org/10.3133/wri024231
|
| [17] |
LIANG D, FALCONER R A, LIN B. Coupling surface and subsurface flows in a depth averaged flood wave model[J]. Journal of Hydrology, 2007, 337(1-2): 147-158. DOI:10.1016/j.jhydrol.2007.01.045 |
| [18] |
MAO X Z, CHEN F Y, YU Q W, et al. Numerical prediction of water desalination in polder reservoir[J]. Journal of Hydraulic Engineering, 2004. |
| [19] |
MEHDIZADEH S S, KETABCHI H, GHOROQI M, et al. Experimental and numerical assessment of saltwater recession in coastal aquifers by constructing check dams[J]. Journal of Contaminant Hydrology, 2020, 231: 103637. DOI:10.1016/j.jconhyd.2020.103637 |
| [20] |
KUAN W K, JIN G, XIN P, et al. Tidal influence on seawater intrusion in unconfined coastal aquifers[J]. Water Resources Research, 2012, 48(2): 136-149. |
| [21] |
MAO X, ENOT P, BARRY D A, et al. Tidal influence on behaviour of a coastal aquifer adjacent to a low-relief estuary[J]. Journal of Hydrology, 2006, 327(1): 110-127. |
| [22] |
WERNER A D, LOCKINGTON D A. Tidal impacts on riparian salinities near estuaries[J]. Journal of Hydrology, 2006, 328(3/4): 511-522. |
| [23] |
XIN P, ROBINSON C, LI L, et al. Effects of wave forcing on a subterranean estuary[J]. Water Resources Research, 2010, 46(12): W12505. |
| [24] |
XIN P, WANG S S J, LU C, et al. Nonlinear interactions of waves and tides in a subterranean estuary[J]. Geophysical Research Letters, 2015, 42: 2277-2284. DOI:10.1002/2015GL063643 |
| [25] |
VAN GENUCHTEN, M TH. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. DOI:10.2136/sssaj1980.03615995004400050002x |
 2021, Vol. 45
2021, Vol. 45


