
文章信息
- 王子蘅, 王振杰, 聂志喜, 张远帆. 2021.
- WANG Zi-heng, WANG Zhen-jie, NIE Zhi-xi, ZHANG Yuan-fan. 2021.
- 声速剖面EOF重构的实测数据采样深度研究
- Research on the sampling depth in the EOF reconstruction of the sound speed profile
- 海洋科学, 45(6): 126-134
- Marine Sciences, 45(6): 126-134.
- http://dx.doi.org/10.11759/hykx20200711001
-
文章历史
- 收稿日期:2020-07-11
- 修回日期:2020-12-29
2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室, 山东 青岛, 266071
2. Laboratory for marine Mineral Resource, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266071, China
声波在水中的良好传播特性使其成为获取和传递水下信息最为有效的手段[1-3]。声速是影响水下多波束系统作业精度的重要外部影响因素, 通过影响声线跟踪的精度, 最终影响到测深精度。多波束测深通过换能器实时接收其发射出的各波束经海底反射和散射后返回的到达角和旅行时[3], 利用声速剖面数据, 由公式计算得到不同波束点对应的水深值。声速剖面是声速的垂直结构分布, 海水的介质特性导致声波的传播轨迹发生弯曲, 要获取波束脚印的确切位置, 需要沿着波束的传播路径追踪声线, 计算波束脚印的水平位移和深度, 即声线跟踪[3]。因此, 声速剖面的正确与否直接影响多波束测深结果的精度和可靠性[4]。
海洋中的声速剖面通常由以下两种方法获得: 直接测量法和间接测量法[4]。直接测量法通过测量声波在海水中已知的固定距离内往返所需的时间或相位来计算声速值。间接测量法利用温盐深测量系统(conductivity, temperature, depth, CTD) 测量海水的温度、盐度及深度等物理量, 再通过声速经验公式计算作业水域内各采样深度的声速值, 进而构成声速剖面。然而在深水大洋进行实际作业时, 受到水深和洋流的影响, 停船投放CTD采集声速剖面数据时间成本较高。采用走航式的抛弃式声速剖面计虽然可以快速有效的获得声速剖面, 但其作业成本随之大大增加。相较于以上方法, 声速剖面重构只需少量的实测声速数据即可实现全海深声速剖面的重构, 提高效率的同时还有效的降低了成本。
由于海洋环境的复杂性, 声速剖面难以用一个简单的函数表示。Davis等[5]证明EOF是在最小均方差意义下反映声速剖面最有效的基函数; 孙文川等[6]论证了EOF重构的声速剖面具有较高的内符合精度, 能较好地描述实际声速剖面; 张志伟等[7]研究表明取前6阶及以上的EOF表示声速剖面可满足多波束测深的精度要求; 张镇迈等[8]采用部分深度的实测剖面, 并基于测区海域内已有的数据, 对全海深声速剖面实现了重构; 张孝首等[9]利用实测CTD数据通过有理拟合延伸和EOF方法实现了深海5 000 m声速剖面场的重构; 李洪超等[10]对不同深度位置的部分声速剖面的重构效果进行了探讨; 张维等[11]在对残缺样本声速合理外延的基础上, 选取声速剖面变化较剧烈深度的3个声速值实现了剖面重构。以上研究表明, 基于EOF方法利用部分实测声速数据重构全海深剖面是可行有效的, 但未对参与重构的实测数据的采样深度给出明确依据。
本文将测区Argo浮标的温盐深数据通过声速经验公式计算得到的声速剖面作为测区历史声速剖面资料, 基于EOF空间函数的方差贡献率选取K(EOF阶次)个最大梯度对应深度处的声速值进行声速剖面重构, 在保证多波束测深精度的前提下实现了对全海深声速剖面的重构。
1 声速剖面EOF表示原理 1.1 声速剖面EOF分解经验正交函数分析方法也称特征向量分析或主成分分析, 是分析矩阵数据的特性、提取主要数据特征量的一种方法[12]。
在某海域采集N个声速剖面: C = [c(1), c(2), …, c(N)], 内插成为M个垂直标准层, 得到声速矩阵CM×N:
| $\begin{array}{*{20}{c}} {{\boldsymbol{C}_{M \times N}} = \left[ {\begin{array}{*{20}{c}} {{c_{1(1)}}}&{{c_{2(1)}}}& \ldots &{{c_{N(1)}}} \\ {{c_{1(2)}}}&{{c_{2(2)}}}& \ldots &{{c_{N(2)}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{c_{1(M)}}}&{{c_{2(M)}}}& \ldots &{{c_{N(M)}}} \end{array}} \right]} , \end{array}$ | (1) |
式中, 每一列为一个声速剖面的标准层插值, 每一行为所有剖面在同一深度的声速。将N条声速剖面每一行进行平均, 得到平均声速剖面
| $\begin{array}{*{20}{c}} {{{\bar C}_{M \times 1}} = \frac{1}{M}\mathop \sum \limits_{i = 1}^M {c_{\left( i \right)}}} , \end{array}$ | (2) |
扩展可得平均声速矩阵
| $\begin{array}{*{20}{c}} {\Delta {\boldsymbol{C}_{M \times N}} = {\boldsymbol{C}_{M \times N}} - {{\bar {\boldsymbol{C}}}_{M \times N}}}, \end{array}$ | (3) |
扰动矩阵的协方差矩阵为:
| $\begin{array}{*{20}{c}} {{\boldsymbol{R}_{M \times M}} = \frac{{\Delta {\boldsymbol{C}_{M \times N}}\Delta \boldsymbol{C}_{M \times N}^T}}{N}} , \end{array}$ | (4) |
其中每个元素rij为:
| $\begin{array}{*{20}{c}} {{r_{ij}} = \frac{1}{N}\mathop \sum \limits_{n = 1}^N \left[ {{c_n}\left( {{z_i}} \right) - \bar c\left( {{z_i}} \right)} \right]\left[ {{c_n}\left( {{z_j}} \right) - \bar c\left( {{z_j}} \right)} \right]} , \end{array}$ | (5) |
将RM×M特征分解, 有:
| $ \boldsymbol{R}_{M \times M} \boldsymbol{F}_{M \times N}=\boldsymbol{D}_{M \times M} \boldsymbol{F}_{M \times N}, $ | (6) |
式中, DM×M为特征值矩阵, 令特征值λi按从大到小顺序排列:
| $ \boldsymbol{D}_{M \times M}=\operatorname{diag}\left[\lambda_{1}, \lambda_{2}, \cdots, \lambda_{M}\right], $ | (7) |
FM×N为特征值对应的特征向量矩阵, 也就是EOF空间函数, 可表示为:
| $ \boldsymbol{F}_{M \times N}=\left[\boldsymbol{f}_{(1)}, \boldsymbol{f}_{(2)}, \cdots, \boldsymbol{f}_{(k)}\right], $ | (8) |
式中, f(k)(k = 1, 2, …, N)为M×1的列向量, 即为确定的第k阶EOF。特征值λi对应的分量f(i)即为第i阶EOF。特征值的大小代表了其对应EOF空间函数对线性空间的影响权重[7], 即越大的特征值对应的特征向量中包含的声速重构信息越丰富。
1.2 声速剖面EOF重构测区内的声速剖面完成EOF分解后, 利用前几阶EOF即可完成测区内任一声速剖面的重构:
| $\begin{array}{*{20}{c}} {c\left( z \right) = \bar c\left( z \right) + \mathop \sum \limits_{i = 1}^K {\alpha _i}{f_i}\left( z \right), i = 1, 2, \cdots , M} , \end{array}$ | (9) |
式中, c(z)为重构的声速剖面; z为各层海水深度;
| $\begin{array}{*{20}{c}} {\Delta {\boldsymbol{C}_{M \times N}} = {\boldsymbol{C}_{M \times N}} - {{\bar {\boldsymbol{C}}}_{M \times N}} = {\boldsymbol{F}_{M \times K}}{\boldsymbol{A}_{K \times N}}} , \end{array}$ | (10) |
则重构系数矩阵AK×N为:
| $\begin{array}{*{20}{c}} {{\boldsymbol{A}_{K \times N}}{\rm{ = }}\boldsymbol{F}_{M \times K}^T\Delta {\boldsymbol{C}_{M \times N}}} \end{array}{\rm{ = }}{\left[ {{a_1}, {a_2}, \cdots , {a_N}} \right]_{K \times N}}, $ | (11) |
式中, ai = [ai(1), ai(2), …, ai(K)]T为每个声速剖面对应的重构系数。得到重构系数后, 即可按式(9)对测区内任一声速剖面进行EOF重构。
2 声速剖面EOF重构的数据采样深度选取方法本文给出了用于声速剖面EOF重构的数据采样深度选取的方法步骤。算法流程图见图 1, 详细步骤和说明如下:
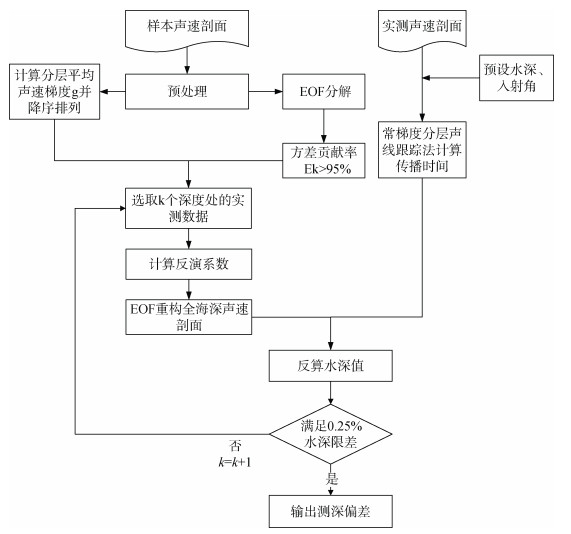 |
| 图 1 声速剖面EOF重构的数据采样深度选取算法流程图 Fig. 1 Algorithm flowchart of data sampling depth selection for SSP EOF reconstruction |
(1) 从中国Argo实时资料中心(http://www.argo.org.cn/)获取某海域温盐压数据, 预处理后利用声速经验公式计算得到采样位置处的声速剖面。目前国内外较为认可的声速经验公式有Chen-Millero, Wilson, Del Grosso及Leroy等, 各模型的温度、盐度、压力的适用范围有所差异。根据文献[13]的研究, Del Grosso, Chen-Millero, C.C.Leroy、Coppens四个经验声速模型在全球海域具有较高的精度及适用性, 文献[14]指出, 在350~1 000 m的深度上, Chen-Millero公式的误差最小, 因此本文选用Chen-Millero声速经验公式计算的声速剖面作为样本声速剖面, 利用Akima插值[15]将声速剖面数据内插到垂直标准层。
(2) 按照1.1节中的方法进行EOF分解, 提取EOF函数, 计算各阶EOF的方差贡献率和累计方差贡献率。方差贡献率[16]指的是每一阶EOF包含声速场信息的百分比。其计算公式为:
| $\begin{array}{*{20}{c}} {{\sigma _i} = \frac{{{\lambda _i}}}{{\sum\limits_{i = 1}^M {{\lambda _i}} }} \times 100\% } , \end{array}$ | (12) |
式中, σi表示第i阶方差贡献率, λi表示协方差矩阵R经降序排列后的第i个特征值。
前K阶EOF对区域的累计贡献率可表示为:
| $\begin{array}{*{20}{c}} {w(K) = {{\mathop \sum \limits_{i = 1}^K {\lambda _i}} \mathord{\left/ {\vphantom {{\mathop \sum \limits_{i = 1}^K {\lambda _i}} {\mathop \sum \limits_{j = 1}^M {\lambda _j}}}} \right. } {\mathop \sum \limits_{j = 1}^M {\lambda _j}}}} , \end{array}$ | (13) |
一般地, 如果w(K)的值大于等于95%, 则认为利用前K阶EOF能较好的表示该区域的主要信息[5]。
(3) 计算测区内每一声速剖面每一深度层的声速梯度, 然后计算平均分层声速梯度:
| ${G_{i, n}} = \frac{{{c_{i + 1, n}} - {c_{i, n}}}}{{{z_{i + 1, n}} - {z_{i, n}}}}, $ | (14) |
| $\overline {{G_i}} = \frac{1}{N}\sum\limits_{n = 1}^N {{G_{i, n}}} , $ | (15) |
式中, ci, n和ci+1, n分别表示第n条声速剖面第
(4) 从新构建的声速层矩阵中选取K个深度处的声速值(即选取K个声速变化最剧烈处的声速值), 结合K阶EOF计算得到重构系数矩阵AK×N, 重构全海深声速剖面。
(5) 基于实测声速剖面, 预设水深值H和初始入射角, 根据分层常梯度声线跟踪法[2], 以H作为约束迭代计算声波的传播时间T:
| $ T={\displaystyle \sum _{i=1}^{Y-1}\frac{{\theta }_{i+1}-{\theta }_{i}}{p{g}_{i}^{2}\Delta {z}_{i}}\mathrm{ln}\left[\frac{{c}_{i+1}}{{c}_{i}}\right]}, $ | (16) |
式中, Y表示实测声速剖面的层数, θi和θi+1分别表示实测剖面第i层和第i+1层的入射角, gi表示实测剖面第i层的梯度, ci和ci+1分别表示实测剖面第i层和第i+1层的声速, Δzi表示第i层的深度差。p为Snell系数:
| $ p=\frac{\sin{\theta }_{i}}{{C}_{i}}=\frac{\sin{\theta }_{i+1}}{{C}_{i+1}}.$ | (17) |
(6) 用重构的声速剖面和T反算波束水深值[6]H′。声波在重构的声速剖面第i层的传播时间ti为:
| $ {t}_{i}=\frac{{{\theta }^{\prime }}_{i+1}-{{\theta }^{\prime }}_{i}}{p{{g}^{\prime }}_{i}^{2}\Delta {z}_{i}}\mathrm{ln}\left[\frac{{{c}^{\prime }}_{i+1}}{{{c}^{\prime }}_{i}}\right], $ | (18) |
式中,
| $ T-{\displaystyle \sum _{i=1}^{J}{t}_{i}} =0,$ | (19) |
式中, J表示使等式成立的ti的个数。所以:
| $H' = \sum\limits_{i = 1}^J {\Delta {z_i}} .$ | (20) |
(7) 计算测深误差
| $\sigma = \frac{{\left| {H - H'} \right|}}{H} \times 100\% .$ | (21) |
定义有效波束比为满足深度限差的波束占总波束的比率[17], 首先统计满足0.25%水深限差要求的波束数数, 然后判断多波束测深的有效波束比是否达到100%, 如果是, 则输出测深偏差, 实验结束, 反之, 则将选取阶数K加1, 重新完成重构系数矩阵的计算以及之后的步骤, 直至符合满足测深精度的要求。
3 实验分析实验数据源于中国Argo资料实时中心发布的《全球Argo浮标剖面观测资料质量再控制数据集》[18], 选取2006—2009年每年1月份的Argo浮标数据。将153.5°W—155W°, 27.5°N—29°N的海区作为区域1; 153.5°W—155.5W°, 22.5°N—24.5°N的海区作为区域2。去除不合格的剖面后, 区域1选取了18个剖面, 区域2选取了15个剖面。
典型深海声速剖面结构如图 2所示[2], 主要划分为三部分: 混合层(由表面层和季节跃变层构成)、主跃层和深海等温层。其中, 声速在混合层和主跃层的变化情况复杂, 而在深海等温层中, 声速随深度的增加呈趋势稳定的正梯度增加, 接近线性变化。因此本文重点对混合层和主跃层这两部分声速变化情况更为复杂的水层的声速剖面进行研究, 统一截取海面至海深1 000 m的深度之间作为本次实验的剖面范围。
 |
| 图 2 深海典型声速剖面图 Fig. 2 Typical deep-sea sound speed profile |
随机选取区域内1条剖面用作检核重构精度, 其余剖面作为已知剖面数据。实验区域内的Argo剖面浮标分布如图 3(a)和(b)所示, 图中“×”点代表已知的样本剖面, “▲”代表用于检核的剖面。
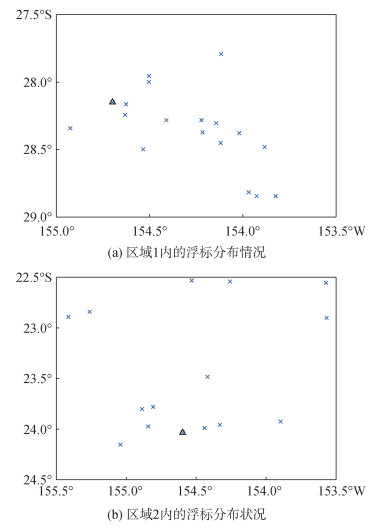 |
| 图 3 实验海域内浮标剖面分布图 Fig. 3 Distribution map of the buoy profiles in the experimental sea area |
(1) Argo剖面浮标测量的是海水的温度、盐度和压力数据, 采用Chen-Millero声速经验公式[19]计算得到相应深度处的声速值:
| $\begin{gathered} c = {c_W}\left( {T, P} \right) + {c_C}\left( {T, P} \right) + A\left( {T, P} \right)S \\ + B\left( {T, P} \right){S^{3/2}} + D\left( P \right){S^2}, \\ \end{gathered} $ | (22) |
式中,
其中, T为温度, ℃; S为盐度; P为压力, bar。
(2) 将计算得到的声速数据利用Akima插值函数内插成1 m的等间距标准层。样本声速剖面结构如图 4。
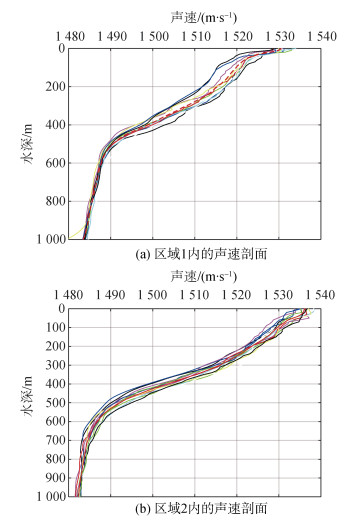 |
| 图 4 声速剖面结构示意图 Fig. 4 Schematic diagrams of SSP |
分别对两个区域的样本声速剖面进行EOF分解, 得到测区EOF空间函数的方差贡献率和累计方差贡献率, 如表 1所示。可以看出, 在区域1中, 前5阶EOF的累计方差贡献率可达97.985%, 在区域2中, 前5阶EOF的累计方差贡献率达95.813%, 均已大于95%, 因此利用前5阶EOF能够较好的表示当前区域的主要信息。
| EOF阶次 | 区域1 | 区域2 | |||
| 方差贡献率/% | 方差累计贡献率/% | 方差贡献率/% | 方差累计贡献率/% | ||
| 1 | 76.973 | 76.973 | 75.057 | 75.057 | |
| 2 | 11.387 | 88.359 | 10.058 | 85.115 | |
| 3 | 4.030 | 92.390 | 5.121 | 90.236 | |
| 4 | 2.775 | 94.164 | 2.905 | 93.141 | |
| 5 | 1.821 | 97.985 | 2.672 | 95.813 | |
图 5给出的是由两个实验海域内的样本声速剖面提取的1~5阶EOF, 可以明显看出, 第1阶EOF空间函数的变化较小, 整体呈趋势稳定, 这表明前几阶EOF中包含了实验海域内的声速场的主要信息, 而2~5阶EOF空间函数的变化明显, 变化集中在浅层区域, 尤其是在越靠后的阶次中, 这反映了声速场相对于平均SSP的细节变化[7]。
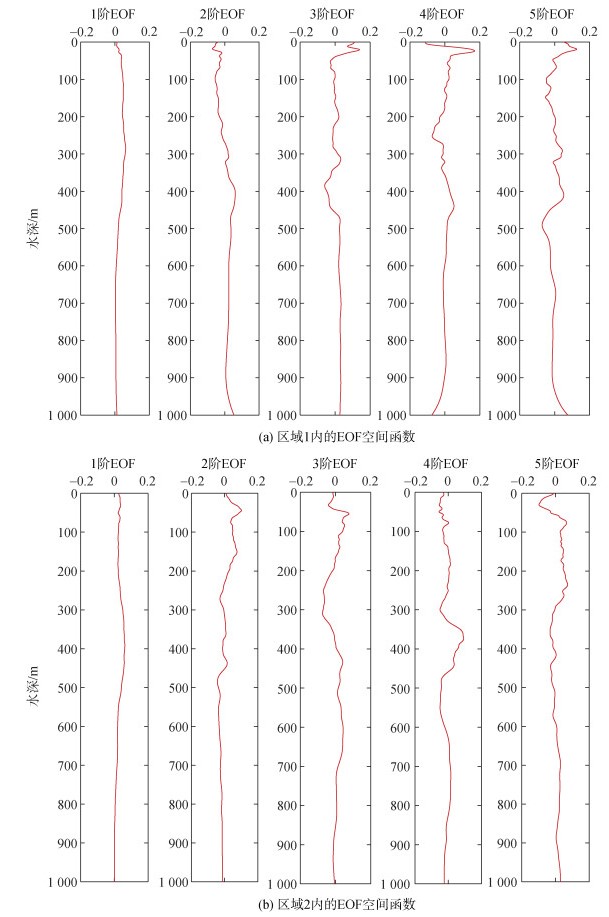 |
| 图 5 1~5阶EOF空间函数 Fig. 5 1~5 order EOFs |
计算每个样本声速剖面每层的梯度变化情况, 得到该区域的平均分层声速梯度及对应的深度位置, 按照平均分层声速梯度由大到小对声速层降序排列, 自上而下选取5个深度处的声速值, 选取结果如表 2所示。
| 序号 | 平均分层声速梯度 | 深度/m | 声速/(m·s–1) | |
| 1 | 区域1 | 0.320 | 23 | 1 526.734 |
| 区域2 | 0.150 | 394 | 1 507.895 | |
| 2 | 区域1 | 0.317 | 22 | 1 526.586 |
| 区域2 | 0.150 | 393 | 1 507.774 | |
| 3 | 区域1 | 0.315 | 24 | 1 526.444 |
| 区域2 | 0.150 | 392 | 1 507.650 | |
| 4 | 区域1 | 0.306 | 21 | 1 526.305 |
| 区域2 | 0.150 | 395 | 1 507.523 | |
| 5 | 区域1 | 0.301 | 25 | 1 526.170 |
| 区域2 | 0.149 | 391 | 1 507.392 |
选取表 2提取的声速值计算重构系数矩阵, 进而重构全海深声速剖面。两个实验海域内声速剖面的重构结果如图 6所示, 重构误差如图 7所示, 区域1的均方根误差为0.514 m/s, 区域2的均方根误差为0.609 m/s。可以看出: 重构声速剖面与实测声速剖面整体符合程度较好; 在两个区域的浅层部分, 尤其是区域1的100 m深度附近和区域2的350 m深度附近, 重构声速剖面与实测声速剖面有明显出入, 这可能是由于只选取了前几阶的EOF空间函数进行重构, 部分阶次的EOF空间函数并不能包含测区声速场的全部信息, 造成了部分信息的损失, 因而出现了一定的偏差。此外, 以500 m水深作为分界, 深层部分的声速剖面重构结果较为稳定, 整体的重构误差较小; 浅层部分的声速剖面重构结果相比较差, 造成该现象的原因可能是浅层部分的海水包含混合层和主跃层, 海洋要素在其中的变化情况复杂, 而在深层海水中已趋于稳定。
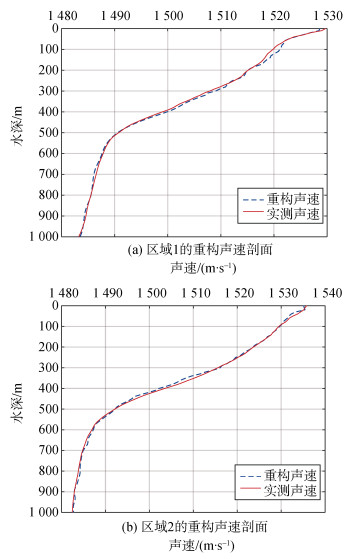 |
| 图 6 重构的声速剖面 Fig. 6 Reconstructed SSP |
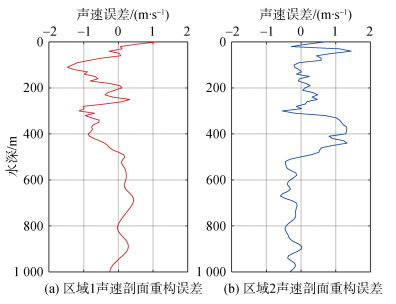 |
| 图 7 声速剖面重构误差 Fig. 7 Error of reconstructed SSP |
在多波束测深中, 利用EOF重构的声速剖面最终都要应用于声线改正。因此对于利用重构的声速剖面进行声线改正能否满足实际应用的要求, 还需要作进一步的检验。美国国家海洋与大气局(national oceanic and atmospheric administration, NOAA)对声速剖面引起的水深误差规定[20]: “若使用的声速剖面与实际声速剖面对测深改正造成的互差超过0.25%水深则视为超限”。本文实验以NOAA的测深限差作为检验声速剖面重构精度的标准, 并结合有效波束比来判断利用EOF重构声速剖面的有效性。设置水深和波束的初始入射角, 基于实测声速剖面, 分层常梯度声线跟踪波束的往返时间, 利用该时间与重构的声速剖面再通过分层常梯度声线跟踪法反算水深, 并与真实水深值进行对比, 比较两者差值是否满足0.25%水深限差, 最后统计有效波束比。
表 3为使用两则区域重构的声速剖面进行多波束测深的结果, 可以看出, 使用重构的声速剖面进行声速改正得到的各波束点水深均符合限差要求, 有效波束比均达到了100%。
| 实验区域 | 最大偏差/m | 有效波束比/% |
| 区域1 | 1.791 | 100 |
| 区域2 | 1.480 | 100 |
本文对重构全海深声速剖面所需实测数据的采样深度进行了研究, 实验证明在对历史声速剖面资料进行分析后, 按照K阶EOF函数方差累计贡献率大于95%, 选取K个最大平均分层声速梯度处的声速值作为已知值, 重构的声速剖面能够满足NOAA对多波束测量声速剖面造成的误差要求, 为实际测量作业中声剖数据的采样深度提供了参考, 提高了工作效率。由于海洋声速易受各种环境复杂性的影响, 因此其他海区的选取阶次及深度会有所不同, 但本文介绍的方法和所得规律性结论具有一定的普适性。
| [1] |
赵建虎. 现代海洋测绘[M]. 武汉: 武汉大学出版社, 2012. ZHAO Jianhu. Modern ocean mapping[M]. Wuhan: Wuhan University Press, 2012. |
| [2] |
刘伯胜, 雷家煜, 刘波声. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010. LIU Bosheng, LEI Jiayu, LIU Bosheng. Hydroacoustics principle[M]. Harbin: Harbin Engineering University Press, 2010. |
| [3] |
赵建虎, 刘经南. 多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008. ZHAO Jianhu, LIU Jingnan. Multi-beam sounding and image data processing[M]. Wuhan: Wuhan University Press, 2008. |
| [4] |
张启国, 陈献, 刘强. 远海多波束水深测量中声速剖面获取方法研究[J]. 海洋测绘, 2019, 39(5): 1-4. ZHANG Qiguo, CHEN Xian, LIU Qiang. Research on the method of the sound speed profile acquisition in deep sea multi-beam sounding[J]. Hydrographic Surveying and Charting, 2019, 39(5): 1-4. DOI:10.3969/j.issn.1671-3044.2019.05.001 |
| [5] |
DAVIS R E. Predictability of sea surface temperature and sea level pressure anomalies over the North Pacific Ocean[J]. J.phys.oceanogr, 1976, 6(3): 249-266. DOI:10.1175/1520-0485(1976)006<0249:POSSTA>2.0.CO;2 |
| [6] |
孙文川, 暴景阳, 金绍华, 等. 声速剖面EOF表示对多波束水深数据的影响研究[J]. 海洋测绘, 2014, 34(6): 21-24. SUN Wenchuan, BAO Jingyang, JIN Shaohua, et al. Study on the effect of sound velocity profile EOF on multi-beam water depth data[J]. Hydrographic Surveying and Charting, 2014, 34(6): 21-24. DOI:10.3969/j.issn.1671-3044.2014.06.005 |
| [7] |
张志伟, 暴景阳, 林建炬. 多波束测量声速剖面EOF表示阶次选取研究[J]. 海洋测绘, 2017, 37(5): 17-21. ZHANG Zhiwei, BAO Jingyang, LIN Jianju. Multi-beam measurement sound velocity profile EOF for order selection study[J]. Hydrographic Surveying and Charting, 2017, 37(5): 17-21. DOI:10.3969/j.issn.1671-3044.2017.05.003 |
| [8] |
张镇迈, 李整林, 戴琼兴. 利用有限深度声速数据重构全海深声速剖面[J]. 声学技术, 2008, 27(5): 106-107. ZHANG Zhenmai, LI Zhenglin, DAI Qiongxing. Sound speed profile reconstruction from the data measured in a limit depth[J]. Technical Acoustics, 2008, 27(2): 106-107. |
| [9] |
张孝首, 周兴华, 唐秋华, 等. EOF重构声速剖面对深水多波束的声速改正分析[J]. 海岸工程, 2020, 39(1): 34-43. ZHANG Xiaoshou, ZHOU Xinghua, TANG Qiuhua, et al. Analysis on correction of deep water multi-beam sound velocity profiles reconstructed by EOF[J]. Coastal Engineering, 2020, 39(01): 34-43. |
| [10] |
李洪超, 赵柯柯, 师军良. 基于EOF的ARGO浮标声速剖面重构[J]. 黄河水利职业技术学院学报, 2017, 29(2): 32-35. LI Hongchao, ZHAO Keke, SHI Junliang. Modeling three-dimensional acoustic field in the ocean by using Argo and EOF[J]. Journal of Yellow River Conservancy Technical Institute, 2017, 29(2): 32-35. |
| [11] |
张维, 黄益旺, 王延意, 等. 利用残缺样本声速重构声速剖面[J]. 声学技术, 2012, 31(4): 371-374. ZHANG Wei, HUANG Yiwang, WANG Yanyi, et al. Sound speed profile reconstruction from incomplete sample data[J]. Technical Acoustics, 2012, 31(4): 371-374. DOI:10.3969/j.issn.1000-3630.2012.04.006 |
| [12] |
丁继胜, 周兴华, 唐秋华, 等. 多波束勘测声速剖面场的EOF表示方法[J]. 武汉大学学报·信息科学版, 2007, 32(5): 446-449. DING Jisheng, ZHOU Xinghua, TANG Qiuhua, et al. Expression of multi-beam echo sounding sound velocity profile with empirical orthogonal functions[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 446-449. |
| [13] |
黄辰虎, 周丰年, 申家双, 等. 全球海域最优声速计算模型的综合选定(二): 精度分析及实际应用[J]. 海洋测绘, 2016, 36(4): 16-20, 30. HUANG Chenhu, ZHOU Fengnian, SHEN Jiashuang, et al. Selection of optimal sound velocity model in the global ocean, Part Ⅱ: Pricision analysis and its application[J]. Hydrographic Surveying and Charting, 2016, 36(4): 16-20, 30. |
| [14] |
吴碧, 陈长安, 林龙. 多种声速经验公式的比较分析研究[J]. 声学技术, 2013, 32(5): 296-298. WU Bi, CHEN Chang-an, LIN Long. Research and comparison of multiple empirical equations for sound velocity[J]. Technical Acoustics, 2013, 32: 32. |
| [15] |
谢骏, 胡均川, 笪良龙, 等. 浅海声速剖面自动分类方法研究[J]. 海洋通报, 2009, 28(3): 76-80. XIE Jun, HU Junchuan, DA Lianglong, et al. Study on automatic classification methodology of sound speed profile in the shallow sea[J]. Marine Science Bulletin, 2009, 28(3): 76-80. |
| [16] |
张伟涛, 张韧, 王辉瓒, 等. 基于Argo观测资料的南海北部海域声速场时空特征分析[J]. 海洋通报, 2013, 32(3): 275-280. ZHANG Weitao, ZHANG Ren, WANG Huizan, et al. Temporal and spatial characteristics of sound velocity field in the northern South China Sea based on Argo observation data[J]. Marine Science Bulletin, 2013, 32(3): 275-280. |
| [17] |
朱小辰. 多波束测深数据处理关键模型及应用研究[D]. 大连: 海军大连舰艇学院, 2011. ZHU Xiaochen. Research on key model and application of multi-beam sounding data processing[D]. Dalian: Naval Dalian Ship Academy, 2011. |
| [18] |
王辉赞, 张韧, 王桂华, 等. 全球Argo浮标剖面观测资料质量再控制数据集用户手册. 2010. 15. WANG Huizan, ZHANG Ren, WANG Guihua, et al. User manual for global Argo buoy profile observation data quality control dataset. 2010. 15. |
| [19] |
CHEN C T. Speed of sound in seawater at high pressures[J]. Acoustical Society of America Journal, 1977, 62(5): 1129-1135. |
| [20] |
NOAA. NOS Hydrographic Surveys Specifications and Deliverables[S]. 1999.
|
 2021, Vol. 45
2021, Vol. 45


