文章信息
- 杨蒙召, 曹奕, 袁红春, 史经伟. 2022.
- YANG Meng-zhao, CAO Yi, YUAN Hong-chun, SHI Jing-wei. 2022.
- 捕食者不同目标策略下的鱼群结构变化仿真与研究
- Simulation of the variation of fish shoal structure under different target selection strategies by predators
- 海洋科学, 46(12): 191-200
- Marine Sciences, 46(12): 191-200.
- http://dx.doi.org/10.11759/hykx20220331002
-
文章历史
- 收稿日期:2022-03-31
- 修回日期:2022-07-13
群体运动是大自然中常见的一种现象, 即大量个体同步移动、转变方向或是改变形状时, 整个群体犹如单一实体一般连贯地移动。它体现在许多生物或非生物群体的行为中, 例如迁徙中的候鸟, 会按照固定队形编成队列, 为了在长途跋涉中尽量减少个体的能量消耗; 又如海洋中的鱼群, 在觅食或游动时会以群体为单位行动, 以混淆捕食者和分散个体所遭遇风险[1, 2]。
群体运动的机理在过去几十年中已经由统计物理学给出解释, 简单来讲是由大量相似单元的互相作用而产生[3]。由REYNOLDS[4]于1987年提出的Boid模型或许是最早广为人知的、在计算机上模拟的群体运动模型; 另有VICSEK[3]提出一种统计物理类型的群集模型, 添加扰动以研究群体运动不同的状态; COUZIN等[5-6]在REYNOLDS的Boid模型进一步优化细节, 为3条规则划分了具体的区域边界。有实验证明3个区域大小的变化会导致鱼群出现不同的状态。过去十几年有不少学者都以Boid模型为基础进行研究, 包括对模型进行扩展优化[7-8], 提出拓扑距离增强群体凝聚力[9], 对原理进行更进一步的探索[10-11], 探讨领导者存在及其功能[12]。Boid模型在模拟鸟群或鱼群上有良好的表现。
捕食者与猎物鱼群的交互是生物系统巧妙平衡的体现, 有研究推测验证了这一系统的平衡有界性[2], 即保证鱼群不会数量骤减也保证捕食者不会因食物不足而消失。在捕食者如何攻击鱼群的研究上, 一些研究者着重于研究鱼群受攻击时的形态变化, 在计算机中模拟并揭示了鱼群受攻击前、过程中和受攻击后的不同群体状态[13]; 另一类发表的研究方法是在观察真实捕猎行为时记录每条鱼的位置信息, 然后在计算机中重现用以计算速度、方向等数据, 用以探究捕食者和鱼群真实的行为方式[14-16]。前者的研究方法着重于形态研究, 并未涉及到行为产生的原因, 后者的研究更加贴近于真实, 然而若是推广到大数量鱼群则所需计算量巨大。故本文更倾向于在模拟环境中进行可能的行为理论猜想与验证。NISHIMURA[17]是率先在模拟环境中研究捕食者目标选择策略的学者, 他提出使用3种不同方法给群体内个体分配优先数, 一段时间内优先数最大的个体被选定为目标, 根据结果评判方法的优劣; 之后DEMŠAR等[1]也发表了相关方面的研究, 与NISHIMURA的不同之处在于使用模糊规则和以视觉感知建立目标选择模型。
NISHIMURA[17]和DEMŠAR[1]两位学者的实验结果分别是通过单位时间内捕获猎物的平均数量和捕获单个猎物的平均时间来判断策略好坏, 在单捕食者场景下结论可靠, 然而若是在多捕食者场景下则不然。通过观察和他人实验验证得出的结论是海洋中高级捕食者往往是合作捕食, 以破坏鱼群结构为阶段性目标, 以此来提升整体捕获率[18]。作者从多捕食者合作捕食的整体效果角度出发, 在单捕食者场景下以鱼群结构被影响程度作为目标策略优劣判断标准, 这同时也可以为研究多捕食者目标策略做铺垫。
作者首先构建鱼群行为模型, 建模捕食者目标选择策略, 设定鱼群的关键参数, 通过不同条件下实验并分析不同策略的有效性, 得出策略的优劣。
1 鱼群行为模型的构建REYNOLDS[4]最早在计算机中实现了对鸟群的模拟, 提出经典的3条行为规则, 即近距离排斥、中距离排列和远距离吸引, 当所有个体都遵循此规则运动时, 模拟结果就非常贴近于真实鸟群行为, 称其为博得(Boid)模型。此模型中个体行为相对简单, 多个个体的行为密集相互作用形成群体, 适用于其他拥有类似特性的自然生物群体, 包括鱼群和陆地动物群等。本文所使用鱼群行为模型基于此模型构建。
本文所使用鱼群模型的思想是将连续的时间分割为离散的时间步, 当前时间步内个体与其周围不同区域内的邻居交互将决定其下一个时间步的前进方向和行进速度。此模型要求每个个体都可以访问群体内所有其他个体的位置、前进方向和速度信息, 与捕食者交互时也要求获得捕食者的相关信息。COUZIN等[5]为Boid模型的3条规则划分了具体的区域边界, 此处给出3区域示意图, 如图 1所示, 图 1中zor表示排斥区域, zoo表示排列区域, zoa代表吸引区域, 3个区域互不重叠。鱼类的视觉盲区也标识在图上,
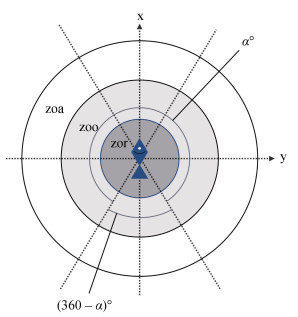 |
| 图 1 以个体为原点的3区域示意图 Fig. 1 Diagram of three regions with a single individual as the origin. |
实验在三维虚拟环境中开展, 设定鱼群中个体的数量N(i=1, 2, …, N), 个体基本属性包括位置ci和单位方向向量
| $ \begin{aligned} \overrightarrow{\boldsymbol{d}}_{\boldsymbol{i}}(\boldsymbol{t}+\boldsymbol{\tau})= & \lambda_r * \overrightarrow{\boldsymbol{D}}_{\boldsymbol{r}}(\boldsymbol{t}+\boldsymbol{\tau})+\lambda_o * \overrightarrow{\boldsymbol{D}}_{\boldsymbol{o}}(\boldsymbol{t}+\boldsymbol{\tau})+ \\ & \lambda_a * \overrightarrow{\boldsymbol{D}}_ \mathit{\boldsymbol{a}}(\boldsymbol{t}+\boldsymbol{\tau})+\lambda_{t g} * \overrightarrow{\boldsymbol{D}}_{\mathit{\boldsymbol{tg}}}(\boldsymbol{t}+\boldsymbol{\tau})+ \\ & \lambda_{a c} * \overrightarrow{\boldsymbol{D}}_{\mathit{\boldsymbol{ac}}}(\boldsymbol{t}+\boldsymbol{\tau})+\lambda_{a p} * \overrightarrow{\boldsymbol{D}}_{\mathit{\boldsymbol{ap}}}(\boldsymbol{t}+\boldsymbol{\tau}), \end{aligned} $ | (1) |
公式(1)中的每一个子项都是系数
| $ \vec{\mathit{\boldsymbol{D}}}_{\boldsymbol{x}}(\boldsymbol{t}+\boldsymbol{\tau})=\frac{\vec{\mathit{\boldsymbol{d}}}_ \mathit{\boldsymbol{x}}(\boldsymbol{t}+\boldsymbol{\tau})}{\left|\vec{\mathit{\boldsymbol{d}}}_ \mathit{\boldsymbol{x}}(\boldsymbol{t}+\boldsymbol{\tau})\right|} * { MaxSpeed }-\overrightarrow{\boldsymbol{d}}_{\boldsymbol{i}}(\boldsymbol{t}), $ | (2) |
经过公式(2)分解后, 产生的差向量将直接作用于个体, 其与个体当前行进方向的合力将会是原始分向量, 若直接将原始分向量作用于个体, 则会产生方向偏差。由方向向量
| $\begin{array}{*{20}{c}} {{\vec {\mathit{\boldsymbol{v}}}_ \mathit{\boldsymbol{i}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) = \frac{{{{\vec {\mathit{\boldsymbol{d}}}}_ \mathit{\boldsymbol{i}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right)}}{{\left| {{{\vec {\mathit{\boldsymbol{d}}}}_ \mathit{\boldsymbol{i}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right)} \right|}} ,}\\ {{c}_{i}\left(t+\tau \right)= {c}_{i}\left(t\right)+{\overrightarrow{\mathit{\boldsymbol{d}}}}_{\mathit{\boldsymbol{i}}}\left(\mathit{\boldsymbol{t}}+\mathit{\boldsymbol{\tau}} \right)*\tau .} \end{array}$ | (3) |
排斥区域规定为以个体为中心点, 半径为rr的圆形区域, 此区域遵循第一条规则“近距离排斥”, 意为这是个体的安全区域, 若有任何其他邻居出现, 则会尝试朝反方向躲避它们, 这是为了维持个体间的最小距离, 使用公式(4)计算排斥向量,
| $ {\vec {\mathit{\boldsymbol{d}}}_ \mathit{\boldsymbol{r}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) = - \mathop \sum \limits_{j \ne i}^{{n_r}} \frac{{{{\vec {\mathit{\boldsymbol{r}}}}_{\mathit{\boldsymbol{ij}}}}\left( \mathit{\boldsymbol{t}} \right)}}{{\left| {{{\vec {\mathit{\boldsymbol{r}}}}_{\mathit{\boldsymbol{ij}}}}\left( \mathit{\boldsymbol{t}} \right)} \right|}}, $ | (4) |
公式(4)中
排列区域规定为环绕在排斥区域周围的一圈环形区域, 环宽为ro。此区域遵循第二条规则“中距离排列”, 意为个体会尝试调整行进方向以对齐其他在此区域内的邻居, 为了维持群体的一致连贯性, 使用公式(5)计算排列向量。
| $ {\vec {\mathit{\boldsymbol{d}}}_ \mathit{\boldsymbol{o}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) = \mathop \sum \limits_{j = 1}^{{n_o}} \frac{{{{\vec {\mathit{\boldsymbol{v}}}}_ \mathit{\boldsymbol{i}}}\left( \mathit{\boldsymbol{t}} \right)}}{{\left| {{{\vec {\mathit{\boldsymbol{v}}}}_ \mathit{\boldsymbol{i}}}\left( \mathit{\boldsymbol{t}} \right)} \right|}} . $ | (5) |
吸引区域规定为整个区域的最外圈的环形区域, 环宽为ra。此区域遵循第3条规则“远距离吸引”, 吸引力是维持群体避免分裂的重要规则, 所以此吸引力指的是其他邻居对此个体的吸引力, 它会尝试靠近其他在吸引区的邻居, 使用公式(6)计算吸引向量。
| $ {\vec {\mathit{\boldsymbol{d}}}_ \mathit{\boldsymbol{a}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) = \mathop \sum \limits_{j \ne i}^{{n_a}} \frac{{{{\vec {\mathit{\boldsymbol{r}}}}_{\mathit{\boldsymbol{ij}}}}\left( \mathit{\boldsymbol{t}} \right)}}{{\left| {{{\vec {\mathit{\boldsymbol{r}}}}_{\mathit{\boldsymbol{ij}}}}\left( \mathit{\boldsymbol{t}} \right)} \right|}}. $ | (6) |
以上3条规则是原始Boid模型所包含的, 然而为了模拟与捕食者或障碍交互, 添加以下规则, 分别是围绕目标、躲避障碍和躲避捕食者。
围绕目标规则是为鱼群设定目标点, 以模拟鱼群盘旋在栖息地, 也是为了便于捕食者选择目标, 设目标点的位置为ctarget, 使用公式(7)计算目标点向量。
| $ {\vec {\mathit{\boldsymbol{d}}}_{\mathit{\boldsymbol{tg}}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) = {c_{{\rm{target}}}} - {c_i}. $ | (7) |
其次是躲避障碍, 为了避免碰撞水中的天然障碍物或是地形边界, 需要转变方向, 这里产生躲避障碍分量的方法是以个体为原点, 以一定密度向世界坐标(世界坐标是定义物理世界的客观坐标, 而以物体中心为原点, 物体朝向为轴的坐标称为本地坐标)的正前方射出射线, 找到和当前行进方向夹角最小的那条作为躲避障碍向量
躲避捕食者规则需要鱼群个体在感知到鲨鱼时, 立刻朝个体与捕食者连接方向的反方向行进, 设捕食者的位置为cp使用公式(8)计算躲避捕食者向量。
| $ {\vec {\mathit{\boldsymbol{d}}}_{\mathit{\boldsymbol{ap}}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) = {c_p} - {c_i}. $ | (8) |
捕食者的基本属性包括位置cp, 单位方向向量
| $ {\vec {\mathit{\boldsymbol{d}}}_ \mathit{\boldsymbol{p}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) = {\lambda _{pac}}*{\vec {\mathit{\boldsymbol{D}}}_{\mathit{\boldsymbol{pac}}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right) + {\lambda _{ptg}}*{\vec {\mathit{\boldsymbol{D}}}_{\mathit{\boldsymbol{ptg}}}}\left( {\mathit{\boldsymbol{t}} + \mathit{\boldsymbol{\tau}} } \right), $ | (9) |
公式(9)中所有方向分量也是经由公式(2)分解后的差向量。基本属性更新方式和躲避障碍规则都与鱼群模型一致, 不再赘述。
此处在NISHIMURA的基础上改进并提出3种可能的目标选择策略: 选择最近个体、选择鱼群中心个体和选择最外围个体。已有多篇论文提出采用第一种策略的捕食者会被鱼群所混淆, 第二种策略模仿捕食者攻击鱼群中心以希望捕获猎物[1], 第3种策略已有许多论文提出了与之相关的观察结果[17]。每种策略会根据鱼群和捕食者的位置、方向和速度分别为鱼群个体分配优先数, 优先数最大的个体会被选择为目标。所选目标在一段时间内是合理的, 然而随着鱼群自然游动, 个体与鱼群的相对位置会发生改变, 故设置时间间隔T以及时更换目标。
策略N: 以鱼群内个体与捕食者的距离为优先数(nearest), 优先函数如公式(10)所示,
| $ {p_i} = - \left| {{c_i} - {c_p}} \right|, $ | (10) |
式中,
策略C: 以鱼群质心为原点, 个体与质心的距离为优先数(most centrical), 优先函数如公式(11)所示,
| $ {p_i} = - \left| {{c_i} - {c_{{\rm{group}}}}} \right|, $ | (11) |
| $ {c_{{\rm{group}}}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^n {c_i}, $ | (12) |
公式(11)中, cgroup表示鱼群质心点, 然而因程序设定所有个体质量相等, 故质心等于中心, cgroup也为鱼群中心点, 使用公式(12)计算其值。
策略P: 选择最外围的目标策略(Most peripheral), 此策略思想较为复杂, 此处给出示意图(图 2)加以说明, 同时优先函数如公式(13)所示,
| $ {p_i} = - \left| {\vec {\mathit{\boldsymbol{c}}}_{\mathit{\boldsymbol{i}}}^\mathit{\boldsymbol{g}} - \beta {M_{j \ne i}}\left( {\left| {\vec {\mathit{\boldsymbol{c}}}_{\mathit{\boldsymbol{j}}}^\mathit{\boldsymbol{g}}} \right|} \right)\frac{{\vec {\mathit{\boldsymbol{c}}}_{\mathit{\boldsymbol{p}}}^\mathit{\boldsymbol{g}}}}{{\left| {\vec {\mathit{\boldsymbol{c}}}_{\mathit{\boldsymbol{p}}}^\mathit{\boldsymbol{g}}} \right|}}} \right|, $ | (13) |
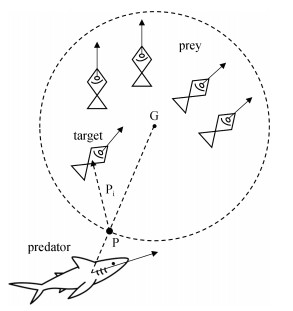 |
| 图 2 “最外围”目标选择策略示意图 Fig. 2 Diagram of "the most peripheral" target selection strategy |
公式(13)中,
鱼群行为模型和捕食者模型中的具体参数参照表 1和表 2, 其具体数值参考了多篇论文[4, 13-14]及多次实验后得出。
| 参数名 | 单位 | 符号 | 值 |
| 猎物长度 | 无量纲 | BL (Body Length) | 3 |
| 排斥区域半径 | 无量纲 | rr | 3 |
| 排列区域环宽 | 无量纲 | ro | 3 |
| 吸引区域环宽 | 无量纲 | ra | 3 |
| 猎物感知范围半径 | 无量纲 | rr+ro+ra | 9 |
| 猎物视角范围 | 度 | α | 300 |
| 猎物最小速度 | 无量纲 | minSpeed | 5 |
| 猎物最大速度 | 无量纲 | maxSpeed | 8 |
| 排斥向量系数 | 无量纲 | λr | 1 |
| 排列向量系数 | 无量纲 | λo | 1 |
| 吸引向量系数 | 无量纲 | λa | 1 |
| 目标向量系数 | 无量纲 | λtg | 1 |
| 躲避障碍向量系数 | 无量纲 | λac | 5 |
| 躲避捕食者向量系数 | 无量纲 | λap | 2 |
| 时间间隔 | 秒 | τ | 1/30 |
| 注: 汇总鱼群行为模型中的参数, “单位”的使用与模型中某些参数的无量纲有关, 表 2同 | |||
| 参数名 | 单位 | 符号 | 值 |
| 捕食者体长 | 无量纲 | PBL | 15 |
| 捕食者视角范围 | 度 | α | 300 |
| 捕食者最小速度 | 无量纲 | minSpeedP | 8 |
| 捕食者最大速度 | 无量纲 | maxSpeedP | 14 |
| 躲避障碍向量系数 | 无量纲 | λpac | 8 |
| 追踪目标向量系数 | 无量纲 | λptg | 1 |
| 策略P系数 | 无量纲 | β | 1 |
为了记录捕食者对鱼群攻击前后鱼群结构的变化, 使用3个关键参数记录鱼群信息, 用以对程序模拟结果进行分析。引入群体极化程度Pgroup (polarization, 定义域[0-1]), 如公式14所示; 群体角动量Mgroup(angular momentum), 如公式15所示。
| $ {P_{{\rm{group}}}}\left( t \right) = \frac{1}{N}\left| {\mathop \sum \limits_{i = 1}^N {{\vec {\mathit{\boldsymbol{v}}}}_{\mathit{\boldsymbol{i}}}}\left( \mathit{\boldsymbol{t}} \right)} \right|, $ | (14) |
| $ {M_{{\rm{group}}}}\left( t \right) = \frac{1}{N}\left| {\mathop \sum \limits_{i = 1}^N \vec {\mathit{\boldsymbol{c}}}_{\mathit{\boldsymbol{i}}}^\mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{t}} \right) \times {{\vec {\mathit{\boldsymbol{v}}}}_{\mathit{\boldsymbol{i}}}}\left( \mathit{\boldsymbol{t}} \right)} \right|, $ | (15) |
公式(15)中的
第3个参数为群体尺寸σ (FlockSize), 如公式16所示,
| $ \sigma \left( t \right) = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^N {{\left| {\vec {\mathit{\boldsymbol{c}}}_{\mathit{\boldsymbol{i}}}^\mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{t}} \right)} \right|}^2}}}{N}} , $ | (16) |
公式(16)中的
本文实验使用基于windows10平台的三维编辑软件Unity, 编辑器版本号为2019.4.29f1, 编程语言为C#。所用电脑配置为处理器R5-4600H, 内存16G, 显卡为处理器核心显卡RX Vega 6。
在虚拟环境中设定100×100×50的封闭立方体地形, 鱼群出生点在地形正中心, 捕食者实例化在偏边界。程序开始运行时优先生成鱼群, 为确保捕食者攻击前鱼群处于稳定状态, 5 s后再生成捕食者。每次运行程序30 s, 以每3帧即每秒十次的频率记录鱼群与捕食者的位置、方向、速度信息。分别在捕食者选择3种策略及鱼群数量规模为100、200和300时运行程序各5次, 记录所生成数据及录制影片。实验在控制变量的前提下运行多次以确保记录到的数据具有普遍性, 并辅以运行时画面以合理解读数据。
4 仿真实现与结果分析 4.1 无捕食者与目标策略P的效果对比与分析此实验在无捕食者与捕食者使用目标策略P的条件下开展, 目的是说明参数的具体意义以及展现捕食者对鱼群的影响。在鱼群数量规模为200、使用目标选择策略P、时长30 s的条件下收集到鱼群尺寸变化曲线及对应的极化程度Pgroup和群体角动量Mgroup (图 3a、3b), 同时对比无捕食者情况下鱼群自然游动的尺寸变化曲线。鱼群于0 s时在一定范围内以随机位置、随机方向生成, 因此0~5 s的前半段鱼群成混乱状态, 对应于图 3a、3b和3c中的0秒开始曲线上扬的部分, 之后鱼群达到稳定, 曲线趋于平缓。
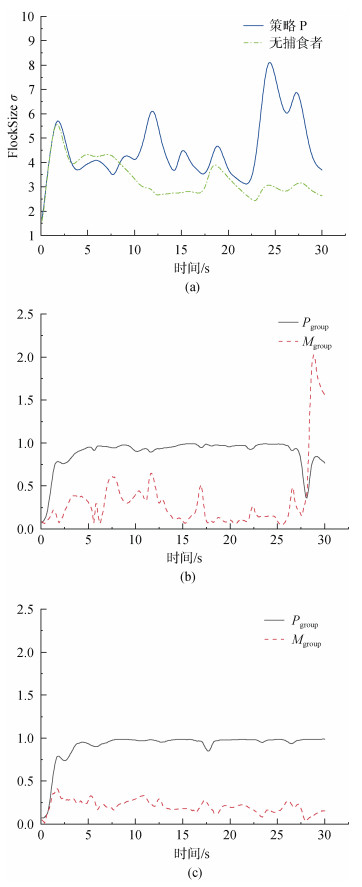 |
| 图 3 群体三种特征曲线图 Fig. 3 Curves of three flock characteristic 注: a. 策略P和无捕食者下群体尺寸曲线; b. 策略P下Pgroup和Mgroup曲线; c. 无捕食者下Pgroup和Mgroup曲线 |
图 3a中策略P的σ曲线相比于无捕食者σ曲线波折程度更大, 有多个突起较高的波峰, 这些波峰对应于视频中鱼群躲避地形边界或是被攻击后散开的行为。策略P的σ曲线中第22.5~30秒内有较大的凸起, 对应捕食者在这期间对鱼群发起的连续两次攻击, 如图 4所示, 其中黄色箭头代表鱼群的大致方向, 红色箭头代表捕食者的大致方向。
 |
| 图 4 捕食者攻击鱼群过程图 Fig. 4 Diagram of a predator attacking fish shoals 注: 红色鱼为被选中的目标; a~c. 第一次攻击过程; d~f. 第二次攻击过程 |
捕食者选定目标后从鱼群后方发起攻击, 鱼群随之朝四周散开, 之后在捕食者后方再聚集, 此为第一次攻击; 捕食者转向之后从鱼群左后方再度攻击, 接着鱼群再次散开、在捕食者后方聚集, 此为第二次攻击。观察图 3b中此时间段的曲线, Pgroup直线下降, 由22.5 s处的0.98下降最多至0.35, 这表示鱼群由方向高度一致转变为较为分散; Mgroup由22.5 s处的0.21先下降至0.04又快速上升至26.6 s处的0.48, 鱼群由稳定状态下的缓慢转向-发现捕食者后的全力向前逃逸-被捕食者突入中心后分散, 此反应常被描述为“喷泉效应”[18], 这对应于第一次攻击。之后又重复了下降-快速上升的过程, 这次Mgroup上升得十分迅速并达到高峰, 鱼群在混乱状态时受到第二次攻击致使其混乱程度更甚。
观察图 3a中无捕食者σ曲线, 在17 s处开始有一低波峰, 对应处的Pgroup曲线略有下降, Mgroup曲线略有上升, 观察视频对应处鱼群正处于地形边界, 做出转向行为, 这与各曲线的变化吻合, 如图 5所示, 其中黄色箭头代表鱼群的大致方向。
 |
| 图 5 鱼群避障过程图 Fig. 5 Diagram of fish shoals avoiding an obstacle 注: a~c. 鱼群遇到地形边界后转向 |
此实验将探讨3种目标选择策略的有效性。在鱼群数量规模200, 捕食者使用3种不同目标选择策略, 时长30 s的条件下各运行5次, 根据所记录数据绘制成群体尺寸变化图和其AUC图(area under curve, 曲线下面积), 如图 6所示, 图 6中N, C, P分别是策略N、策略C和策略P的缩写。
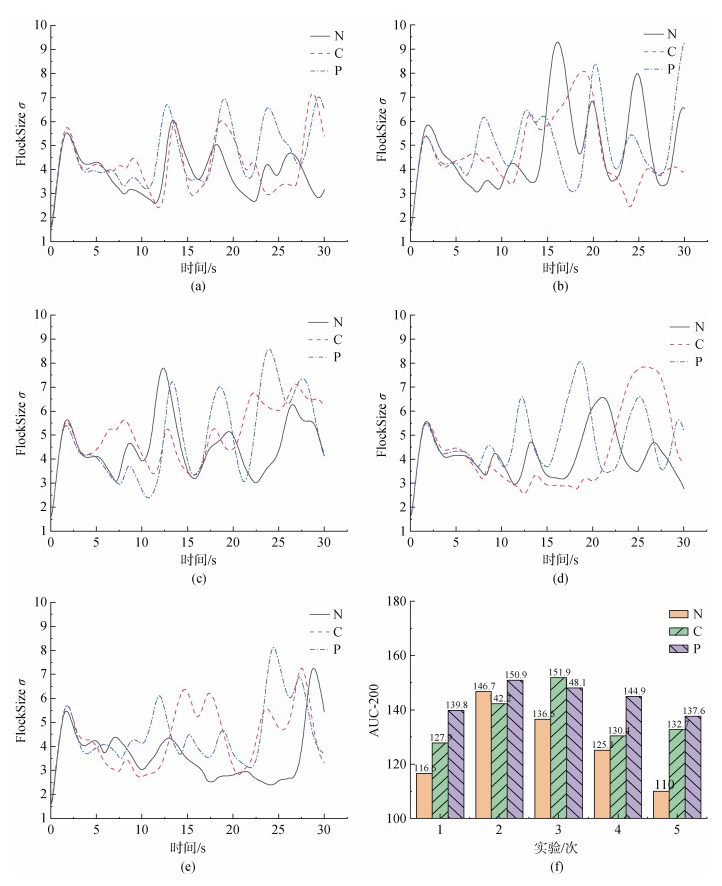 |
| 图 6 鱼群信息图 Fig. 6 Diagram of fish schoals' info 注: a~e. 5次实验群体尺寸曲线图; f. 5次实验AUC对比柱状图 |
由4.1得出, 较高的波峰是由捕食者攻击所致, 而较低的波峰是由鱼群躲避障碍转向所致。图 6f显示, 3种目标选择策略中策略P的效果在5次实验中的4次是最高的, 平均比策略N高14.4%, 平均比策略C高5.9%, 代表其在30 s内对鱼群尺寸的影响是最大的; 策略C次之, 在5次实验中的4次是第二高的, 平均比策略N高8.5%; 策略N往往是最低的。
观察图 6a~6f(此分析在去除0~5 s内鱼群混乱的初始状态导致的高波峰下, 以影响鱼群尺寸大小为攻击评价标准), 策略P的曲线基本每次都出现3个较高的波峰, 代表捕食者每次实验都会发动3次较为有效的攻击; 策略C有时会出现1个高波峰, 有时会出现两到3个较高波峰, 这表示捕食者会发动一次非常有效的攻击或是两三次较为有效的攻击; 策略N出现波峰的次数基本也在3次左右, 然而往往只有一到两个波峰是较高的, 这代表捕食者发动攻击时的效果并不都很理想, 出现类似第2次实验中的整体高效攻击的概率是比较小的。因此判断使用策略P是三者之中对鱼群尺寸影响最大的。
4.3 不同鱼群规模下3种目标选择策略效果对比与分析在证明了策略P对于200数量规模的鱼群是最有效的之后, 应当探讨对于不同规模的鱼群是否有普遍性的结论。此实验在鱼群数量规模分别为100、200和300, 捕食者使用3种不同目标选择策略, 分别在30 s内运行5次, 根据所记录数据绘制AUC柱状对比图, 如图 7所示。
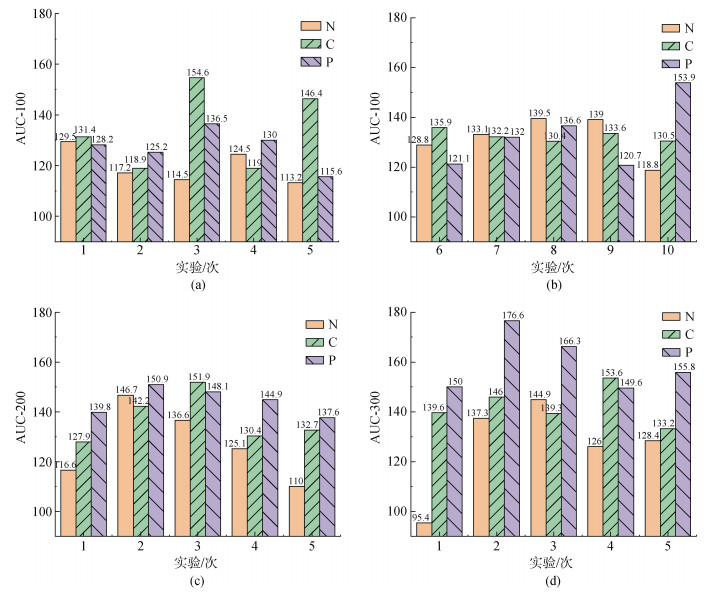 |
| 图 7 3种策略AUC对比柱状图 Fig. 7 Histograms of the AUC comparison of the three strategies 注: a, b. 100鱼群数量规模实验结果柱状图; c. 200鱼群数量规模下实验结果柱状图; d. 300鱼群数量规模下实验结果柱状图 |
观察图 7c和7d可知, 对于200和300数量规模的鱼群, 策略P的柱体5次中4次是最高的, 分别平均比策略N高14.4%和28.1%, 分别平均比策略C高5.9%和13.2%, 其效果依然是最佳的, 在图 7d的结果中显现出的效果甚至有与其他策略进一步拉开差距的趋势; 对于100数量规模的鱼群, 则有不同的表现(因前5次实验并未显示出明显的规律, 故另增加5次实验, 共10次)。观察图 7a和7b, 3种策略的柱体最高的次数不相上下, 并且以平均值来看也未出现7c和7d中明显的数值差距, 这表明它们的效果总体相当。此现象的一种解释是小规模鱼群应对风险的能力较低[2, 17]。群体规模越大, 群体警惕性越高, 会引起捕食者的混淆效应, 即在选择和追踪目标时困惑。无论捕食者使用何种策略, 小规模鱼群都无法使捕食者混淆, 因此3种策略的效果相当。
5 结论本文对鱼群行为模型进行构建; 提出3种捕食者目标选择策略并为其建模, 3种目标策略分别为: 选择最近个体、选择鱼群中心个体和选择最外围个体; 设定了3种描述鱼群的关键参数。以影响鱼群结构的程度作为评判标准, 开展了3类不同实验。首先比较捕食者使用策略P与无捕食者条件下鱼群结构变化, 分析得出群体尺寸变化曲线中高波峰对应捕食者攻击, 低波峰对应于鱼群避障转向, 并验证了捕食者存在会对鱼群结构产生较大影响; 其次在实验中对比了3种目标选择策略的优劣, 得出策略P效果是最优的; 最后在实验中探究3种策略在3种不同数量规模鱼群中的表现, 在200和300数量级鱼群中策略P仍是最优异的, 在100数量级鱼群中3种策略则有着相当的表现, 原因在于小规模鱼群应对风险的能力不足, 无法体现策略的优劣。
捕食者捕获猎物鱼群是大自然中常见的现象, 目前可探究的方向包括多捕食者与鱼群交互、不同鱼群竞争资源又或是两种状况叠加[19], 自然界中的情况往往更加复杂多变。如何在虚拟环境中重现这一景象具有较大的研究价值, 这涉及多方面的知识。本文对于单捕食者策略影响鱼群结构的研究是前期研究中的一部分, 可为多捕食者合作捕猎的研究做铺垫。日后可以在此基础上拓展研究多种策略搭配分割鱼群、提升整体捕食效率等问题。
| [1] |
DEMŠAR J, LEBAR BAJEC I. Simulated predator attacks on flocks: a comparison of tactics[J]. Artificial Life, 2014, 20(3): 343-359. DOI:10.1162/ARTL_a_00135 |
| [2] |
MANNA D, MAITI A, SAMANTA G. Analysis of a predator-prey model for exploited fish populations with schooling behavior[J]. Applied Mathematics and Computation, 2018, 317: 35-48. DOI:10.1016/j.amc.2017.08.052 |
| [3] |
VICSEK T. Universal patterns of collective motion from minimal models of flocking[C]//2008 second IEEE winternational conference on self-adaptive and self-organizing systems. Venice, Italy: IEEE, 2008: 3-11.
|
| [4] |
REYNOLDS C W. Flocks, herds and schools: A distributed behavioral model[C]//Proceedings of the 14th annual conference on computer graphics and interactive techniques. NewYork, United States: ACM, 1987: 25-34.
|
| [5] |
COUZIN I D, KRAUSE J, JAMES R, et al. Collective memory and spatial sorting in animal groups[J]. Journal of Theoretical Biology, 2002, 218(1): 1-11. DOI:10.1006/jtbi.2002.3065 |
| [6] |
WANG W, ESCOBEDO R, SANCHEZ S, et al. The impact of individual perceptual and cognitive factors on collective states in a data-driven fish school model[J]. PLOS Computational Biology, 2022, 18(3): e1009437. DOI:10.1371/journal.pcbi.1009437 |
| [7] |
HERBERT-READ J E, PERNA A, MANN R P, et al. Inferring the rules of interaction of shoaling fish[J]. Proceedings of the National Academy of Sciences, 2011, 108(46): 18726-18731. DOI:10.1073/pnas.1109355108 |
| [8] |
KAWABAYASHI H, CHEN Y W. Interactive system of artificial fish school based on the extended boid model[C]//2008 international conference on intelligent information hiding and multimedia signal processing. Venice, Italy: IEEE, 2008: 721-724.
|
| [9] |
BALLERINI M, CABIBBO N, CANDELIER R, et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study[J]. Proceedings of the National Academy of Sciences, 2008, 105(4): 1232-1237. DOI:10.1073/pnas.0711437105 |
| [10] |
CALOVI D S, LOPEZ U, SCHUHMACHER P, et al. Collective response to perturbations in a data-driven fish school model[J]. Journal of The Royal Society Interface, 2015, 12(104): 20141362. DOI:10.1098/rsif.2014.1362 |
| [11] |
LIU Y, ZHOU Q. Study on group motion based on Boids model[C]//2019 Chinese control conference (CCC). Venice, Italy: IEEE, 2019: 6275-6280.
|
| [12] |
COUZIN I D, KRAUSE J, FRANKS N R, et al. Effective leadership and decision-making in animal groups on the move[J]. Nature, 2005, 433(7025): 513-516. DOI:10.1038/nature03236 |
| [13] |
LEE S H, PAK H, CHON T S. Dynamics of prey-flock escaping behavior in response to predator's attack[J]. Journal of Theoretical Biology, 2006, 240(2): 250-259. DOI:10.1016/j.jtbi.2005.09.009 |
| [14] |
ROMENSKYY M, HERBERT-READ J E, IOANNOU C C, et al. Quantifying the structure and dynamics of fish shoals under predation threat in three dimensions[J]. Behavioral Ecology, 2020, 31(2): 311-321. DOI:10.1093/beheco/arz197 |
| [15] |
ASTARLOA A, LOUZAO M, BOYRA G, et al. Identifying main interactions in marine predator–prey networks of the Bay of Biscay[J]. ICES Journal of Marine Science, 2019, 76(7): 2247-2259. DOI:10.1093/icesjms/fsz140 |
| [16] |
MITCHELL M D, HARBORNE A R. Non-consumptive effects in fish predator–prey interactions on coral reefs[J]. Coral Reefs, 2020, 39(4): 867-884. DOI:10.1007/s00338-020-01920-y |
| [17] |
NISHIMURA S I. A predator's selection of an individual prey from a group[J]. Biosystems, 2002, 65(1): 25-35. DOI:10.1016/S0303-2647(01)00191-5 |
| [18] |
HANDEGARD N O, BOSWELL K M, IOANNOU C C, et al. The dynamics of coordinated group hunting and collective information transfer among schooling prey[J]. Current Biology, 2012, 22(13): 1213-1217. DOI:10.1016/j.cub.2012.04.050 |
| [19] |
AGMOUR I, ACHTAICH N, FOUTAYENI Y. Stability analysis of a competing fish populations model with the presence of a predator[J]. International Journal of Nonlinear Science, 2018, 26(2): 108-121. |
 2022, Vol. 46
2022, Vol. 46


