文章信息
- 孔敏, 王风帆, 耿姗姗, 余佳, 舒雨婷. 2023.
- KONG Min, WANG Feng-fan, GENG Shan-shan, YU Jia, SHU Yu-ting. 2023.
- 模糊层次分析法在浅剖数据质量评价中的应用
- Application of fuzzy analytic hierarchy process in the quality evaluation of sub-bottom profile data
- 海洋科学, 47(10): 65-75
- Marine Sciences, 47(10): 65-75.
- http://dx.doi.org/10.11759/hykx20220728003
-
文章历史
- 收稿日期:2022-07-28
- 修回日期:2023-02-20
海底浅地层剖面(sub-bottom profile)测量是一种基于声学原理的连续走航式探测地球物理方法, 可获取高分辨率海底浅部地层结构、构造及海底地形地貌信息[1-2], 在海洋地质研究[3-6]、海底地貌识别[7]、海底地质灾害[7-8]、海底资源勘探[9-10]及海洋工程勘查[11-12]中发挥了重要作用。针对浅剖数据的采集、处理、应用等方面, 国内外学者[13-16]已开展了多角度的研究, 但对于数据质量评价的研究较少, 尤其缺少系统的评价指标及定量化评价方法。浅剖数据的质量评价目前主要依赖人为主观经验评价, 这导致评价结果以定性评价为主、主观性强, 另外对于数据用户的知识经验要求也比较高, 不利于数据统一的质量分级及针对性地推广应用。构建统一的评价指标体系可以规范数据质量评价流程, 客观定量的评价结果可以为数据的分级管理、合理利用提供参考依据, 使得数据用户快速、全面地了解数据的质量情况, 提高数据的管理及应用效率。层次分析法(Analytic Hierarchy Process, AHP)是一种重要的多准则决策(Multi-criteria Decision Making, MCDM)技术[17], 是一种定性定量相结合的、系统的、层次化的分析方法。该方法最早由SATTY[18-19]提出, 主要通过构建基于复杂问题相互影响关系的模型来将问题转化为简单形式来解决, 适用于对难以完全定量的复杂事件进行综合评价。该方法的原理是根据问题的性质和要达到的目标, 将问题分解为不同的影响因素, 并按照因素间相互影响以及隶属关系将因素按不同的层次聚集组合, 形成一个多层次的分析结构模型, 从而最终使问题归结为最低层(方案层)相对于最高层(目标层)的相对重要权值的确定或相对优劣次序的排定。首先将待评估目标划分成多层次指标体系, 并确定每一层次的指标, 然后通过定性结合定量的方式获取各个指标的权重, 最后进行综合评价。层次分析法可以将人们的决策经验运用到决策中, 通过利用一定的标准对定量指标与定性指标、可见指标与不可见指标等进行共同的测量。该方法能够将决策问题过程当中的定性指标与定量指标实行有效地结合。
模糊层次分析法是对传统层次分析法的扩展, 该方法是结合了层次分析法及模糊数学的一种综合评价技术, 允许在层次分析法中适当地表示主观偏好比较, 由此产生的模糊层次分析法适用于处理涉及主观性决策的不确定性问题, 在战略决策[20]、风险评估[21-22]、资源预测[23-25]、生态评价[26]等方面得到了广泛的应用。
本文将层次分析法应用于浅剖数据质量评价模型的构建, 结合德尔菲法及模糊评价法, 建立了两层的数据评价指标, 确定了不同层次评价指标的权重, 为浅剖数据质量评价提供了一种可行客观的评价模型。
1 方法与流程模糊层次分析法考虑了定性和定量决策标准, 适用于需要结合专家意见的数据质量评价工作, 本文采用的模糊层次分析法主要分为以下几个步骤, 具体见图 1。
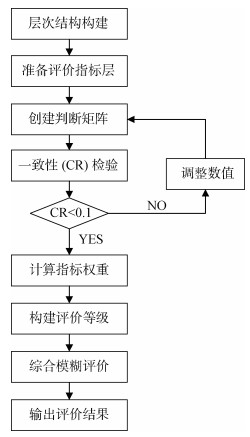 |
| 图 1 模糊层次分析法流程图 Fig. 1 Fuzzy AHP flowchart |
1) 构建层次结构
根据研究目标, 建立层次结构, 包括目标层、准则层和方案层。
2) 准备评价指标层
根据目标层, 确定准则层及方案层的具体内容。本文中的目标层即浅剖数据质量评价, 准则层为评价浅剖数据质量的一级指标, 方案层为评价浅剖数据质量的二级指标。
3) 创建判断矩阵
构建准则层、目标层的两两判断矩阵。根据9度法[23]进行填写, 具体见表 1。
| 标度aij | 定义 |
| 1 | i因素与j因素同等重要 |
| 3 | i因素比j因素略微重要 |
| 5 | i因素比j因素较为重要 |
| 7 | i因素比j因素非常重要 |
| 9 | i因素比j因素绝对重要 |
| 2, 4, 6, 8 | 为以上前后两级之间对应的标度值 |
| 倒数 | 若j因素与i因素比较, 得到的判断值为aji=1/aij |
4) 一致性检验
成对的两两判断矩阵具有一定的人为因素, 并具有相应的主观性, 构建的矩阵大多数情况下不具有完全的一致性[19-20, 24], 需要对判断矩阵的一致性检验, 来判断矩阵的可信程度, 具体可根据一致性比率(CR)进行检验, 具体计算公式:
| $ CR = \frac{{CI}}{{RI}} = \frac{{\left( {{\lambda _{\max }} - n} \right)/\left( {n - 1} \right)}}{{RI}} , $ | (1) |
CI为随机一致性指标, RI为平均随机一致性指标, λmax为矩阵最大特征值, n为矩阵阶数, 其中RI与矩阵阶数相关, 具体值选取可参考表, 本文仅选取了7阶以内的RI值展示。
| n | RI |
| 1, 2 | 0 |
| 3 | 0.52 |
| 4 | 0.89 |
| 5 | 1.12 |
| 6 | 1.26 |
| 7 | 1.36 |
若CR < 0.1, 则说明两两一致性通过检验, 如果CR≥0.1, 则说明没通过一致性检验, 需要重新调整矩阵。
5) 计算指标权重
对各层的指标权重进行归一化计算。
6) 综合模糊评价
通过归一化权指标权重与模糊评价矩阵的乘积计算得到模糊评价向量, 综合所有因素, 计算评价结果。
2 评价模型构建 2.1 指标选取指标选取是进行数据质量评价的第一步, 按层次筛选能够全面反映海洋浅剖数据质量的指标。本文按照层次分析法的原理, 首先确定评价海洋浅剖数据质量(目标层)的一级指标(准则层), 然后确定可对一级指标评价的二级指标(方案层)。浅剖数据质量的直观表现是剖面图像, 首先确定剖面图像质量为一级指标, 高质量的浅地层剖面数据与采集环境及后处理过程也是息息相关, 因此本文将数据测量信息及处理加工信息确定为另外两个一级指标, 本文选取的3个一级指标覆盖了对外业采集阶段、数据处理阶段及最后成果的评价。根据每个一级指标的特征, 选取了相应的二级指标。
1) 数据测量信息, 描述数据相关的外业测量信息, 从测量信息来对数据质量进行评价, 主要包括测线布设、时间信息、定位信息、采样间隔、航速、测量仪器、环境条件等6项二级指标。其中, 测线布设评价要素包括测线布设走向、测线长度、测线间距、有无交叉点; 时间信息评价要素包括时间信息有无、是否存在错误记录; 定位信息评价要素包括定位信息有无、是否存在错误记录; 采样间隔评价要素包括数据项有无、间隔大小; 航速评价要素包括航速稳定性、航速大小; 测量仪器评价要素包括仪器与水深及底质等海底条件的适应性以及仪器参数设置的合理性; 环境条件评价要素包括调查区水深及实时海况条件等。
2) 处理加工信息, 描述数据后处理信息, 从处理信息来对数据质量进行评价, 包括处理后的格式、处理程度、处理说明信息等3个二级指标。其中, 处理后的格式评价要素包括是否为SEGY格式; 处理程度评价要素包括是否对浅剖数据进行了多次波压制、滤波、增益等关键步骤的处理; 处理说明信息评价要素包括是否提供了数据的处理说明。
3) 剖面图像质量, 描述剖面图像的可视化质量, 该项是浅剖数据质量最直观的评价标准, 包括穿透深度、垂直分辨率、水平分辨率、信噪比等4项二级指标。其中, 穿透深度评价要素包括剖面的最大穿透深度; 垂直分辨率、水平分辨率评价指标包括剖面垂直向和水平向最大的分辨率, 信噪比评价指标包括剖面有效信息与噪声信息的比值。评价模型见图 2。
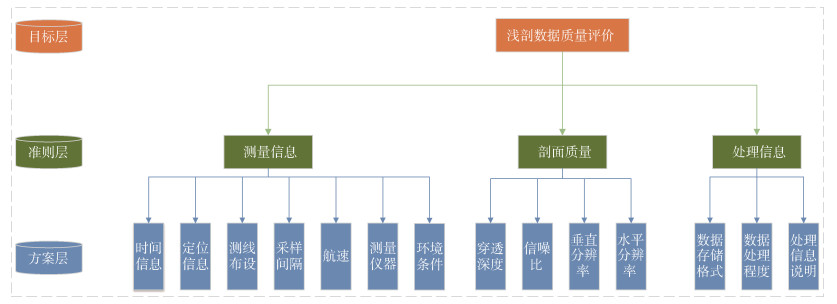 |
| 图 2 浅剖数据质量评价模型 Fig. 2 Model for evaluating the quality of sub-bottom profile data |
本文针对目标层, 构建了一级指标两两判断矩阵共4个, 本文结合德尔菲法, 选取3位专家进行了两两判断矩阵的构建, 构建方式采用9度法, 具体见表 3。
| 测量信息 | 剖面质量 | 处理信息 | |
| 测量信息 | 1, 1, 1 | 1, 4/5, 3/4 | 2, 2.5, 1.5 |
| 剖面质量 | 1, 5/4, 4/3 | 1, 1, 1 | 2, 2.5, 2 |
| 处理信息 | 1/2, 2/5, 2/3 | 1/2, 2/5, 1/2 | 1, 1, 1 |
经计算, 一级指标三者均通过了一致性检验, 3位专家的一致性结果分别为0, 0.005 3, 0。本文综合了3位专家的判断矩阵结果, 赋予3位专家同等权重, 应用算术平均法, 计算得到一级指标判断矩阵, 经对判断矩阵按列归一化处理后得到每个指标的权重值, 具体见表 4。
| 测量信息 | 剖面质量 | 处理信息 | |
| 测量信息 | 1 | 0.850 0 | 2 |
| 剖面图像 | 1.194 4 | 1 | 2.166 7 |
| 处理信息 | 0.522 2 | 0.466 7 | 1 |
该3阶矩阵一致性检验结果为0.023 1, CR < 0.1, 符合一致性要求, 对该矩阵进行按列归一化处理后得到以下矩阵:
| $ A = \left[ {\begin{array}{*{20}{c}} {0.368\;1}&{0.366\;9}&{0.387\;1} \\ {0.439\;7}&{0.431\;6}&{0.419\;4} \\ {0.192\;2}&{0.201\;5}&{0.193\;5} \end{array}} \right] , $ | (2) |
将矩阵按行相加得到行向量
| $ {W_i} = {R_i}/\sum\limits_{j = 1}^n {{R_i}} , $ | (3) |
计算得知Wi={0.374 0, 0.430 2, 0.195 8}, i=1, 2, 3, 测量信息、剖面图像与处理信息在数据质量评价中的权重分别为0.374 0, 0.430 2, 0.195 8, 从这个结果来看, 剖面图像质量是评价海洋浅剖数据质量最重要的指标, 这一步将定性专家经验定量化, 是知识驱动的一个重要应用[23-24]。
2.3 二级指标判断矩阵构建与一级指标判断矩阵构建方式相同, 对每个一级指标下的二级指标进行判断矩阵构建及计算, 同样根据9度标法, 采用德尔菲法选取3位专家进行两两判断矩阵的构建, 一致性结果见表 5, 均小于0.1, 对专家矩阵结果进行同等权重赋值后, 计算得到各二级指标的模糊评价矩阵。
| 测量信息 | 剖面质量 | 处理信息 | |
| 专家1 | 0.017 7 | 0.022 8 | 0.008 9 |
| 专家2 | 0.026 7 | 0 | 0 |
| 专家3 | 0.016 4 | 0.003 9 | 0.008 9 |
1) 测量信息判断矩阵结果
经测量信息为7阶矩阵(表 6), 其中矩阵最大特征值为7.282 7, 经计算CR值为0.034 6, 符合一致性检验。各指标权重经归一化处理后见表 6, 其中定位信息权重最高为0.221 2, 其次分别为环境条件、测线布设、航速与测量仪器, 时间信息权重最低。
| 时间信息 | 定位信息 | 采样间隔 | 测线布设 | 航速 | 测量仪器 | 环境条件 | Wi | |
| 时间信息 | 1 | 0.444 4 | 0.833 3 | 0.611 1 | 0.555 6 | 0.722 2 | 0.555 6 | 0.086 9 |
| 定位信息 | 2.500 0 | 1 | 2.333 3 | 1.500 0 | 1.666 7 | 1.166 7 | 2 | 0.221 2 |
| 采样间隔 | 1.333 3 | 0.444 4 | 1 | 0.888 9 | 0.666 7 | 0.888 9 | 0.555 6 | 0.104 4 |
| 测线布设 | 2 | 0.722 2 | 1.388 9 | 1 | 1.055 6 | 1 | 1 | 0.147 5 |
| 航速 | 1.833 3 | 0.666 7 | 1.666 7 | 1.055 6 | 1 | 1 | 0.777 8 | 0.143 2 |
| 测量仪器 | 1.500 0 | 0.888 9 | 1.166 7 | 1 | 1.222 2 | 1 | 1 | 0.146 7 |
| 环境条件 | 1.833 3 | 0.500 0 | 1.833 3 | 1 | 1.333 3 | 1 | 1 | 0.150 1 |
2) 剖面质量判断矩阵结果
剖面质量为4阶矩阵(表 7), 矩阵最大特征值为4.109 8, CR值为0.041 1, 符合一致性检验。各指标权重经归一化处理后见表 7, 其中垂直分辨率权重最高为0.335 8, 其次分别为穿透深度、信噪比及水平分辨率。这个结果与浅剖调查特征是较为吻合的, 浅剖仪特征之一就是垂直分辨率高。
| 穿透深度 | 信噪比 | 垂直分辨率 | 水平分辨率 | Wi | |
| 穿透深度 | 1 | 1.500 0 | 0.833 3 | 1.5 | 0.276 8 |
| 信噪比 | 0.722 2 | 1 | 0.611 1 | 1.333 3 | 0.207 5 |
| 垂直分辨率 | 1.333 3 | 1.666 7 | 1 | 1.833 3 | 0.335 8 |
| 水平分辨率 | 0.722 2 | 0.833 3 | 0.555 6 | 1 | 0.179 9 |
3) 处理信息判断矩阵结果
处理信息为3阶矩阵(表 8), 矩阵最大特征值为3.010 2, CR值为0.009 9, 符合一致性检验。各指标权重经归一化处理后见表 8, 其中处理后格式权重最高为0.540 7, 其次分别为处理程度、处理信息说明。这个结果与浅剖数据格式多样化特征是相关的, 目前不同浅剖仪自记式格式较多, 目前通用的格式包括SEGY、XTF等, 如果获取的数据集记录格式不通用, 会大大影响数据的应用范围, 有可能数据获得者根本无法读取数据, 所以数据格式对于数据的质量也是一个明显的影响指标。
| 处理后格式 | 处理程度 | 处理信息说明 | Wi | |
| 处理后格式 | 1 | 2 | 3 | 0.540 7 |
| 处理程度 | 0.5 | 1 | 1.833 3 | 0.289 4 |
| 处理信息说明 | 0.333 3 | 0.555 6 | 1 | 0.169 8 |
通过2.3的计算, 获取了二级指标针对一级指标的权重, 为实现通过二级指标对数据质量评价, 需要进一步计算二级指标对于目标层的权重, 计算公式见公式(4):
| $ W_{合成}=W_{二级}×W_{一级}.$ | (4) |
| 一级指标 | 权重 | 二级指标 | 权重 | 合成权重 |
| 测量信息 | 0.374 0 | 时间信息 | 0.086 9 | 0.032 5 |
| 定位信息 | 0.221 2 | 0.082 7 | ||
| 采样间隔 | 0.104 4 | 0.039 0 | ||
| 测线布设 | 0.147 5 | 0.055 2 | ||
| 航速 | 0.143 2 | 0.053 6 | ||
| 测量仪器 | 0.146 7 | 0.054 9 | ||
| 环境条件 | 0.150 1 | 0.056 1 | ||
| 剖面质量 | 0.430 2 | 穿透深度 | 0.276 8 | 0.119 1 |
| 信噪比 | 0.207 5 | 0.089 3 | ||
| 垂直分辨率 | 0.335 8 | 0.144 4 | ||
| 水平分辨率 | 0.179 9 | 0.077 4 | ||
| 处理信息 | 0.195 8 | 处理后格式 | 0.540 7 | 0.105 9 |
| 处理程度 | 0.289 4 | 0.056 7 | ||
| 处理信息说明 | 0.169 8 | 0.033 2 |
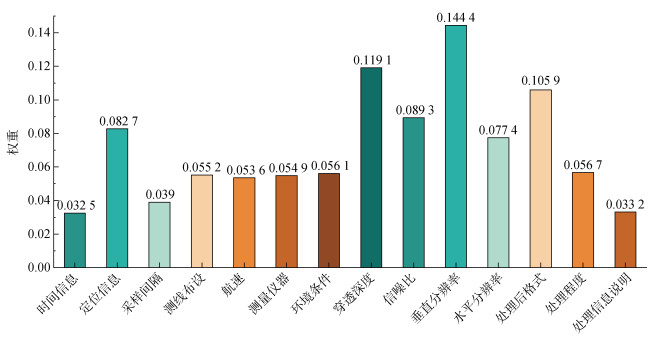 |
| 图 3 浅剖质量评价二级指标合成权重对比图 Fig. 3 Comparison of synthetic weights of secondary indicators for a quality evaluation of the sub-bottom profile data |
根据层次分析法结合德尔菲专家打分法计算获取了海洋浅剖数据各评价指标的权重, 即完成了评价因素集的构建, 见公式(5):
| $ U = \left\{ {\begin{array}{*{20}{c}} {{u_1}, }&{{u_2}, }&{ \cdots , }&{{u_n}} \end{array}} \right\}, \;n = 14 . $ | (5) |
进一步构建评价集, 见公式(6):
| $ V = \left\{ {\begin{array}{*{20}{c}} {{v_1}, }&{{v_2}, }&{ \cdots , }&{{v_m}} \end{array}} \right\}, \;m = 4 . $ | (6) |
本文对浅剖质量评价定为4级, m取值为4, 按照数据质量高低分别为Ⅰ级, Ⅱ级, Ⅲ级, Ⅳ级, 可定性对应为优秀、良好、中等、差等4个级别。
从U到V的模糊映射为R, 即综合评判矩阵R, 见公式(7):
| $ R = \left[ {\begin{array}{*{20}{c}} {{R_1}} \\ {{R_2}} \\ \vdots \\ {{R_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1m}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2m}}} \\ \vdots & \vdots & \vdots & \vdots \\ {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nm}}} \end{array}} \right] , n=14, m=4, $ | (7) |
其中, rn表示un对vm的隶属度大小, 经上一步计算U中每个因素权重可以表示为W, 对应的模糊综合评价模型S可以表示为:
| $ \begin{array}{l} S{\text{ = }}W*R = \left\{ {\begin{array}{*{20}{c}} {{w_1}, }&{{w_2}, }&{ \cdots , }&{{w_n}} \end{array}} \right\}*\left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1m}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2m}}} \\ \vdots & \vdots & \vdots & \vdots \\ {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nm}}} \end{array}} \right] \\ = \left\{ {\begin{array}{*{20}{c}} {{s_1}, }&{{s_2}, }&{ \cdots , }&{{s_m}} \end{array}} \right\} \\ \end{array} , $ | (8) |
其中*表示模糊算法, 本文选取加权平均的算法。
最后根据最大隶属度原则, 确定数据质量等级, 即S最终评价结果为
本文选取的评价浅剖数据共2套, 分别来源于国际网站共享及国内调查, 其中第1套评价数据为美国NCEI(National Center of Environment Information, 国家环境信息中心)于2017年3月发布的浅剖数据, 测区名称为FS1601, 数据分布在马里亚纳海沟北部海域(图 4), 该区域海底地形特征复杂, 呈现出海岭海沟相间的地貌特征, 水深范围550~7 590 m, 该海域底质以深海沉积为主, 包括深海黏土及软泥, 数据集包括坐标数据和SEGY数据。第2套评价数据为国内近海专项调查数据, 数据分布在广东沿海, 海底地形总体上由岸向海倾斜, 比较平缓, 水深0~20 m, 底质类型以近岸粉砂质沉积为主, 数据集包括SEGY数据及相关调查处理报告。
 |
| 图 4 深海浅剖数据测线分布图 Fig. 4 Distribution map of the sub-bottom profile data survey line in a deep sea |
针对浅剖数据评级的指标可直接提取法、间接统计法、可视化成图法等三种方法进行获取。首先对SEGY数据进行道头信息解析, 自动提取存储在道头中的相关信息, 包括指标中的时间信息、定位信息、测量仪器、采样间隔、数据格式等, 其次根据前后相邻点的定位信息与时间拟合航速, 通过对定位数据可视化成图统计获取测线布设信息。穿透深度、垂直分辨率、空间分辨率、信噪比、处理程度等通过软件打开剖面图像并结合测量仪器的测量精度进行评估。
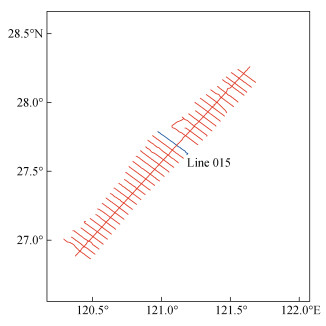 |
| 图 5 浅海浅剖数据测线分布图 Fig. 5 Distribution map of the sub-bottom profile data survey line in a shallow sea |
经指标提取与计算, 获取以下信息: 国际浅剖数据采集时间为2016年, 采样间隔138~368 ms; 定位信息齐全, 定位精度0.1 m; 测量仪器为Edgetech 3300, 采用全频谱技术, 最大作业海深可达7 000 m, 最大穿透深度80 m(黏土), 10 m(粗砂), 分辨率6~10 cm; 调查区平均水深3 578 m, 位于深海区; 调查时海况信息未知; 经计算该数据航速5.8~6.7 kn, 平均航速6.3 kn; 未提供处理说明。国内浅剖数据采集时间为2009年, 采样间隔为80 ms; 定位信息齐全, 定位精度1 m; 测量仪器为Geopulse Boomer, 最大穿透深度80 m, 地层分辨率0.3 m; 调查区平均水深小于20 m, 位于浅海区; 调查时海况良好; 调查航速5~6 kn; 具备详细的数据处理说明文件。
将经过提取的各指标信息及数据提供给专家进行质量评价定级, 其中关于剖面质量的评价需结合专家的主观经验, 专家依据本文设置的4个等级进行每个二类指标定级打分。
3.3 评价结果为保证对数据集质量评价的客观性, 本文选取了3位专家分别对两套浅剖数据进行评价打分, 并对3位专家的评价结果赋予同等权重。对评价结果应用2.5节给出的计算公式, 进行综合计算, 最后根据最大隶属度原则, 判定数据质量, 数据评价结果见表 10、表 11。
| 评价指标 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | 最大隶属度 |
| 时间信息 | 0.333 3 | 0.666 7 | 0.000 0 | 0.000 0 | 良好 |
| 定位信息 | 1.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 优秀 |
| 采样间隔 | 0.000 0 | 0.666 7 | 0.333 3 | 0.000 0 | 良好 |
| 测线布设 | 0.000 0 | 0.333 3 | 0.666 7 | 0.000 0 | 中等 |
| 航速 | 0.666 7 | 0.333 3 | 0.000 0 | 0.000 0 | 优秀 |
| 测量仪器 | 0.333 3 | 0.666 7 | 0.000 0 | 0.000 0 | 良好 |
| 环境条件 | 0.000 0 | 0.000 0 | 0.666 7 | 0.333 3 | 中等 |
| 穿透深度 | 0.000 0 | 0.333 3 | 0.666 7 | 0.000 0 | 中等 |
| 信噪比 | 0.000 0 | 1.000 0 | 0.000 0 | 0.000 0 | 良好 |
| 垂直分辨率 | 0.000 0 | 0.333 3 | 0.666 7 | 0.000 0 | 中等 |
| 水平分辨率 | 0.000 0 | 0.333 3 | 0.666 7 | 0.000 0 | 中等 |
| 处理后格式 | 0.666 7 | 0.333 3 | 0.000 0 | 0.000 0 | 优秀 |
| 处理程度 | 0.000 0 | 0.000 0 | 1.000 0 | 0.000 0 | 中等 |
| 处理信息说明 | 0.000 0 | 0.000 0 | 0.000 0 | 1.000 0 | 差 |
| 评价指标 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | 最大隶属度 |
| 时间信息 | 0.000 0 | 1.000 0 | 0.000 0 | 0.000 0 | 良好 |
| 定位信息 | 0.000 0 | 0.666 7 | 0.333 3 | 0.000 0 | 良好 |
| 采样间隔 | 0.000 0 | 1.000 0 | 0.000 0 | 0.000 0 | 良好 |
| 测线布设 | 0.666 7 | 0.333 3 | 0.000 0 | 0.000 0 | 优秀 |
| 航速 | 0.333 3 | 0.666 7 | 0.000 0 | 0.000 0 | 良好 |
| 测量仪器 | 0.333 3 | 0.333 3 | 0.333 3 | 0.000 0 | 优秀 |
| 环境条件 | 0.000 0 | 1.000 0 | 0.000 0 | 0.0000 | 良好 |
| 穿透深度 | 0.333 3 | 0.666 7 | 0.000 0 | 0.000 0 | 良好 |
| 信噪比 | 0.000 0 | 0.666 7 | 0.333 3 | 0.000 0 | 良好 |
| 垂直分辨率 | 1.000 0 | 0.000 0 | 0.000 0 | 0.000 0 | 优秀 |
| 水平分辨率 | 0.000 0 | 0.666 7 | 0.333 3 | 0.000 0 | 良好 |
| 处理后格式 | 0.333 3 | 0.666 7 | 0.000 0 | 0.000 0 | 良好 |
| 处理程度 | 0.000 0 | 1.000 0 | 0.000 0 | 0.000 0 | 良好 |
| 处理信息说明 | 0.000 0 | 0.000 0 | 1.000 0 | 0.000 0 | 中等 |
经模糊综合评价, 国际深海浅剖数据集的V={0.218 1, 0.358 7, 0.371 2, 0.052 0}, 最大隶属度为Ⅲ级, 通过模糊评价综合评定该数据质量为中等。国内近海浅剖数据集V={0.292 4, 0.573 0, 0.134 6, 0}, 最大隶属度为Ⅱ级, 通过模糊评价综合评定该数据质量为良好。
3.4 结果分析 3.4.1 国际深海浅剖数据评价结果通过本文构建的模糊层次分析法评价模型, 国际深海浅剖数据集综合评价为中等, 根据表 10的每项指标的综合评价结果可以看出, 最大隶属度为优秀、良好的指标主要集中在外业测量信息, 这说明该数据采集时选用的仪器合理, 外业采集过程操作标准, 尤其是航速, 全程控制在6 kn左右, 保障了高质量数据剖面的采集, 但处理程度及最终的剖面成果质量相关指标主要集中在中等与良好之间, 这说明网站共享的这套数据集一方面未开展较好的内业处理, 导致展示的剖面质量不高, 图 6显示存在剖面一定的绕射波, 进一步说明了内业处理程度不够。另外说明深海海域数据由于水深的影响, 即使外业调查工作做得很好, 质量较高的数据获取难度仍较大。
 |
| 图 6 深海浅剖数据剖面图(Line 422) Fig. 6 Sub-bottom data profile in a deep sea (Line 422) |
国内浅海浅剖数据集综合评价为良好, 根据表 11的每项指标的综合评价结果可以看出, 该数据集大部分指标的评价结果等级为良好或优秀, 说明该区域的环境条件、外业采用的仪器、航速控制等保障了数据采集的质量, 另外从剖面的评价结果来看, 数据的内业处理程度也比较高, 从图 7中可以看出, 该数据的最大穿透深度超过100 m, 地层反射界面清晰, 图中展示的垂向分辨率、信噪比等均与评价结果有较高的一致性, 这也反映了本文构建的质量评价模型具有良好的客观性。
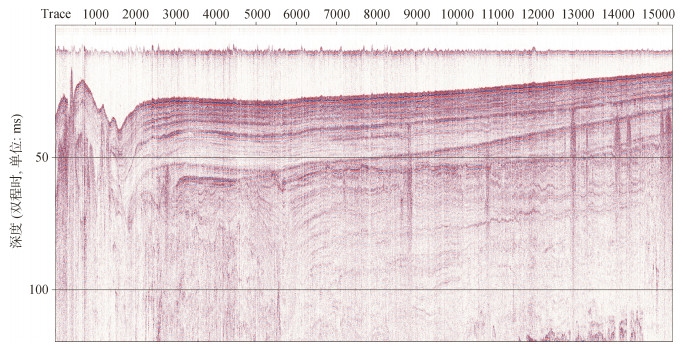 |
| 图 7 浅海浅剖数据剖面图(Line 015) Fig. 7 Sub-bottom data profile in a shallow sea (Line 015) |
模糊层次分析法构建的分层评价指标既能给出客观的定量评价结果, 又可根据评价结果倒推影响数据质量的主要因素, 对于后续数据的应用提供了很好的信息支撑。通过对本文获取的不同来源数据集的质量评价结果, 建议后续对国际深海数据进一步处理, 会更好地提升剖面质量及总体数据质量, 有利于数据的应用。
4 结束语海洋浅剖数据由于具有的采集仪器安装方便、工作效率高、垂直分辨率高等优势, 目前的海洋科考船普遍安装了浅剖仪, 获取了大量的浅剖数据, 但由于数据调查、处理时采用的标准、设置的参数不同, 导致形成的数据集质量参差不齐, 亟需对不同数据集进行质量评价, 以便于数据的后期应用。本文综合了浅剖数据测量、处理及成果剖面图等多方面信息, 构建的基于模糊层次分析法数据质量评价模型, 将以往主要依靠人工经验开展的浅剖数据质量评价工作分解到每个具体的指标项, 具有更好的可操作性, 同时也降低了评价结果的主观性与片面性, 在浅剖数据质量定量评价中得到了较好的应用。针对该模型得到以下几点结论:
(1) 从本文质量评价模型的各评价指标权重来看, 虽然剖面质量是最重要的评价指标, 但外业测量、环境条件、内业处理都会影响浅剖数据的质量, 数据质量评价需考虑多方面因素。
(2) 模糊层次分析评价模型将专家主观经验以知识驱动的形式转成定量化评价指标, 分层多角度的数据质量评价可有效降低因个人主观因素影响和片面性导致的结论误差, 同时有助于全面分析数据质量影响因素。
(3) 本文给出的质量评价模型在不同水深条件下浅剖数据的质量评价中得到了较好的应用, 可以较客观地给出数据质量等级, 为后期数据应用作参考。
(4) 在评价指标分级中进一步细化等级并给予赋分, 可以提升模型评价的定量化程度, 在使用该方法进行数据质量评价时, 可根据需要进行模型等级的定量优化。
| [1] |
刘保华, 丁继胜, 裴彦良, 等. 海洋地球物理探测技术及其在近海工程中的应用[J]. 海洋科学进展, 2005, 23(3): 374-384. LIU Baohua, DING Jisheng, PEI Yanliang, et al. Marine Geophysical Survey Techniques and Their Applications to offshore Engineering[J]. Advances in Marine Science, 2005, 23(3): 374-384. |
| [2] |
杨国明, 朱俊江, 赵冬冬, 等. 浅地层剖面探测技术及应用[J]. 海洋科学, 2021, 45(6): 147-162. YANG Guoming, ZHU Junjiang, ZHAO Dongdong, et al. Development and application of sub-bottom profiler technologies[J]. Marine Sciences, 2021, 45(6): 147-162. |
| [3] |
刘玉萍, 丁龙翔, 杨志成, 等. 利用浅剖资料进行海底底质分析[J]. 物探与化探, 2016, 40(1): 66-72. LIU Yuping, DING Longxiang, YANG Zhicheng, et al. Seabed sediment analysis using sub-bottom profile data[J]. Geophysical and Geochemical Exploration, 2016, 40(1): 66-72. |
| [4] |
方中华, 李攀峰, 杨源, 等. 菲律宾海深水环境下浅地层沉积特征分析[J]. 海洋学报, 2022, 44(3): 53-60. FANG Zhonghua, LI Panfeng, YANG Yuan, et al. Analysis on sedimentary characteristics of shallow strata in deep water environment of Philippine Sea[J]. Haiyang Xuebao, 2022, 44(3): 53-60. |
| [5] |
倪玉根, 夏真, 马胜中. 浅地层剖面揭示琼州海峡的形成时代[J]. 海洋地质与第四纪地质, 2014, 34(4): 79-82. NI Yugen, XIA Zhen, MA Shengzhong. The Opening of Qiongzhou Strait: Evidence from Sub-bottom Profiles[J]. Marine Geology & Quaternary Geology, 2014, 34(4): 79-82. |
| [6] |
沈浩杰. 东海大陆架南缘海域地层声学剖面及地质解释[J]. 沉积学报, 1999, 17(1): 78-83. SHEN Haojie. Sub-bottom profiling and its geological interpretation on the southern margin of continental shelf of the East China Sea[J]. Acta Sedimentologica Sinica, 1999, 17(1): 78-83. |
| [7] |
冯京. 基于高分辨率声学探测的渤海海峡地貌及灾害地质研究[D]. 中国海洋大学, 2014. FENG Jing. Study on Geomorphological and Geohazards in Bohai Strait Based on High Resolution Acoustic Detection[D]. Ocean University of China, 2014. |
| [8] |
FRANCKY S A, KUUS P, BLASCO S, et al. Multiple failure styles related to shallow gas and fluid venting, upper slope Canadian Beaufort Sea, northern Canada[J]. Marine Geology, 2014, 355: 136-149. DOI:10.1016/j.margeo.2014.05.014 |
| [9] |
单晨晨, 邓希光, 温明明, 等. 参量阵浅地层剖面仪在海底羽状流探测中的应用——以ATLAS P70在马克兰海域调查为例[J]. 地球物理学进展, 2020, 35(3): 1183-1190. SHAN Chenchen, DENG Xiguang, WEN Mingming, et al. Application of parametric sub-bottom profile in gas plumes detection: ATLAS P70 in Makran area as an example[J]. Progress of Geophysics, 2020, 35(3): 1183-1190. |
| [10] |
刘伯然, 宋海斌, 关永贤, 等. 南海东北部陆坡冷泉系统的浅地层剖面特征与分析[J]. 地球物理学报, 2015, 58(1): 247-256. LIU Boran, SONG Haibin, GUAN Yongxian, et al. Characteristics and formation mechanism of cold seep system in the northeastern continental slope of South China Sea from sub-bottom profiler data[J]. Chinese Journal of Geophysics, 2015, 58(1): 247-256. |
| [11] |
李海东, 胡毅, 许江, 等. 浅地层剖面系统在福建沿海海底沉船调查中的应用[J]. 海洋技术学报, 2019, 38(1): 79-84. LI Haidong, HU Yi, XU Jiang, et al. Application of sub-bottom profilers in the investigation of seabed shipwreck in Fujian coastal waters[J]. Journal of Ocean Technology, 2019, 38(1): 79-84. |
| [12] |
胡梦涛, 蒋廷臣, 李佳琦, 等. 浅剖数据解译中淤泥层层界提取方法[J]. 测绘通报, 2017, 6: 72-76. HU Mengtao, JIANG Tingchen, LI Jiaqi, et al. The extraction method of silt boundary layer in sub-bottom profiler data interpretation[J]. Bulletin of Surveying and Mapping, 2017, 6: 72-76. |
| [13] |
HENKART P. Chirp sub-bottom profile processing-A review[J]. Sea Technology, 2006, 47(10): 35-38. |
| [14] |
李平, 杜军. 浅地层剖面探测综述[J]. 海洋通报, 2011, 30(3): 344-350. LI Ping, DU Jun. Review on the probing of sub-bottom profiler[J]. Marine Science Bulletin, 2011, 30(3): 344-350. |
| [15] |
冯强强, 温明明, 吴衡, 等. 海洋浅地层剖面资料的数据处理方法[J]. 海洋地质前沿, 2013, 29(11): 49-53, 66. FENG Qiangqiang, WEN Mingming, WU Heng, et al. Data processing methods for marine sub-bottom profiles[J]. Marine Geology Frontiers, 2013, 29(11): 49-53, 66. |
| [16] |
陶华, 李彦杰. 中浅地层剖面质量改进方法及应用[J]. 海洋技术学报, 2017, 36(5): 135-140. LAO Hua, LI Yanjie. Study on the Method and Application of Quality Improvement in Shallow Stratum Profile[J]. Journal of Ocean Technology, 2017, 36(5): 135-140. |
| [17] |
ZHOU K F, ZHANG N N. Mineral prospectivity mapping for Porphyry-type and hydrothermal vein-type copper deposits using fuzzy analytical hierarchy process and geographic information system[J]. Journal of Intelligent & Fuzzy Systems, 2016, 31(6): 3143-3153. |
| [18] |
SAATY T. The Analytic Hierarchy Process[M]. New York: McGraw-Hill, 1980: 287.
|
| [19] |
SAATY T. How to make a decision: the analytic hierarchy process[J]. Interfaces, 1994, 24(6): 19-43. DOI:10.1287/inte.24.6.19 |
| [20] |
CALABRESE A, COSTA R, LEVIALDI N, et al. Integrating sustainability into strategic decision-making: A fuzzy AHP method for the selection of relevant sustainability issues[J]. Technological Forecasting & Social Change, 2019, 155-168. |
| [21] |
张飞飞. 基于模糊网络层次分析法的海上风电项目风险评估研究[J]. 电力与能源, 2019, 40(4): 459-463. ZHANG Feifei. Research on risk assessment of offshore wind power projects based on fuzzy network analytic hierarchy process[J]. Power & Energy, 2019, 40(4): 459-463. |
| [22] |
徐兴路. 基于模糊层次分析法的水运工程质量风险分析与评估[J]. 中国水运, 2021(12): 36-38. XU Xinglu. Risk analysis and evaluation of water transport engineering quality based on fuzzy AHP[J]. China Water Transport, 2021(12): 36-38. |
| [23] |
PAZAND K, HEZARKHANI A, GHANBARI Y. Fuzzy analytical hierarchy process and GIS for predictive Cu porphyry potential mapping: a case study in Ahar–Arasbaran Zone (NW, Iran)[J]. Arabian Journal of Geosciences, 2014, 7(1): 241-251. DOI:10.1007/s12517-012-0774-4 |
| [24] |
马瑶, 赵江南, 廖时理. 模糊层次分析法在西南印度洋中脊46°E—52°E多金属硫化物远景区预测中的应用[J]. 地质科技通报, 2020, 39(6): 75-82. MA Yao, ZHAO Jiangnan, LIAO Shili. Application of fuzzy analytic hierarchy process to mineral prospectivity mapping of polymetallic sulfide deposits in the Southwest Indian ridge between 46° to 52°E[J]. Bulletin of Geological Science and Technology, 2020, 39(6): 75-82. |
| [25] |
SUVAM D, SHANTANU S, PRASANNA K D. GIS-based landslide susceptibility zonation mapping using the analytic hierarchy process (AHP) method in parts of Kalimpong Region of Darjeeling Himalaya[J]. Environmental Monitoring and Assessment, 2022, 194(3): 234. |
| [26] |
ZHANG F, PENG G, XU P, et al. Ecological risk assessment of marine microplastics using the analytic hierarchy process: A case study in the Yangtze River Estuary and adjacent marine areas[J]. Journal of Hazardous Materials, 2022, 425: 127960. DOI:10.1016/j.jhazmat.2021.127960 |
 2023, Vol. 47
2023, Vol. 47


