
文章信息
- 赵健, 蔡瑞阳, 孙伟富, 杨俊钢. 2023.
- ZHAO Jian, CAI Rui-yang, SUN Wei-fu, YANG Jun-gang. 2023.
- 基于海洋气候数据集的区域海平面变化非线性预测
- Prediction of regional sea-level nonlinear change based on ocean climate data records
- 海洋科学, 47(4): 69-78
- Marine Sciences, 47(4): 69-78.
- http://dx.doi.org/10.11759/hykx20210128002
-
文章历史
- 收稿日期:2021-01-28
- 修回日期:2021-03-02
2. 自然资源部 第一海洋研究所, 山东 青岛 266061
2. First Institute of Oceanography, MNR, Qingdao 266061, China
海平面变化所受影响因子较多, 是非线性、非平稳性且多尺度变化的时间序列, 需要长时间且连续的数据集来监测其变化过程[1], 利用传统的统计预报或机器学习进行区域海平面变化的准确预测存在一定的技术难度[2]。近年来, 以经验模式分解(empirical mode decomposition, EMD)为代表的数据分解方法和神经网络模型开始应用于海平面变化预测。EMD是由Huang等[3]提出的一种基于数据驱动的自适应分解方法, 集合经验模式分解(ensemble empirical mode decomposition, EEMD)通过叠加高斯白噪声进行多次分解来消除EMD分解存在的模态混叠现象[4]。近年来各种深度学习算法不断演进, 循环神经网络较为适合处理时间序列数据, 但存在梯度消失、梯度爆炸等问题, 且若采用tanh、relu为激活函数, 则无法处理长时间序列。为解决梯度消失和爆炸等问题以及更好的预测时间序列数据, 循环神经网络逐渐转变为长短期记忆神经网络(long and short-term memory, LSTM), 如今LSTM在长期依赖信息学习及预测方面应用广泛[5]。
中国目前海平面变化研究多局限于季节性信号和低频信号丰富的南海、东海海域, 黄、渤海海域的海平面变化研究相对较少[6]。张吉等[7]利用气象耦合模式模拟了RCP4.5情景下21世纪南海海平面变化趋势, 王国松等[8]构建了多模态融合的神经网络模型预测南海海域海平面变化, 赵健[9]从波形理论出发重构海平面数据, 进行了南海及东海海平面变化监测。本文利用海洋气候数据集中的海平面异常数据, 构建基于EEMD与LSTM的组合预测模型, 并应用到山东半岛近海海平面非线性变化预测中, 可为区域海平面变化预测研究提供参考。
1 海洋气候数据集海洋气候数据集(climate data records, CDRs)[10]是“可用于确定气候变率和气候变化, 具有足够时间长度、一致性和连续性的长时间序列数据, 是开展全球气候变化研究的有效数据”。利用海洋CDRs数据研究海洋变化是应对全球气候变化重要组成部分, 对于时空动态变化范围较大的海洋水体可以较好的揭示其在季节、年际、年代际尺度上的变化[11]。
为加强对中国中高纬度海域海平面变化的研究[12], 本文利用自然资源部第一海洋研究所研制的中国首套长时间序列、高精度、高时空一致性的海洋气候数据集中经数据融合后获取的格网化海平面异常(sea level anomaly, SLA)数据, 对山东半岛近海(34°00′N~38°00′N, 119°00′E~123°00′E)海平面变化非线性趋势进行分析预测。海平面异常数据可以很好地捕捉海洋变化的特征, 能对海平面变化趋势进行准确的监测和评价。本文所采用的SLA数据时间范围为1993年1月—2015年12月, 时间分辨率为1个月, 空间分辨率为25 km, 与验潮站数据比较其精度指标为0.2 mm·a–1[11]。考虑到不同纬度数据密度差异, 在计算区域平均的总体数值时, 采用纬度加权平均方法:
| $ {\overline h _k} = \frac{{\sum\limits_i {\sum\limits_j {{h_{ijk}}cos\left( {{\varphi _j}} \right)} } }}{{\sum\limits_i {\sum\limits_j {{\text{cos}}\left( {{\varphi _j}} \right)} } }}, $ | (1) |
式中, hijk为对应地理位置(i, j)和时间k的数据值; φj为数据点的纬度。
区域平均后的山东半岛近海1993—2015年海平面异常时间序列如图 1所示, 线性拟合可得该时间段山东半岛近海海平面上升速率为3.23 mm·a–1。
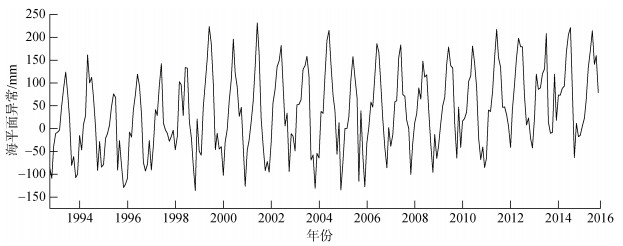 |
| 图 1 区域平均后的1993—2015年山东半岛近海海域海平面异常时间序列 Fig. 1 SLA time series from 1993 to 2015 around the Shandong Peninsula after regional averaging |
原始序列的极值分布不均匀, 或存在混合信号时, 进行EMD分解会产生上下包络线拟合误差, 导致筛选出的分量是固有模式(intrinsic mode functions, IMFs)和异常事件或相邻时间尺度的固有模式组合, 即模态混叠现象。海平面异常数据在采集过程中不可避免存在仪器及噪声的干扰, 利用EMD分解信号会出现模态混叠等问题, 降低预测精度。
Wu等[4]在2005年提出一种以噪声为辅助手段的数据分析方法即EEMD分解。它将原始信号加入若干次白噪声, 把信号和噪声的组合作为待分解信号进行EMD处理, 考虑到白噪声的零均值特性, 对分解结果进行多次平均得到真实分量。EEMD本质是一种叠加高斯白噪声的多次EMD分解[13], 步骤如下:
步骤1: 在序列x(t)加入服从正态分布的白噪声, 有:
| $ {x_i}\left( t \right) = x\left( t \right) + {n_j}\left( t \right). $ | (2) |
步骤2: 对新序列做x(t)进行EMD分解, 求出K个IMF分量ci(t)和一个剩余分量rn(t):
| $ x\left( t \right) = \sum\limits_{i = 1}^k {{c_i}\left( t \right) + {r_n}\left( t \right)} , $ | (3) |
式(3)中, 固有模式分量
步骤3: 重复M次步骤1和步骤2, 每次加入新的白噪声序列;
步骤4: 求M次分解后的IMF分量的整体平均, 作为序列
| $ {c_j}\left( t \right) = \frac{1}{M}\sum\limits_{i = 1}^M {cij\left( t \right)} , $ | (4) |
式(4)中, cij(t)表示第i次加入高斯白噪声后, 分解得到的第j个IMF。
2.2 LSTM网络LSTM是一种特殊的循环神经网络, 可以学习长期依赖信息[14]。它采用记忆单元代替RNN隐含层的神经单元, 在处理长序列输入时有更强的梯度处理能力。LSTM网络由LSTM结构单元串接而成, 每个结构单元决定之前的信息和状态是否保留, 具体结构如下[15]:
1) 决定从细胞状态丢弃什么信息。通过忘记门读取ht–1和xt, 输出数值ft。
| $ f_t=\sigma\left[W_f\left(h_{t-1}, x_t\right)+b_f\right] . $ | (5) |
2) 决定往细胞状态存放什么信息。首先通过输入门决定更新信息it, 然后通过tanh层创建一个新的候选值向量
| $ i_t=\sigma\left[W_i\left(h_{t-1}, x_t\right)+b_i\right], $ | (6) |
| $ \tilde{C_t}=\tanh \left[W_c\left(h_{t-1}, x_t\right)+b_c\right]. $ | (7) |
3) 将旧细胞状态Ct-1与ft相乘, 再加上
| $ C_t=f_t \times C_{t-1}+i_t \times \tilde{C_t}. $ | (8) |
4) 决定输出什么信息。首先, 通过输出门决定输出信息Ot, 然后通过tanh层将其和输出信息Ot相乘得到确定输出部分ht。
| $ O_t=\sigma\left[W_o\left(h_{t-1}, x_t\right)+b_o\right], $ | (9) |
| $ h_t=O_t \times \tanh \left(C_t\right), $ | (10) |
式(5)~(10)中, xt、ht分别为t时刻网络的输入与输出; ft、it、Ot、Ct分别为遗忘门、输入门、输出门和记忆细胞的输出; Wx为权重矩阵; bx为偏置; σ为sigmoid激活函数。
3 基于EEMD和LSTM的组合预测模型EEMD-LSTM组合预测模型主要包括: SLA序列的EEMD分解、各IMF分量的LSTM预测以及预测结果的重构等三部分。首先通过EEMD分解将海平面异常SLA时间序列中具有物理含义的信号提取出来, 得到频域稳定的固有模式分量IMFs; 再利用LSTM算法对得到的各IMF分量分别建立预测模型; 最后将各IMF分量预测结果进行重构叠加, 得到最终的海平面异常预测结果。
3.1 海平面异常时间序列EEMD分解对山东半岛近海1993—2015年间的SLA时间序列进行EEMD分解, 得到7个子序列和一个残差序列共8个IMF分量, 如图 2(a)~(h)所示。借助白噪声的集合扰动进行显著性分析[16]发现IMF7未通过检验, 表明该分量包含真实信号的可能性小, 为白噪声的可能性较大, 建立预测模型时应舍弃。IMF1~ IMF6频率稳定, 分别对应3.97月、11.96月、22.92月、30.56月、137.5月(约11 a)和91.67月(约7 a)周期, 表现为明显的季节变化、年际变化和2~3 a周期变化, 基本包含原始序列的显著周期[17]。表明EEMD分解可以将原始非线性的海平面异常时间序列分解成多个平稳的子序列, 同时保留有物理含义的信号。
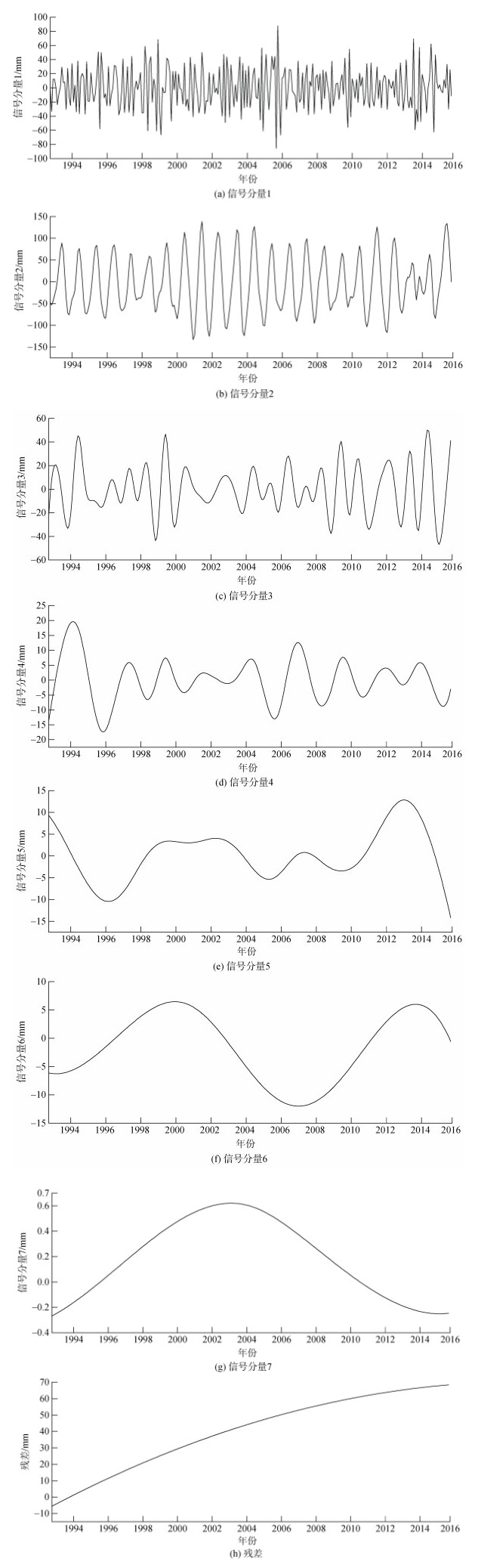 |
| 图 2 山东半岛近海海平面异常时间序列经验模态分解分解结果 Fig. 2 EEMD results of the SLA time series around the Shandong Peninsula |
对EEMD分解后的IMF分量进行预测时, 将1993年1月至2011年5月的数据作为训练数据(约占数据总量的80%), 2011年6月至2015年12月的数据作为检验数据(约占数据总量的20%)。在构建LSTM网络对IMF分量进行预测时, 需选取不同的学习率、迭代次数、衰落因子等超参数, 结合各实验结果选择达到最优预测效果的超参数设置。图 3为IMF1-6分量及剩余分量在LSTM网络检验阶段的预测值与原始IMF数据对比, 实线为IMF分量在检验阶段的原始数据, 虚线为LSTM预测结果。从图 3可以看出, 随着IMF分量趋于平稳模型的预测精度逐渐提高, 预测效果相对较差的高频分量IMF1, 由于存在大量突变点造成预测难度较大, 但其总体振幅及走向与原始数据基本保持一致, 整体预测效果符合预期。
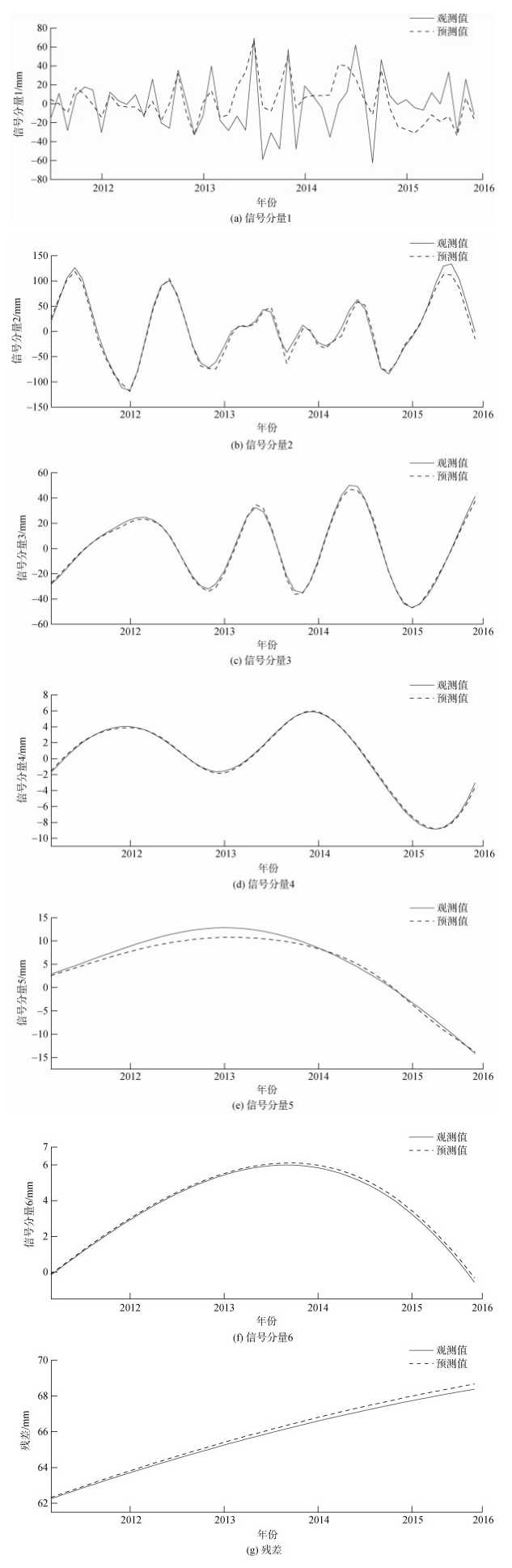 |
| 图 3 检验阶段(2011年6月—2015年12月)各信号分量预测结果与学习样本对比 Fig. 3 Comparison of the predictions of IMF components with the testing data in the testing period (2011.06–2015.12) |
为评价EEMD-LSTM组合模型的预测效果, 将仅采用LSTM模型进行预测与EEMD-LSTM组合模型预测结果进行比对。为避免与原始观测数据比对时产生偏差, 首先对IMF分量进行归一化处理, 再将IMF分量预测结果叠加重构, 最终得到EEMD-LSTM组合模型预测结果, 两种方法检验数据的预测结果如图 4所示。可以看出仅采用LSTM预测结果的峰值和谷值与原始海平面异常观测数据较为接近, 但由于模型存在滞后导致误差相对较大; 而EEMD-LSTM组合模型明显地改善了上述滞后性, 与原始SLA观测数据更为吻合。即采用组合模型预测效果明显优于仅利用LSTM网络对原始SLA观测数据进行预测。海平面异常观测数据经平稳及降噪处理后, 再依据信号的不同变化特征进行多尺度模拟预测效果更好。但由于海平面变化的非平稳性和非线性, 海平面异常时间序列中存在大量的突变点和极值点, 预测误差偏大的点较易出现在时间序列变化的极值点上。
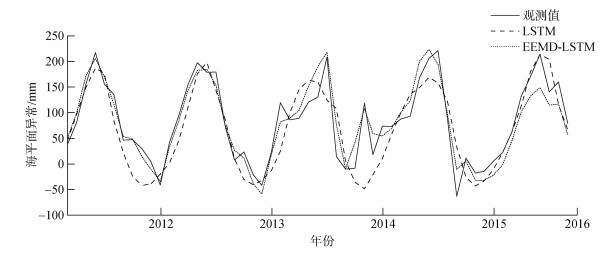 |
| 图 4 LSTM算法预测与EEMD-LSTM组合模型在检验阶段(2011年6月—2015年12月)预测结果对比 Fig. 4 Comparison of predictions between the LSTM model and the EEMD-LSTM combined model (2011.06—2015.12) 注: LSTM为长短期记忆网络模型; EEMD-LSTM为经验模态分解与长短期记忆网络组合模型 |
为定量分析两种方法的预测精度, 采用相关系数(R)、平均绝对误差(MAE)和均方根误差(RMSE)等三个指标进行预测结果的定量评价[18], 结果如表 1所示。从表 1可以看出, EEMD-LSTM组合模型预测结果相关系数R较LSTM网络直接预测提高0.1, 而RMSE与MAE分别降低21.51 mm和15.73 mm, 组合模型预测精度显著提高。
| 模型 | R | RMSE/mm | MAE/mm |
| LSTM | 0.84 | 47.38 | 36.47 |
| EEMD–LSTM | 0.94 | 25.87 | 20.74 |
| 注: LSTM为长短期记忆网络模型; EEMD-LSTM为经验模态分解与长短期记忆网络组合模型; MAE为平均绝对误差; RMSE为均方根误差 | |||
本文采用EEMD-LSTM组合预测模型, 对山东半岛近海未来10年的区域海平面变化趋势进行预测, 结果如图 5所示。图 5中1993—2015年的海平面异常时间序列由实线表示, 未来十年(2016— 2025年)的海平面异常预测结果由虚线表示, 线性拟合得到2016—2025年山东半岛近海海平面上升速率将增大至3.54 mm/a。《2021年中国海平面公报》[19]显示1980—2021年, 黄海沿海海平面上升速率为3.2 mm/a, 预计未来30年, 山东沿海海平面将上升60~160 mm。本文利用海洋气候数据集研究山东半岛近海海平面变化趋势, 预测结果与上述公报研究结论基本相符, 与基于同时间段卫星测高数据的研究结果也较为一致[12], 表明该组合预测模型具有很好的应用价值。
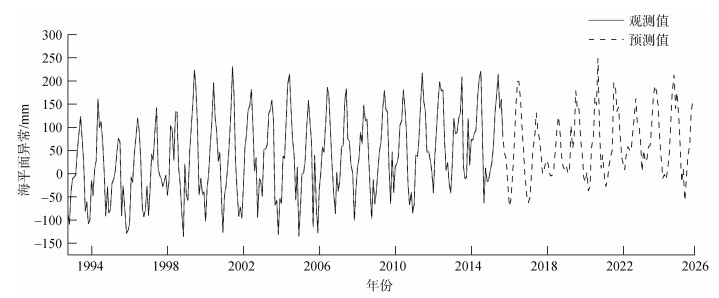 |
| 图 5 基于EEMD-LSTM组合模型的山东半岛近海2016—2025年海平面异常预测结果 Fig. 5 Predicted SLAs with the EEMD–LSTM combined model from 2016 to 2025 around the Shandong Peninsula |
论文基于EEMD-LSTM组合预测模型进行区域海平面变化趋势的预测研究, 能够解决EMD分解算法所带来的模态混叠现象, 保留原始序列的物理信息, 同时改善LSTM网络滞后现象, 极值问题得到缓解, 预测结果更加接近原始观测数据, 在区域海平面变化预测中具有较好的应用价值。
论文使用中国首套高精度、高时空一致性的CDRs数据, 对山东半岛近海未来十年海平面变化进行了预测, 结果表明未来十年山东半岛沿海海平面上升速率将增大至3.54 mm/a–1, 与中国海平面公报研究结果相符, 与基于同时间段卫星测高数据的研究结果也较为一致[12], 验证了海洋CDRs数据和EEMD-LSTM组合预测模型的有效性。同时发现海平面变化预测研究对极值模拟预测能力要求较高[20], 今后可考虑加入海平面的空间特性及其影响因子并开展极值预测方面的研究。
致谢: 感谢自然资源部第一海洋研究所提供的海洋气候数据集CDRs, 感谢审稿专家的意见和建议。
| [1] |
ARMIN A, XIAO L. Estimating sea level rise around Australia using a new approach to account for low frequency climate signals. 2020, 65(10): 2324-2338.
|
| [2] |
赵健, 樊彦国, 张音. 基于EEMD-BP组合模型的区域海平面变化多尺度预测[J]. 系统工程理论与实践, 2019, 39(10): 2713-2722. ZHAO Jian, FAN Yanguo, ZHANG Yin. Multi-scale prediction of regional sea level variations based on EEMD- BP combined model[J]. System Engineering Theory and Practice, 2019, 39(10): 2713-2722. DOI:10.12011/1000-6788-2019-0223-10 |
| [3] |
HUANG N, SHEN Z, LONG S, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [4] |
WU Z, HUANG N. Ensemble empirical mode decomposition: A noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [5] |
杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, 38(S2): 1-6, 26. YANG Li, WU Yuxi, WANG Junli, et al. Research on recurrent neural network[J]. Journal of Computer Applications, 2018, 38(S2): 1-6, 26. |
| [6] |
ZHAO J, FAN Y, MU Y. Sea level prediction in the Yellow Sea from satellite altimetry with a combined least squares-neural network approach[J]. Marine Geodesy, 2019, 42(4): 344-366. DOI:10.1080/01490419.2019.1626306 |
| [7] |
张吉, 左军成, 李娟, 等. RCP4.5情景下预测21世纪南海海平面变化[J]. 海洋学报(中文版), 2014, 36(11): 21-29. ZHANG Ji, ZUO Juncheng, LI Juan, et al. Sea level variations in the South China Sea during the 21st century under RCP4.5[J]. Haiyang Xuebao, 2014, 36(11): 21-29. |
| [8] |
WANG G, WANG X, WU X, et al. Multimodal fusion for sea level anomaly forecasting[P/OL]. 2020-06-15 [2021-01-25]. https://arxiv.org/abs/2006.08209v1.
|
| [9] |
赵健. 中国南海及东海近海测高海平面变化监测与预测[J]. 测绘学报, 2020, 49(5): 670. ZHAO Jian. Sea level change monitoring and prediction using satellite altimetry in south China Sea and east China sea coastal ocean[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(5): 670. |
| [10] |
梁顺林, 唐世浩, 张杰, 等. 全球气候数据集生成及气候变化应用研究[J]. 遥感学报, 2016, 20(6): 1491-1499. LIANG Shunlin, TANG Shihao, ZHANG Jie, et al. Production of the global climate data records and applications to climate change studies[J]. Journal of Remote Sensing, 2016, 20(6): 1491-1499. |
| [11] |
张杰, 孙伟富, 杨俊钢, 等. 海洋气候数据集生成与分析简介[J]. 海洋科学进展, 2019, 37(2): 325-331. ZHANG Jie, SUN Weifu, YANG Jungang, et al. Brief introduction to the first global ocean climate data records(CDRs)of China[J]. Advances in Marine Science, 2019, 37(2): 325-331. DOI:10.3969/j.issn.1671-6647.2019.02.016 |
| [12] |
ZHAO J, CAI R, FAN Y. Prediction of sea level nonlinear trends around Shandong peninsula from satellite altimetry[J]. Sensors, 2019, 19(21): 4770. DOI:10.3390/s19214770 |
| [13] |
WANG T, ZHANG M, YU Q, et al. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal[J]. Journal of Applied Geophysics, 2012, 83: 29-34. DOI:10.1016/j.jappgeo.2012.05.002 |
| [14] |
HOCHREITERS S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [15] |
彭燕, 刘宇红, 张荣芬. 基于LSTM的股票价格预测建模与分析[J]. 计算机工程与应用, 2019, 55(11): 209-212. PENG Yan, LIU Yuhong, ZHANG Rongfen. Modeling and analysis of stock price forecast based on LSTM[J]. Rong fen Computer Engineering and Applications, 2019, 55(11): 209-212. |
| [16] |
易彩. 高速列车轮对轴承状态表征与故障诊断方法研究[D]. 成都: 西南交通大学, 2015. YI Cai. State Characterization and fault diagnosis research on wheel bearing of high-speed train[D]. Chengdu: Southwest Jiaotong University, 2015. |
| [17] |
王慧, 刘克修, 张琪, 等. 中国近海海平面变化与ENSO的关系[J]. 海洋学报(中文版), 2014, 36(9): 65-74. WANG Hui, LIU Kexiu, ZHANG Qi, et al. The relationship between sea level change of China's coast and ENSO[J]. Haiyang Xuebao, 2014, 36(9): 65-74. |
| [18] |
赵健, 樊彦国, 丁宁. 基于最小二乘与径向基函数神经网络的海平面变化预测[J]. 海洋科学, 2018, 42(5): 92-97. ZHAO Jian, FAN Yanguo, DING Ning. Sea level anomaly forecasting using least square and the radial basis function neural network[J]. Marine Sciences, 2018, 42(5): 92-97. |
| [19] |
自然资源部. 2021年中国海平面公报[Z]. 北京: 自然资源部, 2022. Ministry of Natural Resources of the People's Republic of China. China sea level bulletin 2021[Z]. Beijing: Ministry of Natural Resources of the People's Republic of China, 2022. |
| [20] |
PENG H, FANG H. Understanding and reconstructing the coastal sea level variations along the western boundary of the North Pacific[J]. Geoscience Letters: Official Journal of the Asia Oceania Geosciences Society(AOGS), 2020, 7: 1-10. |
 2023, Vol. 47
2023, Vol. 47

