
文章信息
- 田丰林, 王昊, 刘巍, 马颖, 陈戈. 2023.
- TIAN Feng-lin, WANG Hao, LIU Wei, MA Ying, CHEN Ge. 2023.
- 基于传输函数的二/三维全时空连续海洋中尺度涡旋流场实时可视化
- Real-time visualization of 2D/3D full spatiotemporal continuous ocean mesoscale eddy fields based on the transfer function
- 海洋科学, 47(9): 12-27
- Marine Sciences, 47(9): 12-27.
- http://dx.doi.org/10.11759/hykx20220519001
-
文章历史
- 收稿日期:2022-05-19
- 修回日期:2023-07-31
2. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室, 山东 青岛 266237;
3. 青岛市计量技术研究院, 山东 青岛 266000
2. Laboratory for Regional Oceanography and Numerical Modeling, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, China;
3. Qingdao Institute of Measurement Technology, Qingdao 266000, China
海洋大数据体量大, 增长速度快, 数据量已增至PB量级(在数值上大约等于1 000个TB的数据量)[1], 目前利用海洋大数据实现对海洋现象特别是对三维海洋现象的探索效率比较低, 建立从海洋数字孪生技术到海洋可视孪生技术的海洋信息系统是实现高效探索海洋大数据的关键。以虚拟海洋、数据可视化与人机交互系统为关键点的海洋可视孪生技术能够辅助用户高感知地理解数据中蕴含的海洋现象, 实时交互地挖掘其中的海洋规律, 是海洋科学中有价值的研究方向[2]。
海洋中尺度涡旋在海洋环流, 以及海水中温度、盐度和物质输运中扮演着重要角色, 影响人类活动, 它的直径一般为数十至数百千米, 寿命可达数天到数月不等。海洋中尺度涡旋可视化是直观表现中尺度涡旋运动规律的重要工具, 是交互式分析海洋中尺度涡旋特征的重要方法, 是海洋流场数据可视化和海洋数字孪生的重要研究内容。海洋中尺度涡旋可视化是基于流场可视化、涡旋特征提取和交互式传输函数三种技术实现的。
在流场可视化方面, 根据流场数据类型可分为二维流场可视化和三维流场可视化。二维流场可视化方法主要包括基于纹理的方法和基于几何的方法。基于纹理的方法优点是能够详细地描述流场信息, 缺点是算法消耗较大。基于几何的可视化主要采用几何图元(如流线、迹线、脉线等)来表现流场, 其优点是表现形式直观简单、易于表达流场的流动规律, 相比于基于纹理的方法, 能更精确地表达流场的流动方向。三维流场可视化方法主要包括基于线、面和纹理的方法[3], 基于面的方法主要通过构建流面表达了比流线更多的信息, 减小了视觉复杂度, 缺点是算法较复杂, 不适用于复杂流场可视化; 基于纹理的方法优点是能够表达流场的全局信息, 缺点是在三维空间中遮挡严重; 基于线的方法则主要采用流线、迹线、脉线可视化流场, 在三维空间中容易存在遮挡和杂乱的现象。本文采取了基于几何的二维流场可视化方案和基于线的三维流场可视化方案。另外, 针对时变流场, Weiskopf等[4]、Helgeland等[5]、Li等[6]、何珏等[7]、田丰林等[8-10]都采用了迹线-流线时空连续框架的概念, 运用空间连续性与时间连续性[11]来分别反映每一帧上相邻流动要素(如粒子)之间的连贯性和同一流动要素在相邻帧上的连贯性, 虽然流线的空间连续性较好, 但是由于流线仅在头部粒子处, 即迹线与瞬时空间切片的交点处时间连续, 流线的时间连续性较低, 所以需要一种时空连续性更好的框架来可视化不稳定流场。
在涡旋提取方面, 流场涡旋特征提取大致分为基于区域、线、几何曲线和客观方法[12]。基于区域的方法根据局部区域的物理量判断这一区域是否为涡旋, 其优点在于运算简单易于并行, 可视化效率较高, 缺点在于特征值受阈值影响严重, 不能同时提取强涡与弱涡。其他方法的算法时间复杂度高, 难以并行处理, 可视化效率不高, 因此本文选择了基于区域的方法来提取涡旋。基于区域的方法包括Q准则[13]、ow方法[14-15]、λ2方法[16]等, Zhang等[17]认为, 如果涡旋的中心嵌入在Okubo-Weiss(ow)参数W= –2.0×10–12的闭合轮廓内, 则确认涡旋, 并利用ow参数识别海面上的涡旋, 确定涡旋的规模和强度; Chelton等人[18]同样选取了W= –2.0×10–12作为ow参数的阈值, 以确定海洋涡旋的轮廓并自动跟踪涡旋的轨迹。但是这些方法都需要设定阈值, 且对不同涡旋不具有普适性, Liu等[19]提出了基于区域的Ω准则, 该方法无须设置最合适的阈值, 当Ω=0.5时, 能够提取多数涡旋[20]。本文选择了ow准则和Ω准则来比较受阈值影响与不受阈值影响的海洋涡旋提取技术。
在传输函数方面, 传输函数是一组定义了数据值及其相关属性与颜色、不透明度等视觉元素之间映射关系的函数[21], 是海洋现象三维交互特征提取的主要方法, 可以揭示数据中与感兴趣的特征相对应的重要结构[22]。传输函数广泛应用在标量场可视化中, Dinesha等[23]提出一种基于高动态范围(High-Dynamic Range, HDR)技术的传输函数并可视化了孟加拉湾海域的盐度场; Tian等[10]通过手动调节传输函数展现出西太暖池、黑潮入侵以及海洋温度异常等海洋可视化效果; 在矢量场可视化中, Helgeland和Andreassen[24]将传输函数应用于三维流场可视化; Song等[25]将传输函数应用到大气涡旋耗散率场上的云滴轨迹可视化。Matsuoka等[26]设计了海洋流场速度值与温度值的二维传输函数并可实现了黑潮区域的流场的可视化, 直观地展现了流速与温度的相关性。然而手动创建传输函数工作量很大, 而且容易出错[27], 在海洋流场可视化中缺乏可供参考的标准传输函数, 能够对具体海域的涡旋实现最佳的可视化效果, 从而降低用户调节传输函数的难度, 这是目前面向海洋涡旋可视化的传输函数亟待解决的问题。
基于上述方法已有的问题, 本文提出用迹线-迹线全时空连续框架来提高可视化框架的时空连续性, 用基于几何的方法可视化海洋流场, 通过传输函数交互特征值(ow值和Ω值)提取海洋中尺度涡旋, 并构建标准传输函数提高用户交互分析海洋中尺度涡旋的效率, 本文的创新之处在于: (1)首次提出面向海洋中尺度涡旋实时交互可视化的迹线-迹线全时空连续框架, 实现了基于迹线的直观高感知度海洋流场可视化效果; (2)通过交互式传输函数将基于区域的中尺度涡旋提取技术——Ω准则应用到海洋中尺度涡旋可视化中, 降低了涡旋提取对阈值的依赖程度; (3)构建面向海洋中尺度涡旋可视化的传输函数标准形态模式, 优化了海洋中尺度涡旋提取效果, 降低了用户交互传输函数分析海洋中尺度涡旋的难度。
本文的结构安排如下: 第一部分介绍了研究所使用的数据; 第二部分介绍了全时空连续框架和流场可视化方法; 第三部分基于海洋流场全时空连续可视化框架, 实现了涡旋特征提取和基于标准传输函数的中尺度涡旋可视化; 第四部分介绍了海洋中尺度涡旋可视化的实现和两种时空连续框架的性能对比; 第五部分进行了总结与展望。
1 数据集(1) MSLA数据集
MSLA数据集是由法国AVISO(Archiving, Validation and Interpretation of Satellite Oceanographic)提供的格网化数据, 融合了T/P, Jason-1, ERS和ENVISAT等多颗卫星的测高资料, 可从 https://www.aviso.altimetry.fr/en/data/products/sea-surface-height-products/中获得。MSLA-UV速度场纹理数据集覆盖82°N~82°S之间的全球海洋(网格大小为1 080×915)[28]。MSLA-UV数据空间分辨率为0.25°×0.25°, 时间分辨率为1 d, 该数据集提供了基于卫星测高测量的每日全球海平面异常估计值以及绝对地转流的速度, 是满足地转平衡的涡旋流场数据, 侧重于检测海洋的中尺度信号, 主要分为two-sat-merged与all-sat-merged两种类型, 由于all-sat-merged类型的数据质量比较高, 本文使用all-sat-merged类型的数据提高海洋中尺度涡旋可视化的质量。
(2) OMEGA3D数据集
本文选取了CMEMS(http://marine.copernicus.eu/)中的Global Observed Ocean Physics 3D Quasi-Geostrophic Currents (OMEGA3D)数据集。OMEGA3D数据记录了基于观测的准地转流(垂直和水平海流), 是三维环流场数据, 其速度分量包括纬向速度u、经向速度v以及垂向速度w, 空间分辨率为0.25°×0.25°, 时间分辨率为1周, 在垂直方向上从–1 482.5 m到–2.5 m记录了75层数据, 数据层之间的间隔各不相同。本文选择OMEGA3D数据集以利用迹线表现海洋中尺度涡旋的三维效果。
2 全时空连续框架与海洋流场可视化 2.1 全时空连续框架基于海洋流场可视化中的迹线-流线时空连续框架[图 1(a)][7-10], 本文提出了迹线-迹线全时空连续框架[图 1(b)]来实现全时空连续海洋流场可视化。迹线-流线时空连续框架是用迹线表达粒子运动的时间连续性, 用瞬时空间切片上的流线表达流线上各个顶点的空间连续性, 瞬时空间切片上的流线仅在流线头部即粒子处时空连续, 流线上其余顶点与迹线上的各个时刻的粒子没有密切的时空相关性。而迹线-迹线全时空连续框架用迹线来表达粒子运动的时间连续性, 用瞬时空间切片上的迹线投影来展现迹线上各个顶点的空间连续性。通过时空投影, 瞬时空间切片上的迹线投影记录了迹线从t0到t时间段上各个粒子的信息, 迹线投影上的每个顶点与迹线上的粒子都具有密切的时空相关性, 因此迹线-迹线框架是全时空连续的。
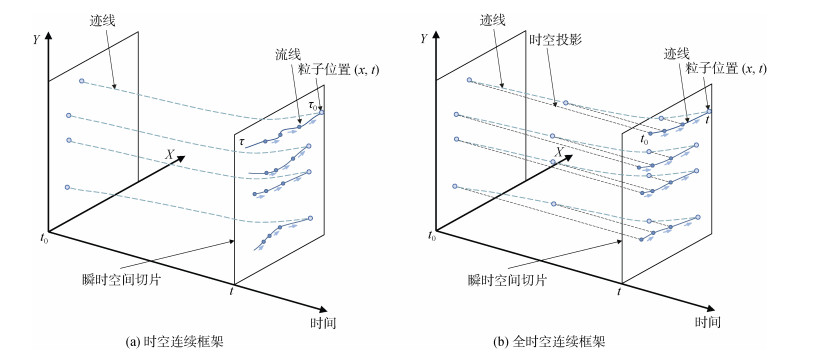 |
| 图 1 时空连续框架与全时空连续框架对比图 Fig. 1 Comparison between spatiotemporal continuous and full spatiotemporal continuous frames 注: (a)为迹线-流线时空连续框架, 由于流线除其第一个顶点外其余顶点时空不连续, 因而该框架不是全时空连续的。(b)为迹线-迹线全时空连续框架, 基于迹线上各个时刻粒子的时空投影, 迹线投影上的顶点与迹线上各个时刻的粒子具有密切的时空相关性, 因而该框架是全时空连续的。图中空心圆点表示在迹线轨迹上各个时刻的粒子, 实心圆点表示流线/迹线上的顶点, t0、t处为瞬时空间切片, 三维时空(x, y, t)由瞬时空间切片充满 |
非定常流场可以定义为u(x, t), 用时间t和位置x确定了这一时空中流场的速度矢量值, 迹线xpath由下面的常微分方程决定:
| dxpath (t;x0,t0)dt=u(xpath (t;x0,t0),t). | (1) |
初始条件xpath(t0; x0, t0)=x0在(x0, t0)处给出, 通过积分求解常微分方程可得迹线的方程如下:
| xpath (t;x0,t0)=x0+t∫t0u(xpath (s;x0,t0),s)ds. | (2) |
在瞬时空间切片上非定常流场可以视作定常流场。流线可以用来可视化流场的结构, 流线由下面的常微分方程决定:
| dxstream (τ;x0,t0)dt=u(xstream (τ;x0,t0),t). | (3) |
τ与t和t0不同, 没有真实的物理意义, 只代表了流线积分的虚拟时间, 以控制流线的长度, 积分后可得流线的方程:
| xstream (τ;x0,t0)=x0+τ∫τ0u(xstream (s;x0,t0),t)ds,τ<τ0, | (4) |
τ<τ0表示流线后向积分, 这样流线的头部粒子一直保持时空连续, 从而构建了时空连续框架。
2.2 海洋流场迹线-迹线全时空连续可视化本文利用基于粒子的迹线图元实现全时空连续框架, 可视化海洋流场。每个迹线图元中包含有数量相同的粒子, 其头部粒子随时间按照迹线方程xpath移动。本文用索引来标记迹线图元上粒子的时间顺序, 第一个索引的粒子位于迹线图元头部, 反映当前时刻头部粒子的位置, 故记为当前粒子; 通过时空投影, 其余索引的粒子反映了同一迹线图元头部粒子在过去各个时刻的位置, 记为历史粒子。相邻索引之间的粒子时间间隔相同, 按索引顺序, 迹线图元的粒子依次记录了从当前时刻到更久远时刻头部粒子的位置。
迹线图元中的粒子属性包括位置和年龄, 在迹线图元初始化时同一图元的粒子位置和年龄相同。迹线图元头部粒子运动时, 其属性随时间发生改变, 迹线图元上其余粒子的位置会各自更新为上一时刻同一迹线图元的前一个索引的粒子位置, 这样, 这一时刻迹线图元的粒子记录了从过去到现在头部粒子的迹线运动, 实现了在任一瞬时空间切片上, 迹线投影——迹线图元上的所有粒子时空连续。图 2描述了迹线图元运动过程。
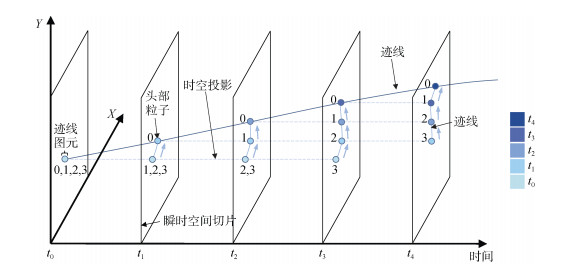 |
| 图 2 迹线图元运动示意图 Fig. 2 Schematic of the pathline element movement |
在该示意图中, 迹线图元由4个粒子组成并在t0时刻初始化, 初始化时迹线图元上粒子的位置相同, 在t0至t4时间段内头部粒子在迹线上运动, 迹线图元上粒子的颜色代表了这一粒子记录了头部粒子在哪一时刻的位置。迹线图元上从头部粒子到图元末端粒子的索引依次为0、1、2、3, 历史粒子的位置会各自更新为上一时刻(前一个瞬时空间切片上)迹线图元的前一个索引的粒子位置, 如在t3瞬时空间切片上, 通过时空投影, 索引为1的粒子位置更新为t2时刻头部粒子(索引0)的位置, 索引为2的粒子位置更新为t2时刻索引为1的粒子位置, 索引为3的粒子位置更新为t2时刻索引为2的粒子位置。这样t3瞬时空间切片上迹线图元的粒子依次记录了头部粒子在t0-t3时刻上的位置, 因此迹线图元上的粒子是全时空连续的。
迹线图元随时间在流场中流动或集聚, 需要对瞬时空间切片上的迹线图元进行密度控制, 保证迹线图元动态均匀分布。本文用迹线图元头部粒子的密度来代替迹线图元的密度, 用径向基函数计算头部粒子的影响域, 即:
| I(x)=∑(‖ | (5) |
式中, x为待求点的位置。索引i为粒子序号。λi为粒子i对待求点的影响比重, 本文中所有粒子比重一致, λi设为1。xi是粒子i的位置。
在瞬时空间切片上, 影响域为:
| I(x, t)=\sum\limits_{i}\sum\limits_{\left\|\boldsymbol{x}-\boldsymbol{x}_{\text {path }}\left(t ; \boldsymbol{x}_i, t_0\right)\right\|_2<R} \lambda_i \varnothing_i\left(\left\|x-x_{\text {path }}\left(t ; x_i, t_0\right)\right\|_2\right), | (6) |
其中R为粒子影响域的半径, 根据3-σ法则, 将高斯函数的标准差σ设置为R/3, 在瞬时空间切片上, 粒子的影响域值都是由中心向边界逐渐减小的, 在粒子聚集处粒子的影响域值叠加, 影响域值较高, 粒子影响域无重叠处, 影响域值为0, 因此影响域函数I(x, t)可以用作记录迹线图元头部粒子在瞬时空间切片上的概率密度。在二维迹线中, 头部粒子的影响范围可以看作圆片, 瞬时空间切片上的头部粒子影响域如图 3所示, 将头部粒子的概率密度渲染到纹理后, 其概率密度纹理如图 4(a)所示; 在三维迹线中, 头部粒子的影响域可以视作球体, 球体之间可以重叠累加, 三维概率密度体纹理由8张RGBA四通道切片组成, 根据头部粒子的深度确定球体投影到哪一层切片的哪一个通道中, 如图 5所示。三维迹线头部粒子概率密度纹理如图 4(b)所示。
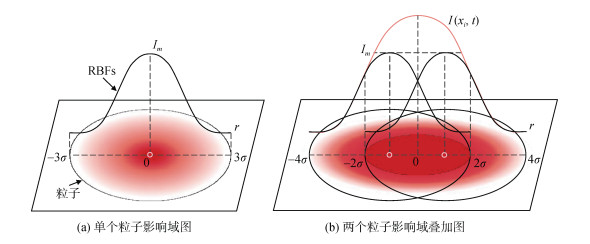 |
| 图 3 二维迹线头部粒子影响域示意图 Fig. 3 Schematic of the particle influence region at the head of the two-dimensional pathline 注: (a)为单个粒子影响域, (b)为两个粒子影响域的叠加。Im为粒子影响域最大值 |
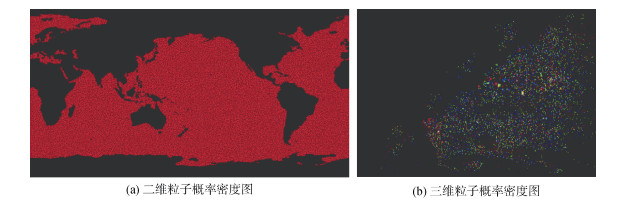 |
| 图 4 二维粒子概率密度图(a)与三维粒子概率密度图(b) Fig. 4 (a) Two-dimensional and (b) three-dimensional particle probability density diagrams 注: (b)中粒子的不同颜色代表粒子的不同深度, 从红色到绿色到蓝色粒子的深度值越来越高 |
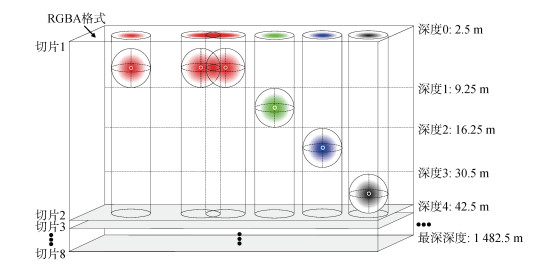 |
| 图 5 三维迹线头部粒子影响域示意图 Fig. 5 Schematic of the particle influence region at the head of the three-dimensional pathline |
迹线图元头部粒子采样概率密度图获取当前位置的密度值, 当密度值过大时, 通过对迹线图元年龄的控制, 加快其“死亡”, 并置为不可见的状态移除迹线图元, 死亡后的迹线图元其头部粒子立即通过Simplex噪声函数[29]获得新的随机位置和“出生”年龄, 并采样随机位置处的密度值, 若密度值较小则播种迹线图元。实现了迹线图元动态均匀分布之后, 将迹线图元上的粒子按照索引顺序首尾相连, 生成迹线。
图 6展现了基于迹线-流线时空连续框架与基于迹线-迹线全时空连续框架的海洋流场可视化效果。在二维定常流场可视化中, 由于迹线与流线重合, 两种时空连续框架对应的可视化效果质量相同。在二维非定常流场可视化中, 迹线-流线时空连续框架只表现了当前时刻的流场结构, 而迹线-迹线全时空连续框架则可以表现涡旋的运动情况。图 6(d)用迹线直观地表现了涡心区域的海流运动, 相比于迹线-流线时空连续框架, 迹线-迹线全时空连续框架更加直观地反映了非定常海洋流场信息。另外全时空连续框架中迹线的时间连续性较高, 不会出现流线上由于从头部到末端时间连续性逐渐降低而导致的线段抖动现象。综上所述, 基于全时空连续框架的流场可视化效果更好。
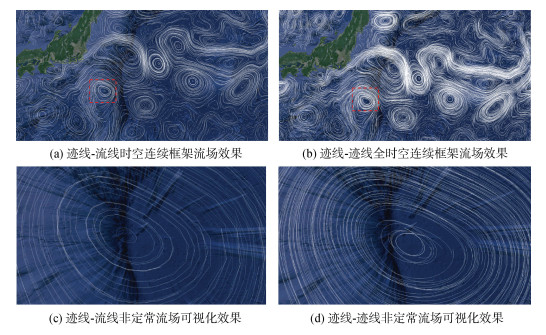 |
| 图 6 海洋非定常流场可视化效果对比图 Fig. 6 Comparison of the visualization of unsteady flow field in oceans 注: (c)、(d)非定常流场可视化效果分别是在(a)、(b)中红色方框区域内的。(d)中涡心区域迹线交叉, 表现了其全时空连续的海流运动, 而(c)中难以观察到涡心的移动 |
图 7展现了基于迹线-迹线全时空连续框架的海洋流场可视化效果。
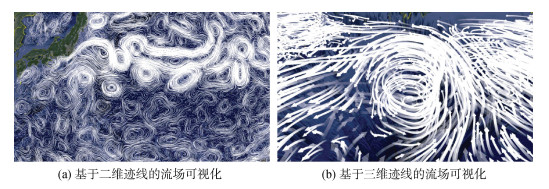 |
| 图 7 基于迹线的海洋流场可视化效果图 Fig. 7 Visualization of ocean flow field based on the pathline 注: 可视化海域为黑潮流域 |
ow准则[14-15]是研究中尺度涡的经典方法[30-31], 通过剪切变形率(Ss), 正交变形率(Sn)以及相对涡度的垂向分量(ω)来定义:
| W=S_{\mathrm{n}}^2+S_{\mathrm{s}}^2-\omega^2, | (7) |
其中,
| S_{\mathrm{n}}=\frac{\delta U}{\delta x}-\frac{\delta V}{\delta y}, \quad S_{\mathrm{s}}=\frac{\delta V}{\delta x}+\frac{\delta U}{\delta y}, \omega=\frac{\delta V}{\delta x}-\frac{\delta U}{\delta y} . | (8) |
U和V分别是纬向上和经向上的速度, 可以由海平面异常(sea level anomaly, SLA, 记为ASL)梯度计算得到(
涡旋一般存在于W为负值且以旋转为主的流域中[32], Zhang等[17]和Chelton等[18]将W= –2.0×10–12作为海洋涡旋提取的阈值。
Nieto等[33]指出了ow准则的局限性, 即ow准则度量了涡旋的绝对强度, 所以严格依赖于阈值的选取, 在不同场景中, 同一阈值不一定都能提取出形态较好的涡旋。
在流场中, 雅可比矩阵J=
| \boldsymbol{S}=\frac{J+J^{\mathrm{T}}}{2}, \boldsymbol{\varOmega}=\frac{J-J^{\mathrm{T}}}{2}. | (9) |
Liu等人[19]提出了Ω准则来降低阈值对涡旋提取的影响。他们将涡度分解为有旋涡度(R)和无旋涡度(
| \varOmega=\frac{(\nabla \times V \cdot R)^2}{\|\nabla \times V\|_2^2 \cdot\|R\|_2^2} \approx \frac{b}{a+b}, | (10) |
其中,
| \left\{\begin{array}{l} a=\operatorname{tr}\left(\boldsymbol{S}^{\mathrm{T}} \boldsymbol{S}\right)=\sum\limits_{i=1}^3 \sum\limits_{j=1}^3\left(S_{i j}\right)^2 \\ b=\operatorname{tr}\left(\boldsymbol{\varOmega}^{\mathrm{T}} \boldsymbol{\varOmega}\right)=\sum\limits_{i=1}^3 \sum\limits_{j=1}^3\left(\Omega_{i j}\right)^2 \end{array},\right. | (11) |
S、Ω分别为应变率张量和涡度张量。
Ω=0.5是涡旋边界提取的阈值[34], 这具有明确的物理意义, 即涡度超过应变。Ω准则度量了涡旋的相对强度, 既能提取强涡也能捕捉弱涡, 降低了阈值对涡旋提取的影响。
本文利用W<–2.0×10–12和Ω>0.5等条件, 构建面向海洋涡旋可视化的标准传输函数, 利用细分计算着色器实时计算迹线特征值并进行颜色映射, 利用迹线的颜色表达海洋中尺度涡旋。
3.2 标准传输函数传输函数是一组定义了数据值及其相关属性与颜色、不透明度等视觉元素之间映射关系的函数[21]。用不透明度控制哪些特征隐藏或显示, 而用颜色来调整要显示特征的视觉效果, 提高特征区间内海洋现象的可感知度。
一维传输函数的映射关系为
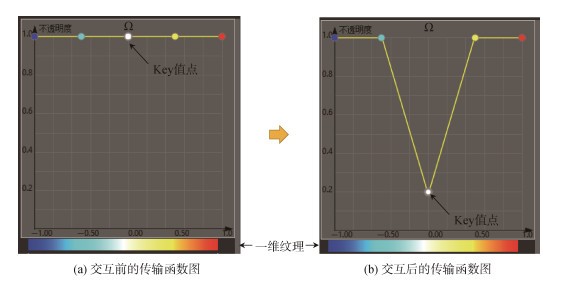 |
| 图 8 传输函数交互原理示意图 Fig. 8 Transfer function interaction principle diagram |
但是目前传输函数存在一些问题, 比如交互方式不够友好、依赖于用户的专业知识、交互效率低下、对具体海域的涡旋没有固定的识别标准、涡旋提取效果不精确等。因此本文提出了一种标准传输函数, 利用此标准传输函数线型可以直接提取中尺度涡旋, 降低用户的操作复杂度。本文中构建标准传输函数所用的数据集是2012年1月1日的MSLA数据, 用二维迹线-迹线全时空连续框架可视化海洋流场。
首先根据特征值类型, 确定适合的传输函数线型以提取涡旋。ow是基于阈值的特征值, 当某点处W>0时被识别为拉伸流, 将符合拉伸流条件的特征值置为0, 并在x=0处设置一个关键点, 取该关键点的颜色为白色, 不透明度为0.2, 从而将拉伸流作为不透明度较低的背景流场。将W<0的区域按照涡度的正负进行区分, 涡度为正时代表气旋涡, 颜色映射为冷色调, 并将特征值x取值为负值; 涡度为负时代表反气旋涡, 颜色映射为暖色调, 并将特征值x取值为正值。之后在识别涡旋的阈值处(W.= –2.0×10–12)设置两个关键点, x=0.001处为识别反气旋涡的关键点, 颜色为暖色调, 不透明度置为最高; x = –0.001处为识别气旋涡的关键点, 颜色为冷色调, 不透明度置为最高。从拉伸流的关键点到识别涡旋的关键点之间颜色和不透明度线性过渡, 以识别涡旋的关键点到x的极值处不透明度始终为最高, 保证提取符合W<–2.0×10–12条件的所有涡旋。本文的ow涡旋提取阈值是面向全球海域的, 这是多次调节传输函数并参考Zhang等[17]的结论得出的。
除了在识别涡旋的阈值关键点之外, 本文在涡旋特征区间内加入了多个特征关键点, 并区分了强涡与弱涡。Nieto等[33]使用–2×10–11作为W参数的阈值以提取涡旋; Tian等[9]使用–2×10–10作为W参数的阈值以提取涡旋。本文比较了利用W = –2.0×10–12(x = ±0.001)、W = –2.0×10–11 (x = ±0.01)与W = –2.0×10–10(x=±0.1)提取涡旋的效果, 如图 9所示。随着W绝对值的增大, 方框区域内的涡旋逐渐消失, 至W = –2.0×10–10时完全消失, 而黑潮延伸体区域的涡旋在W = –2.0×10–10时仍有部分保留, 因此本文将W = –2.0×10–10作为区分黑潮延伸体区域的强涡与周围区域弱涡的阈值点。本文还加入了W = –1.0×10–9 (x = ±0.5)关键点来表现强涡内部涡旋强度更强的区域。本文强涡弱涡的阈值选取是面向黑潮流域的。对比图 9(a)、(c)可得, 相比于以往涡旋可视化选取的W<–2.0×10–10阈值[8-9], 本文提取涡旋的阈值更有利于同时表现强涡与弱涡, 有利于可视化表达更多的涡旋。
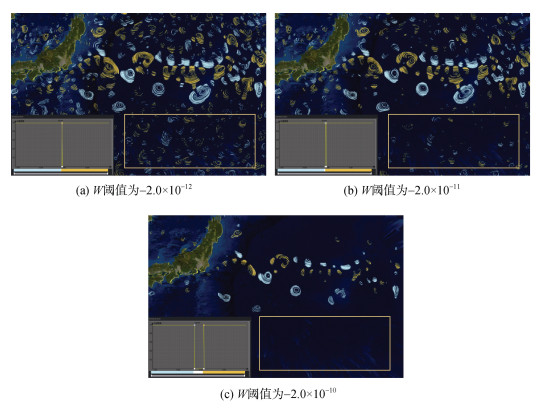 |
| 图 9 基于不同W参数阈值的黑潮流域涡旋提取效果图 Fig. 9 Vortex extraction in Kuroshio basin based on different W parameter thresholds 注: 图中黄色的涡旋为反气旋涡, 青色的涡旋为气旋涡。随着w绝对值的增大, 方框区域内的涡旋逐渐消失, 但是黑潮延伸体区域的涡旋仍然保留。W参数值上限分别为(a) –2.0×10–12, (b) –2.0×10–11, (c) –2.0×10–10 |
Ω方法受阈值影响很小, 本文取Ω=0.5为识别涡旋的阈值, 某点处Ω<0.5时被识别为拉伸流, 将符合拉伸流条件的特征值x置为0, 将Ω>0.5的区域按照涡度的正负进行区分, 涡度为正时代表气旋涡, 颜色映射为冷色调, 并将特征值x取值为负值; 涡度为负时代表反气旋涡, 颜色映射为暖色调, 并将特征值x取值为正值。在x = 0、x = ±0.5和x = ±1处设置关键点, x = 0处的关键点颜色置为白色, 不透明度置为0.2, 从x = 0到x = ±0.5之间颜色和不透明度线性过渡以保留背景流场; 从识别涡旋的关键点到x = ±1处不透明度始终为最高, 保证尽可能提取更多的涡旋。基于Ω特征值的标准传输函数是面向全球海洋的。
在确定了传输函数的线型与关键点之后, 需要对在涡旋特征区间的关键点调色。本文利用了HSV(hue, saturation, value, 即色调、饱和度、明度, 记为H, S, V)彩色系统, 更直观定量地解释关键点的调色。如图 10, H(色调)利用颜色环控制, 用角度度量, 取值范围为0°~360°, 从红色(0°)开始逆时针多次旋转60°依次得到黄色、绿色、青色、蓝色和品红色。通过设置H的数值可以控制关键点的色调。S(饱和度)代表颜色接近颜色环上光谱色的程度, 数值越大越接近光谱色。V表示色彩的明亮程度, 数值越大色彩越明亮。S与V的取值范围都为0~255。HSV系统是面向用户的调色系统, 可感知度更高。本文暖色调选取了H值为0~60的红-黄区间, 按照反气旋涡特征点的数量将H值区间等分并为特征点赋值; 冷色调选取了H值为180~240的青-蓝区间, 按照气旋涡特征点的数量将H值区间等分并为特征点赋值。每个特征点S与V值为最高, 保证特征点的颜色即为颜色环上的光谱色。ow方法特征点与Ω方法特征点的色彩方案如表 1、表 2所示。
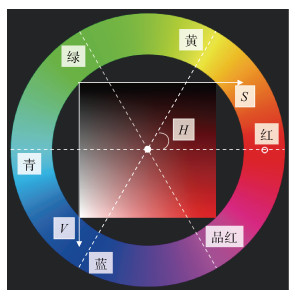 |
| 图 10 HSV调色系统示意图 Fig. 10 Schematic of hue, saturation, and value color-matching system 注: 颜色环为色调区, 以红色为起点, 逆时针旋转角为H值; 色域区为正方形, 从左上角延S轴向右饱和度增大, 从左上角延V轴向下明度增大 |
| ow特征值 | –1.0×10–9 | –2.0×10–10 | –2.0×10–11 | –2.0×10–12 | 2.0×10–12 | 2.0×10–11 | 2.0×10–10 | 1.0×10–9 |
| x | –0.5 | –0.1 | –0.01 | –0.001 | 0.001 | 0.01 | 0.1 | 0.5 |
| H | 240 | 220 | 200 | 180 | 60 | 40 | 20 | 0 |
| S | 255 | 255 | 255 | 255 | 255 | 255 | 255 | 255 |
| V | 255 | 255 | 255 | 255 | 255 | 255 | 255 | 255 |
| RGB | (0, 0, 255) | (0, 85, 255) | (0, 170, 255) | (0, 255, 255) | (255, 255, 0) | (255, 170, 0) | (255, 85, 0) | (255, 0, 0) |
| Ω特征值 | –1.0 | –0.5 | 0.5 | 1.0 |
| x | –1.0 | –0.5 | 0.5 | 1.0 |
| H | 240 | 180 | 60 | 0 |
| S | 255 | 255 | 255 | 255 |
| V | 255 | 255 | 255 | 255 |
| RGB | (0, 0, 255) | (0, 255, 255) | (255, 255, 0) | (255, 0, 0) |
最终得到基于ow特征值与Ω特征值的标准传输函数, 如图 11所示。
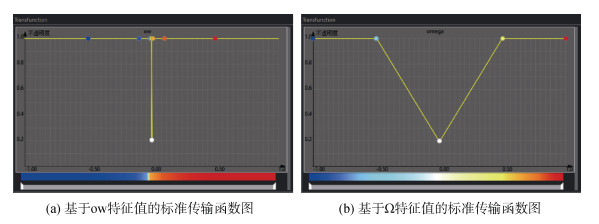 |
| 图 11 标准传输函数图 Fig. 11 Standard transfer function diagram 注: (a)图中横坐标放大了5.0×108倍 |
本文基于ow特征值的标准传输函数综合考虑了多个涡旋提取阈值, 并针对黑潮区域强涡弱涡选取了合适的特征点; 而且标准传输函数的配色设计易于感知定量可控, 实现了从涡旋特征空间到颜色空间的映射, 解决了以往利用RGB彩色系统交互调节传输函数[8-9]难以解释的难题。
利用本文的标准传输函数, 用户可以直接提取海洋涡旋, 如果有更精细的探索涡旋的需求, 可以在标准传输函数基础上在涡旋有效区间内加入更多的关键点。这降低了用户手动调节传输函数的难度, 优化了传输函数的交互性。
3.3 海洋中尺度涡旋可视化效果本文的可视化效果是基于自研渲染引擎实现的, 图 12(a)、(b)展示了基于ow特征值标准传输函数和基于Ω特征值标准传输函数的二维涡旋可视化效果。
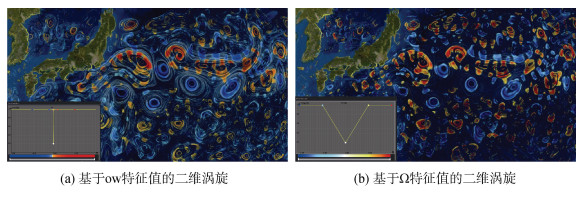 |
| 图 12 二维涡旋可视化效果图 Fig. 12 Two-dimensional vortex visualization 注: (a)为基于ow特征值的标准传输函数, 图中横坐标放大了5.0×108倍; (b)为基于Ω特征值的标准传输函数 |
为了更好地观察海洋涡旋三维结构, 本文将在背景流场区间的传输函数不透明度值设为最低, 得到了图 13所展示的基于标准传输函数的三维涡旋可视化效果。图 13中, 本文利用2012年1月11日的OMEGA3D数据可视化, 其中第一、二行分别为基于ow准则和Ω准则提取的涡旋效果, 第一列为黑潮流域涡旋可视化效果, 第二列为第一列红色方框中的涡旋放大图, 1号为反气旋涡, 2号为气旋涡。冷色调代表气旋涡, 暖色调代表反气旋涡。
 |
| 图 13 三维涡旋可视化效果图 Fig. 13 Three-dimensional vortex visualization |
从图 13(a)、(b)中可以看到, 基于ow的标准传输函数能够较好地区分强涡和弱涡, 图 13(a)、(c)显示, 基于Ω的标准传输函数提取的涡旋数量较基于ow方法多。图 14中在鄂霍次克海域的二维涡旋可视化效果也表明了这一现象, 图 14中红色方框区域内ow准则识别为背景流场, 而Ω准则识别为涡旋, 且基于Ω准则识别的涡旋更饱满, 这是因为ow受阈值影响, 将一部分弱涡识别为背景流场, 而Ω准则受阈值影响很小, 可以尽可能地提取所有涡旋。但是基于Ω方法提取的不同涡旋表现了近似的颜色分布, 不易区分强涡和弱涡, 这是因为Ω方法度量了涡旋的相对强度, 不同的涡旋都具有相对涡旋强度较强的涡核区域, 从而难以区分涡旋的强弱。ow方法则度量了涡旋的绝对强度, 旋转强度与应变强度的差值(绝对强度)在每个涡旋中的范围都不一致, 从而可以用W值表达涡旋的强弱层次。图 12黑潮流域以及图 14鄂霍次克海域的二维涡旋可视化效果显示, ow方法能较好区分强涡弱涡, 而Ω方法较难区分。
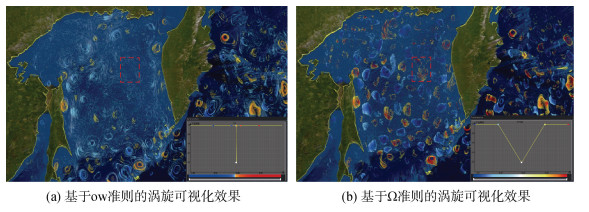 |
| 图 14 鄂霍次克海域二维涡旋可视化效果图 Fig. 14 Visualization of two-dimensional vortexes in Okhotsk Sea area 注: 利用2012年1月1日的MSLA数据可视化。(a)为基于ow准则的涡旋可视化效果, (b)为基于Ω准则的涡旋可视化效果。在红色方框区域内, 基于ow准则识别为无涡旋, 而基于Ω准则识别为有涡旋。传输函数中的W参数的横坐标放大了5.0×108倍, 冷色调代表气旋涡, 暖色调代表反气旋涡 |
本文中尺度涡旋可视化性能如表 3所示, 本文的中尺度涡旋可视化效率都达到了实时交互的性能级别。
| 2D中尺度涡旋可视化 | 3D中尺度涡旋可视化 | |
| ow方法 | 36.3 | 30.4 |
| Ω方法 | 36.5 | 30.9 |
为了验证在海洋中尺度涡旋流场可视化系统中直观观察到的Ω方法相较于ow方法能更全面地提取中尺度涡旋的现象, 本文利用W<–2.0×10–12和Ω>0.5阈值条件离线计算了2012年1月1日的全球MSLA数据(分辨率为1 440×720), 提取海洋中尺度涡旋, 将气旋涡的像素点设为蓝色, 反气旋涡的像素点设为红色, 背景流场设为白色, 并统计了在西北太平洋区域的涡旋数量(见表 4)(忽略了像素点数量小于4的图斑, 此处下限设为4是由于中尺度涡旋的半径为数十至数百km, 以4像素为面积的圆, 直径约为50 km), 涡旋识别区域如图 15所示。
| 气旋涡 | 反气旋涡 | 总数 | |
| ow方法 | 740 | 752 | 1 492 |
| Ω方法 | 782 | 787 | 1 569 |
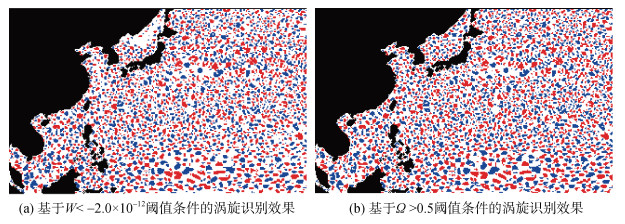 |
| 图 15 西北太平洋海洋中尺度涡旋识别效果图 Fig. 15 Effect map of ocean mesoscale eddy recognition in Northwest Pacific 注: 利用2012年1月1日的MSLA数据识别涡旋。研究范围为0 N°~50 N°, 100 E°~180 E°。(a)为基于W<–2.0×10–12阈值条件的涡旋识别效果, (b)为基于Ω>0.5阈值条件的涡旋识别效果 |
统计结果表明西北太平洋Ω方法提取的涡旋数量多于ow方法。
以上统计结果表明, Ω方法相较于ow方法都能更全面地提取中尺度涡旋。但是海洋中尺度涡旋流场可视化系统的观察效果(图 12, 图 14)表明Ω方法难以区分强涡与弱涡, 而基于ow标准传输函数提取的涡旋的区分效果较好。基于Ω标准传输函数的海洋中尺度涡旋可视化效果表明, 以往利用W<–2.0×10–10的阈值标准[8-9]而遗漏的弱涡同样可以利用Ω方法清晰直观地可视化, 而不应因为涡旋强度过小而舍弃这部分涡旋的识别, 本文的中尺度涡旋可视化效果克服了前人可视化弱涡的缺陷。基于标准传输函数提取的中尺度涡旋效果都能表达涡旋结构的细节, 实现了高感知度的涡旋可视化。
4 基于GPU的算法实现与性能测试 4.1 基于GPU的算法实现本文利用C++和OpenGL实现了基于迹线的涡旋可视化。本文用过程(PASS)来指代渲染流水线, 在一个PASS中集成了多个着色器, 同时也可以设置渲染状态, 它是图形渲染的基本功能模块, 基于多PASS技术涡旋可视化实现步骤如图 16所示。PASS1、PASS2、PASS3分别代表了第一个渲染过程、第二个渲染过程、第三个渲染过程。
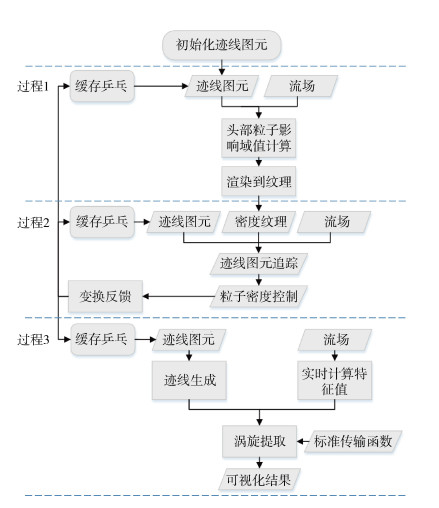 |
| 图 16 海洋涡旋可视化流程图 Fig. 16 Flowchart of ocean vortex visualization |
首先对迹线图元的初始化。对于二维涡旋可视化, 本文在全球海域90°N~90°S、180°W~180°E范围的360×180数量的经纬度网格上, 对每个网格(1°×1°)播种一个迹线图元; 对于三维涡旋可视化, 本文在局部海域0°N~60°N、100°E~180°E、–1 482.5~ –2.5 m的深度(75层数据)上对60×80×75个经纬深度网格播种迹线图元。初始化时同一图元上的粒子位置年龄相同。
在PASS1中迹线图元以面片(PATCH)的IBO (index buffer object)(索引缓冲对象)形式将粒子通过VBO(vertex buffer object)(顶点缓冲对象)传入到PASS1中的顶点着色器, 并在PASS1的片段着色器计算迹线图元头部粒子的影响域值, 最终将渲染结果保存为概率密度图。
在PASS2中实现对迹线图元的追踪和密度控制。顶点着色器接收VBO的迹线图元并将图元传入细分着色器中, 细分着色器接收迹线图元和PASS1的概率密度图, 迹线图元头部粒子采样流场纹理获取速度, 通过4阶龙格-库塔算法更新这一帧迹线图元头部粒子的位置, 迹线图元上其他粒子的位置各自更新为上一帧同一迹线图元的前一个索引的粒子位置(图 2), 从而实现迹线图元上粒子的时空连续。在细分着色器中还实现了迹线图元的密度控制, 保证迹线图元的动态均匀分布。通过PASS2的几何着色器, 将来自细分着色器的迹线图元输出为点图元, 由变换反馈(transform feedback)机制记录到VBO中, 通过设置了与VBO大小状态相同的缓存TBO, 将VBO与TBO构成乒乓缓存(buffer pingponging), 变换反馈机制将PASS2输出的点图元交替写入到VBO或TBO中, 根据IBO保存为面片, 当从VBO中读取上一帧的迹线图元时, TBO负责写入这一帧的迹线图元, 之后变换VBO与TBO的读写状态, 从而使迹线图元不断随着每一帧而更新, 实现了对迹线图元的追踪。
在PASS3中实现迹线的生成和涡旋提取。迹线图元经由顶点着色器传入细分着色器, 而标准传输函数作为一张一维纹理传入细分着色器, 通过对迹线图元上的粒子计算特征值并采样一维纹理, 为迹线图元赋予涡旋特征的颜色。在二维涡旋可视化中, 用等值线细分(isolines)的方式将迹线图元上的粒子细分为迹线上的各个顶点, 通过片段着色器的光栅化阶段后, 生成二维迹线; 在三维涡旋可视化中, 用四边形细分(quads)的方式将迹线图元上的顶点细分为迹管三维模型的顶点, 迹管上的顶点经过片段着色器光栅化阶段后, 生成三维迹线。
本文迹线图元的追踪和迹线的生成都是在GPU端计算运行的, 这充分利用了GPU并行计算的特性, 能够达到较高的性能, 从而实现全时空连续的实时交互高感知度海洋涡旋流场可视化效果, 而目前的海洋流场可视化方案[35-36]则主要在CPU端离线计算流线上各个顶点的位置并生成流线, 之后再将流线数据发送至GPU端进行渲染, 可交互性较低, 并且该方案只能实现稳定流场的可视化效果, 不能实现时空连续的不稳定流场可视化效果, 本文海洋流场可视化为此提供了GPU端的解决方案。
4.2 性能测试本文的性能测试平台基于以下计算机硬件配置: NVDIA GeForce GTX 1050Ti(4 GB显存), Intel Core i7-4790处理器(3.60 GHz), Windows 10 64位专业版系统, 24G内存。可视化窗口的尺寸为1 920×1 080。性能参数以帧率表示(单位f/s)。二维迹线-迹线中迹线图元的数量与二维迹线-流线的粒子数量均为360×180×4, 三维迹线-迹线中迹线图元数量与三维迹线-流线的粒子数量均为60×80×75。图 17是基于迹线-流线时空连续框架的二维、三维流场可视化效率与基于迹线-迹线全时空连续框架的二维、三维流场可视化效率的对比。
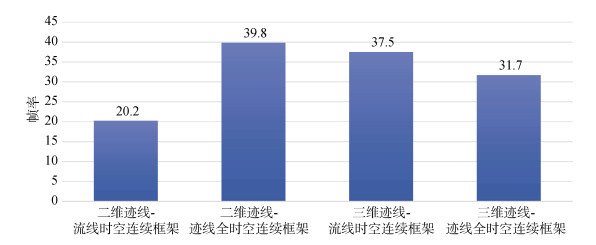 |
| 图 17 基于迹线-流线时空连续框架与基于迹线-迹线全时空连续框架可视化性能对比图 Fig. 17 Comparison of visualization performance between pathline–streamline based spatiotemporal continuous and pathline–pathline based full spatiotemporal continuous frameworks |
在二维流场可视化中, 本文方案的性能优于迹线-流线方案。主要原因是迹线-流线方案中的流线生成利用了几何着色器的将点图元扩充为线段图元的功能, 其中的扩充操作对性能损失影响严重。而本文的方案中迹线图元上的粒子数量都是相同的, 只需要在细分着色器中将迹线图元面片的顶点细分为等值线并渲染为线段, 没有用到几何着色器中的扩充操作, 从而优化了性能。
在三维流场可视化中, 本文方案的性能较迹线-流线方案低, 在迹线-流线方案中, 流线是利用细分着色器将流线头部粒子面片细分为四边形域并渲染为流管生成的, 而迹线-迹线方案中迹线是利用细分着色器将迹线图元面片上的顶点细分为四边形域并渲染为迹管生成的, 本文的方案要求细分着色器处理的面片顶点数量较迹线-流线方案处理的面片顶点数量多, 这是本文方案性能略低的原因。以上性能对比结果表明, 这四种流场可视化的效率都达到了实时可交互的级别。
5 结论本文基于前人对时空连续框架的研究, 创新性地提出了迹线-迹线全时空连续框架, 并应用了两种基于区域的涡旋提取技术——ow准则和Ω准则来提取中尺度涡旋, 构建了面向海洋中尺度涡旋提取的标准传输函数。本文的全时空连续框架方案增强了可视化效果的时空连续性, 在海洋流场可视化中的性能达到交互级别。在两种涡旋提取技术中, ow受阈值影响较大, 不能较全面地提取涡旋, 但是能区分强涡与弱涡的结构; Ω方法则可以尽可能地提取全球海洋涡旋, 但是不同涡旋结构相似, 较难区分强涡与弱涡。基于本文的标准传输函数可以实现对黑潮流域中尺度涡旋的实时提取, 在尽可能提取全部涡旋的同时也能表现涡旋的形态和结构, 降低了用户交互传输函数的复杂度。
未来我们将改进时空连续框架和中尺度涡旋提取技术。首先, 全时空连续框架中迹线会有互相交错的情况, 将客观参考系引入全时空连续框架将会改善迹线空间感知度较低的情况; 针对时变流场, 如何用传输函数可视化流场的时变信息也是一个挑战; 对于三维中尺度涡旋可视化, 如何改善迹线的重叠和混合情况, 提高迹线的空间感知也是亟须解决的问题, 通过引入涡旋核心线可以在一定程度上改善这些情况。我们未来会加强对三维中尺度涡旋轨迹的实时交互可视化, 积极地探索三维涡旋与流场的相互作用, 实时定量化计算海洋中尺度涡旋的体积、动能等涡旋参数, 为研究人员建立感知度更高的孪生海洋交互可视分析平台。
| [1] |
钱程程, 陈戈. 海洋大数据科学发展现状与展望[J]. 中国科学院院刊, 2018, 33(8): 884-891. QIAN Chengcheng, CHEN Ge. Big data science for ocean: present and future[J]. Bulletin of the Chinese Academy of Sciences, 2018, 33(8): 884-891. DOI:10.16418/j.issn.1000-3045.2018.08.018 |
| [2] |
国家自然科学基金委员会地球科学部. 海洋科学学科研究方向与关键词(试用版 2022)[M]. 北京: 国家自然科学基金委员会, 2021: 51-53. National Natural Science Foundation of China, Earth Sciences Division. Directions and key words of marine science and related fields of the national natural science foundation of china(Trial edition 2022) [M]. Beijing: National Natural Science Foundation of China, 2021: 51-53. |
| [3] |
宋汉戈, 刘世光. 三维流场可视化综述[J]. 系统仿真学报, 2016, 28(9): 1929-1936. SONG Hange, LIU Shiguang. Review of 3D Flow Visualization[J]. Journal of System Simulation, 2016, 28(9): 1929-1936. DOI:10.16182/j.cnki.joss.2016.09.001 |
| [4] |
WEISKOPF D, SCHRAMM F, ERLEBACHER G, et al. Particle and texture based spatiotemporal visualization of time-dependent vector fields[C]//IEEE Visualization 2005. Minneapolis, USA: IEEE, 2005: 639-646.
|
| [5] |
HELGELAND A, ELBOTH T. High-quality and interactive animations of 3D time-varying vector fields[J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(6): 1535-1546. DOI:10.1109/TVCG.2006.95 |
| [6] |
LI G S, TRICOCHE X, WEISKOPF D, et al. Flow charts: Visualization of vector fields on arbitrary surfaces[J]. IEEE Transactions on Visualization and Computer Graphics, 2008, 14(5): 1067-1080. DOI:10.1109/TVCG.2008.58 |
| [7] |
何珏, 田丰林, 张昉, 等. 基于实时几何流线生成的二维海流数据交互可视化方法[J]. 海洋技术, 2015, 34(3): 91-96. HE Jue, TIAN Fenglin, ZHANG Fang, et al. Study on the interactive visualization method of 2D ocean current data based on real-time geometric streamline generation[J]. Journal of Ocean Technology, 2015, 34(3): 91-96. |
| [8] |
田丰林, 朱新升, 刘巍, 等. 基于传输函数的中尺度涡旋时空连续可视化[J]. 海洋学报, 2020, 42(9): 119-133. TIAN Fenglin, ZHU Xinsheng, LIU Wei, et al. Time-space continuous visualization of mesoscale vortices based on transfer function[J]. Acta Oceanologica Sinica, 2020, 42(9): 119-133. |
| [9] |
TIAN F L, CHENG L Q, CHEN G. Transfer function-based 2D/3D interactive spatiotemporal visualizations of mesoscale eddies[J]. International Journal of Digital Earth, 2020, 13(5): 546-566. DOI:10.1080/17538947.2018.1543364 |
| [10] |
TIAN F L, MAO Q, ZHANG Y Z, et al. i4Ocean: transfer function-based interactive visualization of ocean temperature and salinity volume data[J]. International Journal of Digital Earth, 2021, 14(6): 766-788. DOI:10.1080/17538947.2021.1886355 |
| [11] |
LARAMEE R S, ERLEBACHER G, GARTH C, et al. Applications of texture-based flow visualization[J]. Engineering Applications of Computational Fluid Mechanics, 2008, 2(3): 264-274. DOI:10.1080/19942060.2008.11015227 |
| [12] |
GÜNTHER T, THEISEL H. The state of the art in vortex extraction[J]. Computer Graphics Forum, 2018, 37(6): 149-173. DOI:10.1111/cgf.13319 |
| [13] |
HUNT J C R. Vorticity and vortex dynamics in complex turbulent flows[J]. Transactions of the Canadian Society for Mechanical Engineering, 1987, 11(1): 21-35. DOI:10.1139/tcsme-1987-0004 |
| [14] |
OKUBO A. Horizontal dispersion of floatable particles in vicinity of velocity singularities such as convergences[J]. Deep Sea Research and Oceanographic Abstracts, 1970, 17(3): 445-454. DOI:10.1016/0011-7471(70)90059-8 |
| [15] |
WEISS J. The dynamics of enstrophy transfer in 2-dimensional hydrodynamics[J]. Physica D Nonlinear Phenomena, 1991, 48(2/3): 273-294. |
| [16] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 332(1): 339-363. |
| [17] |
ZHANG Z G, ZHANG Y, WANG W, et al. Universal structure of mesoscale eddies in the ocean[J]. Geophysical Research Letters, 2013, 40(14): 3677-3681. DOI:10.1002/grl.50736 |
| [18] |
CHELTON D B, SCHLAX M G, SAMELSON R M, et al. Global observations of large oceanic eddies[J]. Geophysical Research Letters, 2007, 34(15): 87-101. |
| [19] |
LIU C Q, WANG Y Q, YANG Y, et al. New omega vortex identification method[J]. Science China Physics, Mechanics and Astronomy, 2016, 59(8): 1-9. |
| [20] |
邵绪强, 刘艺林, 杨艳, 等. 流体的旋涡特征提取方法综述[J]. 图学学报, 2020, 41(5): 687-701. SHAO Xuqiang, LIU Yilin, YANG Yan, et al. A review of vortex feature extraction methods for fluid[J]. Journal of Graphics, 2020, 41(5): 687-701. |
| [21] |
JOBARD B, LEFER W. Unsteady flow visualization by animating evenly-spaced streamlines[J]. Computer Graphics Forum, 2010, 19(3): 31-39. |
| [22] |
KNISS J, KINDLMANN G, HANSEN C. Multidimensional transfer functions for interactive volume rendering[J]. IEEE Transactions on Visualization and Computer Graphics, 2002, 8(3): 270-285. |
| [23] |
DINESHA V, ADABALA N, NATARAJAN V. Uncertainty visualization using HDR volume rendering[J]. The Visual Computer, 2012, 28(3): 265-278. |
| [24] |
HELGELAND A, ANDREASSEN O. Visualization of vector fields using seed LIC and volume rendering[J]. IEEE Transactions on Visualization and Computer Graphics, 2004, 10(6): 673-682. |
| [25] |
SONG Y, YE J, SVAKHINE N, et al. An atmospheric visual analysis and exploration system[J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(5): 1157-1164. |
| [26] |
MATSUOKA D, ARAKI F, YAMASHITA Y. Multiple scatter plots based multi-dimensional transfer function for visualizing ocean simulation data[C]//Asian Simulation Conference. Berlin, Heidelberg: Springer, 2014: 187-200.
|
| [27] |
SHARMA O, ARORA T, KHATTAR A. Graph-based transfer function for volume rendering[J]. Computer Graphics Forum, 2020, 39(1): 76-88. |
| [28] |
LI W Q, CHEN G, KONG Q Q, et al. A VR-Ocean system for interactive geospatial analysis and 4D visualization of the marine environment around Antarctica[J]. Computers & Geosciences, 2011, 37(11): 1743-1751. |
| [29] |
PERLIN K. Improving noise[C]//APPOLLONI T. Proceedings of the 29th annual conference on Computer graphics and interactive techniques. New York, USA: Association for Computing Machinery, 2002: 681-682.
|
| [30] |
WILLIAMS S, HECHT M, PETERSEN M, et al. Visualization and analysis of eddies in a global ocean simulation[C]//Computer Graphics Forum. Oxford, UK: Blackwell Publishing Ltd, 2011, 30(3): 991-1000.
|
| [31] |
CHEN C H, KAMENKOVICH I, BERLOFF P. Eddy trains and striations in quasigeostrophic simulations and the ocean[J]. Journal of Physical Oceanography, 2016, 46(9): 2807-2825. |
| [32] |
杨光. 西北太平洋中尺度涡旋研究[D]. 青岛: 中国科学院研究生院(海洋研究所), 2013. YANG Guang. A study on the mesoscale eddies in the northwestern pacific ocean[D]. Qingdao: Graduate School of the Chinese Academy of Sciences(Institute of Oceanology), 2013. |
| [33] |
NIETO K, MCCLATCHIE S, WEBER E D, et al. Effect of mesoscale eddies and streamers on sardine spawning habitat and recruitment success off Southern and central California[J]. Journal of Geophysical Research: Oceans, 2015, 119(9): 6330-6339. |
| [34] |
LIU C Q, GAO Y S, DONG X R, et al. Third generation of vortex identification methods: Omega and Liutex/Rortex based systems[J]. Journal of Hydrodynamics, 2019, 31(2): 205-223. |
| [35] |
李忠伟, 徐斌, 李永, 等. 基于非结构化三角网格的海洋流场可视化[J]. 图学学报, 2022, 43(3): 486-495. LI Zhongwei, XU bin, LI Yong, et al. Visualization of ocean flow field based on unstructured triangular mesh[J]. Journal of Graphics, 2022, 43(3): 486-495. |
| [36] |
嵇晓峰, 张丰, 王中一, 等. 基于着色模型实时构造的海洋流场动态流线可视化方法研究[J]. 浙江大学学报(理学版), 2020, 47(1): 45-51. JI Xiaofeng, ZHANG Feng, WANG Zhongyi, et al. Research on dynamic streamline visualization of ocean flow field with real-time construction of coloring model[J]. Journal of Zhejiang University(Science Edition), 2020, 47(1): 45-51. |
 2023, Vol. 47
2023, Vol. 47


