
文章信息
- 杨春蕙, 栗小东, 刘琦, 王迎宾. 2023.
- YANG Chun-hui, LI Xiao-dong, LIU Qi, WANG Ying-bin. 2023.
- 机器学习方法在舟山渔场主要经济蟹类生物量估算中的应用
- Application of machine learning methods for estimating the biomass of economically important crabs in the Zhoushan fishery
- 海洋科学, 47(9): 61-70
- Marine Sciences, 47(9): 61-70.
- http://dx.doi.org/10.11759/hykx20221127002
-
文章历史
- 收稿日期:2022-11-27
- 修回日期:2023-03-16
一直以来, 渔业生物量评估基本上以扫海面积法为主, 该方法操作简单、计算方便, 被广泛应用于渔业生物量评估的研究中[1]。但使用该方法须假设评估对象在所研究海域是均匀分布的, 因此, 需要以增加调查站位数量来提高评估的准确性。可见, 目标种类生物量的评估结果与调查的站位数密切相关, 在预算不高的情况下, 评估结果的准确性将会降低。
随着智能化和自动化的发展, 机器学习算法被用于识别渔船行为[2-6]、确定船舶类型[7-10]。除此之外, 机器学习方法被广泛地用于鱼类丰度和分布预测[11-14]、种群鉴定[15]、CPUE标准化[16]以及蟹类、鱼类资源分布与环境因子之间关系的探究[17-19]等方面。例如, 栗小东等[17]运用梯度提升回归树(GBRT)和支持向量机(SVM)这两种机器学习方法, 分析了三疣梭子蟹时空分布与环境因子之间的关系, 结果显示GBRT模型的预测性能较高且模型较为稳定; 陈雪忠等[20]利用历史渔海况数据训练得到的随机森林模型对2010年印度洋长鳍金枪鱼分月渔场的预测, 结果表明预测的渔场位置与实际渔场位置较一致; 张云雷等[21]使用提升回归树模型研究皮氏叫姑鱼(Johnius belangerii) 栖息地中环境与生物之间关系的过程中, 发现提升回归树模型不仅能解释两者之间的复杂关系, 还能够处理生态研究中的各种变量关系。目前基于机器学习方法开展渔业生物量评估的研究鲜见报道[16]。本研究使用随机森林(RF)、梯度提升回归树(GBRT)、极限梯度提升树(XGBoost)3种机器学习方法[22], 根据环境因子与资源调查渔获密度资料的相关关系建立模型, 估算舟山渔场4种主要经济蟹类生物量大小, 并与扫海面积法的估算结果进行了比较分析, 对于探索更为经济、准确的生物量和生物量评估方法, 进而为渔业资源评估和管理提供更有效的技术支持是有意义的尝试。
1 材料与方法 1.1 数据资源数据来自2006年8月, 2007年1月、5月、11月在东海北部海域开展渔业资源底拖网调查所获得的多种经济蟹类数据资料。调查海域范围为121°75′~ 124°25′E、29°75′~31°35′N, 调查区域共设置20个站位(图 1)。调查所用船只为主机功率为184 kW(275HP), 吨位为100 t, 调查船在每一个调查站位拖曳约1 h, 拖速为2 kn。调查同时记录和测定每个站位的底层海水温度(SBT)、底层海水盐度(SBS)以及水深等环境因子。与东海北部海域历史数据[23-29]相比, 此次调查优势经济蟹类组成基本无变化。因此, 选取舟山渔场海域4种优势经济蟹类种作为主要研究对象, 包括: 三疣梭子蟹(Portunus trituberculatus)、双斑鲟(Charybdis bimaculata)、日本鲟(Charybdis japonica)和细点圆趾蟹(Ovalipes punctatus)[23, 30]。海上调查采样及实验室分析方法按照《海洋渔业资源调查规范》(SC/9403—2012)[31]等有关规范、标准进行。
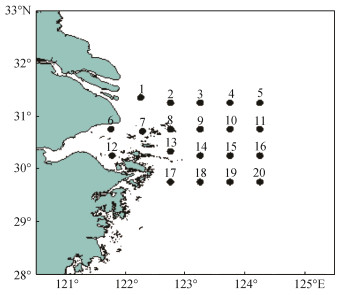 |
| 图 1 调查站位图 Fig. 1 Survey stations of fishery resources |
扫海面积法是根据拖网单位时间的扫海面积和单位时间拖网渔获量估算单位面积内某种渔业资源的绝对数量。采用资源密度计算[32], 其计算公式和步骤如下:
式中, N为计算所得舟山渔场海域4种经济蟹类现存生物量(t), Di为i区的资源密度(t/km2), Ai为i区的面积(km2), 其中:
式中, di为i区的资源密度指数(t/ h), ai为调查船在区每小时扫海面积(km2), E为逃逸率, 本文取E = 0.75[25]。
1.2.2 随机森林随机森林(RF)是基于分类回归树(CART)的一种集成方法[33], 采用了bagging的过程, 通过随机选择生成回归树, 最后利用投票的方式组合得到最终结果或利用预测结果得到最终值[34]。其特点是这些回归树的每一节点的分割变量不再由所有变量竞争产生, 而是由随机选取的变量产生, 且产生每棵树的样本选取是随机的, 生成的每棵树上的节点也是随机产生的。因此, 随机森林所建造的树与树之间是没有关联的, 在计算结果时要对每棵树单独拟合回归, 取平均预测结果作为其预测值[16]。随机森林在建造树时, 对泛化误差使用的是无偏估计, 模型泛化能力强, 且可在有缺失值的情况下维持一定精度。随机森林由于集成调整了学习样本中的细小变化所带来的分类树的不稳定性, 因此与单个分类树相比大大提升了预测精度[35]。
1.2.3 梯度提升回归树梯度提升回归树(GBRT)是一种基于学习器为回归树的组合算法, 主要由残差树、梯度提升和缩减算法3部分组成[36]。它将梯度提升与回归树相结合, 其中每一棵新的回归树拟合学习的都是基于前一棵回归树学习后的残差, 用梯度提升的方法不断降低残差, 对残差的学习也使得回归树变成了残差树[37], 即以损失函数的梯度下降方向为基础建立新的回归树, 最终的输出结果就是每棵回归树输出结果的累加, 从而使结果得到改进[38]。通过多棵决策树结合共同决策, 经过若干次提升法迭代过程后, 输出最终模型[39], 进而缩减算法提升学习效果和速度。
1.2.4 极限梯度提升回归XGBoost (Extreme Gradient Boosting)模型属于GBDT模型的一个改进版本, 其与传统的GBDT最大区别在于: GBDT在优化时只使用泰勒一阶展开, 而XGBoost则使用泰勒二阶展开, 并且XGBoost还引入正则项[40], 是一种基于决策树的集成学习提升方法, 将弱的基分类器组合为更强的分类器[41], 更不容易过拟合。由于它在梯度提升回归树的基础上进行了改进提出的算法, 其优势表现在数据处理效率高效果好泛化能力强主要从以下3个方面进行了优化: 算法本身优化、运行效率优化、健壮性优化[42]。
1.3 环境因子的选择与应用环境因子的选择过程包括两个部分: 优势种特性与环境因子之间的关系以及模型拟合和评估的结果比较[23-24]。4种经济蟹类作为底层游泳动物, 主要受底层海洋环境影响, 影响它们分布的主要环境因素包括底层海水温度、底层海水盐度、水深、pH、叶绿素a浓度[43], 将此5种影响因子作为解释变量, 单位网次渔获量Y作为响应变量, 选择季节作为时间变量。
在筛选模型因子的过程中, 利用方差膨胀因子(VIF)对解释变量进行多重共线性检验[44], 筛选加入模型的环境因子, 当VIF > 3时, 认为该因子存在多重共线性问题, 不予考虑投入建模[17]。
通过逐步回归的方法将环境因子逐个带入模型, 利用方差解释率来评价模型的拟合效果, 方差解释率越高, 表明模型拟合效果越理想。在逐个添加模型因子的过程中, 当方差解释率不再增加时, 则停止添加因子并选择此时的模型为最佳模型[17, 44]。方差解释率的计算方法如下:
式中, Var(residual)为残差方差, Var(y)为原始数据方差。
以上3种模型的构建和检验过程均在R 3.6.3软件实现, 其中RF模型由“randomForest”包构建, GBRT模型由“gbm”包构建, XGBoost模型由“xgboost”包构建。
1.4 模拟分析本研究将基于扫海面积法估算所得调查海域20个站位4种经济蟹类的全部生物量为真实值。根据站位点将调查海域划分为20个等面积棋盘格式分布区域。利用Arcgis软件根据渔业调查海域范围经纬度数据估算调查海域总面积(S), S约为24 142.44 km2。因此, 调查海域所划分的20个等面积棋盘格式分布区域中每部分面积约为1 207.122 km2。
在扫海面积法、RF、GBRT、XGBoost4种方法的建模过程中, 根据数据的特点, 去除数值为空的站点数据后分季节建立模型, 明确某季节可用于建模的站位数量(用n表示), 依次减少直至该季节可用于建模的站位数量的一半, 即每次用于建模的站位数为n, n–1, n–2,
式中, Q为所评估海域几种经济蟹类生物量, n为某季节所用总站位数量, Cpred为评估的各站位生物量之和,
将基于扫海面积法估算所得调查海域20个站位4种经济蟹类的全部生物量设为真实值(q), 将其分别与扫海面积法、RF、GBRT、XGBoost 4种方法在每个站位估算得到的蟹类生物量(Q)作差并取绝对值(
在对舟山渔场四种经济蟹类生物量评估模型的创建过程中, 通过方差解释率来评价RF、GBRT、XGBoost3种机器学习模型的拟合效果(表 1), 结果如表 1所示, 除秋季各环境因子之间不存在共线性问题以外, 其余3个季节环境因子之间均存在不同程度的共线性问题, 通过逐步删除共线性较为严重的因子最终筛选得到各季节建模所使用的环境因子数据。利用方差解释率对筛选所得到的环境因子数据进行组合, 评价不同组合下模型的拟合效果, 得到不同季节情况下RF、GBRT、XGBoost3种机器学习方法的环境因子最优组合结果(表 2)。比较不同模型各季节最优组合可知, 不同季节最优模型所包含的环境因子有所差异, 春季RF和XGBoost模型包含SBT和pH两个环境因子, GBRT模型比二者多包含了环境因子Chlorophyll A; 夏季RF模型包含SBT、Chlorophyll A、WD 3个环境因子, GBRT和XGBoost模型多包含了pH; 秋季3种模型共同拥有Chlorophyll A、SBS两个环境因子; 冬季3种模型共同拥有Chlorophyll A、pH两个环境因子, 且RF和GBRT模型多包含了WD。
| 底层海水温度/℃ | 叶绿素a浓度/μg·L–1 | pH | 水深/m | 底层海水盐度 | |
| 春 | 1.944 164 | 7.251 473 | 5.620 451 | 4.749 669 | 12.433 509 |
| 1.357 245 | 3.089 11 | 1.419 891 | 4.014 682 | ||
| 1.144 541 | 1.053 299 | 1.090 979 | |||
| 夏 | 1.907 438 | 6.012 929 | 2.381 524 | 2.876 606 | 8.043 142 |
| 1.504 922 | 1.769 23 | 1.815 063 | 2.825 75 | ||
| 秋 | 1.569 625 | 1.527 576 | 1.266 961 | 1.440 768 | 1.799 36 |
| 冬 | 8.842 839 | 2.391 905 | 1.580 19 | 1.712 273 | 8.004 365 |
| 2.116 188 | 1.426 461 | 1.711 685 | 3.074 593 | ||
| 1.183 176 | 1.167 253 | 1.029 294 | |||
| 注: 表格空缺处为VIF检验中删去的因子, 每个季节最后一行为筛选后剩余的因子 | |||||
| 季节 | RF | GBRT | XGBoost |
| 春季 | SBT + pH | SBT + Chlorophyll A + pH | SBT + pH |
| 夏季 | SBT + Chlorophyll A + WD | SBT + Chlorophyll A + pH + WD | SBT + Chlorophyll A + pH + WD |
| 秋季 | Chlorophyll A + WD + SBS | Chlorophyll A + pH + SBS | SBT + Chlorophyll A + pH + WD + SBS |
| 冬季 | Chlorophyll A + pH + WD | Chlorophyll A + pH + WD | Chlorophyll A + pH |
剔除站位空值后, 春、夏、秋、冬4季可用站位数分别为14、14、16和16。在逐个减少站位数量时, 扫海面积法、RF、GBRT、XGBoost4种方法在评估研究海域几种经济蟹类生物量情况的结果中都出现了离散度不断增大的情况, 表示评估方法的准确性在逐步降低(图 2), 特别是秋冬两季评估结果离散度随投入站位个数的减少而明显增大, 而当投入站位数量大于12时, 4种方法的预测结果都接近真实值。
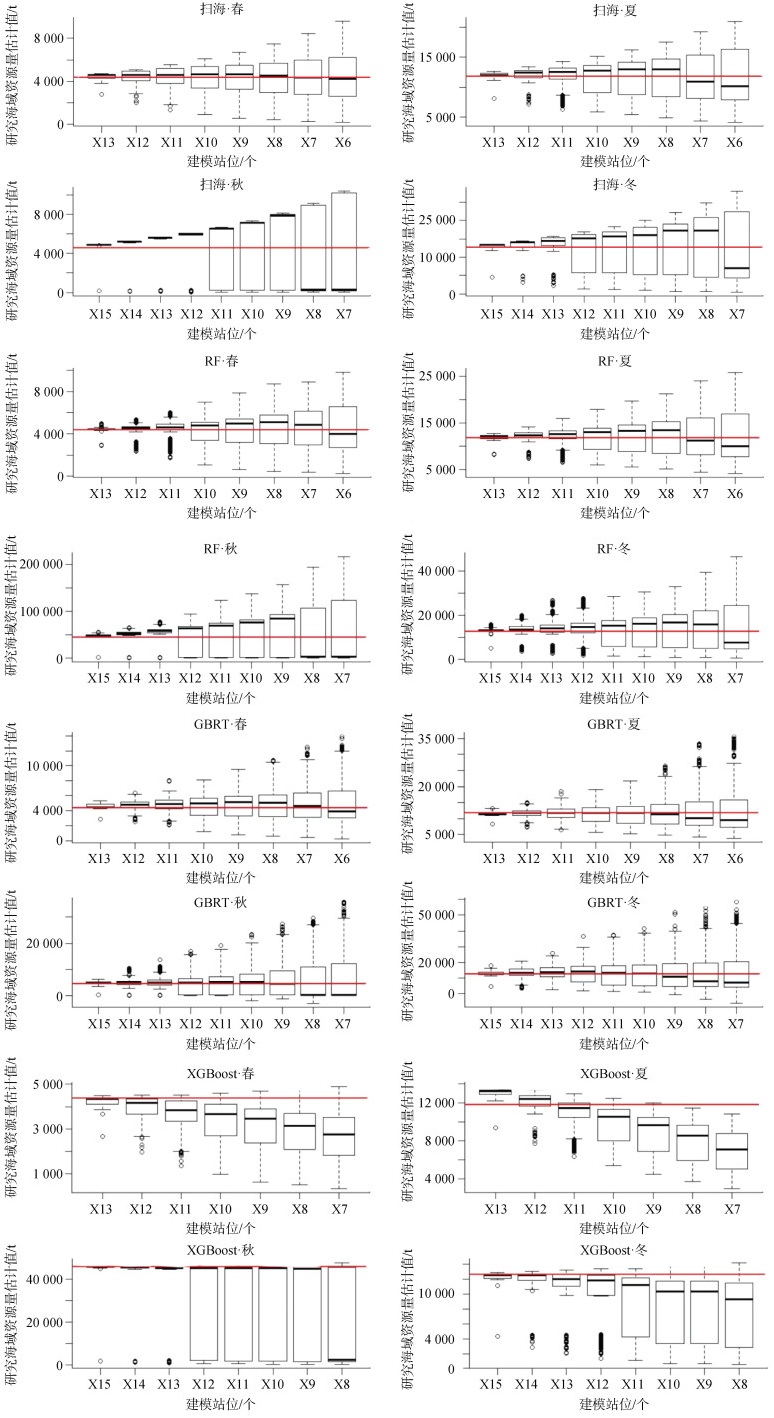 |
| 图 2 扫海面积法、RF、GBRT、XGBoost 4种方法在不同站位数量时生物量评估结果 Fig. 2 Biomass assessment results of the four methods, including the swept area method, RF, GBRT, and XGBoost at different numbers of stations 注: 图中红线代表该季节4种经济蟹类全部生物量的真实值; 箱子表示由大到小排列而成的全部评估数据; 箱子上下缘分别表示该组数据的上四分位数和下四分位数; 横线为该组数据的中位数; 圆圈为异常值 |
当投入的调查站位数量逐渐减少时, 4种方法的评估结果误差均逐渐增大。春季站位间调查数据较为均匀, 3种机器学习方法的评估效果与扫海面积法相比并没有明显优势, 特别是XGBoost的评估结果误差较大且受投入站位数量影响明显; 夏季, GBRT评估效果较好, RF评估结果与扫海面积法结果相似, XGBoost评估结果波动大; 秋季和冬季, GBRT与XGBoost模型评估效果较好, RF评估结果与扫海面积法结果相似(图 2、图 3)。
 |
| 图 3 4种模型评估结果绝对差的比较图 Fig. 3 Comparison of the poor evaluation results of the four models |
扫海面积法是渔业资源生物量评估最常用的方法之一, 本研究中该方法在春季和夏季评估结果优于其他3种机器学习方法, 而在秋季和冬季XGBoost方法评估效果更好。扫海面积法、RF对秋、冬两季经济蟹类生物量出现高估现象(图 2)。春季和夏季4种经济蟹类站位间调查渔获量最大值与最小值之间的差异显著小于秋、冬两季(P < 0.05), 数据分布更为集中且波动平缓。扫海面积法与3种机器学习方法对不同站位数量下生物量进行评估时, 秋冬两季评估结果离散度随投入站位个数的减少而明显增大(图 2、图 3)。这表明极端值和数据分布对于经济蟹类生物量评估方法均有一定程度的影响, 特别是对机器学习方法的性能影响较大。
扫海面积法为基于平均资源密度这一思路进行渔业资源量估测的方法, 即假设资源个体是均匀分布的[45], 因此在数据分布集中的春、夏两季评估效果优势明显。在机器学习方法层面, PENNINGTON[46]认为极端值会极大地影响评估效果, 但盲目地删除极端值也会使评估结果偏离, 未来在进行经济蟹类生物量评估时也可参考国外学者采用的负二项分布、Gamma分布、泊松分布和Δ-分布等多种模型对数据进行估算。除此之外, 渔业资源本身具有一定的流动性和波动性[47], 在评估的过程中无法忽视环境因子与渔业资源分布的关系。不季节不同, 环境因子也会发生变化, 机器学习方法因为考虑到环境因子对评估结果的影响, 考虑范围更加全面、合理。
3.2 模型评估结果差异在大多数情况下RF模型拟合和交叉验证效果很好, 能够应对数据较少、数据集不平衡、特征值遗失等情况[48-50], 但本文中随机森林的优势并未展现。DOMOKOS[51]认为由于随机森林模型是由大量只含部分特征变量的决策树组成, 其预报结果由决策树输出类别的众数决定, 所以由随机森林模型得出的评估结果难以进行人为解释。除此之外, 本文还考虑为RF模型对于含有较多噪声的样本也会发生过度拟合现象[50]。因此在利用RF模型对研究海域资源量生物量进行评估时, 应配合其他方法进行进一步的分析和解释。
GBRT模型作为一种基于残差学习的集成方法, 因其能够在数据异常的情况下分析处理数据, 而被广泛应用于各类型的数据训练中, 但近期有学者, 在对梯度提升回归树的研究中发现[36], 梯度提升回归树算法在处理训练样本时过于粗糙。因为GBRT简单均值函数作为叶节点的预测函数, 在某个叶节点上做输出变量预测时同等考虑所有到达该叶节点的训练样本, 这使得建模时会过度依赖数据的质量, 从而无法达到预测准确。虽然数据量对GBRT模型的最优拟合作用的发挥产生影响, 但可以通过改进模型从而提高拟合效果。吕佳[36]提出可以通过结合K近邻算法的思想对梯度提升回归树模型的预测函数做了改进并修改原梯度提升回归树算法的缩减步长, 让其能自我学习来达到提高模型评估的准确度和效率。综上所述, 随着机器学习方法不断完善和改进, 在未来机器学习方法应用于渔业资源量生物量评估的优势会更加明显。
本研究在3种机器学习方法在应用过程中, 所用到的参数多为默认值, 均未调整为最优拟合作用的情况, 因此会影响机器学习方法对结果评估的准确性, 导致评估结果存在误差、趋势不明显等问题。从模型本身的性质分析可以发现3种机器学习方法还有可以继续优化的空间, 因此在今后的运用中相较于扫海面积法的优势会愈加明显。
3.3 评估方法的经济成本比较本研究使用3种机器学习模型对舟山渔场4种经济蟹类的生物量进行了评估, 并与扫海面积法的估算结果进行了比较。扫海面积法作为传统的渔业资源量生物量评估方法其假设资源个体是均匀分布的, 因此需要较多站位来提高资源量生物量评估的准确性, 在预算不高的情况下难以做到精准实用。而机器学习方法是根据资源和环境因子的相关关系, 评估资源量生物量的分布特征, 从而估算研究海域渔业资源量生物量大小。随着投入站点数目的减少, 在数据波动较大的情况下机器学习方法对生物量的评估效果明显优于扫海面积法。机器学习所用到的环境因子可以从资源调查或者环境监测数据中获得, 不会增加数据获取成本, 且经济效益显著。但在渔业资源分布较为均匀的情况下, 传统的扫海面积法同样得到了较为理想的估算结果。因此, 在研究经费有限的情况下, 采取机器学习方法对经济蟹类生物量评估具有重要意义。
本研究仍存在诸多不足之处, 对于研究海域20个站点的划分, 刻意划分其为等面积的棋盘格式区域, 这是数据误差来源之一。由于剔除了空值方便模型的评估和数据的处理, 一定程度上给4种经济蟹类资源量资源估算带来误差。在今后的研究中, 作者将进一步考虑从真实值的取值方式以及研究海域划分入手, 进一步对数据进行挖掘, 并用热图等方式更为直接地表现出来, 为实际应用过程中, 低成本、高效率的渔业资源评估方法提供理论依据。
| [1] |
詹秉义. 渔业资源评估[M]. 北京: 中国农业出版社, 1995. ZHAN Bingyi. Fishery resources assessment[M]. Beijing: China Agriculture Press, 1995. |
| [2] |
JOO R, BERTRAND S, CHAIGNEAU A, et al. Optimization of an artificial neural network for identifying fishing set positions from VMS data: An example from the Peruvian anchovy purse seine fishery[J]. Ecological Modelling, 2011, 222(4): 1048-1059. DOI:10.1016/j.ecolmodel.2010.08.039 |
| [3] |
宁耀. 基于深度学习的渔船行为识别方法研究[D]. 兰州: 兰州大学, 2020. NING Yao. Fishing behavior recognition method based on the deep learning research[D]. Lanzhou: Lanzhou University, 2020. |
| [4] |
储倩. 基于机器学习的渔船轨迹数据挖掘与行为识别模型[D]. 兰州: 兰州大学, 2021. CHU Qian. Fishing boat trajectory data mining and behavior recognition model based on machine learning[D]. Lanzhou: Lanzhou University, 2021. |
| [5] |
MAZZARELLA F, VESPE M, DAMALAS D, et al. Discovering vessel activities at sea using AIS data: Mapping of fishing footprints[C]//International Conference on Information Fusion, Salamanca, Spain: IEEE, 2014: 1-7.
|
| [6] |
于永照. 基于LightGBM、LGB-NN模型的渔场预报应用研究[D]. 兰州: 兰州大学, 2020. YU Yongzhao. Application research of fishing ground forecast based on LightGBM and LGB-NN model[D]. Lanzhou: Lanzhou University, 2020. |
| [7] |
SOUZA E N D, BOERDER K, MATWIN S, et al. Improving fishing pattern detection from satellite AIS using data mining and machine learning[J]. Plos One, 2016, 11(7): eo158248. |
| [8] |
郑巧玲, 樊伟, 张胜茂, 等. 基于神经网络和VMS的渔船捕捞类型辨别[J]. 南方水产科学, 2016, 12(2): 81-87. ZHENG Qiaoling, FAN Wei, ZHANG Shengmao, et al. Fishing type identification of fishing vessels based on neural network and VMS[J]. Southern Fisheries Science, 2016, 12(2): 81-87. DOI:10.3969/j.issn.2095-0780.2016.02.012 |
| [9] |
KROODSMA D A, MAYORGA J, HOCHBERG T, et al. Tracking the global footprint of fisheries[J]. Science, 2018, 359(6378): 904. DOI:10.1126/science.aao5646 |
| [10] |
HUANG H G, HONG F, LIU J, et al. FVID: Fishing vessel type identification based on VMS trajectories[J]. Journal of Ocean University of China, 2019, 18(2): 403-412. DOI:10.1007/s11802-019-3717-9 |
| [11] |
BARAN P, LEK S, DELACOSTE M, et al. Stochastic models that predict trout population density or biomass on a mesohabitat scale[J]. Hydrobiologia, 1996, 337(1/3): 1-9. |
| [12] |
LEK S, BELAUD A, BARAN P, et al. Role of some environmental variables in trout abundance models using neural networks[J]. Aquatic Living Resources, 1996, 9(1): 23-29. DOI:10.1051/alr:1996004 |
| [13] |
MARAVELIAS C D, HARALABOUS J, PAPACONSTANTINOU C. Predicting demersal fish species distributions in the Mediterranean Sea using artificial neural networks[J]. Marine Ecology Progress Series, 2003, 255: 249-258. DOI:10.3354/meps255249 |
| [14] |
LI Z G, WAN R, YE Z J, et al. Use of random forests and support vector machines to improve annual egg production estimation[J]. Fisheries Science, 2017, 83: 1-11. DOI:10.1007/s12562-016-1033-5 |
| [15] |
HARALABOUS J, GEORGAKARAKOS S. Artificial neural networks as a tool for species identification of fish schools[J]. ICES Journal of Marine Science, 1996, 53(2): 173-180. DOI:10.1006/jmsc.1996.0019 |
| [16] |
杨胜龙, 张禹, 张衡, 等. 不同模型在渔业CPUE标准化中的比较分析[J]. 农业工程学报, 2015, 31(21): 259-264. YANG Shenglong, ZHANG Yu, ZHANG Heng, et al. Comparative analysis of different models in fishery CPUE standardization[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(21): 259-264. DOI:10.11975/j.issn.1002-6819.2015.21.034 |
| [17] |
栗小东, 王晶, 杨春蕙, 等. 基于两种机器学习方法分析东海北部海域三疣梭子蟹(Portunus trituberculatus)时空分布[J]. 海洋与湖沼, 2019, 52(5): 1284-1292. LI Xiaodong, WANG Jing, YANG Chunhui, et al. Spatial and temporal distribution of Portunus trituberculatus in the northern part of the East China Sea based on two machine learning methods[J]. Oceanologia et Limnologia Sincia, 2019, 52(5): 1284-1292. |
| [18] |
LUAN J, ZHANG C L, XU B D, et al. Modelling the spatial distribution of three Portunidae crabs in Haizhou Bay, China[J]. PLoS One, 2018, 13(11): e0207457. DOI:10.1371/journal.pone.0207457 |
| [19] |
栾静, 张崇良, 徐宾铎, 等. 海州湾双斑蟳栖息分布特征与环境因子的关系[J]. 水产学报, 2018, 42(6): 889-901. LUAN Jing, ZHANG Chongliang, XU Binduo, et al. Relationship between double-spotted habitat distribution characteristics and environmental factors in Haizhou Bay[J]. Journal of Fisheries, 2018, 42(6): 889-901. |
| [20] |
陈雪忠, 樊伟, 崔雪森, 等. 基于随机森林的印度洋长鳍金枪鱼渔场预报[J]. 海洋学报(中文版), 2013, 35(1): 158-164. CHEN Xuezhong, FAN Wei, CUI Xusen, et al. Random forest-based longfin tuna fishery forecast in the Indian Ocean[J]. Acta Oceanologica Sinica, 2013, 35(1): 158-164. |
| [21] |
张云雷, 薛莹, 于华明, 等. 海州湾春季皮氏叫姑鱼栖息地适宜性研究[J]. 海洋学报, 2018, 40(6): 83-91. ZHANG Yunlei, XUE Ying, YU Huaming, et al. Habitat suitability study of Pefish in Haizhou Bay[J]. Journal of Oceanography, 2018, 40(6): 83-91. |
| [22] |
GUNDERSON D R. Surveys of fisheries resources[M]. New York: John Wiley and Sons, 1993: 1-31.
|
| [23] |
卢衎尔, 张洪亮, 朱文斌, 等. 浙江近海春、夏季蟹类群落结构及其与环境因子的关系[J]. 水生生物学报, 2019, 43(3): 612-622. LU Caoer, ZHANG Hongliang, ZHU Wenbin, et al. Crab community structure and its relationship with environmental factors in spring and summer offshore Zhejiang[J]. Hydrobiology Journal, 2019, 43(3): 612-622. |
| [24] |
俞存根, 宋海棠, 姚光展. 东海蟹类群落结构特征的研究[J]. 海洋与湖沼, 2005, 36(3): 213-220. YU Cungen, SONG Haitang, YAO Guangzhan. Structure characteristics of crab community in the East China Sea[J]. Oceanologia et Limnologia Sincia, 2005, 36(3): 213-220. |
| [25] |
俞存根, 宋海棠, 姚光展. 东海大陆架海域蟹类资源量的评估[J]. 水产学报, 2004, 1: 41-46. YU Cungen, SONG Haitang, YAO Guangzhan. Assessment of crab resources in the continental shelf area of the East China Sea[J]. Journal of Fisheries, 2004, 1: 41-46. |
| [26] |
徐兆礼. 瓯江口海域夏秋季蟹类数量分布与环境的关系[J]. 水产学报, 2009, 33(2): 237-244. XU Zhaoli. The relationship between the distribution of crab population and the environment in summer and autumn[J]. Journal of Fisheries, 2009, 33(2): 237-244. |
| [27] |
张洪亮, 张龙, 陈峰, 等. 浙江南部近岸海域春季蟹类群落结构特征[J]. 中国水产科学, 2013, 20(5): 1050-1056. ZHANG Hongliang, ZHANG Long, CHEN Feng, et al. Structural characteristics of spring crab community in the coastal waters of southern Zhejiang province[J]. China Fisheries Science, 2013, 20(5): 1050-1056. |
| [28] |
梁金玲, 章守宇, 汪振华, 等. 马鞍列岛海域蟹类群落结构及其多样性[J]. 生态学杂志, 2016, 35(2): 431-440. LIANG Jinling, ZHANG Shouyu, WANG Zhenhua, et al. Crab community structure and diversity in the waters of Maan Islands[J]. Journal of Ecology, 2016, 35(2): 431-440. |
| [29] |
杨刚. 山东近海蟹类群落结构及三疣梭子蟹生长参数、资源量研究[D]. 上海: 上海海洋大学, 2017. YANG Gang. Study on community structure and growth parameters and resources of Shandong[D]. Shanghai: Shanghai Ocean University, 2017. |
| [30] |
徐雪, 唐伟尧, 王迎宾. 舟山渔场及长江口渔场临近海域三疣梭子蟹增殖容量估算[J]. 南方水产科学, 2019, 15(3): 126-132. XU Xue, TANG Weiyao, WANG Yingbin. Estimation of proliferation capacity of swimming crabs in Zhoushan fishery and Yangtze Estuary fishery[J]. Southern Aquatic Sciences, 2019, 15(3): 126-132. |
| [31] |
中华人民共和国国家质量监督检验检疫总局. GB/T 12763.6—2007海洋调查规范第6部分海洋生物调查[S]. 北京: 中国标准出版社2007. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. GB/T 12763.6—2007 Code for Marine survey Part 6 Marine biological survey[S]. Beijing: Standards Press of China 2007. |
| [32] |
耿宝龙, 邱盛尧. 靖海湾三疣梭子蟹增殖放流资源量贡献率的调查研究[J]. 烟台大学学报(自然科学与工程版), 2014, 27(1): 71-74. GENG Baolong, QIU Shengyao. Investigation on the contribution rate of the proliferation and release of swimming crab in Jing Bay[J]. Journal of Yantai University (Natural Science and Engineering edition), 2014, 27(1): 71-74. |
| [33] |
BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. |
| [34] |
LANTZ B. Machine learning with R(2nd ed)[M]. Birmingham: Packt Publishing, 2015.
|
| [35] |
STROBL C, BOULESTEIX A L, ZEILEIS A, et al. Bias in random forest variable importance measures: illustrations, sources and a solution[J]. BMC bioinformatics, 2007, 8: 25. |
| [36] |
吕佳. 梯度提升回归树算法研究及改进[D]. 上海: 上海交通大学, 2017. LV Jia. Research and improvement of the gradient lifting regression tree algorithm[D]. Shanghai: Shanghai Jiao Tong University, 2017. |
| [37] |
FRIEDMAN J H. Greedy function approximation: a gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. |
| [38] |
SAKHNOVICH A. On the GBDT version of the Bäcklund-Darboux transformation and its applications to linear and nonlinear equations and Weyl theory[J]. Mathematical Modelling of Natural Phenomena, 2012, 5(4): 340-389. |
| [39] |
赵卫东, 董亮. 机器学习[M]. 北京: 人民邮电出版社, 2018: 53. ZHAO Weidong, DONG Liang. Machine learning[M]. Beijing: People's Posts and Telecommunications Press, 2018: 53. |
| [40] |
王青松, 谢兴生, 佘颢. 基于CNN-XGBoost混合模型的短时交通流预测[J]. 测控技术, 2019, 38(4): 37-40, 67. WANG Qingsong, XIE Xingsheng, SHE Hao. Short- time traffic flow prediction based on a CNN-XGBoost mixed model[J]. Measurement and Control Technology, 2019, 38(4): 37-40, 67. |
| [41] |
QIAN K, REN Z, DONG F, et al. Deep wavelets for heart sound classification[C]//Proceedings of the 28th International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS). Piscataway: IEEE, 2019
|
| [42] |
吕盼成. 基于集成学习的雅砻江流域中长期径流预报研究[D]. 北京: 华北电力大学, 2021. LV Pancheng. Research on medium and long-term runoff prediction in Yalong River Basin based on integrated learning[D]. Beijing: North China Electric Power University, 2021. |
| [43] |
丁朋朋, 高春霞, 田思泉, 等. 浙江南部近海蟹类群落结构及其与环境因子的关系[J]. 海洋渔业, 2019, 41(6): 652-662. DING Pengpeng, GAO Chunxia, TIAN Siquan, et al. Community structure and its relationship with environmental factors in southern Zhejiang[J]. Marine Fisheries, 2019, 41(6): 652-662. |
| [44] |
KABACOFF R I. R in action: data analysis and graphics with R[M]. Shelter Island: Manning Publications, 2011: 1-474.
|
| [45] |
黄良敏, 李军, 张雅芝, 等. 闽江口及附近海域渔业资源现存量评析[J]. 热带海洋学报, 2010, 29(5): 142-148. HUANG Liangmin, LI Jun, ZHANG Yazhi, et al. Evaluation of the existing quantity of fishery resources in Minjiang Estuary and nearby waters[J]. Journal of Tropical Oceanography, 2010, 29(5): 142-148. |
| [46] |
PENNINGTON M. Estimating the mean and variance from highly skewed marine data[J]. Fishery Bulletin, 1996, 94(3): 498-505. |
| [47] |
陈新军. 海洋渔业资源可持续利用评价[D]. 南京: 南京农业大学, 2001. CHEN Xinjun. Evaluation of the sustainable utilization of marine fishery resources[D]. Nanjing: Nanjing Agricultural University, 2001. |
| [48] |
方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32-38. FANG Kuangnan, WU Jianbin, ZHU Jianping, et al. Review of random forest methods studies[J]. Statistics and Information Forum, 2011, 26(3): 32-38. |
| [49] |
董师师, 黄哲学. 随机森林理论浅析[J]. 集成技术, 2013, 2(1): 1-7. DONG Shishi, HUANG Zhexue. Analysis of random forest theory[J]. Integration Technology, 2013, 2(1): 1-7. |
| [50] |
SEGAL M R. Machine learning benchmarks and random forest regression[J]. Center for Bioinformatics & Molecular Biostatistics, 2004, 1-14. |
| [51] |
DOMOKOS R K, SEKI M P, POLOVINA J J, et al. Oceanographic investigation of the American Samoa albacore (Thunnus alalunga) habitat and longline fishing grounds[J]. Fisheries Oceanography, 2007, 16(6): 555-572. |
 2023, Vol. 47
2023, Vol. 47


