
文章信息
- 华峻巍, 王法明. 2024.
- HUA Junwei, WANG Faming. 2024.
- 基于卫星海面高度资料的太平洋海区涡旋能谱分析
- Power spectra analysis of Pacific Ocean eddies based on satellite altimeter data
- 海洋科学, 48(1): 1-10
- Marine Sciences, 48(1): 1-10.
- http://dx.doi.org/10.11759/hykx20220921003
-
文章历史
- 收稿日期:2022-09-21
- 修回日期:2022-11-19
2. 中国科学院大学, 北京 100049;
3. 中国科学院海洋环流与波动重点实验室, 山东 青岛 266071;
4. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室, 山东 青岛 266237
2. University of the Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Ocean Circulation and Wave, the Chinese Academy of Sciences, Qingdao 266071, China;
4. Laboratory for Ocean and Climate Dynamics, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China
中尺度涡旋在海洋多尺度运动中扮演着承上启下的重要角色。一方面, 它通过斜压不稳定过程从大尺度平均环流中汲取能量, 并以涡-流相互作用的方式将能量逆向传递给大尺度; 另一方面, 它又通过剪切形变影响海洋锋面过程, 为海洋次中尺度运动提供生成条件, 将能量向小尺度方向传递[1]。一般认为, 海洋涡旋动能(eddy kinetic energy, 以下简称EKE)随尺度分布是大气强迫和海洋内部非线性运动共同作用的结果。假定能量注入海洋主要发生在大尺度和能量耗散最终发生在小尺度, 中尺度-次中尺度区间范围内涡旋能谱分布则由海洋自身运动决定。因此, 能谱分析是揭示海洋多尺度运动的重要手段, 在理论研究和资料诊断中得到了广泛应用。
假定空间均匀和各向同性, 经典湍流理论认为能谱分布在惯性区间内遵循k–5/3定律, k为波数[2]。但在地转和层结的双重约束下, 地球流体运动具有准二维运动的特点。受Kraichnan二维湍流理论的启发, 在准地转框架下Charney[2]创立了地转湍流理论(quasi-geostrophic turbulence, 以下简称QT), 认为海洋大气涡旋动能谱分布应为k–3。但该理论不足的是, 未考虑边界影响, 仅适用于描述位涡守恒约束下的大洋内部运动。实际观测的海洋-大气涡旋往往伴随着显著的表面浮力异常和均匀的内部位涡。针对该情况, Blumen[3]假定流体内部位涡为0, 并且认为运动完全由密度异常边界条件驱动, 提出了表面准地转湍流理论(surface quasi-geostrophic turbulence, 以下简称SQT), 其对应的动能谱呈k–5/3分布。由位涡的可逆性原理出发, Klein等[4]进一步证明, 海洋动力过程理论上可以分解为准地转解(由内部位涡强迫)和表面准地转解(由近地表密度强迫)。真实的上层海洋运动往往同时受到外因和内因影响, 可能介于QT和SQT理论描述之间。
卫星高度计的发射对揭示海洋涡旋能谱具有重要意义。根据地转平衡关系, 涡旋动能(K)可由海面高度异常(S)分别在纬向(x)和经向(y)的偏微分以及重力加速度(g)和科式参量(f)计算:
| K=g22f2[(∂S∂x)2+(∂S∂y)2]. | (1) |
海面高度异常的大小直接反映出海洋涡旋流动的强弱。若海面高度异常(sea surface height anomaly, 以下简称SSHA)波数谱为k–m, 涡旋动能谱则为k–2–m。在该条件下, 前述地转湍流理论预测SSHA波数谱服从于k–5分布, SQT预测SSHA波数谱表现为k–11/3分布。因此, 可以利用高度计观测的海面高度异常场计算SSHA谱斜率, 检验经典地转湍流理论在真实海洋中的适用性。Fu[5]首次利用SeaSat高度计数据进行了该方面尝试, 发现在强涡旋区域, SSHA谱接近k–5分布, 而在弱涡旋区域, SSHA谱则表现为k–1。由于SeaSat高度计工作时间短, 信噪比低, 该结果的可信度受到很大限制。后来的GeoSat数据结果有所改进, 强涡旋谱相比k–5而言更接近k–4, 而弱涡旋谱斜率则在–2到–3之间[6]。1992年发射升空的TOPEX/Poseidon(T/P)大大提高了卫星海面高度观测的精度, 深化了人们对中尺度涡旋全球时空分布的认识和理解。基于3 a的T/P数据, Stammer[7]分析发现中纬度海洋涡旋存在一个归一化的普遍波数谱形式k–4.6。此后, 基于多颗卫星高度计融合数据分析, Le Traon等[8]研究结果表明, 在黑潮和南极绕极流等高涡旋动能区域, SSHA谱分布更接近于k–11/3。Xu等[9]利用多年沿轨数据, 对比了SSHA波数谱斜率在不同纬度的分布, 发现70~250 km固定中尺度波段上的SSHA谱斜率存在区域差异: 在高涡旋动能、主要向东流动的洋流中, 如黑潮延伸体、湾流和南极绕极流(Antarctic Circumpolar Current, 以下简称ACC)区域, SSHA谱斜率接近或大于k−4。Zhou等[10]通过去除沿轨高度计数据中的时间不相干信号, 重新研究了SSHA谱斜率的全球分布, 发现低EKE区域的谱斜率可能超过k–3。尽管如此, Xu等[9]报道的谱斜率的地理空间格局仍保持不变。然而, 从沿轨道数据计算SSHA波数谱是基于中尺度湍流是各向同性的假设。因此, 沿轨道的数据不适合诊断波数谱的各向异性, 而基于直接观测和数值模拟的证据有力地表明, 中尺度涡旋是纬向或经向拉长的, 具有各向异性的空间结构, 尤其是在背景流较强的地区。中尺度涡旋的各向异性特征对于理解中尺度涡旋之间以及与洋流之间的相互作用是非常重要的。Stewart等[11]通过检验速度波动的方差椭圆, 诊断了全球海洋中涡旋变率的各向异性。他们的结果显示涡流变率是各向异性的。
上述不同人的研究结果, 针对不同研究区域、应用不同时长的卫星高度计数据, 得出的SSHA谱斜率大体分布在–3至–5之间。该区间范围大于SQT和QT预测的谱斜率区间范围。在探讨理论与实际差别时, 首先要对高度计资料计算的谱斜率差异的显著性进行检验。这需要我们用更长时间序列的SSHA资料进行统计平均, 从而减少谱斜率的估算方差。另外, 尤须指出的是, β效应使得涡旋运动在纬向受到强烈约束, 这种纬向-经向差异是海洋中涡-流相互作用的核心, 对于纬向急流的产生至关重要。以往研究多关注了涡旋随纬度分布(即空间不均匀性), 涡旋的经-纬向对比(即各向异性)则较少涉及。
为深化理解理论假定与实际海洋在空间均匀和各向同性方面的差异, 本文基于卫星观测的近30 a (1993—2022年)SSHA资料进行了波数谱分析, 区分经向和纬向分别计算了赤道波动区、副热带大洋内区、和中高纬度涡旋活跃区在中尺度波段区间的谱斜率, 对比分析了基于各向同性假设由二维快速傅里叶变换积分至一维所得谱结果与一维快速傅里叶变换谱结果的差异, 依据二维波数-频率谱图上频散关系, 并结合准地转湍流理论和线性波动理论探讨波谱斜率随经纬度和方向的变化。
1 数据与方法 1.1 研究数据及预处理为了研究中尺度海洋涡旋, 我们使用了The Copernicus Marine Environment Monitoring Service(以下简称CMEMS)分发的1993—2022年的网格化海平面异常(SSHA)资料进行波数谱的计算。高度计卫星网格化海平面异常根据2012年前后10 a平均值计算。SSHA通过最佳插值估计, 合并不同高度计任务的测量值。该产品由DUACS多任务高度计数据处理系统处理。它几乎实时地服务于欧洲和全世界主要的海洋学和气候预报中心, 处理来自所有高度计任务的数据: Jason-3、Sentinel-3A、HY-2A、Saral/AltiKa、Cryosat-2、Jason-2、Jason-1、T/P、ENVISAT、GFO、ERS1/2。它为各种应用提供了一致且同质量的产品目录, 包括近实时应用和离线研究。为了在延迟时间内生成海平面异常(SSHA)和绝对动态地形(ADT)的地图, 该系统使用了来自名为SEALEVEL*_PHY_L3_REP_OBSERVATIONS_008_*的产品的沿轨高度计任务。最后对所有飞行卫星进行最优插值合并, 计算网格SSHA和ADT。网格SSHA数据由哥白尼海洋环境监测局(CMEMS)分发。数据集被插值到0.25°×0.25°笛卡尔网格分辨率和每日采样。
用于计算谱斜率的太平洋4个典型海区如图 1所示。有涡旋活动剧烈的中高纬度强流区, 含黑潮延伸体(147°E~163°E, 27°N~43°N)和ACC区域(140°E~ 156°E, 41°S~57°S); 涡旋活动相对微弱的副热带南太平洋(128°W~112°W, 17°S~33°S); 赤道波动显著的热带太平洋区域(128°~112°W, 3°N~13°S)。其中黑潮延伸体区域以及ACC区域远离赤道, 因此地转平衡占主导地位。我们希望这种区域的选择可以最小化边界效应。根据每日SSHA计算的波数谱非常不稳定, 尤其是在小断面(< 10°)。统计稳定的波数谱只能通过长期平均获得。在本文中, 我们选择16°×16°的矩形区域计算SSHA波数谱。在快速傅里叶变换(Fast Fourier Transform, 以下简称FFT)之前应用10%余弦锥形窗口。在计算区域内, 利用海面的连续性对所有陆地点进行了插值填充。每个格点首先做时间平均用以获得海表面高度异常距平值, 分别去除经向与纬向线性趋势后再对剩余的数据进行加窗处理, 以进行后面的谱计算。
 |
| 图 1 谱分析的4个目标区域 Fig. 1 Four target regions for spectral analysis |
我们使用的频谱分析是基于信号的快速傅里叶变换, 这使我们能够处理有限长度的采样信号。更长的数据记录可以更好地分解每个频率(波数)的变化, 从而更好地分离频谱中的相邻频率(波数)。然而, 对于波数谱而言, 长时间的空间数据记录可能混合来自不同地理区域的信息, 特别是在热带地区, 其中经向剖面穿过强纬向洋流, 使其动力学解释变得困难。对全球海洋上空的测高数据或模式进行谱分析的不同研究使用了非常不同的数据长度段来计算能谱。一些测高研究使用的数据段长度约为500 km或1 000 km, 长度为10°或20°的矩形区域。谱的计算大多以10°或20°为单位。这些数据段长度对于中纬度地区可能是足够的, 但对于热带地区不适用, 因为此时最大能量可能出现在600~1 000 km波长处。使用比这更短的采样区间会降低最大能量, 并增加从高能低波数到能量较弱高波数的泄漏, 从而降低谱斜率。
在计算SSHA波数谱斜率前, 必须确定用于估计斜率的中尺度波段。Xu等[9]用于计算谱斜率的波长范围是在对SSHA波数谱遵循的幂次定律进行全局评估后选择的: 250 km代表有效涡旋尺度上限Ll, 70 km代表高度计能分辨的尺度下限LS, 低于该值, 频谱主要由测量噪声控制。但是, 该波段不再适用于网格化数据。由于Rossby变形半径Rd和中尺度涡旋的特征长度L均随纬度的增加而减小, 用于计算的中尺度波段并非在所有纬度上都动态等效。因此, 用于计算谱斜率的中尺度波段应随纬度的变化而进行适当的调整。在本文中, 我们沿用Wang等[12]的方法对其进行优化:
| Ll=∫k2H(k)dk∫k3H(k)dk, | (2) |
| Ls=Ll−ΔLcosθ, | (3) |
其中,
我们检验了赤道区域一维SSHA波数谱对不同的窗口的敏感度。首先对测试数据进行如下操作: 去除平均值和线性趋势; 对数据分别乘不同的窗函数以及不加窗处理。由图 2可知除了Tk01窗, 其他窗口会使谱能降低, 在有效中尺度波段尤其显著。而Tk01窗使谱斜率大幅增加, 其余窗函数则使谱斜率。略有增加。为避免能量泄漏致结果不准确, 在本文中我们应用了Tk01窗通过对格点中心跨度16°的所有纬向SSHA谱进行平均, 得到纬向平均能谱; 同理通过对格点中心跨度16°的所有经向SSHA谱进行平均得到经向平均谱:
| Pzonal =fft[SSHA(x,y0)], | (4) |
| Pmeridional =fft[SSHA(x0,y)]. | (5) |
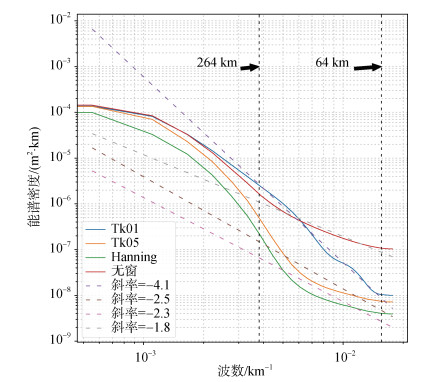 |
| 图 2 数据对不同窗函数的敏感度实验 Fig. 2 Sensitivity experiment of data to different window functions |
为与一维谱结果对比, 我们计算了各向同性SSHA波数谱。对于网格化数据, 对SSHA的矩形区域进行2-D FFT:
| PP(kx,ky)=ftt2[SSHA(x,y)]. | (6) |
然后依据各向同性假设将其积分至一维:
| P(K)=∑K=(k2x+k2y)12,PP(kx,ky), | (7) |
kx与kx分别为纬向与经向波数, 谱斜率则由最小二乘法估计所有落入计算所得中尺度波段内的波数。
1.3 谱的不确定性分析到目前为止, 我们计算的所有谱存在一个问题: 无法评估不确定性。通过肉眼我们可以看出其具有较大的噪音, 通过计算得知, 平均值的误差随平均量增加而减小。将更多的谱平均时, 谱中的不确定性降低。为获得更多可平均的谱, 通常的做法为将一列数据分解成数段, 计算每个段的谱, 并对这些谱进行平均以获得平均谱。在本文中我们每个计算区域经向与纬向天然存在数段数据。由于我们平均平方量(谱振幅), 所以和的分布将遵循χ2分布, 我们将用它来估计不确定性。对于每一段, 在波数上, 估计谱为:
| ˆE(k)=⟨|a(k)|2⟩=1nn∑i=1|a(k)|2, | (8) |
其中, a为复数傅里叶系数, k在本文中为波数, 在一维快速傅里叶变换中每个区域计算的为全部纬向(经向)谱的平均, 即相当于将数据分割为了M段, M为区域内全部纬向(经向)数据的段数, 其中每一段具有两个自由度, 因此其自由度为v=2M。为了估计误差, 整个论点源于一个概念: 存在一个真实谱E(k), 最佳估计谱
计算E和
| ln(ˆEE)=ln(ˆE)−ln(E). | (9) |
定义一个变量, 该变量表示由真实谱归一化的平方和:
| y=νˆEE. | (10) |
当我们有v自由度时,
为得到估计谱
| P(χ2ν,1−α2<νˆEE<χ2ν,α2)=1−α. | (11) |
因此, 如果要计算95%的显著性水平, 我们可将α设置为0.05。这对应于χ2分布上的给定点。我们可以进一步推导这种关系, 以提供真实值在观测值的特定范围内的概率:
| P(νˆEχ2ν,1−α2>E>νˆEχ2ν,α2)=1−α. | (12) |
真实谱E在
图 3展示了两个典型高涡旋动能区域、低涡旋动能区域以及赤道区域, 即由低纬度到中高纬度的经向与纬向一维SSHA波数谱。蓝色与橘色实线与阴影部分分别为SSHA波数谱以及95%置信区间, 绿色红色点状线为有效中尺度波段拟合斜率; 黑色点状线代表进行谱斜率估计的有效中尺度波段。这些谱是在图 1中用红框表示的子区域上计算的。两个向东流动区域的EKE至少比海盆内部的EKE大一个数量级。在黑潮延伸体区域, 中尺度带上的平均纬向SSHA波数谱斜率为–4.4, 平均经向谱斜率为–5.0。在ACC区域, 中尺度带上的平均纬向SSHA波数谱斜率为–4.6, 平均经向谱斜率为–5.4。在低EKE区域, 中尺度带上的平均纬向谱斜率与平均经向谱斜率相同, 与QT理论预测值吻合, 其谱斜率为–4.9与Zhou等[10]的结论一致, 即低涡旋动能区域谱斜率也会超过k–3。在赤道区域, 中尺度带上的平均纬向谱斜率为–4.1, 经向谱斜率为–4.2, 显著低于其它区域且与SQT预测值吻合。值得注意的是, 赤道区域经向SSHA能谱显著高于纬向SSHA能谱, 这是由于赤道区域存在强纬向流及纬向波动。谱斜率是中尺度信号产生和演化的表现。由赤道地区到中高纬度, 经向谱斜率呈现递增趋势, 纬向谱斜率则在中高纬度维持相对稳定。低涡旋动能区域以及赤道区域的经向谱斜率比其他地区平坦, 纬向SSHA波数谱斜率与经向谱斜率接近, SSHA波数谱几乎是各向同性的; 而在东向流动的高涡旋动能区域, 如黑潮延伸体区域以及南极绕极流区域, 经向谱明显比纬向谱陡(谱斜率差值大于0.5), 经向与纬向谱存在显著差异。该结果说明SSHA波数谱确实是各向异性的, 且存在强烈的区域差异。上图描绘的波数谱斜率的空间变化特征的整体趋势与涡旋变化特征的整体分布趋势非常相似。一般来说, 涡旋变化率越高, 谱斜率越陡。较高的谱斜率与高度非线性动力学有关, 而较为平坦的谱则更多与线性动力学有关的论点大致一致[14]。此外, 谱斜率的差异与涡流过程直接相关。在向东流动的高EKE区域, 等密度线向上倾斜至极点, 深海(约1 km)中出现斜压不稳定性, 其尺度大于变形半径。这些中尺度信号增长迅速且持续时间长, 在此期间, 强平均流可以完全拉伸并非线性重塑它们。Wang等[15]进一步指出, 在这些高EKE区域中, 中尺度带上的动能通量是各向异性的, 更多动能在纬向上向大尺度转移, 这导致了纬向谱斜率较为平坦。此外, 这些区域充满了曲流和环流, 这也是高度计观测中的中尺度信号。各区域谱斜率均介于理论预测的k–4与k–5之间。纬向和经向谱斜率之间的差异与中尺度信号的非线性演化密切相关。在演化过程中, 中尺度信号之间相互作用, 它们还与平均流和较小尺度非线性地、不间断地相互作用, 然而, 这些相互作用的许多细节仍然不清楚。此外, 海洋上层的某些小尺度或高频非地转运动, 如次中尺度过程、波浪和内部潮汐, 也会影响中尺度湍流。
 |
| 图 3 四个谱分析区域的经向SSHA波数谱与纬向SSHA波数谱 Fig. 3 Latitudinal and longitudinal SSHA wavenumber spectra of the four spectral analysis regions |
二维快速傅里叶算法所得波数空间内谱能量更多集中在300~1 000 km区间, 由谱形可看出在较大波长处存在显著的能量注入。在波长超过有效中尺度波段的上限时, 谱形开始趋于平稳, 出现“驼峰”。290 km, 215 km除以2π分别对应46 km, 34 km, 这与海洋大部分地区的典型第一模态Rossby变形半径(25~45 km)相当。对于斜压不稳定过程产生的涡流, 第一模态Rossby变形半径是最优选的尺度, 这是主要洋流系统附近主要的涡流产生过程。一旦这些涡旋形成, 它们的尺度往往会通过非线性相互作用增加, 直到尺度足够大, 涡旋可以像Rossby波一样西向传播。因此, 强流附近的涡流尺度接近于或大于第一模态Rossby变形半径。由图 4可知, 高能涡流的波长大于有效中尺度波段上限。基于各向同性假设将二维谱结果积分至一维所得谱斜率基本介于一维经向与纬向谱斜率之间, 仅在赤道区域与一维谱斜率有细微差别。其空间分布模式遵循一维纬向谱斜率的空间分布: 由赤道向中高纬度递增并在中高纬度维持不变。同时, 由网格化过程中的滤波和平滑测量噪声导致的信号损失会使谱变陡。除赤道区域外, 谱斜率与QT预测的k–5吻合较好。赤道区域谱斜率则与SQT预测值接近。综合考虑二维谱斜率以及一维谱斜率, 谱斜率与涡旋能量以及纬度密切相关。考虑到一维谱结果在高EKE区域表现出显著的各向异性特征, 基于各向同性假设积分得到的谱斜率并不能准确表征高EKE区域能谱变化。
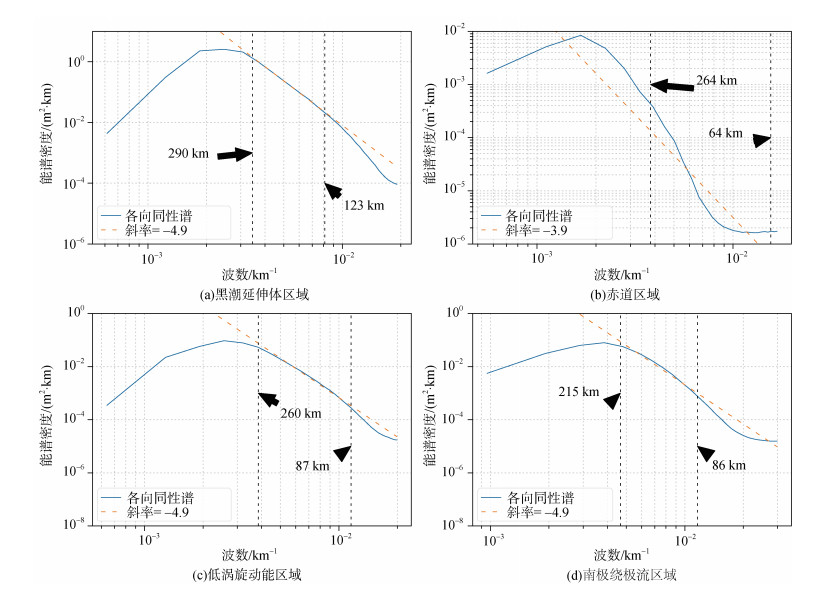 |
| 图 4 2-D FFT结果基于各向同性假设积分至一维所得SSHA波数谱 Fig. 4 2-D FFT results integrated into one-dimensional SSHA wavenumber spectrum based on isotropy assumption |
图 5为27°N纬线上对时间与空间方向进行二维快速傅里叶变换并对谱结果取平均后计算方差绘制(沿频率与经度方向对谱结果平滑处理), 虚线为沿着最大能量密度的脊线, 斜率大致为5.8 cm/s。在二维SSHA频率-波数谱上揭示了中尺度湍流的特征: 其所遵循的频散关系近似位于一条直线上, 与线性Rossby波相关的频散关系曲线有显著差异。由
| ck+ω=0(k>0), | (13) |
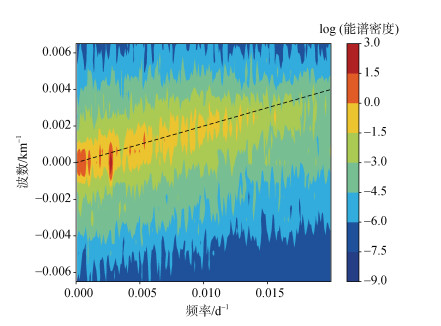 |
| 图 5 黑潮延伸体区域27°N二维SSHA波数频率谱 Fig. 5 27°N 2-D SSHA wavenumber–frequency spectrum in the Kuroshio extension body area |
可求得对应涡旋传播速度约为5.8 cm/s(非常接近Wunsch[16]独立发现的值), 这一结果也突出了中尺度涡旋强烈的非线性特征。特别要注意的是, 虽然大部分能量是沿着波数频率空间中的非频散关系曲线分布的。也有相当一部分能量存在于离这条线很远的地方。非频散关系线几乎与0值附近的第一斜压模态频散曲线相切, 并在较大波数、频率处与正压频散曲线相交。
波数频率谱的组成和结构的理论解释可分为几个类别: 海洋通过背景流的改变、层结以及地形等因素对自由运动进行调控的波动理论; 平均流的破碎导致其变率且由最不稳定模态波的特性表征的不稳定性理论以及包括稳定与不稳定背景流的强迫波理论。所有这三种理论都可以产生波数与频率之间的频散关系。另一类则是只预测波数谱, 没有直接频散关系但通过
图 6显示了研究区域中心纬度35°N的对数频率纬向波数谱能量密度。在该纬度, 频散关系直线斜率变缓, 同时沿着非频散关系直线的能量增加; 在所有频率上,
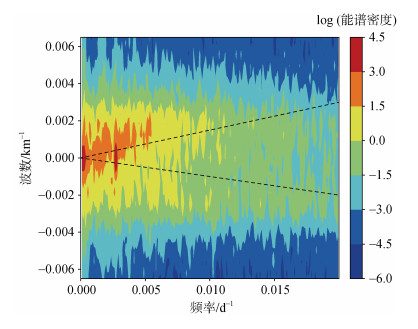 |
| 图 6 黑潮延伸体区域35°N二维SSHA波数频率谱 Fig. 6 35°N 2-D SSHA wavenumber–frequency spectrum in the Kuroshio extension body area |
本研究利用30 a(1993—2022年)太平洋海域几个典型区域网格化高度计资料, 重新对高涡旋动能区以及低涡动能区、赤道地区的SSHA波数谱进行了计算。估计了与纬度有关的中尺度波段上的经向谱斜率与纬向谱斜率。在靠近典型主流系的高能区域, 大部分能量包含在波长超过250 km的波段上, 基于各向同性谱可知宽谱驼峰出现在300~1 000 km波段。有效中尺度波段上限经换算后与海洋大部分地区的第一模态Rossby变形半径接近。根据QT预测, 波长小于250 km时, 能谱基本遵循k–5幂次定律。结果表明, 波数谱斜率除赤道区域外在由涡旋动能强度定义的中尺度区间内高度符合QT理论预测值。在赤道区域, 经向谱斜率与纬向谱斜率皆显著低于其他区域, 其经向谱能显著高于其纬向谱能, 其谱斜率与SQT理论预测值吻合。在热带地区, 海表附近可能存在的Charney不稳定性使得表面准地转湍流理论动力学更具相关性[9]。值得注意的是, SSHA数据的非地转成分部分可能导致谱斜率变平坦。在中高纬度区域, SSHA波数谱斜率明显高于赤道区域, 并且区域间差异显著。在东向流动的高涡旋动能区域, 如黑潮延伸体以及南极绕极流区域, 经向谱斜率与纬向谱斜率的差值更大, 其经向谱斜率远远高于纬向谱斜率, 在该区域SSHA波数谱是各向异性的, 因此基于各向同性假设由二维谱结果积分至一维无法很好表征该区域的中尺度信号演化, 且其谱斜率数值基本介于SQT理论和QT理论预测的理论值之间; 太平洋海域的剩余部分与低涡旋动能区域基本吻合。在EKE较低的区域, 经向谱斜率与纬向谱斜率差异不显著(数值小于0.5), SSHA波数谱几乎是各向同性的。这一结果还表明海洋中尺度湍流的存在有望符合Charney[2], Hua等[17]以及McWilliams[18]所描述的地转湍流特性。对于纬向平均谱斜率, 谱斜率随纬度的增加而变陡, 中高纬度的纬向谱斜率几乎保持不变。与此不同的是, 经向谱斜率随着纬度的增加而逐渐增加。除了中尺度信号的非线性演化在纬向和经向上是各向异性外, 网格化过程也可能对其产生影响。值得补充的是, 纬向谱斜率相比经向谱斜率更加不稳定, 经向谱斜率表现出较好的纬向依赖性, 且其与EKE水平密切相关。综上所述, SSHA波数谱斜率与涡旋动能能级高度相关。SSHA波数谱的各向异性也表明中尺度信号特征长度尺度是各向异性的。中尺度信号的特征长度尺度常被用来确定横向湍流扩散系数的大小。因此, 特征涡长尺度的具体取值影响着海洋模式的模拟, 尤其是用于气候研究的粗分辨率海洋模式。虽然已经做了大量的工作来估计特征涡长尺度, 但特征涡长尺度的各向异性仍然不太为人所知。更精确的特征长度尺度将导致更精确的横向湍流扩散系数值, 这将改进海洋模型的模拟。需要说明的是, 本文未探究结论对不同季节的适用性。同时, 具体谱形与谱斜率会因计算区域的选择而有细微差别。本文的目的不是进行全球讨论, 而是为之提供一个分析框架。
最后, 尽管SSHA波数谱各向异性的证据很强, 但谱斜率的地理分布可能是即时的。目前, 所有测高得到的谱斜率结果, 包括沿轨数据的结果, 波长小于或等于100 km的都会受到测量噪声的影响。在全球范围内对测高波数谱的解释也应谨慎对待。同时, 由于高度计和卫星轨道分布等因素的影响, 网格化SSHA可能会产生人为的各向异性, 这种各向异性表现为波数谱的各向异性。
| [1] |
SCOTT R B, WANG F M. Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry[J]. Journal of Physical Oceanography, 2005, 35(9): 1650-1666. DOI:10.1175/JPO2771.1 |
| [2] |
CHARNEY J G. Geostrophic turbulence[J]. Journal of Atmospheric Sciences, 1971, 28(6): 1087-1095. DOI:10.1175/1520-0469(1971)028<1087:GT>2.0.CO;2 |
| [3] |
BLUMEN W. Uniform potential vorticity flow: Part Ⅰ. Theory of wave interactions and two-dimensional turbulence[J]. Journal of Atmospheric Sciences, 1978, 35(5): 774-783. DOI:10.1175/1520-0469(1978)035<0774:UPVFPI>2.0.CO;2 |
| [4] |
KLEIN P, LAPEYRE G, SIEGELMAN L, et al. Ocean- scale interactions from space[J]. Earth and Space Science, 2019, 6(5): 795-817. DOI:10.1029/2018EA000492 |
| [5] |
FU L L. On the Wavenumber spectrum of oceanic mesoscale variability observed by the SeaSat altimeter[J]. Journal of Geophysical Research: Oceans, 1983, 88(C7): 4331-4341. DOI:10.1029/JC088iC07p04331 |
| [6] |
KHATRI H, SUKHATME J, KUMAR A, et al. Surface ocean enstrophy, kinetic energy fluxes, and spectra from satellite altimetry[J]. Journal of Geophysical Research: Oceans, 2018, 123(5): 3875-3892. DOI:10.1029/2017JC013516 |
| [7] |
STAMMER D. Global characteristics of ocean variability estimated from regional TOPEX/POSEIDON altimeter measurements[J]. Journal of Physical Oceanography, 1997, 27(8): 1743-1769. DOI:10.1175/1520-0485(1997)027<1743:GCOOVE>2.0.CO;2 |
| [8] |
LE TRAON P Y, KLEIN P, HUA B L, et al. Do altimeter wavenumber spectra agree with the interior or surface quasi-geostrophic theory?[J]. Journal of Physical Oceanography, 2008, 38(5): 1137-1142. DOI:10.1175/2007JPO3806.1 |
| [9] |
XU Y S, FU L L. Global variability of the wavenumber spectrum of oceanic mesoscale turbulence[J]. Journal of Physical Oceanography, 2011, 41(4): 802-809. DOI:10.1175/2010JPO4558.1 |
| [10] |
ZHOU X H, WANG D P, CHEN D. Global wavenumber spectrum with corrections for altimeter high-frequency noise[J]. Journal of Physical Oceanography, 2015, 45(2): 495-503. DOI:10.1175/JPO-D-14-0144.1 |
| [11] |
STEWART R H, SHUM C, TAPLEY B, et al. Statistics of geostrophic turbulence in the Southern Ocean from satellite altimetry and numerical models[J]. Physica D: Nonlinear Phenomena, 1996, 98(2/4): 599-613. |
| [12] |
WANG S H, QIAO F L, DAI D J, et al. Anisotropy of the sea surface height wavenumber spectrum from altimeter observations[J]. Scientific Reports, 2019, 9(1): 15896. DOI:10.1038/s41598-019-52328-w |
| [13] |
TCHILIBOU M, GOURDEAU L, MORROW R, et al. Spectral signatures of the tropical Pacific dynamics from model and altimetry: a focus on the meso-/submesoscale range[J]. Ocean Science, 2018, 14(5): 1283-1301. DOI:10.5194/os-14-1283-2018 |
| [14] |
WUNSCH C. Toward a midlatitude ocean frequency– wavenumber spectral density and trend determination[J]. Journal of Physical Oceanography, 2010, 40(10): 2264-2281. DOI:10.1175/2010JPO4376.1 |
| [15] |
WANG S, LIU Z, PANG C G. Geographical distribution and anisotropy of the inverse kinetic energy cascade, and its role in the eddy equilibrium processes[J]. Journal of Geophysical Research: Oceans, 2015, 120(7): 4891-4906. DOI:10.1002/2014JC010476 |
| [16] |
WUNSCH C. The oceanic variability spectrum and transport trends[J]. Atmosphere-Ocean, 2009, 47(4): 281-291. DOI:10.3137/OC310.2009 |
| [17] |
HUA B L, HAIDVOGEL D B. Numerical simulations of the vertical structure of quasi-geostrophic turbulence[J]. Journal of Atmospheric Sciences, 1986, 43(23): 2923-2936. DOI:10.1175/1520-0469(1986)043<2923:NSOTVS>2.0.CO;2 |
| [18] |
MCWILLIAMS J C. Statistical properties of decaying geostrophic turbulence[J]. Journal of Fluid Mechanics, 1989, 198: 199-230. DOI:10.1017/S0022112089000108 |
 2024, Vol. 48
2024, Vol. 48


