
文章信息
- 张群星, 徐昱, 刘娟, 孟静, 王桂霞, 陈旭. 2024.
- ZHANG Qunxing, XU Yu, LIU Juan, MENG Jing, WANG Guixia, CHEN Xu. 2024.
- 跃层厚度对内孤立波能量耗散的影响
- Effect of pycnocline thickness on energy dissipation of internal solitary waves
- 海洋科学, 48(2): 1-14
- Marine Sciences, 48(2): 1-14.
- http://dx.doi.org/10.11759/hykx20230215001
-
文章历史
- 收稿日期:2023-02-15
- 修回日期:2023-06-13
2. 中国海洋大学工程学院, 山东 青岛 266100;
3. 北京应用气象研究所, 北京 100029;
4. 内蒙古师范大学数学科学学院, 内蒙古 呼和浩特 010022
2. College of Engineering Ocean University of China, Qingdao 266100, China;
3. Beijing Institute of Applied Meteorology, Beijing 100029, China;
4. College of Mathematics Science, Inner Mongolia Normal University, Hohhot 010022, China
海洋中的密度分层受温度和盐度影响, 内孤立波的生成、传播过程依赖于密度稳定的层结, 在长距离传播过程中携带巨大的能量并保持自身波形不变[1-2], 对海洋上混合层和深海环境造成影响[3-5]。内孤立波在陆架地形上的破碎在海洋混合和能量耗散中发挥了重要的作用, 影响海洋中营养物质输运及海底沉积物的再悬浮过程, 对海下声信号的传播也会有重要影响[6-10]。
前人针对南海内孤立波开展了众多的观测研究[2, 11-19]。Orr等[16]在南海大陆坡区域对内孤立波的破碎进行了观测, 得到了内孤立波在一定区域内传播过程中的能量耗散率。亚洲声学实验根据潜标观测数据发现南海北部内孤立波是由吕宋海峡传来[20-22], 后续开展的Nonlinear Internal Waves Initiative (NLIWI)及Internal Waves in Straits Experiment (IWISE)试验对南海北部内波的传播演化过程进行了连续观测, 阐明了其传播特征及生成机制[23-26]。于博等[27]在南海观测结果表明内孤立波核心处流速强, 且在核心处水体会因为对流不稳定而发生翻转, 破碎的过程中动能与有效势能存在转化关系。实际海洋环境复杂多变, 加之观测仪器的局限性, 难以进行长时间大范围的海上观测, 特别是内波破碎所致混合观测往往比较缺乏, 目前对海洋中内孤立波的破碎动力过程认识仍然不够充分。
实验室实验和数值模拟是内孤立波研究的有效补充手段, 前人对内孤立波的破碎及能量耗散过程开展了一系列的研究[28–35], 其受到地形高度及背景密度场的共同影响[36]。Vlasenko等[37]利用接近于实际海洋的层结, 内孤立波的振幅及底地形条件, 开展了数值模拟实验, 发现内孤立波的振幅大于0.4× (地形上的水深–跃层位置)时, 内孤立波就会发生破碎。假如地形高度较小且平缓, 内孤立波振幅也较小, 内孤立波大部分能量将透射进入大陆架区域; 假如地形高度较大且陡峭, 内孤立波振幅较大时, 能量将会反射并返回到深海区域[38], 因此, 地形高度是影响内孤立波耗散及波形演变的重要参数[34, 39]。大量的实验室实验[29, 32]及数值模拟[28, 33, 40-41]也针对不同地形坡度对内孤立波的影响进行了研究, 其中地形坡度最大可达到0.417。背景密度场的设置包括完全两层模型、跃层处采用tanh曲线、上层流体密度线性分层下层流体密度均一、全水深采用tanh曲线生成连续层结等几种类型[42]。Arthur等[40]和Allshouse等[43]通过数值模拟针对跃层厚度对混合和输运的影响进行了研究, 其认为存在最佳跃层厚度可以产生最大的质量输运。Hartharn-Evans等[44]研究了背景层结对内孤立波的影响, 发现上层线性分层及全线性层结会影响内孤立波浅化过程中的破碎类型, 密度梯度会抑制内孤立波塌陷破碎的过程。这些针对背景密度场对内孤立波影响的研究, 主要对内孤立波与地形作用之后破碎产生的流体微团进行分析, 包括能量变化及对混合效率的影响等, 缺乏背景密度场对内孤立波整体能量变化及能量耗散影响的了解。而前人针对内孤立波过陆坡地形破碎机制及能量变化做的大量工作, 往往基于两层流体开展, 真实海洋中会存在密度跃层, 因此, 需要对背景层结进行改进。实验条件的限制无法铺设不同跃层厚度的背景层结来进行相应的研究, 数值模拟则可以避免这个问题, 通过改变地形高度、水深比、跃层厚度等条件, 来探究跃层厚度对内孤立波能量变化及能量耗散的影响。实际海洋中随着季节的变化, 跃层强度也会发生变化, 其通常被定义为密度跃层的垂向密度梯度, Delisi等[45]认为跃层强度会影响内孤立波的振幅, 本文将主要针对跃层厚度进行分析。
OpenFOAM作为一款开源CFD计算软件, 具有多方面的优势, 其在内孤立波的模拟中得到的广泛的应用, 通过对源代码的修改可以对完全两层模型和跃层连续模型进行模拟[46-50]。本文将基于OpenFOAM针对连续跃层进行模拟, 突破实验室实验条件的限制, 针对跃层厚度变化对内孤立波传播及与地形作用过程中能量耗散进行分析。
1 数值模型条件与理论计算数值水槽的长度L为15 m, 高度H为0.48 m。采用两种密度层结, 分别为上层0.08 m, 下层0.4 m和上层0.12 m, 下层0.36 m, 上层水厚度为h1, 下层水厚度为h2, 数值水槽示意图如图 1所示。采用不同密度的盐水进行密度分层, 上下层盐水的密度ρ1、ρ2分别为1 030 kg/m3和1 050 kg/m3, 密度分层使用5种跃层厚度δ, 分别为0.01 m、0.03 m、0.05 m、0.08 m、0.16 m。模型中共使用3种实验地形, 斜坡斜率均为0.12, 斜坡地形高度hs分别为0.16 m、0.20 m和0.24 m, 斜坡顶端即hs所示位置放置在10 m处。数值实验中采用重力塌陷法生成内孤立波, 每个地形, 每种层结下进行3组实验, 塌陷高度hd分别为0.08 m、0.16 m、0.24 m, 塌陷区宽度hw为0.4 m, 共计90组工况, 工况设置见表 1。计算时间步长为0.001 s, 0.25 s输出一次数据, 计算时间为120 s。
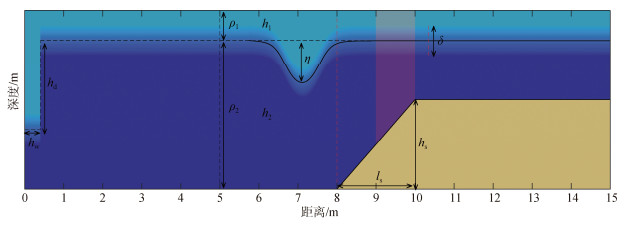 |
| 图 1 数值水槽装置示意图 Fig. 1 Schematic view of the numerical flume 注: 图中浅色表示上层低密度水, 深色表示高密度水, 跃层处渐变颜色表示密度在此连续变化, 跃层厚度为δ。水槽左侧为重力塌陷造波区, hd为塌陷高度, 斜坡长度和高度分别为ls和hs。图中红色区域为数值水槽9~10 m区域 |
| 塌陷高度hd/m | 地形高度hs/m | 上下层水深比 | 跃层厚度δ/m | 总工况 |
| 0.08 | 0.16 | 1∶3 | 0.01 | |
| 0.16 | 0.20 | 1∶5 | 0.03 | |
| 0.24 | 0.24 | 0.05 | ||
| 0.08 | ||||
| 0.16 | ||||
| 3 | 3 | 2 | 5 | 3×3×2×5=90 |
模拟计算使用twoLiquidMixingFoam求解器, 可用于不可压缩流动的模拟, 并得到了广泛的应用[51-54]。所用控制方程如下:
连续性方程:
| ∂ρ∂t+∇⋅(ρV)=0, | (1) |
ρ是密度,
动量方程:
| ∂ρv∂t+∇⋅(ρVV)−∇⋅τ=−gh∇ρ−∇prgh , | (2) |
输运方程加入了扩散项:
| ∂α∂t+∇⋅(Vα)=∇⋅[(Dab+Dt)∇α], | (3) |
Dab是层流扩散系数,
使用体积分数的加权平均值计算每个单元中多相流体的所有物理性质。例如, 流体混合物的密度可以表示为
数值模拟基于有限体积法对控制方程进行离散[57], 时间导数项采用后向差分离散格式进行离散, 梯度离散格式采用高斯线性方法, 速度对流项采用高斯线性方法, 体积分数输运项离散格式采用“Gauss van Leer”方法, 湍流动能项离散格式采用“Gauss limited Linear”方法, 限制器系数为1。拉普拉斯项的离散化采用“Gauss linear corrected”。网格体心到面心的插值格式采用线性方法。面法向梯度离散格式采用“corrected”方法。对于压力-速度的耦合采用PIMPLE算法[58-59]。
1.3 网格及边界条件设置网格生成使用blockMesh, 采用三维笛卡尔坐标系, 将y方向上的网格数设为1, 生成y方向上只有1层的准二维网格, 网格数为1 500×480×1。大振幅内孤立波模拟的准确性更依赖于垂向的网格坐标, 本文中垂向网格分辨率大于水平网格分辨率[37, 60-61]。整体的网格采用3个block块进行创建, 不同的block块通过面匹配进行连接。x, z方向上边界条件全部设置为固壁边界, y方向上的面边界设置为empty。
1.4 背景密度场设置海洋中的跃层厚度可达数百米, 需要对以往的模拟方式进行改进, 不再使用常用的完全两层密度分层模型或者线性层结。Schlitzer[62]对World Ocean Circulation Experiment(WOCE)中获得的18 000多个密度剖面数据进行分析, 发现在大多数情况下可以采用双曲正切曲线来描述海洋中的密度变化。背景密度场可用以下的公式来进行生成:
| ρ0(z)=ρc−Δρ2tanh[2(z+H2)δtanh−1(0.975)], | (4) |
其中
| N(z)=√−g dρ0(z)ρc dz, | (5) |
其在z=h2位置处浮频率最大。图 2为水深比为1∶5时密度剖面及浮频率示意图。不同跃层厚度密度曲线中, 跃层厚度为0.16 m时, 密度曲线变化最为平缓, 浮频率最大值也更小。图中黑色实线为实验室使用电导率仪所测得密度剖面, 及相应浮频率。对比实验浮频率的结果来看, 其变化趋势与跃层厚度为0.05 m时更加接近。
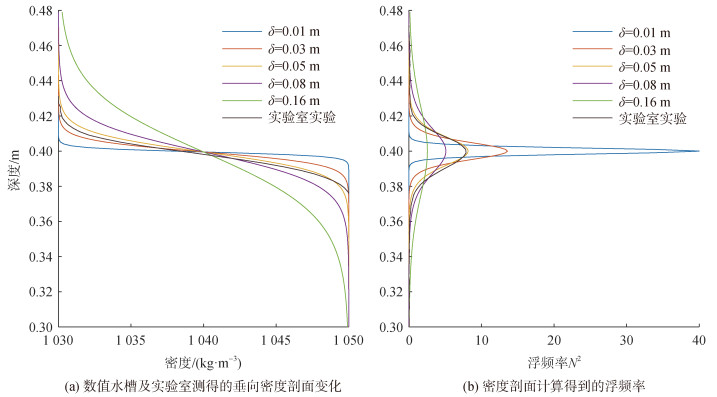 |
| 图 2 密度剖面及浮频率 Fig. 2 Density profiles and Brunt–Väisälä frequencies 注: (a)为数值水槽5种跃层厚度初始场的垂向密度剖面变化及实验室测得的垂向密度剖面, (b)为根据密度剖面计算得到的浮频率 |
内孤立波的能量包括动能(EK)和有效势能(EAP)。数值水槽采用准二维网格进行计算, 最终的输出结果为水平方向的流速u和垂向的流速w, 单位体积的EK[63]计算公式为
| EK=L∫0H∫012ρ(u2+w2)dzdx, | (6) |
得到内孤立波传播过程中的动能。
EAP[64]的计算公式为:
| EAP=L∫0H∫0ρwg(z−h2)dzdx, | (7) |
公式(7)中
本文采用直接法计算湍耗散率, 湍耗散率的定义为:
| ϵ=2\nu {S}_{ij}{S}_{ij}=\nu \frac{\partial {u}_{i}}{\partial {x}_{j}}\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right) , | (8) |
式中
| {ϵ}_{D}=\nu \left[4{\left(\frac{\partial u}{\partial x}\right)}^{2}+4{\left(\frac{\partial w}{\partial z}\right)}^{2}+3{\left(\frac{\partial u}{\partial z}\right)}^{2}+3{\left(\frac{\partial w}{\partial x}\right)}^{2}+6\left(\frac{\partial u}{\partial z}\frac{\partial w}{\partial x}\right)+4\left(\frac{\partial u}{\partial x}\frac{\partial w}{\partial z}\right)\right] , | (9) |
式中运动学黏度系数v=1.335×10–6 m2/s, 运动学黏度系数取值参照密度为1 030~1 050 kg/m3温度为10 ℃的氯化钠溶液[66]。
1.7 理查德森数计算内孤立波在传播及与地形作用过程中, 跃层处伴随着强烈的流速剪切, 进一步触发剪切不稳定的发生。Miles[67-68]和Howard[69]研究分层流体剪切流动时发现当理查德森数大于1/4时流场才会足够稳定。理查德森数的定义为:
| R i(z)=-g \frac{\mathrm{d} \rho}{\mathrm{d} z} / \rho_0\left(\frac{\partial u}{\partial z}\right)^2, | (10) |
g是重力加速度, ρ为密度场, ρ0为参考密度, 这里取为1 050 kg/m3, μ是水平速度。理查德森数小于1/4时流场会变得不稳定, 剪切效应增强。
2 结果与分析 2.1 内孤立波波速Michallet等[32]研究发现在两层流体中随着混合效应的增加, 内孤立波的波速会减小, 而跃层厚度的增加, 增强混合效应进而会导致波速减小。对于波速这里采用两层流体波速c0来进行无量纲化,
| {c_0} = \sqrt {g'\frac{{{h_1}{h_2}}}{{{h_1} + {h_2}}}} , | (11) |
其中, g′=g(ρ2 – ρ1)/ρ2。水平坐标采用振幅η对上层水深h1进行无量纲化, 内孤立波的振幅随着塌陷高度的增加而线性增加, 在同一塌陷高度下, 跃层厚度的增加, 内孤立波的振幅也会增加。根据模拟得到的结果(图 3), 所有工况下, 波速都呈现出相同的规律, 即波速随振幅的增加而增加, 随跃层厚度的增加而减小, 与前人结果一致。
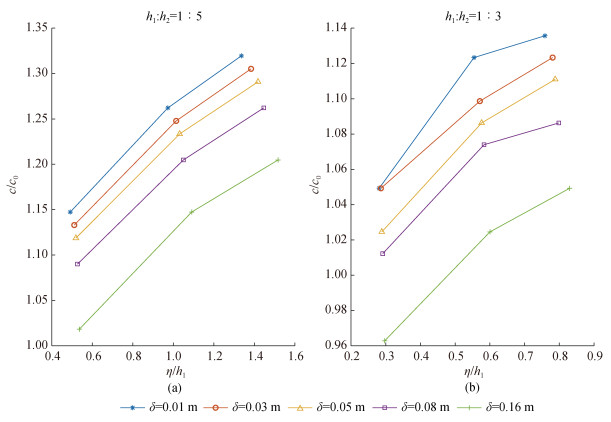 |
| 图 3 波速对比 Fig. 3 Comparison of wave velocities |
内孤立波从能量变化角度可以分为4个阶段, 分别为生成阶段、传播阶段、作用阶段及透射传播阶段。下文以地形高度0.24 m、水深比为1∶5、塌陷高度为0.24 m为例, 来探讨内孤立波能量在不同阶段的变化。在生成阶段, 初始场状态下, 有效势能最大, 动能最小为0, 随着重力调整的过程, 有效势能迅速减小, 动能开始增大, 不同跃层厚度工况下内孤立波的动能有效势能演化趋势基本一致。在内孤立波完整的波形生成后即t=20 s后为传播阶段, 跃层厚度为0.01 m工况下能量衰减明显更强。图 4 (b)为内孤立波到达数值水槽中7 m位置处跃层附近水平流速u的垂向梯度, 这表征了流速的剪切, 跃层厚度为0.16 m工况下流速剪切最小, 跃层位置处的剪切效应相应较弱, 导致的能量耗散也更弱, 所以可以解释图 4 (a)中, 跃层厚度越大其能量耗散也会更弱。内孤立波作用阶段, 其与地形相互作用, 在斜坡顶部发生破碎, 上下层的流体发生剧烈的混合, 能量耗散强烈。这个过程中还伴随着有效势能与动能的再分配, 在地形的作用下有效势能与动能相互转换, 有效势能的值会大于动能。跃层厚度的变化导致内孤立波能量再分配过程产生明显的差别。内孤立波透射通过地形向水槽后端传播的过程称为透射传播阶段, 内孤立波经过作用阶段的剧烈能量耗散使得振幅往往变化很大, 经过地形后逐步恢复到稳定传播的内孤立波, 稳定后这一阶段与第二阶段性质接近, 这里不做重点分析。
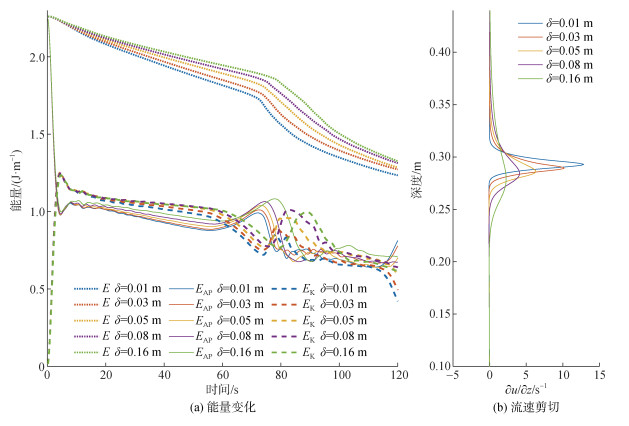 |
| 图 4 内孤立波能量变化及垂向流速剪切 Fig. 4 Changes in internal solitary wave energy and vertical velocity shear |
本文将重点关注内孤立波传播阶段及作用阶段, 基于大量的数值模拟结果, 对能量演化进行系综分析。从图 4(a)的能量曲线变化曲线可知, 内孤立波在传播阶段的能量耗散速度基本一致, 而作用阶段能量耗散明显增强。对内孤立波的能量变化可以分为两部分进行分析: 一部分为传播阶段中的能量耗散, 另一部分则为作用阶段的能量耗散。传播阶段能量耗散为内孤立波传播到6 m位置与7 m位置处总能量差。作用阶段能量耗散为内孤立波传播到8 m处与11 m位置处的能量差除以3, 再减去传播阶段能量耗散。图 5(a)—(c)所示为3种地形高度下传播阶段的能量耗散, 当振幅较小时, 跃层厚度对能量耗散差异影响很小, 随着振幅的增大, 跃层厚度对内孤立波传播阶段的能量耗散影响更加明显, 跃层厚度越小, 其带来的能量耗散更强。图 5(d)—(f)为作用阶段的能量耗散计算结果, 在地形高度为0.16 m[图 5(d)]时, 其与地形相互作用较弱, 所以不同跃层厚度带来的能量耗散差别很小。随着地形高度的增加, 在图 5(e)—(f)中水深比为1∶5时, 跃层厚度从0.01~0.08 m, 跃层厚度越大能量耗散越来越弱, 跃层厚度达到0.16 m时, 能量耗散开始增加; 当水深比为1∶3时, 跃层位置与地形顶部更加接近, 与地形相互作用更加剧烈, 以图 5(f)为例, 跃层厚度从0.01~0.05 m, 能量耗散随着跃层厚度的增加而减弱, 当跃层厚度大于0.05 m时, 能量耗散会随着跃层厚度增加而增强。且图 5(f)中两种水深比工况下塌陷高度最大时, 跃层厚度为0.16 m时能量耗散会有明显的增加。
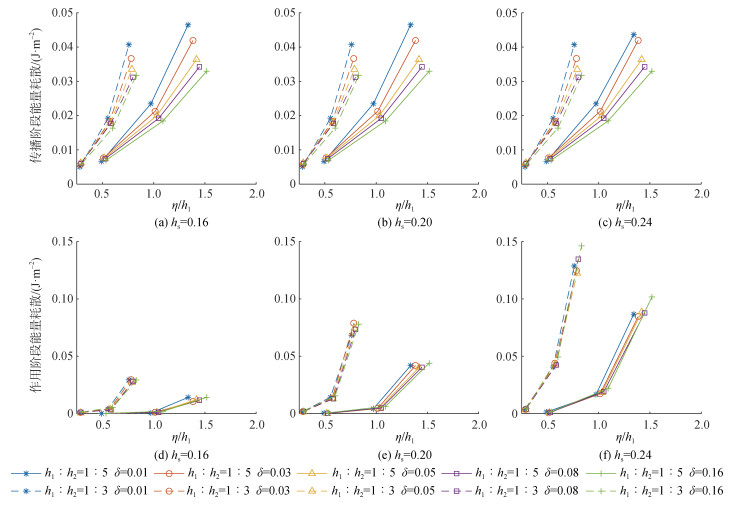 |
| 图 5 内孤立波传播过程中能量耗散及与地形作用过程中能量耗散 Fig. 5 Energy dissipation during propagation of internal solitary waves and its interaction with topography |
上文对内孤立波在传播阶段和作用阶段跃层厚度对能量耗散产生的影响进行了分析。演化过程中的能量耗散包括动能耗散及有效势能耗散, 但不能确定能量耗散中有效势能还是动能耗散占主导作用, 以及跃层厚度在其中的影响, 所以将动能耗散与有效势能耗散的比值结果进行了对比, 传播阶段与作用阶段耗散占比关系将单独给出。动能耗散与有效势能耗散计算方法与上文中能量耗散计算方法一致, 计算内孤立波到达不同位置处的动能差及有效势能差。
图 6(a)—(c)所示为传播阶段, 大部分工况下势能耗散大于动能耗散; 跃层厚度在其中的作用更加明显, 相同塌陷高度下, 跃层厚度从0.01 m增加到0.08 m, 动能耗散占比越来越小, 当跃层厚度达到0.16 m时, 动能耗散占比开始增加, 说明跃层厚度在大于0.08 m时, 在背景层结的作用下, 势能耗散减弱。此外, 传播阶段的动能耗散占比会随着振幅的增加先增大后减小。在作用阶段, 小振幅工况下跃层厚度对动能有效势能耗散比影响较大, 与传播阶段规律相同, 跃层厚度越小动能耗散占比越大, 当内孤立波与地形相互作用较强时, 以图 6(f)中地形高度为0.24 m为例, 在最大振幅时5种跃层厚度的动能耗散有效势能耗散比最为接近, 内孤立波发生破碎, 流体混合及能量耗散过程剧烈, 跃层厚度的影响较小, 所以最终的动能有效势能耗散比计算结果较为接近。综合所有数值模拟结果, 在内孤立波传播及作用阶段均为势能耗散大于动能耗散, 且随着跃层厚度的增加, 动能耗散会逐渐减小, 当跃层厚度较大后, 动能有效势能耗散比值会增大, 原因是在层结的影响下, 有效势能耗散减小。
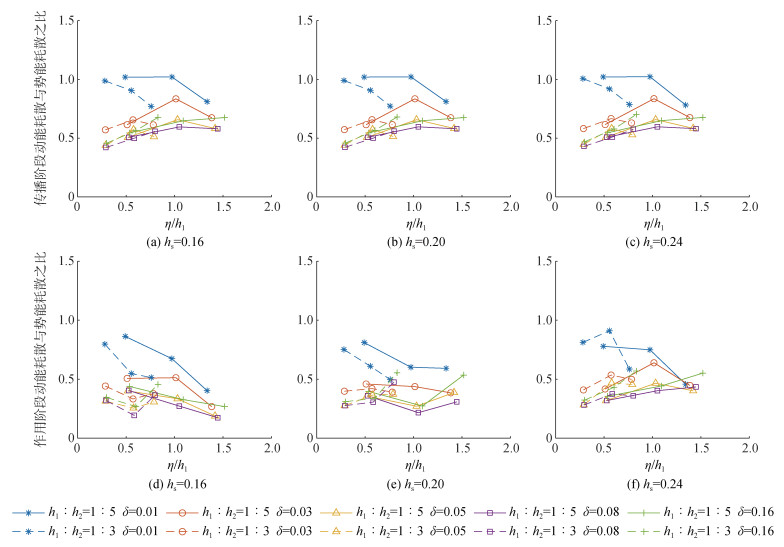 |
| 图 6 内孤立波传播过程及作用过程动能耗散比有效势能耗散 Fig. 6 Dissipation of kinetic energy to available potential energy during the propagation and interaction of internal solitary waves |
Turkington等[70]证明了对于非线性内孤立波动能总大于有效势能。Lamb等[71]对不同振幅动能有效势能比进行了计算, 动能有效势能比最大值可达到1.3, Klymak等[17]在南海发现动能有效势能比可达到1.4, 而内孤立波在浅化过程中最大为1.5[72]。同样以地形高度0.24 m、水深比为1∶5、塌陷高度为0.24 m为例, 内孤立波生成后向右传播的过程中, 有效势能耗散大于动能耗散, 动能有效势能比持续增加, 到达斜坡地形前达到极大值, 即图 7(a) 55 s附近, 动能有效势能比极大值取值在传播阶段, 最大值是由于内孤立波与地形相互作用产生, 出现在作用阶段。动能有效势能比达到极大值之后, 湍耗散率积分增强[图 7(b)], 内孤立波开始与地形相互作用。在作用阶段动能向有效势能转化, 动能有效势能比减小达到极小值。动能有效势能比达到极小值之后, 内孤立波发生破碎, 有效势能转化为动能, 增强波致涡旋、湍流等更小尺度的混合。因此可以选取这两个极值点, 其很好地划分了内孤立波与地形相互作用的各个阶段, 进一步讨论跃层厚度带来的能量变化差异。内孤立波到达陆坡区域时, 动能有效势能比开始减小, 陆坡区域的理查德森数平均值也逐渐减小[图 7(c)], 发生破碎之后不同跃层厚度的演化规律变得不同。
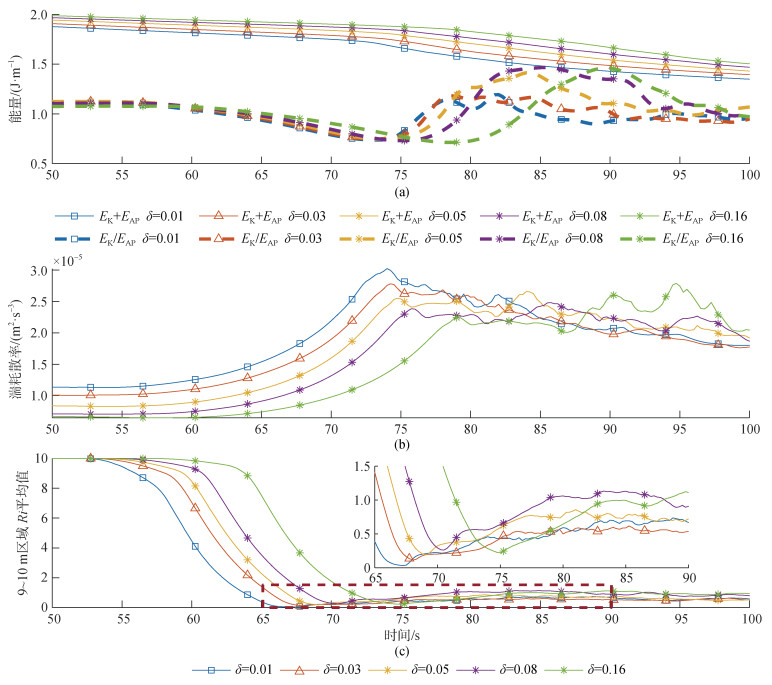 |
| 图 7 内孤立波能量、动能有效势能比、湍耗散及9~10 m区域内理查德森数平均值 Fig. 7 Energy, kinetic energy to available energy ratio, turbulent dissipation of internal solitary waves, and averaged Richardson numbers in the 9–10-m zone |
这里的湍耗散率积分为对直接法计算所得湍耗散率进行整场积分, 再进行时间积分得到的结果。图 8为在不同地形水深条件下, 动能有效势能比的极大值、极小值及湍耗散率对比图。在传播阶段, 图 8(a)—(c)可以看到, 振幅越小, 动能有效势能比极大值更大。这是因为在内孤立波传播过程中, 振幅比较小时, 跃层处的水平流速剪切导致的动能耗散更弱, 所以动能有效势能比达到的极大值更大, 随着跃层厚度从0.01 m增加到0.05 m, 动能势能比极大值随着跃层厚度的增加而增加, 跃层厚度从0.08~0.16 m, 内孤立波动能势能比所达到的极大值随着跃层厚度的增加开始减小。在作用阶段内孤立波动能有效势能比达到极小值, 其反映了内孤立波在与地形相互作用过程中的能量再分配, 动能有效势能比达到的极小值越小, 在地形上动能向有效势能转化的能量越多, 内孤立波能够达到的波陡就会越大。图 8(d)—(f)中小振幅工况达到的动能有效势能极小值与对应工况下动能有效势能极大值基本一致, 随跃层厚度的变化规律也相同。其中跃层厚度达到0.08 m时动能有效势能比极小值演化趋势发生转折, 以图 8(f)中水深比为1∶5最大塌陷高度下五种跃层厚度工况为例, 当跃层厚度达到0.08 m时, 动能势能比随着跃层厚度增大而减小, 跃层厚度达到0.16 m时, 动能有效势能比极小值明显小于跃层厚度为0.01 m工况下的结果。从能量转化的角度来看, 跃层厚度比较小时, 层结的作用会抑制动能向有效势能的转化, 随着跃层厚度的增加, 跃层处流速剪切带来的能量耗散减少, 动能能量随跃层厚度增加而增加, 所以动能有效势能比极小值随跃层厚度增大而增大, 跃层厚度达到0.08 m后, 层结对能量转化的影响减弱, 动能向有效势能转化增强, 动能有效势能比极小值随跃层厚度增大而减小。因此, 跃层厚度会影响内孤立波能量再分配过程。
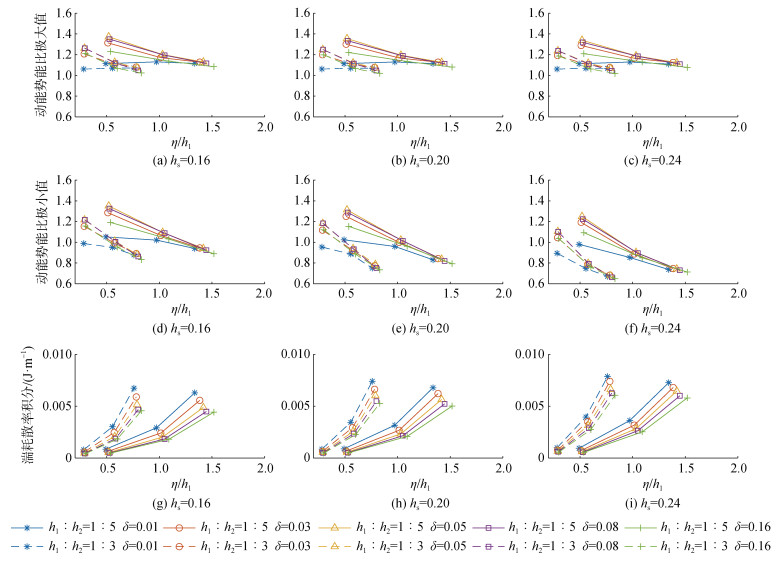 |
| 图 8 动能势能比的极大值、极小值对比及湍耗散率曲线 Fig. 8 Comparison of maximum and minimum values of the kinetic energy–available potential energy ratio and turbulent dissipation |
为了更直观地了解跃层厚度对内孤立波动能有效势能极大值极小值及能量耗散的影响, 这里分析了密度场及湍耗散率变化。图 9(a)—(t)为地形高度0.24 m、水深比为1∶5、塌陷高度为0.24 m工况下不同跃层厚度内孤立波动能有效势能比达到极大值、极小值时密度场及湍耗散率变化。在传播阶段, 图 9(a)—(e)为动能有效势能比极大值时的密度场, 此时内孤立波波谷还未到达斜坡上方, 波前已经开始与地形相互作用。图 9(k)—(o)为动能有效势能比极大值时的湍耗散率结果, 跃层厚度越小, 跃层处的湍耗散率也更强, 所以导致跃层厚度小于0.05 m时, 跃层厚度越小其达到的动能有效势能比极大值越小。在作用阶段, 图 9(f)—(j)为跃层厚度从0.01 m至0.16 m动能有效势能比达到极小值时密度场变化, 此时在内孤立波在浅化效应下动能转换为有效势能, 波陡达到最大, 图 9(f)—(g)中跃层厚度0.01 m及0.03 m工况下跃层处已经产生开尔文-亥姆兹不稳定(简称KH不稳定), 而跃层厚度为0.05 m、0.08 m及0.16 m时[图 9(h)—(j)]则不存在。图 7(c)对数值水槽9~10 m区域内计算得到的理查德森数进行空间平均, 跃层厚度为0.01 m时, 区域内理查德森数达到的平均值最小, 此时流场内流速剪切最强, 同时图 9(p)中跃层处湍耗散率最强, 跃层厚度从0.01 m增加到0.08 m, 流速剪切逐渐减弱, 理查德森数平均值逐渐增大, 界面处的KH不稳定消失; 当跃层厚度达到0.16 m时, 理查德森数平均值减小, 能量耗散增强。因此, 跃层厚度的增加会抑制界面处不稳定过程的发展, 随着跃层厚度的增加能量耗散逐渐减小, 而跃层厚度变大超过临界值后, 层结变化的影响超过流速剪切的变化, 流场内翻转混合效应增强, 能量耗散进一步增加。
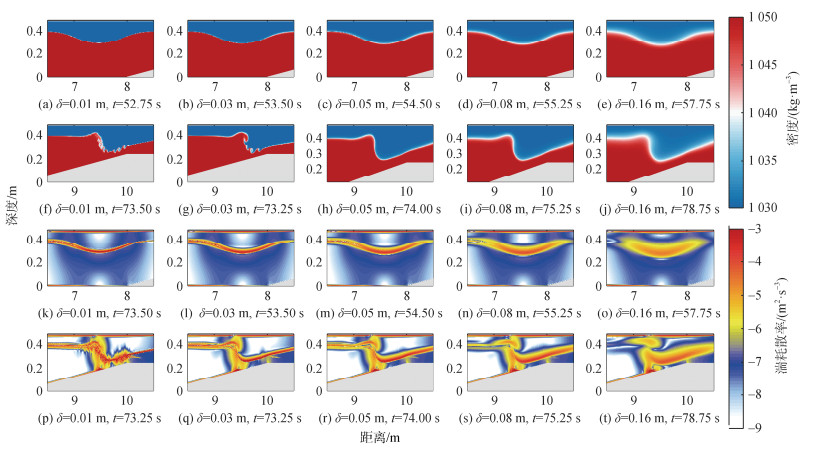 |
| 图 9 内孤立波动能有效势能比极大值、极小值时刻的密度场与湍耗散率 Fig. 9 Diagram of the density field and turbulent dissipation rate at the points of maximum and minimum kinetic energy to the available potential energy of internal solitary waves |
本文基于开源CFD计算软件OpenFOAM使用twoLiquidMixing求解器模拟了不同跃层厚度下内孤立波过斜坡地形的过程。首先分析了跃层厚度对波要素的影响, 随着跃层厚度的增加, 波速减小, 内孤立波振幅增加。并将内孤立波整个过程中分为4个阶段, 分别为生成阶段、传播阶段、作用阶段、透射传播阶段, 对传播阶段及作用阶段的能量再分配过程及能量耗散进行了计算, 跃层厚度在其中的影响主要表现为:
(1) 跃层厚度与跃层处流速剪切存在着负相关关系。相同工况下跃层厚度越小, 跃层处流速剪切越强。
(2) 跃层厚度对能量再分配及能量耗散过程有重要的影响。当跃层厚度较小时, 随着跃层厚度的增加, 内孤立波能量耗散减弱, 动能有效势能比的极值逐渐增大, 动能耗散比有效势能耗散持续减小, 当跃层厚度超过0.08 m时, 规律相反。
(3) 在湍流混合与能量耗散机制方面。跃层厚度小时, 跃层处的流速剪切强烈, 存在强烈的混合过程, 理查德森数平均值较小, 易引起KH不稳定的产生, 随着跃层厚度的增加界面处剪切效应减弱, 理查德森数平均值逐渐变大, KH不稳定消失, 当跃层厚度继续增加超过临界值之后, 理查德森数变小, 内孤立波破碎时流体的翻转混合过程加强, 引起强烈的能量耗散。
(4) 随着塌陷高度的增加, 内孤立波波速逐渐增加, 传播阶段及作用阶段的能量耗散也会逐渐增强, 动能有效势能比极大值极小值逐渐减小, 水深比为1∶5时, 相同塌陷高度下内孤立波波速及传播阶段能量耗散大于水深比为1∶3工况下, 作用阶段能量耗散及动能有效势能比极大值极小值规律相反, 地形高度的增加会增加作用阶段的能量耗散, 对传播阶段能量耗散影响不大。
| [1] |
CHRIS G. Mixing with latitude[J]. Nature, 2003, 422(6931): 477-478. DOI:10.1038/422477a |
| [2] |
OSBORNE A R, BURCH T L. Internal solitons in the Andaman Sea[J]. Science, 1980, 208(4443): 451-460. DOI:10.1126/science.208.4443.451 |
| [3] |
DUDA T F, LYNCH J F, IRISH J D, et al. Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea[J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1105-1130. DOI:10.1109/JOE.2004.836998 |
| [4] |
HELFRICH K R, MELVILLE W K. Long nonlinear internal waves[J]. Annual Review of Fluid Mechanics, 2006, 38(1): 395-425. DOI:10.1146/annurev.fluid.38.050304.092129 |
| [5] |
SUSANTO R, MITNIK L, ZHENG Q. Ocean internal waves observed in the Lombok Strait[J]. Oceanography, 2005, 18: 80-87. |
| [6] |
INALL M E, RIPPETH T P, SHERWIN T J. Impact of nonlinear waves on the dissipation of internal tidal energy at a shelf break[J]. Journal of Geophysical Research: Oceans, 2000, 105(C4): 8687-8705. DOI:10.1029/1999JC900299 |
| [7] |
MOUM J N, FARMER D M, SMYTH W D, et al. Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf[J]. Journal of Physical Oceanography, 2003, 33(10): 2093-2112. DOI:10.1175/1520-0485(2003)033<2093:SAGOTA>2.0.CO;2 |
| [8] |
SANDSTROM H, OAKEY N S. Dissipation in internal tides and solitary waves[J]. Journal of Physical Oceanography, 1995, 25(4): 604-614. DOI:10.1175/1520-0485(1995)025<0604:DIITAS>2.0.CO;2 |
| [9] |
MA X, YAN J, HOU Y, et al. Footprints of obliquely incident internal solitary waves and internal tides near the shelf break in the northern South China Sea[J]. Journal of Geophysical Research: Oceans, 2016, 121(12): 8706-8719. DOI:10.1002/2016JC012009 |
| [10] |
RIVERA-ROSARIO G, DIAMESSIS P J, LIEN R C, et al. Formation of recirculating cores in convectively breaking internal solitary waves of depression shoaling over gentle slopes in the south China Sea[J]. Journal of Physical Oceanography, 2020, 50(5): 1137-1157. DOI:10.1175/JPO-D-19-0036.1 |
| [11] |
NEW A L, PINGREE R D. Large-amplitude internal soliton packets in the central Bay of Biscay[J]. Deep Sea Research Part A: Oceanographic Research Papers, 1990, 37(3): 513-524. DOI:10.1016/0198-0149(90)90022-N |
| [12] |
ALFORD M H, PEACOCK T, MACKINNON J A, et al. The formation and fate of internal waves in the South China Sea[J]. Nature, 2015, 521(7550): 65-69. DOI:10.1038/nature14399 |
| [13] |
VLASENKO V, STASHCHUK N, INALL M E, et al. Tidal energy conversion in a global hot spot: On the 3-D dynamics of baroclinic tides at the Celtic Sea shelf break[J]. Journal of Geophysical Research: Oceans, 2014, 119(6): 3249-3265. DOI:10.1002/2013JC009708 |
| [14] |
NAM S, SEND U. Direct evidence of deep water intrusions onto the continental shelf via surging internal tides[J]. Journal of Geophysical Research: Oceans, 2011, 116: C05004. |
| [15] |
FU K H, WANG Y H, LEE C P, et al. The deformation of shoaling internal waves observed at the Dongsha Atoll in the northern South China Sea[J]. Coastal Engineering Journal, 2016, 1650001. |
| [16] |
ORR M H. Nonlinear internal waves in the South China Sea: Observation of the conversion of depression internal waves to elevation internal waves[J]. Journal of Geophysical Research: Oceans, 2003, 108(C3): 3064. |
| [17] |
KLYMAK J M, PINKEL R, LIU C, et al. Prototypical solitons in the South China Sea[J]. Geophysical Research Letters, 2006, 33(11): 2006GL025932. DOI:10.1029/2006GL025932 |
| [18] |
柯自明, 尹宝树, 徐振华, 等. 南海文昌海域内孤立波特征观测研究[J]. 海洋与湖沼, 2009, 40(3): 269-274. KE Ziming, YIN Baoshu, XU Zhenhua, et al. The characteristics of internal solitary waves at wenchang in the South China Sea[J]. Oceanologia et Limnologia Sinica, 2009, 40(3): 269-274. DOI:10.3321/j.issn:0029-814X.2009.03.003 |
| [19] |
吴凡, 杨永增, 熊学军, 等. 相同尺度地形与背景流共振生成内孤立波机制[J]. 海洋科学进展, 2022, 40(2): 197-208. WU Fan, YANG Yongzeng, XIONG Xuejun, et al. Mechanism of internal solitary waves generated by the resonance of same-scale terrain and background current[J]. Advances in Marine Science, 2022, 40(2): 197-208. |
| [20] |
ZHAO Z, ALFORD M H. Source and propagation of internal solitary waves in the northeastern South China Sea[J]. Journal of Geophysical Research: Oceans, 2006, 111(C11): C11012. |
| [21] |
RAMP S R, TANG T Y, DUDA T F, et al. Internal solitons in the northeastern South China Sea part I: sources and deep water propagation[J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1157-1181. DOI:10.1109/JOE.2004.840839 |
| [22] |
YANG Y J, TANG T Y, CHANG M H, et al. Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies[J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1182-1199. DOI:10.1109/JOE.2004.841424 |
| [23] |
ALFORD M H, LIEN R C, Simmons H, et al. Speed and evolution of nonlinear internal waves transiting the South China Sea[J]. Journal of Physical Oceanography, 2010, 40(6): 1338-1355. DOI:10.1175/2010JPO4388.1 |
| [24] |
LI Q, FARMER D M. The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea[J]. Journal of Physical Oceanography, 2011, 41(7): 1345-1363. DOI:10.1175/2011JPO4587.1 |
| [25] |
LIEN R C, HENYEY F, MA B, et al. Large-Amplitude internal solitary waves observed in the northern South China Sea: properties and energetics[J]. Journal of Physical Oceanography, 2014, 44(4): 1095-1115. DOI:10.1175/JPO-D-13-088.1 |
| [26] |
RAMP S R, PARK J H, YANG Y J, et al. Latitudinal structure of solitons in the South China Sea[J]. Journal of Physical Oceanography, 2019, 49(7): 1747-1767. DOI:10.1175/JPO-D-18-0071.1 |
| [27] |
于博, 黄晓冬, 董济海, 等. 南海陆坡区约束流核型内孤立波观测研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(3): 1-7. YU Bo, HUANG Xiaodong, DONG Jihai, et al. Observation of a trapped core internal solitary wave in South China Sea[J]. Periodical of Ocean University of China, 2016, 46(3): 1-7. |
| [28] |
AGHSAEE P, BOEGMAN L, LAMB K G. Breaking of shoaling internal solitary waves[J]. Journal of Fluid Mechanics, 2010, 659: 289-317. DOI:10.1017/S002211201000248X |
| [29] |
BOEGMAN L, IVEY G N, Imberger J. The degeneration of internal waves in lakes with sloping topography[J]. Limnology and Oceanography, 2005, 50(5): 1620-1637. DOI:10.4319/lo.2005.50.5.1620 |
| [30] |
HELFRICH K R, MELVILLE W K. On long nonlinear internal waves over slope-shelf topography[J]. Journal of Fluid Mechanics, 1986, 167(1): 285-308. |
| [31] |
LA FORGIA G, TOKYAY T, ADDUCE C, et al. Numerical investigation of breaking internal solitary waves[J]. Physical Review Fluids, 2018, 3(10): 104801. DOI:10.1103/PhysRevFluids.3.104801 |
| [32] |
MICHALLET H, IVEY G N. Experiments on mixing due to internal solitary waves breaking on uniform slopes[J]. Journal of Geophysical Research: Oceans, 1999, 104(C6): 13467-13477. DOI:10.1029/1999JC900037 |
| [33] |
NAKAYAMA K, SATO T, SHIMIZU K, et al. Classification of internal solitary wave breaking over a slope[J]. Physical Review Fluids, 2019, 4(1): 014801. DOI:10.1103/PhysRevFluids.4.014801 |
| [34] |
SUTHERLAND B R, BARRETT K J, IVEY G N. Shoaling internal solitary waves[J]. Journal of Geophy sical Research: Oceans, 2013, 118(9): 4111-4124. DOI:10.1002/jgrc.20291 |
| [35] |
吴凡. 南海北部内孤立波特征分析及潮地共振产生内波的机制研究[D]. 青岛: 自然资源部第一海洋研究所, 2021. WU Fan. Research on the mechanism of internal solitary waves generated by the resonance of the same- scale terrain and background current[D]. Qingdao: The First Institute of Oceanography, SOA, 2021. |
| [36] |
GARRETT C, KUNZE E. Internal tide generation in the deep ocean[J]. Annual Review of Fluid Mechanics, 2007, 39(1): 57-87. DOI:10.1146/annurev.fluid.39.050905.110227 |
| [37] |
VLASENKO V, HUTTER K. Numerical experiments on the breaking of solitary internal wavesover a slope–shelf topography[J]. Journal of Physical Oceanography, 2002, 32(6): 1779-1793. DOI:10.1175/1520-0485(2002)032<1779:NEOTBO>2.0.CO;2 |
| [38] |
KLYMAK J M, LEGG S, PINKEL R. A simple parameterization of turbulent tidal mixing near supercritical topography[J]. Journal of Physical Oceanography, 2010, 40(9): 2059-2074. DOI:10.1175/2010JPO4396.1 |
| [39] |
郭钰林, 孟静, 徐昱, 等. 内孤立波与平顶海山作用的能量耗散实验研究[J]. 海洋与湖沼, 2021, 52(4): 846-859. GUO Yulin, MENG Jing, XU Yu, et al. Laboratory study on energy dissipation of internal solitary waves in guyots[J]. Oceanologia et Limnologia sinica, 2021, 52(4): 846-859. |
| [40] |
ARTHUR R S, KOSEFF J R, FRINGER O B. Local versus volume-integrated turbulence and mixing in breaking internal waves on slopes[J]. Journal of Fluid Mechanics, 2017, 815: 169-198. DOI:10.1017/jfm.2017.36 |
| [41] |
XU C Z, STASYNA M. Instability and cross-boundary-layer transport by shoaling internal waves over realistic slopes[J]. Journal of Fluid Mechanics, 2020, 895: R6. DOI:10.1017/jfm.2020.389 |
| [42] |
HARTHARN-EVANS S, STASTNA M, CARR M. Dense pulses formed from fissioning internal waves[J]. Environmental Fluid Mechanics, 2022, 23(2): 1-17. |
| [43] |
ALLSHOUSE M R, SWINNEY H L. Dependence of internal wave bolus transport on pycnocline thickness[J]. Geophysical Research Letters, 2020, 47(14): e2020GL086952. DOI:10.1029/2020GL086952 |
| [44] |
HARTHARN-EVANS S G, CARR M, STASTNA M, et al. Stratification effects on shoaling internal solitary waves[J]. Journal of Fluid Mechanics, 2022, 933: A19. DOI:10.1017/jfm.2021.1049 |
| [45] |
DELISI D P, ORLANSKI I. On the role of density jumps in the reflexion and breaking of internal gravity waves[J]. Journal of Fluid Mechanics, 1975, 69(3): 445-464. DOI:10.1017/S0022112075001516 |
| [46] |
于宗冰, 邹丽, 马鑫宇, 等. 基于OpenFOAM软件的内孤立波生成模拟及试验[J]. 中国海洋平台, 2020, 35(5): 27-34. YU Zongbing, ZOU Li, MA Xinyu, et al. Simulation and test of internal solitary wave generation based on OpenFOAM software[J]. China Offshore Platform, 2020, 35(5): 27-34. |
| [47] |
DING W, AI C, JIN S, et al. Numerical investigation of an internal solitary wave interaction with horizontal cylinders[J]. Ocean Engineering, 2020, 208: 107430. DOI:10.1016/j.oceaneng.2020.107430 |
| [48] |
LI J, ZHANG Q, CHEN T. ISWFoam: a numerical model for internal solitary wave simulation in continuously stratified fluids[J]. Geoscientific Model Development, 2022, 15(1): 105-127. DOI:10.5194/gmd-15-105-2022 |
| [49] |
MENG Q, ZHANG C. A third-order KdV solution for internal solitary waves and its application in the numerical wave tank[J]. Journal of Ocean Engineering and Science, 2016, 1(2): 93-108. DOI:10.1016/j.joes.2016.03.002 |
| [50] |
ZOU L, YU Y, SUN Z, et al. CFD Simulation of internal solitary wave using the Volume-of-fluid method within OpenFOAM[J]. DEStech Transactions on Computer Science and Engineering, 2018, mmsta: 19617. |
| [51] |
RODI W, CONSTANTINESCU G, STOESSER T. Large-eddy simulation in hydraulics[M]. London: CRC Press, 2013.
|
| [52] |
KILLINGSTAD P E. A study of dead water resistance reynolds averaged navier stokes simulations of a barge moving in stratified waters[D]. Oslo: University of Oslo, 2018.
|
| [53] |
XIE P, CHU V H. Openfoam simulation of gravity- current head impact on a structure on the sea floor[C]//CALVO L 3 8th IAHR World Congress. Panama: International Association for Hydro-Environment Engineering and Research, 2019: 4128-4136.
|
| [54] |
WANG C A, XU D, GAO J P, et al. Numerical study of surface thermal signatures of lee waves excited by moving underwater sphere at low Froude number[J]. Ocean Engineering, 2021, 235: 109314. DOI:10.1016/j.oceaneng.2021.109314 |
| [55] |
MARU W, HOLLAND D, LAKSHMANAN S, et al. Multiphase flow and mixing quantification using computational fluid dynamics and magnetic resonance imaging[J]. Flow Measurement and Instrumentation, 2021, 77: 101816. DOI:10.1016/j.flowmeasinst.2020.101816 |
| [56] |
SANTOS R R C, VIANNA S S V. Stratified flows and associated shear instabilities modelling over an inclined plan[J]. Process Safety and Environmental Protection, 2020, 136: 169-181. DOI:10.1016/j.psep.2020.01.027 |
| [57] |
MOUKALLED F, MANGANI L, DARWISH M. Erratum to: The finite volume method in computational fluid dynamics[M]. Cham: Springer International Publishing, 2015.
|
| [58] |
ISSA R I. Solution of the implicitly discretised fluid flow equations by operator-splitting[J]. Journal of Computational Physics, 1986, 62(1): 40-65. DOI:10.1016/0021-9991(86)90099-9 |
| [59] |
CARETTO L S, GOSMAN A D, PATANKAR S V, et al. Two calculation procedures for steady, three-dimensional flows with recirculation[C]//CABANNES H, TEMAM R. Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics. Berlin, Heidelberg: Springer, 1973: 60-68.
|
| [60] |
MICHALLET H, BARTHÉLEMY E. Experimental study of interfacial solitary waves[J]. Journal of Fluid Mechanics, 1998, 366: 159-177. DOI:10.1017/S002211209800127X |
| [61] |
VLASENKO V, BRANDT P, RUBINO A. Structure of large-amplitude internal solitary waves[J]. Journal of Physical Oceanography, 2000, 30(9): 2172-2185. DOI:10.1175/1520-0485(2000)030<2172:SOLAIS>2.0.CO;2 |
| [62] |
SCHLITZER R. Electronic atlas of WOCE hydrographic and tracer data now available[J]. Eos, Transactions American Geophysical Union, 2000, 81(5): 45-45. |
| [63] |
SUTHERLAND B R, KEATING S, SHRIVASTAVA I. Transmission and reflection of internal solitary waves incident upon a triangular barrier[J]. Journal of Fluid Mechanics, 2015, 775: 304-327. DOI:10.1017/jfm.2015.306 |
| [64] |
LAMB K G. On the calculation of the available potential energy of an isolated perturbation in a density-stratified fluid[J]. Journal of Fluid Mechanics, 2008, 597: 415-427. DOI:10.1017/S0022112007009743 |
| [65] |
DORON P, BERTUCCIOLI L, KATZ J, et al. Turbulence characteristics and dissipation estimates in the coastal ocean bottom boundary layer from PIV data[J]. Journal of Physical Oceanography, 2001, 31(8): 2108-2134. DOI:10.1175/1520-0485(2001)031<2108:TCADEI>2.0.CO;2 |
| [66] |
黄鹏起, 陈旭, 孟静, 等. 内孤立波破碎所致混合的实验研究[J]. 海洋与湖沼, 2016, 47(3): 533-539. HUANG Pengqi, CHEN Xu, MENG Jing, et al. An experimental study on mixing induced by internal solitary wave breaking[J]. Oceanologia et Limnologia Sinica, 2016, 47(3): 533-539. |
| [67] |
MILES J W. On the stability of heterogeneous shear flows. Part 2[J]. Journal of Fluid Mechanics, 1963, 16(2): 209-227. DOI:10.1017/S0022112063000707 |
| [68] |
MILES J W. On the stability of heterogeneous shear flows[J]. Journal of Fluid Mechanics, 1961, 10(4): 496. DOI:10.1017/S0022112061000305 |
| [69] |
HOWARD L N. Note on a paper of John W. Miles[J]. Journal of Fluid Mechanics, 1961, 10(4): 509. DOI:10.1017/S0022112061000317 |
| [70] |
TURKINGTON B, EYDELAND A, WANG S. A computational method for solitary internal waves in a continuously stratified fluid[J]. Studies in Applied Mathematics, 1991, 85(2): 93-127. DOI:10.1002/sapm199185293 |
| [71] |
LAMB K G, NGUYEN V T. Calculating energy flux in internal solitary waves with an application to reflectance[J]. Journal of Physical Oceanography, 2009, 39(3): 559-580. DOI:10.1175/2008JPO3882.1 |
| [72] |
KLYMAK J M, MOUM J N. Internal solitary waves of elevation advancing on a shoaling shelf[J]. Geophysical Research Letters, 2003, 30(20): 2003GL017706. DOI:10.1029/2003GL017706 |
 2024, Vol. 48
2024, Vol. 48


