文章信息
- 张明琪, 徐永生, 杨树国. 2024.
- ZHANG Mingqi, XU Yongsheng, YANG Shuguo. 2024.
- 多尺度耦合经验正交分解法反演海洋次表层温盐结构
- Inversion of ocean subsurface temperature and salinity structure by multiscale coupled empirical orthogonal decomposition
- 海洋科学, 48(3): 1-12
- Marine Sciences, 48(3): 1-12.
- http://dx.doi.org/10.11759/hykx20221124003
-
文章历史
- 收稿日期:2022-11-24
- 修回日期:2023-02-16
2. 中国科学院海洋研究所, 山东 青岛 266071;
3. 崂山实验室, 山东 青岛 266061;
4. 中国科学院大学, 北京 100094
2. Institute of Oceanography, Chinese Academy of Sciences, Qingdao 266071, China;
3. Laoshan Laboratory, Qingdao 266061, China;
4. University of Chinese Academy of Sciences, Beijing 100094, China
卫星遥感凭借快速、高效获取地球表面大量实时观测数据的能力, 成为人类了解和认知地球的必要途径。目前, 中国遥感卫星已发展成为拥有气象、海洋等系列卫星的对地观测系统[1-2]。海洋三维温盐场属于海洋核心动力要素, 精准描述海洋次表层温盐结构非常重要且富有挑战性。对于海洋内部现场的观测, 受多方面因素的限制, 数据往往稀疏和缺失。卫星遥感也无法直接探测海洋内部热力信息。然而经过多年的发展和观测, 遥感技术已经积累了庞大的海表面观测数据, 因此基于海表层卫星遥感观测间接推测海洋次表层温盐结构有非常重要的研究意义[3]。
温度和盐度是海水的基本物理性质, 它们的分布表征海洋的动态过程, 并对生物地球化学循环具有重要的影响[4-5]。近年来, 人们通过各种各样的方法不断地探索海洋次表面的温盐结构。海洋的次表层结构都会受到表层参数的影响, 并且可以借助卫星观测数据和数值模拟方法进行解释, 以得出深海温盐结构的关键参数[6]。Khedouri等[7]通过卫星高度计数据来估算海洋次表层温度; Fischer[8]基于多元投影法, 使用海表面高度异常(sea surface height anomaly, 简称SSHA)和海表面温度异常(sea surface temperature anomaly, 简称SSTA)估计了赤道的垂直温度结构; Fox等[9]通过经验回归建立了海面高度与海面温度与次表面温盐的回归模型, 并且以此为基础构建了美国海军使用的The Modular Ocean Data Assimilation System (MODAS)系统; 王喜东等[10]根据MODAS系统统计出了海面温度异常、海面高度异常与温度剖面异常之间关系, 并利用卫星海表面温度和卫星海面高度重构了三维海洋温度场。此外还有很多基于统计回归的重构方法[11-15], 这类方法利用卫星表面观测对海洋三维温盐场进行重构, 对温盐场有良好的描述能力, 但是缺乏温盐场垂直梯度的约束。除了回归方法外, Ali等[16]表明, 可以使用神经网络从表面参数确定海洋次表层的温盐结构。Wu等[17]使用了多个卫星测量和一种名为自组织图(Self-Organizing Map, 简称SOM)的神经网络算法, 对海洋次表面的温盐结构进行了估算; Su等[18-19]采用支持向量机、随机森林等多种方法对全球海洋温盐场重构进行探索并取得较好的精度结果。此外, 聂旺琛等[20]利用广义回归神经网络算法重构了全球海洋三维温盐场。人工智能重构主要集中在大尺度温盐场重构上, 然而对于小尺度的温盐场重构效能尚不明确。
本文提出一种基于多尺度耦合经验正交分解(Multi-scale coupled empirical orthogonal function, 简称MCEOF)的三维温盐场多尺度重构方法, 通过多层重构迭代的过程得到包含多尺度特征信息的重构三维温盐场。该方法引入了多尺度重构的思想, 从不同的空间尺度进行重构, 提高了温盐场及其垂直梯度的重构精度。同时该温盐重构模型的构建, 为高精度温盐场的重构方案给予了参考, 也为进一步优化模型, 比如增加海表面盐度、风场等约束条件来提高重构精度提供了思路。
1 数据 1.1 数据来源本文使用的数据集有: 1)卫星遥感海面温度数据(sea surface temperature, 简称SST)和卫星海表面高度数据(sea surface height, 简称SSH); 2)历史观测温盐场数据; 3)气候态数据。
文中选取的SST数据为REMSS(Remote Sensing Systems)多源卫星融合daily SST产品(https://data.remss.com/sst/daily/mw/v05.0/netcdf/), 其分辨率为0.25°×0.25°。
卫星高度数据来自于Aviso+提供的0.25°×0.25°的网格化海面高度异常数据daily SSH产品(https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-level-global?tab=form), 该数据融合了TOPEX/ POSEIDON、JASON等卫星资料。
历史观测温盐场数据选取的是全球海洋ARGO (array for real-time geostrophic oceanography)温盐数据(https://data-ARGO.ifremer.fr/geo/pacific_ocean/), 包括从2001—2020年, 研究区域内所有的温盐剖面。
气候态数据选取美国国家海洋数据中心提供的WOA18(World Ocean Atlas 2018)温盐数据集(https://www.ncei.noaa.gov/access/world-ocean-atlas-2018/)。
1.2 数据处理本文使用ARGO数据集对重构方法进行测试, 选取的重建区域为143°~155°E, 28°~40°N的12°×12°矩形区域, 将所有的剖面数据随机打乱, 随机选取3/4的温盐剖面建立重构模型, 利用剩下1/4的数据剖面进行模型验证。
在建立模型前, 需要对区域内的数据集进行严格的筛选和处理。本文只重构试验区域内0~1 000 m深度内的温盐剖面, 以此来验证模型, 所以要删除1 000 m以浅区域空值率大于5%的温盐剖面, 然后将温盐剖面用线性插值法插值为标准深度的剖面数据, 本文选取的标准深度与WOA18气候态的标准深度保持一致。除此之外, 删去温盐度数据变化不稳定的剖面。最后, 将SST、SSH以及气候态数据根据时空位置与ARGO温盐剖面相匹配, 总计得到约21 000条剖面, 其中训练集数据约15 000条, 测试集数据约6 000条。
2 方法 2.1 EOF重构方法经验正交分解(empirical orthogonal function, 简称EOF)也叫做特征向量分析, 它主要被用于分析矩阵数据中的特征, 进而提取数据中的主要特征量。本文主要是利用EOF方法对三维温盐场的垂向模态进行提取, 对于任意测试集的分析点, 将其附近的历史温度和盐度的深度剖面组成一个新的耦合温盐剖面矩阵X, 然后对矩阵X进行经验正交分解。
| $ \boldsymbol X = \left( {\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{12}}}& \cdots &{{T_{1i}}}& \cdots &{{T_{1N}}} \\ {{T_{21}}}&{{T_{22}}}& \cdots &{{T_{2i}}}& \cdots &{{T_{2N}}} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{T_{k1}}}&{{T_{k2}}}& \cdots &{{T_{ki}}}& \cdots &{{T_{kN}}} \\ {{S_{11}}}&{{S_{12}}}& \cdots &{{S_{1i}}}& \cdots &{{S_{1N}}} \\ {{S_{21}}}&{{S_{22}}}& \cdots &{{S_{2i}}}& \cdots &{{S_{2N}}} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{S_{k1}}}&{{S_{k2}}}& \cdots &{{S_{ki}}}& \cdots &{{S_{kN}}} \end{array}} \right), $ | (1) |
式中
| $ \boldsymbol P = {\boldsymbol E_{{\text{EOF}}}}^{\text{T}} · \boldsymbol X . $ | (2) |
分析前m个主成分与海面温度和海面高度的相关关系, 并利用多元线性回归建立每个主成分与剖面的经度、纬度、海面温度和海面高度的回归关系:
| $ \widehat {{\boldsymbol P_i}} = {b_1} + {b_2}*{L_\text{lon}} + {b_3}*{L_\text{lat}} + {b_4}*{S_\text{SST}} + {b_5}*{S_\text{SSH}} , $ | (3) |
式中i=1, 2,
| $ \hat {\boldsymbol{X}} = {\boldsymbol E_\text{EOF}} · \hat {\boldsymbol {P}}. $ | (4) |
得到对应位置的重构温盐剖面。
2.2 多尺度耦合正交分解考虑到固定尺度窗口的EOF分解得到的只是固定尺度的垂向温盐特征, 而对其他尺度的温盐信息捕捉能力较为缺乏, 为了提取不同尺度的三维温盐场信息, 本文提出了一种多尺度耦合正交分解(MCEOF)回归法来开展三维温盐场重构工作。
MCEOF的主要思想是: 首先通过EOF分解, 利用前m个模态, 即在大尺度上温盐场的主要特征, 重构出依赖于前m个模态的训练集重构温盐场
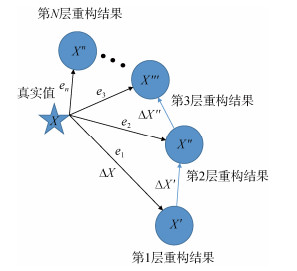 |
| 图 1 模型误差分析 Fig. 1 Model error analysis |
本文以三层MCEOF为例进行分析, 如图 2, 第1层MCEOF是将观测温盐剖面构成的矩阵X提取主成分, 使用多元线性回归构造主成分与剖面的经度、纬度、海面温度和海面高度的函数关系:
| $ \boldsymbol P = f\left( {{L_\text{lon}}, {\text{ }}{L_\text{lat}}, {\text{ }}{S_\text{SST}}, {\text{ }}{S_\text{SSH}}} \right) , $ | (5) |
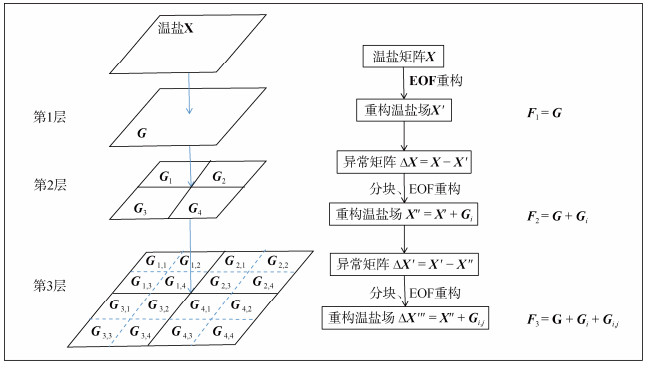 |
| 图 2 MCEOF重构流程图 Fig. 2 Flow chart of MCEOF-based reconstruction |
进而重构得到第1层重构温盐场
接下来计算第2层MCEOF, 第1层重构温盐场与观测温盐场的异常值为
| $ {\hat {\boldsymbol {P}}_i} = {f_i}\left( {{L_\text{lon}}, {L_\text{lat}}, \widehat {{S_\text{SST}}}, \widehat {{S_\text{SSH}}}} \right), $ | (6) |
式中
| $ \boldsymbol {X}_{i}^{″}=\boldsymbol {X}^{\prime } +\boldsymbol {E}_\text{EOF, i}·{\widehat{\boldsymbol {P}}}_{i} $ | (7) |
记为
同理进行第3层MCEOF重构, 第2层重构温盐场与第1层重构温盐场的异常值为
| $ {\hat{\boldsymbol {P}}_{1, i}} = {f_{1, i}}\left( {{L_\text{lon}}, \;{L_\text{lat}}, \;{{\widehat {{S_\text{SST}}}}^{'}}, \;{{\widehat {{S_\text{SSH}}}}^{'}}} \right), $ | (8) |
式中
分别为
| $ {\boldsymbol {X}^{‴}}_{1, i}=\boldsymbol {X}^{\prime } + \boldsymbol {X}_{1}^{″} + \boldsymbol {E}_{\text{EOF, 1, }i}·{\widehat{{\boldsymbol P}}}_{1, i} , $ | (9) |
记为
本文利用所构造的数据集, 对MCEOF重构模型进行验证, 分别建立了不同的MCEOF重构对照分析, 进行多次重复试验, 并将其结果与多元线性回归(Multiple Linear Regression, 简称MLR)重构方法进行比较。
3.1 EOF模型对空间尺度参数的响应关系在温盐重构过程中, 空间尺度越大, 包含的特征越多, 很难捕捉到最主要的特征。因此本文将研究区域划分为12°×12°、6°×6°、3°×3°和1°×1°, 利用EOF重构模型重构不同空间尺度上的温盐场, 分析空间尺度大小对重构结果的影响。
本文计算了EOF重构方法在不同空间尺度上的重构温盐场与ARGO测试温盐场的均方根误差(图 3), 在整体上EOF重构方法的均方根误差均小于MLR重构方法, EOF方法的精度相比于MLR方法有了明显的提升。同时在12°×12°、6°×6°和3°×3°区域内, 随着空间尺度的减小, 重构温盐场的均方根误差逐渐减小, 这是因为不同区域内影响温盐场的主要特征不同, 越小的研究区域越有利于捕捉温盐场的局部特征, 能有效地提高温盐场的重构精度。而1°×1°区域重构温盐场的均方根误差大于3°×3°区域, 这取决于研究区域内数据量的大小, 在实际温盐场重构中, 1°×1°范围内的温盐剖面数量较少, 重构模型难以准确获取完整的温盐特征, 并且模型的精度与稳定性容易受少数异常值的影响, 不足以支撑模型准确地获取其主要特征, 从而影响了重构温盐场的精度。
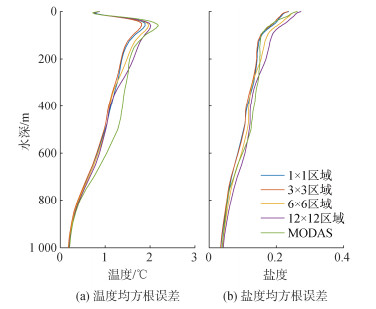 |
| 图 3 不同空间尺度EOF重构温盐场的均方根误差 Fig. 3 Root mean square errors of the EOF reconstruction of temperature and salt fields at different spatial scales |
因此, 对比不同空间尺度范围内EOF模型重构温盐场的精度, 随着空间尺度的减小, 重构温盐场的均方根误差也逐渐减小, 但由于历史观测温盐场数量过少的原因, 限制了模型的优越性, 重构结果在3°×3°区域内达到最佳。
3.2 MCEOF模型敏感度分析本文的温盐场重构方法中涉及到的敏感因素主要有分层的层数以及分层的尺度组合, 为了验证MCEOF重构模型的敏感度和稳定性, 本文根据不同的分层数和分层的尺度组合, 设计了如表 1的13个组合, 分别对每个组合进行5次重复试验, 该重复试验将制作的数据集随机打乱, 随机选取其中3/4的数据作为训练集, 剩余1/4的数据作为测试集, 对每个组合求5组重复试验的平均均方根误差, 作为重构精度的评判标准, 均方根误差越小, 其重构精度越高。
| 组合 | 层数 | 分层情况 | 温度平均均方根误差/℃ | 盐度平均均方根误差 |
| 1 | 4 | 12×12, 6×6, 3×3, 1×1 | 1.200 | 0.143 |
| 2 | 4 | 12×12, 6×6, 2×2, 1×1 | 1.200 | 0.143 |
| 3 | 4 | 12×12, 4×4, 2×2, 1×1 | 1.198 | 0.144 |
| 4 | 3 | 12×12, 6×6, 3×3 | 1.149 | 0.141 |
| 5 | 3 | 12×12, 6×6, 2×2 | 1.158 | 0.141 |
| 6 | 3 | 12×12, 4×4, 2×2 | 1.157 | 0.142 |
| 7 | 2 | 12×12, 6×6 | 1.185 | 0.144 |
| 8 | 2 | 6×6, 3×3 | 1.170 | 0.141 |
| 9 | 2 | 6×6, 2×2 | 1.172 | 0.142 |
| 10 | 2 | 4×4, 2×2 | 1.169 | 0.139 |
| 11 | 1 | 6×6 | 1.258 | 0.154 |
| 12 | 1 | 3×3 | 1.184 | 0.140 |
| 13 | 1 | 2×2 | 1.183 | 0.140 |
如表 1所示, 不同分组实验重构温盐场中, 差异主要体现在温度的重构精度, 盐度的重构精度变化很小, 所以下面主要讨论温度重构精度。通过观察不同分层层数的重构精度发现, 将研究区域分为3层后, MCEOF的重构精度都达到最高, 其余分层方式重构精度由高到低依次为2层、1层、4层; 值得注意的是, 分层层数为4层的组合, 其重构精度会降低, 这是由于该区域内温盐剖面数量较少, 难以提取完整的温盐特性, 模型不能获取其主要特征, 从而降低了模型的重构精度, 因此得到随着MCEOF重构分层数的增加, 重构精度也会增加, 并且分为3层后, 其温盐场重构精度最高。
对相同分层数的不同尺度组合包含2°×2°和3°×3°的组合精度相差不大, 由于2°×2°区域内数据量少的原因, 使其重构精度略有降低, 得到重构精度最高的组合为组合4(12×12, 6×6, 3×3), 因此选择组合4中的尺度参数与层数参数来构建最终的次表层温盐重构模型。
3.3 MCEOF模型重构精度分析本文以组合4(12°×12°、6°×6°、3°×3°)的区域划分为例, 进行MCEOF重构计算, 以此验证MCEOF重构方法的有效性。
首先提取耦合历史观测温盐矩阵的主要特征, 得到对应前4个模态上的特征投影, 即前4个主成分, 分别分析前4个主成分与海面温度异常和海面高度异常的相关性。
图 4(a)表示第1层MCEOF中前4个主成分与海面高度异常的散点图, 其对应主成分的方差贡献率分别为98.90%、0.96%、0.15%和0.04%, 根据图中主成分和海面异常的散点图分布, 得到海面高度异常和第一主成分、第二主成分都有明显的正相关关系, 它们的相关系数分别为0.91、0.93, 但是相关关系并不是线性关系, 而是一种接近指数相关的非线性关系; 海面高度异常和第三主成分存在弱正相关关系, 相关系数为0.23。
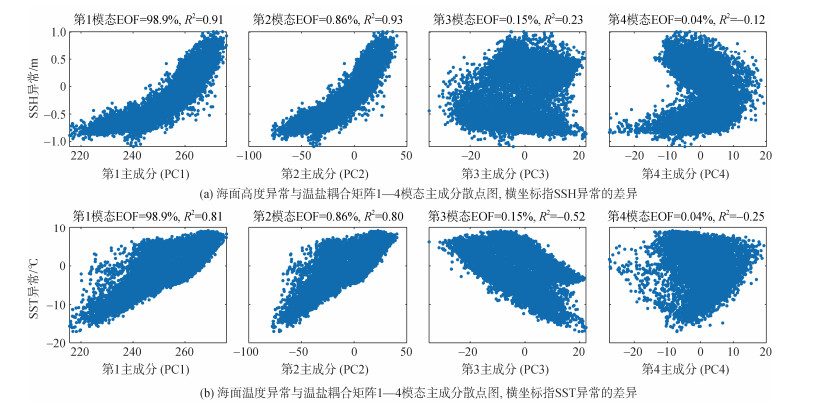 |
| 图 4 第1层MCEOF主成分与海面异常数据的散点分析图 Fig. 4 Scatter analysis plot of the first layers of principal MCEOF components with sea surface anomaly data |
图 4(b)表示前4个主成分与海面温度异常的散点图, 温度异常和第一主成分、第二主成分都存在明显的正相关关系, 相关系数分别为0.81、0.80; 和第三主成分存在明显的负相关关系, 相关系数为–0.52, 并且其相关关系都接近于线性关系。为了便于测试模型, 假设海面高度和海面温度与主成分之间的关系都是线性关系, 建立温盐重构模型, 从而通过公式(2)计算第1层MCEOF的重构温盐场。
通过图 4发现, 在大尺度的EOF分析中, 温度异常和高度异常的散点图明显分成了两簇, 说明除了大尺度上最明显的特征之外, 还有一些中、小尺度的特征也会对温盐场的重构有很重要的作用。因此, 利用本文提出的MCEOF思想, 根据第1层EOF的重构温盐场, 计算其与观测温盐场误差矩阵, 除去大尺度的主要特征, 然后对误差场进行重构, 提取主要特征除外的次要特征, 以此构建第2层尺度的重构模型。
在第2层MCEOF重构中, 将研究区域划分为6°×6°的四个区域, 对每个区域的误差场进行MCEOF分析, 提取其前4个主成分, 分别分析前4个主成分与海面高度误差、温度误差的相关性。
根据图 5, 前4个主成分的方差贡献率分别为58.10%、20.20%、8.92%和4.67%, 前4个主成分的方差贡献率达到90%, 能够表现误差场的主要特征。海面高度异常与第一主成分、第三主成分存在正相关关系, 相关系数为0.43、0.39, 与第二主成分有正相关性, 相关系数为0.30, 两者的相关关系都接近于线性相关; 海面温度异常与第二主成分只有弱负相关关系, 其相关系数分别为–0.29。选取前4个主成分构造三维温盐场的第2层重构模型, 根据公式(5)计算出第2层MCEOF的重构温盐场。
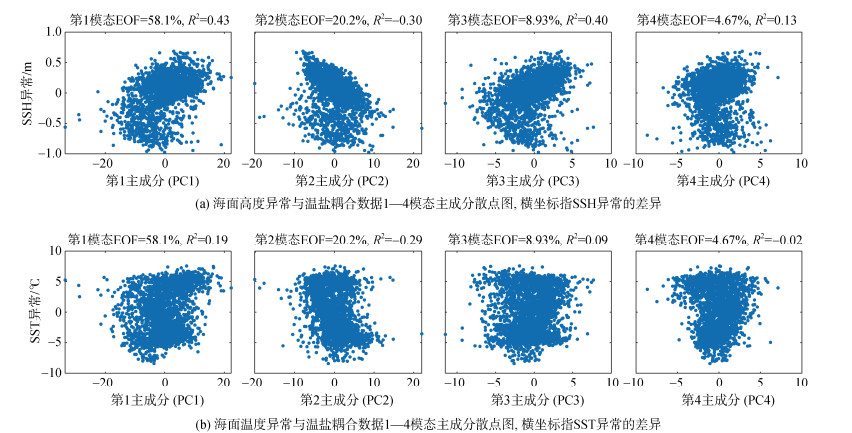 |
| 图 5 第2层MCEOF主成分与海面异常数据的散点分析图 Fig. 5 Scatter analysis plot of the second layers of principal MCEOF components with sea surface anomaly data |
通过图 5发现, 去除大尺度的主要特征后, 海面温度异常和海面高度异常的散点图仍有分为两簇的现象, 说明去除中尺度主要特征之后, 更小尺度的特征仍会对温盐场的重构有很重要的作用。从而在两层MCEOF的基础上, 再次计算第1层重构温盐场和第2层重构温盐场的异常场, 进行EOF分解。
在6°×6°分块区域的基础上, 继续将每个区块均分为3°×3°的研究区域, 建立3°×3°区域上的第3层MCEOF重构。对每个区域的误差场进行EOF特征提取, 提取了其前4个主成分, 分别对海面高度和海面温度与每个主成分之间的相关性进行分析。
如图 6所示, 前4个主成分的方差贡献率达到90%, 能够表现误差场的主要特征。在除去前两个尺度上的主要、次要特征后, 海面高度异常和海面温度异常仍然和主成分之间存在相关关系。海面高度异常与第一主成分存在负相关关系, 且接近线性相关; 海面温度异常与第二主成分存在弱负相关关系, 与第三主成分存在弱正相关关系, 且其相关关系都接近线性相关。选取前4个主成分构造第三层EOF温盐重构模型, 根据公式(7)计算出三层MCEOF(3 layer MCEOF, 简称3L_MCEOF)的重构温盐场。
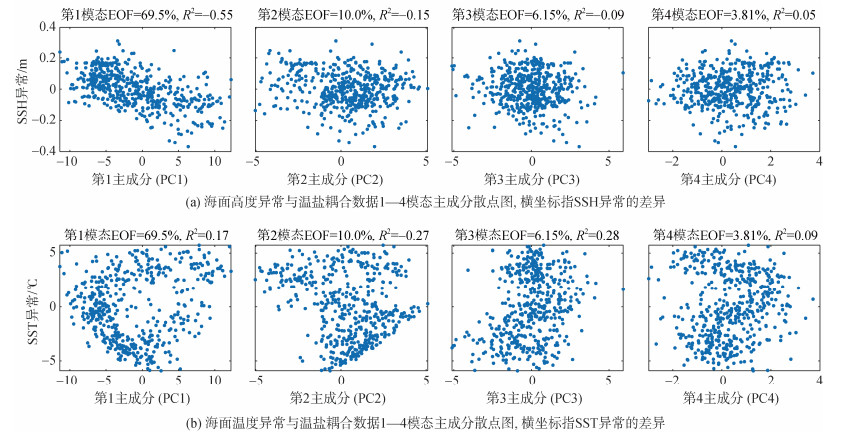 |
| 图 6 第三层MCEOF主成分与海面异常数据的散点分析图 Fig. 6 Scatter analysis plot of the third layers of principal MCEOF components with sea surface anomaly data |
为了验证MCEOF重构方法的优越性, 本文准备了组合4对应的MCEOF重构模型、3°×3°区域内的EOF重构模型和3°×3°区域MLR重构法三个对照组分别做多次重复试验, 通过计算多次实验结果的平均均方根误差, 对温盐场的重构精度进行比较。
图 7中, 相比传统的多元线性回归方法(MLR), 使用EOF重构和MCEOF分层重构方法后, 重构温度和盐度场的精度都得到了提升, 总体来看, MCEOF重构的精度最高。针对图 7温度均方根误差图, 在混合层深度处, 所有重构方案温度的均方根误差都达到最大值, EOF重构的均方根误差为1.86, MCEOF重构的均方根误差为1.76, 其精度分别较EOF重构提升了约0.1 ℃; 在0~350 m深度处, MCEOF的重构精度相比于EOF有明显的提升, 而在350 m以深的区域, 两种重构方法的精度大致相同, 但还是可以看出, MCEOF的重构精度高于EOF重构, 进一步说明了多尺度EOF重构方法的有效性。
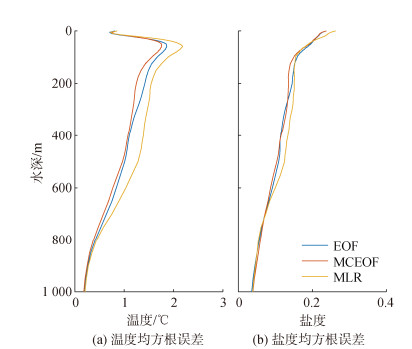 |
| 图 7 MCEOF重构温盐场均方根误差对比 Fig. 7 Comparison of the RMSEs of MCEOF-reconstructed temperature and salt fields |
从图 7盐度均方根误差对比中看出, EOF和MCEOF重构的盐度精度都高于MLR重构方法, 并且从总体看出, MCEOF重构精度达到最高, 虽然盐度精度的提升较小, 但对于海洋在声学场等方面的研究仍然有很大的作用。
除此之外, 本文对对照组重构温盐场的垂直梯度与ARGO观测温盐剖面垂直梯度的均方根误差也进行了分析(图 8)。所有重构温盐场与观测温盐场垂直梯度的均方根误差都符合气候态与观测温盐场垂直梯度均方根误差的变化趋势。MCEOF重构的温盐场垂直梯度在200 m以深区域, 其均方根误差有明显的提升, 并且MCEOF重构温盐场垂直梯度的精度达到最高。这说明通过不断去除大尺度的主要特征, 对温盐场的精度和其垂直梯度的精度都会有明显的改善。MCEOF温盐重构工作提高了重构温盐场的垂直梯度, 这一特点在研究海洋声学场、潜艇的信号接收等方面都有非常重要的作用。
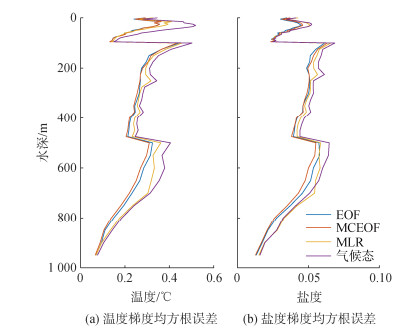 |
| 图 8 三层MCEOF重构温盐梯度均方根误差对比 Fig. 8 Comparison of the RMSEs of MCEOF-reconstructed temperature and salinity gradients |
本文选择组合4的MCEOF重构三维温盐场与HYCOM模式数据进行对比, 分析海洋三维温盐场的空间特征。
HYCOM模式数据采用由等深坐标和等密度坐标相结合的垂向混合坐标, 可以提供海洋数值模式的初始场, 也可以将HYCOM模式数据同化到海洋数值再分析和预报系统中, 毛庆文等[21]就用HYCOM模式数据来评估由其构建的三维温盐场系统的性能。本文通过对比HYCOM模式温盐场和MCEOF重构温盐场, 分析其深度垂向断面以及水平切面的差异, 来评估重构温盐场对实际海洋的信息捕捉能力。
本文选取36°36′N, 从138°E~150°E的HYCOM垂向断面, 观测时间为2019年12月20日, 由3.2的分析可知, 不同重构方案在深层区域的均方根误差都比较接近, 所以本文主要分析0~500 m的深度断面。
图 9(a)(左)的HYCOM温度断面中, 在150°~153°E之间, 等温线有明显的凸起; 同时在144°~149°E之间, 等温线也有凸起的特征。图 9(a)(右)中MCEOF温度重构结果与HYCOM模式数据相比, 重构温度场不仅反映了上层温度的变化特征, 还反映了真实的温盐场的内部状况, 在150°~153°E和144°~149°E之间的两个温度凸起也得到了良好的反映。同样在图 9(b)中, MCEOF盐度重构结果也能够很好地反映出150°~153°E之间, HYCOM模式数据明显的凸起特征, 并且其深度断面的变化趋势也符合盐度模式数据。
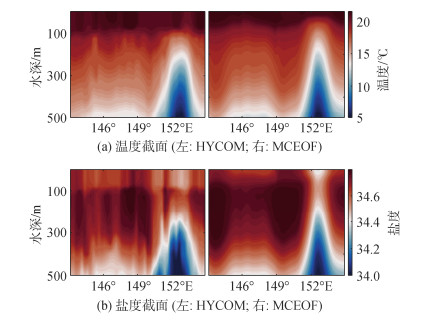 |
| 图 9 MCEOF重构温度(a)和盐度(b)的垂向截面对比 Fig. 9 Comparison of the vertical cross-sections of MCEOF- reconstructed temperature (a) and salinity (b) fields |
除深度截面的对比之外, 本文还对区域内不同深度的水平切面进行分析。选择整片区域内, 2019年12月20日的HYCOM数据和组合4的MCEOF重构温盐场进行水平切面的对比。
综合对比50 m, 450 m和800 m深度处HYCOM模式数据和MCEOF重构温盐的切面结果(图 10), MCEOF重构的温盐场与HYCOM模式数据的温盐场分布特征大致保持一致, 符合海洋真实温盐场的变化趋势, 并且MCEOF重构结果中温度的分布情况更加符合真实温盐场。
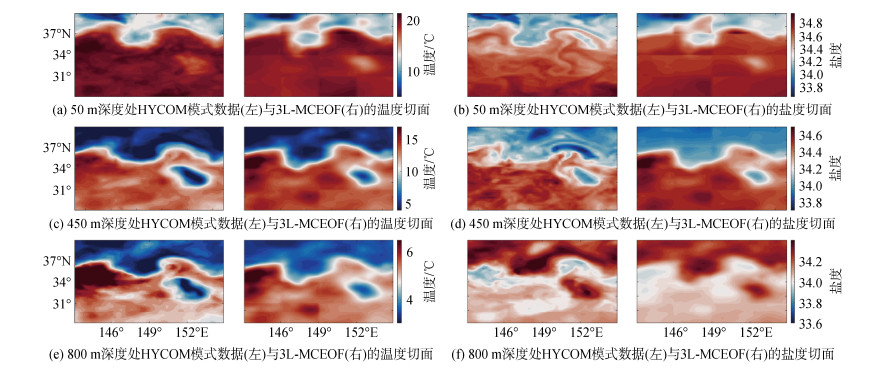 |
| 图 10 MCEOF重构温盐场与HYCOM模式数据水平切面对比 Fig. 10 Horizontal-section comparison between MCEOF-reconstructed temperature and salinity fields and HYCOM data |
通过对MCEOF重构结果的均方根误差, 以及从不同角度(纵向, 横向)与HYCOM数据的比较得出, MCEOF重构方法能有效提高海洋三维温盐场的重构精度, 并且能良好地体现海洋内部的变化特征, 有效地捕捉到海洋中内部信息。
3.5 卫星观测误差对重构模型影响的量化评估通过上述几个角度的研究分析发现, 重构温盐场的精度与重构区域的尺度有很重要的关系, 在拥有足够数据量的前提下, 选取的重构区域尺度越小, 重构温盐场的精度越高。除此之外, 本文重构模型的输入参量是卫星海表面温度和卫星高度计数据, 然而卫星观测其真实海洋存在一定的误差, 为了进一步评估卫星观测的误差对三维温盐场的影响, 本文接下来选取组合4的MCEOF重构温盐场模型, 分别将选取卫星海表数据和真实海表数据作为输入参量进行三维温盐场重构, 其中真实海表面温度数据选取ARGO温度剖面的表层温度; 高度数据是利用ARGO温盐剖面数据, 使用Olbers等[22]的定义来计算的动力高度。
根据图 11, 将真实海表面数据作为输入参数进行重构的精度明显高于卫星海表面数据作为输入参数的精度。在约80 m深度处, 两种重构结果的均方根误差都达最大值, 并且观测海表重构的精度要大于卫星海表重构精度; 在100 m~500 m深度区域, 观测重构的精度有了明显的提升, 并且在约300 m深度处提升最大, 该位置的温度均方根误差较卫星重构均方根误差减小0.4, 其精度提升了27.24%。这也进一步表明, 在本文提出的MCEOF方法中, 三维温盐场重构精度与海面参量的准确率有密切关系, 即越接近真实海洋的表面的海面观测, 能使其重构三维温盐场越加真实。
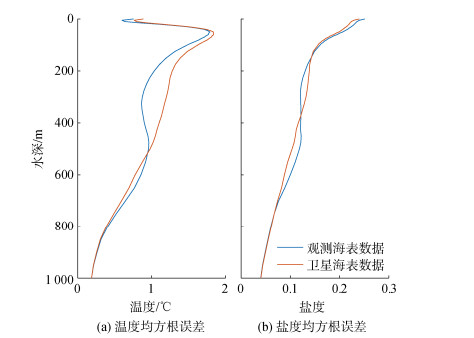 |
| 图 11 不同输入参量重构结果均方根误差对比 Fig. 11 Comparison of the root mean square errors of reconstruction results for different input parameters |
利用多年海洋遥感海表面信息和ARGO历史观测温盐数据, 开展了基于多尺度EOF特征分解的海洋三维温盐场重构工作。将观测温度场和盐度场组成的耦合矩阵进行经验正交分解, 提取主要特征, 通过多元线性回归构建主成分与观测点的经纬度、海面高度和海面温度的回归关系, 利用位置和海面信息重构温盐剖面。为了验证EOF温盐重构方法, 本文建立了12°×12°、6°×6°、3°×3°和1°×1°EOF的四种重构方案, 并且与同尺度MLR方法进行对比。结果显示, 小尺度温盐场重构的精度有明显的提升, 并且对比同尺度MLR方法, 其与真实温盐场的偏差更小。同时, 小尺度的温盐重构能更准确地重构海洋的三维温盐场的垂直梯度特征。
考虑到不同尺度温盐场表现的主要特征不同, 本文在EOF温盐重构方法的基础上, 提出了一种多尺度思想, 通过去除大尺度的主要特征, 继续使用EOF重构模型, 提取除大尺度主要特征外其他尺度的次要特征, 以此计算更精确的重构温盐场。本文设计了不同的重构方案, 并对其与MLR方法进行比较, 结果显示, MCEOF重构模型的精度高于EOF模型的重构精度, 并且随着模型层次的细化, 重构温盐场的精度也逐渐提高。同时, EOF方法重构的温盐场精度要高于MLR方法的重构精度。此外, MCEOF重构温盐场的垂直梯度比其余方法均有一定的提升。对比HYCOM模式数据, MCEOF重构能良好地体现海洋内部的变化特征, 有效地捕捉到海洋中内部信息。本文还分析了卫星观测的精度对海洋温盐场重构的影响。结果显示, 卫星海表面信息越接近于真实海表面信息, 三维温盐场重构结果提升越大。
| [1] |
赖积保, 康旭东, 鲁续坤, 等. 新一代人工智能驱动的陆地观测卫星遥感应用技术综述[J]. 遥感学报, 2022, 26(8): 1530-1546. LAI Jibao, KANG Xudong, LU Xukun, et al. A review of land observation satellite remote sensing application technology with new generation artificial intelligence[J]. National Remote Sensing Bulletin, 2022, 26(8): 1530-1546. |
| [2] |
刘建强, 叶小敏, 兰友国. 我国海洋卫星遥感大数据及其应用服务[J]. 大数据, 2022, 8(2): 75-88. LIU Jianqiang, YE Xiaomin, LAN Youguo. Remote sensing big data from Chinese ocean satellites and its application service[J]. Big Data Research, 2022, 8(2): 75-88. |
| [3] |
黎文娥, 苏华, 汪小钦, 等. 多源卫星观测的全球海洋次表层温度异常信息提取[J]. 遥感学报, 2017, 21(6): 881-891. LI Wene, SU Hua, WANG Xiaoqin, et al. Estimation of global subsurface temperature anomaly based on multisource satellite observations[J]. Journal of Remote Sensing, 2017, 21(6): 881-891. |
| [4] |
STEWART R H. Introduction to physical oceanography[M]. Englewood Ciffs: Prentice Hall, 2008: 25-32.
|
| [5] |
TALLEY L D, PICKARD G L, EMERY W J, et al. Descriptive physical oceanography[M]. San Diego: Academic Press, 2011: 29-65.
|
| [6] |
SU H, WU X B, YAN X H, et al. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: A support vector machine approach[J]. Remote Sensing of Environment: An Interdisciplinary Journal, 2015, 160: 63-71. DOI:10.1016/j.rse.2015.01.001 |
| [7] |
KHEDOURI E, SZCZECHOWSKI C, CHENEY R E. Potential oceanographic applications of satellite altimetry for inferring subsurface thermal structure[J]. Oceans, 1983, 15: 274-280. |
| [8] |
FISCHER M. Multivariate projection of ocean surface data onto subsurface sections[J]. Geophysical Research Letters, 2000, 27(6): 755-757. DOI:10.1029/1999GL010451 |
| [9] |
FOX D N, TEAGUE W J, BARRON C N, et al. The Modular Ocean Data Assimilation System (MODAS)[J]. Journal of Atmospheric and Oceanic Technology, 2002, 15(1): 22-28. |
| [10] |
王喜冬, 韩桂军, 李威, 等. 利用卫星观测海面信息反演三维温度场[J]. 热带海洋学报, 2011, 30(6): 10-17. WANG Xidong, HAN Guijun, LI Wei, et al. Reconstruction of ocean temperature profile using satellite observations[J]. Journal of Tropical Oceanography, 2011, 30(6): 10-17. DOI:10.3969/j.issn.1009-5470.2011.06.002 |
| [11] |
FIEDLER P C. Surface manifestations of subsurface thermal structure in the California Current[J]. Journal of Geophysical Research: Oceans, 1988, 93(C5): 4975-4983. DOI:10.1029/JC093iC05p04975 |
| [12] |
CARNES M R, MITCHELL J L, DEWITT P W. Synthetic temperature profiles derived from GEOSAT altimetry: comparison with air-dropped expendable bathythermograph profiles[J]. Journal of Geophysical Research: Oceans, 1990, 95(C10): 17979-17992. DOI:10.1029/JC095iC10p17979 |
| [13] |
CARNES M R, TEAGUE W J, MITCHELL J L. Inference of Subsurface thermohaline structure from fields measurable satellite[J]. Journal of Atmospheric and Oceanic Technology, 1994, 11(2): 551-566. DOI:10.1175/1520-0426(1994)011<0551:IOSTSF>2.0.CO;2 |
| [14] |
PASCUAL A and GOMIS D. Use of surface data to estimate geostrophic transport[J]. Journal of Atmospheric and Oceanic Technology, 2003, 20(6): 912-926. DOI:10.1175/1520-0426(2003)020<0912:UOSDTE>2.0.CO;2 |
| [15] |
汤博, 侯一筠, 殷玉齐, 等. 利用卫星遥感海面温度、高度联合反演南海北部三维温度场[J]. 海洋科学, 2019, 43(11): 1-10. TANG Bo, HOU Yijun, YIN Yuqi, et al. Inversion of the three-dimensional temperature field in the northern part of the South China Sea based on the remote satellite sea surface temperature and height[J]. Marine Sciences, 2019, 43(11): 1-10. DOI:10.11759/hykx20190312002 |
| [16] |
ALI M M, SWAIN D, WELLER R A. Estimation of ocean subsurface thermal structure from surface parameters: A neural network approach[J]. Geophysical Research Letters, 2004, 31(20): L20308. |
| [17] |
WU X B, YAN X H, JO Y H, et al. Estimation of subsurface temperature anomaly in the North Atlantic using a self-organizing map neural network[J]. Journal of Atmospheric & Oceanic Technology, 2012, 29(11): 1675-1688. |
| [18] |
SU H, WU X B, LU W F, et al. Inconsistent subsurface and deeper ocean warming signals during recent global warming and hiatus[J]. Journal of Geophysical Research: Oceans, 2017, 122: 8182-8195. |
| [19] |
SU H, ZHANG H J, GENG X P, et al. OPEN: A new estimation of global ocean heat content for upper 2000 meters from remote sensing data[J]. Remote Sensing, 2020, 12(14): 1-17. |
| [20] |
聂旺琛, 王喜冬, 陈志强, 等. 基于神经网络的全球三维温盐场重构技术研究[J]. 热带海洋学报, 2022, 41(2): 1-15. NIE Wangchen, WANG Xidong, CHEN Zhiqiang, et al. Research and application of global three-dimensional thermohaline reconstruction technology based on neura Network[J]. Journal of Tropical Oceanography, 2022, 41(2): 1-15. |
| [21] |
毛庆文, 储小青, 严幼芳, 等. 南海三维动态温盐场重构系统的设计与实现[J]. 热带海洋学报, 2013, 32(6): 1-8. MAO Qingwen, CHU Xiaoqing, YAN Youfang, et al. A three-dimensional temperature and salinity reconstruction system in the South China Sea[J]. Journal of Tropical Oceangraphy, 2013, 32(6): 1-8. |
| [22] |
OLBERS D, GOURETSKY V, SEISS G, et al. Hydrographic atlas of the Southern Ocean[M]. Bremen: Alfred Wegener Institute, 1992: 17-18.
|
 2024, Vol. 48
2024, Vol. 48


