文章信息
- 张昱昊, 宋金宝, 刘长龙. 2024.
- ZHANG Yuhao, SONG Jinbao, LIU Changlong. 2024.
- 涌浪对大气边界层风廓线的影响
- Influence of swell on the wind profile in atmospheric boundary layer
- 海洋科学, 48(3): 13-25
- Marine Sciences, 48(3): 13-25.
- http://dx.doi.org/10.11759/hykx20230427001
-
文章历史
- 收稿日期:2023-04-27
- 修回日期:2023-08-13
Monin–Obukhov相似性理论[1](Monin–Obukhov Similar Theory, MOST)成功描述了剪切和浮力作用下的大气湍流运动规律, 建立了近地面层气象要素廓线规律的普遍表达式。然而与平坦的陆地不同, 海洋中波浪的存在对低层大气和上层海洋的动力过程有重要影响。准确理解波浪在海气相互作用中的贡献, 对海洋–大气耦合模式、天气和波浪预报等有重要意义。
一般认为, 海洋上方的风驱动波, 产生风浪, 动量通量由大气向海洋传递(符号为正)。基于Charnock关系[2], MOST也被广泛应用于计算海表动量通量和风速廓线上。然而, 外部传来的快速传播的涌浪进入低风速区时, 由于其传播速度大于局地风, 会发生一些异常现象, 最早由Harris[3]在实验室发现在波浪上方存在一股微弱的风, 并命名为波驱动风。随后大量的现场观测[4-11]和大涡模拟(Sullivan等[11])的结果表明, 在低风速和涌浪存在的情况下, 动量通量会出现从海面到大气向上传递的现象(符号为负), 其原因在于, 涌浪会诱导一个向上传递的波致应力, 其会使总应力减小, 甚至反转方向, 并在顺风向协谱上出现一个与涌浪同频率的谱峰[12-14]。当向上传递的波致应力出现时, 会使风廓线在近海面梯度增大, 整体更平滑, 甚至出现近海面风速最大值, 且平均风速随高度增加而减小的现象。因此, 传统的MOST无法刻画涌浪影响下的风廓线特征。Babanin等[15]的研究也指出, 当观测仪器部署在海浪边界层(直接受波浪影响的区域)内时, 基于MOST的对数廓线会失效。然而Edson等[16]认为, 只要将MOST应用于海浪边界层以上的湍流统计, 其在海洋表层依然有效; Huang等[17], Liu等[18]在分析实测数据时发现涌浪的作用局限在海浪边界层内, 而与海浪边界层以上的湍流结构无关, 且在大气近中性层结下, 海浪边界层上方风速满足对数廓线, 而海浪边界层以内风速则会偏离拟合的对数风廓线。
与风浪情况不同, 当涌浪存在时, 海浪边界层可以到达相当高的高度, 致使几乎所有的浮标观测都会受到涌浪的影响, 因此拖曳系数在中低风速下很分散(Hogstrom等[12]), 给海气界面众多过程的研究带来了很大的不确定性。为了描述涌浪对海气边界层风廓线的影响, 人们提出了一些简单的模型, 如Kudryavtsev等[19]基于海浪边界层的两层近似提出了涌浪与大气互作用的单波模型。该两层模型的结果可以用来解释近海面正梯度、上方负梯度的波浪驱动风的形成, 再现了Harris[3]的实验室实验结果。Makin[20]通过引入科氏力的影响和推广混合长度的定义, 将该模型扩展到整个大气边界层。相同的模型也被Hanley等[21], Song等[22]用于研究表面波对大气边界层风廓线的影响。Semedo等[10]基于常通量层假设提出了一个模型, 模型风廓线与实测风廓线在有明显涌浪信号时一致性良好。
虽然先前的研究从不同角度揭示了涌浪对海气边界层风廓线的影响, 但仍然存在许多重要的科学问题值得进一步探讨。以往研究聚焦于中性条件下涌浪对风廓线的影响, 然而, 在低风速下, 浮力是影响大气边界层的另一个关键因素。Jiang[23]利用大涡模拟指出, 在涌浪海况下, 大气稳定度起着重要的作用, 在稳定条件下, 平均风廓线、湍流结构可以被涌浪显著地改变。以往研究考虑将Ekman模型引入来描述海洋大气边界层, 但MOST却具有更简单、广泛的适用性。同时由于在实际海洋中进行多层湍流观测的难度高, 缺乏实测数据, 导致理论模型往往缺乏实测数据的统计检验。针对上述问题, 本文通过比较考虑涌浪影响的Ekman模型和常通量层模型的结果, 研究科氏力对风廓线的影响。并探讨不同大气层结下MOST在海浪边界层内外的适用性, 以及使用大量数据分析波致应力影响下的风廓线模型的准确性。
本文内容安排如下: 第1节介绍了研究涌浪对风廓线影响的常通量层模型和Ekman模型, 以及应用于海浪边界层之上的MOST; 第2节对比了近中性条件下两种模型在理想实验中的结果, 并使用常通量层模型考察涌浪存在时不同大气层结下MOST在海浪边界层内外的适用性; 第3节展示了模型与实测数据的对比结果; 第4节为结论与展望。
1 研究方法与研究数据 1.1 常通量层模型参考Semedo等[10], Zou等[24], 基于常通量层假设, 总动量通量τtot, 即风应力不随高度z变化:
| $ \frac{{\partial {\tau _\text{tot}}}}{{\partial z}} = 0. $ | (1) |
在涌浪存在时, 海气边界层内风应力可分解为黏性应力、湍流应力和波致应力之和:
| $ {\tau _\text{tot}} = {\tau _\text{vis}} + {\tau _\text{t}} + {\tau _\text{w}} = u_*^2, $ | (2) |
其中, τt为湍流应力, τw为波致应力, τvis为黏性应力, μ*为摩擦速度。黏性应力在海表外可忽略。基于一阶闭合法, 湍流应力可参数化为平均风速梯度与涡黏度系数之积:
| $ {\tau _\text{t}} = {K_\text{m}}\frac{{\partial U}}{{\partial z}}, $ | (3) |
其中U为平均风速, Km为涡黏度系数。一般认为, 波致应力τw随高度呈指数衰减, 即:
| $ {\tau _\text{w}}\left( z \right) = {\tau _\text{w}}\left( 0 \right){{\rm{e}}^{ - Akz}}, $ | (4) |
其中k为波数, 参考Semedo等[10], A取2, 海表面的波致应力τw(0)可表示为:
| $ {\tau _\text{w}}\left( 0 \right) = \frac{1}{2}\frac{{{\rho _\text{w}}}}{{{\rho _\text{a}}}}\frac{{\beta g{a^2}}}{c}, $ | (5) |
其中, ρa为空气密度, ρw为海水密度, g为重力加速度, a为波的振幅, c为波相速度, β为波增长/衰减率。这样, 波致应力可以如下表示:
| $ {\tau _\text{w}}\left( z \right) = \frac{1}{2}\frac{{{\rho _\text{w}}}}{{{\rho _\text{a}}}}\frac{{\beta g{a^2}}}{c}{{\rm{e}}^{ - 2kz}}. $ | (6) |
对于一个海浪谱, 波致应力可以表示为所有波分量贡献的积分:
| $ {\tau _\text{w}}\left( z \right) = \frac{{{\rho _\text{w}}}}{{{\rho _\text{a}}}}\mathop \smallint \limits_0^{{\infty }} \frac{{\beta gS\left( f \right)}}{c}{{\rm{e}}^{ - 2kz}}{\rm{d}}f. $ | (7) |
根据式(2)和(3), 风廓线表达式为:
| $ U\left( z \right) = \mathop \smallint \limits_{{z_0}}^z ({\tau _\text{tot}} - {\tau _\text{w}})K_\text{m}^{ - 1}{\rm{d}}z, $ | (8) |
其中, z0定义为海表粗糙长度, 根据Makin等[25], Makin和Kudryavtsev [26], 其表达式为:
| $ {z_0} = 0.1\frac{\nu }{{{u_{*0}}}}, $ | (9) |
其中v为空气运动黏度, u*0为海表处的湍流摩擦速度,
| $ U\left( z \right) = \frac{{{\tau _\text{tot}}}}{{\kappa {u_*}}}\ln (\frac{z}{{{z_0}}}) - \frac{{{\tau _\text{w}}\left( 0 \right)}}{{\kappa {u_*}}}\mathop \smallint \limits_{{z_0}}^z \frac{{{{\rm{e}}^{ - 2kz}}}}{z}{\rm{d}}z . $ | (10) |
根据MOST, 在非中性条件下, 无量纲风廓线剪切可以表示为大气稳定度的函数:
| $ \frac{{\kappa z}}{{{u_*}}}\frac{{\partial U}}{{\partial z}} = \phi \left( \zeta \right), $ | (11) |
其中
| $ {K_\text{m}} = \frac{{\kappa {u_*}z}}{{\phi \left( \zeta \right)}}. $ | (12) |
将式(12)代入式(8), 可以得到非中性条件下的风廓线:
| $ U\left( z \right) = \frac{{{\tau _\text{tot}}}}{{\kappa {u_*}}}\left[ {\ln \left( {\frac{z}{{{z_0}}}} \right) - \psi \left( \zeta \right)} \right] - \frac{{{\tau _\text{w}}\left( 0 \right)}}{{\kappa {u_*}}}\mathop \smallint \limits_{{z_0}}^z \frac{{\phi \left( \zeta \right){{\rm{e}}^{ - 2kz}}}}{z}{\rm{d}}z , $ | (13) |
其中
参考Hanley等[21], Song等[22], 考虑科氏力影响时, 动量方程变为如下形式:
| $ \frac{{\partial {\tau _\text{tot}}}}{{\partial z}} - i{f_\text{c}}\left( {U - {U_{\rm{g}}}} \right) = 0, $ | (14) |
其中
| $ U = 0, z = 0, $ | (15) |
| $ U = {U_{\rm{g}}}, z \to \infty . $ | (16) |
令
| $ \frac{\partial }{{\partial z}}\left( {{K_\text{m}}\frac{{\partial {U_\text{E}}}}{{\partial z}}} \right) - i{f_\text{c}}{U_\text{E}} + {T_\text{w}} = 0, $ | (17) |
| $ {U_\text{E}} = - {U_{\rm{g}}}, z = 0, $ | (18) |
| $ {U_\text{E}} = 0, z \to \infty , $ | (19) |
其中:
| $ \begin{gathered} {T_\text{w}}\left( z \right) = \frac{{\partial {\tau _\text{w}}\left( z \right)}}{{\partial z}} = {T_\text{wx}}\left( z \right) + i{T_\text{wy}}\left( z \right) = \\ \;\; - 2\frac{{{\rho _\text{w}}}}{{{\rho _\text{a}}}}\smallint \omega K\beta E\left( {k, \theta } \right){{\rm{e}}^{ - 2kz}}{\rm{d}}k{\rm{d}}\theta \\ \end{gathered} , $ | (20) |
其中
| $ {K_\text{m}}\left( z \right) = \kappa {u_{*0}}\left( {z + {z_0}} \right), $ | (21) |
其中
| $ \left( {z + {z_0}} \right)\frac{{{\partial ^2}{U_\text{E}}\left( z \right)}}{{\partial {z^2}}} + \frac{{\partial {U_\text{E}}\left( z \right)}}{{\partial z}} - \frac{{i{f_\text{c}}}}{{\kappa {u_{*0}}}}{U_\text{E}}\left( z \right) = - \frac{{{T_\text{w}}\left( z \right)}}{{\kappa {u_{*0}}}}, $ | (22) |
其通解形式为:
| $ {U_\text{E}}\left( z \right) = {B_1}{I_0}\left( \xi \right) + {B_2}{K_0}\left( \xi \right) + {\varPsi _0}\left( z \right), $ | (23) |
其中I0和K0分别为0阶第一和第二类修正Bessel函数,
| $ {\varPsi _0}\left( z \right) = \frac{2}{{\kappa {u_{*0}}}}\left\{ \begin{gathered} {I_0}\left( \xi \right)\mathop \smallint \limits_z^\infty {K_0}\left( {\xi {'}} \right){T_\text{w}}\left( {z{'}} \right){\rm{d}}z{'} - \hfill \\ {K_0}\left( \xi \right)\mathop \smallint \limits_z^\infty {I_0}\left( {\xi {'}} \right){T_\text{w}}\left( {z{'}} \right){\rm{d}}z{'} \hfill \\ \end{gathered} \right\} , $ | (24) |
其中
根据边界条件(19), 可得B1=0, 根据边界条件(18), 可得:
| $ {B_2} = - \frac{2}{{\kappa {u_{*0}}}}\left\{ \begin{gathered} \frac{{{I_0}\left( {{\xi _0}} \right)}}{{{K_0}\left( {{\xi _0}} \right)}}\mathop \smallint \limits_0^\infty {K_0}\left( \xi \right){T_\text{w}}\left( z \right){\rm{d}}z - \hfill \\ \mathop \smallint \limits_0^\infty {I_0}\left( \xi \right){T_\text{w}}\left( z \right){\rm{d}}z \hfill \\ \end{gathered} \right\} - \frac{{{U_{\rm{g}}}}}{{{K_0}\left( {{\xi _0}} \right)}}, $ | (25) |
其中
| $ \begin{gathered} U\left( z \right) = {U_\text{E}}\left( z \right) + {U_{\rm{g}}} = \frac{2}{{\kappa {u_{*0}}}}\left\{ {\left[ {{I_0}\left( \xi \right) - \frac{{{I_0}\left( {{\xi _0}} \right){K_0}\left( \xi \right)}}{{{K_0}\left( {{\xi _0}} \right)}}} \right]\mathop \smallint \limits_0^\infty {K_0}\left( \xi \right){T_\text{w}}\left( z \right){\rm{d}}z} \right. \\ \left. {\; + \mathop \smallint \limits_0^z \left[ {{K_0}\left( \xi \right){I_0}\left( {\xi '} \right) - {I_0}\left( \xi \right){K_0}\left( {\xi '} \right)} \right]{T_\text{w}}\left( {z'} \right){\rm{d}}z'} \right\} + \left[ {1 - \frac{{{K_0}\left( \xi \right)}}{{{K_0}\left( {{\xi _0}} \right)}}} \right]{U_{\rm{g}}} \\ \end{gathered} . $ | (26) |
根据式(21)、(26), 湍流应力可表示为:
| $ + \xi \mathop \smallint \limits_0^z \left[ {K_0^{'}\left( \xi \right){I_0}\left( {\xi '} \right) - I_0^{'}\left( \xi \right){K_0}\left( {\xi '} \right)} \right]{T_\text{w}}\left( {z'} \right){\rm{d}}z' - \sqrt {i{f_\text{c}}\kappa {u_*}\left( {z + {z_0}} \right)} \frac{{K_0^{'}\left( \xi \right)}}{{{K_0}\left( {{\xi _0}} \right)}}{U_{\rm{g}}}, $ | (27) |
海表处湍流应力可表示为:
| $ {\tau _\text{t}}\left( 0 \right) = F\left( {{z_0}, {u_{*0}}} \right) = \frac{1}{{{K_0}\left( {{\xi _0}} \right)}}\left\{ {\mathop \smallint \limits_0^\infty {K_0}\left( \xi \right){T_\text{w}}\left( z \right){\rm{d}}z - \sqrt {i{f_\text{c}}\kappa {u_*}{z_0}} K_0^{'}\left( {{\xi _0}} \right){U_{\rm{g}}}} \right\}, $ | (28) |
海表湍流摩擦速度u*0可表示为:
| $ u_{*0}^2 = \left| {{\tau _\text{t}}\left( 0 \right)} \right| = {\left\{ {\left[ {\text{Re} (F} \right){]^2} + \left[ {\text{Im} (F} \right){]^2}} \right\}^{\frac{1}{2}}}. $ | (29) |
当给定z=36 m处风速U36时, 地转风Ug可通过下式计算:
| $ {U_{\rm{g}}} = \frac{{{F_1}\left( {z, {u_{*0}}} \right){|_{z = 36}}}}{{1 - {K_0}\left( {{\xi _{36}}} \right)/{K_0}\left( {{\xi _0}} \right)}}, $ | (30) |
其中:
| $ \begin{gathered} {F_1}\left( {z, {u_{*0}}} \right){|_{z = 36}} = {U_{36}} - \frac{2}{{\kappa {u_{*0}}}}\left[ {{I_0}\left( {{\xi _{36}}} \right) - \frac{{{I_0}\left( {{\xi _0}} \right){K_0}\left( {{\xi _{36}}} \right)}}{{{K_0}\left( {{\xi _0}} \right)}}} \right] \hfill \\ \cdot \mathop \smallint \limits_0^\infty {K_0}\left( \xi \right){T_\text{w}}\left( z \right){\rm{d}}z + \mathop \smallint \limits_0^{36} \left[ {{K_0}\left( {{\xi _{36}}} \right){I_0}\left( {\xi '} \right) - {I_0}\left( {{\xi _{36}}} \right){K_0}\left( {\xi '} \right)} \right] \hfill \\ {T_\text{w}}\left( {z'} \right){\rm{d}}z'\} . \hfill \\ \end{gathered} $ | (31) |
随后, 可通过式(20)、(26)、(29)、(30)迭代计算摩擦速度u*0和风廓线U(z)。
1.3 海浪边界层以上的MOST一般而言, 在风浪条件下, 可以通过海表粗糙长度z0的参数化结合MOST来求解风廓线, 例如海气耦合响应实验COARE算法[16, 28]等。然而, 涌浪存在时, 观测通常都在涌浪影响下, 并且由于向上传递的波致应力的存在, 波浪对风廓线的影响无法通过现有的z0参数化来表示。因此, 传统的基于MOST的风廓线模型是不适用的。但由于波致应力随高度呈指数衰减, 在海浪边界层以上, 风应力由湍流应力所主导, 式(13)右边第二项趋于常数, 波致应力对风廓线剪切的影响消失。观测同样表明海浪边界层以上的风廓线依然符合MOST的剪切规律, 在中性层结下, 可以直接使用对数廓线外推, 在非中性层结下, 风廓线可以表示为:
| $ U\left( z \right) = \frac{{{u_*}}}{\kappa }\left[ {\ln\left( {\frac{z}{{{z_0}}}} \right) - \psi \left( \zeta \right)} \right] . $ | (32) |
此时, 我们将u*和z0作为未知参数, 结合海浪边界层之上的多层数据求解, 即可得到外推风廓线(32)。
1.4 实测数据介绍本文使用的实测数据来自广东茂名博贺附近的海上气象观测平台, 经纬度为(21°26′30″N, 111°23′ 30″E), 平台在距离海平面8 m、20 m、28 m和36 m处各安装了一套涡相关观测系统, 包括超声风速仪、CO2/H2O分析仪、红外辐射仪和温湿探头等, 用于测量三个方向的风速、超声虚温和水汽等脉动。除此之外, 我们在海底布放了一套海浪观测设备(AWAC; Nortek, Rud, Norway)用于观测海浪和海流信息。涡相关观测系统的采样频率为20 Hz, 海浪观测设备每3 h进行一次采样, 采样时长2 048 s, 采样频率为1 Hz。湍流和波浪数据观测时间均从2012年2月15日至5月8日。为确保数据的有效性, 在分析数据之前我们对其进行了严格的预处理, 包括去除野点, 倾斜校正和去除趋势[29]。预处理之后得到2 636个长度为10 min的数据, 图 1展示观测期间的风向、浪向和波龄(cp/U8, cp为海浪谱峰相速度, U8为实测8 m高度处平均风速)分布情况, 观测期间, 风向浪向夹角多为锐角, 且涌浪占优(cp/U8 > 1.2)情况较多, 为我们的研究提供了很好的基础。随后, 我们筛选顺风向涌浪情况下的数据, 再根据湍流数据计算大气稳定度情况, 将筛选得到的数据分为不稳定层结(
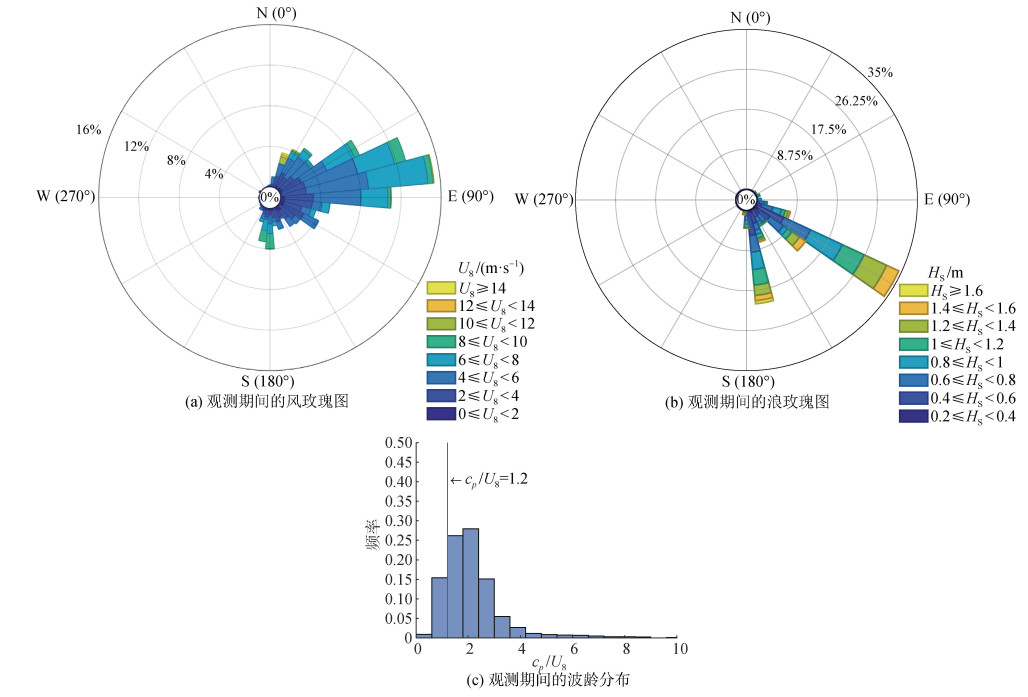 |
| 图 1 观测期间数据概况 Fig. 1 Data overview during the observation period 注: 风向和浪向定义为来向 |
在所有模型所需参数中, 最缺乏观测证据的参数就是波生长/衰减率β, 根据Belcher等[31], 其表达式为:
| $ \beta = \frac{{{\rm{d}}E/{\rm{d}}t}}{E} = {c_\beta }\omega \frac{{{\rho _\text{a}}}}{{{\rho _\text{w}}}}{\left( {\frac{{{u_{*0}}}}{c}} \right)^2}, $ | (33) |
其中, E为海浪能量, ω为角频率, cβ为波增长/衰减率系数, 对于风浪, cβ取值为32±16[32], 对于涌浪, cβ取值为负数。参考Hanley等[21], 为方便起见, 我们假设存在单一沿风向传播的涌浪, 将式(33)代入式(6), 结合深水频散关系ω2=gk, 此时波致应力表达式为:
| $ {\tau _\text{w}}\left( z \right) = \frac{1}{2}{c_\beta }u_{*0}^2{\left( {ak} \right)^2}{{\rm{e}}^{ - 2kz}}. $ | (34) |
首先考察中性条件下常通量层模型和Ekman模型的差异, 取ρa=1.2 kg/m3, ρw=1 025 kg/m3, 科氏力参数fc=10−4 /s。假设涌浪波数k=0.05 rad/m, 振幅a=4 m, 并给定z=36 m处风速U36=5 m/s, 由于衰减率系数的不确定性[21, 33], cβ分别取值−30, −50, −75和−100。定义全部参数后, 分别计算常通量层模型和Ekman模型在100 m边界层内的结果, 结果如图 2和图 3所示, 其中zk为归一化的高度。可以看到, 考虑涌浪影响的Ekman模型和常通量层模型在不同波浪衰减率系数下求得的风廓线在100 m边界层内基本吻合。与Song等[22]的结果相似, cβ的取值对风廓线有重要影响, 在cβ < −50时, 顺风向风廓线出现近海面超地转射流, 并在风速极大值上方随高度呈负梯度减小并趋于地转风, 近海面风速极大值的大小随波浪衰减率系数绝对值
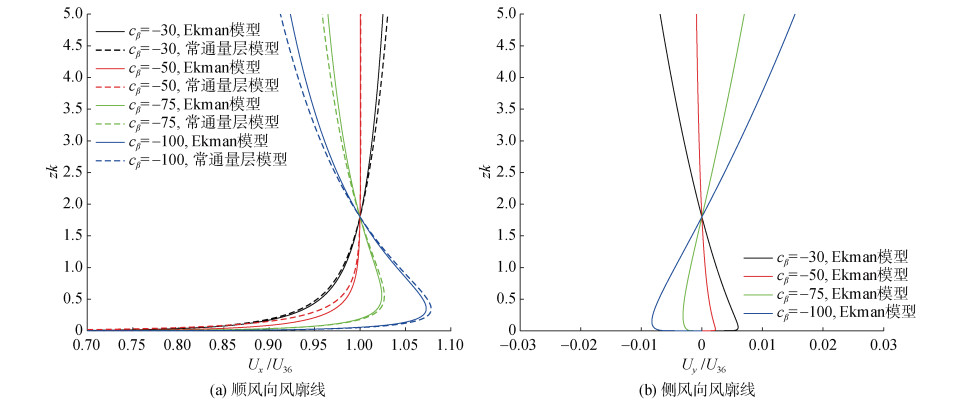 |
| 图 2 Ekman模型和常通量层模型的风廓线对比 Fig. 2 Comparison of the wind profiles generated using the Ekman and constant flux layer models |
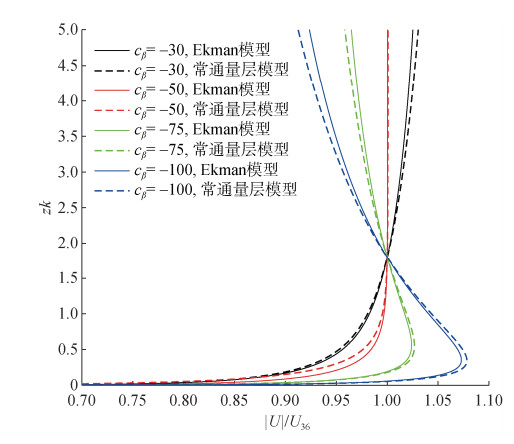 |
|
图 3 Ekman模型和常通量层模型风速大小 |
由于MOST只能刻画湍流边界层的特征, Drennan等[34]、Miller等[35]和Smedman等[36]提出, 在涌浪存在情况下, MOST会失效。而Liu等[18]在分析实测数据时发现, 在顺风向涌浪存在时, 使用对数廓线拟合20 m以上风速效果良好, 而8 m处风速小于上三层风速拟合结果, 说明涌浪存在时, 一定高度以上风廓线依然符合MOST的规律。同时, 在低风速条件下, 浮力对湍流会产生显著影响, Zou等[24]研究非中性条件下涌浪对风廓线的影响时发现, 稳定度影响显著, 稳定层结下风廓线梯度增大, 不稳定层结下风廓线更平滑。针对上述问题, 接下来考察不同大气层结情况下涌浪对海气边界层风廓线的影响以及MOST在波边界层内外的适用性, 我们使用常通量层模型继续研究。根据Hogstrom等[30], 我们取不稳定条件下无量纲剪切函数
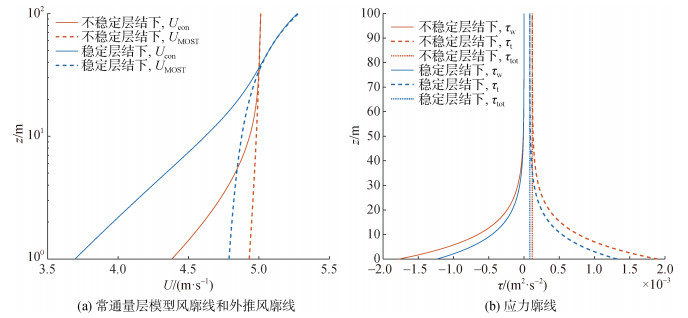
首先考察中性条件的情况, 假设存在一波数k=0.05 rad/m, 振幅a=5 m的涌浪, 给定z=36 m处风速U36=5 m/s, 取cβ=−30, 计算常通量层模型的风廓线Ucon, 如图(4)a所示, 在高度为对数的坐标轴下可以发现, 受波致应力的影响, 风廓线在近海面梯度增大, 不符合中性条件下传统的对数廓线规律。由于波致应力随高度呈指数衰减, 根据式(32), 当我们利用MOST外推波边界层以上的风廓线时, 得到一条对数
风廓线UMOST, 其在约20 m以上几乎与常通量层模型吻合, 然而在20 m以下出现偏差。模型的结果重现了Liu等[18]研究中发现的顺风向涌浪存在时观测的8 m处风速小于由上层风速拟合得到的对数风廓线的现象, 且与Babanin等[15]在风浪条件下研究中发现的规律相反。需要注意的是, 相较于常通量层模型的结果, 外推的风廓线给出了一个极小的粗糙长度, 我们可以认为, 这个极小的粗糙长度包含了涌浪使风廓线整体增速的效应, 从而使MOST在涌浪存在时至少能刻画波边界层之上风廓线的特征。然而在波边界层之内, MOST无法刻画波致应力的影响, 因此其与常通量层模型结果出现偏差。图 4(b)展示了风应力随高度的变化, 波致应力随高度呈指数衰减, 在30 m以上, 波致应力逐渐趋于0, 随后风应力由湍流应力所主导。
 |
| 图 4 中性层结下的风廓线和风应力廓线 Fig. 4 Wind profile and wind stress profile under neutral stratification |
如图 5所示, 不稳定与稳定的大气层结条件给出了与中性层结相似的结果, 外推的风廓线在约z > 20 m时与常通量层模型结果基本吻合, 在稳定条件下, 风廓线整体梯度相对更大, 不稳定情况下, 风廓线整体更平滑。这与Jiang[23]的单波的大涡模拟结果相似。非中性条件下风应力随高度的变化与中性条件类似, 波致应力均在约30 m以上逐渐消失, 随后风应力由湍流应力所主导。
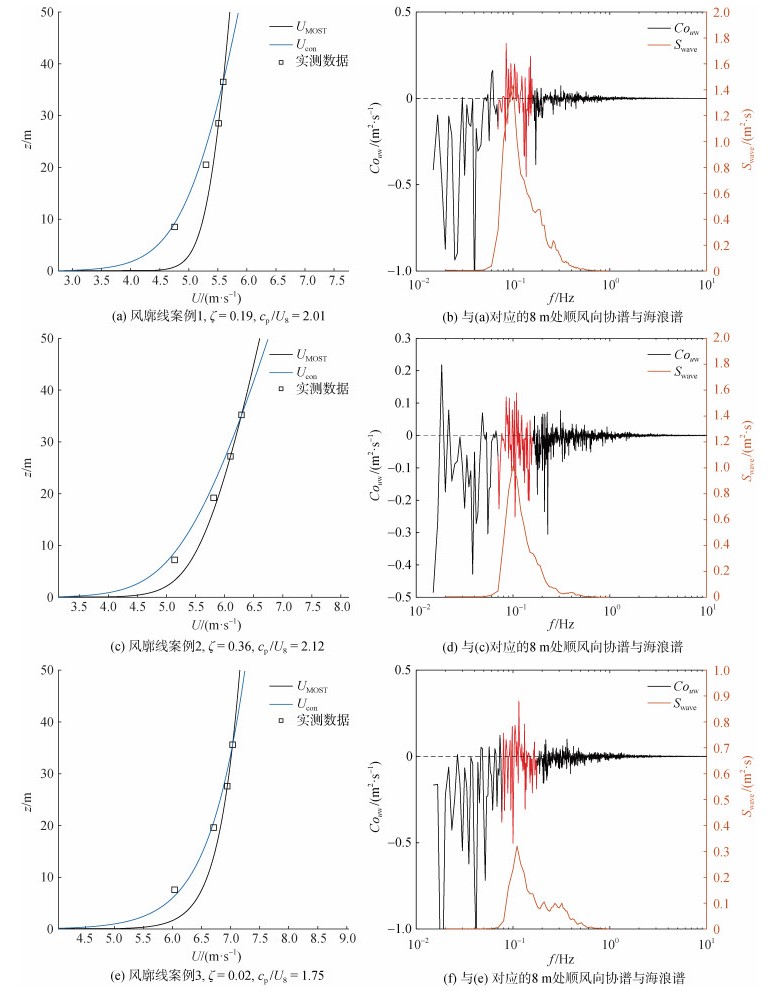
3 实测数据对比参考Hanley和Belcher[21], 取cβ=−30, 使用实测36 m处平均风速和海浪谱S(f)计算常通量层模型的风廓线Ucon, 使用实测的28 m, 36 m处风速外推基于MOST的风廓线UMOST, 将结果与实测的四层风速进行比较。图 6展示了不稳定层结下几个案例的UMOST, Ucon和实测数据的对比, 左侧为风廓线, 右侧展示了对应的海浪谱和通过8 m处湍流数据绘制的顺风向协谱Couw。可以看到, 受涌浪的影响, 协谱在海浪谱峰频率附近出现了波相干扰动, 表明涌浪引起向上的动量通量; 外推风廓线显著大于8 m处风速, 表明涌浪致使近海面风剪切增大, MOST在海浪边界层内失效。而常通量层模型在8 m处与实测数据较为接近。图 7展示了稳定层结下的结果, 可以看到, 在不同的大气稳定度和波龄大小下, 外推风廓线均在8 m处显著大于实测风速, 而常通量层模型的风廓线在8 m处与实测数据较为接近。由于衰减率系数存在不确定性, 常通量层模型可以通过调整cβ的取值获得与8 m处实测数据更为接近的结果。
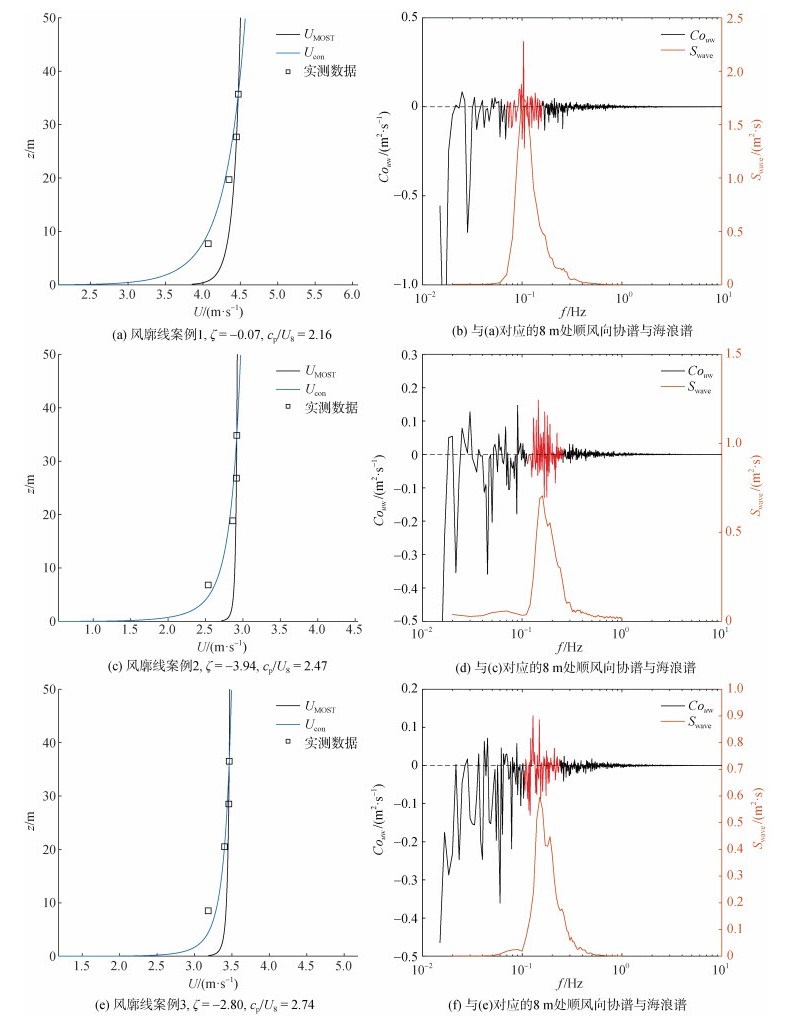 |
| 图 6 不稳定层结下的风廓线案例以及对应的海浪谱与8 m处顺风向协谱Couw Fig. 6 Several wind profile cases under unstable stratification with corresponding wave spectra and cospectra in the downwind direction Couw at 8 m |
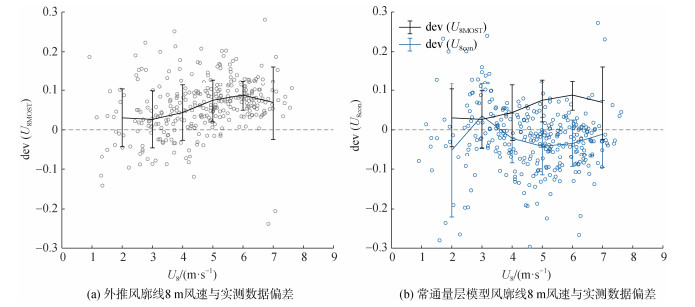
通过求解外推风廓线和常通量层模型的风廓线得到其在8 m处的风速U8MOST和U8con, 计算其与实测数据的相对偏差dev(U8MOST)和dev(U8con)并进行统计, 图 8展示了不稳定层结下的结果, 相较于U8MOST, U8con明显更接近实测风速U8, 而U8MOST明显偏大。图 9展示了稳定层结下的结果, 虽然在稳定层结下常通量层模型依然比外推风廓线更接近实测风速, 但依然存在一定偏差。为研究稳定层结下出现偏差的原因, 我们将式(13)和计算Obukhov长度时使用的摩擦速度u*采用湍流摩擦速度
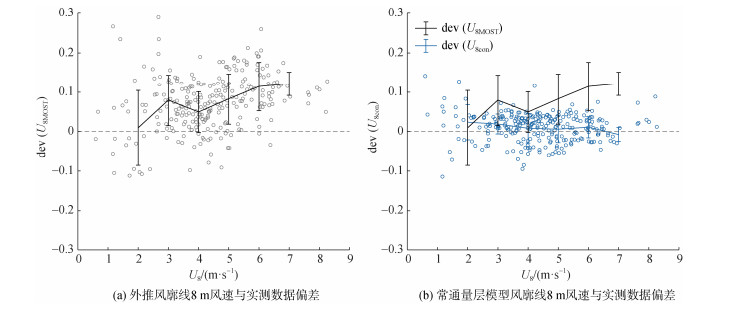 |
| 图 8 不稳定层结下, 模型风廓线8 m处风速与实测数据的相对误差 Fig. 8 Relative error between wind speed at 8 m of model wind profiles and measured data under unstable stratification |
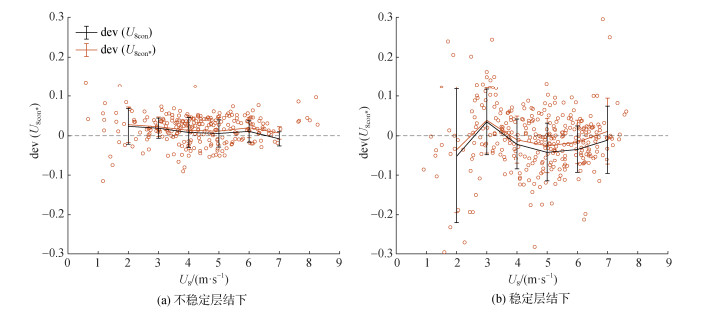 |
| 图 10 使用湍流摩擦速度计算的常通量层模型结果与实测数据的相对误差 Fig. 10 The relative error between the results of the constant flux layer model calculated using turbulent friction velocity and measured data |
本文比较了考虑涌浪影响的Ekman模型与常通量层模型, 两种模型的理想实验给出了相似的结果, 风廓线对不同的波浪衰减率系数cβ有较高敏感性, 在
与实测数据的对比给出了与理想实验一致的结果, 相比外推风廓线, 考虑涌浪影响的常通量层模型计算得到的8 m处风速与实测数据非常接近, 证明MOST无法刻画涌浪存在时海浪边界层内的风廓线特征, 涌浪对风廓线的影响不可忽略。然而, 稳定条件下, 常通量层模型的结果略离散, 可能有以下几点原因, 首先是常通量层模型计算过程中使用的摩擦速度, 将其替换为湍流摩擦速度后, 在稳定层结下效果得到了可见的提升, 因此在使用常通量层模型计算时, 或许使用湍流摩擦速度而非总摩擦速度才更加合理; 然后是稳定条件下无量纲剪切函数
| [1] |
MONIN A S, YAGLOM A M. Statistical fluid mechanics[M]. Cambridge, Massachusetts, USA: MIT Press, 1971.
|
| [2] |
CHARNOCK H. Statistics and aerodynamics of the sea surface[J]. Nature, 1956, 177(4498): 62-64. DOI:10.1038/177062a0 |
| [3] |
HARRIS D L. The wave-driven wind[J]. Journal of the Atmospheric Sciences, 1966, 23(6): 688-693. DOI:10.1175/1520-0469(1966)023<0688:TWDW>2.0.CO;2 |
| [4] |
VOLKOV Y A. Turbulent flux of momentum and heat in the atmospheric surface layer over a disturbed sea- surface[J]. Izvestiya Atmospheric and Oceanic Physics, 1970, 6(12): 770-774. |
| [5] |
SMEDMAN A, HOGSTROM U, BERGSTROM H, et al. A case study of air-sea interaction during swell conditions[J]. Journal of Geophysical Research: Oceans, 1999, 104(C11): 25833-25851. DOI:10.1029/1999JC900213 |
| [6] |
SMEDMAN A S, TJERNSTROM M, HOGSTROM U. The near-neutral marine atmospheric boundary-layer with no surface shearing stress - a case-study[J]. Journal of the Atmospheric Sciences, 1994, 51(23): 3399-3411. DOI:10.1175/1520-0469(1994)051<3399:TNNMAB>2.0.CO;2 |
| [7] |
DONELAN M A, DRENNAN W M, KATSAROS K B. The air-sea momentum flux in conditions of wind sea and swell[J]. Journal of Physical Oceanography, 1997, 27(10): 2087-2099. DOI:10.1175/1520-0485(1997)027<2087:TASMFI>2.0.CO;2 |
| [8] |
RUTGERSSON A, SMEDMAN A S, HOGSTROM U. Use of conventional stability parameters during swell[J]. Journal of Geophysical Research: Oceans, 2001, 106(C11): 27117-27134. DOI:10.1029/2000JC000543 |
| [9] |
GRACHEV A A, FAIRALL C W. Upward momentum transfer in the marine boundary layer[J]. Journal of Physical Oceanography, 2001, 31(7): 1698-1711. DOI:10.1175/1520-0485(2001)031<1698:UMTITM>2.0.CO;2 |
| [10] |
SEMEDO A, SAETRA O, RUTGERSSON A, et al. Wave- induced wind in the marine boundary layer[J]. Journal of the Atmospheric Sciences, 2009, 66(8): 2256-2271. DOI:10.1175/2009JAS3018.1 |
| [11] |
SULLIVAN P P, EDSON J B, HRISTOV T, et al. Large-eddy simulations and observations of atmospheric marine boundary layers above nonequilibrium surface waves[J]. Journal of the Atmospheric Sciences, 2008, 65(4): 1225-1245. DOI:10.1175/2007JAS2427.1 |
| [12] |
HOGSTROM U, SAHLEE E, SMEDMAN A S, et al. Surface stress over the ocean in swell-dominated conditions during moderate winds[J]. Journal of the Atmospheric Sciences, 2015, 72(12): 4777-4795. DOI:10.1175/JAS-D-15-0139.1 |
| [13] |
HOGSTROM U, SAHLEE E, SMEDMAN A S, et al. The transition from downward to upward air-sea momentum flux in swell-dominated light wind conditions[J]. Journal of the Atmospheric Sciences, 2018, 75(8): 2579-2588. DOI:10.1175/JAS-D-17-0334.1 |
| [14] |
ZOU Z, SONG J, LI P, et al. Effects of swell waves on atmospheric boundary layer turbulence: a low wind field study[J]. Journal of Geophysical Research: Oceans, 2019, 124(8): 5671-5685. DOI:10.1029/2019JC015153 |
| [15] |
BABANIN A V, MCCONOCHIE J, CHALIKOV D. Winds near the surface of waves: observations and modeling[J]. Journal Of Physical Oceanography, 2018, 48(5): 1079-1088. DOI:10.1175/JPO-D-17-0009.1 |
| [16] |
EDSON J B, JAMPANA V, WELLER R A, et al. On the exchange of momentum over the open ocean[J]. Journal of Physical Oceanography, 2013, 43(8): 1589-1610. DOI:10.1175/JPO-D-12-0173.1 |
| [17] |
HUANG J, ZOU Z S, ZENG Q C, et al. The turbulent structure of the marine atmospheric boundary layer during and before a cold front[J]. Journal of the Atmospheric Sciences, 2021, 78(3): 863-875. DOI:10.1175/JAS-D-19-0314.1 |
| [18] |
LIU C L, LI X Y, SONG J B, et al. Characteristics of the marine atmospheric boundary layer under the influence of ocean surface waves[J]. Journal of Physical Oceanography, 2022, 52(6): 1261-1276. DOI:10.1175/JPO-D-21-0164.1 |
| [19] |
KUDRYAVTSEV V N, MAKIN V K. Impact of swell on the marine atmospheric boundary layer[J]. Journal of Physical Oceanography, 2004, 34(4): 934-949. DOI:10.1175/1520-0485(2004)034<0934:IOSOTM>2.0.CO;2 |
| [20] |
MAKIN V K. On the possible impact of a following- swell on the atmospheric boundary layer[J]. Boundary- Layer Meteorology, 2008, 129(3): 469-478. DOI:10.1007/s10546-008-9320-z |
| [21] |
HANLEY K E, BELCHER S E. Wave-driven wind jets in the marine atmospheric boundary layer[J]. Journal of the Atmospheric Sciences, 2008, 65(8): 2646-2660. DOI:10.1175/2007JAS2562.1 |
| [22] |
SONG J, FAN W, LI S, et al. Impact of surface waves on the steady near-surface wind profiles over the ocean[J]. Boundary-Layer Meteorology, 2014, 155(1): 111-127. |
| [23] |
JIANG Q F. Influence of swell on marine surface-layer structure[J]. Journal of the Atmospheric Sciences, 2020, 77(5): 1865-1885. DOI:10.1175/JAS-D-19-0098.1 |
| [24] |
ZOU Z S, ZHAO D L, ZHANG J A, et al. The influence of swell on the atmospheric boundary layer under nonneutral conditions[J]. Journal of Physical Oceanography, 2018, 48(4): 925-936. DOI:10.1175/JPO-D-17-0195.1 |
| [25] |
MAKIN V K, KUDRYAVTSEV V N, MASTENBROEK C. Drag of the sea-surface[J]. Boundary-Layer Meteorology, 1995, 73(1/2): 159-182. |
| [26] |
MAKIN V K, KUDRYAVTSEV V N. Coupled sea surface-atmosphere model - 1. wind over waves coupling[J]. Journal of Geophysical Research: Oceans, 1999, 104(C4): 7613-7623. DOI:10.1029/1999JC900006 |
| [27] |
SONG J B. The effects of random surface waves on the steady Ekman current solutions[J]. Deep-Sea Research Part I: Oceanographic Research Papers, 2009, 56(5): 659-671. DOI:10.1016/j.dsr.2008.12.014 |
| [28] |
FAIRALL C W, BRADLEY E F, HARE J E, et al. Bulk parameterization of air-sea fluxes: updates and verification for the COARE algorithm[J]. Journal of Climate, 2003, 16(4): 571-591. DOI:10.1175/1520-0442(2003)016<0571:BPOASF>2.0.CO;2 |
| [29] |
ZOU Z S, ZHAO D L, LIU B, et al. Observation-based parameterization of air-sea fluxes in terms of wind speed and atmospheric stability under low-to-moderate wind conditions[J]. Journal of Geophysical Research: Oceans, 2017, 122(5): 4123-4142. DOI:10.1002/2016JC012399 |
| [30] |
HOGSTROM U. Non-dimensional wind and temperature profiles in the atmospheric surface-layer - a re-evaluation[J]. Boundary-Layer Meteorology, 1988, 42(1/2): 55-78. |
| [31] |
BELCHER S E, HUNT J C R. Turbulent shear-flow over slowly moving waves[J]. Journal of Fluid Mechanics, 1993, 251: 109-148. DOI:10.1017/S0022112093003350 |
| [32] |
PLANT W J. A relationship between wind stress and wave slope[J]. Journal of Geophysical Research: Oceans, 1982, 87(Nc3): 1961-1967. DOI:10.1029/JC087iC03p01961 |
| [33] |
PIERSON W J, MOSKOWITZ L. A proposed spectral form for fully developed wind seas based on similarity theory of S a Kitaigorodskii[J]. Journal of Geophysical Research: Atmospheres, 1964, 69(24): 5181-5190. DOI:10.1029/JZ069i024p05181 |
| [34] |
DRENNAN W M, KAHMA K K, DONELAN M A. On momentum flux and velocity spectra over waves[J]. Boundary-Layer Meteorology, 1999, 92(3): 489-515. DOI:10.1023/A:1002054820455 |
| [35] |
MILLER S, FRIEHE C, HRISTOV T, et al. Wind and turbulent profiles in the surface layer over ocean waves[M]. Oxford, UK: Clarendon Press, 1999.
|
| [36] |
SMEDMAN A, HOGSTROM U, SAHLEE E, et al. Observational study of marine atmospheric boundary layer characteristics during swell[J]. Journal of the Atmospheric Sciences, 2009, 66(9): 2747-2763. DOI:10.1175/2009JAS2952.1 |
| [37] |
BAAS P, STEENEVELD G J, DE WIEL B, et al. Exploring self-correlation in flux-gradient relationships for stably stratified conditions[J]. Journal of the Atmospheric Sciences, 2006, 63(11): 3045-3054. DOI:10.1175/JAS3778.1 |
| [38] |
潘伟, 邹仲水, 宋金宝, 等. 低风速涌浪条件下浪致应力的研究[J]. 海洋学报, 2021, 43(10): 1-9. PAN Wei, ZOU Zhongshui, SONG Jinbao, et al. Studies Of Wave-Induced Stresses Under Swell-Dominated Low Wind Speed Condition[J]. Haiyang Xuebao, 2021, 43(10): 1-9. |
 2024, Vol. 48
2024, Vol. 48