文章信息
- 王艳明, 郭云水, 王锐. 2024.
- WANG Yanming, GUO Yunshui, WANG Rui. 2024.
- 基于灰色多元变权组合预测模型对山东省海水养殖产量预测
- Prediction of mariculture production in Shandong Province using a gray multiple variable weight combination prediction model
- 海洋科学, 48(3): 50-63
- Marine Sciences, 48(3): 50-63.
- http://dx.doi.org/10.11759/hykx20231016004
-
文章历史
- 收稿日期:2023-10-16
- 修回日期:2023-12-28
海水养殖是中国海洋渔业的重要组成部分。海水养殖产品不仅满足人们对海鲜和海产品的需求, 还能够为改善国民膳食结构和提高健康水平做出重要贡献。此外, 海水养殖技术的应用, 有力地弥补了中国海洋资源的不足, 推动了中国海洋经济的快速发展, 为渔民增加收入、改善生活水平、提高生活质量提供了新的途径, 同时也是中国建设海洋强国的重要战略之一。山东省拥有3 345 km长的海岸线, 约占中国海岸线总长度的1/6, 拥有众多的岛屿和优质的滩涂、港湾、浅海, 具备大力发展海水养殖得天独厚的优势与条件, 为中国海水养殖大省。多年来, 山东省着力推进“海上粮仓”建设, 2022年海水养殖总产量突破556.1×105 t。准确测度山东省海水养殖产量, 不仅有助于山东省制定科学合理的海洋渔业发展规划, 还为水产养殖生产调控和养殖产业结构调整提供必要的科学依据。
用于海水养殖预测的模型较多, 目前科学的海水养殖产量预测方法大多基于线性回归、时间序列等, 包括利用相关性分析、灰色模型、多元回归模型、神经网络模型等算法进行预测, 如基于灰色GM(1, 1)模型对中国及各地区海水养殖总产量的预测[1-3]; 基于优化波动影响的灰色马尔科夫修正模型对中国水产品产量进行预测[4]; 基于LS分析方法的海水养殖产量预测模型[5]; 基于小波变换-DGM(2, 1)模型对中国海水养殖品产量的预测[6]; 基于改良后的MGM(1, N)模型对中国水产品产量的预测分析[7]; 基于ARMAV模型对国内海洋捕捞与海水养殖产量的预测分析[8]; 基于Verhulst模型对青岛市海水养殖产量的预测[3]; 以及对虾相对产量预测的人工神经网络模型[9]等。
组合预测理论是由外国学者BATES等[10]于1969年首次提出, 为了从原始序列中有效提取更多信息, 同时弥补单项模型的不足和充分利用各模型的优点。由于单项模型无法全面包含预测信息, 通过线性或非线性的方式将单项模型进行组合, 这种组合方式可以提高预测结果的准确性。同一事件可以从不同层次、不同角度出发使用不同的方法进行预测, 单项模型组合可以充分利用各个模型的优点。王书平等[11]通过构建基于时间序列方法、ANN、SVM和EMD的组合预测模型, 对中国铜的价格进行预测分析其未来走势。邓思源等[12]构建基于XGBoost-LSTM神经网络的变权组合预测模型, 用于预测大坝变形, 预测结果与工程实际情况吻合度更高, 具有较好的适用性和可推广价值。PAI等[13]结合ARIMA和SVM模型预测股票价格, 研究表明组合预测模型能够发挥单项模型的优势, 显著降低预测误差。此外, 还有一些学者利用灰色模型和时间序列模型的组合预测模型, 对建筑物沉降监测数据和深基坑深层水平位移数据进行预测, 均取得了良好的效果[14-17]。卢奇等[18]基于GM(1, 1)、多元线性回归和神经网络利用标准差法构建出能源消费预测模型, 并验证了该组合模型的有效性。在变权组合模型的研究中, 权重的确定是关键, 张鹏等[19]通过对定权组合模型和变权组合模型的比较, 发现变权组合模型更符合实际需要, 更适用于时间序列数据的预测。苏丽敏等[20]提出了一种综合考虑权重不确定性和预测误差变化性的变权组合预测方法, 为变权重组合预测模型的权重计算提供了一种新的思路。
与以往研究不同, 本文在充分考虑多因素影响的基础上, 综合各个学者对养殖产量预测的研究成果, 选取出能较为准确预测海水养殖产量的LSTM神经网络模型、灰色GM(1, N)模型和偏最小二乘回归模型, 创新性地利用变权组合的方式结合灰色GM(1, N)模型、偏最小二乘回归模型和长短期记忆神经网络模型组成灰色多元变权组合预测模型, 将建立的新模型应用于山东省海水养殖产量预测中, 并创新利用新陈代谢GM(1, 1)模型结合灰色多元变权组合预测模型的预测结果对海水养殖各品种产量进行预测, 填补了山东省的海水养殖总产量和各品种产量预测的空缺, 为山东省的海水养殖总产量和各品种产量预测提供科学有效的数学模型和预测的精确度。
1 预测模型设计 1.1 单项模型的选择 1.1.1 长短期记忆神经网络预测模型(LSTM)本文选用了一种擅长处理时间序列问题的特殊的循环神经网络, 在原始的循环神经网络的基础上, 通过增加多个门控单元来调节记忆门与遗忘门之间的平衡, 捕获数据长期以来之间的关系, 长短期记忆神经网络(LSTM)和门控单元解决了原始神经网络数据依赖问题。
长短期记忆神经网络的3个门控单元, 加强了对数据的控制, 有效防止了神经网络的梯度爆炸与梯度消失, 增强了神经网络的学习能力。长短期记忆神经网络的神经元结构如图 1所示。
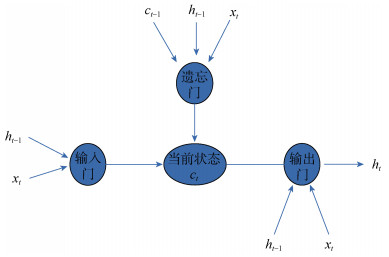 |
| 图 1 长短期记忆神经网络神经元结构图 Fig. 1 Neuron structure diagram of the long short-term memory neural network |
图 1中, 遗忘门单元使得神经网络根据t时刻的输入xt和t–1时刻的输出ht–1来决定从神经元状态中选择忘记信息, 通过遗忘门的xt与上一时刻的输出ht–1经过f=(W1x+W1h)计算, 计算后得到的值再经过sigmoid激活函数将其映射到(0, 1)之间。通过将上一时刻的状态ct–1与f相乘来忘记取值接近0的信息, 记忆取值接近1的信息。在神经网络忘记信息后, 最新t时刻的信息通过输入门控单元加入到状态ct–1中, 形成新的状态ct。
长短期记忆神经网络得出最新状态ct, 输出门根据当前的最新状态ct与上一时刻的输出ht–1以及当前的输入xt来决定当前时刻的输出ht。
长短期记忆神经网络的各个单元的定义为:
| $ \left\{\begin{array}{c}i=\text{sigmoid}\left({W}_{i}\left[{h}_{t-1},{x}_{t}\right]\right)\left(输入门\right)\\ f=\text{sigmoid}\left({W}_{f}\left[{h}_{t-1},{x}_{t}\right]\right)\left(遗忘门\right)\\ o=\text{sigmoid}\left({W}_{o}\left[{h}_{t-1},{x}_{t}\right]\right)\left(输出门\right)\\ {c}_{t}=f^*{c}_{t-1}+i^*z\left(新状态\right)\\ {h}_{t}=o^*tanh{c}_{t}\left(输出\right)\end{array} \quad , \right.$ | (1) |
相比于传统统计预测方法, LSTM神经网络能够更好地处理非线性关系, 传统的统计预测方法通常假设数据是线性相关的, 而LSTM神经网络可以处理非线性关系, 并能够自适应地学习输入数据之间的复杂关系。LSTM神经网络还能够处理长期依赖关系, LSTM神经网络中的长短时记忆单元可以通过门控机制来处理长期依赖关系, 可以捕捉到数据中的长期趋势和周期性。在实际预测中, 数据缺失是很常见的情况, LSTM神经网络可以通过填充缺失数据或者使用插值方法来预测缺失数据的值。
1.1.2 灰色GM(1, N)基础模型灰色预测模型适用于处理样本量小、贫信息的问题。GM(1, N)模型[21]是多变量灰色系统建模方法的基本模型, GM(1, N)模型相比于GM(1, 1)灰色模型可对多因素作动态、整体的分析, 可以研究变量序列与相关因素序列间的动态变化关系。该模型包括一个研究变量和N-1个影响因子变量。GM(1, N)时间响应函数为:
| $ \begin{gathered} \hat x_1^{\left( 1 \right)}\left( {k + 1} \right) = \left( {\hat x_1^{\left( 0 \right)}(1) - \frac{1}{a}\mathop \sum \limits_{i = 2}^N {b_i}x_i^{\left( 1 \right)}\left( {k + 1} \right)} \right){\text{e}^{ - ak}} \\ \; + \frac{1}{a}\mathop \sum \limits_{i = 2}^N {b_i}x_i^{\left( 1 \right)}\left( {k + 1} \right) \\ \end{gathered} , $ | (2) |
其中,
| $ \hat x_1^{\left( 0 \right)}\left( {k + 1} \right) = \hat x_1^{\left( 1 \right)}\left( {k + 1} \right) - \hat x_1^{\left( 1 \right)}\left( k \right). $ | (3) |
根据式(3)我们得到预测值
| $ s_1^2 = \frac{I}{{n - 1}}\sum {{{\left( {\hat x_1^{\left( 0 \right)}\left( i \right) - \overline {\hat x_1^{\left( 0 \right)}} } \right)}^2}} , $ | (4) |
| $ s_2^2 = \frac{I}{{n - 1}}\sum {{{\left( {E_1^{\left( 0 \right)}\left( i \right) - \overline {E_1^{\left( 0 \right)}} } \right)}^2}} , $ | (5) |
| $ C = \frac{{{s_2}}}{{{s_1}}}, $ | (6) |
| $ p = p\left\{ {\left| {E\left( k \right) - \bar E} \right| < 0.6745{s_1}} \right\}. $ | (7) |
| 精度等级 | 平均相对误差( |
方差比(C) | 小误差概率(P) |
| 一级 | 0.01 | 0.35 | 0.95 |
| 二级 | 0.05 | 0.50 | 0.80 |
| 三级 | 0.10 | 0.65 | 0.70 |
| 四级 | 0.20 | 0.80 | 0.60 |
偏最小二乘法是一种稳健的统计分析方法, 常用于处理解释多重共线性严重、样本量少、变量个数多的数据资料, 特别适用于数据探索性分析。与其他模型相比, 偏最小二乘法具有简单稳健、易于定性解释和预测精度较高等优点。在使用偏最小二乘方法时, 无需剔除任何解释变量或样本点。然而, 偏最小二乘法的缺点是无法对解释变量与反应变量之间的关系作出精确的定量解释。
偏最小二乘回归是一种用于建立于存在多重相关性的多组自变量和多组因变量回归模型的方法。相对于传统的多元线性回归, 偏最小二乘法可以通过降低数据的维度来减少模型中自变量之间的共线性, 从而提高回归模型的预测精度。它结合了主成分分析和典型相关分析的成分变量进行回归。主成分分析是一种无监督学习方法, 它可以将高维数据转换为低维数据, 从而减少数据的维度。而典型相关分析则是一种有监督学习方法, 它可以找到两个多变量之间的最大相关性, 从而建立它们之间的预测模型。在偏最小二乘回归中, 不要求每个成分内部信息量都最大, 因此不能使用组内累计贡献率来确定使用多少主成分。相反, 只能使用对因变量的预测效果来评估使用多少主成分。这意味着我们可以使用更少的主成分来建立预测模型, 从而减少模型的复杂度。因此, 偏最小二乘法使用交叉验证来评估模型的精度, 而不像主成分分析一样使用累计贡献率。交叉验证是一种常用的模型评估方法, 它可以将数据集划分为训练集和测试集, 从而评估模型的泛化性能。
在本文中, 我们采用偏最小二乘回归方法建立双对数线性回归模型, 其数学形式如式(8)所示:
| $ \ln y = {a_0} + {a_1}\ln{x_1} + {a_2}\ln{x_2} + \ldots + {a_n}\ln{x_n}, $ | (8) |
其中, ai(i=1, 2,
本文以LSTM神经网络模型、灰色GM(1, N)模型和偏最小二乘回归模型预测结果为基础, 利用方差倒数法构建出一种变权多元组合预测模型, 记实际观测序列为
| $ \left\{ {\frac{{{{\hat y}_t} = \mathop \sum \limits_{i = 1}^m \left( {{w_{it - 1}}{{\hat y}_{it}}} \right)}}{{{w_{it}} = \frac{{1/{e_{it}}}}{{\mathop \sum \nolimits_{i = 1}^m 1/{e_{it}}}},t = 1,2,\text{L}}}} \right.. $ | (9) |
本文综合考虑山东省海水养殖产量的影响因素及数据的可取性, 对影响海水养殖产量的因素进行相关性分析, 为使最终结果更加切合实际结果, 本文在数据选择上参考现有的水产养殖相关文献[23-29]得出海水养殖产量受海水养殖面积、海水投放鱼苗数量、海水苗种总产值、海洋渔业人口数量、海洋专业从业人员数量、海水加工品总量、水产品出口金额、水产技术推广机构数量、水产技术推广实有人数、水产技术推广机构经费、渔民人均纯收入、海水养殖产品生产者价格指数、年末海洋机动渔船拥有量、渔业灾情造成的直接经济损失、水产品数量损失等多种因素的影响, 利用相关分析计算各指标相关系数, 选出与海水养殖产量最具相关性的指标。
在此基础上最终选取海水养殖面积(公顷)、海水苗种总产值(×105元)、海水加工品总量(t)、水产品出口金额(×105美元)、水产技术推广机构经费总计(×105元)、渔民人均纯收入(元/人)为主要影响因素。海水养殖相关数据来自《中国渔业统计年鉴》[30]。相关性分析结果如表 2所示。
| 因变量 | 自变量 | 相关系数 |
| 海水养殖产量 | 海水养殖面积 | 0.963 |
| 海水苗种总产值 | 0.946 | |
| 海水加工品总量 | 0.948 | |
| 水产品出口金额 | –0.721 | |
| 水产技术推广机构经费总计 | 0.951 | |
| 渔民人均纯收入 | 0.967 |
表 2计算结果表明, 在2002年—2022年的21年间山东省海水养殖产量与多个变量之间存在相关性。其中, 海水养殖面积与产量之间呈现很强的正相关关系, 海水养殖面积是衡量养殖规模和潜力的重要指标。扩大海水养殖面积可以增加养殖的容量和产量, 通过监测和分析海水养殖面积的变化, 可以预测产量的增长趋势。海水苗种总产值与产量也存在较强的正相关关系, 苗种是海水养殖的基础, 通过增加投放的苗种数量可以优化养殖产品的结构、促进产量的增长, 从而满足市场的需求。此外养殖苗种的充足供应也是养殖产能和效益的重要保证。海水加工品总量与养殖产量之间也存在较强的正相关关系, 提高海水加工品总量可以增加养殖后产业链收益, 增加养殖产品的附加值, 从而提高养殖的积极性和总体效益。水产品出口金额与养殖产量之间存在负相关关系, 这可能是因为高通胀和贸易战等因素对近些年山东省海水养殖产品出口量造成了一定的负面影响, 同时当海水养殖产量增加时, 可能会导致市场供应过剩的情况, 进而导致养殖产品的价格下降, 对出口金额产生负面影响。水产技术推广机构经费与产量之间存在较强的正相关关系, 增加经费可以提高技术推广的质量和效果, 从而促进养殖产量的增长。渔民人均纯收入与产量之间存在很强的正相关关系, 渔民收入提高有利于调动渔民养殖积极性和养殖技术的升级, 从而提高养殖产量和效益。因此, 在制定养殖规划和决策时, 需要综合考虑各种因素的影响, 以确保养殖产量和效益的平衡和稳定。
2.2 模型预测结果 2.2.1 灰色GM(1, N)模型预测结果按照GM(1, N)的建模原理, 拟合2002年—2016年的山东省海水养殖产量, 计算拟合相对误差。结合表 1精度检验等级参照表并根据拟合结果计算平均相对误差
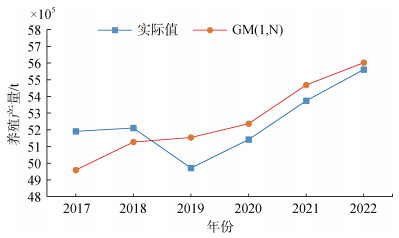 |
| 图 2 GM(1, N)单项模型预测曲线图 Fig. 2 Prediction curve of GM(1, N) single-item mode |
本文通过采用双对数回归模型来消除量纲的影响, 并进行拟合和预测。自变量和因变量取对数后的相关系数计算值如表 3所示。
| lny | lnx1 | lnx2 | lnx3 | lnx4 | lnx5 | lnx6 | |
| lny | 1 | ||||||
| lnx1 | 0.943** | 1 | |||||
| lnx2 | 0.858** | 0.939** | 1 | ||||
| lnx3 | 0.923** | 0.959** | 0.894** | 1 | |||
| lnx4 | –0.756** | –0.747** | –0.737** | –0.643** | 1 | ||
| lnx5 | 0.964** | 0.944** | 0.904** | 0.885** | –0.727** | 1 | |
| lnx6 | 0.983** | 0.925** | 0.872** | 0.886** | –0.742** | 0.982** | 1 |
| 注: **表明在0.01水平(双侧)上显著相关 | |||||||
为了消除多重共线性的影响并提高模型的预测精度, 本文采用偏最小二乘回归方程结合Python建立了预测模型。通过对偏最小二乘回归的建模原理和交叉有效性检验进行研究, 本文提取了6个成分, 最终得到了山东海水养殖产量的偏最小二乘回归预测方程, 其具体形式如式(10)所示:
| $ \begin{gathered} \ln y = 0.023\ln{x_1} + 0.014\ln{x_2} + 0.037\ln{x_3} \\ \; - 0.002\ln{x_4} + 0.122\ln{x_5} + 0.102\ln{x_6} \\ \end{gathered} , $ | (10) |
由表 3可知, 各自变量之间存在较强的相关性, 这可能导致多重共线性问题, 从而影响模型的预测准确性。所以我们采用的是偏最小二乘回归模型来降低自变量之间的相关性, 从而提高模型的预测精度。在使用Python进行建模时, 我们分为训练集和测试集, 并对自变量和因变量进行对数转换等预处理操作。使用Python中的偏最小二乘回归函数来建立模型, 并设置保留的主成分数量, 使用交叉验证等方法来评估模型的性能, 并选择最优的主成分数量。最后使用建立好的偏最小二乘回归模型来预测目标变量的值。
根据得到的偏最小二乘回归方程拟合2002年— 2016年的山东海水养殖产量, 从而得到2017年—2022年山东省海水养殖产量预测值。拟合相对误差和预测相对误差结果如表 4和表 5所示, 预测平均相对误差为1.72%, 预测曲线如图 3所示。
| 年份 | 真实值 | GM(1, N) | 偏最小二乘回归 | LSTM神经网络 | |||
| 拟合值 | 误差/% | 拟合值 | 误差/% | 拟合值 | 误差/% | ||
| 2002 | 3 262 069 | 3 258 807 | 0.00 | 3 206 356 | 1.71 | 3 258 198 | 0.12 |
| 2003 | 3 360 712 | 3 362 246 | 0.05 | 3 385 143 | 0.73 | 3 361 714 | 0.03 |
| 2004 | 3 418 840 | 3 334 221 | 2.48 | 3 514 265 | 2.79 | 3 408 906 | 0.29 |
| 2005 | 3 580 294 | 3 626 007 | 1.28 | 3 513 651 | 1.86 | 3 576 409 | 0.11 |
| 2006 | 3 735 008 | 3 782 535 | 1.27 | 3 750 777 | 0.42 | 3 724 221 | 0.29 |
| 2007 | 3 535 277 | 3 567 574 | 0.91 | 3 646 965 | 3.16 | 3 551 528 | 0.46 |
| 2008 | 3 613 510 | 3 522 417 | 2.52 | 3 632 540 | 0.53 | 3 598 629 | 0.41 |
| 2009 | 3 814 304 | 3 856 646 | 1.11 | 3 877 332 | 1.65 | 3 806 678 | 0.20 |
| 2010 | 3 962 643 | 3 927 491 | 0.89 | 4 042 023 | 2.00 | 3 962 535 | 0.00 |
| 2011 | 4 134 775 | 4 157 323 | 0.55 | 4 156 557 | 0.53 | 4 139 233 | 0.11 |
| 2012 | 4 362 443 | 4 424 892 | 1.43 | 4 400 462 | 0.87 | 4 345 068 | 0.40 |
| 2013 | 4 566 350 | 4 507 862 | 1.28 | 4 493 819 | 1.59 | 4 563 696 | 0.06 |
| 2014 | 4 799 107 | 4 671 784 | 2.65 | 4 708 151 | 1.90 | 4 807 258 | 0.17 |
| 2015 | 4 995 654 | 4 949 156 | 0.93 | 4 968 401 | 0.55 | 4 978 103 | 0.35 |
| 2016 | 5 127 840 | 5 069 604 | 1.14 | 5 105 857 | 0.43 | 5 125 208 | 0.05 |
| 平均相对误差/% | 1.23 | 1.38 | 0.20 | ||||
| 年份 | 真实值 | GM(1, N) | 偏最小二乘回归 | LSTM神经网络 | |||
| 拟合值 | 误差/% | 拟合值 | 误差/% | 拟合值 | 误差/% | ||
| 2017 | 5 190 836 | 4 958 476 | 4.48 | 5 130 182 | 1.17 | 5 257 798 | 1.29 |
| 2018 | 5 210 855 | 5 126 868 | 1.61 | 5 069 748 | 2.71 | 5 232 212 | 0.41 |
| 2019 | 4 970 985 | 5 154 330 | 3.69 | 5 122 773 | 3.05 | 5 135 837 | 3.32 |
| 2020 | 5 141 394 | 5 236 438 | 1.85 | 5 232 727 | 1.78 | 5 269 809 | 2.50 |
| 2021 | 5 373 842 | 5 468 436 | 1.76 | 5 322 405 | 0.96 | 5 290 189 | 1.56 |
| 2022 | 5 560 794 | 5 602 224 | 0.75 | 5 425 422.312 | 2.43 | 5 508 394.6 | 0.94 |
| 平均相对误差/% | 2.36 | 2.02 | 1.67 | ||||
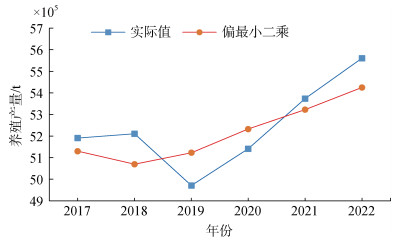 |
| 图 3 偏最小二乘回归模型预测曲线图 Fig. 3 Prediction curve of partial least squares regression model |
用LSTM神经网络对数据进行拟合, 用6个影响因素(海水养殖面积(公顷)、海水苗种总产值(×105元)、海水加工品总量(t)、水产品出口金额(×105美元)、水产技术推广机构经费总计(×105元)、渔民人均纯收入(元/人)对海水养殖产量(t)进行预测, 所以LSTM的inputsize为6, 输出大小为1, 将其隐层层数为1, 单向的LSTM网络。学习率为0.0001, 使用5 000次循环对2002年—2016年的数据进行模型训练。而后, 使用2017年—2022年的数据进行测试, 得到预测值之后, 依据预测误差确定各个预测方法的权重, 拟合相对误差和预测相对误差结果如表 4和表 5所示, 预测曲线如图 4所示。
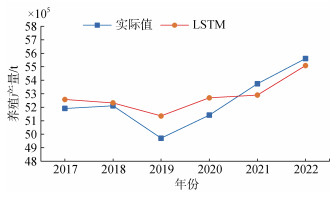 |
| 图 4 长短期记忆神经网络模型预测曲线图 Fig. 4 Prediction curve of the long short-term memory neural network mode |
LSTM神经网络模型拟合平均误差为0.20%, 远低于其他各单项模型拟合平均误差, 显示出LSTM神经网络在海水养殖产量预测上的优势。但单一的LSTM神经网络预测模型也并非完美的, 在对2017年—2022年数据的预测上, LSTM神经网络预测平均相对误差为1.67%, 预测误差高于其他单项模型, 且对2019年因各种突发情况引起的实际海水养殖产量的下跌并未做到很好的预测, 所以本文尝试利用GM(1, N)预测模型、偏最小二乘回归预测模型和LSTM神经网络模型组成灰色多元变权组合预测模型, 以提高预测的精确度。
2.2.4 各单项模型预测结果分析通过各单项模型对2002年—2017年拟合结果可以看出, LSTM神经网络平均相对误差为0.20%, 拟合效果最好; 偏最小二乘法拟合平均相对误差为1.38%, 模型拟合效果最差。机器学习相比于传统统计计算方法在数据拟合方面具有一定优势, 预测上也较其他方法更加准确, LSTM神经网络模型预测效果最佳, 平均预测误差为1.67%; 偏最小二乘法预测效果第二, 平均预测误差为2.02%; GM(1, N)模型预测效果最差, 平均预测误差为2.36%。
根据GM(1, N)模型、偏最小二乘回归方程模型以及BP神经网络模型的预测结果, 经过对比2017年—2022年实际值与预测值, 可以发现不同模型对山东省海水养殖产量的准确度不同, 具有一定的差异, 有些单项模型的预测值大于真实值, 而有些单项模型的预测值小于真实值。由于不同的预测模型适用于不同的对象, 其适用性也有所不同。因此, 采用组合预测的方法可以综合各种方法的优势, 并综合应用不同信息的数据, 以有效地消除单一预测模型的劣势, 从而提高预测精度。
2.2.5 灰色多元变权组合预测模型预测结果不同的预测模型适用于不同的对象, 其适用性也有所不同。在计算各单项模型权重时, 我们采用相对误差作为参考, 对相对误差较大的模型赋予较小的权重, 对相对误差较小的模型赋予较大的权重。通过对3种预测模型进行拟合和预测的平均误差分析, 发现若利用拟合值来建立定权组合预测, 可能无法对每个样本点预测误差较小的模型赋予较大权重, 从而影响预测精度。为了更好地综合LSTM神经网络模型和各单项预测模型的优点, 采用变权重方法建立组合预测模型。通过利用方差倒数法来计算各样本点的3个单项预测模型的权重, 该方法基于方差的概念, 通过计算每个样本点的方差倒数来确定权重值, 从而使得预测误差较小的模型获得较大的权重。根据方差倒数法的式(2)进行计算, 各单项预测模型的权重如表 6所示。
| 年份 | 权重 | ||
| GM(1, N) | 偏最小二乘回归 | LSTM神经网络 | |
| 2002 | — | — | — |
| 2003 | 0.298 8 | 0.001 2 | 0.700 0 |
| 2004 | 0.013 5 | 0.010 6 | 0.976 0 |
| 2005 | 0.007 1 | 0.003 4 | 0.989 5 |
| 2006 | 0.033 9 | 0.308 0 | 0.658 1 |
| 2007 | 0.198 7 | 0.016 6 | 0.784 7 |
| 2008 | 0.016 3 | 0.373 3 | 0.610 4 |
| 2009 | 0.031 0 | 0.014 0 | 0.955 0 |
| 2010 | 0.000 0 | 0.000 0 | 1.000 0 |
| 2011 | 0.036 2 | 0.038 8 | 0.925 1 |
| 2012 | 0.060 2 | 0.162 4 | 0.777 4 |
| 2013 | 0.002 1 | 0.001 3 | 0.996 6 |
| 2014 | 0.004 0 | 0.007 9 | 0.988 0 |
| 2015 | 0.091 5 | 0.266 3 | 0.642 2 |
| 2016 | 0.002 0 | 0.014 1 | 0.983 9 |
采用变权重方法对各单项模型进行修正, 能够更好地综合各单项预测模型的优点, 提高预测精度和可靠性。该方法不仅考虑了每个样本点的预测误差, 还能够对每个单项预测模型的优劣进行精细权衡, 从而更好地适应实际预测需求。
结合式(1)和式(2)对山东省海水养殖产量进行了拟合和预测。首先对2002年—2016年的数据进行拟合, 再对2017年—2022年的数据进行预测。为避免用现实预测现实的逻辑悖论, 首先预测2017年— 2019年山东省海水养殖产量, 检验相对误差, 再根据2017年—2019年实际数据调整组合预测权重值, 对2020年—2022年数据进行预测。
由于未来年份实际值是未知的, 所以在利用误差来构造权重时, 方差倒数法无法计算出各单项预测模型的变权重系数。因此, 我们选择利用当年预测值来代替当年实际值, 即
| $ \begin{array}{*{20}{c}} {{s_{it}} = {{\left( {{y_t} - {{\hat y}_{it}}} \right)}^2},} \\ {{w_{it}} = \frac{{s_{it}^{ - 1}}}{{\mathop \sum \nolimits_{i = 1}^m s_{it}^{ - 1}}},t = n + 1,n + 2,\text{L}}, \\ {\begin{array}{*{20}{c}} {{{\hat y}_{t + 1}} = \mathop \sum \limits_{i = 1}^m \left( {{w_{it}}{{\hat y}_{it + 1}}} \right)} \end{array},} \end{array} $ | (11) |
同时, 根据灰色多元变权组合预测模型的拟合及预测结果, 计算相对误差, 结果如表 7和表 8所示, 预测曲线如图 5所示。
| 年份 | 真实值 | 拟合值 | 误差/% |
| 2002 | 3 262 069 | — | — |
| 2003 | 3 360 712 | 3 361 901 | 0.035 |
| 2004 | 3 418 840 | 3 409 016 | 0.287 |
| 2005 | 3 580 294 | 3 576 552 | 0.105 |
| 2006 | 3 735 008 | 3 734 376 | 0.017 |
| 2007 | 3 535 277 | 3 556 302 | 0.595 |
| 2008 | 3 613 510 | 3 610 046 | 0.096 |
| 2009 | 3 814 304 | 3 809 214 | 0.133 |
| 2010 | 3 962 643 | 3 962 535 | 0.003 |
| 2011 | 4 134 775 | 4 140 559 | 0.140 |
| 2012 | 4 362 443 | 4 358 867 | 0.082 |
| 2013 | 4 566 350 | 4 563 488 | 0.063 |
| 2014 | 4 799 107 | 4 805 923 | 0.142 |
| 2015 | 4 995 654 | 4 972 871 | 0.456 |
| 2016 | 5 127 840 | 5 124 824 | 0.059 |
| 平均相对误差/% | 0.16 | ||
| 年份 | 真实值 | 预测值 | 误差/% |
| 2017 | 5 210 855 | 5 225 934 | 0.289 |
| 2018 | 4 970 985 | 5 151 863 | 3.639 |
| 2019 | 5 141 394 | 5 135 196 | 0.121 |
| 平均相对误差/% | 1.25 | ||
| 2020 | 5 141 394 | 5 241 859 | 1.954 |
| 2021 | 5 373 842 | 5 340 925 | 0.613 |
| 2022 | 5 560 794 | 5 558 463 | 0.042 |
| 平均相对误差/% | 0.87 | ||
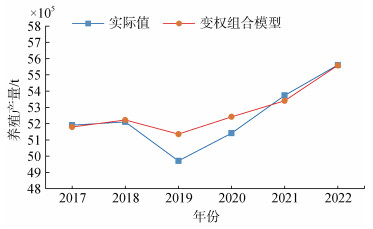 |
| 图 5 灰色多元变权组合预测模型预测曲线图 Fig. 5 Prediction curve of the gray multivariate variable weight combination prediction model |
从表 4和表 7中可以看出, 偏最小二乘回归模型的拟合平均相对误差最大, 为1.38%, GM(1, N)模型的拟合平均相对误差为1.23%, 排名第三; 长短期记忆神经网络模型的拟合结果较好, 拟合平均相对误差为0.20%, 排名第二。而灰色多元变权组合预测模型的拟合平均相对误差为0.16%, 低于各单项模型平均相对误差, 说明灰色多元变权组合预测模型能够更好地综合各个单项预测模型的优点, 提高拟合精度和可靠性。从表 5和表 8中可以看出, 在预测2017年— 2022年山东省海水养殖产量时, 各个单项预测模型和灰色多元变权组合预测模型的预测平均相对误差大小排名顺序有所变化。灰色多元变权组合预测模型的平均相对预测误差最小, 其中2017年—2019年平均预测误差为1.25%, 2020年—2022年平均预测误差为0.87%。LSTM神经网络预测模型的平均相对预测误差为1.67%, 偏最小二乘回归预测模型的平均相对预测误差为2.02%, GM(1, N)预测模型的平均相对预测误差为2.36%。这也说明了灰色多元变权组合预测模型在预测精度方面具有较大的优势。经实证分析, 灰色多元变权组合预测模型在预测山东省海水养殖产量方面表现出色。相较于现有的海水养殖预测模型, 该模型的预测精度更高, 为分析和测度中国海水养殖行业情况提供了一种有效的统计模型和全新的分析思路。各单项模型与组合模型预测结果如图 6所示。
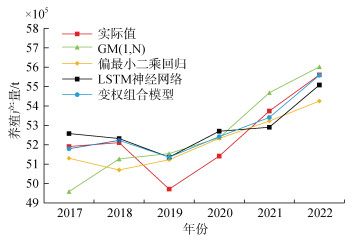 |
| 图 6 各单项模型与组合模型预测结果曲线图 Fig. 6 Curve chart of prediction results for each single model and combination model |
根据新信息优先原理, 通过利用2002年—2022年山东海水养殖产量6个影响因素的数据, 利用灰色GM(1, 1)模型来预测2023年—2025年的数据, 各影响因素预测结果如表 9所示。
| 年份 | 海水养殖面积/公顷 | 海水苗种总产值/万元 | 海水加工品总量/t | 水产品出口金额/(105美元) | 水产技术推广机构经费总计/(105元) | 渔民人均纯收入/(元·人–1) |
| 2023 | 5 589 844 | 620 112 | 745 623 | 6 662 501 | 474 649 | 36 696 |
| 2024 | 5 668 675 | 626 409 | 768 250 | 6 657 495 | 473 233 | 40 377 |
| 2025 | 5 748 617 | 632 771 | 791 563 | 6 652 493 | 471 821 | 44 426 |
为了对2023年—2025年山东省海水养殖产量趋势进行预测, 首先利用各影响因素的预测值计算出3种单项预测模型对2023年—2025年山东省海水养殖产量的预测值, 再结合式(11)计算出基于灰色多元变权组合预测模型的山东省2023年—2025年海水养殖产量。山东省海水养殖产量预测值如表 10所示, 变化趋势如图 7所示。
| 年份 | 海水养殖产量/t |
| 2023 | 5 649 101 |
| 2024 | 5 708 263 |
| 2025 | 5 792 817 |
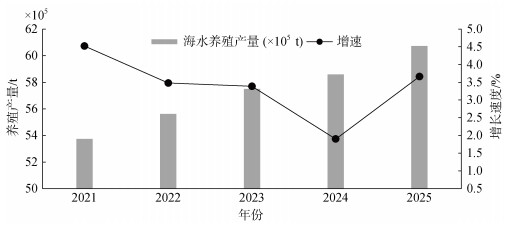 |
| 图 7 2021年—2026年山东省海水养殖产量变化趋势 Fig. 7 Trend exhibited by changes in mariculture production in Shandong province from 2022 to 2026 |
从图 7可以看出, 为了保障中国粮食安全, 深入推进“海上粮仓”建设, 中国已从多方面展开布局, 提出了许多重要战略举措, 颁布有关政策, 推动海水养殖总体产量持续上升。山东省拥有得天独厚的海洋资源和良好的海洋生态环境, 可以为海水养殖业提供必要的条件和保障。在政府的大力支持和推动下, 山东省海水养殖业的发展前景广阔, 预计到2025年山东省海水养殖产量将可达到579.3×105 t。虽然海水养殖产量增长速度将会有所放缓, 但平均增长速度仍约为3.11%。山东省大力实施海洋强省建设行动, 不断开创“海上粮仓”建设新局面, 为中国粮食安全提供了重要的保障, 山东省政府应继续加大对海水养殖产业的支持和投入, 推动其健康、可持续发展, 为山东省经济的发展和人民的生活提供更加坚实的保障。
2.3.3 山东省海水养殖各品种产量预测山东省作为中国海水养殖大省, 其鱼类、甲壳类、贝类、藻类4大海水养殖品种相比于全国其他沿海省份产量较好, 其中2022年山东省鱼类总产量为83 786 t排名第五, 甲壳类总产量229 131 t排名第三, 贝类总产量4 429 358 t位居全国第一, 藻类总产量692 025 t位居全国第二。山东省是中国北方海参主要产区, 自2003年起山东海参养殖产量一直位于全国第一, 其特殊的海岸地理位置, 非常适合人工养殖海参产业发展, 又因为养殖海参的起源地是从山东发展起来, 形成较大规模后, 向外地漫延, 山东地域养殖海参技术目前领先于其他地区, 为中国的海参养殖产业发挥了巨大作用, 所以本文除对4大类海水养殖品种进行预测, 还加上了海参产量的预测。2022年山东省海参养殖产量高达100 165 t。为研究鱼类、甲壳类、贝类、藻类以及海参产量的未来走势, 本文利用新陈代谢GM(1, 1)模型对2012年—2022年近11年的4类海水养殖品种及海参产量占总产量比例进行预测, 结合灰色多元变权组合预测模型对山东省海水养殖产量预测结果, 对2023年—2025年4类海水养殖品种及海参产量进行预测, 预测结果如表 11所示, 预测曲线如图 8所示。
| 年份 | 鱼类产量 | 甲壳类产量 | 贝类产量 | 藻类产量 | 海参产量 |
| 2023 | 76 032.3 | 239 809.1 | 4 438 962.7 | 690 274.9 | 98 695.2 |
| 2024 | 69 038.0 | 251 000.6 | 4 448 602.0 | 688 382.4 | 97 166.3 |
| 2025 | 62 687.0 | 262 714.4 | 4 458 262.4 | 686 495.1 | 95 661.1 |
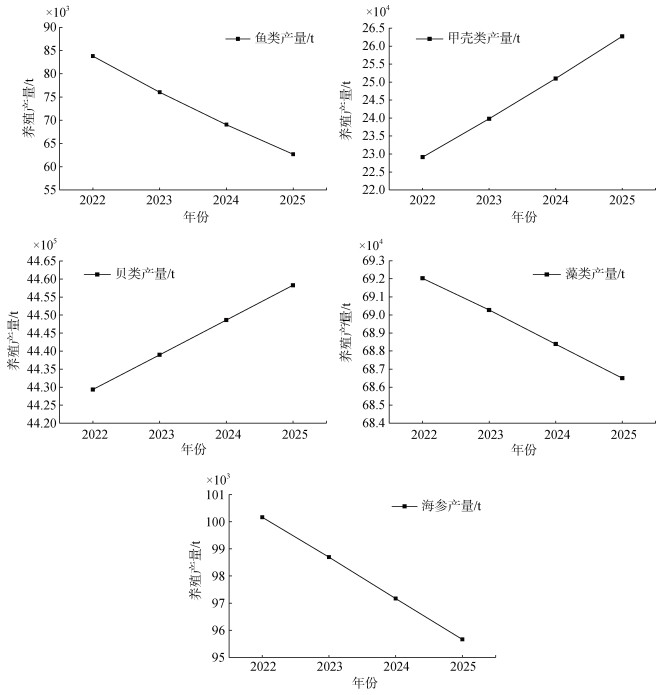 |
| 图 8 山东省海水养殖各品种产量预测曲线图 Fig. 8 Prediction curve for the production of mariculture varieties in Shandong province |
由图 8和表 11可知, 预计到2025年山东省鱼类、甲壳类, 贝类、藻类以及海参海水养殖产量将分别达到6.27×105、26.27×105、445.83×105、68.65×105和9.57×105 t。山东省未来3年海水养殖生产中鱼类、藻类产量将呈现出持续下降的趋势, 平均增长速度分别为–9.2%、–0.3%, 鱼类养殖成本高、效率低、周期较长, 导致养殖动力不足, 养殖规模缩小。而藻类由于山东省实施科学规划布局养殖生产等一系列措施, 这些措施虽然有利于水产养殖业的长远发展, 但也限制了部分养殖区域的规模和产量, 导致鱼类和藻类养殖面积呈现出持续下滑的趋势。而甲壳类、贝类产量均呈现出持续增长的趋势、平均增长速度分别为4.70%、0.2%。虽然甲壳类、贝类增长速度较为缓慢, 但因产量数值较大, 带动山东省海水养殖总产量增长较为明显, 其中2022年山东省鱼类、甲壳类、贝类、藻类、海参总产量分别占山东省海水养殖总产量1.51%、4.14%、80.03%、12.50%、1.81%, 可见山东省海水养殖产量的增长主要依靠贝类产量的增长。海参近几年产量波动较大, 生产稳定性较差, 且未来预期产量将有所下滑, 平均增长速度为–1.50%。山东省作为中国海参养殖的龙头省份, 近10年来总产量一直维持在80 000~102 000 t范围内波动。海参作为高收益高价值产品, 有关部门可以提高重视, 加大力度鼓励海参养殖, 进一步提高海水养殖的经济收益。
3 结论通过基于灰色多元变权组合预测模型对山东省海水养殖产量进行预测时, 预测结果精度显著优于LSTM神经网络预测模型和其他单项预测模型的预测结果。在预测山东省海水养殖产量时, GM(1, N)模型、偏最小二乘回归模型、LSTM神经网络模型预测精度分别为97.64%、97.98%、98.33%, 而灰色多元变权组合预测模型预测精度为99.13%, 预测精度高于各单项模型。根据预测结果, 预计2023年—2025年, 山东省海水养殖产量将逐步上升, 2022年—2025年山东省海水养殖产量平均增速将达到3.11%, 相比于2017年—2021年山东省海水养殖产量的平均增速0.87%有所上升, 预计到2025年山东省海水养殖产量将可达到579.28×105 t, 鱼类、甲壳类、贝类、藻类以及海参海水养殖产量将分别达到6.27×105、26.27×105、445.83×105、68.65×105和9.5×105 t。测试表明灰色多元变权组合预测模型是可行的, 可以满足山东省海水养殖产量预测的基本要求, 具有一定的推广价值。同时, 灰色多元变权组合预测模型的数据分析框架可应用于全国以及各地区水产品产量研究、其他各种类农副产品产量研究。
山东省2022年海参养殖产量占全国海参养殖产量的40.3%, 海参是一种高价值的水产品, 在不损害市场供求的前提下, 提高海参养殖的产量, 可以带来更高的利润和产值, 可为当地海水养殖业的发展提供重要的支撑, 山东省应加强海参养殖产业的推广, 鼓励更多的农民和企业参与到海参养殖中来。山东省海水养殖各品种产量预测结果表明, 贝类养殖产量的增加对山东省海水养殖产量增加的影响程度最大, 2022年山东省贝类养殖产量占山东省海水养殖总产量的80.03%, 未来3年贝类养殖产量将持续增加, 平均增速为0.2%。贝类养殖生产具有投资少、见效快、产量高、效益大及管理方便等特点, 其产业发展十分迅猛, 目前已形成了育苗、养成、饲料、加工、出口等行业组成的产业体系[31], 这些特点使得贝类养殖的成本更低, 利润率更高, 从而增加海水养殖经济收益和产值。
总的来说, 山东省的海水养殖产业发展较为成熟, 具有一定的优势和特点。为提高未来海水养殖产量, 山东省应该: (1)加强海水养殖的科技创新, 提高养殖技术水平和效益。鼓励企业增加研发投入, 加强技术创新, 提高养殖品种的质量和产出效率; (2)扩大海水养殖面积, 增加海水苗种总产值。政府可以提供财政支持等政策扶持, 鼓励企业增加养殖面积, 同时加强对海水养殖的管理和监督, 确保养殖行为的合法合规; (3)加强海水产品的加工和销售渠道建设, 提高海水加工品总量和水产品出口金额。政府可以鼓励企业开拓国内外市场, 加强对海水产品的质量监管, 确保产品的质量和安全; (4)加强水产技术推广, 提高参与水产技术推广人数和水产技术推广机构经费。政府可以加大对水产技术推广的投入, 加强技术培训和技术指导, 提高渔民的技术水平和生产效益; (5)提高渔民人均纯收入, 激发渔民的积极性和创造性。政府可以通过税收减免、社会保障等方式提高渔民的实际收入, 同时加强对渔业资源的保护和管理, 确保渔业的可持续发展。
研究山东省海水养殖产量的未来趋势, 将有助于山东省进行“海上粮仓”的建设, 促进海水养殖业可的持续发展, 为山东省的农业生产提供新的发展思路和路径, 同时也将为山东省海洋强省建设与海洋经济发展注入新的动力和活力。
| [1] |
黄松钱, 王卫民, 曾聪, 等. 基于灰色新陈代谢GM(1, 1)模型的中国水产品年总产量的预测[J]. 中国农学通报, 2012, 28(17): 126-131. HUANG Songqian, WANG Weimin, ZENG Cong, et al. Prediction of the annual total output of aquatic products in China based on the Grey Metabolism GM (1, 1) Model[J]. Chinese Journal of Agriculture, 2012, 28(17): 126-131. |
| [2] |
纪建悦, 张任晗, 褚磊. 基于灰色新陈代谢GM(1, 1)模型的我国海水养殖产量预测研究[C]//第十九届中国管理科学学术年会论文集. 北京: 《中国管理科学》编辑部, 2017: 6. JI Jianyue, ZHANG Renhan, CHU Lei. Research on the prediction of China's mariculture yield based on the grey metabolism GM (1, 1) model[C]// Proceedings of the 19th China management science academic annual conference. Beijing: Editorial Department of China Management Science, 2017: 6. |
| [3] |
杜小伟, 刘群. 灰色GM(1, 1)模型和Verhulst模型在青岛市海水养殖产量预测中的应用[J]. 浙江海洋学院学报(自然科学版), 2011, 30(5): 420-425. DU Xiaowei, LIU Qun. The application of grey GM (1, 1) model and Verhulst model in predicting the yield of marine aquaculture in Qingdao[J]. Journal of Zhejiang Ocean University (Natural Science Edition), 2011, 30(5): 420-425. |
| [4] |
乔松珊, 张建军. 基于灰色马尔可夫修正模型的水产品产量预测[J]. 中国渔业经济, 2013, 31(1): 105-109. QIAO Songshan, ZHANG Jianjun. Prediction of aquatic product output based on grey Markov modified model[J]. Fishing Industry in China Economy, 2013, 31(1): 105-109. |
| [5] |
王连龙, 塔莉. 湖南水产养殖业生产能力探析[J]. 安徽农业科学, 2011, 39(29): 17950-17952. WANG Lianlong, TA Li. Analysis on the production capacity of aquaculture industry in Hunan[J]. Agricultural Science, 2011, 39(29): 17950-17952. |
| [6] |
舒服华. 基于小波变换-DGM(2, 1)模型的海水养殖品产量预测[J]. 海南热带海洋学院学报, 2021, 28(5): 99-105, 128. SHU Fuhua. Prediction of mariculture product yield based on wavelet transform DGM (2, 1) model[J]. Journal of Hainan Tropical Ocean University, 2021, 28(5): 99-105, 128. |
| [7] |
张丽梅, 王成智, 赵学达. 基于MGM(1, n)模型的中国水产品产量时间序列的实证分析[J]. 大连海洋大学学报, 2014, 29(5): 520-524. ZHANG Limei, WANG Chengzhi, ZHAO Xueda. Empirical analysis of time series of China's aquatic product output based on MGM (1, n) model[J]. Journal of Dalian Ocean University, 2014, 29(5): 520-524. |
| [8] |
张丽梅, 王雪标, 李久奇, 等. 基于ARMAV模型的国内海洋捕捞与海水养殖产量的分析[J]. 大连海洋大学学报, 2011, 26(2): 157-161. ZHANG Limei, WANG Xuebiao, LI Jiuqi, et al. Analysis of domestic marine fishing and mariculture yield based on ARMAV model[J]. Journal of Dalian Ocean University, 2011, 26(2): 157-161. |
| [9] |
蔡煜东, 姚林声. 对虾相对产量预测的人工神经网络模型[J]. 水产科学, 1993, 10: 25-27. CAI Yudong, YAO Linsheng. Artificial neural network model for forecasting relative yield of shrimp[J]. Fisheries Science, 1993, 10: 25-27. |
| [10] |
BATES J M, GRANGER C W J. Combination of forecasts[J]. Operations Research, 1969, 4: 19-22. |
| [11] |
王书平, 胡爱梅, 吴振信. 基于多尺度组合模型的铜价预测研究[J]. 中国管理科学, 2014, 22(8): 21-28. WANG Shuping, HU Aimei, WU Zhenxin. Research on copper price prediction based on multi-scale combination model[J]. China Management Science, 2014, 22(8): 21-28. |
| [12] |
邓思源, 周兰庭, 王飞, 等. 大坝变形的XGBoost-LSTM变权组合预测模型及应用[J]. 长江科学院院报, 2022, 39(10): 72-79. DENGA Siyuan, ZHOU Lanting, WANG Fei, et al. XGBoost-LSTM variable weight combination prediction model for dam deformation and its application[J]. Journal of the Yangtze River Academy of Sciences, 2022, 39(10): 72-79. |
| [13] |
PAI P, LIN C. A hybrid ARIMA and support vector machines model in stock price forecasting[J]. Omega, 2004, 6: 487-505. |
| [14] |
刘江, 王征博, 刘成, 等. 灰色-时序组合模型在建筑沉降预测中的应用[J]. 北京测绘, 2018, 32(2): 214-217. LIU Jiang, WANG Zhengbo, LIU Cheng, et al. Application of grey time series combination model in building settlement prediction[J]. Beijing Surveying and Mapping, 2018, 32(2): 214-217. |
| [15] |
鲁玉芬, 方从严, 开明. 灰色-时序组合模型在建筑物沉降预测中的应用[J]. 科技和产业, 2022, 22(8): 315-318. LU Yufen, FANG Congyan, KAI Ming. Application of grey time series combination model in building settlement prediction[J]. Science and Industry, 2022, 22(8): 315-318. |
| [16] |
张磊, 兰孝奇, 向荣荣, 等. 灰色时序组合模型在基坑水平位移预测中的应用[J]. 勘察科学技术, 2016, 203(4): 47-50. ZHANG Lei, LAN Xiaoqi, XIANG Rongrong, et al. The application of grey time series combination model in predicting horizontal displacement of foundation pits[J]. Survey Science and Technology, 2016, 203(4): 47-50. |
| [17] |
霍成胜, 王成栋, 孟军海, 等. 基于灰色时序组合模型的基坑监测预测[J]. 黄金科学技术, 2014, 22(5): 79-83. HUO Chengsheng, WANG Chengdong, MENG Junhai, et al. Prediction of foundation pit monitoring based on grey time series combination model[J]. Gold Science and Technology, 2014, 22(5): 79-83. |
| [18] |
卢奇, 顾培亮, 邱世明. 组合预测模型在我国能源消费系统中的建构及应用[J]. 系统工程理论与实践, 2003, 3: 24-30. LU Qi, GU Peiliang, QIU Shiming. Construction and application of combination forecasting models in China's energy consumption system[J]. Systems Engineering Theory and Practice, 2003, 3: 24-30. |
| [19] |
张鹏. 组合预测中变权与定权的应用比较[J]. 统计与决策, 2018, 34(17): 80-82. ZHANG Peng. Comparison of application of variable weight and fixed weight in combination forecasting[J]. Statistics and Decision, 2018, 34(17): 80-82. |
| [20] |
苏丽敏, 宋艳红, 何慧爽. 考虑权重不确定性的变权重组合预测方法[J]. 统计与决策, 2019, 35(11): 60-63. SU Limin, SONG Yanhong, HE Huishuang. Variable weight combination prediction method considering weight uncertainty[J]. Statistics and Decision, 2019, 35(11): 60-63. |
| [21] |
邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002: 282-285. DENG Julong. Grey theory basis[M]. Wuhan: Huazhong University of Science and Technology Press, 2002: 282-285. |
| [22] |
王学萌, 罗建军. 灰色系统方法简明教[M]. 成都: 成都科技大学出版社, 1993: 79. WANG Xuemeng, LUO Jianjun. A concise tutorial on grey system methods[M]. Chengdu: Chengdu University of Science and Technology Press, 1993: 79. |
| [23] |
李彦平, 王城佳, 刘大海, 等. 海域要素投入对海水养殖业发展影响的实证分析[J]. 海洋环境科学, 2023, 42(1): 72-79. LI Yanping, WANG Chengjia, LIU Dahai, et al. Empirical analysis of the impact of sea area factor input on the development of marine aquaculture industry[J]. Marine Environmental Science, 2023, 42(1): 72-79. |
| [24] |
张莹, 韩立民, 秦宏. 我国海水养殖生态效率影响因素分析[J]. 海洋与湖沼, 2022, 53(5): 1288-1298. ZHANG Ying, HAN Limin, QIN Hong. Analysis of factors affecting ecological efficiency of mariculture in China[J]. Oceanologia et Limnlolgia Sinica, 2022, 53(5): 1288-1298. |
| [25] |
丁然, 张曦. 我国海水养殖产量与相关影响因子的灰色关联度分析[J]. 渔业信息与战略, 2014, 29(3): 183-191. DING Ran, ZHANG Xi. Grey correlation analysis of China's seawater aquaculture production and related influencing factors[J]. Fisheries Information and Strategy, 2014, 29(3): 183-191. |
| [26] |
陈琦. 我国海水养殖产量的波动特征及影响因素分析[J]. 统计与决策, 2018, 34(21): 98-102. CHEN Qi. Analysis of fluctuation characteristics and influencing factors of seawater aquaculture production in China[J]. Statistics and Decision, 2018, 34(21): 98-102. |
| [27] |
李海涛, 茆毓琦. 基于启发式Johnson算法优化BP神经网络的水产养殖产量预测模型[J]. 渔业现代化, 2017, 44(6): 19-23, 31. LI Haitao, MAO Yuqi. Optimization of BP neural network based on heuristic Johnson algorithm for aquaculture yield prediction model[J]. Fisheries Modernization, 2017, 44(6): 19-23, 31. |
| [28] |
李海涛, 刘泰麟. 基于决策树优化的BP神经网络在海参养殖产量预测中的应用[J]. 水产学杂志, 2019, 32(5): 71-75. LI Haitao, LIU Tailin. Application of BP neural network based on decision tree optimization in predicting the yield of sea cucumber farming[J]. Journal of Fisheries, 2019, 32(5): 71-75. |
| [29] |
秦宏, 叶川川, 张莹. 海水养殖生态经济系统状态评价研究——以山东省为例[J]. 经济问题, 2017, 457(9): 100-105, 113. QIN Hong, YE Chuanchuan, ZHANG Ying. Study on the evaluation of the state of seawater aquaculture ecological economic system – taking Shandong Province as an example[J]. Economic Issues, 2017, 457(9): 100-105, 113. |
| [30] |
农业部渔业局. 中国渔业统计年鉴[M]. 北京: 中国农业出版社, 1992-2022. Fishery Bureau of the Ministry of Agriculture. Fishing industry in China statistical yearbook[M]. Beijing: China Agriculture Press, 1992-2022. |
| [31] |
翟毓秀, 郭萌萌, 江艳华, 等. 贝类产品质量安全风险分析[J]. 中国渔业质量与标准, 2020, 10(4): 1-25. ZHAI Yuxiu, GUO Mengmeng, JIANG Yanhua, et al. Quality and safety risk analysis of shellfish products[J]. China Fisheries Quality and Standards, 2020, 10(4): 1-25. |
 2024, Vol. 48
2024, Vol. 48

