
文章信息
- 王声虎, 姜楚华, 陈俊华, 李浩, 吴思儒. 2024.
- WANG Shenghu, JIANG Chuhua, CHEN Junhua, LI Hao, WU Siru. 2024.
- Savonius型转轮三角阵列减流性能研究
- Research on the flow reduction performance of a Savonius hydrokinetic rotor with a triangular array
- 海洋科学, 48(3): 64-74
- Marine Sciences, 48(3): 64-74.
- http://dx.doi.org/10.11759/hykx20231017001
-
文章历史
- 收稿日期:2023-10-17
- 修回日期:2023-12-25
2. 宁波大学科学技术学院机械工程与自动化学院, 浙江 宁波 315300
2. Faculty of Mechanical Engineering and Automation, College of Science and Technology Ningbo University, Ningbo 315300, China
海洋养殖为人类带来优质蛋白, 备受人们喜爱, 全球大力发展海洋养殖。但受近海环境污染, 养殖密度过高, 严重影响近海养殖质量及效益[1], 由此向水质优良的开放海域发展养殖成为当下热点趋势。然而开放海域较大的流速对养殖鱼类耐流能力是带来较大的负面影响[2], 例如, 中华倒刺鲃(Spinibarbus sinensis)幼鱼1、2 bl/s训练组氨基酸含量高于对照组和4 bl/s训练组[3], 同时, 较大的流速还会影响养殖设施结构安全[4-5], 对此采用阻力型的Savonius转轮(Savonius Hydrokinetic Rotor, SHR)作为减流设施部件, 开展减流防护性能研究, 为海洋渔业养殖设施防护和营造鱼类适宜栖息地提供理论支撑。SHR结构简单, 制造成本低, 启动特性高[6], 被广泛用于风力发电和海洋能捕获[7]。流体通过其中心对称分布的叶片时, 形成非对称阻力, 产生转矩驱动转轮绕其中心旋转从而获取能量[8], 并且流体经过叶片作用后, 在转轮尾部形成涡流, 改变尾流分布, 尾流场呈现流速衰减效应。它的自身结构对尾流场也有一定影响, 例如叶片的几何参数、叶片弧角、级数尾流影响减流性能[9-11]。YAO等[12]采用计算流体力学(Computational Fluid Dynamics, CFD)数值计算方法, 对单个SHR的后方流场进行数值模拟, 分析尾流速度场变化规律, 表明SHT具有较好的减流性能, 并发现叶尖速对其减流性能有较大影响。BAO等[13]研究了SHT的消波功能在海洋牧场中对设备防护具有一定作用。ZHAO等[14]发现在公海环境下半潜式水产养殖平台中渔网对减流起着重要作用。此外, LIU等[15]也发现渔网对半潜式水产养殖平台减流和提高结构强度作用明显。
研究Savonius转轮阵列减流性将有助于提高工程应用性能。前期已有国内学者对SHR阵列机组捕能性能开展了部分研究, MYCEK等[16]研究表明, 上游转子的存在会影响下游转子动力性能。ZHANG等[17]使用高时间分辨率粒子图像测速(Time-resolved particle image velocimetry, TR-PIV)技术和CFD技术分析了转子角度和转子间距的影响, 定义了3个不同的区域, 即速度上升区、速度下降区和速度恢复区, 它们是下游转子对上游转子影响的指示器。NAG等[18]研究了线性排列的两个转子获得最佳性能的排列间距; 并研究ANSYS CFX中3种不同的排列方式(三角排列和交错排列)在不同转速下和距离下, 3个转子在4D距离下达到最佳捕能性能。PAN[19]发现2个叶轮时, 上游叶轮的尾流与下游叶轮旋转诱导的流动发生相互作用, 两叶轮间距增大时这种作用减弱, 并且, 三叶轮方案的整体做功能力和单个叶轮的力矩特性均较好。MALKI等[20]优化了转子之间的排列方式, 提高阵列输出功率。CHAWDHARY等[21]详细阐述了三角形布置的水平轴涡轮机的尾流特性和流场。
以上学者研究重点关注SHR转轮阵列捕能性能, 对其尾流场的时空演变规律及尾流场流速衰减性能并没有细致研究, 难以为渔场减流防护工程提供理论支撑。本研究采用CFD数值模拟方法, 结合实验验证, 开展不同阵列排布参数以及其他关键参数对SHR转轮阵列减流性能影响研究。
1 研究方法 1.1 SHR几何参数本次研究是在单个SHR减流效果的基础上, 对等腰三角形阵列形式下的不同形状参数在不同条件下的减流性能进行了数值模拟和实验验证。数值模拟使用Star CCM+水动力仿真软件进行模拟计算。为减小不必要的换算, 模拟选择的建模大小与实物大小完全相同。模拟和实验的几何模型参数参考YAO[12]实验中的最佳能量捕获和最佳减流能力的结构: 重叠率为0.15的半圆形双叶轮机。具体尺寸见表 1, 对应尺寸参数如图 1所示。
| 参数 | 符号 | 公式 | 值 |
| 转子高度 | H | — | 0.24 m |
| 转子直径 | D | — | 0.182 m |
| 叶片直径 | d | — | 0.1 m |
| 端面直径 | D0 | — | 0.2 m |
| 高径比 | RHD | 1.32 | |
| 重叠率 | e | 0.15 | |
| 叶片曲率 | ε | 1 |
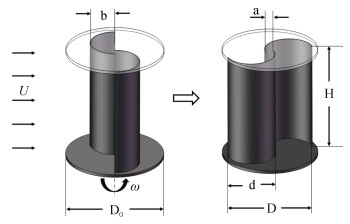 |
| 图 1 SHR结构图 Fig. 1 Structure chart of SHR |
图 2展示了三角阵列重要结构参数: LX为上游rotor1与下游转子x方向的中心距离; LY为rotor2和rotor3之间y方向中心距。叶尖速比(TSR: Tip Speed Ratio)是研究减流的重要因素。
| TSR=ωD2U, | (1) |
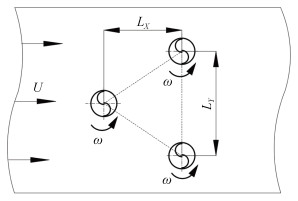 |
| 图 2 三角排列参数示意图 Fig. 2 Schematic of triangular arrangement parameters |
其中ω为角速度(rad/s); U为来流流速(m/s)。
1.2 减流标准拟定减流研究需要分析的衰减长度La和衰减系数Ca如下。衰减长度La可以衡量SHR降低流速的空间范围, 衰减系数Ca可以衡量其降低流速的幅度大小。定义Ca仅大于0.2时, 才具有减流效果。
| La=LD, | (2) |
| Ca=U−uU, | (3) |
其中L是Ca为0.2时的最远距离; u是下游某监测点平均流速。
针对上述, 需获取SHR不同三角形状参数阵列下游多处流速u和目标流速最远触及长度L。以中国佘山附近流速为例, 某日平均流速约为0.94 m/s, 最大可达1.51 m/s(数据来自中国国家海洋科学数据中心)。因此, 此次研究将来流流速设定为1.5 m/s。
1.3 三角阵列结构参数LX和LY的影响研究首先, 对参数LY大小进行多组仿真与实验, 距离大小表示为转子直径(D)的倍数, 即2D、3D和4D。然后对参数LX进行多组仿真与实验, 距离大小选取2D、3D和4D。最后选取最佳减流效果的形状参数, 得到最佳LX和LY。
1.4 关键运动参数的影响研究在得到最佳三角排列形状参数后, 再研究影响减流性能的其他参数。首先, 空载条件下, 实验发现SHR以TSR=1.37旋转, 这与TALUKDAR等[22] SHR空载实验发现的两叶片旋转相对应, 因此选取了0.1~1.2一共12个不同的TSR, 观察转子的减流性能, 以确保SHR旋转时对来流形成阻力, 消耗来流能量。其次, 考虑到实际海洋中, 不同位置拥有不同流速, 因此, 选择3种相对较高的流速进行了模拟与实验, 观察并分析不同流速对减流性能的影响。最后, 设置了不同排布方向(即改变了3个转子不同旋转方向), 分析其对减流效果的影响, 如图 3和图 4所示。图 3(a)显示为凹面相邻时rotor1和rotor3旋转方向相同, 图 3(b)显示为rotor1和rotor2旋转方向相同; 图 4(a)显示凸面相邻时, rotor1和rotor2旋转方向相同, 图 4(b)显示为rotor1和rotor3旋转方向相同。通过这4种不同排列方式, 研究其对减流效果的影响。
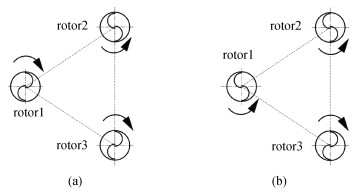 |
| 图 3 下游凹面相邻 Fig. 3 Concave adjacent a. rotor1和rotor3同向; b. rotor1和rotor2同向 |
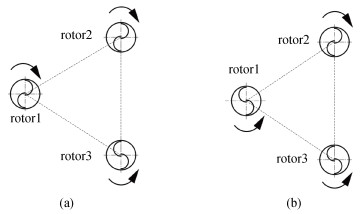 |
| 图 4 下游凸面相邻 Fig. 4 Convex adjacent a. rotor1和rotor2同向; b. rotor1和rotor3同向 |
SHR在轴向具有完全一致的几何形状, 并且, 为了减少计算时间和提高仿真效率, 此次仿真选用二维CFD进行模拟计算。
2.1.1 模拟域大小与边界条件为便于足够区域观察尾流场, 计算域长度设置为45D, 宽度与水池宽度一致为7D。模拟域中左侧为速度入口, 右侧为压力出口, 上下边界为对称面。
2.1.2 网格划分与模型选择计算域网格划分如图 5所示, 3个SHR的旋转域选用了多面体网格, 静止域选用了切割体网格, 如图 5(a)所示。为了更清楚地仿真出3个旋转域内部流场情况, 多面体网格基础尺寸更加细化, 如图 5(b)所示。由于旋转域附近可能存在复杂涡流, 因此对其附近静止域实行4层网格加密。SHR叶片表面选用了10个棱柱层网格, 以便提高叶片与水流接触精度。此外, 对3个旋转域和静止域临界表面生成了相同尺寸的棱柱层, 为了减小数值传输误差。
 |
| 图 5 网格划分图 Fig. 5 Meshing diagram |
网格数量和尺寸的变化对测量转子周围的流体流动起重要作用。在三角阵列中, 相同条件下, 细化5种不同网格级别, 可以从表 2中看出同一监测点在网格数为第3级别时平均流速变化稳定。因此, 选择第3级别网格设置。
| 细化级别 | 节点数 | 内部面数 | 单元网格数 | 流速/(m·s–1) |
| 级别1 | 248 632 | 264 812 | 76 842 | 1.12 |
| 级别2 | 425 716 | 495 162 | 130 454 | 1.24 |
| 级别3 | 757 312 | 841 869 | 245 095 | 1.33 |
| 级别4 | 1 232 487 | 1 303 481 | 384 501 | 1.32 |
| 级别5 | 1 457 843 | 1 525 487 | 508 514 | 1.33 |
考虑到研究网格数量和计算机计算速度, 选用雷诺平均方程法。它可以将流动质量、动量和能量方程进行统计平均(如下), 忽略湍流脉动, 只考虑平均运动并且对空间要求不高, 可以较大程度缩减计算工作量。
| ∂∂tρU+∇⋅ρU=−∇p+∇⋅τ, | (4) |
另外, 选用雷洛平均纳维斯托克斯(The Reynolds-Averaged Navier-Stokes, RANS)标准k-ε模型进行湍流模拟。动量方程变为:
| ∂ρU∂t+∇⋅(ρUU)−∇⋅(μeff∇U)=−∇p′+∇⋅(μeff∇U)T+SM, | (5) |
其中SM是体积力, μeff是有效黏度为:
| μeff=μ+μt, | (6) |
对于k-ε湍流模型, 湍流黏度μt为:
| μt=Cμk2ε, | (7) |
其中Cμ为常数。
假设时间离散化为一阶隐式格式, 最大时间步长为0.01 s, 确保转轮的旋转角度在一个时间步长内小于1°。
2.2 水池验证实验水池为直冲式循环水池, 水池长20 m, 水池下方设有一水泵, 用于提供水的动力。水泵可通过控制器调节转速实现水流大小调节, 可将自由流加速到最高2.5 m/s。水池设置水深0.8 m, 可将转轮全部浸没。SHR实物选用不锈钢材质制造, 如图 6(a)所示, 转子高度H为0.24 m, 转子单个叶片直径d为0.1 m, 上下端面直径D0为0.2 m, 并且叶片曲率ε为1, 两个叶片重叠率e为0.15。3个相同的SHR安装在铝型材上, 可方便实现位置调节。图 6(c)所示, 3个SHR通过同步带传动, 实现相同的TSR。实验中需要通过阻尼装置控制转轮转速, 从而获得所需的TSR, 为了方便控制并保证精度, 采用伺服电机替代阻尼装置, 基于伺服电机速度控制模式, 准确控制转轮转速, 转轮转速低于其空载时转速, 实则电机提供反向扭力, 电机起制动作用。转子上方安装有一扭矩转速传感器, 可实时测量0~20 N/m的扭矩。此外, 流速测量选用的是多普勒流速流量仪, 测量范围为0.02~10.00 m/s, 分辨率为2 mm, 精度±0.2%。在模拟和实验中都设置了10列测速探头, 并布置在下游转轮之后, 如图 7所示。每列中平均分布11个测速点, L1~L10分别距离rotor2和rotor3连线0.6D、1.2D、1.8D、2.4D、3.6D、5.4D、7.2D、9D、10.8D、12.6D(沿X轴方向)。临近转轮, 水分子运动更复杂, 因此设置的测速点更加密集, 而下游水流相对稳定, 所以设置的测速点更加分散。
 |
| 图 6 实验测试装置实物图 Fig. 6 Water tank experiment verification diagram a. SHR实物图; b. SHRs在水池中安装空间位置图; c. 水池实验仪器安装位置图; d. 试验水池 |
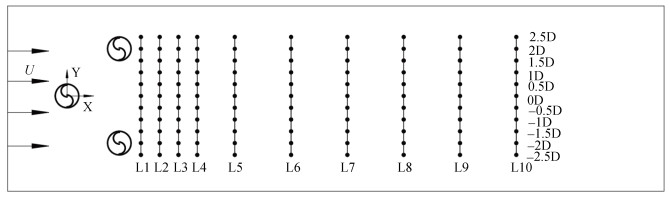 |
| 图 7 尾流场测速点分布图 Fig. 7 Velocity measurement point distribution map |
为了研究数值模型的可靠性, 对三角阵列下在不同TSR下进行了模拟和实验, 选取下游3个不相同测速点位, 测量模拟与实验之间的误差, 相对误差计算如下:
| 相对误差=实验值−模拟值实验值×100%. | (8) |
结果如图 8所示。可以发现模拟和实验趋势相同, 但又存在差异, 是由于实验时水池产生的流速不稳定, 并且流速在下游具有一定的自衰减, 导致实验数据整体大于模拟数据。对比发现, 在相同流速和转速内显示出显著的一致性, 最大相对误差值约为16%, 最小相对误差值约为2%, 良好的一致性验证模拟过程的准确性。
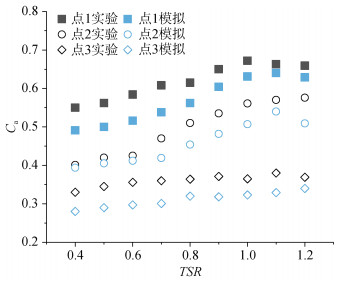 |
| 图 8 实验与仿真结果对比 Fig. 8 Comparison of the experimental and simulation results |
当流场达到稳态时, 各列测速点流速呈周期性规律。所以在此次研究中, 讨论流速大小时, 可以应用各个监测点的平均流速。
3 结果分析 3.1 转轮阵列减流原理对某一位置的SHR三角排列进行了仿真验证发现: 静止时, 3个转子所产生的尾流场无法自动形成稳定流场, 因此在后方产生不稳定的尾流场, 如图 9(a)所示; 而旋转中的3个SHR会在后方会形成规律性涡流, 这些涡流在两侧水流的作用下逐渐消失, 并在后方形成稳定的流场, 如图 9(b)所示。因此阵列SHR旋转时的减流效果好于静止时的减流效果。
 |
| 图 9 SHR旋转和静止对比图 Fig. 9 Comparison of SHR rotation and static a. SHR静止时模拟图; b. SHR放置时模拟图 |
通过图 9(b)发现, rotor3下游所产生的涡流比rotor2下游所产生的涡流更多, 降低流速效果更好。这是因为SHR中心对称结构所决定的, 如图 10所示, rotor1旋转时所产生的涡流会被rotor2下半凹面阻挡, 流向rotor3上半凸面, 并且rotor2下方叶尖处粒子产生剧烈运动, 生成小范围高速低压区域, 加上rotor1后方涡流的阻挡作用(白色圆形区域内), 粒子将沿着狭窄通道来到rotor2和rotor3之间。之后上部分粒子继续沿着rotor2下方凹面外表面向上运动, 但下部分粒子会受到rotor3后方涡流的阻碍向斜上方运动。因此, 在上述综合作用下, rotor2后方涡流小于rotor3后方的涡流。此外, 外侧流场被下游两个转子阻挡后也形成了高速区域(红色矩形框内), 这进一步阻止了外部流场进入下游低速区, 这样下游会形成稳定的低速区域。对此影响尾流场的可能参数是三角排列各转轮间的中心距、转速和旋转方向。所以以下研究开始针对这3个因素展开。
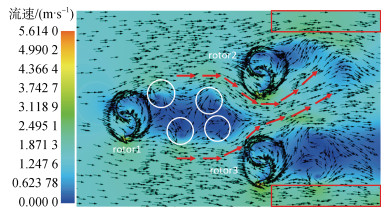 |
| 图 10 速度矢量图 Fig. 10 Velocity vector plot |
为了探究三角排列中, 参数LX和LY(图 2)各自对降低流速的影响, 分别测试了不同大小的LX和LY。首先, 将LX的大小保持不变, 测试了在相同TSR条件下, 自由流速为1.5 m/s时, LY分别为2D、3D、4D时, 尾流场的变化规律。
如图 11所示, 可以发现, 当LY=2D时, 下游的流场蓝色更加聚集, 并且rotor2和rotor3中间的小范围加速与它们产生的涡流很快抵消, 最后形成稳定的减流区; 当LY=3D时, rotor2和rotor3中间的加速区有一部分侵入下游减流区域, 所以在尾流中间有部分绿色区域; 当LY=4D时, rotor2和rotor3中间的加速区很大一部分侵入下游减流区域, 阻挡了上下两个SHR尾流汇合。
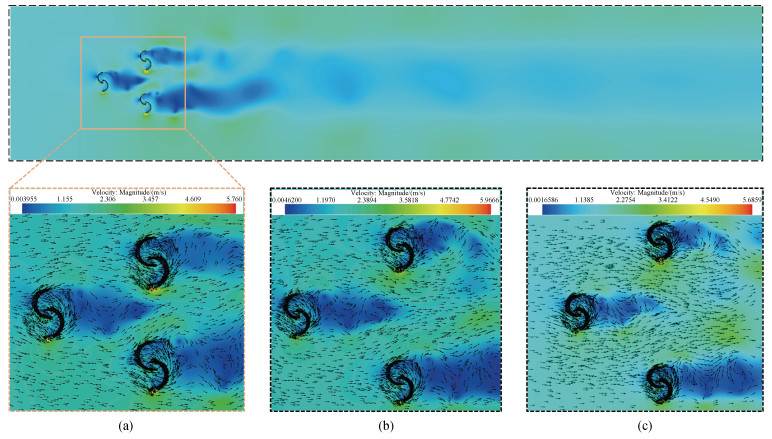 |
| 图 11 LY变化时的局部模拟图 Fig. 11 Partial simulation diagram for varying LY a. LY=2D; b. LY=3D; c. LY=4D |
图 12(a)显示了当LY=2D时各列在不同测速点位的流速。可以看出在L1~L5之间出现两个突变低值, 分别位于点1.5D和点–1D处, 这与图 11(a)所示的蓝色区域一致。而–1D处的突变更低, 最低处可达0.2 m/s, 这验证了rotor3下游涡流越多, 降低流速效果越好。L5~L10势逐渐变得平稳, 两个波谷逐渐重合, 流速也逐渐增大。L1~L10两端(2.5D和–2.5D)处, 流速都在初始流速1.5 m/s以上, 这是由于rotor2的上端叶尖附近和rotor3的下端叶尖附近水流颗粒急速运动, 导致两端流速大于初始流速, 但随着外部流场和内部场(–2D~2D)的共同作用下, 两端流速在下游逐渐降低。当LY=3D时, 流速分布有所改变, 如图 12(b)所示, 观察到两个突变出现在2D和–1.5D处, 但在0.5D和0D出现了一个突变高值, 正是上面所述的部分加速区域侵入导致平均流速增大。
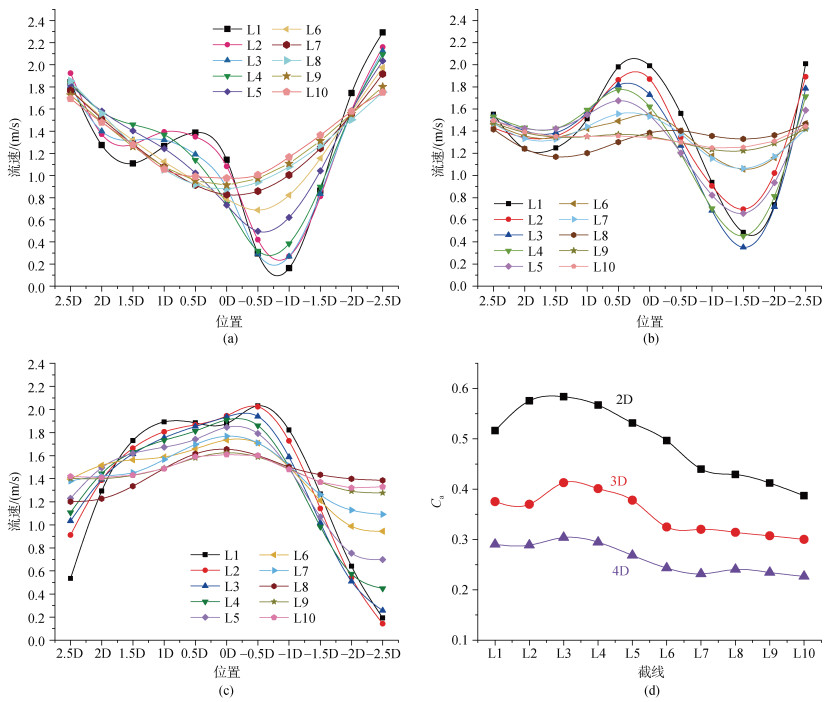 |
| 图 12 LY为2D、3D和4D时的减流效果 Fig. 12 Flow reduction effect when LY is 2D, 3D and 4D a.平均流速(LY=2D); b. 平均流速(LY=3D); c. 平均流速(LY=4D); d. 流速衰减系数(Ca) |
此外, 在下游L7~L10区间的流速逐渐趋于恢复至1.5 m/s附近, 降低流速效果不如LY=2D时的效果。当LY=4D时, 如图 12(c)所示, 出现了两个突变高值, 并合并至一个大峰值, 其绝大部分点位流速都高于1.2 m/s, 只有在L1-L7两端有少数流速低于1.2 m/s, 因此, 降低流速效果也不如LY=2D时的效果。图 12(d)显示了3种排列下的10个截线衰减系数, 可以明显看出, LY=2D时每个截线Ca都大于3D和4D的截线Ca, 并且流速都是呈先增大后减小的趋势, 都在L3处达到流速最小值, L3之后流速逐渐恢复。
对比了LY之后, 研究了不同大小的LX的影响。如图 13中3幅图分别显示了当LY=2D时, 在相同TSR下, 自由流速为1.5 m/s, LX为2D, 3D和4D的仿真结果图。图 13中的(a)(b)(c)显示了不同测速点位平均流速大小, 图 13(d)显示了3种排列截线的平均流速, 可以清楚看出, 不同的LX的大小对下游流速影响较小, 其中当LX=3D时, 下游平均流速最小, 但与其他两种排列相差不大。此外, 流速大小随下游距离增加而增加。
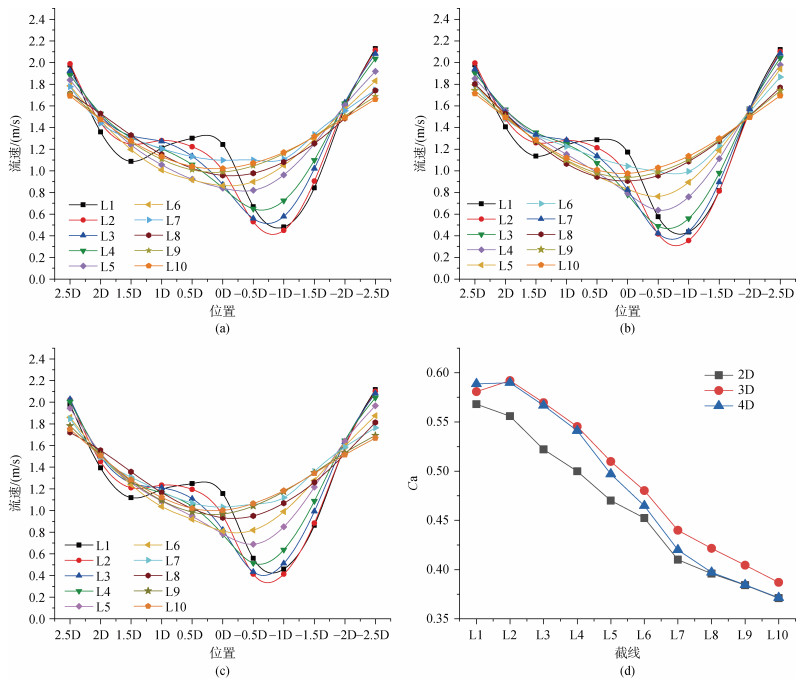 |
| 图 13 LX为2D、3D和4D时的减流效果 Fig. 13 Flow reduction effect when LX is 2D, 3D and 4D a.平均流速(LX=2D); b. 平均流速(LX=3D); c. 平均流速(LX=4D); d. 流速衰减系数(Ca) |
选取固定参数LX=3D和LY=2D, 流速1.5m/s的条件下, 对TSR=0.1-1.2进行研究, 分析不同TSR对降低流速的影响。结果如图 14所示, 图中可以看出当TSR=0.1~0.8时, Ca随着TSR的增大而增大, 当TSR=0.9~1.1时, Ca的变化趋于稳定, 并在TSR= 1.0和1.1时达到最大, TSR=1.2时, Ca降低, 减流效果减弱。
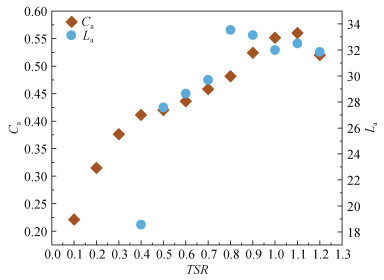 |
| 图 14 叶尖速比减流影响图 Fig. 14 Diagram showing flow reduction effect for different TSRs |
由于TSR小于0.3时, 下游无法形成稳定的尾流场, 因此无法测得La。从图中可以看出, La首先随TSR的增大呈上升趋势, 当TSR=0.8时, La的模拟值和实验值达到最大值33.541D和35.5D。
3.4 初始流速的影响将不同初始流速作为研究对象, 分析相同阵列下的不同初始流速对减流性能的影响。选取U=1.5、U=1.2和U=1.0 m/s 3种初始流速, 并分别让其在3种不同TSR(即0.9, 1.0和1.1)下进行模拟。结果如表 3所示, 虽然初始流速不同, 3种TSR下都具有较大的Ca和La, 并且结果均在相同小范围中浮动, 说明不同的初始流速只会影响下游流速的绝对数值, 并不影响其减流性能。
| U/(m·s–1) | TSR | Ca | La |
| U=1.5 | 0.9 | 0.513 89 | 33.15 |
| 1.0 | 0.55 13 | 32.0 | |
| 1.1 | 0.588 59 | 31.52 | |
| U=1.2 | 0.9 | 0.527 | 33.3 |
| 1.0 | 0.538 9 | 32.7 | |
| 1.1 | 0.566 7 | 32.5 | |
| U=1.0 | 0.9 | 0.596 4 | 33.7 |
| 1.0 | 0.577 5 | 33.4 | |
| 1.1 | 0.543 | 32.9 |
从上述可知, 下游两个转子rotor2和rotor3相邻的两个叶片对尾流场影响较大, 因此, 研究了下游两个转子不同排布方向对减流效果的影响。将下游两个转轮对称排布时, 可分成凸面相对和凹面相对。并且, 将上游rotor1也分别分为和rotor2同向旋转和rotor3同向旋转这两种情况。将上述一共4种排列方式, 分别让其在0.9、1.0、1.13种不同的TSR下进行模拟。
结果如下表 4所示, 当凸面相对时, 上游转子的旋转方向会影响下游转子涡流生成的数量。当rotor1和rotor2同向时, rotor3下游会产生更多的涡流; 反之, 当rotor1和rotor3同向旋转时, tuebine2会产生更多的涡流。但是, 凸面相对的两种情况, 不会影响最终的减流效果。当凹面相对时, 上游转子的旋转方向则不会影响下游转子涡流产生数量, 并且, 整个流速场呈对称分布。但是, 由于下游转子中间侵入的高速水流无法排出, 所以一直往下游延伸, 最终导致减流效果减弱。此外, 虽然凹面相对排列时, 拥有更大的La, 但是下游1.2 m/s的流速线更加狭窄和细长。
| 下游SHRs | 转向 | TSR | Ca | La |
| 凸面相邻 | 1-2同向 | 0.9 | 0.605 74 | 31.2 |
| 1 | 0.613 41 | 31.6 | ||
| 1.1 | 0.673 48 | 32.1 | ||
| 1-3同向 | 9 | 0.576 24 | 30.8 | |
| 1 | 0.598 80 | 31.95 | ||
| 1.1 | 0.613 48 | 32.1 | ||
| 凹面相邻 | 1-2同向 | 0.9 | 0.448 56 | 34.8 |
| 1 | 0.463 41 | 35.5 | ||
| 1.1 | 0.464 85 | 35.8 | ||
| 1-3同向 | 9 | 0.475 87 | 35.7 | |
| 1 | 0.499 54 | 36.2 | ||
| 1.1 | 0.524 36 | 36.7 |
本文对三角阵列下的Savonius转轮减流性能进行了数值模拟和实验分析。首先, 研究了三角阵列参数LX和LY对减流效果的影响。其次, 研究了不同叶尖速比、不同初始来流流速、不同旋转方向对减流性能的影响。结果如下:
1) 下游两个转轮中, 产生更多涡流的一侧, 拥有更好的减流性能。并且当形状参数LX不变, LY=2D时最大衰减系数Ca比LY=3D时高29.28%, 比LY=4D时高47.93%。当LY为2D时, LX为3D时, 最大衰减系数Ca比LX=2D时高4.05%, 比LX=4D时高0.37%。
2) 对TSR为0.1~1.2范围内的三角阵列研究发现, TSR为0.9~1.1区间时, 拥有更高的Ca和更大的La, 因此减流性能更好。对初始流速为1.0、1.2和1.5 m/s的3种流情况分析发现, 不同的初始流速不会影响三角阵列的减流性能。
3) 对下游两个转轮凹面相邻和凸面相邻两种不同旋转方向发现, 凸面相邻时, 上游转子旋转方向的仅会影响下游转轮产生的涡流, 不会影响减流性能。凹面相对时, 尾流场呈对称分布, 减流性能相对减弱。
| [1] |
CAI R S, LIU K X, TAN H J. The impact, risks, and adaptation strategies of climate change on China's oceans and coastal zones[J]. China Population, Resources, and Environment, 2020, 30(9): 1-8. |
| [2] |
钱振家, 徐金铖, 余友斌, 等. 水流对鱼类游泳行为和生理代谢的影响的研究进展[J]. 中国农学通报, 2022, 38(32): 133-138. QIAN Zhenjia, XU Jincheng, YU Youbin, et al. Research progress on the effects of water flow on swimming behavior and physiological metabolism of fish[J]. Chinese Journal of Agriculture, 2022, 38(32): 133-138. |
| [3] |
李秀明. 运动训练对中华倒刺鲃幼鱼生长的影响及其机理研究[D]. 重庆: 西南大学, 2013. LI Xiuming. Research on the effect of sports training on the growth of juvenile Spinibarbus sinensis and its mechanism[D]. Chongqing: Southwest University, 2013. |
| [4] |
ZHAO Y P, BAI X D, DONG G H, et al. Numerical analysis of the elastic response of a floating collar in waves[J]. Ocean Engineering, 2015, 95(1): 175-182. |
| [5] |
LADER P F, ENERHAUG B. Experimental investigation of forces and geometry of a net cage in uniform flow[J]. IEEE Journal of Oceanic Engineering, 2005, 30(1): 79-84. DOI:10.1109/JOE.2004.841390 |
| [6] |
CUEVAS-CARVAJAL N, CORTES-RAMIREZ J S, JULIAN A, et al. Effect of geometrical parameters on the performance of conventional savonius vawt: a review[J]. Renewable & Sustainable Energy Reviews, 2022, 161: 112314. |
| [7] |
AKWA J V, HORACIO A V, PETRY A P. A review on the performance of savonius wind turbines[J]. Renewable & Sustainable Energy Reviews, 2012, 16(5): 3054-3064. |
| [8] |
姚建均, 李凤甡, 王贤成, 等. Savonius型水轮机减流特性数值模拟研究[J]. 哈尔滨工程大学学报, 2020, 41(6): 870-876. YAO Jianjun, LI Fengshen, WANG Xiancheng, et al. Numerical simulation study on flow reduction characteristics of Savonius type water turbine[J]. Journal of Harbin Engineering University, 2020, 41(6): 870-876. |
| [9] |
KANG C, LIU H, YANG X. Review of fluid dynamics aspects of Savonius-rotor-based vertical-axis wind rotors[J]. Renewable & Sustainable Energy Reviews, 2014, 33: 499-508. |
| [10] |
NADHIEF M I, PRABOWOPUTRA D M, HADI S, et al. Experimental study on the effect of variation of blade arc angle to the performance of savonius water turbine flow in pipe[J]. The International Journal of Robotics Research, 2020, 9(5): 779-783. |
| [11] |
KUMAR A, SAINI R P, SAINI G, et al. Effect of number of stages on the performance characteristics of modified Savonius hydrokinetic turbine[J]. Ocean Engineering, 2020(Dec. 1 Pt. 2): 217. |
| [12] |
YAO J, LI F, CHEN J, et al. Parameter analysis of savonius hydraulic turbine considering the effect of reducing flow velocity[J]. Energies, 2020, 13(1): 24. |
| [13] |
BAO L, WANG Y, JIANG C, et al. Research on wave and energy reduction performance of floating breakwater based on s-shaped runner[J]. Energies, 2022, 15: 5148. |
| [14] |
ZHAO Y P, LIU H F, BI C W, et al. Numerical study on the flow field inside and around a semi-submersible aquaculture platform[J]. Applied Ocean Research, 2021, 115: 102824. |
| [15] |
LIU H F, BI C W, XU Z, et al. Hydrodynamic assessment of a semi-submersible aquaculture platform in uniform fluid environment[J]. Ocean Engineering, 2021, 237: 109656. |
| [16] |
MYCEK P, GAURIER B, GERMAIN G, et al. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part Ⅱ: Two interacting turbines[J]. Renewable Energy, 2014, 68: 876-892. |
| [17] |
ZHANG Y, KANG C, ZHAO H, et al. Effects of in-line configuration of drag-type hydrokinetic rotors on inter-rotor flow pattern and rotor performance[J]. Energy Conversion and Management, 2019, 196: 44-55. |
| [18] |
NAG A K, SARKAR S. Performance analysis of helical Savonius hydrokinetic turbines arranged in array[J]. Ocean Engineering, 2021, 12: 241. |
| [19] |
PAN C, KANG C, ZHANG W. Numerical study on the combination and interference of vertical axis spiral wind turbines[J]. Journal of Solar Energy, 2018, 39(8): 7. |
| [20] |
MALKI R, MASTERS I, WILLIAMS A J, et al. Planning tidal stream turbine array layouts using a coupled blade element momentum-computational fluid dynamics model[J]. Renewable Energy, 2014, 63(1): 46-54. |
| [21] |
CHAWDHARY S, HILL C, YANG X, et al. Wake characteristics of a TriFrame of axial-flow hydrokinetic turbines[J]. Renewable Energy, 2017, 109: 332-345. |
| [22] |
TALUKDAR K P, SARDAR A, KUCKARNI V, et al. Parametric analysis of model Savonius hydrokinetic turbines through experimental and computational investigations[J]. Energy Conversion and Management, 2018, 158: 36-49. |
 2024, Vol. 48
2024, Vol. 48


