
文章信息
- 王丽娜, 宋悦, 王旭东, 吕路莹, 董昌明. 2024.
- WANG Lina, SONG Yue, WANG Xudong, LÜ Luying, DONG Changming. 2024.
- 融合图卷积和注意力机制的GRU海面温度预测模型
- A GRU–sea surface temperature prediction model integrating graph convolution and an attention mechanism
- 海洋科学, 48(5): 1-12
- Marine Sciences, 48(5): 1-12.
- http://dx.doi.org/10.11759/hykx20230523002
-
文章历史
- 收稿日期:2023-05-23
- 修回日期:2023-08-25
2. 南方海洋科学与工程广东省实验室(珠海), 广东 珠海 519080;
3. 南京信息工程大学 海洋科学学院, 江苏 南京 210044
2. Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519080, China;
3. School of Marine Sciences, Nanjing University of Information Science and Technology, Nanjing 210044, China
海面温度(sea surface temperature, SST)是驱动全球水循环的重要参数[1-4], 在海洋和大气之间的物质、能量和动量交换中发挥重要作用。海面温度异常易导致干旱、洪涝等自然灾害出现。因此, SST精确预测对海洋环境[5]、海洋研究[6]等领域具有重要意义。
目前, 海面温度预测方法大致分为两类: 数值方法[7]和数据驱动方法[8]。数值方法通常利用动力学和热力学方程描述海面温度变化, 需要大量的运算时间[9]。近年来, 随着深度学习的发展, 一些深度学习方法逐渐应用于SST预测领域。传统循环神经网络用于预测海面温度, 但其会出现梯度消失或梯度爆炸问题, 无法应用于长期序列预测领域[10]。为解决长期的时间依赖性问题, 长短期记忆(long short-term memory, LSTM)[11]和门控循环单元(gated recurrent unit, GRU)[12]被提出。Zhang等[13]提出将LSTM网络应用于SST预测, 取得较优的预测性能。Xiao等[14]提出了将LSTM网络与Adaboost算法相结合的集成学习模型预测SST, 避免了模型过拟合。贺琪等[15]提出了一种基于EMD-GRU模型的海面温度预测方法, 有效提升了预测精度。
上述方法在预测SST值时仅考虑了非线性时间相关性, 忽略了其空间相关性。孙苗等[16]提出了基于卷积神经网络(convolutional neural networks, CNN)和LSTM相结合的方法, 考虑了SST的时空特征, 实现了对南海海面温度的预测。张雪薇等[17]提出了基于ConvGRU的SST预测模型, ConvGRU模型融合了卷积神经网络和门控循环单元(gated recurrent unit, GRU), 考虑了时空数据的异质性[18], 实现了SST时空特征的同时处理。然而CNN不能表达节点间的空间关联性, 难以提取拓扑图的空间特征。由于图卷积神经网络(graph convolutional network, GCN)将每个节点视为图结构中的一个顶点, 通过聚合邻近节点之间的信息来表示目标节点的新特征, 可以捕获节点之间的空间相关性, 有学者将GCN代替CNN, 开展相关研究。Sun等[19]将GCN与LSTM神经网络相结合, 提出时间序列图网络(TSGN)来预测SST。该模型使用不同的组件来捕获空间和时间相关性, 忽略了时空数据的异质性[18]。由于连续SST数据具有很强的时空相关性, 无论是特定时间SST数据的空间关系, 还是特定位置数据的时间变化, 都不能孤立地观察, 不同时间不同地点的SST值可能是相关的[20-21]。海域的地形并非是单一的海水, 海域中还可能存在陆地或岛屿。因此, 应用图卷积(graph convolution, GC)以图形拓扑表示节点之间的关系, 有重要的实际意义。GC能够捕捉节点之间的空间相关性, 并通过聚合相邻节点的信息来获得目标节点的特征表示。
综上, 本文将海洋表面空间特征构建成图形拓扑结构, 应用GC充分提取其空间特征, 同时考虑时空数据的异质性, 提出了一种融合图卷积和注意力机制的GRU海面温度预测模型。首先, 把GRU的矩阵乘法替换为图卷积运算, 构成门控图卷积(graph convolutional recurrent unit, GCRU)层来提取数据的时空信息; 其次, 引入注意力机制对GCRU层的输出信息分配概率权重, 重要信息分配更高的权重系数, 指导预测过程更有效; 最终, 使用一个全连接的输出层输出海面温度预测结果。实验结果表明, 本模型在东海和渤海研究区域未来1 d、3 d和7 d的SST值均取得较高预测精度。
1 基础理论 1.1 问题定义在本节中, 首先对海面温度预测问题进行定义。使用图形表示SST数据, 每次记录每个网格节点即经纬交叉节点的SST值, 根据网格上有效的SST数据定义图结构。由于图形可以全面地描述不规则数据, 与全网格数据需求相比, 图结构表示更加灵活。
定义1: 将SST数据的网络拓扑结构描述为G = (Vt, E, A), Vt是一组有限的顶点, 对应格点空间的n个有效SST值点。其中, 海洋中的陆地(如海岸、岛屿)没有有效的SST观测值; E是一组边, 表示节点之间的连通性。A表示加权邻接矩阵, 其定义如式(1)所示。
| Aij={q⋅exp(−d2ijσ2),i≠j且exp(−d2ijσ2)≥ε1−q,i=j, | (1) |
式中:
定义2: 将海洋表面空间格点温度视为节点属性特征, 并表示为特征矩阵
| [Xt+1,⋯,Xt+T]=f(G;Xt−(n−1),⋯,Xt−1,Xt), | (2) |
式中: n是给定历史时间序列的长度; T是预测的时间序列长度。
1.2 GCN概述GCN可以对图数据的复杂关系和相互依赖性进行建模, 受到了广泛的关注和研究。GCN将节点之间的关系转换为图的邻接矩阵, 以捕捉拓扑结构产生的依赖关系, 通过聚合邻居结点的信息来提取空间特征, 在获得图节点表示的同时考虑了相邻节点的影响[23]。
GCN中的卷积模式包括频谱域图卷积和空间域图卷积, 本研究使用频谱模式构建GCN模型, 在傅里叶域中将给定邻接矩阵A和特征矩阵X构造图滤波器。图滤波器作用于图的节点, 在考虑图节点和节点的一阶相邻域的情况下, GCN执行频谱卷积运算来取代CNN中的卷积运算, 以捕捉图的空间特征, 然后根据分层传播规则来堆叠多个网络。多层GCN模型可以表示为
| H(l+1)=σ(˜D−12˜A˜D−12H(l)θ(l)), | (3) |
式中:
为了防止过平滑现象发生, GCN的层数一般会设置成1~2层。在本研究中, 选择公式(4)来获得空间相关性。
| f(X,A)=σ(⌢ARelu(⌢AXW0)W1), | (4) |
式中: X是特征矩阵; A是邻接矩阵;
Recurrent Neural Network(RNN)是处理序列数据的最广泛使用的递归神经网络模型, 然而传统RNN存在梯度消失和爆炸等问题, 在中长期预测任务中有一定局限性[24]。LSTM是RNN的一种变体, 为此类问题提供了解决方案。LSTM单元设置了输入门、遗忘门和输出门, 以控制输入值、记忆值和输出值。在LSTM基础上, GRU只设置了更新门和重置门, 减少训练时间, 提高了训练效率, 同时具有等效的预测精度。鉴于此, 本文采用GRU模型来捕获时间依赖性。GRU结构如图 1所示。
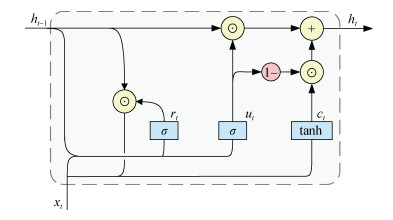 |
| 图 1 GRU结构 Fig. 1 Structure of the gated recurrent unit |
GRU可以通过如下公式进行描述
| ut=σ(xtWxu+ht−1Whu+bu), | (5) |
| rt=σ(xtWxr+ht−1Whr+br), | (6) |
| ct=tanh(xtWxc+(rt⊙ht−1)Whc+bc), | (7) |
| ht=ut⊙ht−1+(1−ut)⊙ct, | (8) |
式中:
注意力机制模拟了人脑注意力在特定时刻对特定区域关注的情况, 从而有选择性地获取更多有效信息, 忽略无用信息。注意力机制分为软注意力和硬注意力。软注意力是指在选择信息的时候, 对t个输入信息进行加权平均, 再输入到神经网络中计算。
在当前的研究中, 使用软注意力模型来学习GRU输出信息不同的重要性, 模型结构如图 2所示。
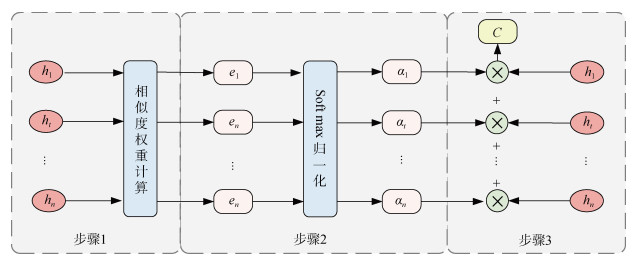 |
| 图 2 注意力机制结构 Fig. 2 Structure of the attention mechanism |
图 2中,
步骤1: 采用多层感知机(Multi-layer Perceptron, MLP)作为评分函数对每个时刻的数据进行相似度权重计算, 如公式(9)所示。
| ei=w(2)(w(1)H+b(1))+b(2), | (9) |
其中,
步骤2: 使用Softmax函数对这些相似度权重进行归一化处理, 如公式(10)所示。
| αi=exp(ei)∑tj=1exp(ej). | (10) |
步骤3: 将归一化后的注意力权重与输入数据进行加权计算得到
| Ci=t∑j=1αj×hj. | (11) |
本节描述融合图卷积和注意力机制的GRU海面
温度预测模型。GCRU-ATT模型由输入层、GCRU层、注意力层和全连接输出层组成, 其中GCRU层内部有图卷积(Graph Convolution, GC)运算, 模型结构如图 3所示。
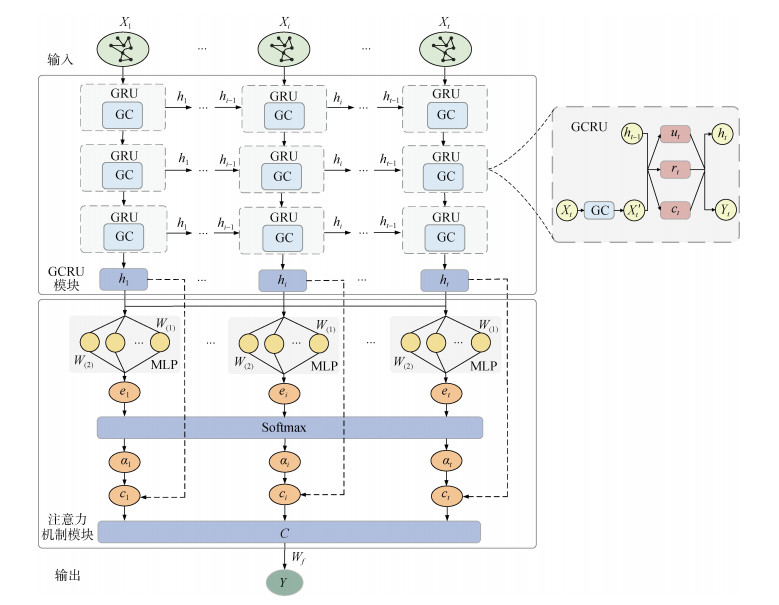 |
| 图 3 GCRU-ATT模型结构图 Fig. 3 Model structure diagram of the graph convolutional recurrent unit–attention mechanism |
首先, 将获得的邻接矩阵和t个历史时间序列的SST数据,
依次, 使用GC操作代替GRU循环单元的更新门
| ut=σ(f(A,Xt)W′fu+ht−1W′hu+b′u), | (12) |
| rt=σ(f(A,Xt)W′fr+ht−1W′hr+b′r), | (13) |
| ct=tanh(f(A,Xt)W′fc+(rt⊙ht−1)W′hc+b′c), | (14) |
| ht=ut⊙ht−1+(1−ut)⊙ct. | (15) |
接着, 将3个GCRU层叠加构成1个模块组, 整个结构包含多个GCRU模块组。其中每个GCRU层隐藏状态的输出作为下一个GCRU层的输入。
再者, 引入注意机制关注重要信息。将GCRU模块的最终隐藏状态信息输入注意力模块, 以获得SST序列数据的重要性。在注意力模型中, 使用多层感知机作为评分函数, 其中
最终, 使用全连接层输出预测结果Y。
3 实验分析 3.1 数据集SST为AVHRR卫星遥感数据, 是由美国国家海洋和大气管理局(national oceanic and atmospheric administration, NOAA)提供的最优插值数据集。分别选取东海和渤海海域的部分区域作为研究对象, 其中东海研究区域为27°45′~32°30′N和123°~126°45′E, 渤海研究区域为37°15′~41°00′N和117°30′~121°30′E, 空间分辨率为0.25°×0.25°。实验数据包含2003年1月1日—2022年12月31日共20 a的日均SST值。将前80%数据作为训练集, 10%数据作为验证集, 余10%数据作为测试集。分别选取东海和渤海海域的部分区域作为研究对象预测未来1 d、3 d和7 d的SST。数据统计信息如表 1所示。
| 数据集 | 东海 | 渤海 |
| 时间范围 | 2003/1/1—2022/12/31 | 2003/1/1—2022/12/31 |
| 覆盖区域 | 27°45′~32°30′N 123°~126°45′E |
37°15′~41°00′N 117°30′~121°30′E |
| 节点数量 | 320 | 272 |
| 训练样本数 | 5 844 | 5 844 |
| 验证样本数 | 730 | 730 |
| 测试样本数 | 730 | 730 |
本文数据预处理过程包括以下几部分:
(1) 数据截取: 从全球数据集中分别截取渤海和东海相应经纬度范围的SST数据;
(2) 对SST数据进行归一化处理, 如式(16)所示。
| XN=X−min | (16) |
式中,
(3) 不同数据集制作: 使用滑动窗口的方法在时间维度上进行切割SST数据, 按8∶1∶1的方式划分训练集、验证集和测试集;
(4) 构造特征矩阵: 将海洋表面空间格点SST信息视为节点属性特征, 并表示为特征矩阵
(5) 构造邻接矩阵: 依据公式(1)计算邻接矩阵。
数据预处理流程如图 4所示。
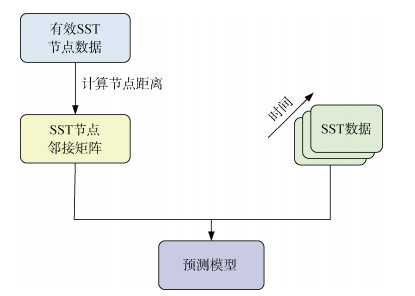 |
| 图 4 预处理流程图 Fig. 4 Preprocessing flow chart |
实验环境如表 2所示。
| 名称 | 版本 |
| 操作系统 | Windows10 |
| CPU | Intel Core i5-7200U |
| GPU | NVIDIA RTX 2060 GPU |
| 编程语言 | Python 3.6 |
| 框架 | Tensorflow1.14 |
本文采用平均绝对误差(averaged mean absolute error, Eama), 均方根误差均值(averaged root mean square error, Earms)和绝对误差(absolute error, Ea)作为评价指标来衡量模型的预测误差和精度。其中, i、j为空间格点坐标, K为样本个数, I表示纬向总格点数, J表示经向总格点数。
| {E_{{\text{ama}}}} = \frac{1}{K}\sum\nolimits_{k = 1}^K {\frac{1}{{I \cdot J}}} \sum\nolimits_{i = 1}^I {\sum\nolimits_{j = 1}^J {\left| {{h_{\text{p}}}\left( {i, j} \right) - {h_{\text{o}}}\left( {i, j} \right)} \right|} } , | (17) |
| {E_{{\text{arms}}}}{\text{ = }}\frac{1}{K}\sum\nolimits_{k = 1}^K {\sqrt {\frac{1}{{I \cdot J}}\sum\nolimits_{i = 1}^I {\sum\nolimits_{j = 1}^J {{{\left( {{h_{\text{p}}}(i, j) - {h_{\text{o}}}(i, j)} \right)}^2}} } } } , | (18) |
| {E_{\text{a}}} = \left| {{h_{\text{p}}}\left( {i, j} \right) - {h_{\text{o}}}\left( {i, j} \right)} \right| . | (19) |
考虑节点对于图结构的影响, 本文引入了一个参数
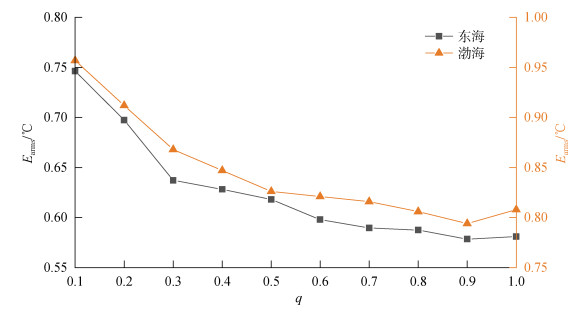 |
| 图 5 最优参数q Fig. 5 Optimal parameter q |
为验证模型的可行性, 在参数设置相同条件下, 选择不同的模块完成模型的变体实验, 分别评估不使用图卷积的GRU、GRU-ATT模型和不使用注意力机制的GCRU模型性能。本研究预测未来1 d、3 d和7 d的SST值, 使用Earms和Eama评估该方法的有效性。Earms和Eama越小, 该方法的预测性能越优。本文模型与其变体模型在东海、渤海的研究区域上对比结果分别如图 6、图 7所示。整体而言, 预测精度随着预测时间的增加而降低, 也即Earms和Eama值在增加。本文模型GCRU-ATT在Eama和Earms指标上均性能最优, 变体模型GRU表现最差; 比较GCRU-ATT模型与GRU-ATT模型, 空间特征提取减小了模型的预测误差; 对比GCRU-ATT模型与GCRU模型, 通过加入注意力机制对GRU层输出信息分配不同的权重注意力, 关注重要信息, 进一步提高了SST的预测精度。以预测7 d的SST为例, GCRU-ATT模型在东海测试集7 d预测的Earms和Eama值比GCRU模型分别减小了0.162 ℃和0.127 ℃, 比GRU-ATT模型分别减小了0.109 ℃和0.073 ℃; GCRU-ATT模型在渤海测试集7 d预测的Earms和Eama值比GCRU模型分别减小了0.097 ℃和0.063 ℃, 比GRU-ATT模型分别减小0.062 ℃和0.026 ℃。实验表明GCRU-ATT模型取得最优的预测性能。
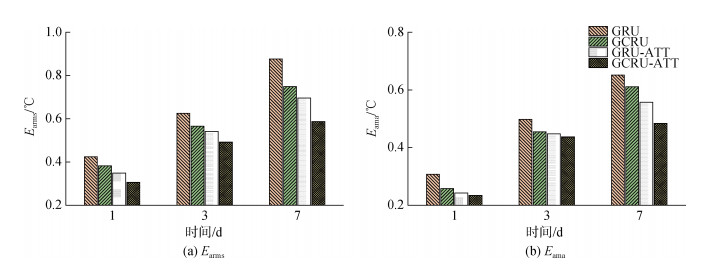 |
| 图 6 变体模型在东海测试集上的对比结果 Fig. 6 Comparison of the results of ablation models on the ECS test set |
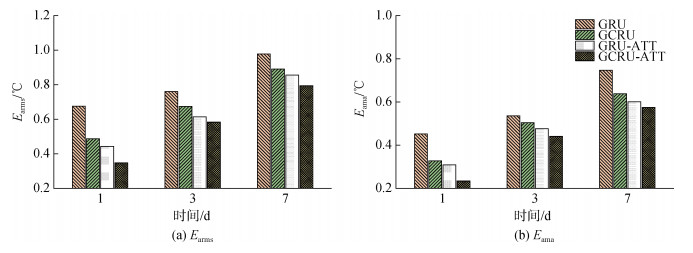 |
| 图 7 变体模型在渤海测试集上的对比结果 Fig. 7 Comparison of the results of ablation models on the BS test set |
基于空间和时间特征提取, 将本文模型与现有模型CNN-LSTM[16]、ConvGRU[17]、TSGN[19]进行比较, 可以发现: (1)TSGN模型预测性能优于CNN-LSTM。TSGN模型由GCN和LSTM模块构成, 其中GCN能捕获节点之间的空间相关性, 比CNN-LSTM模型预测性能优, 但TSGN和CNN-LSTM模型均使用不同的组件来捕获空间和时间相关性, 未考虑时空数据的异质性。(2)ConvGRU的预测性能优于CNN-LSTM, 由于ConvGRU包含卷积计算提取空间特征, 通过GRU模块提取时间特征, 同时学习时间和空间特征, 考虑了时空数据的异质性; 而CNN-LSTM首先学习空间特征, 然后是时间特征, 未考虑时空数据的异质性。(3)GCRU-ATT模型的预测性能优于ConvGRU和TSGN模型, 由于ConvGRU模型忽略了空间节点之间的关联性, 而TSGN模型未考虑时空数据的异质性。本文所提GCRU-ATT模型考虑时空数据的异质性, 通过构建无向图捕获空间节点间的依赖, 同时引入注意力机制对输出信息分配不同的权重注意力, 关注重要信息, 提高了SST的预测精度。
以东海历史SST作测试集, 将CNN-LSTM、TSGN、ConvGRU和本文模型共4个模型进行不同预测步长预测, 测试结果如图 8所示。由图 8可知, 本文模型的Earms和Eama均低于其他三个模型, 其预测误差在所有模型中最小, 性能最优。GCRU-ATT模型在未来1 d、3 d和7 d预测的Earms分别为0.306 ℃、0.514 ℃、0.587 ℃; ConvGRU模型次之, Earms分别为0.356 ℃、0.623 ℃、0.794 ℃; TSGN模型的预测性能优于CNN-LSTM模型, Earms分别为0.387 ℃、0.678 ℃、0.839 ℃; CNN-LSTM模型总体上预测性能最差, Earms分别0.429 ℃、0.698 ℃、0.939 ℃。同理, Eama指标上GCRU-ATT模型取得最优结果。
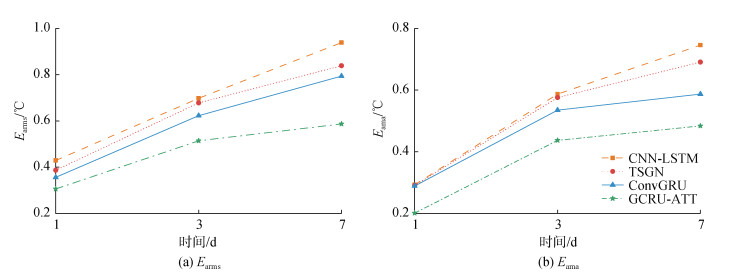 |
| 图 8 不同模型在东海测试集上的误差统计 Fig. 8 Comparisons of error statistics among different models on the ECS test set |
以渤海历史SST作测试集, 将CNN-LSTM、TSGN、ConvGRU和本文模型共4个模型进行不同预测步长预测, 测试结果如图 9所示。由图 9可知, 本文模型的Earms和Eama均低于其他3个模型, 其预测误差在所有模型中最小, 性能最优, 该结论与东海做测试集的预测结果相同。GCRU-ATT模型在1 d、3 d和7 d预测步长的Earms分别为0.348 ℃、0.583 ℃和0.794 ℃。ConvGRU模型次之, 不同预测步长的Earms分别为0.439 ℃、0.678 ℃和0.833 ℃。TSGN模型的预测性能优于CNN-LSTM模型, 不同预测步长的Earms分别为0.497 ℃、0.701 ℃和0.954 ℃。CNN-LSTM模型总体上预测性能最差, 不同预测步长的Earms分别为0.544 ℃、0.737 ℃、0.996 ℃。同理, Eama指标上GCRU-ATT模型取得最优结果。
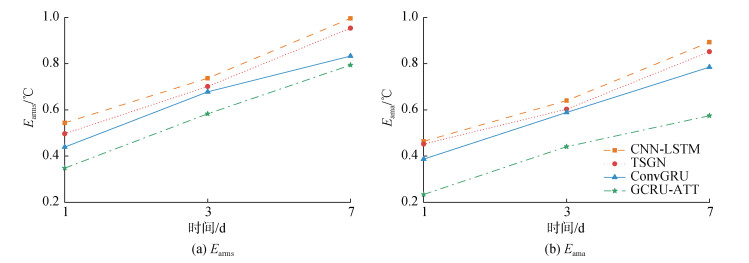 |
| 图 9 不同模型在渤海测试集上的误差统计 Fig. 9 Comparisons of error statistics among different models on the BS test set |
表 3展示了CNN-LSTM、TSGN、ConvGRU和本文模型共4个模型在东海和渤海SST测试集上的误差统计, 表中加粗数字表示最优误差指标。在所有预测范围内, 与渤海数据集相比, 所有方法在东海数据集上都取得了更好的性能。这是因为东海的纬度较渤海低, 温差比渤海小, 而渤海靠近内陆, 易受海陆冷热交替的影响, 温差较大。从表 3可以看出, 不同预测步长的SST预测精度不同, 预测精度随着预测序列长度的增加而降低。GCRU-ATT模型与其他模型比较, 预测性能最优。
| 区域 | 模型 | Earms/℃ | Eama/℃ | |||||
| 1 | 3 | 7 | 1 | 3 | 7 | |||
| 东海 | CNN-LSTM | 0.429 | 0.698 | 0.939 | 0.293 | 0.587 | 0.746 | |
| TSGN | 0.387 | 0.678 | 0.839 | 0.291 | 0.576 | 0.691 | ||
| ConvGRU | 0.356 | 0.623 | 0.794 | 0.289 | 0.535 | 0.587 | ||
| GCRU-ATT | 0.306 | 0.514 | 0.587 | 0.219 | 0.437 | 0.484 | ||
| 渤海 | CNN-LSTM | 0.544 | 0.737 | 0.995 | 0.464 | 0.640 | 0.893 | |
| TSGN | 0.497 | 0.701 | 0.954 | 0.452 | 0.603 | 0.852 | ||
| ConvGRU | 0.439 | 0.678 | 0.833 | 0.387 | 0.589 | 0.785 | ||
| GCRU-ATT | 0.348 | 0.583 | 0.794 | 0.234 | 0.441 | 0.575 | ||
为更好地展示GCRU-ATT模型的预测结果, 选取东海研究区域2022年1月1日至2022年1月7日共7 d的SST预测, 对观测值、预测值和绝对误差值进行可视化, 如图 10所示。因为原始数据的分辨率问题, 海表面温度预测图存在一些细节变化规律的预测误差, 因此使用了克里金插值方法来弥补这些误差。对应本文的东海研究区域, 其中观测值和预测值的图像颜色由蓝色至红色变化, 对应SST值由小至大, 蓝色越深代表SST值越低, 红色越深代表SST值越高; 绝对误差值由蓝色至红色变化对应误差由小至大, 蓝色越深代表误差越小, 红色越深代表误差越大。由观测值可知, 研究区域的右上角温度偏高, 原因是水的比热容大, 冬季远海区域SST值比近海高; 由预测值可知, 该模型的预测值与观测值高度相似, 表明本模型的预测效果较好; 由绝对误差可知, 随着预测天数增加, 预测误差增大。本模型的预测效果良好, 误差整体偏小。但仍有部分区域的预测出现较大误差, 主要集中在研究区域的左上角, 第7 d时最大误差达到了1.75 ℃。
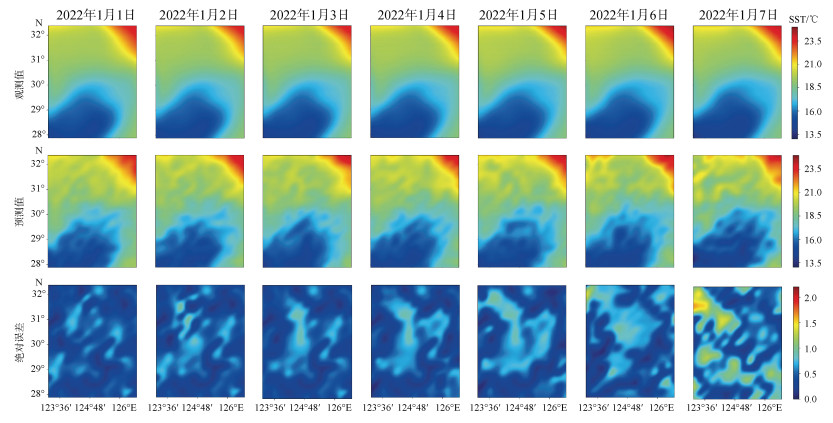 |
| 图 10 东海研究区域2022年1月1日至2022年1月7日周预测的每日SST值与每日绝对误差对比 Fig. 10 Comparisons of the daily sea surface temperature and daily absolute errors of the weekly prediction in the areas selected from ECS. The date range is from 1 January 2022 to 7 January 2022 |
选取渤海研究区域2022年1月1日至2022年1月7日共7 d的SST预测, 对观测值、预测值和绝对误差值进行可视化, 如图 11所示。渤海研究区域地形复杂, 存在较多的陆地和海域的混合区域, 其中, 陆地区域对应可视化图像中的深蓝色。真实SST值和预测SST值由蓝色至红色变化, 对应SST值由小至大; 绝对误差值由蓝色至红色变化, 对应误差值由小变大。整体上, 随着预测天数增加, 预测误差增大。由观测值可知, 该图清晰反映了海岸线的轮廓; 由预测值可知, 该模型在渤海研究区域仍展现了较好的预测效果; 由绝对误差图可知, 该模型误差主要集中在研究区域的海岸线附近。第7 d部分海域SST值最大误差达到2.03 ℃。
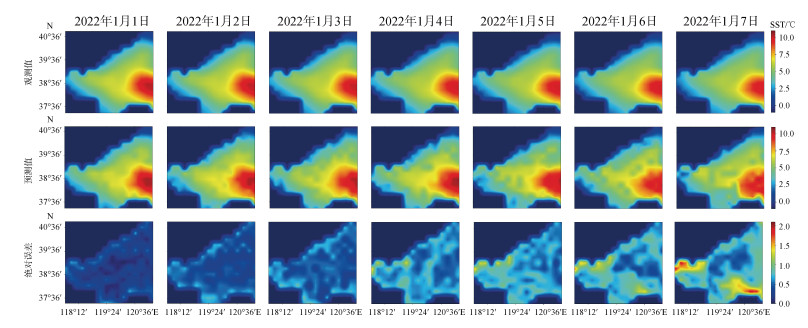 |
| 图 11 渤海研究区域2022年1月1日至2022年1月7日周预测的每日SST值与每日绝对误差对比 Fig. 11 Comparisons of the daily sea surface temperature and daily absolute errors of the weekly prediction in the areas selected from ECS. The date range is from 1 January 2022 to 7 January 2022 |
为更好地说明GCRU-ATT模型的预测性能, 在东海研究区域和渤海研究区域分别随机选择一个观测点(东海: 30°7′30″N, 126°7′30″E, 渤海: 38°37′30″N, 119°37′30″E)。应用本文所提模型对所选取的两个观测点进行测试, 图 12展示了本文模型在东海和渤海两个位置未来1 d、3 d和7 d的预测结果。
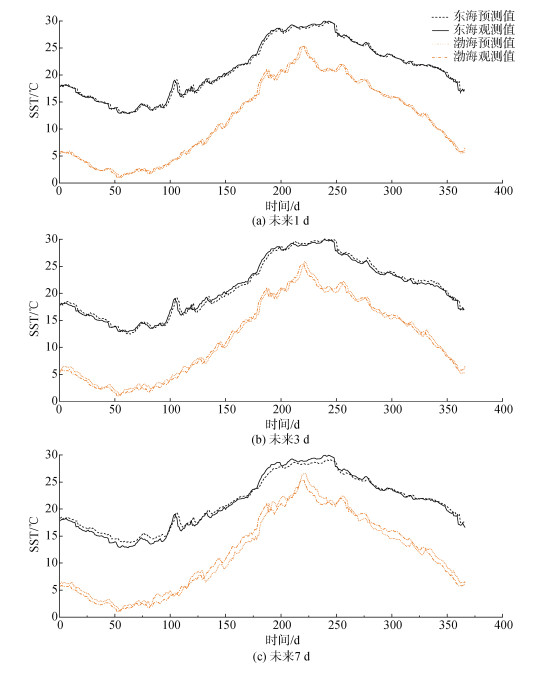 |
| 图 12 GCRU-ATT模型在东海和渤海研究区域2022年测试集上不同时间步长的预测结果 Fig. 12 Forecast results of the graph convolutional recurrent unit–attention mechanism model at different time steps on the ECS and BS test sets of 2022 |
GCRU-ATT模型的预测结果表明, 无论东海还是渤海观测点, 该模型在不同的预测步长上都能获得良好的预测结果, 预测值与实际值拟合良好, 预测的偏差很低。尽管模型在最值的预测是有偏差的, 并且预测性能随着预测长度的增加而降低, 但这并不影响模型预测的准确性和稳定性。
4 结论本文将海面温度空间分布构建网状拓扑图, 提出了一种同时捕捉全局时间和空间相关性的海面温度预测方法GCRU-ATT。本方法应用图卷积来捕获空间依赖关系, 使用GRU网络捕捉连续历史SST值的动态时间变化, 引入注意机制关注重要信息, 提高预测精度。选择东海和渤海研究区域, 应用GCRU-ATT模型对所提出的SST预测任务进行测试。结果表明, 在不同预测步长上, GCRU-ATT模型的预测精度均优于CNN-LSTM、TSGN和ConvGRU模型, 证明了该模型在实际SST预测的有效性, 但是影响SST变化还有其他环境因素如太阳辐射、大气运动等, 未来的研究可以考虑引入多个参数对模型进一步优化, 以提高SST的预测精度。
| [1] |
SUMNER M D, MICHAEL K J, BRADSHAW C J A, et al. Remote sensing of Southern Ocean Sea surface temperature: implications for marine biophysical models[J]. Remote Sensing of Environment, 2003, 84(2): 161-173. |
| [2] |
陆雪, 刘子洲, 翟方国. 近18 a山东半岛南部海域海面温度的长期变化研究[J]. 海洋科学, 2023, 47(4): 37-53. LU Xue, LIU Zizhou, ZHAI Fangguo. Long-term changes in sea surface temperature in sea areas to the south of the Shandong Peninsula over the past 18 years[J]. Marine Sciences, 2023, 47(4): 37-53. |
| [3] |
CONSTABLE A J, MELBOURNE-THOMASJ, CORNEYS P, et al. Climate change and Southern Ocean ecosystems Ⅰ: how changes in physical habitats directly affect marine biota[J]. Global Change Biology, 2015, 20(10): 3004-3025. |
| [4] |
李玲莉, 王林慧, 宋军, 等. 两类El Niño事件对中国近海及毗邻海域海表温度的影响[J]. 海洋科学, 2021, 45(4): 51-63. LI Lingli, WANG Linhui, SONG Jun, et al. Effects of two types of El Niño events on the sea surface temperature in China's offshore and adjacent seas[J]. Marine Sciences, 2021, 45(4): 51-63. |
| [5] |
RÜHMKORFF S, WOLF F, VAJEDSAMIEI J, et al. Marine heatwaves and upwelling shape stress responses in a keystone predator[J]. Proceedings of the Royal Society B, 2023, 290(1991): 20222262. DOI:10.1098/rspb.2022.2262 |
| [6] |
CASTROS L, WICKG A, STEELE M. Validation of satellite sea surface temperature analyses in the Beaufort Sea using UpTemp buoys[J]. Remote Sensing of Environment, 2016, 187: 458-475. |
| [7] |
KRISHNAMURTI T N, CHAKRABORTY A. Seasonal prediction of sea surface temperature anomalies using a suite of 13 coupled atmosphere–ocean models[J]. Journal of Climate, 2006, 19(23): 6069-6088. DOI:10.1175/JCLI3938.1 |
| [8] |
ZHU L Q, LIU Q, LIU X D, et al. RSST-ARGM: a data-driven approach to long-term sea surface temperature prediction[J]. EURASIP Journal on Wireless Communications and Networking, 2021, 171. |
| [9] |
STOCKDALET N, BALMASEDAM A, VIDARD A. Tropical Atlantic SST prediction with coupled ocean– atmosphere GCMs[J]. Journal of Climate, 2006, 19(23): 6047-6061. |
| [10] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. |
| [11] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [12] |
WANG W H, WEI F R, DONG L, et al. MINILM: Deep self-attention distillation for task-agnostic compression of pre-trained transformers[J]. Advances in Neural Information Processing Systems, 2020, 33: 5776-5788. |
| [13] |
ZHANG Q, WANG H, DONG J Y, et al. Prediction of sea surface temperature using long short-term memory[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1745-1749. |
| [14] |
XIAO C, CHEN N, HU C, et al. Short and mid-term sea surface temperature prediction using time-series satellite data and LSTM-AdaBoost combination approach[J]. Remote Sensing of Environment, 2019, 233: 111358. |
| [15] |
贺琪, 胡泽煜, 徐慧芳, 等. 基于经验模态分解-门控循环模型的海表温度预测方法[J]. 激光与光电子学进展, 2021, 58(24): 2415005. HE Qi, HU Zeyu, XU Huifang, et al. Sea surface temperature prediction method based on empirical mode decomposition-gated recurrent unit model[J]. Laser & Optoelectronics Progress, 2021, 58(24): 2415005. |
| [16] |
孙苗, 赵龙飞, 孔祥超. 一种基于深度学习的海表面温度预测方法——以南海为例[J]. 海洋信息技术与应用, 2021, 36(4): 25-31. SUN Miao, ZHAO Longfei, KONG Xiangchao. A SST prediction method based on deep learning: take the South China Sea case as an example[J]. Journal of Marine Information Technology and Application, 2021, 36(4): 25-31. |
| [17] |
张雪薇, 韩震. 基于ConvGRU深度学习网络模型的海表面温度预测[J]. 大连海洋大学学报, 2022, 37(3): 531-538. ZHANG Xuewei, HAN Zhen. Prediction of sea surface temperature based on ConvGRU deep learning network model[J]. Journal of Dalian Ocean University, 2022, 37(3): 531-538. |
| [18] |
冯宁, 郭晟楠, 宋超, 等. 面向交通流量预测的多组件时空图卷积网络[J]. 软件学报, 2019, 30(3): 759-769. FENG Ning, GUO Shengnan, SONG Chao, et al. Multicomponent spatial-temporal graph convolution networks for traffic flow forecasting[J]. Journal of Software, 2019, 30(3): 759-769. |
| [19] |
SUN Y, YAO X, BI X, et al. Time-series graph network for sea surface temperature prediction[J]. Big Data Research, 2021, 25(4): 100237. |
| [20] |
ZHENG G, LI X F, ZHANG R H, et al. Purely satellite data–driven deep learning forecast of complicated tropical instability waves[J]. Science Advances, 2020, 6(29): eaba1482. |
| [21] |
YANG Y T, DONG J Y, SUN X, et al. A CFCC-LSTM model for sea surface temperature prediction[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 207-211. |
| [22] |
YU B, YIN H T, ZHU Z X. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting[J]. arXiv preprint arXiv: 1709.04875, 2017.
|
| [23] |
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv, 2016: 1609. 02907.
|
| [24] |
BENGIO Y, SIMARD P, FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. |
| [25] |
LI M, HUANG P Y, CHANG X, et al. Video pivoting unsupervised multi-modal machine translation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 45(3): 3918-3932. |
| [26] |
GASTEIGER J, BOJCHEVSKI A, GÜ NNEMANN S. Predict then propagate: Graph neural networks meet personalized page Rank[J]. arXiv preprint arXiv, 2018: 1810.05997.
|
 2024, Vol. 48
2024, Vol. 48

