
文章信息
- 李昭毅, 孙虎元, 蔡振宇, 孙立娟. 2024.
- LI Zhaoyi, SUN Huyuan, CAI Zhenyu, SUN Lijuan. 2024.
- 基于Sine-SSA-BP人工神经网络的腐蚀速率预测研究
- Corrosion rate prediction based on Sine-SSA-BP artificial neural network
- 海洋科学, 48(8): 17-28
- Marine Sciences, 48(8): 17-28.
- http://dx.doi.org/10.11759/hykx20240312001
-
文章历史
- 收稿日期:2024-03-12
- 修回日期:2024-04-22
2. 中国科学院海洋研究所 海洋环境腐蚀与生物污损重点实验室, 山东 青岛 266071;
3. 中国科学院大学, 北京 100049;
4. 中国科学院海洋大科学研究中心, 山东 青岛 266071
2. Key Laboratory of Marine Environmental Corrosion and Bio-Fouling, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China
海洋工程用钢在海洋资源开发中有着广泛应用。然而, 钢结构在海水这种强电解质环境中腐蚀速度会大大加快, 寿命大幅缩短, 可靠性也大大降低, 而且腐蚀导致的材料失效往往也会带来非常严重的事故[1-4]。海洋环境非常复杂, 不仅体现在海水中的电解质种类复杂, 而且还有众多不同种类的生物, 这些因素都会影响碳钢在海水中的腐蚀速率。对海洋钢结构的腐蚀情况进行充分的预测, 掌握其腐蚀规律, 不仅能够减少由于腐蚀失效带来的损失, 而且能促使海洋经济向更加可持续的方向发展。
不同钢材在不同海域的腐蚀过程和腐蚀速率存在显著差异。对于X80钢, 温度、盐度和溶解氧对腐蚀的影响更为显著[5], 而对于耐候钢, 其中添加少量合金元素(Cu、P、Cr、Ni等), 可以在腐蚀过程中形成致密的锈层[6-9]。因此, 耐候钢的耐腐蚀性由该层的形成决定[10-11]。而对于不锈钢, 局部腐蚀是它在海洋环境中的主要腐蚀类型, 这可归因于多种因素, 包括氧浓度理论[12]、钝化溶解理论[13]和IR液滴理论[14-15]。缝隙腐蚀中的腐蚀程度也受到以下因素的影响: 离子浓度、表面位置、外部应力、材料形状和环境pH[16-20]。不同材料主要的腐蚀机制往往大相径庭, 附着在其表面的各种化合物也是如此。例如, 海洋动物的大小从微米级的生物到以厘米为单位的巨大生物, 都可能附着在金属表面[21-22]。如果不加以控制, 它们的随意生长和附着会严重影响金属的可靠性[23-25]。
因此, 针对不同材料进行高效、快速、准确的预测对于大型海洋工程来说意义重大。腐蚀速率预测需要大量的腐蚀数据, 而这些数据可能需要几年甚至几十年的积累。而且相对于其他数据, 腐蚀数据积累难度较大, 需要与不同的要素相对应[26]。
由于腐蚀测试实验涉及多种样品类型、漫长的测试周期、复杂的测试环境, 而且需要较大的经济开销, 目前对腐蚀速率的预测更依赖于经验模型[27]。早在多年前, 某些经验模型已用于腐蚀研究[28]。例如, Melchers[29]开发了一个模型来研究时间和平均水温与浸入海洋环境中的低合金钢腐蚀之间的关系。他发现, 影响腐蚀的主要因素是平均水温。然而, 研究表明, 海洋中的金属腐蚀是一个高度复杂的过程, 涉及许多变量。因此, 例如最大似然估计[30]、多元线性回归[31]和普通最小二乘法等仅能涉及较少影响因素和较小体量数据的经典方法并不适合于今天的大规模数据驱动研究。
在人工智能数据飞速发展的时代, 机器学习具有高效、低误差、适应海量数据且可针对不同材料随时调整的优势。用于提高在海洋大气中SiO2纳米结构铜绿青铜腐蚀预测的准确性[32]、用于识别海洋生物的GA-BP预测模型[33]、用于通过Q235钢腐蚀产物的图像分析确定腐蚀状态的BP神经网络[34]和用于预测海洋工程材料腐蚀速率的GA-BP-预测模型[35], 这些只是机器学习在部分领域中应用的个别案例。在腐蚀预测中, BP神经网络的优势同样存在, 通过机器学习对腐蚀速率进行合理的预测, 既可以充分利用腐蚀数据对未来腐蚀情况进行预测, 而且也可以缩短腐蚀试验的周期, 更加适合于对钢结构未来的腐蚀情况进行预估。
1 基本原理 1.1 麻雀搜索优化算法(SSA) 1.1.1 算法基本原理麻雀搜索算法(SSA)是一种群智能优化算法, 其灵感来源于麻雀实时寻找食物和识别威胁[36], 带领团队即时躲避危险, 以确保其生存的能力。
在麻雀寻找食物的过程中, 既有发现者, 也有加入者。发现者是群体中寻找食物的成员, 当其寻找到食物时, 它会将食物信号传递给其他麻雀, 发现者在整个麻雀群体中拥有着最高的能量储备, 这相当于在算法中具有高适应度, 能量储备越高的麻雀越易于最先发现食物分布最密集的位置, 跟随其进行食物搜索的麻雀数量也就越多。
当麻雀意识到危险, 或者说任何麻雀的安全值超过临界阈值时, 它会发送危险信号提醒麻雀群体。在收到信息后, 处于危险区域的麻雀会向安全地区移动, 并在新的区域继续搜索食物。
在种群中, 每只麻雀的位置会随时间不断变化, 适应度相对较低的麻雀会去追随适应度较高的麻雀, 适应度越低, 其飞离当前搜索位置到另一随机位置的可能就越高, 甚至可能飞离种群。每只麻雀的身份都是不稳定的, 任何一只麻雀都可以成为发现者, 也有可能飞离种群, 在寻找食物时会有所不同。当麻雀发现能量密度更高的食物来源时, 其自身的适应度随着其自身能量储备的提高而提高, 它就会成为能量储备较高的发现者。
随后, 跟随新发现者寻找食物的麻雀的身份变成了加入者。在整个种群中, 发现者与加入者的比例是恒定的。在麻雀种群中, 发现者觅食位置的能量密度随着适应度的下降而下降。这种方法实际上在一定程度上减轻了群智能方法容易陷入局部最优的问题。为了找到最佳的食物来源, 加入者在觅食过程中不断接收来自适应度强的发现者的信号。为了争夺资源, 一些加入者也会立即关注效率更高的发现者。
1.1.2 算法实现首先, 众多麻雀在种群中位置不同, 为将麻雀的身份和位置简单数据化表达, 将麻雀种群定义为一个矩阵, 将矩阵中的每个元素定义为种群中不同的麻雀, 如式(1)所示:
| Xm×n=[x11⋯x1n⋮⋱⋮xm1⋯xmn]. | (1) |
矩阵的维数n对应于优化的目标变量数量的大小, 需解决问题中的变量数量越高, 其在人工神经网络内部的层数也就越多, 所对应的麻雀种群活动范围越大。麻雀的数量用数字m表示。每只麻雀的适应度如式(2)所示:
| Fx=[f([(x1,1x1,2…x1,n)])f([(x2,1x2,2…x2,n)])⋮f([(xm,1xm,2…xm,n)])], | (2) |
其中f表示每个个体的适应度。
在整个麻雀种群中, 发现者数量占大多数。他们有足够的能量储备来寻找食物, 发现能量储备高的区域。适应度较低的加入者会追随适应度较高的发现者, 以跟随他们获取到更多的食物。因此, 麻雀种群中大多数麻雀寻找食物的方向由适应度高的发现者决定, 适应度较高的发现者也因其有较高的能量储备, 有更广泛的食物搜索范围。发现者在寻找食物的过程中位置不断变化, 该算法的设计原理规定发现者的位置更新如式(3)所示:
| Xt+1i,j={Xti,j·exp(−iα·itemmax),如果R2<ST,(a)Xti,j+Q·L, 如果R2≥ST,(b) | (3) |
式中, t表示算法的当前迭代次数。j=1, 2, 3, …, n。itemmax表示最大迭代数。Xi, j表示第i只麻雀在第j维中的位置信息。α(α∈(0, 1])是一个随机数。R2(R2∈[0, 1])和ST(ST∈[0, 1])分别表示预警值和安全值。Q是服从正态分布的随机数。L是一个1行n列的矩阵, 矩阵中的所有元素都是1。
当环境安全时, 种群中的所有麻雀都会应用公式(3)中等式(a)的原则寻找食物。当麻雀的安全值大于预警值时, 代表着该麻雀感受到危险, 并会向周围发出信号, 该麻雀周围的个体接收到信号后将会离开危险区域, 重新到下一个区域继续搜寻食物。在所有麻雀的安全值小于预警值后, 麻雀位置的更新将应用公式(3)中等式(b)。
同时, 加入者的位置也会随发现者的位置变化而变化, 加入者位置更新的算法原理如式(4)所示:
| Xt+1i,j=(Q⋅exp(−Xworst−Xti,ji2),如果i>n/2,Xt+1p+|Xti,j−Xt+1p|⋅A+⋅L, 否则,), | (4) |
Xp是目前发现者在食物搜索中占据的最佳位置。Xworst表示搜索范围中最差的位置。A表示一个具有1行n列的矩阵。矩阵中的所有元素值取为1或–1中的随机数。A+=AT(AAT)–1。当i > (n/2)时, 代表第i个加入者的适应度较低, 它将飞往其他地点搜寻食物。
在麻雀种群觅食的过程中, 威胁是随机出现的, 且所有麻雀在觅食过程中都有可能注意到威胁。该算法的原理通过式(5)实现:
| Xt+1i,j={Xtbest+β·|Xti,j−Xtbest|,如果fi>fg,Xti,j+K·(|Xti,j−Xworst|(fi−fw)+ε), 如果fi=fg, | (5) |
Xbest是整个搜索范围内的最佳位置。β是均值为0、方差为1的正态分布随机数步长控制参数。K(K∈[–1, 1])。fi是麻雀的当前适应度值。fg和fw分别是当前范围内的最佳和最差适应度值。ε是最小的常数。简单来说, 当麻雀的适应度达到最佳适应度时, fi > fg代表当前麻雀i易于受到危险的威胁, fi=fg代表当前麻雀i已经意识到了来自危险的威胁, 其将会向较为安全的麻雀所在区域靠拢。
1.2 混沌映射麻雀搜索优化算法(Sine-SSA)在麻雀搜索优化算法中, 相对于传统的群智能优化算法, 其确实在一定程度上减轻了群智能优化算法容易陷入局部最优解的问题, 但与粒子群算法[37]、人工蜂群算法[38]、蚁群优化算法[39]等众多群智能优化算法相同, 它们存在一个普遍问题[40-41], 就是算法最初, 种群在初始化时, 每个个体的位置是随机分布的, 这就有可能导致个体分布不均匀, 进而复现局部最优的问题。因此, 为了实现种群中个体的更均匀分布, 我们认为在种群初始化时添加一个优化过程, 以将种群中每个个体的位置充分打乱, 使其分布更加均匀。因此, 本文通过引入Sine混沌映射来使麻雀搜索优化算法的种群充分初始化。
Sine混沌映射是一种单峰映射, 可以通过方程式(6)表达:
| xk+1=αsin(πxk), | (6) |
x是迭代序列值。k[k∈[0, +∞)]是一个整数, α是一个系统参数。
在模型开发期间, 将数据导入SSA-BP腐蚀速率预测模型后, 所得到的预测数据与实际数据的误差出现了一些问题, 在指定特定数量的训练样本时, 模型预测的误差大量上升, 最高误差近8%。
最初, 我们认为可能问题出现在腐蚀数据与环境数据时间轴对应中, 但是经过重新调整匹配后, 这一现象仍然存在, 而且误差相较于调整前有所上涨, 因此确定问题并非出在数据中。在算法运行初期, 由于麻雀搜索优化算法自身有一定的减轻陷入局部最优问题的能力, 群智能优化算法所存在的普遍问题被忽略, 因此, 模型优化的目标就来到了对种群进行充分初始化。因此, 本文将Sine混沌映射融入算法, 使得麻雀种群可以充分初始化, 充分打乱位置。该方法可以减少提高种群分布的均匀性。
2 Sine-SSA-BP腐蚀速率预测模型搭建 2.1 数据采集 2.1.1 实验材料所有来自实际海上测试的腐蚀速率数据都用于模型训练。表 1展示了实验用钢Q345qENH(以下简称Q345)的基本元素组成。将钢板切割成10 mm×10 mm× 10 mm。铜线被焊接到10 mm×10 mm的正方形表面上。使用透明水晶胶封装侧面及顶部焊接铜线的面。只有底部10 mm×10 mm的工作面暴露在外。之后, 依次用目数为160、400、800、1 600和2 000的砂纸将工作表面抛光至镜面。
| C | Si | Mn | P | S | Cr | Ni | Cu | Fe |
| 0.17 | 0.19 | 1.52 | 0.025 | 0.001 | 0.029 | 0.014 | 0.013 | Balance |
课题组自研了一种腐蚀传感器, 传感器在放入海水中后, 可以自动记录材料的腐蚀速率, 并存储在设备内。设备规格如表 2所示。3个电极组成了测试装置。利用腐蚀电化学方法来测量通过在指定环境、指定材料的腐蚀速率。腐蚀传感器的原理是使用电化学测试中的弱极化曲线[42]测试方法来确定材料的实时腐蚀速率。测试中的所有数据均来自科考船实海测试。利用腐蚀传感器实时监测走航水中Q345钢的腐蚀速率, 并与船载CTD、PH、溶解氧、氮传感器所采集的环境参数数据进行对应, 最终得到的数据会被导入金属腐蚀速率预测模型进行学习训练, 并划分部分数据进行验证, 以对模型的预测准确度进行评估。
| 工作环境 | 电流精确度 | 腐蚀速率精确度 | 电源 | 尺寸 | 数据测试间隔 |
| 深度为4 m的走航水 | 1 μA/cm2 | 0.01 mm/a | 220 V AC | 290 mm×210 mm× 80 mm | 60 s |
在BP神经网络中, 多层感知(multi layer perceptron, MLP)是最常用的神经网络模型之一[43], 模型包含输入层、输出层和隐含层, 人为确定输入层的数量和内容后, 由神经网络模型输入隐含层, 在隐含层中不断调整输入层的权重, 最终确定适应度最高的权重, 并将最终计算结果传递到输出层。在本研究中, 输入层是在海洋环境中对腐蚀速率产生影响的环境因素。基于航次所收集的数据, 输入层包含电导率、pH、温度、盐度、溶解氧和氮。海洋环境中的Q345钢腐蚀速率是输出层。隐含层的数量根据经验公式[44]由输入层和输出层计算, 再进行各隐含层数量误差的测试, 最终筛选出误差最低的隐含层数量, 计算公式如式(7)所示:
| L=√γ+δ+φ, | (7) |
L是隐含层的数量, γ和δ分别是输入层和输出层的数量。φ(φ∈[0, 10])是校正系数。在将所采集的数据整理导入测试后, 对比不同数量隐含层的误差, 隐藏层的数量及其相应的MSE(mean square error, 均方误差)计算如图 1所示。
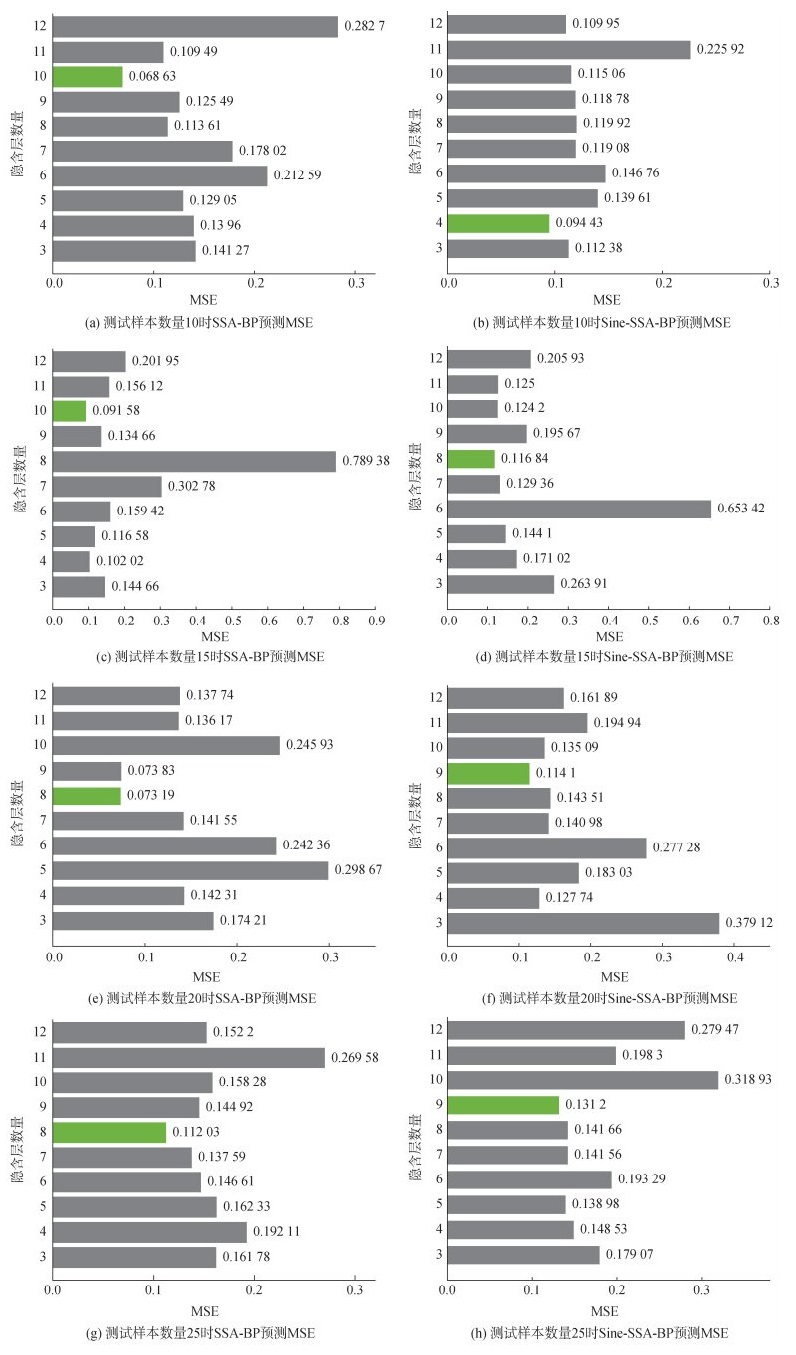 |
| 图 1 SSA-BP腐蚀速率预测模型(左)和Sine-SSA-BP腐蚀速率预测模型在隐含层数量为10 (a, b), 15 (c, d), 20 (e, f), 25 (g, h)下的MSE Fig. 1 Mean square error (MSE) of sparrow search optimization algorithm-back propagation (SSA-BP) corrosion rate prediction model (left) and Sine-SSA-BP corrosion rate prediction model with 10 (a, b), 15 (c, d), 20 (e, f), and 25 (g, h) hidden layers |
本研究中所建立的BP神经网络MLP模型的架构图如图 2所示, 输入层为影响海洋中金属腐蚀速率的因素, 输出层为金属腐蚀速率。对模型进行多次调试后, 训练次数确定为1 000次, 学习速率设置为0.01, 训练最小误差设定为0.000 1。SSA优化算法中, 初始种群规模设定为30, 最大迭代数设定为50, 安全值设定为0.6, 发现者比例设定为0.7, 加入者比例设定为0.3, 察觉到危险的麻雀数量比例设定为0.2。
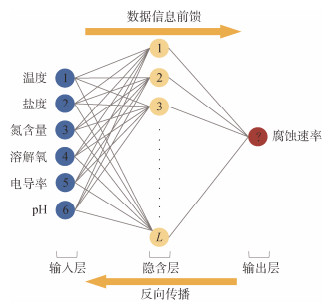 |
| 图 2 BP神经网络腐蚀速率预测模型架构 Fig. 2 Architecture of BP neural network corrosion rate prediction model |
本实验使用了在蓝海101号自然科学基金委渤黄海秋季航次所收集的数据(航次编号NORC2022-01)。航次收集到腐蚀速率数据21 469个, CTD等环境参数数据8 746个。CTD等环境参数数据和腐蚀速率数据与数据采集时间有关。根据工作人员记录显示, 设备时钟与船载CTD时钟相差2 min。因此, 在处理过程中, 所收集到的腐蚀数据与CTD等环境参数数据相对应时, 应向前错开2 min。采用的CTD等环境参数数据所对应的海深为4 m。根据时间轴进行对应后, 将本次测试学习的数据进行了整理。在测试中, BP腐蚀速率预测模型, SSA-BP腐蚀速率预测模型、Sine-SSA-BP腐蚀速率预测模型同时导入数据进行测试, 提高测试效率, 同时便于作对比。图 3是模型学习测试的整体架构图。
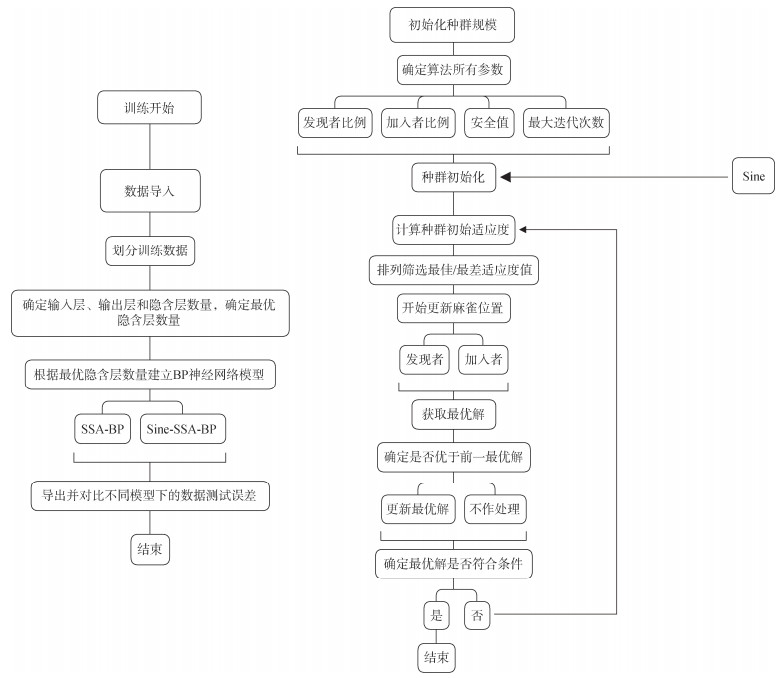 |
| 图 3 整体训练测试架构 Fig. 3 Training and testing architecture |
在已有的研究中[45-46], BP神经网络模型误差的检验与验证往往仅对一个数据集划分固定数量的学习和测试样本来进行预测对比, 忽略了当预测样本发生变化时所带来的预测结果变化, 因此, 为了避免此问题, 初步测试实验分别将测试样本确定为10个、15个、20个和25个, 在进一步测试中, 测试样本的数量将由5个逐个增加到30个。
测试结束后, 分别收集BP、SSA-BP、Sine-SSA-BP腐蚀速率预测模型对测试样本集的每个腐蚀速率的预测值, 与真实值进行比较, 计算与真实值间的误差, 分别绘制3种预测模型在测试样本数量分别为10、15、20、25个时的误差情况图、预测值与真实值对照图, 分别如图 4、图 5所示。同时, 为了更加直观地对误差情况进行对比, 分别计算三种模型预测结果的平均绝对误差、均方误差、均方根误差和平均绝对百分比误差, 其计算方法如下所示:
 |
| 图 4 测试样本数量为10(a), 15(b), 20(c)和25(d)时BP、SSA-BP、Sine-SSA-BP腐蚀速率预测模型的学习预测误差 Fig. 4 Learning prediction errors of BP, SSA-BP, and Sine-SSA-BP corrosion rate prediction models with 10 (a), 15 (b), 20 (c), and 25 (d) test sample sizes |
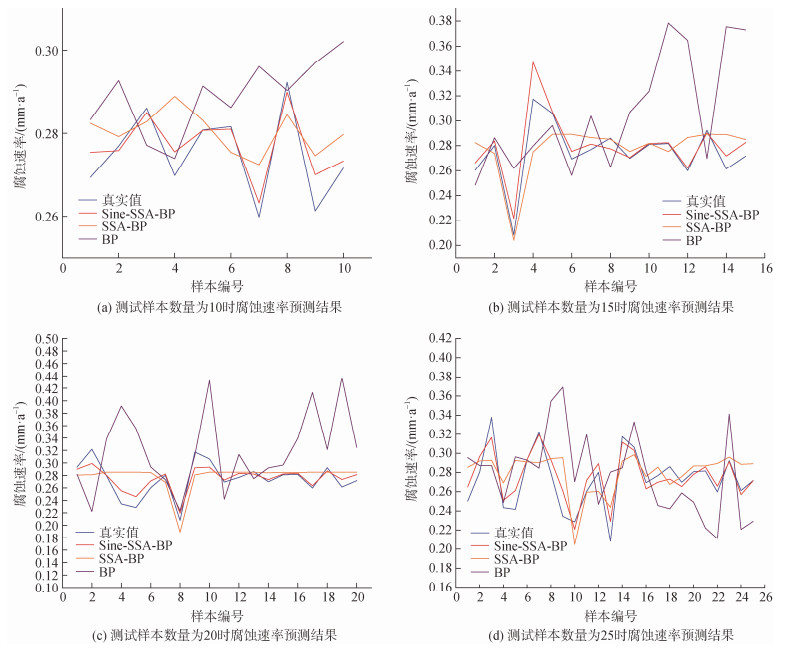 |
| 图 5 测试样本数量分别为10(a)、15(b)、20(c)和25(d)时BP、SSA-BP、Sine-SSA-BP腐蚀速率预测模型的预测值与真实值比较 Fig. 5 Comparison of predicted values and true values of BP, SSA-BP, and Sine-SSA-BP corrosion rate prediction models with test sample sizes of 10 (a), 15 (b), 20 (c), and 25 (d), respectively |
MAE: Mean Absolute Error, 意为平均绝对误差, 计算方法为计算误差后取绝对值, 计算其平均值, 能够最直观地反映误差情况, 该值越小, 则误差越小。计算方法如式(8)所示:
| MAE=1nn∑i=1|yi−ˆyi|. | (8) |
MSE: Mean Square Error, 意为均方误差, 计算方法为计算误差后, 取其平方和, 计算其平均值, 该值越小, 则误差越小, 计算方法如式(9)所示:
| MSE=1nn∑i=1(yi−ˆyi)2. | (9) |
RMSE: Root Mean Square Error, 意为均方根误差, 是MSE的算数平方根, 该值可以表示预测值与实际值的离散化程度[47], 该值越小, 则误差越小, 计算方法如式(10)所示:
| RMSE=√1nn∑i=1(yi−ˆyi)2. | (10) |
MAPE: Mean Absolute Percentage Error, 意为平均绝对百分比误差, 计算方法为误差率的绝对值求和后取平均值, 该值可以表示测试模型的整体误差[47], 该值越小, 则误差越小其计算方法如式(11)所示:
| MAPE=1nn∑t=1|At−FtAt|. | (11) |
计算结果如表 3所示。
| 样本数量 | 模型 | MAE | MSE | RMSE | MAPE |
| 10 | BP | 0.020 573 | 0.000 509 66 | 0.022 576 | 7.61% |
| SSA-BP | 0.008 805 5 | 0.000 105 74 | 0.010 283 | 3.25% | |
| Sine-SSA-BP | 0.003 08 | 0.000 016 718 | 0.004 089 | 1.15% | |
| 15 | BP | 0.046 844 | 0.003 562 3 | 0.059 685 | 17.53% |
| SSA-BP | 0.013 74 | 0.000 324 03 | 0.018 001 | 4.96% | |
| Sine-SSA-BP | 0.006 728 | 0.000 098 713 | 0.009 935 | 2.47% | |
| 20 | BP | 0.061 228 | 0.006 805 5 | 0.082 495 | 23.10% |
| SSA-BP | 0.019 751 | 0.000 625 08 | 0.025 002 | 7.48% | |
| Sine-SSA-BP | 0.008 92 | 0.001 346 2 | 0.011 603 | 3.31% | |
| 25 | BP | 0.061 279 | 0.005 558 8 | 0.074 557 | 23.67% |
| SSA-BP | 0.020 801 | 0.000 681 42 | 0.026 104 | 7.93% | |
| Sine-SSA-BP | 0.009 192 | 0.000 135 51 | 0.011 641 | 3.53% |
为了更详细对比SSA-BP和Sine-SSA-BP腐蚀速率预测模型对于测试样本数量变化的误差提升程度, 研究中将测试样本的数量由5个逐个增加至30个, 并计算每次测试的MAPE, 绘制对比图, 结果如图 6所示。
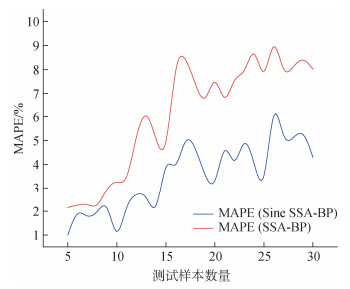 |
| 图 6 测试样本数量由5上升到30时SSA-BP、Sine-SSA-BP腐蚀速率预测模型的MAPE变化 Fig. 6 Mean absolute percentage error (MAPE) changes in the SSA-BP and Sine-SSA-BP corrosion rate prediction models as the number of test samples increases from 5 to 30 |
在测试方法上, 为了防止模型预测结果的随机性, 分别在个人计算机平台及中科曙光超级计算机平台进行测试, 对比验证所得训练结果。
3 测试结果图 4是在多次进行学习计算并且所得数据误差稳定之后, 使用学习预测结果创建的。腐蚀速率误差=该样本腐蚀速率真实值–该样本腐蚀速率预测值。SSA-BP腐蚀速率预测模型和Sine-SSA-BP腐蚀速率预测模型的误差显著低于BP腐蚀速率预测模型, 且Sine-SSA-BP腐蚀速率预测模型优于SSA-BP腐蚀速率预测模型。图 5展示了3个模型的预期结果与实际值之间的比较。Sine-SSA-BP腐蚀速率预测模型和SSA-BP腐蚀速率预测模型的结果都非常接近实验中任何数量的测试样本的实际值。Sine-SSA-BP腐蚀速率预测模型以少量样本预测大量样本时, 随着测试样本数量的增加, 其能够更好地抵御误差快速上升的问题。表 3和图 6提供了初步的证据。
根据预测结果分别计算3种模型的MAE、MSE、RMSE和MAPE, 结果如表 3所示。BP腐蚀速率预测模型的预测MAPE为7.611 2%、17.532 7%、23.095 6%、23.665 9%, SSA-BP腐蚀速率预测模型的预测MAPE分别为3.251 7%、4.955 4%、7.480 4%、7.926 6%, Sine-SSA-BP腐蚀速率预测模型的预测MAPE分别为1.145 5%、2.469 6%、3.311%、3.526 4%, 预测准确度Sine-SSA-BP > SSA-BP > BP。为了确认上文中的初步判断, 本文将不同数量的测试样本重新输入到先前学习的样本中, 在所有数据中随机抽取30个测试样本, 测试样本数量从5逐渐增加到30。并且本文在不同数量的测试样本下测试并计算了SSA-BP腐蚀速率预测模型和Sine-SSA-BP腐蚀速率预测模型的MAPE, 如图 6所示。Sine-SSA-BP腐蚀速率预测模型的平均MAPE值为3.500 2%, SSA-BP腐蚀速率预测模型的平均MAPE值为6.090 0%, 而且在每一个样本数量情况下, Sine-SSA-BP腐蚀速率预测模型预测MAPE均低于SSA-BP。
4 结论(1) Sine混沌映射可以将群智能优化算法中的种群充分初始化, 避免群智能优化算法所普遍存在的易陷入局部最优解的问题, 提高群智能优化算法搜寻最优解的准确度。在本文研究中, Sine-SSA-BP腐蚀速率预测模型相较于SSA-BP腐蚀速率预测模型预测精确度提升明显, 当测试样本数量分别为10、15、20、25时, Sine-SSA-BP腐蚀速率预测模型平均绝对百分比误差MAPE为1.145 5%、2.469 6%、3.311%、3.526 4%, 均远优于SSA-BP、BP腐蚀速率预测模型。
(2) 在测试样本数量随机变化时, Sine-SSA-BP腐蚀速率预测模型的MAPE均优于SSA-BP腐蚀速率预测模型, 验证了其对于Q345钢海洋腐蚀速率预测的可靠性, 为海洋金属腐蚀速率的预测提供了一种新的方法。
致谢: 本研究的资料及样品采集得到国家自然科学基金委员会共享航次计划项目(项目批准号: 42149901)的资助。该航次(航次编号: NORC2022-01)由“蓝海101”号科考船实施, 在此致谢。
| [1] |
HOU B R, LI X G, MA X M, et al. The cost of corrosion in China[J]. NPJ Materials Degradation, 2017, 1(1): 4. DOI:10.1038/s41529-017-0005-2 |
| [2] |
SONG D, HAO J, YANG F L, et al. Corrosion behavior and mechanism of Cr-Mo alloyed steel: Role of ferrite/bainite duplex microstructure[J]. Journal of Alloys and Compounds, 2019, 809: 151787. DOI:10.1016/j.jallcom.2019.151787 |
| [3] |
ZHANG J, WANG J, ZHANG B B, et al. Fabrication of anodized superhydrophobic 5083 aluminum alloy surface for marine anti-corrosion and anti-biofouling[J]. Journal of Oceanology and Limnology, 2020, 38(4): 1246-1255. DOI:10.1007/s00343-020-0036-3 |
| [4] |
YANG D, HUANG Y L, LI J Q, et al. Corrosion behavior of Q235B carbon steel in simulated seawater pumped storage system under operational conditions[J]. Journal of Oceanology and Limnology, 2020, 38(5): 1537-1547. DOI:10.1007/s00343-020-0043-4 |
| [5] |
高杨, 孙虎元, 孙立娟. X80管线钢在黄海海水中的初期腐蚀行为[J]. 腐蚀与防护, 2018, 39(5): 327-331, 358. GAO Yang, SUN Huyuan, SUN Lijuan. Initial corrosion behavior of X80 pipeline steel in the Yellow Sea[J]. Corrosion and Protection, 2018, 39(5): 327-331, 358. |
| [6] |
WANG Z F, LIU J R, WU L X, et al. Study of the corrosion behavior of weathering steels in atmospheric environments[J]. Corrosion Science, 2013, 67: 1-10. DOI:10.1016/j.corsci.2012.09.020 |
| [7] |
MORCILLO M, DÍAZ I, CANO H, et al. Atmospheric corrosion of weathering steels. Overview for engineers. Part I: Basic concepts[J]. Construction and Building Materials, 2019, 213: 723-737. DOI:10.1016/j.conbuildmat.2019.03.334 |
| [8] |
WU W, CHENG X Q, ZHAO J B, et al. Benefit of the corrosion product film formed on a new weathering steel containing 3% nickel under marine atmosphere in Maldives[J]. Corrosion Science, 2020, 165: 108416. DOI:10.1016/j.corsci.2019.108416 |
| [9] |
WANG P J, MA L W, CHENG X Q, et al. Influence of grain refinement on the corrosion behavior of metallic materials: A review[J]. International Journal of Minerals, Metallurgy and Materials, 2021, 28: 1112-1126. |
| [10] |
HAO L, ZHANG S X, DONG J H, et al. Atmospheric corrosion resistance of MnCuP weathering steel in simulated environments[J]. Corrosion Science, 2011, 53(12): 4187-4192. DOI:10.1016/j.corsci.2011.08.028 |
| [11] |
MORCILLO M, DÍAZ I, CHICO B, et al. Weathering steels: From empirical development to scientific design. A review[J]. Corrosion Science, 2014, 83: 6-31. DOI:10.1016/j.corsci.2014.03.006 |
| [12] |
MEARS R B, EVANS U R. Corrosion at contact with glass[J]. Transactions of the Faraday Society, 1934, 30: 417-423. DOI:10.1039/tf9343000417 |
| [13] |
CHANG H Y, PARK Y S, HWANG W S. Initiation modeling of crevice corrosion in 316L stainless steels[J]. Journal of Materials Processing Technology, 2000, 103(2): 206-217. DOI:10.1016/S0924-0136(00)00462-3 |
| [14] |
PICKERING H W, CHO K, NYSTROM E. Microscopic and local probe method for studying crevice corrosion and its application to iron and stainless steel[J]. Corrosion Science, 1993, 35(1/4): 775-783. |
| [15] |
XU Y, PICKERING H W. The initial potential and current distributions of the crevice corrosion process[J]. Journal of the Electrochemical Society, 1993, 140(3): 658. DOI:10.1149/1.2056139 |
| [16] |
SZKLARSKA-SMIALOWSKA Z, MANKOWSKI J. Crevice corrosion of stainless steels in sodium chloride solution[J]. Corrosion Science, 1978, 18(11): 953-960. DOI:10.1016/0010-938X(78)90030-6 |
| [17] |
PELLIER J, GERINGER J, FOREST B. Fretting-corrosion between 316L SS and PMMA: Influence of ionic strength, protein and electrochemical conditions on material wear. Application to orthopaedic implants[J]. Wear, 2011, 271(9/10): 1563-1571. |
| [18] |
AOYAMA T, SUGAWARA Y, MUTO I, et al. In situ monitoring of crevice corrosion morphology of type 316L stainless steel and repassivation behavior induced by sulfate ions[J]. Corrosion Science, 2017, 127: 131-140. DOI:10.1016/j.corsci.2017.08.005 |
| [19] |
SHOJAEI E, MIRJALILI M, MOAYED M H. The influence of the crevice induced IR drop on polarization measurement of localized corrosion behavior of 316L stainless steel[J]. Corrosion Science, 2019, 156: 96-105. DOI:10.1016/j.corsci.2019.04.030 |
| [20] |
MU J, LI Y Z, WANG X. Crevice corrosion behavior of X70 steel in NaCl solution with different pH[J]. Corrosion Science, 2021, 182: 109310. DOI:10.1016/j.corsci.2021.109310 |
| [21] |
GUENTHER J, WALKER-SMITH G, WARÉN A, et al. Fouling-resistant surfaces of tropical sea stars[J]. Biofouling, 2007, 23(6): 413-418. DOI:10.1080/08927010701570089 |
| [22] |
MYAN F W Y, WALKER J, PARAMOR O. The interaction of marine fouling organisms with topography of varied scale and geometry: a review[J]. Biointerphases, 2013, 8(1): 30. DOI:10.1186/1559-4106-8-30 |
| [23] |
HUNSUCKER K Z, RALSTON E. Marine biofouling and its prevention[J]. Marine Technology Society Journal, 2017, 51(2): 3. DOI:10.4031/MTSJ.51.2.7 |
| [24] |
XIAO J, HAN J, ZHANG F, et al. Numerical simulation of crystallization fouling: taking into account fouling layer structures[J]. Heat Transfer Engineering, 2017, 38(7/8): 775-785. |
| [25] |
ZHOU Z Y, POURHASHEM S, WANG Z G, et al. Distinctive roles of graphene oxide, ZnO quantum dots, and their nanohybrids in anti-corrosion and anti-fouling performance of waterborne epoxy coatings[J]. Chemical Engineering Journal, 2022, 439: 135765. DOI:10.1016/j.cej.2022.135765 |
| [26] |
LI X G, ZHANG D W, LIU Z Y, et al. Materials science: Share corrosion data[J]. Nature, 2015, 527(7579): 441-442. DOI:10.1038/527441a |
| [27] |
YAMASHITA M, MIYUKI H, MATSUDA Y, et al. The long term growth of the protective rust layer formed on weathering steel by atmospheric corrosion during a quarter of a century[J]. Corrosion Science, 1994, 36(2): 283-299. DOI:10.1016/0010-938X(94)90158-9 |
| [28] |
PAIK J K, THAYAMBALLI A K, PARK Y I, et al. A time-dependent corrosion wastage model for seawater ballast tank structures of ships[J]. Corrosion Science, 2004, 46(2): 471-486. DOI:10.1016/S0010-938X(03)00145-8 |
| [29] |
MELCHERS R E. Modeling of marine immersion corrosion for mild and low-alloy steels—Part 2: Uncertainty estimation[J]. Corrosion, 2003, 59(4): 335-344. DOI:10.5006/1.3277565 |
| [30] |
CHERNOZHUKOV V, HONG H. Likelihood estimation and inference in a class of nonregular econometric models[J]. Econometrica, 2004, 72(5): 1445-1480. DOI:10.1111/j.1468-0262.2004.00540.x |
| [31] |
ABROUGUI K, GABSI K, MERCATORIS B, et al. Prediction of organic potato yield using tillage systems and soil properties by artificial neural network (ANN) and multiple linear regressions (MLR)[J]. Soil and Tillage Research, 2019, 190: 202-208. DOI:10.1016/j.still.2019.01.011 |
| [32] |
MÉNDEZ-FIGUEROA H, COLORADO-GARRIDO D, HERNANDEZ-PEREZ M, et al. Neural networks and correlation analysis to improve the corrosion prediction of SiO2-nanostructured patinated bronze in marine atmospheres[J]. Journal of Electroanalytical Chemistry, 2022, 917: 116396. DOI:10.1016/j.jelechem.2022.116396 |
| [33] |
LIU J X, ZHANG L, LI Y F, et al. Deep residual convolutional neural network based on hybrid attention mechanism for ecological monitoring of marine fishery[J]. Ecological Informatics, 2023, 77: 102204. DOI:10.1016/j.ecoinf.2023.102204 |
| [34] |
ZHANG X X, GAO Z M, XIU Y, et al. Image analysis of synthesized corrosion products applied to in-situ analysis of Q235 steel under simulated marine atmosphere[J]. International Journal of Electrochemical Science, 2019, 14(2): 1713-1724. DOI:10.20964/2019.02.76 |
| [35] |
MA L, DONG H. Prediction of corrosion rate of Q235 steel under the marine environment[C]//IOP Conference Series: Earth and Environmental Science. IOP Publishing, 2018, 170(3): 032130.
|
| [36] |
GHAREHCHOPOGH F S, NAMAZI M, EBRAHIMI L, et al. Advances in sparrow search algorithm: a comprehensive survey[J]. Archives of Computational Methods in Engineering, 2023, 30(1): 427-455. DOI:10.1007/s11831-022-09804-w |
| [37] |
杨万里, 周雪婷, 陈孟娜. 基于Logistic映射的新型混沌简化PSO算法[J]. 计算机与现代化, 2019(12): 15-20. YANG Wanli, ZHOU Xueting, CHEN Mengna. New chaotic simplified particle swarm optimization algorithm based on Logistic mapping[J]. Computer and Modernization, 2019(12): 15-20. |
| [38] |
匡芳君, 徐蔚鸿, 金忠. 自适应Tent混沌搜索的人工蜂群算法[J]. 控制理论与应用, 2014, 31(11): 1502-1509. KUANG Fangjun, XU Weihong, JIN Zhong. Artificial bee colony algorithm based on self-adaptive Tent chaos search[J]. Control Theory & Application, 2014, 31(11): 1502-1509. |
| [39] |
刘明霞, 游晓明, 刘升. 基于聚度的自适应动态混沌蚁群算法[J]. 计算机工程与应用, 2019, 55(3): 15-22. LIU Mingxia, YOU Xiaoming, LIU Sheng. Adaptive dynamic chaotic ant colony algorithm based on degree of aggregation[J]. Computer Engineering and Applications, 2019, 55(3): 15-22. |
| [40] |
IBRAHIM R A, ABD ELAZIZ M, LU S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization[J]. Expert Systems With Applications, 2018, 108: 1-27. DOI:10.1016/j.eswa.2018.04.028 |
| [41] |
TENG Z J, LV J L, GUO L W. An improved hybrid grey wolf optimization algorithm[J]. Soft Computing, 2019, 23: 6617-6631. DOI:10.1007/s00500-018-3310-y |
| [42] |
SUN H Y. Techniques for Corrosion Monitoring (Electrochemical polarization technique based on the nonlinear region weak polarization curve fitting analysis), Second Edition[M]. Woodhead Publishing, 2021: 79-98.
|
| [43] |
TANTY R, DESMUKH T S. Application of artificial neural network in hydrology—A review[J]. International Journal of Engineering & Technical Research, 2015, 4(6): 184-188. |
| [44] |
WANG F L, LIU G L, WANG J Q. An unconstrainted optimization method based on BP neural network[C]// 2010 International Conference on E-Product E-Service and E-Entertainment. IEEE, 2010: 1-4.
|
| [45] |
李海涛, 袁森. 基于遗传算法和BP神经网络的海洋工程材料腐蚀预测研究[J]. 海洋科学, 2020, 44(10): 33-38. LI Haitao, YUAN Sen. Corrosion prediction of marine engineering materials based on genetic algorithm and BP neural network[J]. Marine Sciences, 2020, 44(10): 33-38. |
| [46] |
肖荣鸽, 王栋, 王勤学. 基于ASO-BP神经网络的海底油气管道腐蚀速率预测[J]. 化学工业与工程, 2022, 39(6): 109-116. XIAO Rongge, WANG Dong, WANG Qinxue. Prediction of corrosion rate of submarine oil and gas pipelines based on ASO-BP neural network[J]. Chemical Industry and Engineering, 2022, 39(6): 109-116. |
| [47] |
肖荣鸽, 靳帅帅. 基于WOA-BP算法的海底管道腐蚀速率预测[J]. 海洋科学, 2022, 46(6): 116-123. XIAO Rongge, JIN Shuaishuai. Prediction of the submarine pipeline corrosion rate based on the whale optimization algorithm and back propagation (WOA-BP) algorithm[J]. Marine Sciences, 2022, 46(6): 116-123. |
 2024, Vol. 48
2024, Vol. 48


