文章信息
- 张瑞, 类淑河, 管长龙, 王红. 2015.
- ZHANG Rui, LEI Shu-He, GUAN Chang-Long, WANG Hong. 2015.
- 波流信号交叉谱估计方法比较
- COMPARISON AMONG METHODS FOR CROSS-SPECTRA ESTIMATION BETWEEN WAVE AND CURRENT
- 海洋与湖沼, 46(4): 725-731
- Oceanologia et Limnologia Sinica, 46(4): 725-731.
- http://dx.doi.org/10.11693/hyhz20141100322
-
文章历史
- 收稿日期:2014-11-17
- 改回日期:2015-02-13
2. 中国海洋大学物理海洋实验室 青岛 266100
2. Key Laboratory of Physical Oceanography, Ocean University of China, Qingdao 266100, China
海洋中波浪和海流几乎总是同时存在。大到钱塘江的怒潮,小到近海浮游生物的“随波逐流”都与波流相互作用有密不可分的关系(高山,2003)。理论分析、数值模拟、实验研究和现场观测等多种手段被广泛用于研究波流相互作用。一般来说,波浪主要通过海面风应力、波致辐射应力和底应力等影响海流。海流则主要通过水深变化和随时空变化的流场影响波浪。两者相互作用的影响极为广泛,例如,流使波浪及波浪谱变形、流浪场的相互作用、波和流影响结构物载荷、运动及被动标量运输等(王涛等,1999)。通过波流相互作用的深入讨论,可以更好地解释海洋动力现象及其演变过程。
交叉谱(cross-spectrum)可视为互相关函数的傅里叶变换。作为一种统计工具,它可用于分析不同时间序列对应频率分量之间的相互关系。由交叉谱得到的凝聚谱可刻画两个序列在频域内的相关性。在物理海洋方面,这些统计工具尽管已被应用于海流的相互作用研究,但是用于探讨波流相互作用的研究工作仍相对较少。袁耀初等(2002)基于南海东北部锚定测流站450m以浅长达77d的Long Ranger ADCP测流资料以及2000m与2300m处长达7个月左右的测流资料,通过加窗周期图法进行交叉谱估计,发现2000m与2300m流速时间序列在周期为2个多月和1个多月的振动有很好的相关性,100m与2300m流速时间序列在周期为15.5d和2d等的振动有很好的相关性。McKone(2003)基于IAS(Intra-Americas Sea)不同地点的NLOM模拟海流数据,采用Welch方法和MTM方法进行交叉谱估计,发现年周期振动均存在强烈的相关性,其中一部分地点之间在9、6、4、2.4个月周期振动也存在相关性,而采用带通滤波器滤掉年周期信号后,4个月和2.4个月已不存在相关性,6个月的相关性程度也明显减弱。
实际观测中,得到的时间序列长度是有限且离散的。交叉谱分析把有限长度数据得到的交叉谱估计作为真实谱的近似。交叉谱估计方法大致可分为非参数方法和参数方法两类。非参数估计方法包括周期图法(Jenkins et al,1968)、Welch方法(Welch,1967; Carter,1987)、多窗谱方法(Multitaper Method,简称“MTM方法”)(Thomson,1982)、最小方差无失真响应方法(The Minimum Variance Distortionless Response Method,简称“MVDR方法”)(Benesty et al,2005)等。参数估计方法主要针对AR模型、MA模型、ARMA模型等进行参数建模,具体的方法包括最大熵估计方法(Strand ,1977)、协方差法(Kay,1988)等。参数交叉谱估计方法虽然具有一些优势如提高了频率分辨率等,但其统计性能很难从数学上给出解析式,相比之下非参数估计方法应用更加广泛。一种好的谱估计方法不一定对任何场合都有良好的估计性能,应依据具体应用实例选择恰当的方法(黄建国,1991)。采用多种方法进行交叉谱估计并对比选择,可以避免对伪峰的误识别,有望给出更合理的结果。
本文主要目标是寻找适合于波流信号的交叉谱估计方法。第一部分介绍三种主要的非参数交叉谱估计方法,即Welch方法、MTM方法和MVDR方法。第二部分利用数值模拟,从相关信号的检测能力和分辨能力两个方面对三种方法进行了比较。第三部分给出风浪实验数据凝聚谱估计,并对三种方法的估计结果进行分析比较。第四部分给出相应的结论与讨论。
1 交叉谱及其估计方法 1.1 交叉谱及相关概念设二维零均值平稳时间序列{Xt,Yt},t = 0,±1,±2,...,则Xt与Yt的互相关函数定义为
| ${R_{XY}}(\tau ) = E[{X_t}{Y_{t + \tau }}]$ \quad $\tau = 0, \pm 1, \pm 2, \cdots $ | (1) |
其中E[]表示数学期望。
若$\sum\limits_{s = - \infty }^\infty {\left| {{R_{XY}}(\tau )} \right|} < \infty $,则非标准化的交叉谱密度函数(简称“交叉谱”)定义为
| ${S_{XY}}(f) = \sum\limits_{\tau = - \infty }^\infty {{R_{XY}}(\tau ){e^{ - i2\pi f\tau }}} $ | (2) |
交叉谱一般是复值的,单位为(Xt的单位)(Yt的单位)/(频率单位Hz)。写成极坐标形式为
| ${S_{XY}}(f) = {\alpha _{XY}}(f){e^{i{\phi _{XY}}(f)}}$ | (3) |
其中αXY(f)为交振幅谱(cross-amplitude spectrum),表示Xt、Yt在频率f上的相关程度。
为排除量纲的影响,对交振幅谱标准化并引入相干谱(coherency spectrum)。记Xt的单谱为SXX(f),Yt的单谱为SYY(f),则两信号的相干谱可表示为
| ${w_{XY}}(f) = \left| {\frac{{{S_{XY}}(f)}}{{{{\{ {S_{XX}}(f){S_{YY}}(f)\} }^{1/2}}}}} \right|$ | (4) |
相干谱表征了Xt、Yt在频率f上的相关程度大小,在频域内刻画了两个序列的相关性。粗略地讲,相干谱为频域上的相关系数。
实际应用中,多采用相干谱的平方表示频域内信号之间的相关性,称为凝聚谱(magnitude-squared coherence),其表达式为:
| ${\rm{Msc}}(f) = \frac{{{{\left| {{S_{XY}}(f)} \right|}^2}}}{{{S_{XX}}(f){S_{YY}}(f)}}$ | (5) |
显然,相干谱与凝聚谱都是无量纲的,在[0,1]区间内取值。该值越接近于1,表明二者在相应频率分量上的相关性越强。特别地,若wXY(f)=0或Msc(f)=0,说明Xt、Yt在频率f上是不相关的; 若对所有频率均有wXY(f)=1或Msc(f)=1,说明Xt和Yt 在频域上是完全相关的。
1.2 交叉谱估计类似于单个信号的谱估计,周期图法是估计交叉谱的基本方法,但其估计方差往往较大,且容易造成频谱泄漏。
Welch方法是经典的交叉谱估计方法。其基本思想是: 先对数据进行分段(允许其间有重叠),然后对每一段数据进行加窗交叉谱估计,最后对各段交叉谱求平均。这种方法对周期图法进行了改进: 一方面通过分段估计再取平均,提高了交叉谱估计的自由度,从而减小了误差; 另一方面通过加窗减少泄露,从而降低了估计偏差。
MTM方法的基本思想是以一簇数据窗代替单一数据窗,对每一数据窗所构成的时间序列进行傅里叶变换,再加权平均。数据窗可采用正交离散扁长的球体序列(Discrete Prolate Spheroidal Sequences)。与Welch方法相比,MTM方法不需要主观定义分辨率,而且交叉谱估计的自由度大于2,有效地减小了估计的误差和偏差。
MVDR方法(Capon,1969)在阵列信号中有广泛的应用,其基本思想是保证期望方向上的阵列响应,同时减少阵列输出中的干扰,从而改善天线阵列的分辨率。MVDR方法亦可用于交叉谱和凝聚谱估计,且比Welch方法分辨率更高(Benesty et al,2005)。特别地,可选取傅里叶矩阵这一特殊的酉阵进行凝聚谱估计。
若已估计出交叉谱和单谱,可进一步估计交振幅谱、相干谱和凝聚谱。记交叉谱估计为ŜXY(f),Xt,Yt的单谱估计相应为 ŜXX(f)、ŜYY(f),则交振幅谱估计可表示为
| ${\hat \alpha _{XY}}(f) = \left| {{{\hat S}_{XY}}(f)} \right|$ | (6) |
相干谱估计可表示为
| ${\hat w_{XY}}(f) = \left| {\frac{{{{\hat S}_{XY}}(f)}}{{{{\{ {{\hat S}_{XX}}(f){{\hat S}_{YY}}(f)\} }^{1/2}}}}} \right|$ | (7) |
凝聚谱估计可表示为
| $M\hat sc(f) = \frac{{{{\left| {{{\hat S}_{XY}}(f)} \right|}^2}}}{{{{\hat S}_{XX}}(f){{\hat S}_{YY}}(f)}}$ | (8) |
以往的研究(Koopmans,1974; Bortel et al,2007; Gallet et al,2011)详细讨论了凝聚谱的临界值: 采取Welch方法进行估计时,每段有50%的重叠且使用Hanning窗,则ŜXX(f)、ŜYY(f)渐近服从自由度为${\widehat {\rm{S}}_{XX}}(f)$,${\widehat {\rm{S}}_{XX}}(f)$的χ2分布(Percival et al,1993)。这一结果可用于凝聚谱的非零相关性检验: 在显著性水平α下,凝聚谱估计的临界值为1-α2/(ν-2),其中ν为自由度,超过这一临界值,可以认为两序列在相应频率上显著相关。
2 模拟数据分析为比较三种估计方法的相关信号的检测能力和频率分辨能力,同时验证前面的临界值结果,参考前人的研究(Benesty et al,2005),进行了一系列数值模拟实验。
模拟时间序列Xt,Yt由下式产生
| ${X_t} = \sum\limits_{i = 1}^n {{A_i}\cos (2\pi {f_i}t)} + \sum\limits_{j = 1}^m {{B_i}\cos (2\pi f_j^xt)} + {\varepsilon _{1,t}}$ | (9) |
| ${Y_t} = \sum\limits_{i = 1}^n {{C_i}\cos (2\pi ({f_i}t + {\phi _i})} ) + \sum\limits_{j = 1}^r {{D_i}\cos (2\pi f_j^yt} ) + {\varepsilon _{2,t}}$ | (10) |
其中n,m,r为正整数,Ai,Bi,Ci,Di为有理数,ε1,t,ε2,t是独立的高斯白噪声过程且其期望为0。在Yt中,相位φ1,φ2,φn是随机变量。Xt和Yt的相同频率为fi,i=1,2,...,n,Xt的特有频率为fjx,j=1,2,...,m,Yt的特有频率为fjy,j=1,2,...,r。则理论凝聚谱为
| $coh(f) = \left\{ {\begin{array}{*{20}{c}} {1,}&{f = {f_1},{f_2}, \cdot \cdot \cdot ,{f_n}}\\ {0,}&{} \end{array}} \right.$ | (11) |
这里给出三对模拟结果:
第一对序列长度取1024,采样频率为1Hz,Ai,Bi,Ci,Di均为1。选取两者的相同频率为f1=0.10,f2=0.20,f3=0.21,f4=0.22,f5=0.23,f6=0.24; f7=0.45,Xt的特有频率为f1x=0.07,Yt的特有频率为f1y=0.32。其中频率 f2、f3、f4、f5和f6非常靠近,这样便于考察各方法的频率分辨能力。分别采用Welch方法(Hanning窗,窗长度256)、MTM方法(分辨率带宽4/1024)、MVDR方法(窗宽256,分辨率为400)进行凝聚谱估计,并做非零相关性检验。在显著性水平0.05下,得到的临界值为0.41,具体结果如图 1中a、b、c所示。
第二对改变序列长度为4096。做非零相关性检验,在显著性水平0.05下,临界值为0.10,具体结果如图 1
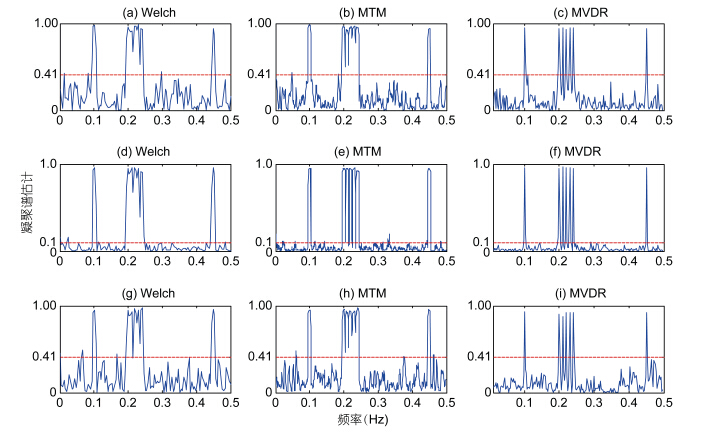 |
| 图 1 凝聚谱估计(三对数值模拟) Fig. 1 Estimation on magnitude-squared coherence(numerical simulation on three pairs of data)a、b、c分别为Welch、MTM、MVDR方法对第一对模拟数据的凝聚谱估计; d、e、f分别为Welch、MTM、MVDR方法对第二对模拟数据的凝聚谱估计;g、h、i分别为Welch、MTM、MVDR方法对第三对模拟数据的凝聚谱估计 中d、e、f所示。 |
第三对序列增加特有频率的个数,Xt的特有频率为f1x=0.07; f1x=0.30; f1x=0.40,Yt的特有频率为f1y=0.01; f1y=0.15; f1y=0.48。做非零相关性检验,在显著性水平0.05下,临界值为0.41。结果如图 1中g、h、i所示。
相关信号的检测能力可通过观察显著相关的频率是否能够被检测出来进行判断。当凝聚谱估计值大于临界值时,相应分量是显著相关的。由图 1可以看出,三种方法均能检测出存在相关性的频率,但Welch方法和MTM方法的估计结果存在伪峰。
可通过考查相近且相关程度相同的频率分量并观察其凝聚谱估计曲线是否存在两个对应的可分辨的尖峰来衡量分辨能力。由图 1可知,在相近的频率f2、f3、f4、f5、f6上,MVDR方法的估计谱能够清晰地分辨每一个频率点,每个频率点上的峰狭窄且互不交叠; Welch方法的估计谱可以勉强分辨出存在相关的频率点,但是一些谱峰连在一起; MTM方法的估计结果也能够显示出具有相关性的频率点,但其峰较宽,分辨率介于MVDR和Welch两种方法之间。
此外,在第一对数值模拟的基础上,从改变模拟数据长度、变换共有频率、增加特有频率的个数、改变振幅系数、加大噪声方差等方面进行了系统的模拟。结论与以上实验类似: MVDR方法的分辨率最高,不易出现伪峰; Welch方法分辨率较差,容易出现伪峰; MTM方法的估计性能介于两者之间。
3 实验室波流数据分析 3.1 数据及其预处理为了解以上三种方法在具体应用中的差异,我们在中国海洋大学物理海洋实验室的大型风-浪-流水槽中进行了波流实验。水槽长65m,宽1.2m,高1.5m,实验时水深0.7m左右。分别选定距离出风口30m、34.2m、39.7m三个风区位置进行实验。在每个风区位置,风速分别设定为6.35、7.0、7.5、8.0和9.0m/s,实测风速在设定水平上下5%—10%范围内波动。波面位移采用实验室自主研发的OUC-2型钽丝测波仪(以下简称“测波仪”)测量,采样频率约为26.78Hz。水下的流速采用声学多普勒流速测量仪(以下简称“ADV”)测量,可探测探头下方10cm位置的三维流速,测量深度分别位于15、20、25、30、35和40cm,垂直方向有重复观测,采样频率为25Hz。实验时,先开动流机,机械造波5分钟,然后搅动水槽内的水体,使水中杂质均匀散布于水体中。为便于ADV测量,流机流速范围设定为0—40cm/s。之后停止机械造波,待水面平静后,设定风速,并启动风机造风。波面起伏平稳后,同步开始测波仪、ADV的数据采集,测量记录波面位移与水下给定深度处的流速。受到测波仪处理记录的限制,每次记录时间长度为10分钟(类淑河,2010)。
不失一般性,选取其中三对实验数据信号进行研究。第一对是风区长度39.7m、风速6.35m/s、ADV探头深度20cm情形下的波面位移和铅直流速信号,记为pair I。第二对是风区长度34.2m、风速8.0m/s、ADV探头深度25cm情形下的波面位移和铅直流速信号,记为pair II。第三对是风区长度30m、风速9.0m/s、ADV探头深度40cm情形下的波面位移和铅直流速信号,记为pair III。其中波面位移时间序列有15000个点,铅直流速时间序列约有14000个点。为进行交叉谱分析,对铅直流速序列进行线性插值,使其与波面位移的15000个点一一对应。鉴于流速数据不平稳,所以采用Butterworth滤波器滤去频率小于0.5Hz的信号,即去除低频信号,然后对波面位移和预处理之后的铅直流速序列进行零均值化处理。
3.2 凝聚谱估计由于实验室数据足够长,研究中首先将数据均进行分段。每段包括1024个数据点,且相互无重叠,由此共分为14段。对每段数据分别用Welch方法、MTM方法、MVDR方法进行凝聚谱估计,参数选择与模拟数据分析相同。最后对14段凝聚谱估计取平均,并进行非零相关性检验,在显著性水平0.05下,得到的临界值为0.054。三对信号的平均凝聚谱估计结果如图 2所示。
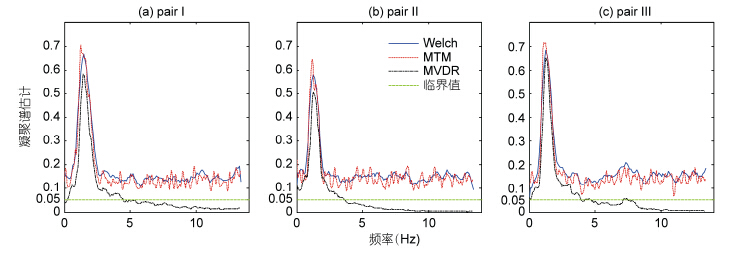 |
| 图 2 三对风浪实验信号的凝聚谱估计 Fig. 2 Estimation on magnitude-squared coherence of three pairs of wind-wave experiment data a、b、c分别为 pair I、pair II、pair III 实验信号的凝聚谱估计 |
不难看出,Welch和MTM方法的估计结果相近,在整个可识别频率范围内凝聚谱的估计值均高于临界值,是显著相关的。MVDR方法给出的估计在谱峰频率fp附近即主导波频段内(Babanin,2009)与Welch和MTM方法的估计结果走势一致,估计值略低,但在高频段,大约在1.5fp之后,有一个明显的指数衰减趋势,而在3fp之后,凝聚谱估计值小于临界值,相关性不显著。
分别对三对实验信号采用Welch、MTM、MVDR方法估计得到的14段凝聚谱对应谱值求方差后再取平均,得到各自的平均方差。第一对信号三种方法对应的平均方差分别为0.0318、0.0272、0.0178; 第二对信号分别为0.0260、0.0208、0.0139; 第三对信号则为0.0319、0.0266、0.0194。显然,MVDR方法得到的平均方差最小,此方法最稳定。
三种方法给出的凝聚谱估计均表明波流信号在主导波频段上存在显著的相关性。然而高频段的信号极容易被噪声干扰甚至掩盖。就此实验数据而言,并不能判断高频段波流信号是否一直存在显著的相关。另一方面,模拟数据分析发现,MVDR方法提供的估计有更强的频率识别与分辨能力; 且实验数据分析表明,MVDR方法得到的平均方差最小,估计结果更稳定。因而,在这三种方法提供的凝聚谱估计中,MVDR方法的估计结果更为可靠,即波流信号仅在主导波波段内存在显著相关性。
图 3中分别给出了三对数据的波面位移单谱估计、铅直流速单谱估计和MVDR方法给出的凝聚谱估计(为便于比较,估计结果均取对数)。由图可知,波面谱只有一个尖峭的主峰,与铅直流速谱谱形相似。凝聚谱与两个单谱的谱形走势大体一致,但谱峰较宽,在稍高于谱峰对应的频率的较宽的频段内,仍保持较高的凝聚谱谱值。这表明,在这一频率范围内,表面波动与水下铅直流速存在很强的相关性。
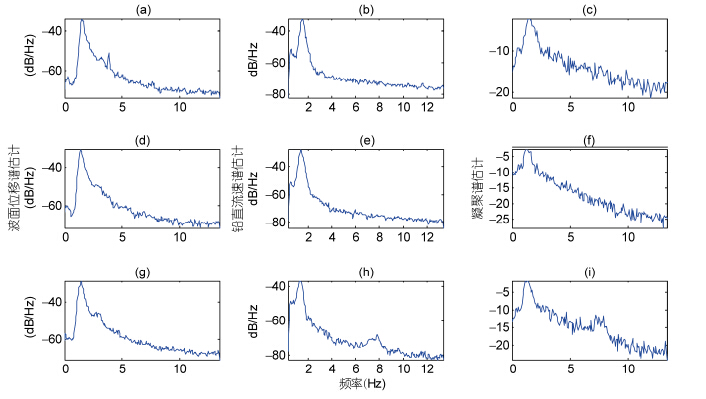 |
| 图 3 三对风浪实验信号的波面位移谱估计、铅直流速谱估计、凝聚谱估计 Fig. 3 Estimation of wave spectrum,current spectrum,and magnitude-squared coherence of three pairs of wind-wave experiment data a、b、c分别为pair I、pair II、pair III的波面位移谱估计; d、e、f分别为pair I、pair II、pair III的铅直流速谱估计; g、h、i分别为pair I、pair II、pair III的凝聚谱估计 |
本文讨论了Welch、MTM和MVDR三种交叉谱估计方法,在波流信号相关性分析中的应用,并通 过数值模拟,从检测相关信号能力和分辨率能力两个方面评估了三种估计方法的性能。我们发现,Welch方法能够鉴别出相近的相关频率,但分辨率不高,且容易出现伪峰; MTM方法出现的伪峰较Welch方法少,分辨率能力仍较差; 而MVDR方法既能够检测到相关信号,又不容易出现伪峰,分辨率较高,在三种方法中估计性能最优。
分别采用三种方法估计了实验室三对波面位移与铅直流速信号的凝聚谱。结果表明,在以谱峰频率为中心的主导波频段,三种方法给出的凝聚谱估计结果相近,均高于临界值,表明波流信号在此频率区间内显著相关。在高频段,估计结果存在差异。在高于1.5fp之后的频段,MVDR给出的估计有衰减趋势,在3fp之后变得不显著,而Welch方法和MTM方法给出的凝聚谱却在整个高频段均大于临界值,即使在很高的频段上,波流信号仍显著相关。本文研究表明,MVDR的估计结果更加合理。
在进行交叉谱估计和单谱估计时,各种估计方法都面临诸多参数选择问题,如Welch方法中窗宽、重叠比例与窗类型的选取。选择的参数不同,估计结果也会有差异。Priestley(1981)指出,相对于窗类型和重叠比例的选择,截断点即窗宽的选取对估计结果影响更大。我们数值模拟的结果也表明,选择不同的窗、变换重叠比例等,估计结果变化不大,但改变窗宽,得到的估计结果会有明显不同。另外,在进行非零相关性检验时,临界值是通过Welch方法估计的自由度进行检验的,而对于MTM方法和MVDR方法来说,这一临界值是否适合,还有待进一步验证。
在实验室波流信号相关性分析的讨论中,仅采用了具有代表性的三对数据,得到的一些物理海洋方面的结论可能不具有一般性,需要在未来的工作中深入研究。
| 王涛, 李家春, 1999. 波流相互作用研究进展. 力学进展, 29(3): 331—343 |
| 类淑河, 2010. 风浪破碎的随机性、非线性和能量耗散特征研究. 青岛: 中国海洋大学博士学位论文 |
| 袁耀初, 赵进平, 王惠群等, 2002. 南海东北部450m以浅水层与深层海流观测结果及其谱分析. 中国科学(D辑), 32(2): 163—176 |
| 高 山, 2003. 二维数值波浪水槽模式的建立和应用及浪流相互作用研究. 青岛: 中国海洋大学博士学位论文 |
| 黄建国, 1991. 现代谱分析的发展及应用(二). 数据采集与处理, 6(1): 33—45 |
| Babanin A V, 2009. Breaking of ocean surface waves. Acta Physica Slovaca, 59(4): 305-535 |
| Benesty J, Chen J D, Huang Y A, 2005. A generalized MVDR spectrum. IEEE Signal Processing Letters, 12(12): 827-830 |
| Bortel R, Sovka P, 2007. Approximation of statistical distribution of magnitude squared coherence estimated with segment overlapping. Signal Processing, 87(5): 1100-1117 |
| Capon J, 1969. High-resolution frequency-wave number spectrum analysis. Proceedings of the IEEE, 57(8): 1408-1418 |
| Carter G C, 1987. Coherence and time delay estimation. Proceedings of the IEEE, 75(2): 236-255 |
| Gallet C, Julien C, 2011. The significance threshold for coherence when using the Welch’s periodogram method: Effect of overlapping segments. Biomedical Signal Processing and Control, 6(4): 405-409 |
| Jenkins G M, Watts D G, 1968. Spectral Analysis and its Applications. San Francisco: Holden Day, 256-300 |
| Kay S M, 1988. Modern spectral estimation. New Jersey : Prentice Hall, 446-471 |
| Koopmans L H, 1974. The Spectral Analysis of Time Series. New York: Academic Press, 281-285 |
| McKone K P, 2003. Multiple Methods of Spectral Analysis with Applications to the Florida Current. Ph.D. Thesis, Dept. of Marine Science, University of Southern Mississippi, Hattiesburg, MS. pp 120 |
| Percival D B, Walden A T, 1993. Spectral Analysis for Physical Applications. Cambridge: Cambridge University Press, 289-295 |
| Priestley M B, 1981. Spectral Analysis and Time Series. London New York: Academic Press, 654-726 |
| Strand O N, 1977. Multichannel complex maximum entropy (autoregressive) spectral analysis. IEEE Transactions on Automatic Control, 22(4): 634-640 |
| Thomson D J, 1982. Spectrum estimation and harmonic analysis. Proceedings of the IEEE, 70(9): 1055-1096 |
| Welch P D, 1967. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Transactions on Audio and Electroacoustics, 15(2): 70-73 |
 2015, Vol. 46
2015, Vol. 46


