
中国海洋湖沼学会主办。
文章信息
- 张卓, 宋志尧. 2015.
- ZHANG Zhuo, SONG Zhi-Yao. 2015.
- 江苏近海潮流湍流切应力研究
- DISTRIBUTION OF TURBULENT SHEAR STRESS IN JIANGSU OFFSHORE, EAST CHINA SEA
- 海洋与湖沼, 46(5): 995-1000
- Oceanologia et Limnologia Sinica, 46(5): 995-1000.
- http://dx.doi.org/10.11693/hyhz20150100008
-
文章历史
- 收稿日期: 2015-01-11
- 收修改稿日期: 2015-04-28
2. 江苏省地理信息资源开发与利用协同创新中心 南京 210023;
3. 江苏省大规模复杂系统数值模拟重点实验室 南京 210023
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China;
3. Jiangsu Provincial Key Laboratory for Numerical Simulation of Large Scale Complex Systems, School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, China
湍流运动是流体力学研究的重要课题,它对河口混合与泥沙输运产生重要影响(周济福等,2000)。湍流在水流在平均流动方向的基础上增加了湍流应力的影响,其分量包括三个正应力和三个切应力,正应力主要体现在对水流压强的影响,而切应力主要体现在对流速分布的影响。目前关于潮流、潮汐的研究较多地采用数值模拟(朱学明等,2012; 齐继峰等,2013; 林作梁等,2013),由于潮流的主要流动方向是水平方向,垂直方向的流速相比水平流速至少要小一个量级,因此水平方向的切应力对流速垂向分布有重要影响,而它的分布和变化特征一直是水动力学的经典课题之一,受到众多学者的关注(Anwar et al,1980; 李浩麟,1992; 卢金友等,2005; 朱长军等,2007)。
相比于河道和明渠水流,潮流是周期性往复流或旋转流,比河道和明渠的恒定水流更加复杂。乐肯堂等(2003)曾假定垂直湍流粘性系数为常数,推导出潮流Ekman方程解析解。徐鹏等(2013)对强潮狭长海湾中垂直涡粘系数分布和底部拖曳系数的变化进行了观测分析,发现垂直涡粘系数大致呈抛物线分布。经典流速分布公式对数分布基于湍流切应力线性分布的假设,具有良好的适应性,在大多数时段的潮流分布可以用对数分布来拟合,尤其是在涨急或落急前后。但在转流期间,对数分布误差较大。更重要的是,很多看似拟合很好的流速分布,推得的粗糙高度却是不合理的。Collins等(1998)的研究表明,经过一致性分析后,潮间带的潮流真正满足对数关系的不到40%,并且认为潮流的加速和减速效应是使潮流速偏离对数分布的重要原因之一。一些学者将对数分布与实测的偏差归结于湍流切应力线性分布假设的不合理。Bowden等(1952)的观测表明,湍流切应力在高潮位1/4周期后满足线性分布,而在高潮位时与线性分布偏离较大。Kironto等(1995)的实验表明,在加速条件下,湍流切应力呈上凹型曲线,在减速条件下,湍流切应力呈下凹型曲线。李浩麟(1992)根据经验型的指数分布,得到了指数形式的潮流切应力分布模式; Song等(2009)通过动力学方程从理论上导出能反映潮流加速和减速作用的湍流切应力二次幂函数分布表达式; Ni等(2009)以二次分布为基础得到双对数水流分布模式; Ni等(2012)进一步推出了紊流切应力三次幂函数分布式。目前多数学者认为潮流切应力偏离线性分布,但切应力具体表达形式还没有定论,也缺少对切应力分布影响因素的分析。另外还有一些学者通过实际观测发现在某些海域湍流切应力仍然在多数情况下满足线性分布(Elliott,2002; Rippeth et al,2002)。
本文对潮流动力方程作简化假设,得到切应力传播方程。湍流切应力由底部逐渐向上传播扩散,推导出切应力随潮周期变化的垂向分布表达式,发现计算得到的切应力偏离线性分布,但也不同于指数分布或幂函数分布。根据江苏近海潮流流速的实测数据计算潮流切应力分布,与本文方程对比,发现本文的湍流切应力分布式能较好地反映潮周期内切应力分布变化特征。最后根据切应力垂向分布表达式分析了导致切应力偏离线性分布的主要因素,探讨了以往研究在不同海域得到切应力分布不同结论的原因。
1 切应力的垂向分布潮流运动方程可表达为
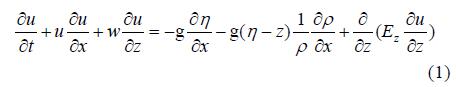
式中u,w分别是x,z方向的流速; η是潮位; Ez是垂向涡粘系数; g是重力加速度。
将(1)对z求导,在地形变化较缓且无淡盐水混合的情形下,可以忽略对流项和斜压项,并注意到湍流切应力和流速的关系: 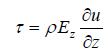 ,可以得到
,可以得到

上式就是湍流切应力的控制方程。从方程的形式可以看出,此方程属于扩散方程,显示湍流切应力从底层向中上层传播的物理特性。这里假设湍流粘性系数是常数,根据Elliott(2012)实测研究,在距离海底5m以上将涡粘系数作常数化处理其结果比较接近实测,而江苏近海深槽平均深度大约在20m。因此可以认为在近底层以外大多数深度范围内(2)式的假设是合理的。由于近底层内(又称常应力层)的切应力分布可近似为不变,因此在以下推导过程中可以理解为将底部边界条件施加在近底层上边即(z=-h=-0.8D,D是总水深约20m,h是近底层到水面的深度)。
设(2)的解形式为

将(3)代入(2)可得

解得
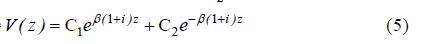
其中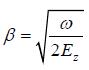 。
。
于是可以得到
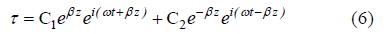
取实数部分即为
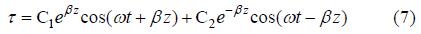
(7)式需要确定两个积分常数C1和C2,一般可采用底面边界条件和表面边界条件确定:
对于表面,z=0时,

对于底面,z=-h时,
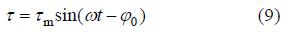
根据实测资料,可将底面边界条件简化近似为正弦波动,τm是底部最大切应力。
通过(8)可得C1=-C2,将其代入(7),由底面边界条件(9)可得: z=-h时,
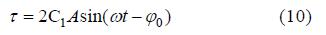
其中
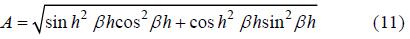

由此可得

若设 ,则(7)可以转化为
,则(7)可以转化为
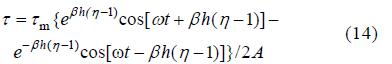
可以看到,湍流切应力的相位和振幅在不同水深处不同,并非简单的幂指数分布。
2 近海潮流切应力的计算和对比验证研究区域选择江苏近海,该区域在东海前进波和黄海旋转波的相互作用下,形成辐射状的沙脊群和潮流通道。该海区主要以正规半日潮为主,弶港至小洋口潮差最大,平均潮差3.9m,从小洋口向南潮差逐渐减小。平均水温最低月为2月,最高水温为8月,南北海域表层分别为27.4°C和26.8°C,底层分别为26.0°C和24.2°C。在该海域几个主要的潮流通道,涨落潮流速很大,垂线平均速度可达1.5m/s以上。近年来有众多学者对该海区的潮流特征进行了研究(陈斌等,2011; 张存勇,2012)。
2013年9月7日14: 00至9月8日15: 00,在江苏洋口港附近海域,进行了海洋水文观测。表 1和图 1列出了某点(121°24′29.72″,32°30′54.00″)前15个小时的流速剖面,图 2是该点站位图。从表 1可以看出,该区域潮流基本以往复流为主,科氏力可以忽略。到达指定位置后采用船舶锚定观测,误差控制在一个船长之内,并在测验过程中随时检查测船位置。在一条垂线上采用了6个流速仪(SLC92型海流计,流速测量精度≤±1.5%,流向精度≤±4°)同时进行测量,得到了大潮2周期的流速剖面。
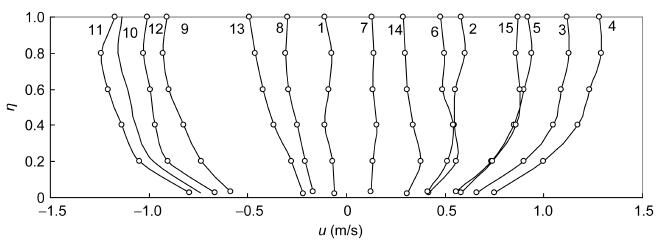 |
| 图 1 大潮流速剖面Fig. 1 Velocity profiles over spring tidal cycles 图上部各折线的序号代表时间次序 |
 |
| 图 2 测点站位图Fig. 2 Location of measurement |
| 序号 | 时间 | 垂向平均流速(m/s) | 垂向平均流向(°) |
| 1 | 09-07 13: 00 | 0.09 | 275 |
| 2 | 09-07 14: 00 | 0.55 | 90 |
| 3 | 09-07 15: 00 | 1.01 | 94 |
| 4 | 09-07 16: 00 | 1.14 | 94 |
| 5 | 09-07 17: 00 | 0.83 | 92 |
| 6 | 09-07 18: 00 | 0.51 | 85 |
| 7 | 09-07 19: 00 | 0.16 | 63 |
| 8 | 09-07 20: 00 | 0.28 | 298 |
| 9 | 09-07 21: 00 | 0.83 | 280 |
| 10 | 09-07 22: 00 | 1.06 | 277 |
| 11 | 09-07 23: 00 | 1.13 | 277 |
| 12 | 09-08 00: 00 | 0.95 | 278 |
| 13 | 09-08 01: 00 | 0.38 | 277 |
| 14 | 09-08 02: 00 | 0.32 | 90 |
| 15 | 09-08 03: 00 | 0.81 | 95 |
Bowden(1959)曾经用流速剖面计算潮流切应力,这里用他的方法得到江苏近海湍流切应力并以此作为实测验证数据。忽略科氏力和平流项,潮流的动量方程可写为
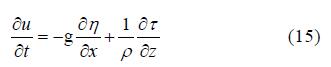
对上式作垂向平均可得:
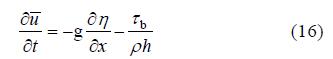
式中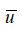 是垂向平均的流速,τb是底部切应力。
是垂向平均的流速,τb是底部切应力。
对上面2式分别从底部到某一深度作垂向积分可得:

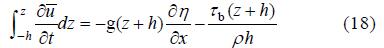
将上(17)和(18)两式相减可得:
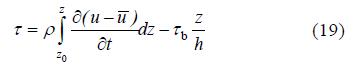
上式第一项是潮流加速运动引起的附加切应力,加
速度越大,这一项就越大,切应力就越偏离线性分布; 反之,如果潮流变成恒定流动,这一项变为0,切应力就完全呈线性分布。第二项则是底摩擦引起的线性切应力项。
在用实测资料计算(19)式右边第一项时,可先数值积分,然后对时间离散求得:
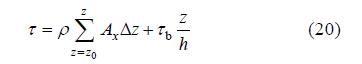
式中 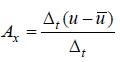 ,Δt代表时间差分算子。
,Δt代表时间差分算子。
图 3是根据图 1所示流速剖面,应用公式(20)计算得到的切应力分布(用点表示),图 3(a),(b),(c),(d)分别包含落潮加速、落潮减速、涨潮加速、涨潮减速四个过程,每个点的序号代表潮流时间的先后次序,和图 1的流速剖面对应,每个序号之间相差1h。
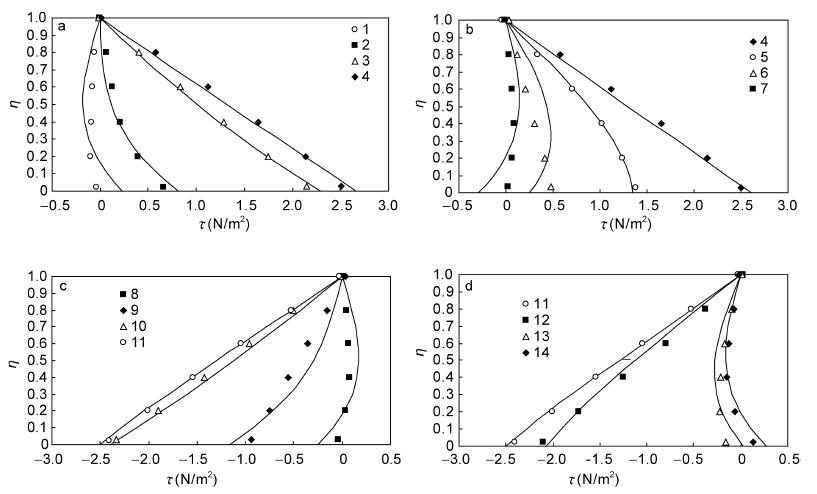 |
| 图 3 潮周期内湍流切应力的变化过程 Fig. 3 The variation of the stress profiles over a tidal cycle |
将实测流速剖面得到的切应力分布和式(14)比较,发现当βh取1—2左右时,二者比较相似(图 2)。实测海区的平均水深度在20m,半日潮对应的角频率ω约为0.00022rad/s,垂直湍流粘性系数 Ez约为0.01m2/s. 这样得到的βh约为2.2,跟公式结果比较接近。这说明本文公式结果可以反映实际潮流切应力的周期性变化。
从图 2可以看到,湍流切应力曲线在加速时上凸,而减速的时下凹,主要是因为越近底相位越超前、越近水面相位越落后的缘故,而在涨急落急时刻,切应力接近线性分布。该结论与以往研究的结论完全一致。本文虽然对涡粘系数作了常数简化处理,在近底 层处存在一定误差(主要在离底面0.2D范围内),海域层结效应可能也对公式精度产生影响,但总体上仍能很好地反映潮流过程中湍流切应力随时间的变化特征。
3 讨论式(14)也可写为
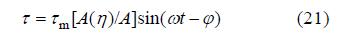
其中 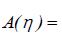
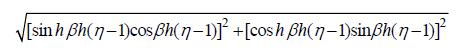
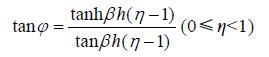
上式表明,湍流切应力的分布从底层到表层存在相位差,相位差大小跟具体位置有关。而振幅从底层到表层逐渐减小但并非简单的线性或二次分布,而是复杂的双曲分布多项式。除了垂直位置以外,影响切应力振幅和相位的主要参数为 βh,该参数是个无量纲数记为Ri

该参数代表了潮流加速作用与涡粘性的相互关系。Ri越大,潮流加速作用越强,振幅就越偏离线性(图 4),相位在垂向的差异就越大(图 5)。Ri越小,则代表涡粘性强,切应力就更接近线性分布。水深对切应力分布的影响主要体现在水深越大,摩擦力作用从底部传递到表层所需要的时间越长,这也会使切应力偏离线性分布。从江苏近海的实测数据来看,Ri在1—2之间,主要与水深变化密切相关,水深越深测得的湍流切应力越有可能偏离线性分布,这也解释了为什么有些学者测得的湍流切应力较符合线性分布,而另外一些学者得到的湍流切应力明显偏离线性的现象。
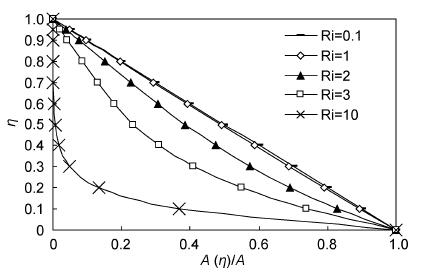 |
| 图 4 紊流切应力振幅沿水深的变化Fig. 4 Distribution of the amplitude in water depth |
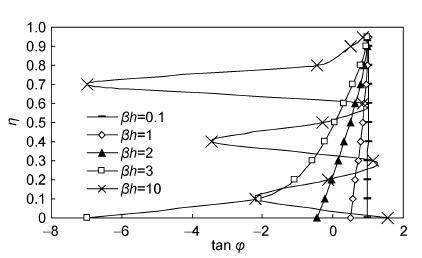 |
| 图 5 湍流切应力相位随水深变化Fig. 5 Distribution of the phase in water depth |
通过潮流动力方程推得湍流切应力扩散方程,并解出湍流切应力垂向分布,并与近海潮流流速观测计算得到的切应力进行比较,得到如下结论:
(1)本文得到的湍流切应力公式能够反映潮流湍流切应力在不同潮流阶段(加速、减速、涨急、落急)的分布特征; 只有在涨急、落急前后基本符合线性分布,在加速和减速阶段明显偏离线性分布。
(2)通过分析切应力分布公式,发现无量纲数 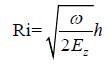 决定了切应力分布偏离线性的程度: 该值越大,切应力分布偏离线性约大,该值越小,切应力: 越接近线性分布。根据江苏近海实测数据,发现一般近岸潮流Ri值在1—2左右,水深是影响其变化的主要因素,水深越大Ri也越大,越有可能发现实测湍流切应力偏离线性的情况。
决定了切应力分布偏离线性的程度: 该值越大,切应力分布偏离线性约大,该值越小,切应力: 越接近线性分布。根据江苏近海实测数据,发现一般近岸潮流Ri值在1—2左右,水深是影响其变化的主要因素,水深越大Ri也越大,越有可能发现实测湍流切应力偏离线性的情况。
(3)本文仅考虑潮流加减速影响下的湍流切应力分布。实测结果经常含有风和密度流的影响,这使湍流切应力分布较为复杂,但本文的结果可以为分析实测切应力分布提供参考。
| 乐肯堂,庄国文,宋金宝等, 2003.海洋底边界层中实测海流的垂直分布Ⅱ.潮流边界层.海洋与湖沼, 34(2):187-193 |
| 卢金友,徐海涛,姚仕名, 2005.天然河道水流紊动特性分析.水利学报, 36(9):1029-1034 |
| 朱长军,张金良,江恩惠等, 2007.明渠含沙水流的垂线流速分布特性研究.长江科学院院报, 24(5):1-3 |
| 朱学明,鲍献文,宋德海等, 2012.渤、黄、东海潮汐、潮流的数值模拟与研究.海洋与湖诏, 43(6):1103-1113 |
| 齐继峰,曹圣山,郭可采等, 2013.基于FVCOM的獐子岛附近海域三维潮汐潮流数值模拟.海洋与湖沼, 44(6):1469-1478 |
| 张存勇, 2012.连云港近岸海域潮流垂直结构及其季节变化.海洋通报, 31(4):391-396 |
| 李浩麟, 1992.潮汐水流垂线流速分布与河床阻力的研究.水利学报,(11):57-62, 80 |
| 陈斌,周良勇,刘健等, 2011.废黄河口海域潮流动力与悬沙输运特征.海洋科学, 35(5):73-81 |
| 周济福,李家春, 2000.河口混合与泥沙输运.力学学报, 32(5):523-531 |
| 林作梁,朱学明,鲍献文等, 2013.基于FVCOM的泉州湾海域三维潮汐与潮流数值模拟.海洋学报, 35(1):15-24 |
| 徐鹏,刘志宇,毛新燕等, 2013.强潮狭长海湾中垂直涡黏性系数与底拖曳系数的估计.中国海洋大学学报(自然科学版), 43(8):1-7 |
| Anwar H O, Arkins R, 1980. Turbulence measurements in simulated tidal flow. Journal of Hydraulic Division, 106(8):1273-1289 |
| Bowden K F, Fairbarn L A, 1952. A determination of the frictional forces in a tidal current. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 214(1118):371-392 |
| Bowden K F, Fairbairn L A, Hughes P, 1959. The distribution of shearing stresses in a tidal current. Geophysical Journal International, 2(4):288-305 |
| Collins M B, Ke X, Gao S, 1998. Tidally-induced flow structure over intertidal flats. Estuarine, Coastal and Shelf Science, 46(2):233-250 |
| Elliott A J, 2002. The boundary layer character of tidal currents in the Eastern Irish Sea. Estuarine, Coastal and Shelf Science, 55(3):465-480 |
| Kironto B A, Graf W H, 1995. Turbulence characteristics in rough non-uniform open-channel flow. Proceedings of the Institutions of Civil Engineers-Water Maritime and Energy, 112(4):336-348 |
| Ni Z H, Song Z Y, Wu L C, 2009. Study on the double-logarithmic profile of tidal flow velocity in the near-bed layers. Acta Oceanologica Sinica, 28(6):84-92 |
| Ni Z H, Song Z Y, Zhang X J et al, 2012. A modification to vertical distribution of tidal flow Reynolds stress in shallow Sea. China Ocean Engineering, 26(3):431-442 |
| Rippeth T P, Williams E, Simpson J H, 2002. Reynolds stress and turbulent energy production in a tidal channel. Journal of Physical Oceanology, 32(4):1242-1251 |
| Song Z Y, Ni Z H, Lv G N, 2009. Vertical distribution of tidal flow Reynolds stress in Shallow Sea. China Ocean Engineering, 23(2):267-275 |
 2015, Vol. 46
2015, Vol. 46


