
中国海洋湖沼学会主办。
文章信息
- 黄鹏起, 陈旭, 孟静, 李敏, 万伟. 2016.
- HUANG Peng-Qi, CHEN Xu, MENG Jing, LI Min, WAN Wei. 2016.
- 内孤立波破碎所致混合的实验研究
- AN EXPERIMENTAL STUDY ON MIXING INDUCED BY INTERNAL SOLITARY WAVE BREAKING
- 海洋与湖沼, 47(3): 533-539
- Oceanologia et Limnologia Sinica, 47(3): 533-539.
- http://dx.doi.org/10.11693/hyhz20150800218
-
文章历史
- 收稿日期:2015-08-15
- 改回日期:2015-11-21
2. 广东海洋大学海洋与气象学院 湛江 524088
2. Guangdong Ocean University, College of Ocean and Meteorology, Zhanjiang 524088, China
海洋内波是密度稳定层结的海水中一种普遍存在的波动现象。共振相互作用、对流不稳定和剪切不稳定等机制引起内波破碎, 使其等密度面发生翻转, 产生湍流和不可逆的能量耗散(梁建军等, 2012)。内波破碎是海洋内部跨等密度面混合的主要来源(Garrett et al, 2007), 能量在此过程中从较大尺度向较小尺度传递, 对海洋环境产生重要的影响。
许多证据表明, 底地形是影响海洋混合的一个重要因素(Ledwell et al, 2000; Nikurashin et al, 2010; Klymak et al, 2012)。连续分层流体中内波传到倾斜地形时, 由于能量束反射前后与水平方向夹角不变, 反射后能量集中, 易发生破碎, 此时会产生强烈的湍流混合。在数值模拟和实验室研究中, 对内波破碎的研究主要集中于两层流体中的内孤立波经过正弦、三角、椭圆或斜坡地形破碎。
实验室环境中, Ivey等(1989)进行了对连续层结流体中内波在斜坡边界破碎导致的垂向混合的研究。他们将混合效率定义为因混合增加的势能与入射波的动能损失之比, 它由流体的稳定度决定, 其上限约为0.2。Helfrich(1992)进行了两层流体中下凹形内孤立波在斜坡上传播的实验, 获得破碎与湍斑的发生位置, 估算了第一模态波从破碎点转到垂向混合时的能量损失大约为15%±5%。Michallet等(1999)是Ivey等(1989)实验的后续。他们对 下凹形内孤立波在均一坡度的斜坡上的浅化效应和破碎进行实验研究, 在使造波区混合尽可能小的条件下生成大振幅内波。他们发现波长LW与斜坡特征长度LS的比值决定了从斜坡反射的能量总量, 当LW/LS=0.5时混合效率达到最大值25%; 而LW/LS大于或小于0.5, 混合效率都减小。杜辉等(2014)研究了两层流体内孤立波在斜板上的破碎, 分析内孤立波能量发现, 能量损失出现跃升是其发生破碎的重要特征, 而这是由于地形效应导致的内孤立波破碎和混合, 加剧了能量损失。
数值实验方面, 李丙瑞等(2010)在两层流体中模拟了三维小振幅内行进波在白噪声强迫下破碎的过程, 在剪切作用大到足以克服层结反向力矩作用时最大混合率为0.18; 这与Li等(2015)模拟二层流体中内孤立波经过三角地形破碎, 障碍参数为1时达到的最大混合率0.16较为接近。Klymak等(2012)结合现场观测数据, 模拟了内潮经过Hawaii Ridge破碎, 得到湍耗散率为10-8—10-4m2/s3量级, 比实测值高出1—2个量级。
对内波湍耗散率的研究主要为海洋实测。Moum等(2003)在Oregon大陆架的海中观测到两个内孤立波在20分钟之内传播经过传感器, 他们计算的内孤立波界面处耗散率的量级在10-7—10-5m2/s3之间, 而且可以发现波形后部的耗散率大于波前, 这可能是波形后部变陡造成的。而Klymak等(2008)基于Thorpe位移计算的在Kaena Ridge内潮与地形作用破碎引起湍耗散在10-7—10-6m2/s3量级。
本文在二维内波水槽两层流体中采用重力塌陷法造内孤立波, 在斜坡上破碎。使用PIV技术测量破碎时的流场结构, 计算内波破碎时的湍耗散率以分析混合的影响, 重点聚焦到内波破碎时各物理量的时间演化特征, 定量刻画混合过程。
1 实验设置本实验在中国海洋大学海洋与大气学院的流体力学实验室中进行, 主要设备布局如图 1所示。实验水槽尺寸为3m×0.15m×0.3m, 本文中定义水平方向为x, 垂直方向为z。角度θ指斜坡角度, ρ1、ρ2分别为上、下层的初始密度, h1、h2分别为上、下层的初始厚度, H为水槽内初始总水深。
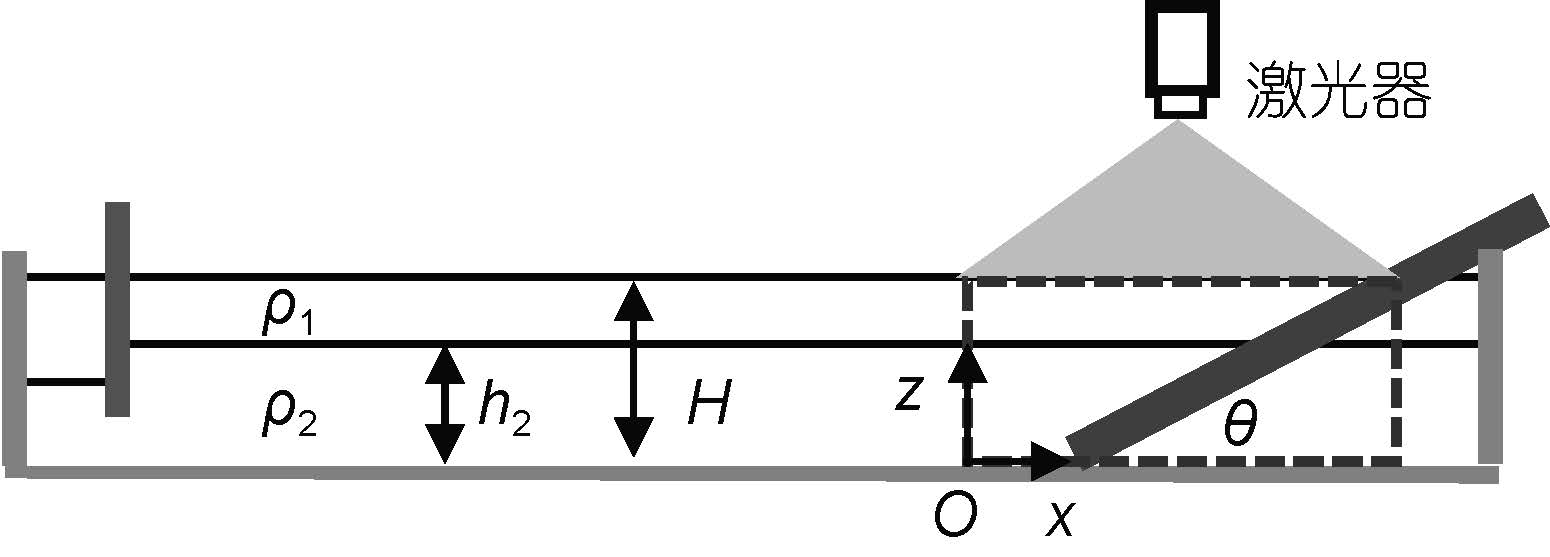 |
| 图 1 实验装置示意图 Fig. 1 Schematic diagram of experimental design |
实验条件如表 1所示, 其中染色实验1用于提取波要素, 实验2—4为PIV实验, 配置两层流体时加入了粒径50μm的示踪粒子。重力塌陷法中塌陷高度的定义为: 插入左侧挡板、往封住水体中注入上层水后挡板两侧上下层界面的高度差, 4组实验中塌陷高度η从2cm变化至9cm。CCD位于右侧, 其分辨率为1920×1080像素, 拍摄帧率设为50帧/s, 即两幅相邻照片的时间间隔为0.02s, 图 1中红色虚线框为拍摄视场, 实验2—4中视场长约40cm。
| 实验 | 角度θ(°) | ρ2/ρ1 | h2/H |
| 1 | 16.4 | 1.024 | 0.792 |
| 2 | 18.0 | 1.029 | 0.793 |
| 3 | 22.8 | 1.021 | 0.800 |
| 4 | 30.0 | 1.019 | 0.800 |
提取某一断面的波形时间序列分析可得波要素如振幅、波速和周期。使用PIVlab(开源PIV软件, Thielicke et al, 2014)获取速度场: 先对原始图像进行预处理减小过亮粒子的影响, 采用FFT window deformation算法, 查询窗口大小为16×16像素, 得到流场并对结果进行过滤和插值。
考虑到内孤立波流场的特殊性, 在计算脉动速度时不能单纯地时间或空间平均。本文使用的方法是识别出原始照片中界面坐标, 在每个水平位置处对上下层分别整层平均得到平均速度。用瞬时速度减去平均速度求出脉动速度, 然后用脉动速度的空间分布或时间序列计算湍耗散率、湍动能。
计算湍耗散率的空间分布, 本文使用“直接法”(direct method)。该方法基于湍耗散率的定义式
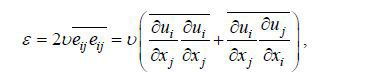 (1)
(1)其中, ui为脉动速度, xi和xj为坐标(下标i和j可取值1或3, 分别代表水平、垂直方向), υ0.00135cm2/s为运动学黏度(10°C, 密度为1.03—1.05g/cm3的氯化钠溶液), 上划线表示取平均。由于平面PIV无法测出所有项, 运用连续方程和湍流的各向同性假设可将(1)式简化为(Doron et al, 2001)
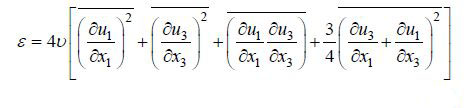 (2)
(2)参考Moum等(2003)的方法, 用断面的速度时间序列计算湍耗散率的方法同样基于定义, 将(1)式简化为以下形式
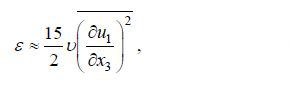 (3)
(3)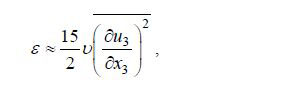 (4)
(4)或是
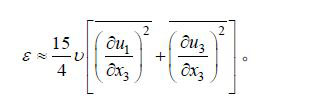 (5)
(5)湍动能(TKE)由下式计算
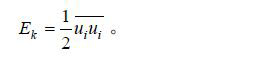 (6)
(6)
涡度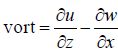
实验中采集的图像如图 2所示, 其中a为实验2塌陷高度2cm, b为实验3塌陷高度5cm, c为实验4塌陷高度9cm的图像, 1—4分别为内孤立波传播、等密度面变陡、破碎、冲击水上涌的过程。
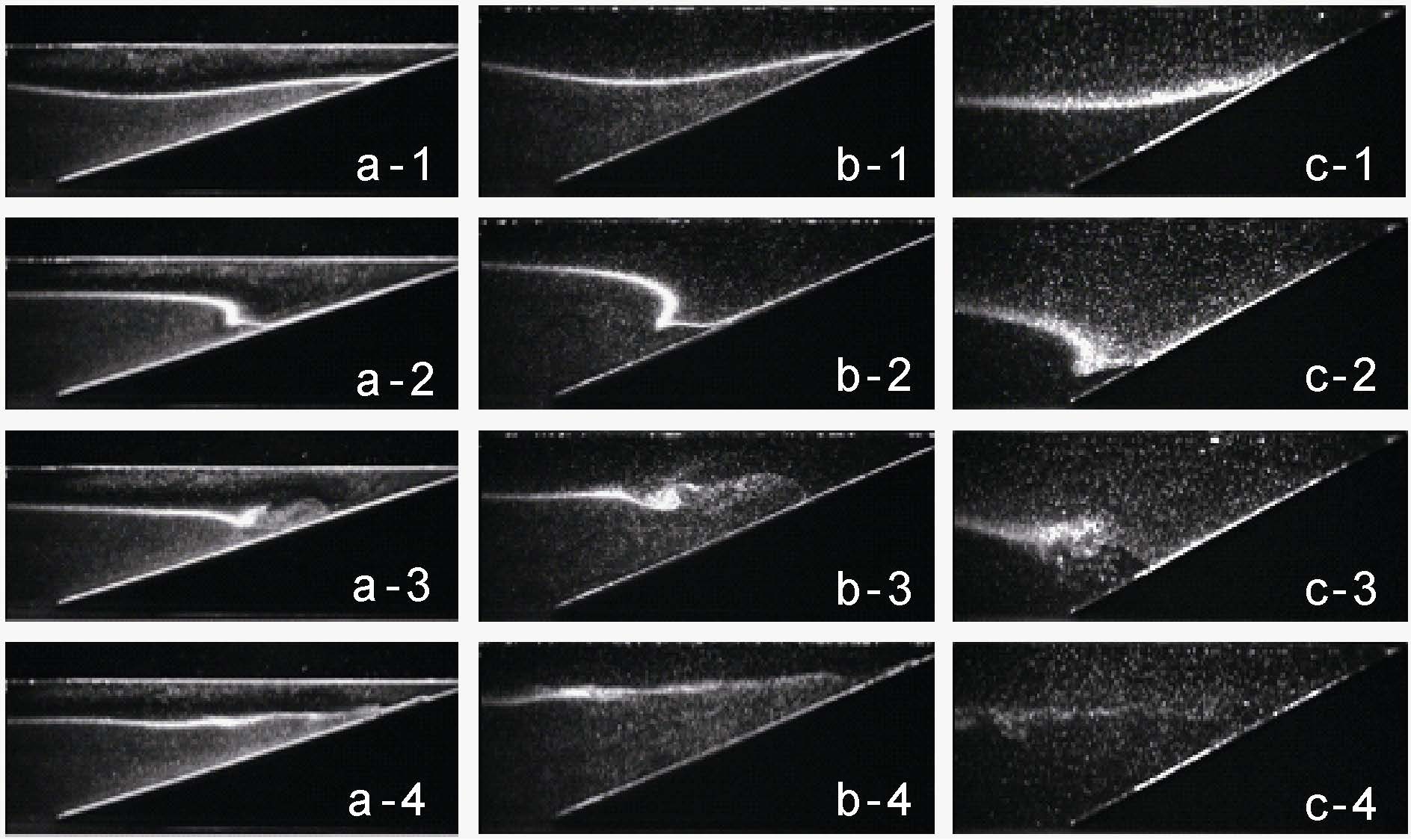 |
| 图 2 实验2—4原始照片 Fig. 2 Images of Experiments 2—4 |
分析斜坡左侧断面时间序列, 拟合得到塌陷高度η与内孤立波振幅a关系如图 3, 可看出两者呈良好的线性正相关。
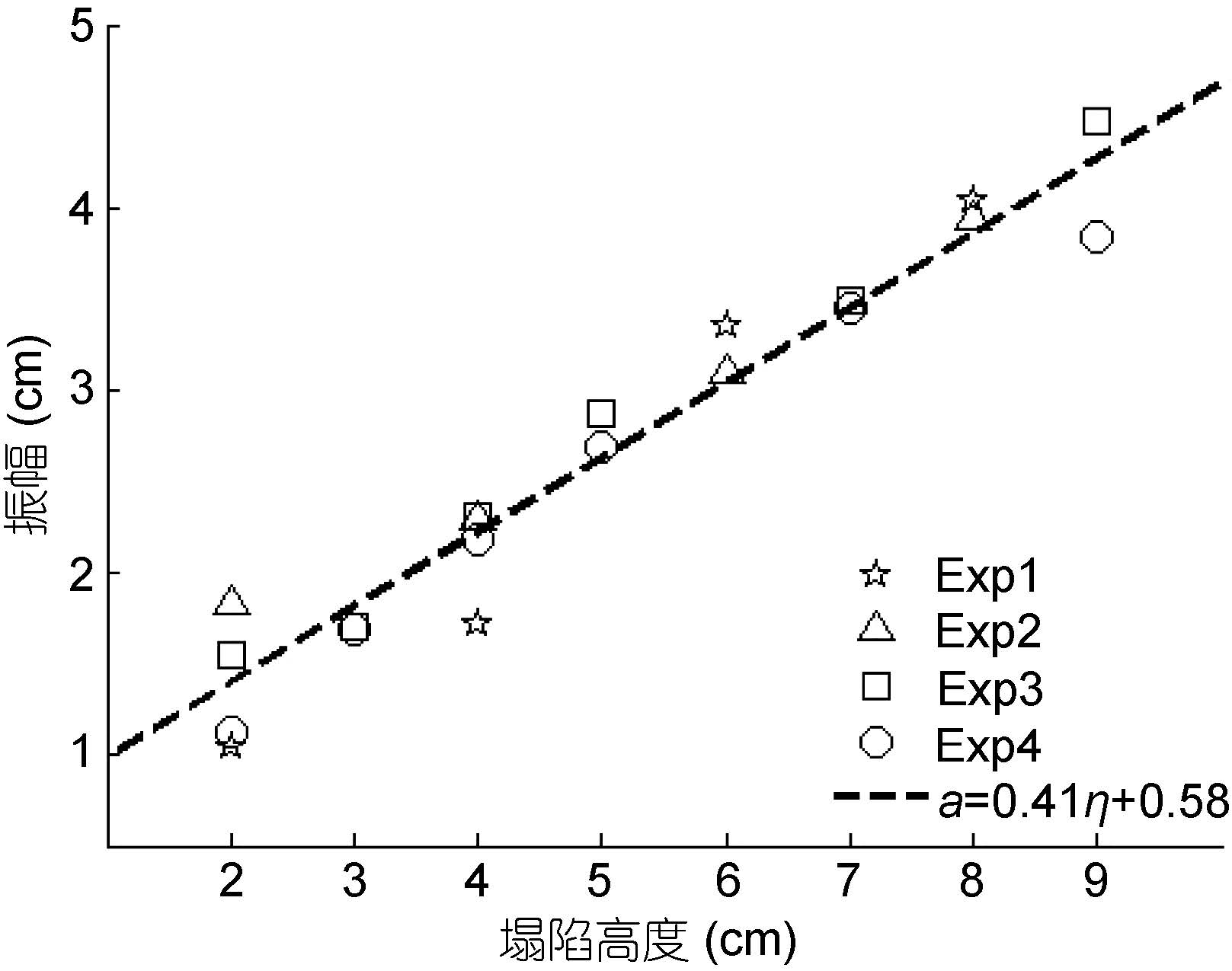 |
| 图 3 塌陷高度η与入射波振幅a关系 Fig. 3 Relation between collapse height and incident wave amplitude |
分析所有实验图像得到速度场, 可知所有实验中的流速大小在0—10cm/s之间。从图 4a可以看到入射波的流动可用界面处的剪切描述: 入射波上层流体与波速同向流动, 下层流体反向流动, 反射波反之。图 4b垂直速度时间序列则呈现明显的波前下降流、波后上升流特点。
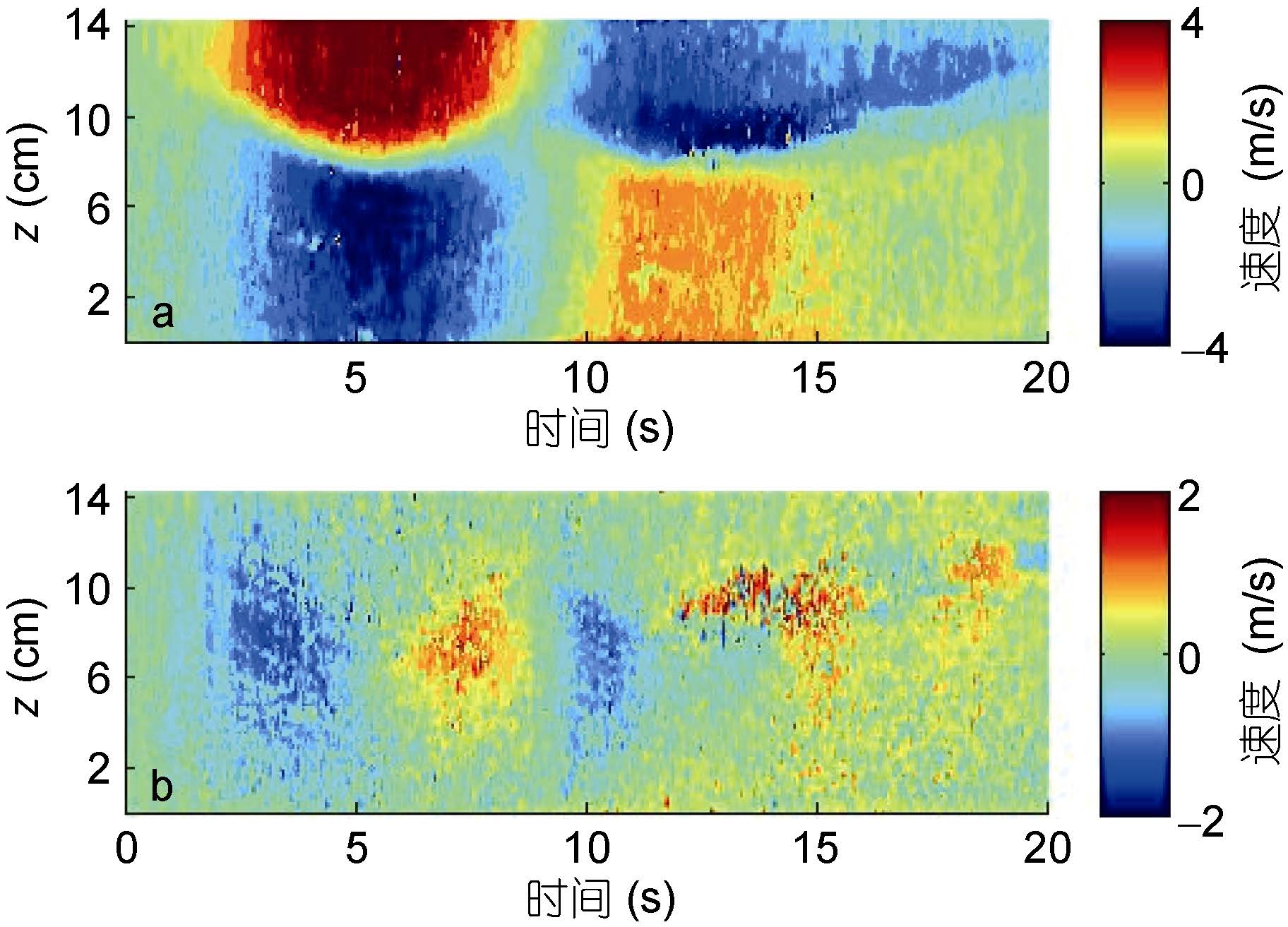 |
| 图 4 视场x=2cm断面速度时间序列 Fig. 4 Velocity time series at x=2cm profile in the field of view |
从速度的空间分布图(图 5)观察到这一相对对称的流动于波后近底部处首次发生变形, 波谷下速度沿斜坡向下, 波后则向上, 导致逆压力梯度的产生; 随后内波的等密度面发生翻转呈“Z”形, 这是因为右上方的水体继续向右运动, 而波面以上、被斜坡下部阻挡的水体则向左挤压, 致使原本在该处波面以下的水体向右沿斜板向上运动, 此时波前变缓波后变陡, 导致了波形的破碎。压力梯度增大, 波后垂向速度增大, 变得不稳定, 重流体被抬升到轻流体中, 波后产生强逆时针涡旋(图 5a, x=15cm斜坡上方处), 反过来又将轻的粒子带到波后的下方; 图 5b中可以看到破碎过程的继续发展, 涡旋强度和范围增大, 斜板右上方水体仍向右运动但速度减小。
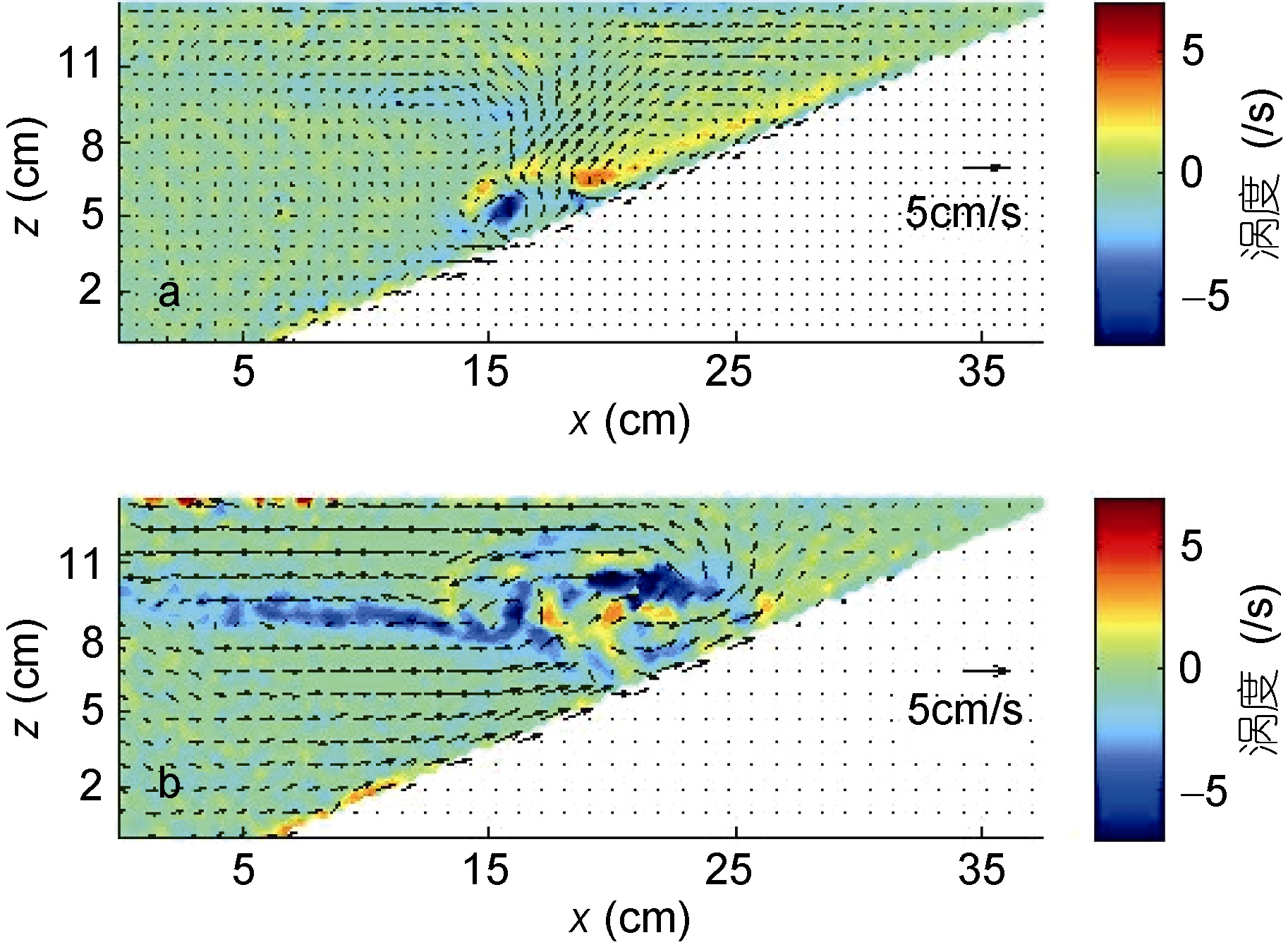 |
| 图 5 破碎阶段两个典型速度场空间分布, 背景等值线为涡度 Fig. 5 Two typical patterns of spatial distribution of velocity field during breaking; the background contour is vorticity |
该部分水体随后受到斜板阻碍, 产生向左的速度。上层左侧的水体则已经作为反射波向左运动了, 此时的流场可用上层的离岸流和下层沿斜坡向上的强底流描述, 破碎区域中出现向右运动速度的极大值, 运动方向较为杂乱, 冲击水的运动速度很大; 冲击水在斜坡上运动达到最高点, 反射波离开视场后, 整个场流速都变得很小。
3.2 湍耗散使用上述脉动速度空间分布的直接法求出每隔 0.5s全场的耗散率, 在内孤立波传播时的界面处、破碎区域的整个下层耗散都很强。取每个时刻场中最大值绘制出整个实验过程标准化的最大湍耗散率ε、平方涡度vort2和湍动能TKE的时间序列图如图 6。最大湍耗散率量级在10-6—10-4m2/s3, 图 6a中可以看到3个物理量的时间序列都有明显的的双峰特征。当内波进入视场后, 耗散率增大到一定值后维持不变, 遭遇斜坡地形之后非线性增强, 耗散率也再次上升形成第一个峰值。随后整个场的耗散率都在1s内骤减, 这是因为整个场的脉动速度急剧减小, 而破碎还未发生, 此时耗散率量级同非线性增强前相同。当破碎开始发展后耗散率开始逐渐增大, 形成第二个峰值, 最后随着反射波传播离开视场而减小。图 6b中较大振幅内波的耗散率的第二个峰值远小于第一个峰 , 可能是较大振幅内波在破碎前非线性增强的阶段, 耗散率大大增加, 与之相比破碎阶段的耗散率过小, 不能形成一个显著的峰。对比a中第二个峰的值可以看出两者大小相当, 因此可以认为b中破碎过程耗散第一个峰的能量更多。3个物理量全场平均的时间序列也有类似的双峰特征, 平均湍耗散率和湍动能与最大值时间序列变化较一致; 而不同的是振幅较大时, 平方涡度入射和反射过程的两个峰值大小相当。
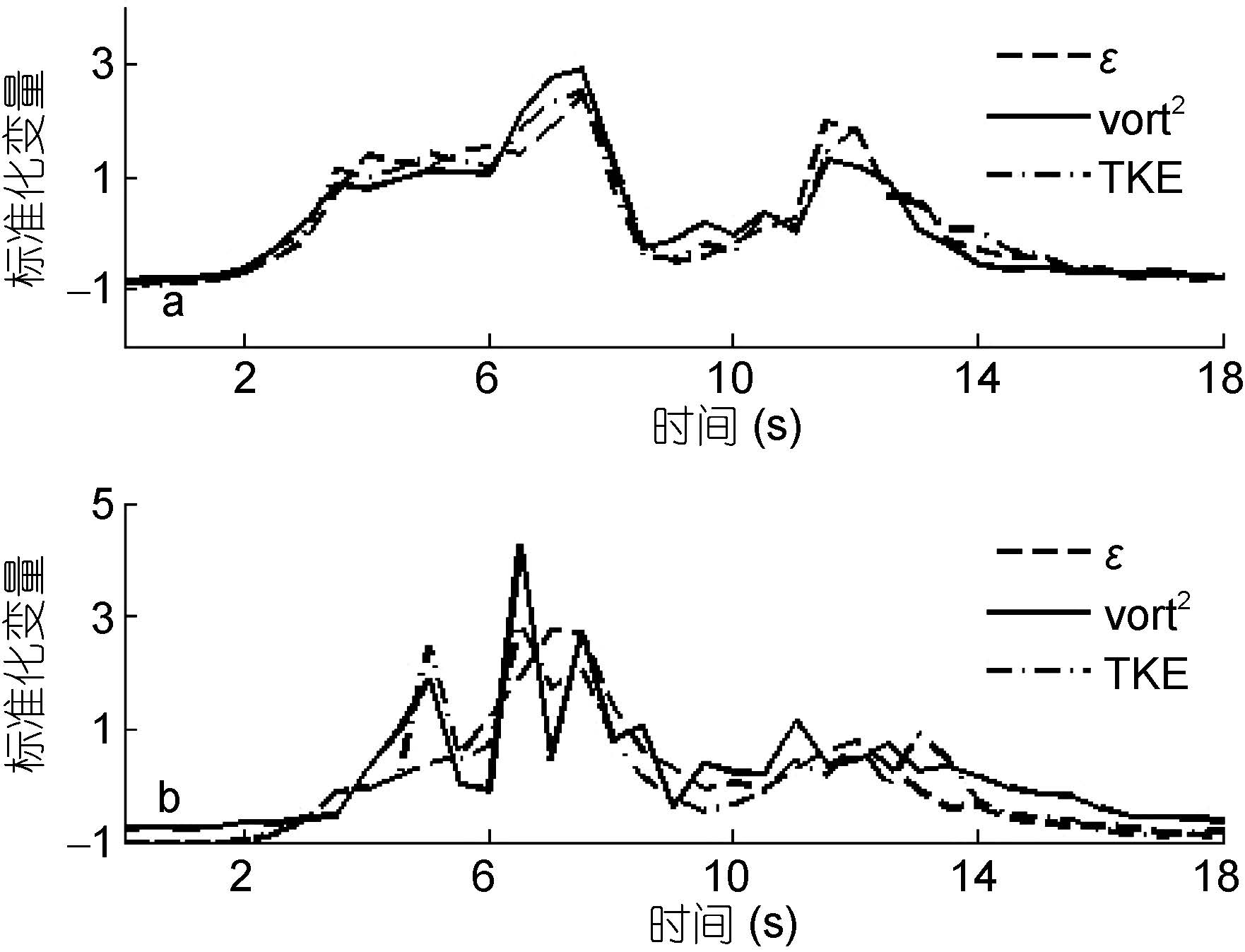 |
| 图 6 标准化最大湍耗散率ε、平方涡度vort2、湍动能TKE的时间序列 Fig. 6 Time series of normalized maximum turbulence dissipation rate, square vorticity, and turbulence kinetic energy(TKE) |
从表 2其他塌陷高度的最大湍耗散率还能够观察到不同角度下内孤立波的耗散率之间的区别: 实验2—4的斜坡角度不断增加, 而实验2和4中8、9cm塌陷高度的耗散率量值大小相当, 这说明尽管振幅变大, 但由于斜坡角度增大, 限制了破碎的发展。这一关系也可以从实验3和4中的9cm塌陷高度的耗散率曲线看出, 同一塌陷高度下, 斜坡角度增大, 造成实验4的耗散率小于实验3, 仅为其一半左右。这一关系可以更明显地从3组实验的小振幅(塌陷高度2cm)内波耗散率中观察到。因为角度增大, 小振幅内波更多的是反射而非破碎, 导致这一阶段的耗散率较小, 最大值仅在10-5m2/s3量级。
| 实验序号- 斜坡角度 Exp-θ(°) | 塌陷 高度 (cm) | 最大湍 耗散率 (10-5m2/s3) | 塌陷 高度 (cm) | 最大湍 耗散率 (10-5m2/s3) |
| 2-18 | 2 | 5.90 | 8 | 14.80 |
| 3-22.8 | 2 | 3.68 | 9 | 32.41 |
| 4-30 | 2 | 1.55 | 9 | 17.75 |
对应图 6a, 两个峰值时刻对应的湍耗散率、湍动能和平方涡度的空间分布如图 7所示, 可以发现3者的分布特征十分相似: 峰值1时刻斜坡上的上下层界面处由于内波的非线性增强而产生了各要素的极大值; 峰值2时刻则是由于破碎后反射波造成的上下层流速剪切形成波后较大的湍流能量耗散。George等(1991)提到涡度的均方根在均质、各向同性假设下与耗散率仅相差一个系数即运动学黏度, 这个结论与本文结果符合较好, 平方涡度与湍耗散率的相关系数在0.7—0.9之间, 相关性较高。由于强剪切的存在, 湍动能在界面处总是很大, 说明此处有很强的湍流扰动, 脉动速度有跨越等密度面的分量。
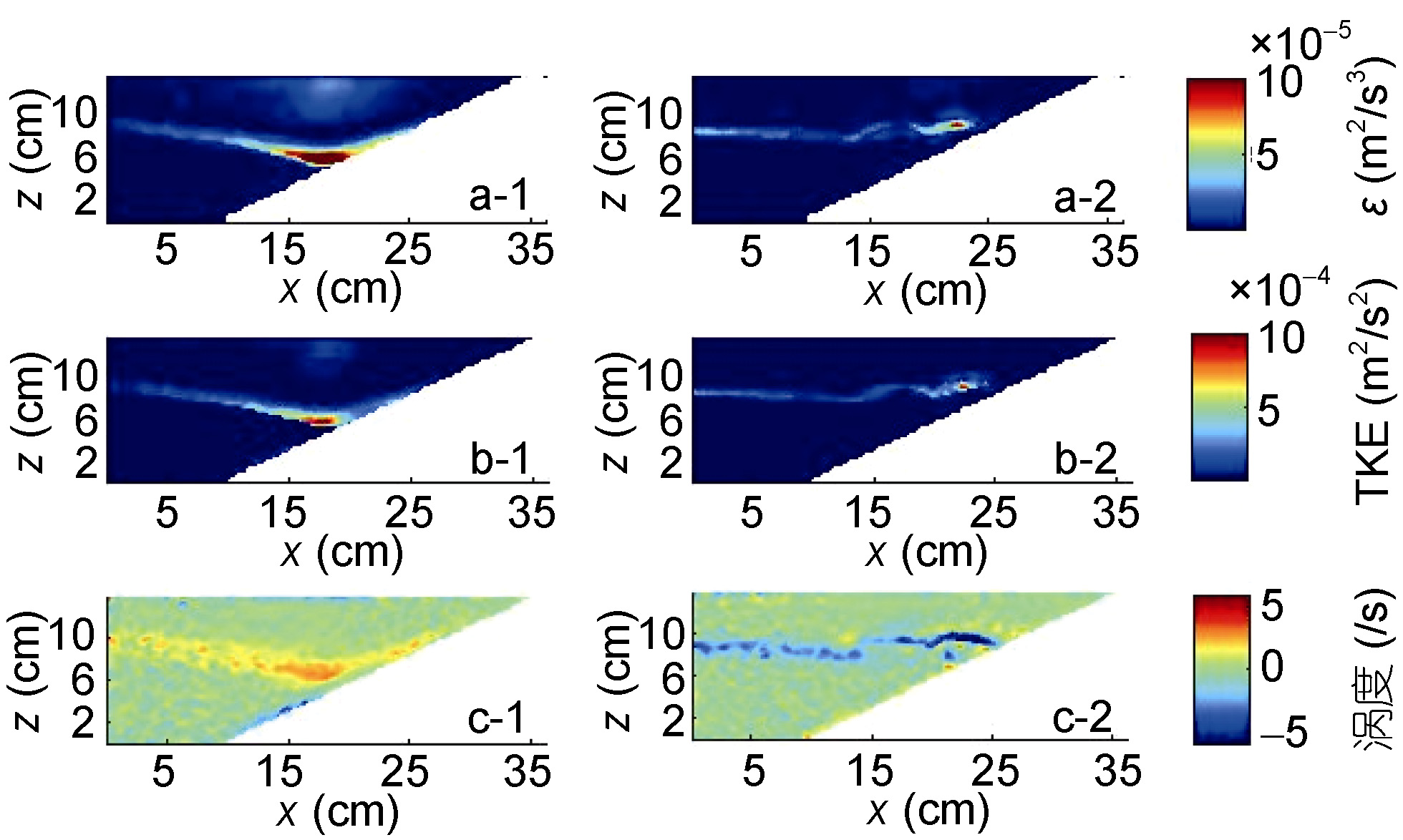 |
| 图 7 两个峰值时刻a: 湍耗散率ε, b: 湍动能TKE和c: 涡度空间分布 Fig. 7 Spatial distribution at the peak time |
取每组实验中最大湍耗散率和湍动能、平方涡度的时间序列中第二个峰值作出其与内孤立波无因次振幅(入射波振幅/上层厚度)关系如图 8所示, 拟合得到关系曲线。由图 8a可以观察到无因次振幅小于0.9时, 振幅与最大湍耗散之间呈平方关系, 而无因次振幅大于0.9, 湍耗散率随振幅增加的趋势变缓或不变, 说明在一定水深、厚度比和密度比的限制下, 内孤立波破碎引起的湍流强度和耗散不会随振幅无限增大。平方涡度、最大湍动能与入射波振幅呈平方关系。
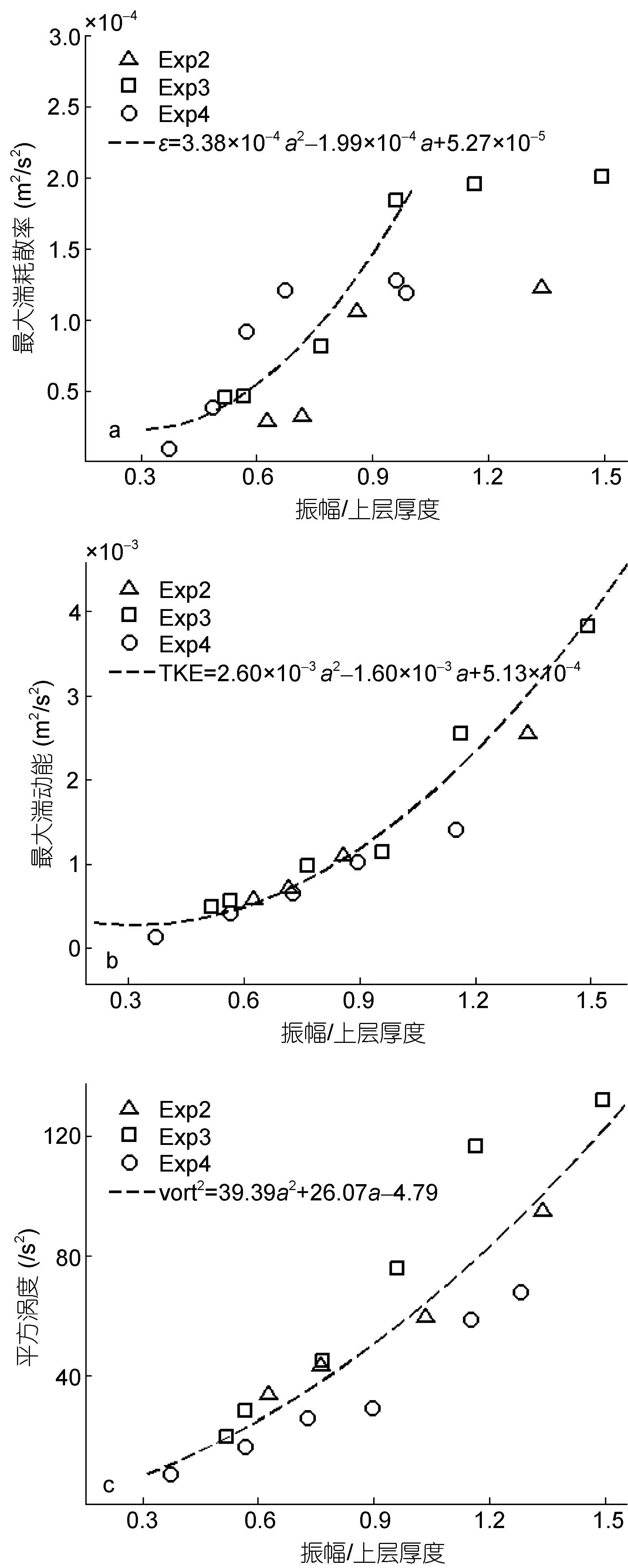 |
| 图 8 最大湍耗散率ε(a)、湍动能TKE(b)和平方涡度vort2(c)与无因次入射波振幅关系 Fig. 8 The fitted line of dimensionless amplitude vs maximum ε(a), TKE(b), and square vorticity(c) |
用时间序列方法求得耗散率分布可以看到, 由于不严格满足各向同性假设, 图 9中a与c的分布特征较为一致, 而两者与b差别较大。随着波的传播波谷逐渐经过断面, 界面处的耗散率增大, 可以观察到破碎时(第8—14s), 在第7s左右波形突然变陡, 斜坡底部也出现了一个耗散率的极大值。随后的反射波形已经难以分辨, 界面处的混合仍然很强, 下层由于湍流扰动也零星分布有较大的耗散率。计算的湍耗散比Moum等(2003)和Klymak等(2008)大1个量级。考虑到实验室测量湍耗散通常大于海洋实测值, 我们认为本文计算的湍耗散率量级是正确的。但是如果要更好地比较海洋与实验室模拟的内孤立波界面处的湍耗散, 还需要改变实验设置中的层结条件, 这仍有待进一步的探究。
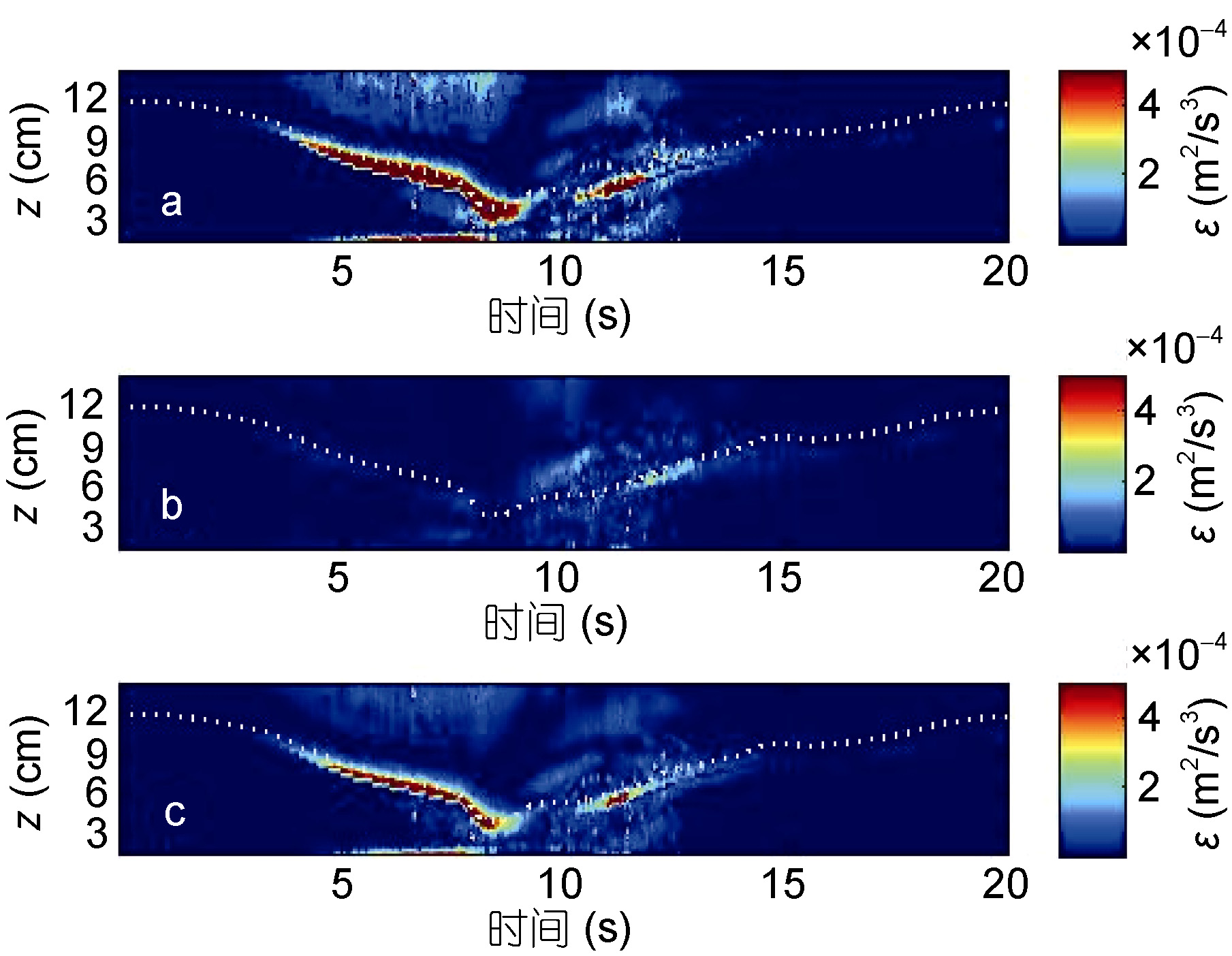 |
| 图 9 实验3塌陷高度η=9cm, x=9.8cm断面上湍耗散率的时间序列 Fig. 9 The time series of turbulence dissipation rate when η=9cm, x=9.8cm in Experiment 3 |
下面就实验和计算中可能出现的误差进行讨论。首先由于实验所用示踪粒子密度约为1.05g/cm3, 介于两层流体密度之间, 导致上层表面不可避免地有一层漂浮的粒子以及上下层界面处粒子聚集, 会使分析速度产生误差。使用PIVlab时采用16×16像素的查询窗口, 即3mm×3mm左右, 可能会平滑掉一些微小的速度脉动, 而且在分析速度的后期处理时手动选取一个流速的范围, 这一步骤有可能会带来误差。在计算过程方面, 脉动速度的计算是本文的一个难题, 也是产生误差的根源。首先因为求平均速度的方法的特殊性, 必须要识别出内孤立波的上下界面, 这一步骤由人工手动完成, 并且只是大致识别几个点, 其它位置由线性插值得到, 并非完全严格地贴合界面; 在内波破碎阶段, 上下层界面十分模糊, 难以识别。在对速度求微分时采用中心差分, 经过与向后差分比较, 发现向后差分造成计算耗散率值偏高。
4 结论与展望本文进行了两层流体第一模态内孤立波传播、在斜坡上破碎、反射的实验室模拟, 得到以下结论:
(1)内孤立波传播的速度场可以用界面的剪切、上下层流速反向来描述。经过地形时内波波前变缓、波后变陡, 等密度面发生翻转, 波面下方产生逆时针的涡旋, 沿斜坡上运动形成冲击水, 反射波的离岸流在界面处造成明显的Kelvin-Helmholtz夹卷。
(2)湍耗散率和湍动能的分布都与涡度十分类似。当内波即将破碎时非线性增强, 这3个量都增大, 然后随着波的变形而迅速降低, 破碎发生后又增大, 最大值在界面靠近斜坡的冲击水后部, 形成时间序列中的两个峰值。
(3)使用直接法和湍流谱拟合法计算的湍耗散率的量级在10-7到10-4m2/s3之间, 比实测海洋内孤立波传播时界面处耗散率以及内潮遇地形破碎的量级范围10-7—10-5m2/s3大1个量级。
(4)各组实验中, 无因次振幅小于0.9时, 全场所有时间内最大湍耗散率与内孤立波振幅呈平方关系。最大湍动能、平方涡度与无因次振幅的关系则呈现良好的平方关系。总体来看, 入射波振幅较小时斜坡角度越大, 破碎越弱; 振幅较大时破碎程度最大的斜坡角度为22.8°。但由于实验次数有限, 该角度值有待检验。
本文在实验室条件下研究内孤立波破碎所致湍耗散, 其条件与实际海洋有很大的差别。本文是实验室内波破碎湍耗散率计算的首次尝试, 仍需更多实验来对以上初步结果进行分析和讨论。
 2016, Vol. 47
2016, Vol. 47


