
中国海洋湖沼学会主办。
文章信息
- 张成网, 王金虎, 陈旭, 徐洋. 2017.
- ZHANG Cheng-Wang, WANG Jin-Hu, CHEN Xu, XU Yang. 2017.
- 内波远距离传播演化的实验研究
- LABORATORY EXPERIMENTS ON LONG-RANGE PROPAGATION AND EVOLUTION OF INTERNAL WAVES
- 海洋与湖沼, 48(3): 475-482
- Oceanologia et Limnologia Sinica, 48(3): 475-482.
- http://dx.doi.org/10.11693/hyhz20161200270
-
文章历史
- 收稿日期:2016-12-05
- 收修改稿日期:2017-02-15
2. 中国海洋大学物理海洋教育部重点实验室 青岛 266100
2. Key Laboratory of Physical Oceanography, Ocean University of China, Qingdao 266100, China
内波是发生在层结稳定海洋内部的一种波动现象, 其回复力主要为弱化重力和科氏力。作为海洋能量级串中非常重要的一个环节(Garrett, 2003), 内波对维持海洋现有背景层结和大尺度环流结构具有非常重要的作用(Munk et al, 1998; Wunsch et al, 2004)。由于内波可以将生成源地附近的能量传递到大洋内部并为海洋混合提供能量, 因此内波的传播和演化问题有十分重要的研究意义(Alford et al, 2007; Zhao et al, 2010)。
内波特殊的频散关系, 决定了内波能量传播方向与水平方向的夹角α满足:
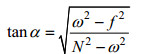 (1)
(1)其中, ω为内波圆频率, f为惯性频率, 在非旋转情况下f=0, 浮性频率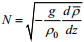
在内波生成源地附近, 现场观测资料和实验室实验结果均证实了内波具有明显的射线结构(Althaus et al, 2003; Cole et al, 2009; 王金虎等, 2016), 其中内波能量沿射线方向传播, 射线与水平方向的夹角满足频散关系(式1)。由于在源地附近, 内波射线容易发生反射(Rodenborn et al, 2011)和共振(Wang et al, 2015)等现象, 因此内波射线能量衰减迅速。Althaus等(2003)通过分析现场全深度剖面资料发现内波射线在经过海表面反射后能量迅速衰减, 同时射线结构不再清晰可见。另一方面, 在远离内波生成源地的大洋内部, 卫星遥感和现场观测资料均发现了低模态斜压内波(Rainville et al, 2006; Zhao et al, 2009)。这些低模态内波携带的能量最远可以传到距离生成源地几千公里的海域(Zhao et al, 2012)。在数值模拟方面, Xu等(2016)指出南海内潮波的能量可以跨越深海盆地传播至距离生成源地1000-1500公里的海域。对于内波射线和低模态内波的关系, 一种普遍的观点是内波射线是由不同垂向模态结构叠加而成, 其中高模态内波在局地发生耗散(Klymak et al, 2010; Johnston et al, 2011)。但是对于内波由射线结构向低模态结构的演变过程缺少必要的现场观测和实验结果。其中现场观测由于空间分辨率较低, 因此无法对内波的传播过程进行准确的刻画(Rainville et al, 2006); 而实验室研究多数只考虑了内波在源地附近的生成问题(Gostiaux et al, 2007; Zhang et al, 2008), 对于生成内波的进一步传播演化缺少足够的研究。综上所述内波在源地生成后的传播演化过程还缺少清晰的物理图像。
本文通过实验研究内波在源地生成后的传播演化规律。为了同时观测内波的近场和远场结构, 实验中同时采用两台CCD相机对实验区域进行拍摄。使用粒子图像测速法(PIV)(Dalziel et al, 2007)测量得到内波在不同区域的速度场, 根据实验结果分别对内波在近场和远场的时空结构进行分析。实验结果定量给出了内波能量的衰减过程, 并讨论了低模态内波的传播规律。
1 实验与方法 1.1 实验设置本文的实验是在中国海洋大学物理海洋重点实验室的二维内波水槽中进行的, 二维水槽长500cm, 宽15cm, 高40cm。为了模拟海洋中的分层现象, 实验中采用经典的“双缸法”(Hill, 2002)放置了深度为14.8cm的线性分层水, 实验中分层水的密度剖面通过电导率仪进行测量, 浮力频率N=1.04rad/s。为了在实验过程中保持流动的二维性, 实验中使用与二维水槽具有同样宽度的模型地形。如图 1所示, 模型地形为顶部用圆弧连接的三角形, 地形长32.0cm, 高6.8cm, 斜面坡度为24.5°。地形顶部圆弧的弧度为49°, 圆弧半径为4.4cm。为了模拟海洋中的正压潮流, 实验中利用偏心圆柱使地形产生正弦运动, 其中偏心圆柱的偏心距为0.5cm, 远小于模型地形的水平尺寸。偏心圆柱通过电机驱动, 实验中圆频率ω=0.42。模型地形被放置在一块薄PVC板上, 板子通过金属件与驱动装置相连。在实验中我们将坐标系建立在模型地形的中心位置, 地形底部中心为坐标原点, 水槽的长度方向为x轴, 高度方向为z轴。由此可以得到正压潮流的流速U(t)满足关系式(2)
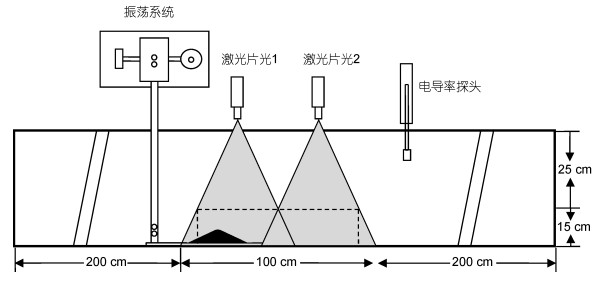 |
| 图 1 实验装置示意图 Fig. 1 The sketch of the experiment setup |
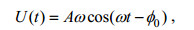 (2)
(2)其中, A为地形的最大位移, 即偏心圆柱的偏心距, ω为振荡圆柱的圆频率, Φ0为流速的初始相位。在实验中我们将零时刻定义为正压潮流由x轴正方向转为负方向的时刻, 因此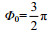
内波的速度场通过粒子图像测速法(PIV)(Dalziel et al, 2007)进行定量测量。在实验中由于需要同时测量内波近场和远场的速度, 因此采用了双PIV系统。双PIV系统由两个光源系统、两个CCD相机和示踪粒子组成。其中光源系统采用两个功率为3W的激光器, 其发射的激光通过柱形凹透镜展片后展成0.5mm厚的片光, 利用这一片光将观测平面内的粒子照亮。实验中采用的示踪粒子为聚苯乙烯粉末, 直径为50μm, 密度约为1040kg/m3。实验中分别用两个CCD摄像机对内波近场和远场区域进行拍摄。在实验室内波研究中, 由于其尺度远小于真实海洋, 耗散作用较强。因此本文将近场区域定义为内波生成源点到内波经过表面和底部反射之间的区域, 远场区域定义为内波射线经过两次反射以外的区域。CCD相机的镜头焦距为50mm, 像素为1600×1200, 每个像素点对应的实际距离为0.3mm。对于每次实验, 在地形振荡10个周期后进行图像采集, 此时内波流速到达稳定状态; 采集8个周期的内波流速, 每个周期采集20张图像。
1.2 数据分析对于采集的原始图像利用PIVlab程序包进行流场计算(Thielicke et al, 2014)。本实验中每个子窗口的大小为8个像素点。接下来将分析得到的流场数据插值到标准的网格点上, 网格点水平和垂直方向的分辨率均为0.25cm。由于实验中采用单一强迫源, 因此内波能量主要集中在强迫频率内。为了更好地展示实验结果, 我们采用带通滤波的方法提取基频部分的内波流速。滤波时采用4阶Butterworth滤波器, 选取谱峰值1/10所对应的频率作为截止频率, 这样既可以排除噪音信号的干扰又可以最大程度的提取内波能量。为了便于比较实验结果, 文中定义了内波归一化流速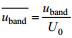
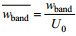
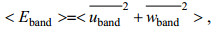 (3)
(3)其中, 
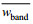
为了分析内波的垂向结构, 我们对带通滤波后的内波流速uband, wband进行垂向模态分解, 控制其垂向结构的本征方程(Gill, 1982)为:
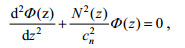 (4)
(4)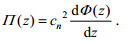 (5)
(5)其中, Φ(z)和Π(z)分别为垂向流速wband和水平流速uband的垂向模态函数。式(4) 的边界条件采用平底刚盖边界条件, 即Φ(0)。N为浮性频率, 在实验中N为常数。Cn为第n个模态的本征值, 在非旋转情况下也为第n个模态内波对应的相速度, H为水深。在计算中我们用前10个模态对实测流速进行拟合, 进而得到各模态垂向流速和水平流速的振幅An和Bn。前三个模态对应的Φ(z)和Π(z)以及各模态的本证值Cn如图 2所示。为了计算各模态能量在传播中的变化规律, 参照内波的归一化强度 < Eband > 定义了各模态内波的归一化强度 < En > :
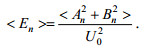 (6)
(6)
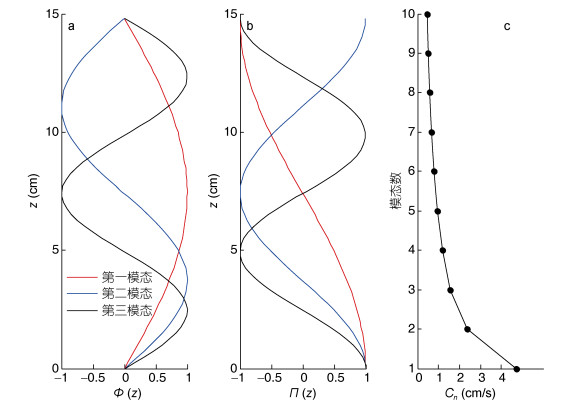 |
| 图 2 内波流速的垂向模态结构和各模态的本征值 Fig. 2 Modal structures and eigenvalues of the internal wave 注: a:垂向流速的垂向模态函数Φ(z); b:水平流速的垂向模态函数Π(z); c:各模态的本征值Cn |
内波近场区域的归一化流速矢量图(图 3)给出了内波归一化水平流速和垂向流速在一个正压潮周期内的空间分布情况。图 3a、b、c、d为

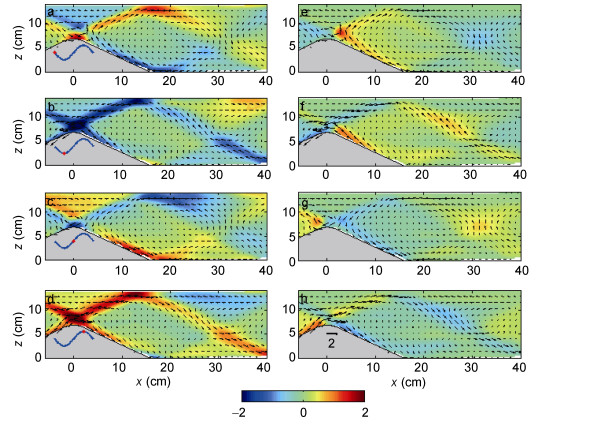 |
图 3 近场区域内波归一化流速在不同时刻的矢量图
Fig. 3 Near-field normalized velocity vectors at different moment
注:左侧四张图表示水平带通流速 , 右侧四张图表示垂向带通流速 , 右侧四张图表示垂向带通流速 。红色圆点代表正压潮相位 。红色圆点代表正压潮相位
|
图 4给出了内波归一化流速矢量在远场区域的分布情况。在远场区域, 由于内波射线经过了表面和底层两次反射, 高模态内波能量衰减显著, 因此射线结构较近场(图 3)相比不再清晰可见。这一结果与Althaus等(2003)在夏威夷海域的现场观测结果较为一致。另一方面, 在远场区域依然存在较为清晰的低模态内波, 这一特点尤其体现在低模态内波的水平流速上。由图 4a、b、c、d可以发现低模态内波信号在一个正压潮周期内向x轴正方向传播。在图 4a、b中可以发现低模态内波表层水平流动的流向为x轴负方向, 底层水平流动的流向为x轴正方向; 在图 4c、d中可以发现低模态内波表层水平流动的流向为x轴正方向, 底层水平流动的流向为x轴负方向。这是因为在实验中远场区域的观测范围接近于第一模态内波的半波长(L1/2=35.4cm)。
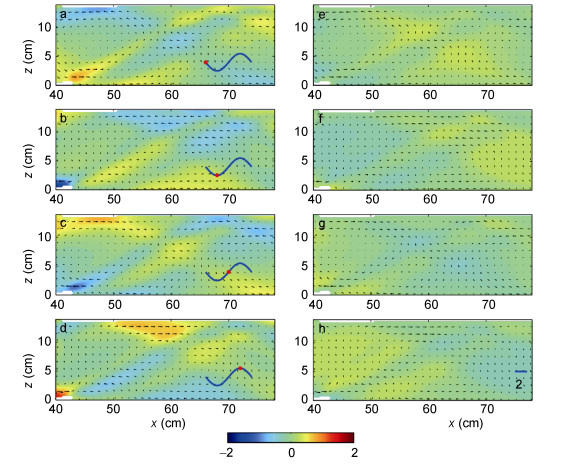 |
| 图 4 远场区域内波归一化流速在不同时刻的矢量图 Fig. 4 Far-field normalized velocity vectors at different moment |
我们将内波近场和远场的测量结果进行合并, 得到一个正压潮周期内内波水平归一化流速

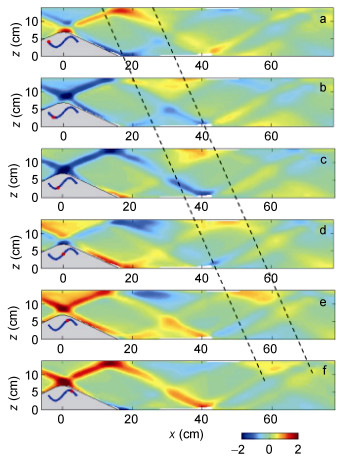 |
图 5 内波水平归一化流速  |
为了定量给出这一低模态内波传播的相速度, 我们给出了内波表层(z=14cm)水平归一化流速
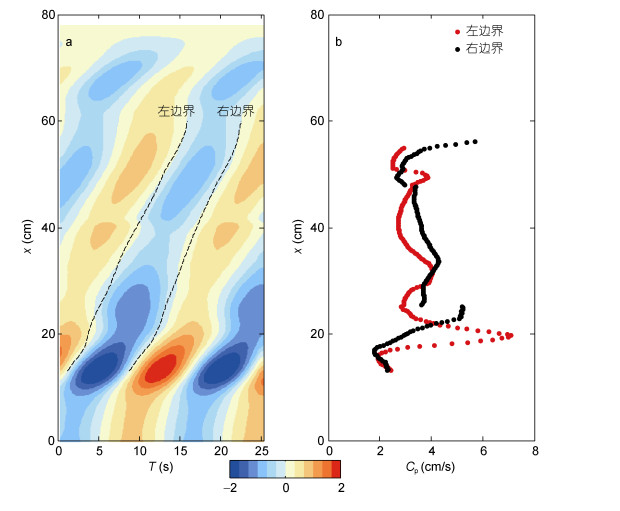 |
图 6 内波表层水平流速的时间断面图及低模态内波相速度
Fig. 6 Time section of surface horizontal velocity of internal waves and the phase speed Cpof low-mode internal waves
注: a:内波表层(z=14cm)水平归一化流速 的时间断面分布图; b:由左右边界计算得到的低模态内波相速度 的时间断面分布图; b:由左右边界计算得到的低模态内波相速度
|
图 7a为内波归一化强度 < Eband > 的空间分布图, 为了更清晰地分析内波能量, 图中颜色条的坐标采用了对数坐标。由图可知在地形上方内波能量主要集中在内波射线范围内, 这与以往的内波实验观测结果较为一致(Wang et al, 2015)。当内波射线离开地形经过表面反射后, 内波射线能量显著减弱。我们分别在入射内波射线和反射内波射线上定义了三条线段, 如图 7a中黑色线段所示。对三条线段上内波强度 < Eband > 积分, 得到内波射线在反射前后和传播过程中的能量变化情况, 积分范围为各线段上内波能量极值1/10所对应的区域。其中在反射前, 内波射线(线段1) 的积分强度为5.85, 在反射后内波射线不同位置处(线段2和线段3) 的积分强度分别为2.82和3.24。由此可知, 内波射线反射后的平均强度约为反射前的51.8%, 这表明内波射线在经过反射时能量损失显著。另一方面, 内波射线在传播过程中由于发生耗散, 能量沿射线传播方向应逐渐减弱。但是反射内波射线在下游位置(线段3) 的能量却大于反射射线上游位置(线段2)。造成这一现象的原因是地形底部生成的内波射线与地形顶部生成的内波射线发生了非线性相互作用, 进而造成了内波能量空间上的不对称性。其中加强区的内波能量较减弱区的内波能量增加了15%。
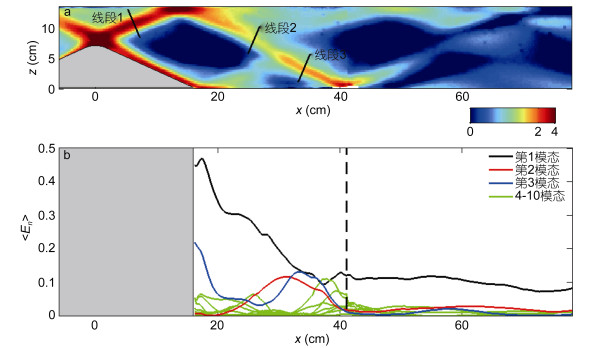 |
| 图 7 各模态内波归一化强度分布图 Fig. 7 Diagram of the normalized internal wave strength in different vertical modes 注: a:内波归一化强度 < Eband > 的空间分布图。b:各垂向模态内波的归一化强度 < En > 沿x轴的分布。黑色虚线为近场区域和远场区域的分界线。 |
图 7b为各垂向模态内波的归一化强度 < En > 沿x轴的变化。其中地形上方由于水深变化剧烈, 不宜进行垂向模态分解, 因此用灰色阴影标记。在地形以外区域给出了前十个垂向模态内波能量 < En > 的变化情况。如图所示, 在近场区域各模态能量均发生显著衰减, 同时各模态内波的极值位置分布存在差异。这是由于在这一区域进行垂向模态分解时受到了地形底部生成内波射线的影响, 对于内波射线的相互作用区域需要用高模态内波进行拟合, 因此各模态内波的变化规律较为复杂。在内波的远场区域(图 7b中黑色虚线以外区域), 由于高模态内波能量衰减显著, 因此能量主要集中在垂向第一模态内波上。在这一区域第一模态内波能量基本保持不变, 如图 7b中黑线所示。而高模态能量迅速衰减(4—10模态), 如图 7b中绿线所示。第二、三模态内波能量也远小于第一模态内波能量。其中第一模态内波归一化能量 < E1 > 约为0.09;第二模态和第三模态的归一化能量振幅 < E2 > 、< E3 > 分别为0.02和0.01。第一模态内波的能量在远场传播过程中衰减缓慢, 在远场范围内(约第一模态内波半波长)损失约为20%。
3 结论本文通过实验室研究的方法定量分析了内波的远距离传播演化规律, 得出以下结论:
(1) 在内波生成的近场区域内波主要表现为射线结构, 但在内波射线外的阴影区域仍然有内波能量分布。由于内波射线的相互作用, 造成了内波射线能量在空间上出现非对称性。加强区域的内波射线能量较减弱区的内波能量增加15%。
(2) 在内波传播的远场区域, 高模态内波能量衰减显著, 内波射线结构不再清晰可见。实验中存在一个明显的低模态内波信号。其传播相速度Cp= 3.05cm/s, 介于理论的第一模态和第二模态相速度之间。
(3) 内波射线的能量在反射时衰减显著, 内波能量损失约为50%。在远场区域, 内波能量主要集中在第一模态, 在第一模态内波半波长的距离上能量损失约为20%。
| 王金虎, 陈旭, 徐洋, 2016. 粗糙地形对内波生成影响的实验研究. 海洋与湖沼, 47(4): 707–713 |
| Alford M H, Zhao Z X, 2007. Global patterns of low-mode internal-wave propagation. Part Ⅱ:group velocity. J Phys Oceanogr, 37(7): 1849–1858 DOI:10.1175/JPO3086.1 |
| Althaus A M, Kunze E, Sanford T B, 2003. Internal tide radiation from Mendocino Escarpment. J Phys Oceanogr, 33(7): 1510–1527 DOI:10.1175/1520-0485(2003)033<1510:ITRFME>2.0.CO;2 |
| Cole S T, Rudnick D L, Hodges B A, et al, 2009. Observations of tidal internal wave beams at Kauai Channel, Hawaii. J Phys Oceanogr, 39(2): 421–436 DOI:10.1175/2008JPO3937.1 |
| Dalziel S B, Carr M, Sveen J K, et al, 2007. Simultaneous synthetic schlieren and PIV measurements for internal solitary waves. Meas Sci Technol, 18(3): 533–547 DOI:10.1088/0957-0233/18/3/001 |
| Garrett C, 2003. Internal tides and ocean mixing. Science, 301(5641): 1858–1859 |
| Gill A E, 1982. Atmosphere-Ocean Dynamics. London: Academic Press, 662 |
| Gostiaux L, Dauxois T, 2007. Laboratory experiments on the generation of internal tidal beams over steep slopes. Phys Fluids, 19: 028102 DOI:10.1063/1.2472511 |
| Hill D F, 2002. General density gradients in general domains:the "two-tank" method revisited. Exp Fluids, 32(4): 434–440 DOI:10.1007/s00348-001-0376-5 |
| Johnston T M S, Rudnick D L, Carter G S, et al, 2011. Internal tidal beams and mixing near Monterey Bay. J Geophys Res, 116(C3): C03017 |
| Klymak J M, Legg S, Pinkel R, 2010. A simple parameterization of turbulent tidal mixing near supercritical topography. J Phys Oceanogr, 40(9): 2059–2074 DOI:10.1175/2010JPO4396.1 |
| Munk W, Wunsch C, 1998. Abyssal recipes II:energetics of tidal and wind mixing. Deep Sea Res Part I, 45(12): 1977–2010 DOI:10.1016/S0967-0637(98)00070-3 |
| Rainville L, Pinkel R, 2006. Baroclinic energy flux at the Hawaiian Ridge:observations from the R/P FLIP. J Phys Oceanogr, 36(6): 1104–1122 DOI:10.1175/JPO2882.1 |
| Rodenborn B, Kiefer D, Zhang H P, et al, 2011. Harmonic generation by reflecting internal waves. Phys Fluids, 23(2): 026601 DOI:10.1063/1.3553294 |
| Thielicke W, Stamhuis E J, 2014. PIVlab-towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J Open Res Softw, 2(1): e30 |
| Wang J H, Chen X, Wang W, et al, 2015. Laboratory experiments on the resonance of internal waves on a finite height subcritical topography. Ocean Dyn, 65(9-10): 1269–1274 DOI:10.1007/s10236-015-0874-2 |
| Wunsch C, Ferrari R, 2004. Vertical mixing, energy, and the general circulation of the oceans. Annu Rev Fluid Mech, 36: 281–314 DOI:10.1146/annurev.fluid.36.050802.122121 |
| Xu Z H, Liu K, Yin B S, et al, 2016. Long-range propagation and associated variability of internal tides in the South China Sea. J Geophys Res, 121(11): 8268–8286 DOI:10.1002/jgrc.v121.11 |
| Zhang H P, King B, Swinney H L, 2008. Resonant generation of internal waves on a model continental slope. Phys Rev Lett, 100(24): 244504 DOI:10.1103/PhysRevLett.100.244504 |
| Zhao Z X, Alford M H, 2009. New altimetric estimates of mode-1 M2 internal tides in the central North Pacific Ocean. J Phys Oceanogr, 39(7): 1669–1684 DOI:10.1175/2009JPO3922.1 |
| Zhao Z X, Alford M H, Girton J B, 2012. Mapping low-mode internal tides from multisatellite altimetry. Oceanography, 25(2): 42–51 DOI:10.5670/oceanog |
| Zhao Z X, Alford M H, MacKinnon J A, et al, 2010. Long-range propagation of the semidiurnal internal tide from the Hawaiian Ridge. J Phys Oceanogr, 40(4): 713–736 DOI:10.1175/2009JPO4207.1 |
 2017, Vol. 48
2017, Vol. 48


