中国海洋湖沼学会主办。
文章信息
- 袁业立, 庄展鹏, 杨光兵. 2017.
- YUAN Ye-Li, ZHUANG Zhan-Peng, YANG Guang-Bing. 2017.
- 湍流混合输运通量的数学物理描述基础——高确定性闭合的湍流二阶矩和基本特征量控制方程组
- BASIS OF MATHEMATICAL AND PHYSICAL DESCRIPTION FOR TURBULENCE MIXING TRANSPORT FLUXES——THE GOVERNING EQUATIONS FOR HIGH-DETERMINACY CLOSURE TURBULENCE SECOND-ORDER MOMENT AND THE BASIC CHARACTERISTICS
- 海洋与湖沼, 48(5): 895-911
- Oceanologia et Limnologia Sinica, 48(5): 895-911.
- http://dx.doi.org/10.11693/hyhz20170300075
-
文章历史
- 收稿日期:2017-03-28
- 收修改稿日期:2017-06-09
2. 青岛海洋科学和技术国家实验室区域海洋动力学与数值模拟功能实验室 青岛 266237
2. Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, China
在Yuan等(2012)的文章中, 按照系统科学关于子系统划分的控制机制原则(许国志, 2000), 考虑Boussinesq近似海洋运动方程组所显示的控制力及其平衡状态(Kamenkovich, 1977), 可将海洋运动区隔为控制机制互不叠置的四类。它们分别为: (1) 湍流, 它是分子黏性-传导-扩散力控制的次小尺度运动, 不论这种控制力是静态平衡的, 还是动态平衡的。湍流的近各向同性统计属性是给出高确定性二阶矩闭合原理的数学物理基础。(2) 波动, 它主要包括海浪和内波, 是受重力控制和处于动态平衡的运动。重力波动是一类可以用局域时间平稳和水平均匀来描述的小尺度和次中尺度运动。(3) 涡旋, 它是受重力控制和处于静态平衡的亚中尺度运动。这里, 涡旋暂时是一类完全用定义来规定的海洋运动。它和波动是一对运动, 同样受重力控制, 只是分别处于不同的平衡状态。(4) 环流, 是所有剩余较大尺度运动的总和, 它主要受地转力控制, 也包括受引潮力和热学-化学力控制的中尺度和大尺度运动。
这里所给出的海洋运动四类划分办法, 前两类的湍流和波动, 其定义与Wunsch等(2004)所给出的一样。第三类的涡旋专门指受重力控制和处于静态平衡的亚中尺度运动。至于第四类的环流主要指剩余较大尺度运动的总和。值得注意的是按定义规定的涡旋类运动, 它既不是地转力控制的中尺度涡旋, 也不是构成湍流结构的大、小涡旋。它实际上是一种重力涡旋, 是对环流起侧向混合作用的运动主体。
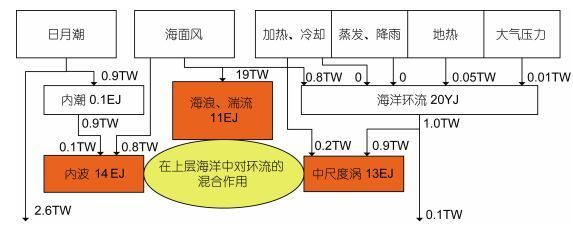 |
|
图 1 对环流起混合作用的三个主要运动模块及其与环流之间的能量学关联示意图 Fig. 1 The schematic diagram of the three main mixing modules to the general circulation as well as their energetic relevance 注:最上层方框表示一些可能的能量输入源, 第二、第三层方框为海洋中主要的能量蓄积形式。给出不同蓄积形式所含能量的估计值, 单位为EJ (1018J)、YJ (1024J), 并给出输入源到能量蓄积、不同能量蓄积形式之间以及能量蓄积向外输出的能量估计值, 单位为TW (1012W)。海浪等中小尺度运动(红色方框)以上层海洋混合(黄色椭圆)的形式将能量耗散或输送到环流, 使能量平衡得以维持。 [引自Wunsch等(2004)图 5] |
考虑到有严格控制机制定义的前三类运动:湍流、波动和涡旋, 都与环流有明显的时-空尺度差异, 且表现出一定程度的随机性, 本文将采用理论上具有各态历经含义, 分别在前三类运动集合上定义的Reynolds平均, 代替有更多各态历经不确定性的时-空区间Reynolds平均, 作为运动类分解的基本运算。它们分别是
(1) 在湍流集合上定义的Reynolds平均
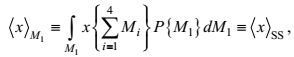 (1)
(1)其中
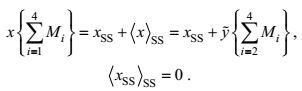 (2)
(2)(2) 在波动集合上定义的Reynolds平均
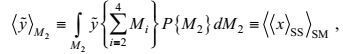 (3)
(3)其中
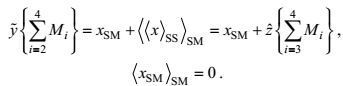 (4)
(4)(3) 在涡旋集合上定义的Reynolds平均
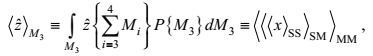 (5)
(5)其中
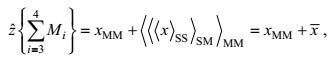
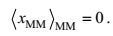 (6)
(6)这里, M1、M2、M3、M4分别表示湍流、波动、涡旋、环流的运动集合, 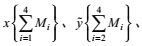
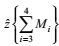
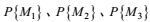
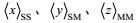
将所定义的这三种Reynolds平均依次作用于Boussinesq近似的海洋运动方程和边界条件, 经过简单的分解演算, 可得到湍流、波动、涡旋、环流四类运动的控制方程组集。容易证明, 四类运动控制方程组集是海洋运动控制方程组的分解, 而后者又是前者的合成。海洋运动控制方程组和所分解的四类运动控制方程组集是描述各类海洋运动相互作用的, 自洽的和一致的控制方程组集。
在海洋动力系统框架下忽略温度方程的压力作用部分, 湍流控制方程可以写成:
运动方程:
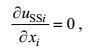 (7)
(7)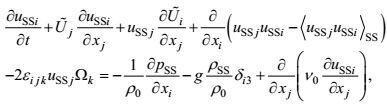 (8)
(8)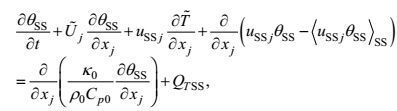 (9)
(9)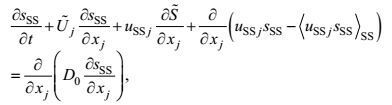 (10)
(10)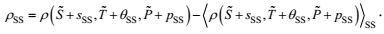 (11)
(11)边界条件:
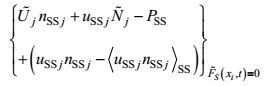 (12)
(12)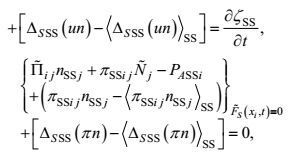 (13)
(13)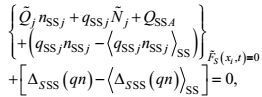 (14)
(14)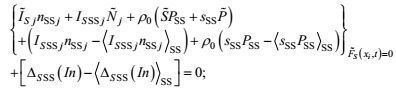 (15)
(15)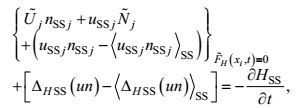 (16)
(16)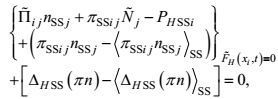 (17)
(17)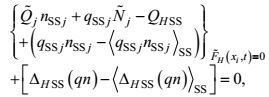 (18)
(18)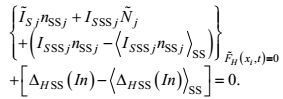 (19)
(19)其中分子动量通量、热量通量和盐量通量可写成Newton形式
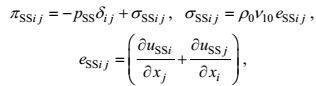 (20)
(20)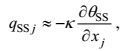 (21)
(21)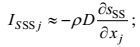 (22)
(22)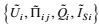
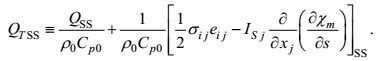 (23)
(23)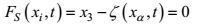
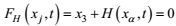
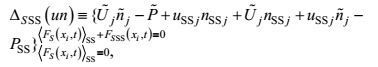 (24)
(24)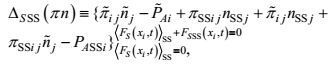 (25)
(25)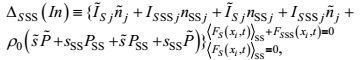 (26)
(26)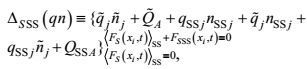 (27)
(27)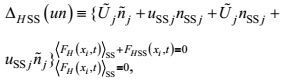 (28)
(28)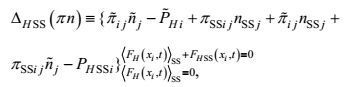 (29)
(29)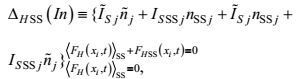 (30)
(30)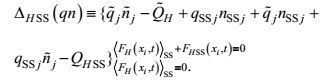 (31)
(31)这里, 运动方程表明, 湍流的局域变化, 除受非线性力偏差、重力、地转力、压力梯度力的作用以外, 还受较大尺度运动, 即波动-涡旋-环流合成运动的平流输运、速度剪切和温度-盐度梯度的生成作用, 以及受较小尺度运动, 即分子运动的黏性-传导-扩散作用。边界条件表明, 在海面和海底上湍流受淡水、动量、热量和盐量的分子输运通量作用。
鉴于在其他类运动控制方程组中, 湍流总是以输运通量剩余项的形式对它们起着搅拌混合的作用, 所以, 高确定性闭合二阶矩和基本特征量控制方程的导出, 它们的解析或数值求解以及湍流搅拌混合系数的解析估计等就成为湍流动力学研究的主要课题。
1.2 湍流二阶矩控制方程的导出为简单起见, 仅以符号
运动方程
 (32)
(32)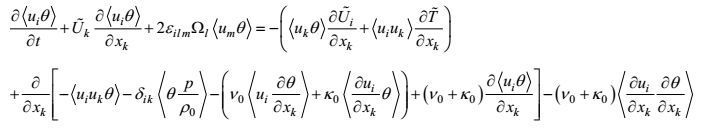 (33)
(33)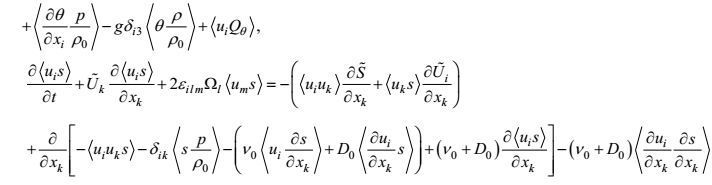 (34)
(34)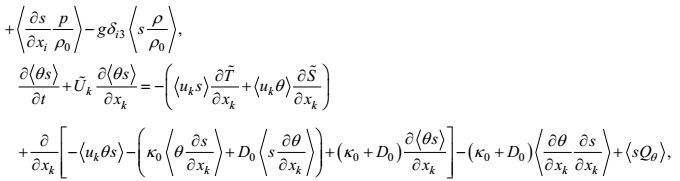 (35)
(35)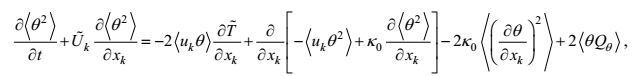 (36)
(36)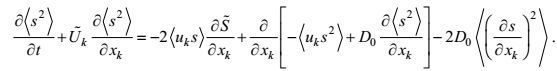 (37)
(37)边界条件
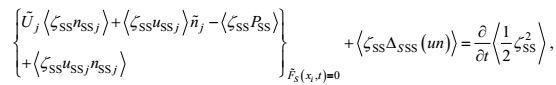 (38)
(38)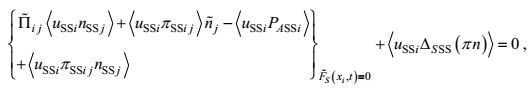 (39)
(39)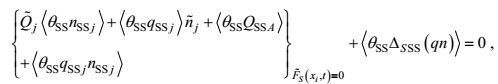 (40)
(40)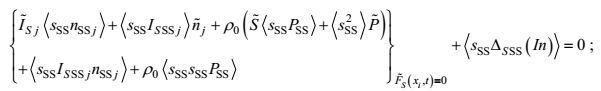 (41)
(41)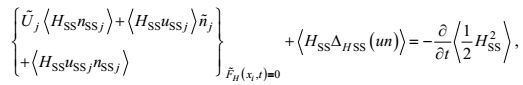 (42)
(42)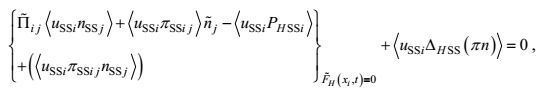 (43)
(43)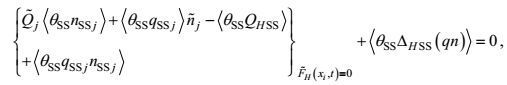 (44)
(44)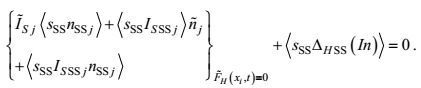 (45)
(45)虽然15个二阶矩方程对15个二阶矩是封闭的, 13个海面海底边界条件对13个二阶矩输入通量也是确定的。但是由于在方程中有三阶矩、变形-压力和梯度-压力项, 在边界条件中有三阶矩和边界替代附加项的出现, 这里的封闭和确定实际上只是形式的。所导出的湍流二阶矩控制方程还需要作非二阶矩项的闭合处理。
2 高确定性闭合的湍流二阶矩控制方程 2.1 高确定性的湍流二阶矩闭合原理所谓二阶矩闭合原理指的是, 按分子黏性-传导-扩散力控制的次小尺度湍流所具有的近各向同性属性和所遵守的物理规律所提出的非二阶矩项闭合处理办法(是勋刚, 1994)。所谓高确定性指的是, 按海洋湍流的最新研究成果(Baumert et al, 2005), 所给出的闭合有量纲参变量和无量纲系数普适形式。这种高确定性闭合原理可以归纳为五条。
(1) 非二阶矩项可以用湍流二阶矩: 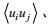
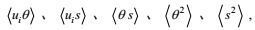

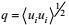
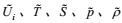
(2) 非二阶矩项的闭合结果应与原始项有相同的物理属性, 闭合模拟结果不应出现物理上不可能的量值和现象。非二阶矩项的闭合结果应与原始项有相同的数学属性, 如对称性、不变性、置换性、迹等于零等。
(3) 非二阶矩项的闭合结果应与原始项有相同的量纲, 可以按量纲分析的π定理给出它们的闭合表示或按Fourier律表示的与合成运动梯度比例的湍流输运通量表示。这些关系式的有量纲参变量和无量纲系数可以按其量纲分析表示和湍流基本物理模型特征尺度高确定地给出。
(4) 湍流的基本物理模型是它的大、小涡旋结构。两类涡旋的基本量纲量和特征尺度可分别高确定性地表示为: (A)大涡旋特征尺度, 以特征量k和ε作为基本量纲量, 可以高确定性地表示为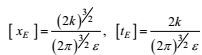
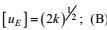
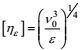
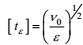
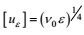
采用更有直观意义的大涡旋基本量纲量:混合长度lD和速度模q, 其特征尺度可分别表示为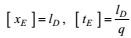
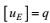
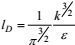
(5) 作为湍流的基本物理模型, 其大、小涡旋被认为满足两种结构属性, (A)动能结构不变性, 即有大、小涡旋的动能梯度不变关系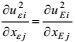
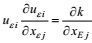
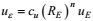
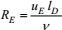
按所提出的高确定性闭合原理, 本文对所导出的二阶矩方程组, 作各非二阶矩项的闭合处理。
2.2.1 闭合的湍流速度-速度二阶矩方程速度-速度二阶矩方程(32) 的闭合主要包括
(1) 输运通量剩余项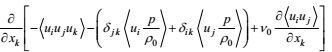
湍流输运是一种大涡旋行为。按所引入的闭合原理第一、二和三条, 速度-速度输运通量剩余项可写成
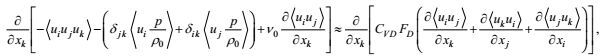 (46)
(46)其中量纲为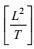
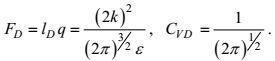 (47)
(47)(2) 分子耗散项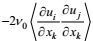
分子耗散是一种小涡旋行为。在严格各向同性情况下, 分子耗散项可以写成
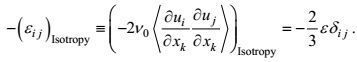 (48)
(48)比拟这个结果, 按闭合原理的第一条, 近各向同性的分子耗散项可写成
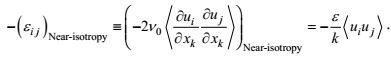 (49)
(49)为了构成变形-压力项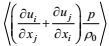
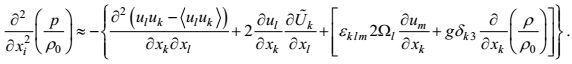 (50)
(50)如果所关注的空间点与边界(自由海面和固体海底)的距离较大于Poisson方程基本解的影响半径, 这样, 方程的解可写成右端项在无限空间中的基本解积分形式
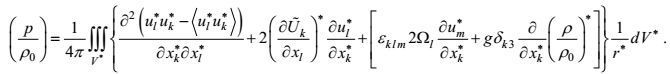 (51)
(51)这里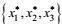
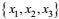
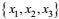
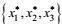
进一步, 取变形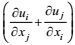
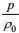
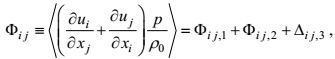 (52)
(52)其中
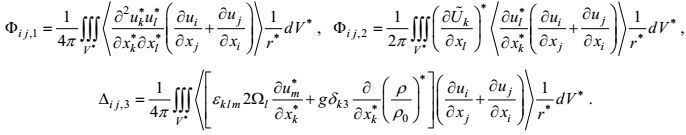 (53)
(53)(3) 第一变形-压力项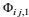
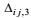
考虑到第一和第三变形-压力项仅与湍流量有关, 而第二变形-压力项则含有一个合成运动因子, 可先在合成运动速度空间变化为零的情况下, 讨论第一和第三变形-压力项的闭合处理。这时, 变形-压力项退化为
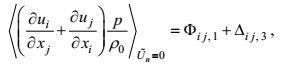 (54)
(54)速度-速度二阶矩方程退化为
 (55)
(55)a. 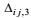
可以证明(见是勋刚, 1994), 对于无限空间中的任意内点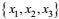
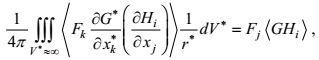 (56)
(56)其中Fk为任意常数向量, G和Hi为任意广义的标量函数和向量函数。实际上, 对远离边界的任意点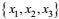
由表示式(53) 的第三式和积分关系(56), 在远离边界的内点上, 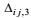
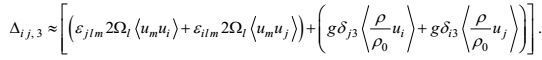 (57)
(57)b. 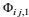
将所导得的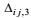
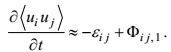 (58)
(58)引入湍流的非各向同性量度量
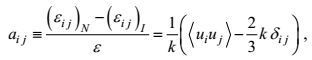 (59)
(59)则有
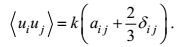 (60)
(60)这样, 将这个表示式代入退化方程(58), 考虑到动能耗散率的定义式: 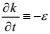
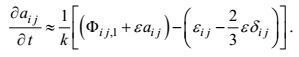 (61)
(61)由于这个方程右端方括号内的第二个圆括号都是迹为零的, 因此, 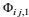
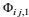
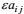
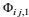
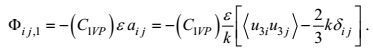 (62)
(62)这里, (C1VP)为所引入的无量纲第一变形-压力系数。
(4) 第二变形-压力项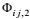
同样, 考虑到合成运动的空间尺度远大于Poisson方程基本解的影响半径, 对合成运动因子做中值处理后, 第二变形-压力项可以写成两个因子的乘积形式
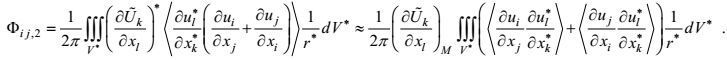 (63)
(63)考虑第二变形-压力项的数学属性和非二阶矩项闭合原理的第一和第三条, 仅与湍流速度有关的后一因子可写成速度二阶矩的线性形式, 它按下标k, l与合成运动速度梯度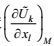
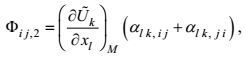 (64)
(64)其中
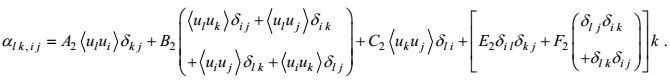 (65)
(65)这里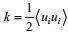
a.第一运动学条件, 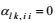
由于第二变形-压力项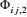
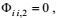
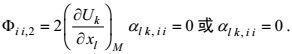 (66)
(66)这就是所谓的第一运动学条件。将表示式(65) 代入第一运动学条件, 则可得
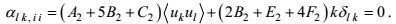 (67)
(67)这样, 有待定常数满足的两个代数方程
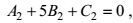 (68)
(68)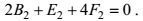 (69)
(69)b.第二运动学条件, 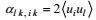
比较式(63) 和(64), 有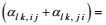
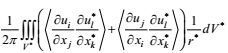
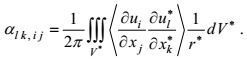 (70)
(70)将这个结果乘以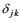
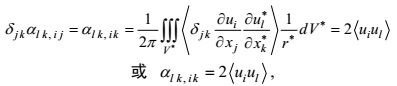 (71)
(71)这就是所谓的第二运动学条件。将表示式(65) 代入第二运动学条件, 则有
 (72)
(72)从而, 有待定常数满足的另外两个代数方程
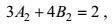 (73)
(73)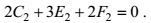 (74)
(74)最后, 解代数方程(68)、(69) 和(73)、(74), 可得用待定常数C2表示的系数关系
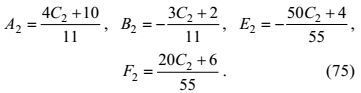 (75)
(75)将所得结果代入表示式(63), 则可得第二变形-压力项的闭合形式
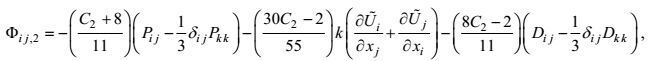 (76)
(76)其中
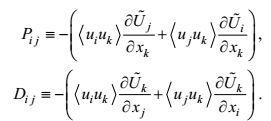 (77)
(77)由于闭合的第二变形-压力项(76), 其第一项形式上具有生成项的意义, 常取它作为第二变形-压力项的近似式
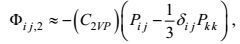 (78)
(78)其中(C2VP)称为无量纲第二变形-压力系数。这样, 将所导得的表示式(62)、(78) 和(57) 代入表示式(52), 则可得变形-压力项实用闭合表示
 (79)
(79)最后, 将表示式(46)、(49)、(79) 代入方程(32), 则得闭合的速度-速度二阶矩方程
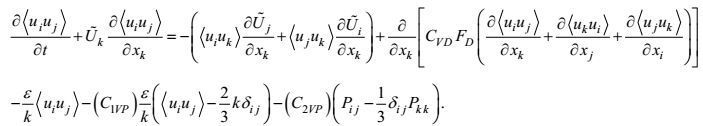 (80)
(80)在目前的高确定性闭合原理中, 仍没有给出无量纲系数(C1VP)和(C2VP)的普适表示。
2.2.2 闭合的湍流速度-温度和速度-盐度二阶矩方程速度-温度和速度-盐度二阶矩方程(33) 和(34) 的闭合主要包括
(1) 输运通量剩余项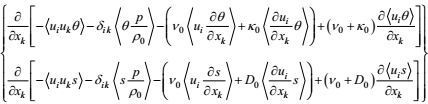
湍流输运是一种大涡旋行为。按所引入的闭合原理第一和第三条, 速度-温度和速度-盐度通量剩余项的闭合形式可分别写成
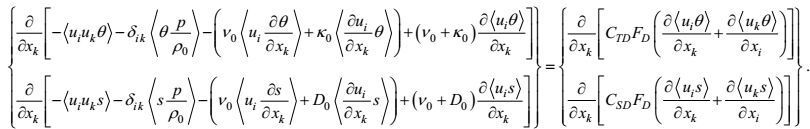 (81)
(81)这里, 量纲为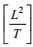
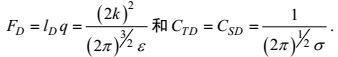 (82)
(82)按Kolmogorov-Prandtl关系, 其中湍流Prandtl数σ和所引入的梯度Richardson数Rg分别确定为
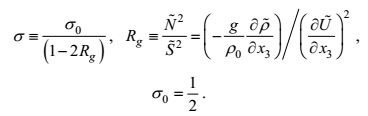 (83)
(83)(2) 分子耗散项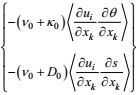
分子耗散是一种小涡旋行为, 它可以被认为是近各向同性的。这样, 由改变坐标指向不变性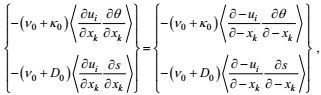
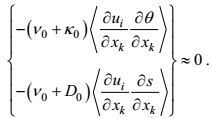 (84)
(84)(3) 梯度-压力项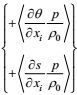
将湍流压力的估计式(51) 代入梯度-压力项, 可以得到
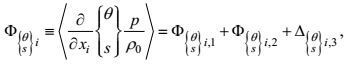 (85)
(85)其中
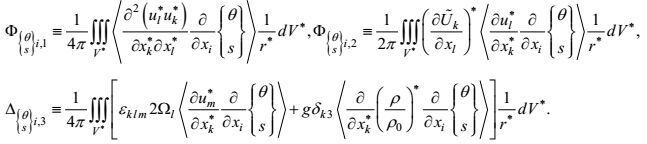 (86)
(86)a.第一梯度-压力项的闭合
梯度-压力项表示式(86) 的第一项仅是湍流量的函数, 描述的是一种大涡旋行为。按闭合原理的第一和第三条, 它可表示为温度-速度和盐度-速度二阶矩
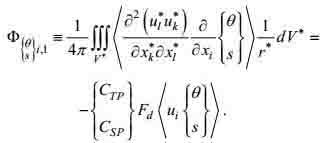 (87)
(87)这里, Fd为量纲为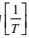
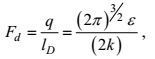 (88)
(88)而后者仍为两个待定无量纲系数。
b.第二梯度-压力项的闭合
先对第二梯度-压力项中的合成运动做中值处理, 再参照积分关系式(56), 对于远离边界的任意内点有第二梯度-压力项的闭合形式
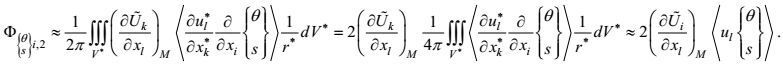 (89)
(89)c.第三梯度-压力项的闭合
同样, 考虑积分关系(56), 有第三梯度-压力项的闭合形式
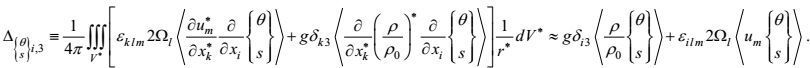 (90)
(90)将闭合估计式(87)、(89) 和(90) 代入(85) 式, 则得温度-速度和盐度-速度二阶矩方程的梯度-压力项闭合形式
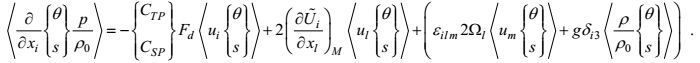 (91)
(91)最后, 将闭合形式(81)、(84) 和(91) 代入方程(83) 和(84), 则得速度-温度和速度-盐度二阶矩方程的闭合形式
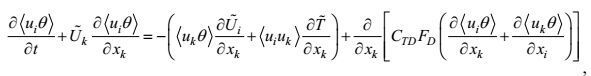 (92)
(92)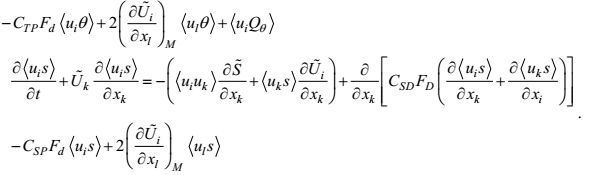 (93)
(93)统观所导出的三个闭合二阶矩方程(80)、(92) 和(93), 它们的重力和地转力有关项都消失。这表明, 次小尺度近各向同性湍流的二阶矩行为, 实际上与重力和地转力无关。压力观测作为确定相关无量纲系数(C1VP), (C2VP)和CTP, CSP普适表示的实测依据, 但至今在湍流尺度上仍缺少现场测量能力。
2.2.3 闭合的湍流温度、盐度二阶矩方程温度、盐度二阶矩方程(35)、(36)、(37) 的闭合主要包括
(1) 输运通量剩余项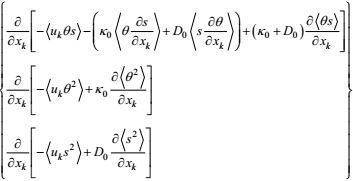
温度-盐度积和温度、盐度平方的输运是一种大涡旋行为。按所引入的闭合原理第一和第三条, 输运通量剩余项的闭合形式可写成
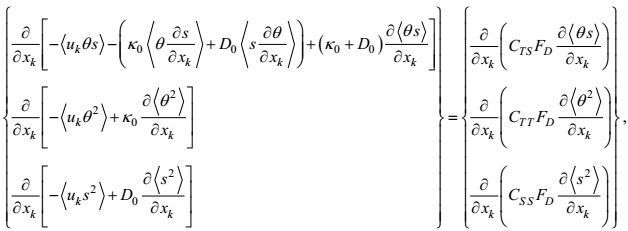 (94)
(94)其中量纲为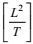
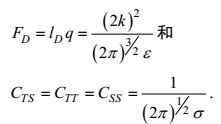 (95)
(95)(2) 分子耗散项: 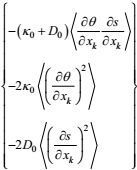
分子耗散是一种小涡旋行为。参照先前的处理结果(49), 按所引入的闭合原理第一条, 分子耗散项也可以写成高确定的闭合形式
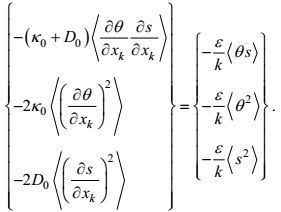 (96)
(96)将(94) 和(96) 式代入方程(35)、(36)、(37), 则可得温度、盐度二阶矩方程的闭合形式
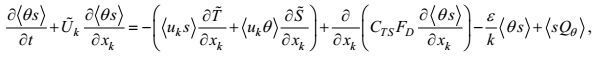 (97)
(97)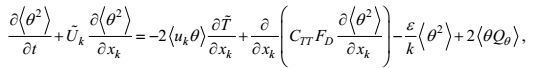 (98)
(98)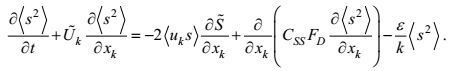 (99)
(99)这样, 本文完成了对所有湍流二阶矩方程的闭合处理。在高确定性闭合原理下这些方程的形式变得几乎完全确定, 仅有的不确定待定系数是来自变形-压力项的(C1VP), (C2VP)和梯度-压力项的CTP, CSP。
2.2.4 闭合的二阶矩边界条件湍流二阶矩边界条件是关系式(12) —(19) 所描述的海面和海底淡水、动量、热量和盐量输运通量平衡。其中非二阶矩项主要是关系式中出现的三阶矩项和因为采用波动-涡旋-环流合成运动边界替代所生成的附加项构成。可按具体情况, 给出这些边界条件高确定性的实用形式。
3 高确定性闭合的湍流基本特征量控制方程 3.1 湍流基本特征量方程在湍流二阶矩方程的闭合过程中, 所引入的两个基本特征量k和ε还需要进一步确定。这样, 导出它们的控制方程和实现这些方程的高确定性闭合就成为本章的主要研究内容。
3.1.1 湍流动能方程的导出对闭合的湍流速度-速度二阶矩方程, 取j=i可得动能
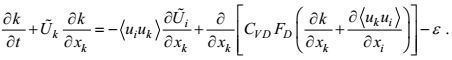 (100)
(100)这个方程与变形-压力项和梯度-压力项无关, 湍流动能方程的有量纲参变量和无量纲系数实际上是高确定性的。
3.1.2 湍流动能耗散率方程的导出按湍流动能耗散率的定义式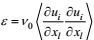
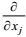
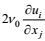
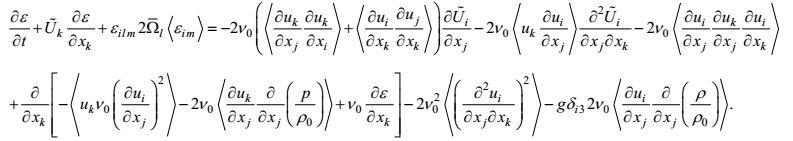 (101)
(101)这个方程的左端三项分别是湍流动能耗散率的时间变化项、合成运动输运项和地转效应项, 右端第一、第二和第三项分别是第一、第二大尺度作用产生项和涡动变形产生项, 第四项是输运通量剩余项, 第五项是分子耗散项, 第六项是重力变形-梯度项。
3.2 高确定性闭合的湍流基本特征量方程鉴于导出湍流动能方程的速度-速度二阶矩方程是经过高确定性闭合处理的, 所以需做闭合的基本特征量方程就只剩下动能耗散率方程了。
3.2.1 动能耗散率方程诸项的量级估计由于动能耗散率方程(101) 诸项, 有的描述的是大涡旋行为, 有的是小涡旋行为, 这样, 首先需要弄清大、小涡旋的尺度关系。按闭合原理第五条所包括的大、小涡旋速度相似性, 有
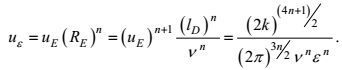 (102)
(102)将这个关系式代入动能结构不变性关系, 可以推导出关系式
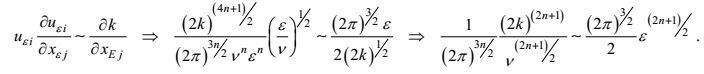 (103)
(103)由于这个导出关系应当是物理普适的, 它不应该取决于运动和流体属性, 这样, 有
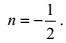 (104)
(104)将这个结果代入大、小涡旋尺度关系则有如表 1所列的动能耗散率方程各项的量级估计。
| 项名 | 对流 | 产生Ⅰ | 产生Ⅱ | 变形产生 | 输运剩余 | 耗散 |
| 量级 | 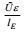 | 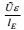 | 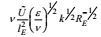 | 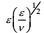 | 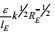 | 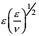 |
| 标准 | 1 | 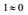 | 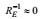 | 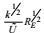 | 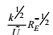 | 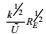 |
虽然按表 1的第一产生项与对流项有相同的量级, 但是, 在湍流尺度远小于合成运动时, 由各向同性湍流统计理论结果
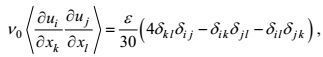 (105)
(105)可导得
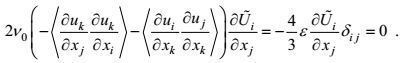 (106)
(106)这个结果表明, 对于近各向同性湍流的第一产生项实际上是接近于零的。
由表 1还可以看到, 第二产生项具有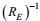
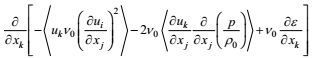
按高确定性闭合原理的第一和第三条, 大涡旋输运通量剩余项的闭合可写成
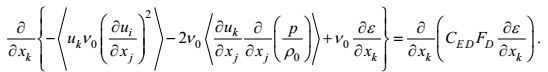 (107)
(107)其中量纲为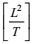
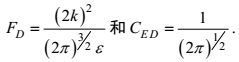 (108)
(108)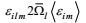
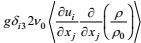
所导出湍流动能耗散率方程的左端第三项和右端第六项分别是地转项和重力项。它们分别因各向同性的改变坐标指向不变性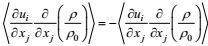
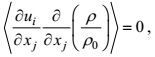 (109)
(109)和因张量运算关系而有
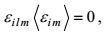 (110)
(110)而消失。
这样, 经过以上四条闭合处理, 动能耗散率方程可简单地写成
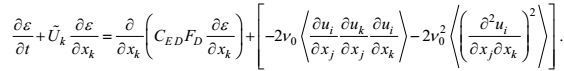 (111)
(111)它的右端项实际上仅包括变形产生项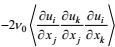
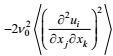
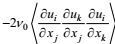
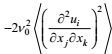
湍流动能耗散率方程这两项的闭合, 其传统做法是, 将动能耗散率方程的变形产生项和分子耗散项各自与动能方程的剪切不稳定产生项和分子耗散率项做成比例闭合处理
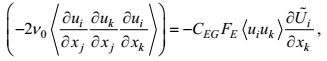 (112)
(112)和
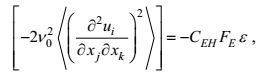 (113)
(113)其中量纲为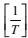
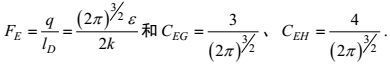 (114)
(114)最后, 有现行高确定性闭合的湍流动能耗散率方程
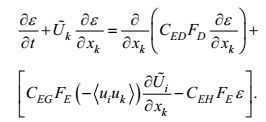 (115)
(115)在关于饱和湍流的后续研究中, 这种非独立的闭合做法, 会带来基本特征量方程的相当不确定性。本文不得不在没有更好的闭合处理办法之前, 回归到求助于现场实验研究, 得到另一个独立的基本特征量实验关系。
3.3 高确定性闭合的湍流基本特征量海面边界条件除湍流基本特征量方程所显示的合成运动速度剪切生成机制以外, 特征量的变化还受到海面通量过程的影响。这里所讲的海面通量过程主要包括破碎和非破碎海浪决定的两种。在破碎海浪决定的情况下, 可以按破碎海浪统计理论(Yuan et al, 2009)给出海面边界条件。
3.3.1 海浪破碎能量损耗决定的海面湍流动能输入海浪破碎能量损耗决定的海面湍流动能输入可以写成
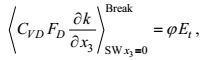 (116)
(116)其中Et是破碎海浪统计理论所导得的总能量损耗率, 它实际上只有很少的一部分φ, 在破碎过程中被转变为湍流动能。大部分破碎能量将因作用于波峰附近, 而以不均匀空间分布的形式, 重新回到海浪运动中。转化为湍流动能的小部分, 实际上就是海浪破碎耗散源函数Sdis所包含的那一部分, 这样, 这个份数可以写成
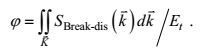 (117)
(117)关系式(116) 给出的是一个关于湍流动能的第二类海面边界条件。
3.3.2 海浪破碎卷入深度决定的海面湍流混合长度按闭合原理的第四条, 海面湍流混合长度可以写成
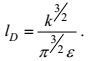 (118)
(118)这样, 以破碎海浪统计理论导得的卷入深度hen作为海面湍流混合长度lD的量度, 对表示式(118) 作海浪集合上的Reynolds平均, 有
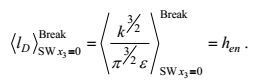 (119)
(119)关系式(119) 的后一个等式表明的是动能耗散率的第一类海面边界条件。
3.3.3 非破碎海浪决定的海面湍流动能输入至于非破碎海浪决定的情况下, 湍流被认为是一种由连续介质诱导的次小尺度运动, 这样, 有
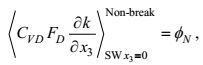 (120)
(120)其中φN表示的是, 与海浪水质点运动相关联的次小尺度海面过程决定的对海洋湍流的动能输入。它是一个关于特征量k的第二类海面边界条件。
3.3.4 非破碎海浪决定的海面湍流混合长度取海面水质点运动范围的一半, 即海浪的平均振幅, 作为海面湍流大涡旋尺度的量度。这样, 有非破碎海浪决定的海面湍流混合长度为
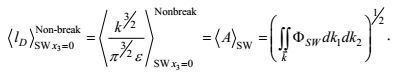 (121)
(121)其中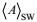
基于系统科学和物理海洋学相结合所提出的海洋动力系统理论, 本文在以下三个方面改善了对湍流混合输运通量研究的认识基础。
(1) 海洋动力系统控制方程组集显示, 湍流、波动、涡旋、环流, 按其较大特征尺度合成运动的平流输运项和速度剪切、温度-盐度梯度生成项和其较小特征尺度运动的输运通量和剩余项, 形成完整的相互作用海洋运动系统。其中最小尺度的湍流和最大尺度的环流则只分别有更小尺度的分子黏性-传导-扩散项和没有更大尺度运动的平流输运项和剪切-梯度生成项。
(2) 湍流, 在其他三类较大尺度运动的控制方程组中总是以输运通量剩余项的形式出现, 它是对三类运动混合的主要运动主体。这样, 闭合的湍流二阶矩和基本特征量控制方程就成为海洋混合研究的主要数学物理描述基础。这方面本文所提供的进展包括:
a.本文在总结海洋湍流研究最新成果的基础上, 提出了五条湍流二阶矩控制方程高确定性闭合原理。这里所谓高确定性, 一方面, 还仅限于非压力相关项有量纲参变量和无量纲常数普适表示的给出; 另一方面, 提出一种按湍流涡旋结构基本量纲量表示和控制方程描述项量纲分析结果, 确定有量纲参变量和无量纲常数的普适办法。
b.所提出的五条高确定性闭合原理可以构成完整的湍流二阶矩和基本特征量控制方程的闭合体系, 它们是湍流混合输运通量剩余量的数学物理描述基础。
c.所提出的现行湍流基本特征量方程组显示, 动能耗散率方程是采用比例于动能方程的速度剪切生成项和分子耗散率项, 闭合处理其变形产生项和分子耗散项的。这种闭合处理办法不能保证两个基本特征量方程的相互独立性。这是目前湍流研究还不得不回归到现场试验这条原始研究路线的主要原因。建立独立的基本特征量方程组是当下湍流研究必须解决的重要理论课题。
(3) 按海洋动力系统控制方程组集, 在除极薄边界层以外的海洋内部, 湍流主要是由波动-涡旋-环流合成运动的速度剪切和温、盐梯度生成项而成长, 而对波动、涡旋、环流起着重要的搅拌混合作用。这样不难理解, Wunsch的海洋混合主体:海浪+湍流混合模块(是勋刚, 1994), 其物理本质实际上就是这里所提出的波动生湍流混合, 它在近海面层中被称为海浪生湍流混合。作者在1999年(Yuan et al, 1999), 基于Prandtl湍流混合模型所导出的半经验半理论混合系数解析表示, 取得了很好的模拟效果(Qiao et al, 2004)。实际上, 采用本文所给出的二阶矩和基本特征量控制方程, 结合动能耗散率的现场测量分析结果, 可以动力学地导出包括海浪和内波的波动生湍流混合系数(Wunsch et al, 2004)。这些工作都证明, 建立湍流输运通量描述数学物理基础的重要意义。
| 许国志, 2000. 系统科学. 上海: 上海科技教育出版社, 17-40 |
| 是勋刚, 1994. 湍流. 天津: 天津大学出版社, 84-101 |
| Baumert H Z, Simpson J H, Sündermann J, 2005. Marine Turbulence: Theories, Observations, and Models. Cambridge, UK: Cambridge University Press, 27-29 |
| Kamenkovich V M, 1977. Fundamentals of Ocean Dynamics. Amsterdam, Netherlands: Elsevier Science, 1-78 |
| Qiao F L, Yuan Y L, Yang Y Z, et al, 2004. Wave-induced mixing in the upper ocean: Distribution and application to a global ocean circulation model. Geophysical Research Letters, 31(11): L11303 |
| Wunsch C, Ferrari R, 2004. Vertical mixing, energy, and the general circulation of the oceans. Annual Review of Fluid Mechanics, 36(1): 281–314 DOI:10.1146/annurev.fluid.36.050802.122121 |
| Yuan Y, Qiao F, Hua F, et al, 1999. The development of a coastal circulation numerical model: 1. Wave-induced mixing and wave-current interaction. Journal of Hydrodynamics, Series A, 14(4B): 1–8 |
| Yuan Y L, Han L, Hua F, et al, 2009. The Statistical theory of breaking entrainment depth and surface whitecap coverage of real sea waves. Journal of Physical Oceanography, 39(1): 143–161 DOI:10.1175/2008JPO3944.1 |
| Yuan Y, Zhuang Z, Yang G et al, 2017. An Analytic Estimation of the Turbulence Mixing Coefficient Generated by the Sea Waves. Journal of Physical Oceanography(Submitted) |
| Yuan Y L, Qiao F L, Yin X Q, et al, 2012. Establishment of the ocean dynamic system with four sub-systems and the derivation of their governing equations set. Journal of Hydrodynamics, Series B, 24(2): 153–168 DOI:10.1016/S1001-6058(11)60231-X |
 2017, Vol. 48
2017, Vol. 48

