
中国海洋湖沼学会主办。
文章信息
- 尤再进, 尹宝树, 石洪源. 2017.
- YOU Zai-Jin, YIN Bao-Shu, SHI Hong-Yuan. 2017.
- 应用“跨零-能量”法估算海洋波浪再生能资源
- NEW WAVE ANALYSIS METHOD "ZERO CROSSING-ENERGY BALANCE" FOR ESTIMATION OF RENEWABLE OCEAN WAVE ENERGY
- 海洋与湖沼, 48(5): 926-931
- Oceanologia et Limnologia Sinica, 48(5): 926-931.
- http://dx.doi.org/10.11693/hyhz20170500110
-
文章历史
- 收稿日期:2017-05-04
- 收修改稿日期:2017-06-01
2. Coastal Research Centre, University of Queensland, Brisbane QLD 4072, Australia;
3. 中国科学院海洋环流与波动重点实验室 青岛 266071;
4. 中国科学院海洋研究所 青岛 266071;
5. 青岛海洋科学与技术国家实验室 青岛 266237;
6. 中国科学院大学 北京 100049
2. Coastal Research Centre, University of Queensland, Brisbane QLD 4072, Australia;
3. Key Lab of Ocean Circulation and Waves, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China;
4. Institute of Oceanology, Chinese Academy of Science, Qingdao 266071, China;
5. National Oceanographic Centre, Qingdao 266237, China;
6. University of Chinese Academy of Science, Beijing 100049, China
海洋波能量如此巨大, 覆盖面广, 可持续。海洋波能的可发电资源通常用波能流密度来定量描述, 目前常用的波能流经验公式是P≈0.5Hs2T, 其中, P是波流能密度(kW/m), Hs是有效波高(m), T是波浪周期(s)。该公式是由深水线性波浪理论推导而来, 计算每米波峰宽度方向从海平面到海底面整个水体蕴蓄的波功率(万勇等, 2014; 江兴杰等, 2015)。有限水深的波能流估算为P=CgE, 其中E是波浪能, Cg是波群传播速度(王绿卿等, 2014; Bernardino et al, 2017)。但是, 现有波能流的估算方法存在几大缺陷:第一, 估算的波能流与驱动波浪发电装置发电的波能流几乎毫无相关。比如, 离岸漂浮式的波浪发电装置主要是利用海平面附近水体内的波浪能量来驱动电机发电, 而现有估算公式是计算从海平面到海底面整个水体蕴藏的波能流。所以, 目前波能流的估算方法过高估算了可以利用的海洋波能资源。除非新一代离岸漂浮式波浪发电装置是充分庞大, 能够采集从海平面到海底整个水体的波浪能量。第二, 有限水深的波能流计算公式是水深的函数, 但是离岸漂浮式的波浪发电装置只与海表面附近水体内的波能量有关, 与整个水深储存的总波浪能几乎无关(Cornejo-Bueno et al, 2016)。第三, 应用线性波浪理论推导的深水波能流公式来估算有限水深下的不规则波能流可能会导致比较大的计算误差(Wan et al, 2015), 尤其在风浪成长的情况下。第四, 现有两种波浪分析方法, 时域的跨零法和频域的波谱法, 通常给出不同计算结果的波能(白志刚等, 2014; Liang et al, 2014)。
本文将介绍一种“跨零-能量”波浪分析的新方法, 推导有限水深条件下的不规则波浪的波能和波能流的计算公式, 讨论波能流估算方法和当前产业化的波浪发电装置的相关性。
1 规则波浪的波能和波能流计算 1.1 波能的垂向分布波浪能是在单位波峰线宽度内和沿波浪传播方向一个波长的从海平面到海底面水体范围内所储存的波浪势能Ep和波浪动能EK两部分之和, 其中波势能的高程参考面是海平面。波浪势能是因水质点偏离它的平衡位置而产生, 而波浪动能是由于水质点的运动而生成的能量(Dean et al, 1991)。相对于高程海平面位置(z=0), 波势能和静止水体的总势能Ep1估算为(邹志利, 2009)
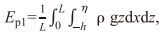 (1)
(1)其中L是波长, η(t)为相对于海平面的波表面高程, h为平均水深, dxdz单位宽微元水体的体积, ρgdxdz是该微元水体的重量, ρ为海水密度, g为重力加速度, x为微元水体的水平距离, z为微元水体的位置高程, ρgzdxdz为微元水体的势能。在没有波浪时, 相对于海平面位置的静止水体势能Ep2是
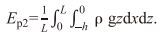 (2)
(2)根据式(1) —(2), 波浪引起的单宽波峰线长度的一个波长范围内的平均波势能, 也就是由于波浪引起的水体总势能增加量为
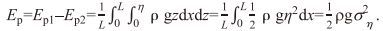 (3)
(3)其中ση2是波面高程数据η(t)的方差值, 式(3) 没有涉及任何假设, 波面的形状可以是不规则的。由式(3) 可知, 波浪势能Ep是由波浪面水体高于海平面而产生, 主要蕴蓄在海平面以上的水体内(0≤z≤η)。假设波面方程是简单的规则波, 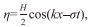
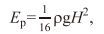 (4)
(4)其中假设了波面形状是简单的规则波, 而式(3) 的波浪势能计算公式是精确解。
波动能EK是由于水体质点运动而产生, 单位宽度的微元水体的体积为dxdz, 其动能表达式为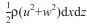
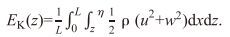 (5)
(5)当式(5) 中水质点速度(u, w)由线性波浪理论来计算时, EK(z)可以表达为
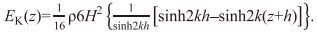 (6)
(6)当z= -h时, 式(6) 中整个水体内包含的波动能EK表达为
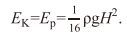 (7)
(7)所以, 储蓄在海平面到海底面的整个水体内的波浪势能Ep和动能EK之和是
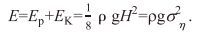 (8)
(8)上式中的波能由波高H或者波面的方差ση2来计算。
图 1给出了波动能EK沿水深的垂直分布。在浅水区内(kh≤π/10), 波动能沿水深的分布是线性的; 在过渡区(π/10 < hk < π), 随水深增大, 60%以上的波动能集中于上层水体内(z/h > -0.5);在深水区(kh≥π), 70%以上的波动能集中于靠近海表面的水体内(z/h > -0.2)。为了避免迭代波浪色散方法来求解有限水深的波浪数k, You (2009)应用深水波浪数ko直接定义三个水深区域:浅水区内(koh≤0.1), 过渡区(0.1 < koh < π), 深水区(koh≥π)。
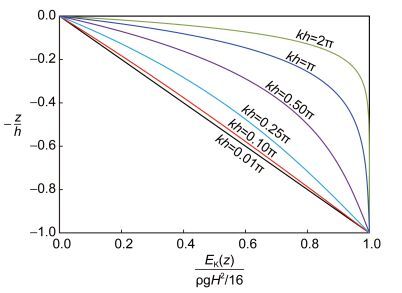 |
| 图 1 波动能EK在浅水区(kh≤π/10)、过渡区(π/10 < hk < π)和深水区(kh≥π)的垂向分布规律 Fig. 1 Vertical distribution of kinematic wave energy EK with water depth in shallow, intermediate and deep waters |
波能流是描绘波浪传播/输送波能量的能力。在风区内, 因风输入海水体能量, 使得水体产生波浪运动。在风区外, 波浪还能够保持自由运动, 将波能量继续向前传播, 直到波浪破碎, 消耗波浪自身的大量能量, 其余的波能量消耗在波浪的海滩爬高上。应用线性波浪理论, 从波表面到任意水深z的波能流可以计算为
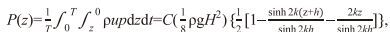 (9)
(9)其中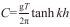
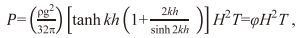 (10)
(10)其中φ(kh)是相对水深kh的函数, 海水密度取ρ=1028.1kg/m3, 重力加速度g=9.81m/s2, 波高取m计算, 波周期取s计算, 波能流P单位是W/m。在深水条件下(kh≥π), 式(10) 进一步简化为
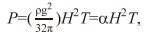 (11)
(11)其中P单位是W/m (P≈1000H2T), 波高计算的单位是m, 周期的计算单位是s。式(11) 只是波高和周期的一个简单函数, 与水深h无关, 进一步改写为P=Hrms2T(kW/m)。
图 2中给出了波能流P(z)从海平面到任意一个水下高程z的垂直分布。由图 2可见, 在浅水区内(kh≤π/10), 波能流沿水深分布是线性的; 在深水区(kh≥π), 70%以上的波能流集中在海表面附近的水体内(z/h > -0.2);在过渡区(π/10 < hk < π), 随着水深kh的增加, 波流能由沿水深均匀分布逐渐地集中海表面附近的水体内。值得一提的是, 式(9) 是波能流从海表面累积到任意一个水下位置z的表达式, 首次定量地描绘了波能流的垂直分布, 从而能够精确地确定波浪发电装置在水下的最佳安装位置。而式(10) 是线性波浪从海表面到海底的单宽波峰线断面的总能流表达式。
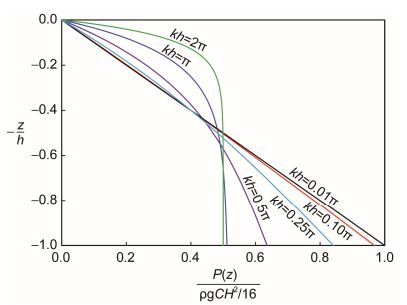 |
| 图 2 线性波浪的波能流P(z)在浅水区(kh≤π/10), 过渡区(π/10 < hk < π)和深水区(kh≥π)的垂向分布 Fig. 2 Vertical distribution of wave energy flux with water depth in shallow, intermediate and deep waters |
海洋波浪具有不规则性, 其波高和周期都是随时间随机变化。对于现场采集的海洋波浪数据η(t), 现有波浪分析方法有两种:时域的跨零法和频域的波谱法。时域跨零法分析波高和周期的概率分布以及它们的联合分布, 而频域波谱法给出波能随频率的分布。本文介绍最近建立的“跨零—能量”波浪分析法(You et al, 2013), 将海洋不规则波转换成规则波, 再应用线性波浪理论推导出的相关公式, 最后推导出不规则波浪的波能和波能流计算公式。
为了使读者更好地了解“跨零-能量”分析法, You等(2013)的方法简单介绍如下。设η(t)是n个不规则波浪的观测波面高程数据(图 3), 观测时间段为D, 假设海况在观测时间内是稳定的。图 3中的任意一个不规则波浪都可以变换成具有同周期的规则波
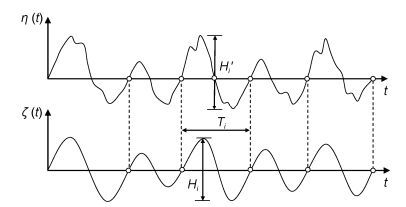 |
| 图 3 任意n个不规则波浪由“跨零—能量”法转换成n个规则波 Fig. 3 Any n irregular waves transformed into n regular waves (H, T) with zero crossing and energy balance method |
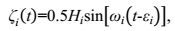 (12)
(12)其中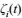
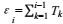
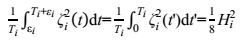 (13)
(13)其中t′=t-εi是一个新时间变量。根据式(12), 这n个规则波浪的波面高程方差σζ2可以写成
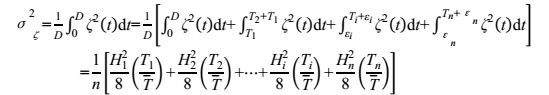 (14)
(14)式中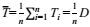
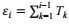
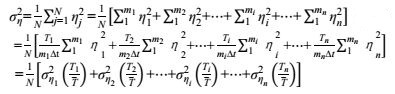 (15)
(15)其中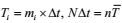
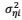
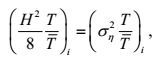 (16)
(16)上式中的第i个规则波高Hi确定为
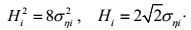 (17)
(17)将式(15) 代入式(14) 中, 最后我们推导了一个n个不规则波浪和转换后的n个规则波浪的转换守恒方程
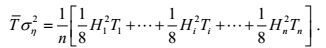 (18)
(18)其中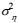
式(18) 就是“跨零-能量”波浪分析法, 它和傅里叶转换方法或者波谱方法有类似点。波谱方法是假设实际海面η(t)有许多振幅不等、频率不同的余/正弦线性叠加而成来近似模拟海面η(t), 而式(18) 是假设实际海面η(t)的n个不规则波可以由n个振幅不等但周期相同的规则波来代替, 每个不规则波浪可以转换成一个规则波, 而且它们拥有相同的波能量和周期。式(18) 首次将频域的波谱法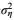
海洋波浪的波面η(t)是不规则波面组成(见图 3)。如果假设海洋波谱是窄谱或者不规则波的跨零周期几乎相等(Ti≈T), 在式(18) 的方程两边同时乘以同一常项ρg, 同时再除以T, 这样不规则波浪的波面方差值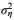
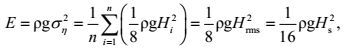 (19)
(19)其中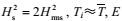
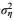
在实际的海况下, 每个不规则波的跨零周期一般是不相等, 也称为有限宽波谱, 通常符合正态分布(You, 2009a)。根据大量的现场数据, You等(2001)推导了几个特征波浪周期之间的关系
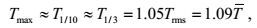 (20)
(20)其中T是平均周期。根据式(18), 小于平均周期T的波浪周期T和平均周期T的比值总满足T < T, 式(18) 中的小于平均周期的项应该满足不等式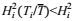
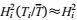
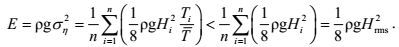 (21)
(21)由上式推出以下两个重要结论
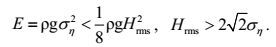 (22)
(22)根据式(22) 可知, 窄波谱假设在一般情况下都是高估了海洋波浪能; 应用计算特征波高Hrms的关系式, 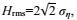
根据式(19) 和(22), 海洋波浪能的统一表达是
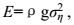 (23)
(23)其中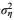
海洋深水波浪(kh≥π)和过渡区波浪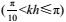
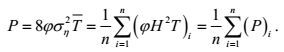 (24)
(24)其中Ti=T, (P)i是第i个不规则波浪转换成规则波的波能流, 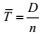
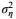
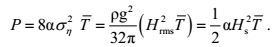 (25)
(25)其中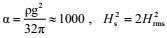
对于非窄波谱分布的深水区波浪(Ti≠T), 根据深水规则波的波能流表达式(11), 在式(18) 的两边同时乘以一个常数α, 非窄波谱的深水波浪的波能流可以估算为
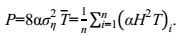 (26)
(26)根据式(25) 和式(26), 非窄波谱和窄波谱分布的深海波能流均可计算为
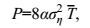 (27)
(27)其中P的单位是W/m。
对于非窄波谱分布的过渡区波浪, 根据过渡区规则波的波能流表达式(11), 在式(18) 方程的两边同时乘以一个常数φ, 平均波能流P可以估算为
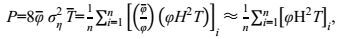 (28)
(28)其中
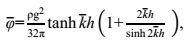 (29)
(29)其中k是平均波浪数, 取平均波浪周期T来计算平均波浪数。在式(28) 的推导中, 应用了波浪周期变化范围小的事实(φ/φ≈1), You等(2013)通过分析大量的现场波浪数据发现, 过渡区的波浪周期变化范围是T=(0.5-1.5)T, 式(20) 给出了几个波周期特征值之间的关系。
3 波浪发电装置的波能流估算目前波浪发电装置可以划分为两大类:岸边固定式和离岸漂浮式。岸边固定式的波浪发电装置一般安装在岩石海岸边, 采集整个水深的波能量, 它的发电功率是破碎波高Hb、波周期T的函数, 但破碎波高由当地水深决定, 如Hb=γ×h, γ是一个常数, h是当地平均水深。在波浪破碎区, 线性波浪理论不再适用。岸边固定式的波浪发电机的输出功率Wg要远小于破碎区外的有限水深波能流P, 具体的Wg和P的关系需要由具体的发电装置来确定。
现有大部分波浪发电装置属于离岸漂浮式。这些装置漂浮在海表面, 采集海表面附近水体内的波能量, 与海平面以下水体中蕴蓄的波能流无关。所以离岸漂浮式的输出功率Wp远远小于式(27) 或者(28) 中估算的波能流P。如果只考虑海平面附近的波势能, 离岸漂浮式的输出功率近似为由式(27) 计算波能流P的一半, 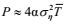
本文应用“跨零-能量”波浪分析的新方法, 成功地将海洋不规则波浪η(t)转换成规则波浪ζ(t), 再应用线性波浪理论来计算波能和波能流。基于这种“跨零-能量”波浪分析方法, 现有两种传统的波浪分析法, 跨零法和波谱法, 通过式(18) 首次定量地统一起来, 推导了有限水深的海洋波能为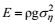
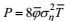
| 万勇, 张杰, 孟俊敏, 等, 2014. 基于ERA-Interim再分析数据的OE-W01区块波浪能资源评估. 资源科学, 36(6): 1278–1287 |
| 王绿卿, 冯卫兵, 唐筱宁, 等, 2014. 中国大陆沿岸波浪能分布初步研究. 海洋学报, 36(5): 1–7 DOI:10.11978/j.issn.1009-5470.2014.05.001 |
| 白志刚, 魏茂兴, 2014. 基于时域模型的一种新的波浪能计算方法. 天津大学学报(自然科学与工程技术版), 47(6): 491–497 |
| 江兴杰, 杨永增, 王道龙, 等, 2015. 浅水环境下波浪能能流密度计算方法研究. 海洋学报, 37(9): 1–9 |
| 邹志利, 2009. 海岸动力学. 4版. 北京: 北京人民交通出版社, |
| Bernardino M, Rusu L, Soares C G, 2017. Evaluation of the wave energy resources in the Cape Verde Islands. Renewable Energy, 101: 316–326 DOI:10.1016/j.renene.2016.08.040 |
| Cornejo-Bueno L, Nieto-Borge J C, García-Díaz P, et al, 2016. Significant wave height and energy flux prediction for marine energy applications: A grouping genetic algorithm-Extreme Learning Machine approach. Renewable Energy, 97: 380–389 DOI:10.1016/j.renene.2016.05.094 |
| Dean R G, Dalrymple R A, 1991. Water Wave Mechanics for Engineers & Scientists. Singapore: World Scientific Publishing Company, 353 |
| Liang B C, Fan F, Liu F S, et al, 2014. 22-Year wave energy hindcast for the China East Adjacent Seas. Renewable Energy, 71: 200–207 DOI:10.1016/j.renene.2014.05.027 |
| Wan Y, Zhang J, Meng J M, et al, 2015. Exploitable wave energy assessment based on ERA-Interim reanalysis data-A case study in the East China Sea and the South China Sea. Acta Oceanologica Sinica, 34(9): 143–155 DOI:10.1007/s13131-015-0641-8 |
| You Z J, Hanslow D, 2001. Statistical distribution of nearbed wave orbital velocity under irregular waves. In: Proceedings of the 15th Australasian Coastal and Ocean Engineering Conference, the 8th Australasian Port and Harbour Conference. Barton: Institution of Engineers |
| Y ou, Z J, 2009a. Statistical distribution of nearbed wave orbital velocity in intermediate coastal water depth. Coastal Engineering, 56: 844–852 DOI:10.1016/j.coastaleng.2009.04.005 |
| You Z J, 2009. A close approximation of wave dispersion relation for direct calculation of wavelength in any coastal water depth. Applied Ocean Research, 30: 133–139 |
| You Z J, Nielsen P, 2013. Extreme coastal waves, ocean surges and wave runup. In: Finkl Charles W, ed. Coastal Hazards. Netherlands: Springer |
 2017, Vol. 48
2017, Vol. 48

