中国海洋湖沼学会主办。
文章信息
- 李宏杰, 徐永生. 2017.
- LI Hong-Jie, XU Yong-Sheng. 2017.
- 北太平洋副热带逆流区涡旋动能谱的季节性变化及其机制
- SEASONAL VARIATION IN EDDY KINETIC ENERGY SPECTRUM AND ITS MECHANISM IN THE NORTH PACIFIC SUBTROPICAL COUNTERCURRENT
- 海洋与湖沼, 48(5): 932-943
- Oceanologia et Limnologia Sinica, 48(5): 932-943.
- http://dx.doi.org/10.11693/hyhz20161200290
-
文章历史
- 收稿日期:2016-12-30
- 收修改稿日期:2017-03-14
2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
高质量的卫星高度计数据可以观测全球海洋环流变化, 而且提供了可以探索其动力学机制的一个工具。海流变化由中尺度涡决定, 其时间尺度为50—200天, 空间尺度为100—500km。多年来, 许多学者充分利用了卫星高度计的观测数据对海洋中的中尺度涡进行了大量研究。例如, 卫星高度计的观测表明, 在北赤道副热带逆流(STCC)区, 其范围大致在18°—27°N, 黑潮以东至夏威夷岛以西的区域(Yoshida et al, 1967; 管秉贤, 1987; 李凤荣等, 2004), 存在大量中尺度涡旋, 呈纬向舌状分布(见图 1)。这些涡旋在向西移动的过程中强度不断增大, 并对黑潮的流量产生重要影响(Kobashi et al, 2002; Yoshida et al, 2011)。Aoki等(1996)和Qiu (1999)等认为STCC区具有很强的平均涡动能(EKE), 且随季节变化, 在夏季最大, 冬季最小。刘秦玉等(2000)等利用T/P卫星测高资料和海洋气候模式(POCM)对STCC区的海面高和流场的波动现象进行了研究, 发现其波动周期约为90天, 波长在450—850km之间。胡瑞金等(2002)采用小波分析的方法也在该区域发现了一个强的振荡区, 其振荡周期为58—139天。Stammer (1998)和Qiu (1999)的研究都认为, STCC海区具有较强涡动能是斜压不稳定的结果。Noh等(2007)以及Qiu等(2010)进一步指出在春季, STCC与西向的北赤道流(NEC)之间的速度垂向剪切较强, 形成较强的斜压不稳定, 而在秋季, STCC与NEC之间的速度垂向剪切较弱, 使得季节斜压不稳定也变弱。Chang (2014)等利用数值模式验证了斜压不稳定对STCC区涡旋动能季节变化所起的决定作用。然而, 在中尺度涡旋演变中, 涡旋互相作用所扮演的角色, 特别是涡旋相互作用对海洋各种运动形式中的长度尺度有何影响尚不很清楚。评估非线性涡旋作用的有效诊断工具是由Frisch (1995)提出的能量谱分析法。许多海洋学家利用了高度计数据来研究能量谱的空间尺度, 发现在大于罗斯贝变形尺度上存在着动能的逆向串级(Scott et al, 2005; Tulloch et al, 2011; Arbic et al, 2013), 其原因很可能是受到斜压不稳定的强迫, 并由于正压化而停止逆向串级。
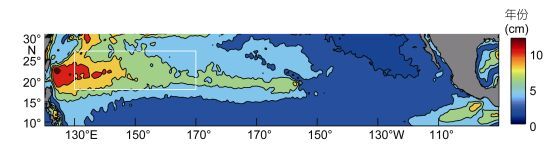 |
| 图 1 北太平洋副热带地区的海表面高度异常的均方根(根据1993年1月到2015年12月期间经过180天高通滤波的MSLA数据) Fig. 1 Root-mean-square sea surface height anomaly in the North Pacific Subtropical Zone based on 180-day of high-pass filtered altimeter data from January 1993 to December 2015 注:白色的矩形为STCC区 |
本文根据Qiu等(2010), Kobashi等(2012)等人研究成果将STCC区范围限定为18°—27°N, 130°— 170°E。我们利用长达23年的高度计测高资料和世界大洋地图集2013(WOA 13) 气候态的月平均温盐数据集, 通过诊断动能谱及其涡旋尺度的季节变化, 探索斜压不稳定对涡动能季节变化的影响, 以及动能串级对涡旋尺度变化的关系, 以期弄清STCC区涡旋产生、非线性演进的动力学机制, 在研究涡旋尺度的季节变化和各向异性这些具有挑战性的问题上取得一点进展。选择STCC区有两个原因: (1) 其他的高能区, 像湾流、黑潮及其延伸区、东澳大利亚流、南极绕极流, 由于强流的正压性及邻近海流和海底地形的影响使得涡旋的相互作用过程可能很复杂。(2) STCC区相较于北太平洋的其它区域, 涡旋动能有更显著的季节变化, 如图 2所示。这对区分涡旋的生成, 相互作用及衰退过程很有意义。
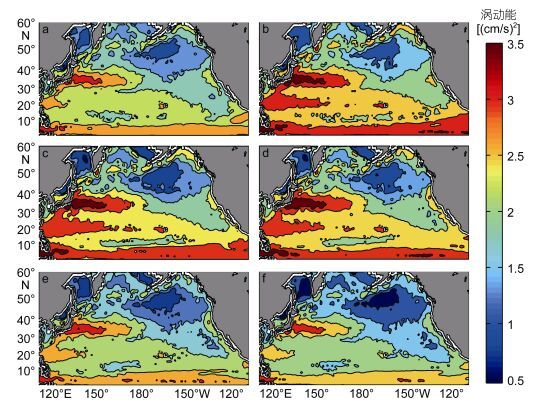 |
| 图 2 北太平洋地区涡动能的双月分布(根据1993年1月到2015年12月高度计MSLA数据, 动能场取log10) Fig. 2 Bimonthly mean EKE distribution in the North Pacific based on satellite altimeter MSLA data from January 1993 to December 2015, the kinetic energy field was plotted in log10 注: a, b, c, d, e, f分别代表 1—2月, 3—4月, 5—6月, 7—8月, 9—10月, 11—12月平均的涡动能 |
AVISO (2015) 卫星高度计数据, 由法国国家空间研究中心(CNES)提供。AVISO有多种资料产品, 我们使用的是由多颗卫星融合的网格化的海平面高度异常(MSLA)数据及绝对动力地形(MADT)数据。数据长度是从1993.1到2015.12, 时间间隔为一天, 水平分辨率为0.25°×0.25°。所选数据范围设定为: 0°—60°N, 120°—80°W, 覆盖了STCC区。
1.2 WOA温盐数据WOA13提供了气候态月平均的温度数据和盐度数据, 其水平分辨率为1°×1°, 垂直方向上有57个等深层。文本根据Chu等(1998)发展起来的P-Vector方法, 直接从温盐数据计算出STCC区从海面到海洋内部各层深度上的绝对地转流。
2 涡旋动能相关量的计算方法 2.1 涡旋动能利用MSLA数据, 我们根据地转关系直接计算涡旋动能, 公式为
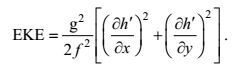 (1)
(1)其中g是重力加速度, f是科氏参数, h′是海表高度异常数据。
2.2 动能谱密度为了计算动能谱密度的分布, MSLA数据先进行如下的预处理。(1) 将STCC区域按经度分成8个互相重叠的子区域, 每个子区域的大小为10.5°×10.5°。子区域的中心从135°E开始, 间隔5°直到170°E。其次, 每个子区域内, 每天的MSLA数据减去一个用最小二乘法拟合的线性平面而去掉线性趋势。然后用汉宁窗平滑边界, 以便进行傅里叶变换(DFT)。将处理好的MSLA数据, 再利用地转关系求出地转速度u,v, 并根据公式
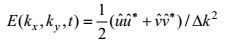 (2)
(2)计算动能谱密度。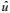
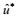
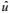
根据Qiu等(2008), 引入水平方向上的准地转动量方程
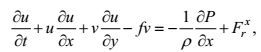 (3)
(3)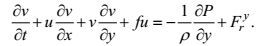 (4)
(4)其中, Frx, Fry是摩擦项。将式(3, 4) 分别与速度的共轭相乘并进行傅里叶变换, 得到动能谱密度的演化方程:
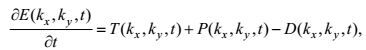 (5)
(5)其中
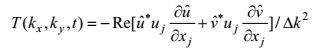 (6)
(6)是动能谱转移项, 它表示由于涡旋的互相作用, 动能谱在不同空间模式上的再分配(Qiu et al, 2008), 其中Re表示取实部。P(kx, ky, t)表示可利用的势能向动能转移的速率, D(kx, ky, t)表示由于摩擦等作用能量耗散的速率。取长期的时间平均, ∂E/∂t项比其它项小一个数量级, 于是可得能量的平衡方程(Qiu et al, 2008)
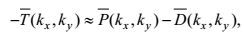 (7)
(7)当T(kx, ky)<0时, 强迫项大于耗散项, 意味着在空间模式(kx, ky)上有能量的输入。而当T(kx, ky)>0时, 强迫项小于耗散项, 意味着在空间模式(kx, ky)上有能量的输出。为求动能谱通量, 首先定义各向同性的波数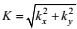
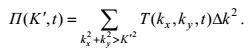 (8)
(8)当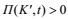
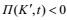
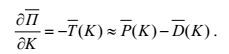 (9)
(9)由此可知, 当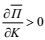
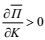
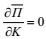
为分析STCC区的斜压不稳定, 我们采用两层半的斜压模式(Qiu, 1999), 即把海洋分成两个活跃的上层和一个无限深的下层。在第一层, 我们假设平均层厚度为H1, 平均水平流速为U1, 代表向东的STCC流。在第二层, 平均层厚度为H2, 平均水平流速为U2, 对应于向西的北赤道流(NEC)。每一层的密度为ρn (n=1, 2, 3)。在准地转假设下, 扰动位涡的控制方程为:
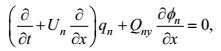 (10)
(10)其中φn是扰动流函数, Qn是气候态平均位涡, 取n=1, 2。在Un是常数的假设下,
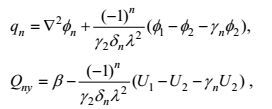
这里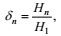
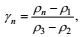
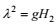
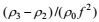
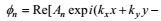
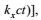
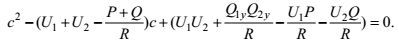 (11)
(11)其中
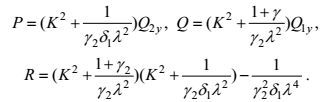
设式(10) 的复数解是c=cr+ici, 当ci≠0时, 式(9) 有不稳定的波解, 对应的斜压增长率为kci。
通过推导, 可得到不稳定波解或者斜压增长率存在的必要条件是:
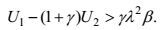 (12)
(12)可见, 较大的水平速度的垂向剪切U1-U2及较小的层结γ, 有助于斜压不稳定的产生。
3 动能谱及其尺度的季节变化根据式(1), 我们可得到STCC区23年内涡动能的时间序列, 如图 3a所示。可以看出涡动能除了年际变化外, 还存在着季节变化。为更明显起见, 我们计算23年内气候态月平均的涡动能及其标准差。由图 3b可知, 在5—6月份, 平均的涡动能达到最大值, 约为400cm2/s2, 其标准差为65cm2/s2。而在12—1月份, 平均的涡动能有最小值, 约为400cm2/s2, 标准差为34cm2/s2。由于STCC区的涡动能与东向的STCC流密切相关, 我们给出经向平均的气候态月平均涡动能沿不同经度的分布。由图 4可以看出, 每月的涡动能大体上向东逐渐减小。这说明STCC向东流的过程中, 中尺度的涡动能不断耗散。
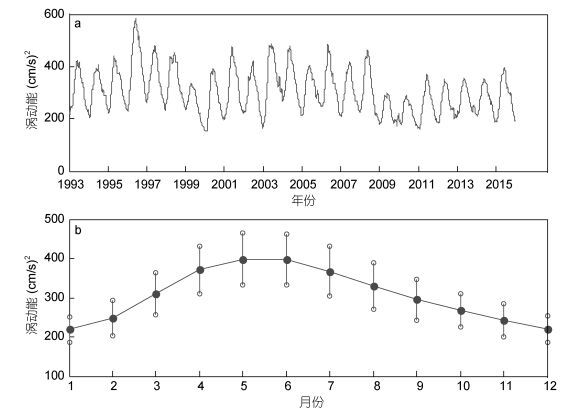 |
| 图 3 STCC区平均涡动能的时间序列(a)及其逐月分布(b) Fig. 3 The average time series (a) of eddy kinetic energy and the monthly distribution (b) in the STCC region 注:竖直线表示标准差 |
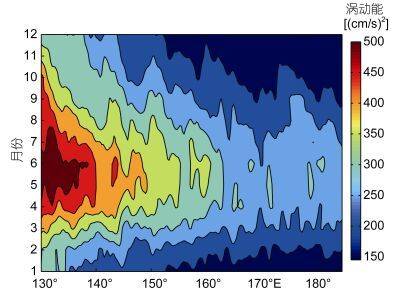 |
| 图 4 STCC区涡旋动能(经向平均)的经向-时间分布 Fig. 4 The meridional-time distribution of EKE averaged meridionally in the STCC regions |
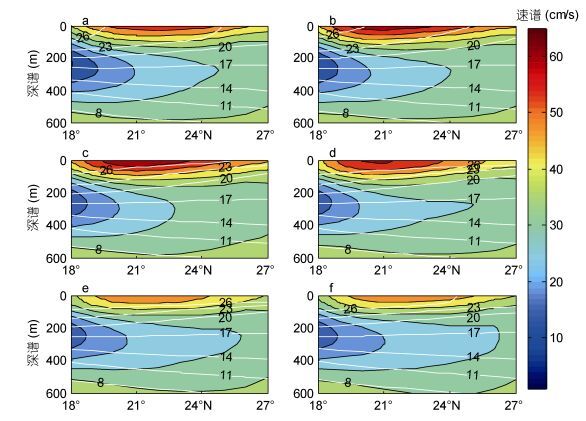
为了进一步弄清涡动能在不同空间尺度上的季节演变, 我们根据式(2) 计算二维动能谱密度, 并取每两个月的平均值, 结果如图 5所示。可以看出动能谱密度有着显著的季节变化, 且分布在一定范围的波数空间内。3—4月份的动能谱密度开始增强, 且在较小波数ky的方向上占的比重也增加了, 这意味着经向上的动能增加了。到了5—6月份, 动能谱密度达到最大。在7—8月份, 动能谱密度在较大波数ky的方向上占据优势, 此时动能主要分布在纬向上。11月以后, 动能谱密度明显减弱, 但仍然主要分布在纬向上。为了进一步看出水平尺度上动能谱密度的季节变化, 及其在中尺度涡附近的变化, 我们计算STCC区在不同季节内一维动能谱密度, 并根据Chelton (1998)的方法, 利用WOA13的温盐资料求罗斯贝变形半径。结果如图 6所示, 其中图 6中的竖直线对应的罗斯贝变形尺度为379km。可以看出, 在STCC区内, 动能谱密度随着尺度的减少(波数增加)而降低。从季节变化看, 在冬季1—2月动能谱密度最低, 且在小于罗斯贝变形尺度的范围内, 谱斜率大于1k-3; 在夏季5—6月动能谱密度最高, 谱斜率达到1k-3。另外, 为了考查涡旋尺度的季节变化, 我们采用下面的式(13) 计算涡旋能量尺度, 它常用来表示中尺度涡的长度尺度:
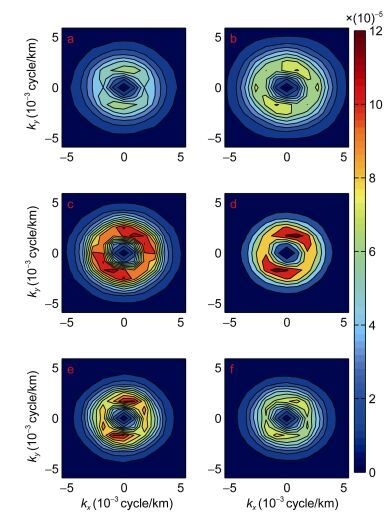 |
| 图 5 STCC区二维动能谱密度的季节分布 Fig. 5 Distribution of bimonthly EKE power spectral density as a function of kx and kyin the STCC regions 注: a, b, c, d, e, f分别代表 1—2月, 3—4月, 5—6月, 7—8月, 9—10月, 11—12月平均的功率谱密度。单位为(m/s)2/(cycle/km)2 |
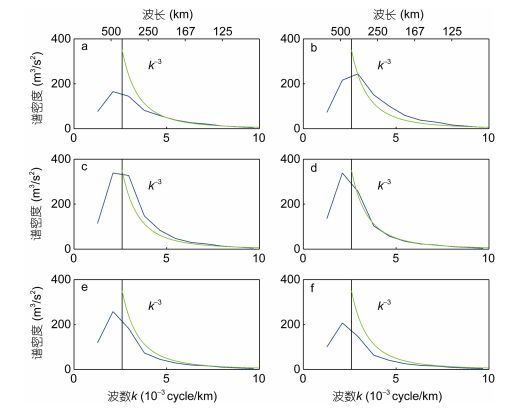 |
| 图 6 STCC区一维动能谱密度的双月分布 Fig. 6 Bimonthly EKE power spectral density distributions as a function of wavenumber k in the STCC region 注:绿线的谱斜率为k-3黑色的竖线为罗斯贝变形长度位置。a, b, c, d, e, f分别代表 1—2月, 3—4月, 5—6月, 7—8月, 9—10月, 11—12月平均的功率谱密度 |
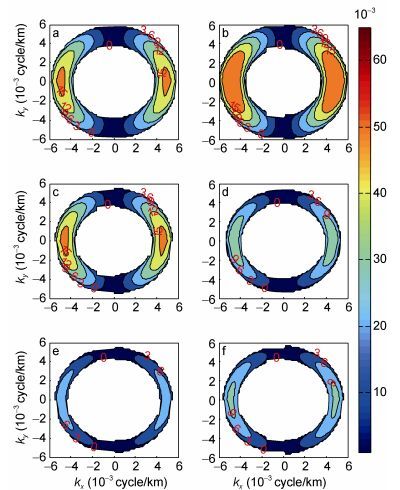
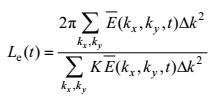 (13)
(13)这里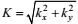
由图 7蓝线可以看出, 涡旋能量尺度的季节变化较为明显。在春季3月份能量尺度最小, 约为200km。在秋季8—9月份能量尺度最大, 约为335km。通过与图 7绿线所示的涡动能比较, 不难发现, 能量尺度最大的月份比涡动能最大的月份滞后2—3个月。这表明涡动能达到最大后, 通过涡旋的相互作用, 涡旋的尺度仍继续增长。这与后面分析的动能逆向串级有密切关系。
 |
| 图 7 STCC区涡旋的能量尺度(蓝线)及涡旋动能(绿线)的逐月分布 Fig. 7 The energy-containing scale (blue line) and EKE (green line) averaged over the STCC-NEC region vs month |
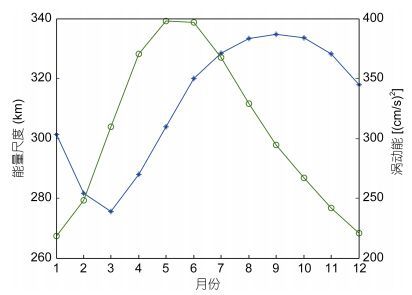
STCC区涡动能的季节变化已被Kobashi等(2002)确认, Qiu (1999)也指出STCC区涡动能的季节变化与斜压不稳定有关。我们通过WOA13气候态月平均的温盐数据, 结合两层半的斜压模式, 进一步探讨斜压不稳定与涡动能季节变化的联系。为此, 我们首先给出在STCC区不同季节内从海表面到600m水深处纬向平均的温度T分布情况。图 8的等值线反映了T随纬向和深度的变化, 其间隔为3℃。明显可见, 在400m水深以下, 等温线普遍朝着赤道方向向上倾斜, 且等温线的弯曲程度比较稳定, 几乎不随季节而变化。与此相对照的是, 在海表面到大约200m水深的海洋上层, 等温线则朝着赤道方向向下倾斜。上层海洋等温线的季节变化是由于受到风和浮力作用强弱的影响。进入冬季11月份以后, 由于海表面冷却, 海洋上层均匀分布的等温线发生了改变。在春季, 上层海洋的等温线弯曲程度最大。而到了夏季, 海表面变暖, 表面浮力减弱, 陡峭的等温线变得平缓。在秋季9—10月份上层海洋等温线的倾斜度最低。上层等温线弯曲程度的变化反映了海水密度的变化, 决定着海水层结的强弱, 从而影响斜压不稳定。另一方面, 斜压不稳定又与水平流速的垂向剪切有关。为此, 我们利用WOA13月平均的温盐数据, 结合P-Vector法, 计算出STCC区域不同季节内从海表面到600m水深, 纬向平均的地转流U。图 8颜色图给出了U随纬向和深度的分布。由此可以看出, 在海表到150m深的地方, 地转流基本上满足U > 0, 它代表了向东的北赤道副热带逆流。而在150m以下的海洋下层, 地转流U < 0它则代表了西向的北赤道流(NEC)。另外可以看出在STCC区的上层, 水平纬向速度U有着明显的季节变化。在春末夏初最大, 冬季1—2月份最小。在下层的NEC区, U的变化不是特别大。这意味着水平速度垂向剪切有着明显的季节变化。
 |
| 图 8 STCC-NEC区在不同月份等温线的深度-纬度断面(等值线)及纬向速度U(y, z)深度纬度断面(填色) Fig. 8 Depth-latitude section of the thermal (contours) and the zonal velocity (color) zonally averaged in the STCC-NEC 注: a, b, c, d, e, f分别代表 1—2月, 3—4月, 5—6月, 7—8月, 9—10月, 11—12月的双月平均值 |
根据海洋动力学, 水平速度的垂向剪切及层结不稳定的增加, 都会产生斜压不稳定。Qiu (1999)指出斜压不稳定是STCC区涡动能季节变化的主要原因。为了进一步证实这个结论, 我们利用两层半的斜压模式, 计算斜压增长率的季节分布。根据纬向流的分布, 我们将STCC-NEC区所在海域按如下方式分成三层:从海表到150m深的海水层作为第一层, 150—500m海水层作为第二层, 500m以下的海水为第三层。并利用WOA13气候态月平均的温盐数据, 计算出在不同的等深层次上, STCC区平均的位势密度ρ(z)及水平速度U。主要参数总结在表 1中。使用这些参数及其他的参数值, 利用式(11), 可计算出波数空间上的斜压增长率kci。图 9给出了STCC-NEC区斜压增长率的双月分布, 其中等值线的间隔为0.003。由此看出在不同季节内, 只有对特定范围的波长才会出现斜压不稳定。3—4月份不稳定的波长范围最大, 介于160—290km, 其中斜压最不稳定的波长(简称为斜压不稳定尺度)为200km。而9—10月份不稳定的波长范围最小, 介于180—230km。通过与能量尺度对比, 我们发现斜压不稳定的尺度比能量尺度小很多, 这很可能是由于涡旋的互相作用产生了逆向串级, 涡旋的尺度不断变大, 使得能量尺度要大于斜压不稳定的尺度, 后面部分将对此进行论证。
| 月份 | 第一层速度(m/s) | 第二层速度(m/s) | 第一层位势密度(kg/m3) | 第二层位势密度(kg/m3) | 第三层位势密度(kg/m3) | 层结γ |
| 1—2月 | 0.008 | -0.033 | 23.7σθ | 25.6σθ | 27.2σθ | 1.26 |
| 3—4月 | 0.016 | -0.032 | 23.8σθ | 25.6σθ | 27.2σθ | 1.16 |
| 5—6月 | 0.017 | -0.030 | 23.5σθ | 25.6σθ | 27.2σθ | 1.38 |
| 7—8月 | 0.009 | -0.031 | 23.1σθ | 25.6σθ | 27.2σθ | 1.62 |
| 9—10月 | -0.001 | -0.032 | 23.0σθ | 25.6σθ | 27.3σθ | 1.74 |
| 11—12月 | 0.001 | -0.033 | 23.2σθ | 25.7σθ | 27.3σθ | 1.66 |
 |
| 图 9 STCC-NEC区在二维波数空间的斜压增长率的双月分布(单位:/天) Fig. 9 Bimonthly baroclinic growth rate as a function of kx and ky in the STCC-NEC regions (unit: /day) 注: a, b, c, d, e, f分别代表 1—2月, 3—4月, 5—6月, 7—8月, 9—10月, 11—12月平均的斜压增长率 |
除了斜压不稳定的尺度随着季节变化, 从图 9我们还发现, 斜压不稳定的增长率也有显著的季节变化。3—4月份最大, 其最大增长率对应的时间尺度为(kci)-1≈51天。作为比较, 9—10月份, 斜压不稳定的增长率最低, 其最大增长率对应的时间尺度为130天。这一结论与Qiu (1999)的结果相比时间尺度稍小, 很大程度上与我们选择的分层有关, 在下面的4.3部分将进行阐述。需要指出的是最大斜压增长率出现的月份比涡动能最大值出现的月份滞后约2个月, 这与最大增长率对应的时间尺度(51天)比较吻合, 这表明斜压不稳定产生的扰动需要经过两个月左右的增长, 演变为振幅足够大的涡旋, 涡动能才能达到最大值。另一方面, 由图 9可以看出, 在不稳定增长率对应的波数空间中, 具有较大纬向波数kx和较小经向波数ky的点对应着更大的增长率。这说明斜压不稳定的尺度主要发生在经向尺度上, 这与3—4月份由图 5显示的涡动能在经向尺度上的增加是一致的。最后, 为了说明斜压不稳定季节性变化的原因, 我们给出了STCC区斜压最大增长率, 以第一层和第二层平均的速度差ΔU作为水平速度U的垂向剪切以及层结γ的季节分布, 如图 10所示。可以看出, 春季3月份水平速度的垂向剪切最大, 层结最小, 对应的斜压最大增长率最大, 而10月份恰好相反。这就表明由于水平速度的垂向剪切和层结的季节性变化, 导致了斜压不稳定的季节变化。
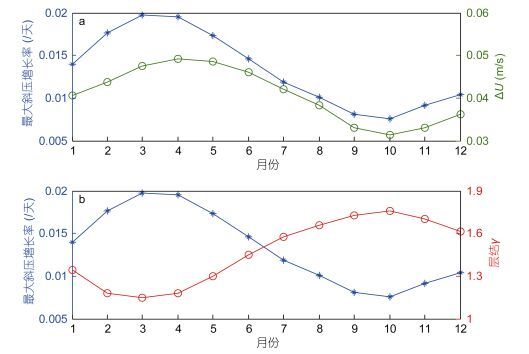 |
| 图 10 STCC区最大斜压增长率(蓝)和水平速度垂向剪切(绿)及层结(红)的逐月分布 Fig. 10 The maximum baroclinic growth rate (blue), zonal velocity shear (green), and the stratification (red) averaged over the STCC region vs month |
前面我们利用两层半的斜压模式, 将STCC-NEC区分成三层, 进行了斜压不稳定分析。由式(11) 及图 10看出, 斜压增长率与水平流速的垂向剪切ΔU成正相关, 而与及密度层结γ的大小成负相关。当分层方式不同时, γ会发生明显的变化, 从而对斜压不稳定产生影响。为此, 我们将STCC区的上层保持不变, 第二层的深度依次取为300、350、400m, 根据前面的方法, 分别计算斜压最大增长率及斜压不稳定的尺度, 结果如图 11a、b所示。可以看出, 不同的分层有相同的季节分布特征, 斜压最大增长率都在3月份最大, 10月份最小。另一方面, 随着第二层深度的增加, 斜压最大增长率不断减小。斜压增长率的这种变化与层结的变化密切相关, 如图 11c所示。第二层深度的增加, 导致层结增强, 进而使得斜压增长率变小。另外, 根据图 11b, 可以看出, 斜压不稳定尺度的季节变化与分层也有关系。第二层深度越大, 斜压不稳定的尺度也越长。除了以上的分层方式, 我们也探讨了其他的分层方式。例如将第一层的深度设定为125m, 第二层的深度分别取为300、350、400m, 所得结论也是相似的。为方便起见, 本文后面的讨论, 均以4.2部分提出的分层方式为依据。
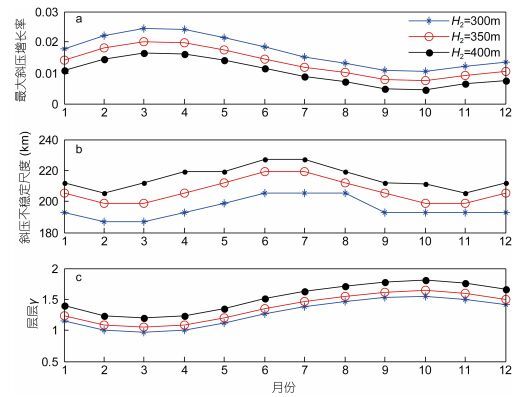 |
| 图 11 SCTT-NEC区不同分层对斜压不稳定性的季节性影响 Fig. 11 Seasonal effects of different delamination on the baroclinic instability in the SCTT-NEC region 注: a:斜压最大增长率的逐月变化; b:斜压不稳定尺度的季节变化; c:层结的季节变化。蓝、红、黑线分别表示第二层深度H2=300, 350, 400m对应的值 |
前面指出涡旋的能量尺度比斜压不稳定尺度大, 可能是由于动能逆向串级造成的, 而动能逆向串级的原因与斜压不稳定也密切相关。为证实这点, 我们首先根据式(5) 计算动能谱的转移项T(kx, ky, t)。图 12给出了T(kx, ky, t)的季节分布, 每幅图的虚线表示在STCC区根据4.2部分计算的斜压不稳定波数范围。从中可以看出, 在不稳定的窗口内, 动能谱转移项大部分是负的。由式(6) 可以得出在中尺度范围内, 强迫项大于耗散项。这表明斜压不稳定将部分势能转化为涡动能, 为中尺度涡旋的产生提供了能源。另一方面, 在水平波长大于300km的区域内, 动能谱转移项大部分是正的。这表明大部分的动能向大尺度转移。特别指出, 5—6月份, 动能谱转移项以纬向尺度为主, 这意味着涡旋互相作用产生的逆向串级使得动能从经向尺度向纬向尺度转移。
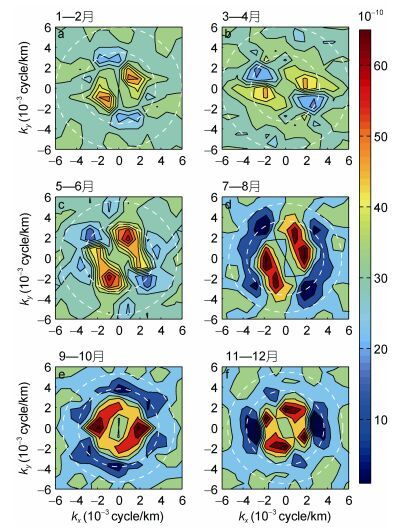 |
| 图 12 STCC区动能谱转移项的双月分布 Fig. 12 Bimonthly spectral energy transfer in the STCC region 注:白色的虚线表示斜压不稳定的范围。a, b, c, d, e, f分别代表 1—2月, 3—4月, 5—6月, 7—8月, 9—10月, 11—12月的双月平均值 |
为了从水平尺度上看出动能串级的季节变化, 我们根据式(7), 计算每两个月平均的动能谱通量Π(K, t), 如图 13所示。可以看出在每个季节内都普遍存在动能逆向串级。动能谱通量在1—2月份最小, 3—4月份增强, 在5—6月份达到最大, 之后又逐渐减小。另一方面, 从尺度变化看, 斜压不稳定尺度(图 12中红线表示)与谱通量的入射尺度(图 13中黑线所示)相比稍小, 但比较接近。这表明斜压不稳定达到最大后, 动能才能逆向串级, 即向大尺度转移。比如5—6月份, 能量入射尺度与斜压不稳定尺度非常吻合, 约为210km。9—10月份, 斜压不稳定尺度约为200km, 而能量入射尺度为224km。可见在3—4月份, 斜压不稳定最强时, 逆向串级发生的尺度也较小; 而9—10月份, 斜压不稳定较弱时, 逆向串级发生的尺度也较大。同时, 我们看到能量尺度(图 13中的绿线), 要大于斜压不稳定的尺度, 这正是动能逆向串级的结果。当动能逆向串级在达到能量尺度后并没有停止, 而是继续向大尺度转移; 而当涡旋尺度一旦超过能量尺度, 就很接近动能串级的驻足尺度。这意味着在稍大于能量尺度的附近, 能量的净输入和净输出达到平衡。
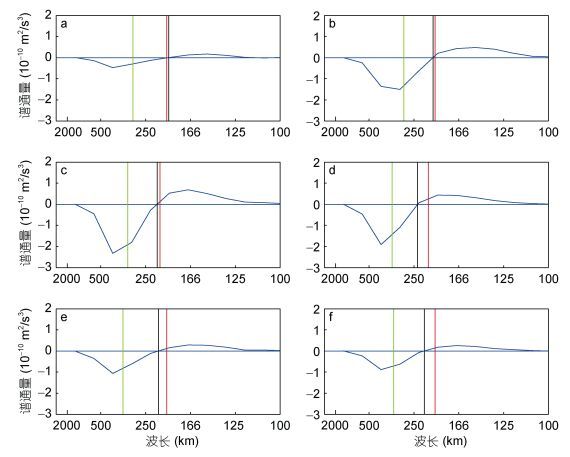 |
| 图 13 STCC区动能通量的双月分布 Fig. 13 Bimonthly spectral kinetic energy flux vs total wavenumber k in the STCC regions 注:黑线表示能量入射尺度, 红线表示斜压不稳定尺度, 绿线表能量尺度。a, b, c, d, e, f分别代表 1—2月, 3—4月, 5—6月, 7—8月, 9—10月, 11—12月的双月平均值 |
本文利用了23年的卫星高度计MSLA和MADT数据, 考察了北太平洋副热带逆流区动能谱的季节变化及其空间尺度分析。结合WOA13气候态月平均的温盐数据集, 本文求出了气候态的地转流。利用准地转湍流的斜压不稳定理论, 特别是斜压两层半模式, 和动能串级的理论, 我们对STCC区涡旋动能谱的季节演变及其涡旋尺度的变化可归纳分为三个阶段:
(1) 增长阶段(3—4月)
3月份, 由层结所导致的地转流的垂向剪切达到年内最大值。此时, 斜压增长率也达到最大值, 涡动能开始快速增长, 斜压不稳定的尺度约为200km, 动能逆向串级开始加强, 使得能量尺度为280km。
(2) 成熟阶段(5—8月)
斜压不稳定引起的扰动持续增长, 使得涡动能的最大值出现在5—6月份, 此时动能谱斜率约为1k-3, 斜压不稳定的尺度为210km, 动能逆向串级也最大, 能量尺度达到了约300km。7—8月份, 斜压不稳定仍然提供涡动能, 涡动能还维持着较高的水平, 而且逆向串级使能量尺度持续增加。
(3) 衰退阶段(9—2月)
9—10月份, 随着地转流垂向剪切的减弱以及层结的强化, 斜压不稳定的增长率也大幅减少, 涡动能不断降低。此时斜压不稳定的尺度减少至200km左右。由于逆向串级, 能量尺度仍旧是增加的, 达到最大值335km。进入1月, 涡动能降到最低, 动能谱斜率大于1k-3, 动能串级的减弱使能量尺度也减少。
总之, 斜压不稳定是涡旋动能产生并增长的能量来源, 也为涡旋互相作用提供了动力。与Qiu (1999)和Kobashi等(2002)的结果相比, 本文分别在二维及一维空间尺度上展示了STCC区涡旋动能谱的季节变化及其特征, 并给出了中尺度涡的长度尺度即能量尺度及其动能谱斜率的季节变化规律。通过计算动能谱转移项的季节变化, 本文进一步确认了斜压不稳定是涡旋能量变化的原因。通过计算动能谱通量及其入射尺度, 驻足尺度的季节变化, 我们发现只有当达到或超过斜压不稳定的尺度时, 在涡旋的互相作用下, 涡旋动能才发生逆向串级。当涡旋尺度超过能量尺度时, 能量的净输入和净输出达到平衡。此外, 本文也表明斜压不稳定发生的方向以经向尺度为主, 但是随后的涡旋互相作用使得动能逆向串级将经向尺度的动能向纬向尺度转移, 这很可能与β效应有关。由于缺少高分辨率的模式数据, 本文没有给出由于斜压不稳定产生的势能向涡动能转移量的季节变化。另外涡旋动能的耗散过程, 是以大尺度的流体向海洋深处转移、然后与海底互相作用而耗散殆尽, 还是在海洋上层串级为能量较大的小尺度涡然后耗散尽, 这些问题需要进一步的研究。
| 刘秦玉, 杨海军, 鲍洪彤, 等, 2000. 北太平洋副热带逆流的气候特征. 大气科学, 24(3): 363–372 |
| 李荣凤, 游小宝, ChuP, 2004. 西北太平洋等位势密度面上的东向副热带逆流. 中国科学D辑地球科学, 34(11): 1083–1089 |
| 胡瑞金, 刘秦玉, 2002. 热带太平洋海平面高度年变化与季节内变化特征. 海洋与湖沼, 33(3): 303–313 |
| 管秉贤, 1987. 副热带逆流二十年研究概况. 黄渤海海洋, 5(4): 65–72 |
| Aoki S, Imawaki S, 1996. Eddy activities of the surface layer in the western North Pacific detected by satellite altimeter and radiometer. J Oceanogr, 52(4): 457–474 DOI:10.1007/BF02239049 |
| Arbic B K, Polzin K L, Scott R B, et al, 2013. On eddy viscosity, energy cascades, and the horizontal resolution of gridded satellite altimeter products. J Phys Oceanogr, 43(2): 283–300 DOI:10.1175/JPO-D-11-0240.1 |
| Chang Y L, Oey L Y, 2014. Analysis of STCC eddies using the Okubo-Weiss parameter on model and satellite data. Ocean Dyn, 64(2): 259–271 DOI:10.1007/s10236-013-0680-7 |
| Chelton D B, deSzoeke R A, Schlax M G, 1998. Geographical variability of the first baroclinic Rossby radius of deformation. J Phys Oceanogr, 28(3): 433–460 DOI:10.1175/1520-0485(1998)028<0433:GVOTFB>2.0.CO;2 |
| Chu P C, Fan C W, Cai W J, 1998. P-vector inverse method evaluated using the modular ocean model (MOM). J Oceanogr, 54(2): 185–198 DOI:10.1007/BF02751694 |
| Frisch U, 1995. Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press, 296 |
| Kobashi F, Kawamura H, 2002. Seasonal variation and instability nature of the north pacific subtropical countercurrent and the Hawaiian lee countercurrent. J Geophys Res, 107(C11): 3185 DOI:10.1029/2001JC001225 |
| Kobashi F, Kubokawa A, 2012. Review on North Pacific Subtropical Countercurrents and Subtropical Fronts: role of mode waters in ocean circulation and climate. J Oceanogr, 68(1): 21–43 DOI:10.1007/s10872-011-0083-7 |
| Noh Yign, Young Y B, You S H, 2007. Seasonal variation of eddy kinetic energy of the North Pacific subtropical countercurrent simulated by an eddy-resolving OGCM. Geophys. Res. Lett, 34(7): 488–501 |
| Qiu B, 1999. Seasonal eddy field modulation of the North Pacific subtropical countercurrent: TOPEX/Poseidon observations and theory. J Phys Oceanogr, 29(10): 2471–2486 DOI:10.1175/1520-0485(1999)029<2471:SEFMOT>2.0.CO;2 |
| Qiu B, Chen S M, 2010. Interannual variability of the north pacific subtropical countercurrent and its associated mesoscale eddy field. J Phys Oceanogr, 40(1): 213–225 DOI:10.1175/2009JPO4285.1 |
| Qiu B, Scott R B, Chen S M, 2008. Length scales of eddy generation and nonlinear evolution of the seasonally modulated south pacific subtropical countercurrent. J Phys Oceanogr, 38(7): 1515–1528 DOI:10.1175/2007JPO3856.1 |
| Scott R B, Wang F M, 2005. Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry. J Phys Oceanogr, 35(9): 1650–1666 DOI:10.1175/JPO2771.1 |
| Stammer D, 1998. On eddy characteristics, eddy transports, and mean flow properties. J Phys Oceanogr, 28(4): 727–739 DOI:10.1175/1520-0485(1998)028<0727:OECETA>2.0.CO;2 |
| Tulloch R, Marshall J, Hill C, et al, 2011. Scales, growth rates, and spectral fluxes of baroclinic instability in the ocean. J Phys Oceanogr, 41(6): 1057–1076 DOI:10.1175/2011JPO4404.1 |
| Wang S H, Liu Z L, Pang C G, 2015. Geographical distribution and anisotropy of the inverse kinetic energy cascade, and its role in the eddy equilibrium processes. J Geophys Res, 120(7): 4891–4906 DOI:10.1002/2014JC010476 |
| Yoshida K, Kidokoro T, 1967. A subtropical counter-current in the North Pacific: an eastward flow near the subtropical convergence. J Oceanogr Soc Japan, 23(2): 88–91 DOI:10.5928/kaiyou1942.23.88 |
| Yoshida S, Qiu B, Hacker P, 2011. Low-frequency eddy modulations in the Hawaiian lee countercurrent: observations and connection to the pacific decadal oscillation. J Geophys Res, 116(C12): C12009 DOI:10.1029/2011JC007286 |
 2017, Vol. 48
2017, Vol. 48


