中国海洋湖沼学会主办。
文章信息
- 岑显荣, 郭双喜, 鲁远征, 屈玲, 周生启. 2017.
- CEN Xian-Rong, GUO Shuang-Xi, LU Yuan-Zheng, QU Ling, ZHOU Sheng-Qi. 2017.
- 冲绳海槽热液柱动力过程的数值模拟
- NUMERICAL SIMULATION OF THE DYNAMICAL PROCESSES OF HYDROTHERMAL PLUMES IN OKINAWA TROUGH
- 海洋与湖沼, 48(6): 1435-1445
- Oceanologia et Limnologia Sinica, 48(6): 1435-1445.
- http://dx.doi.org/10.11693/hyhz20170500148
-
文章历史
- 收稿日期:2017-05-30
- 收修改稿日期:2017-09-25
海底热液活动普遍发育在地质构造不稳定的区域, 如大洋中脊、弧后盆地以及板内火山等, 是地壳和海洋之间进行能量和物质交换的主要通道。迄今为止, 已发现的海底热液地点超过300处, 其中较为活跃的包括西太平洋边缘的冲绳海槽和马努斯海盆, 东太平洋海隆(EPR), 以及中大西洋洋中脊(MAR)等热液区。
海底热液活动的突出表现是高温的热液流体从海底喷出, 形成黑烟囱状的羽流。如图 1所示, 这些热液流体的密度低于周围海水, 因此当其从热液喷口喷出后会向上漂浮, 但它不会无限制的上升, 而是在上升过程中把周围的海水卷挟进来, 当到达最大上升高度zmax时, 形成“顶帽”, 热液流体与周围海水的混合物停止上升, 或者受洋流的影响或者受自己内部动力学等因素的影响向两边扩散形成一个密度平衡面, 此面被称为中性浮力面, 其高度称为中性浮力面高度zn。整个过程形成类似羽状的物理化学异常水体, 这个异常水体通常被称为热液柱(曾志刚, 2011)。热液柱是热液系统将自身的能量输入海水的主要形式, 是研究现代海底热液活动环境效应的主要物理化学对象。从动力学角度上看, 热液喷口的热通量、体积通量和湍流强度等要素为热液柱的产生提供了动力条件, 而海水层结、底流、潮汐流、地转效应等环境要素则影响热液柱的物质和能量输运过程。对热液柱的运动特征和动力学机制的充分认识, 是研究热液系统的成矿规律、生物群落分布特征的基础, 也是准确地估计全球热液活动输出的热通量和物质通量的前提。
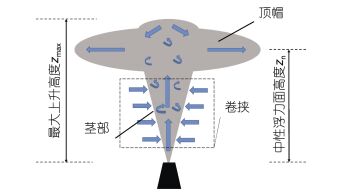 |
| 图 1 热液柱示意图 Fig. 1 Schematic view of a hydrothermal plume |
目前, 对热液柱动力过程的研究仍不充分。起初, 人们从热羽流的一些理论模型出发, 对羽流的动力学方程进行简化, 推导出羽流流动的一些经验公式, 并应用于指导热液活动的现场观测。Morton等(1956)开创性地提出了经典的热羽流模型(该模型后来被称为MTT模型), 他们认为羽流的卷挟速率与羽流上升速度成正比, 并对羽流的一维守恒方程组进行了求解, 得到了羽流的最大上升高度与初始动力条件之间的关系式。MTT模型随后被广泛应用于热液柱的研究, 用来探寻观测的羽状特性(如上升高度或轴线温度)与热源热通量的关系。Speer等(1989)在MTT模型的基础上加入了背景温度与盐度梯度因素, 揭示了太平洋洋中脊和大西洋洋中脊的热液柱在形态方面的差异。后来, Rudnicki等(1992)在Speer等(1989)的工作的基础上发展了一套有限差分法, 并应用于大西洋洋中脊TAG热液区热液柱的研究, 计算了其热通量、物质通量以及金属颗粒物的浓度分布, 认为TAG热液区的热液柱只携带了其中了50%的热量, 其余的热量则以弥散流的方式释放。需要指出的是, 上述这些经验公式的应用范围有限, 难以细致地描述热液柱的温度、速度以及热液产物的分布, 更难以反映热液柱的湍流输运特性及详细的卷挟过程, 因此无法深入地理解热液柱的动力过程。
实验模拟可以在实验室内再现热液柱, 并验证理论模型的一些结论。例如, Carazzo等(2012)进行了一系列的羽流室内实验, 研究了初始密度层结和颗粒物浓度对羽流动力过程的影响。张巍等(2016)利用实验方法在线性层结的盐水中模拟了羽流的运动过程, 重新确定了羽流最大上升高度公式中的经验常数。然而, 这些羽流的室内实验通常只能模拟理想化的热液过程, 很多实际的因素, 如海底的水流、喷口处剧烈的温度梯度、海底的高压极端环境等条件, 目前都难以在实验室中全部实现, 因而大大制约了实验模拟成果同现场资料的结合。
现场观测方面, 过去和现在开展的海底热液调查活动, 积累了很多宝贵的现场数据。例如, Xu等(2014)在采用声呐方法对热液柱的速度进行了测量, 并计算了热液柱的体积通量和热通量; Wen等(2016)在日本南部的吐噶喇群岛测量了热液柱的温度、浊度以及甲烷浓度等水文数据, 并拍摄了热液柱视频。然而, 由于海底热液活动普遍发生在水深千米以上的高压环境, 且热液流体的温度通常高达300℃以上, 利用常规的海洋仪器难以进行多方位、长时间的原位观测。尽管目前也有科学家使用水下机器人(ROV)或载人深潜器等设备可对热液柱的理化参数进行精确测量(Escartin et al, 2015; Zhang et al, 2017), 但仍需耗费大量的人力物力, 费用极其昂贵。海底热液活动的调查已进行了半个多世纪, 但仍有许多问题有待解决, 如深海热液调查技术和设备的研发、采样和取样所带来的环境破坏等等(黄丁勇等, 2011)。
如今, 随着计算机硬件水平的快速发展, 以及流体动力学模型(特别是湍流模型)的不断完善, 使用计算流体力学(Computational Fluid Dynamics, 简称CFD)方法对热液柱进行模拟, 已成为研究热液系统物理过程的有效手段。CFD方法主要基于完整的Navier-Stokes方程组, 建立热液柱的动力学模型, 并利用数值方法进行求解, 从而获得热液柱的速度、温度和示踪物浓度等信息。比起理论模型和室内实验, CFD的最大优势是可以获得高温高压环境下热液柱的速度场、温度场和湍流耗散率等物理量的所有细节, 从而分析热液柱卷挟的详细过程及其热质输运规律。Lavelle等(1997; 2013)采用非静力海洋模式, 以太平洋胡安德富卡洋脊的热液区为对象, 系统地研究海水了在不同的喷口初始参数、海底横流、内潮、旋转和层结等各种条件影响下, 热液柱的生成和发展过程。Tao等(2013)以大西洋洋中脊的Nibelungen热液区为对象, 借助开源的CFD软件Gerris, 利用l-k湍流模型研究了热液柱的湍流混合和卷挟过程、以及热液柱在横流影响下的运动特征, 并提出了在横流作用下羽流最大上升高度的标度律公式。Jiang等(2014)利用二维轴对称模型对西南太平洋ABE热液区的热液柱进行了CFD模拟, 发现热液柱的“顶帽”区域存在回流现象。在国内, 温竹青(2010)应用FLUENT软件模拟了大西洋洋中脊TAG热液区羽流喷发后在海底的扩散形态, 得到了喷发温度、热源半径、喷发初始速度对热液柱的影响规律。
在本文中, 我们结合冲绳海槽热液活动的现场观测数据, 通过k-ε湍流模型模拟热液柱的动力过程。根据数值模拟的结果, 研究热液柱的运动和动力特征, 及其卷挟过程的变化规律, 最终评估海底热液系统输出的物质和能量通量。
1 数据与方法 1.1 冲绳海槽热液区的理化和环境参数冲绳海槽属弧后盆地, 位于琉球海沟和琉球岛弧向大陆一侧(图 2), 是菲律宾海板块在琉球海沟向欧亚大陆俯冲的结果。整个冲绳海槽南北长约1300km, 北部宽达230km, 最大水深约1200m, 南部宽达60—100km, 最大水深约2300m(曾志刚, 2011)。冲绳海槽的中部是热液活动较活跃的地区。2014年4月, 我国“科学”号科考船执行中国科学院海洋先导性科技专项的西太平洋海底热液调查任务, 航次目标为采集冲绳海槽热液区及邻近区域水体、沉积物、生物等样品以及水文和流场数据, 为深部水体环境和深海生态系统研究提供基础图件、样品和相关环境信息参数。该航次共完成25个站位的地质、水文、生物作业, 获得了水体不同层位的深度、温度、盐度、溶解氧、甲烷、浊度等理化环境参数。
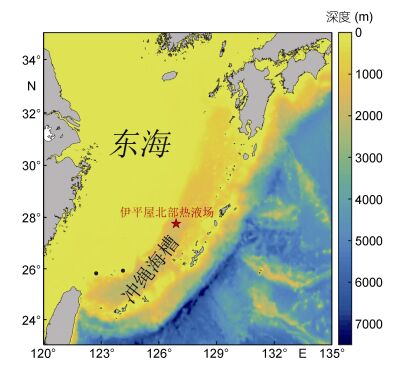 |
| 图 2 冲绳海槽及伊平屋北部热液区示意图 Fig. 2 The Okinawa Trough and the Iheya North hydrothermal field |
本文选取冲绳海槽中部地区的伊平屋北部热液区作为背景区域, 重点关注综合大洋钻探计划第331次钻探(Takai et al, 2011)的C0016站位(126°53.80′, 27°45.50′N)附近的热液柱。据现场观测显示(Takai et al, 2011), 在C0016站位附近的北部大烟囱(North Big Chimney), 其烟囱体高约20m, 顶部直径约6m;根据ROV测距激光束估算, 热液喷口的直径约10—20cm, 热液流体温度高达311℃。另外, 根据2014年冲绳海槽热液航次的观测资料, 在位于C0016站位东边的W8站位(126°53.86′, 27°47.47′, 水深1046m), CTD数据显示:测量最大深度处(约1026m)海水的温度约为4.38℃(相应的盐度约为34.57), 并随着深度的减小温度(盐度)大致呈线性地增加(减小); 960m以深的底层水存在明显的浊度异常, 而且浊度随深度增加而迅速增加。一般来说, 喷口附近的浊度会明显高于背景浊度值(陈小丹等, 2015), 因此W8站位出现的浊度异常预示该站位与实际喷口的位置非常接近。从图 3可以看到, 在深度960—980m(离海底66—86m)的范围内, 存在明显的温度和盐度异常, 推测这个深度范围很可能是热液柱的中性浮力层或最大上升高度的区间。因此, 本文以W8站位的CTD数据作为数值模拟的背景参数, 以求更真实地反演该热液柱的动力过程。
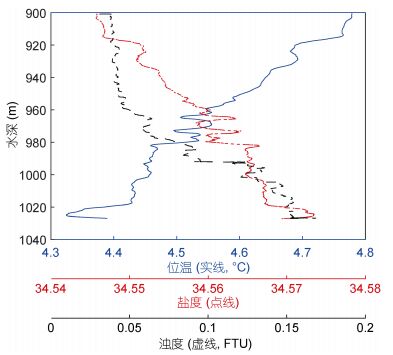 |
| 图 3 W8站位底层水的位温、盐度和浊度分布 Fig. 3 The distribution of potential temperature, salinity, and turbidity of the bottom water at station W8 |
热液柱的流动通常处于湍流状态。在直接数值模拟尚未普及的时候, 基于Reynolds时均方程的k-ε湍流模型目前仍是研究湍流的有效工具之一, 已被成功应用于西南太平洋劳海盆ABE热液区热液柱的模拟(Jiang et al, 2014), 再现了热液柱的动力过程。这里, 我们也将采用k-ε模型来模拟热液柱的湍流流动。由于W8站位的最大水深所对应的水压约为10.62MPa, 喷口流体温度为311℃, 热液柱因而处于高温高压的环境。对于密度的计算, 我们采用非线性的海水状态方程(Sun et al, 2008), 它在温度0—374℃、压力0.1—100MPa、盐度0—40的变化范围内都适用, 能反映热液流体在上升过程中引起的密度的剧烈变化。
如图 4a所示, 在几何上我们采用二维轴对称模型, 以喷口中心线作为对称轴, 计算区域半径100m(约为中性浮力层半径的3倍), 高度200m(约为热液柱最大上升高度的3倍), 以消除边界的反射对计算结果的影响; 喷口被简化为直径D=0.1m的圆形区域, 置于离海底20m、顶部直径6m的烟囱体之上(图 4b)。在边界条件方面, 计算域顶部设为压力出口, 底部以及烟囱体为固壁, 侧边为对称边界; 喷口设为速度入口, 由于喷口的流速难以进行直接测量, 故采用Jiang等(2014)建议的渐近方法进行推算, 给定流速0.15m/s, 流体温度311℃。至于初始条件, 由于本文不考虑海底背景潮流的影响, 因此把背景流场的初始流速设为零, 初始温度分布则依据对W8站位的位温数据进行线性拟合, 把海底的初始温度设为Tbottom=4.38℃(对应的密度为ρbottom=1026.772kg/m3), 随离底距离线性增加, 在顶部处的温度设为Ttop= 5.308℃(对应的密度为ρtop=1026.725kg/m3), 由此得到的背景浮力频率为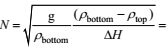
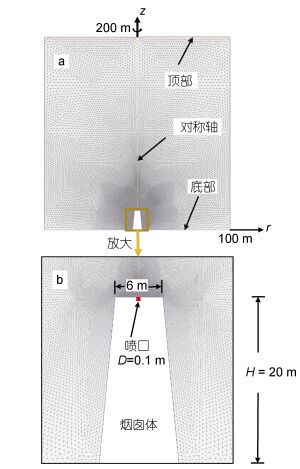 |
| 图 4 网格与边界条件(a)与烟囱体及喷口位置的局部放大(b) Fig. 4 Mesh and boundary conditions (a) and zoomed-in display near the chimney and the vent (b) |
图 5显示的是热液柱在不同时刻的速度矢量及温度等值线的分布。在羽流发展的初始时刻(图 5a), 从喷口出来的高温流体与周围的水体温差较大, 在离喷口大约4.5m的地方, 羽流的上升速度最明显, 中心线的最大上升速度约为0.35m/s, 这与Xu等(2013)在Main Endeavour Field热液区的羽流流速测量结果(0.11—0.24m/s)相近。从图 5a还可以看到, 在300s时热液柱的形状以茎部结构为主, “顶帽”结构还不明显, 这是由于热液流体此时正处于快速上升的阶段, 热液柱的半径比其高度小很多而造成的; 而在羽流尾端的两侧, 随着羽流上升的加速和因此形成的卷挟作用, 周边水体不断补充, 因而在茎部两侧形成两个较强烈的涡旋。在600s时, 随着羽流不断上升, 热液柱的半径显著增大, 导致其体积不断增大, 浮力逐渐减小, 羽流的加速度开始减小, 温度等值线显示此时已产生明显的“顶帽”结构, 但依然可以看到茎部两侧的涡旋(图 5b); 在2000s时, 羽流顶部的浮力减小到零, 热液柱开始在中性浮力面高度zn沿水平方向扩散, 垂向剪切作用的减弱导致其茎部侧边的涡旋开始消失, 而羽流的尾端则在惯性作用下到达最大上升高度zmax(图 5c); 最后, 羽流进入准稳态发展阶段, 热液流体以热液柱为载体沿中性浮力面高度向四周扩散, 此过程反复循环, 并且热液柱一直维持具有“顶帽”和茎部结构特征的“蘑菇云”形态(图 5d)。
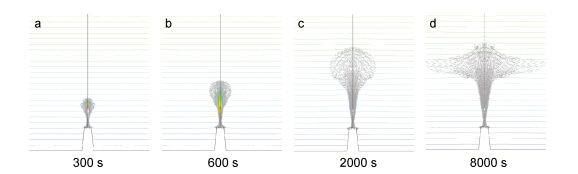 |
| 图 5 热液柱在不同时刻的演化 Fig. 5 The evolution of a hydrothermal plume at different stages |
湍动能耗散率ε(单位为W/kg)代表在分子黏性作用下由湍流动能转化为热能的速率, 耗散率越高, 湍流混合越强。图 6显示的是沿热液柱中心线的湍动能耗散率的变化过程。这里, 我们把ε=1×10-9W/kg的位置定义为羽流的边缘。由图 6可知, 从开始到第一个振荡周期(约2094s)的时间里, 羽流不断上升, 在2000s的时候到达最高位置(约68m), 羽流的平均上升速度约为0.035m/s; 随后, 羽流进入准稳态阶段, 其边缘的最高点在羽流最大上升高度zmax(约64m)位置附近振荡。
 |
| 图 6 羽流中心线的湍流耗散率的时间-高度演化 Fig. 6 The time-height diagram of the dissipation rate along the plume's centerline |
在热液柱的现场观测中, 羽流的最大上升高度zmax是探测热液喷口位置、反演热通量等热液流体性质的重要依据。若能准确预测羽流的最大上升高度, 那么热通量便可以利用式(1)进行间接估算, 从而评估热液活动对岩石、海水、生物等环境的影响情况(曾志刚, 2011)。羽流所能上升的最大高度由喷口的初始浮力通量B0和背景层结参数N两者共同决定。这里, 我们把zmax定义为羽流中心线处的垂向速度第一次降为0的位置。根据MTT模型的预测, zmax与B0和N之间满足如下关系式:
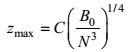 (1)
(1)在使用上面的MTT经验公式时, 式中的B0应取渐近浮力通量Basymp(asymptotic buoyancy flux), 其中Basymp=gβT(Texit-Tbottom)Q0, βT为热膨胀系数。需要注意的是, 喷口的实际浮力通量应为
MTT模型中的经验系数C是通过大量羽流室内实验的数据分析得到的, 一般建议取为3.76(Turner等, 1987)。为了进一步验证MTT模型的经验系数C的适用情况, 我们根据不同的层结强度设计了四种工况(如表 1), 模拟结果如图 7所示。整体而言, MTT理论模型的预测结果与CFD模拟的结果两者吻合良好(图 7a), 特别是对于工况1—3等几种层结较弱的工况, zmax的模拟值跟理论值相比其平均误差为9.7%。为确定经验系数C, 我们对CFD模拟的最大上升高度进行线性回归分析, 具体结果如图 7b所示。本文的模拟结果显示, 经验系数取值为C=3.46 (R2= 0.9321), 比建议值(C=3.76)偏小8%左右。在羽流室内实验中, 张巍等(2016)得到的经验系数为C=4.03 (R2= 0.9326), 比建议值偏大7%左右。需要说明的是, 本文只模拟了四种工况, 在对C作回归分析时, 样本数偏少, 这可能是造成计算结果与建议值有一定偏差的原因。对于冲绳海槽的热液柱, MTT模型的经验系数应选取比一般建议值更小的取值, 才能更好预测其最大上升高度。此外, 从工况1的结果来看, 尽管本文预测的羽流最大上升高度(63.62m)比MTT模型预测结果(72.62m)更接近实测值(约66m), 但考虑到CFD模型的假设及边界条件与热液柱的真实物理过程仍有一定差别, CFD模拟结果与实测结果不可避免地也会存在一定的偏差, 这需要更多的现场数据进行检验。
| 工况 | Tbottom(℃) | Ttop(℃) | N (rad/s) | B0(m4/s3) | zn(m) | zmax(m) | zn/zmax | zmax理论值(m) | 误差 |
| 1 | 4.38 | 5.308 | 0.001498 | 0.000469 | 48.97 | 63.62 | 0.770 | 72.62 | -12.4% |
| 2 | 4.38 | 7.5 | 0.003036 | 0.000469 | 31.11 | 40.17 | 0.774 | 43.18 | -6.98% |
| 3 | 4.38 | 12.38 | 0.005930 | 0.000469 | 21.83 | 28.56 | 0.764 | 26.02 | 9.76% |
| 4 | 4.38 | 24.38 | 0.012339 | 0.000469 | 15.51 | 20.26 | 0.769 | 14.99 | 35.16% |
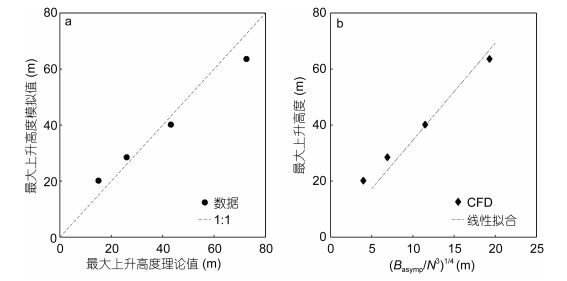 |
| 图 7 羽流的最大上升高度的模拟值与理论值的比较(a)以及标度律关系(b) Fig. 7 Comparison between the simulated and theoretical maximum rising height of the plume (a) and the scaling relationship with buoyancy flux and stratification (b) |
另外, 热液柱中性浮力面高度与最大上升高度之比η=zn/zmax是研究羽流扩散机制的重要参数。在热液柱的现场观测中, 通过水文示踪(温度异常)或者光学示踪(浊度异常)等途径估计的羽流最大上升高度仍存在一些不确定性。相较而言, 中性浮力面层的羽流信号更易探测, 因此从中性浮力层估算热通量也是热液研究的一种常用手段(陈小丹等, 2016)。从表 1可以看到, ηCFD的平均值为0.769, 与Turner(1973)推导的羽流的解析解结果(ηtheory=0.761)十分接近, 也与Devenish等(2010)的大涡模拟结果相近(ηLES=0.765)。结合前面对于MTT模型经验系数的回归分析, 可建立估算中性浮力面高度的标度律公式:
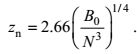 (2)
(2)根据热液柱的速度场对羽流的几何特征参数进行反演, 是研究羽流半径变化规律的主要手段之一(Xu et al, 2014)。在羽流的不同高度位置, 可利用该高度处的最大垂向速度wmax, 对羽流上升速度w进行归一化: w*=w/wmax; 类似地, 利用离喷口的垂向距离z-H对径向距离r进行归一化: r*=r/(z-H)。归一化后的速度分布如图 8a所示, 可见羽流的垂向速度基本满足高斯分布。使用高斯函数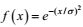
在MTT理论模型中, 羽流的半径b与高度z之间满足如下线性关系:
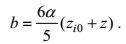 (3)
(3)式中的α为卷挟因子, 在MTT模型中α=0.093; zi0为MTT模型中虚拟喷口到实际喷口的距离, z为羽流到实际喷口的距离。利用数值模拟结果: z=10m处的半径bz=10=0.0985×10=0.985m, 我们得到zi0=0.535m。从图 8b可以看到, 在离喷口25m的范围内, CFD模拟得到的羽流半径与MTT理论解两者基本一致。
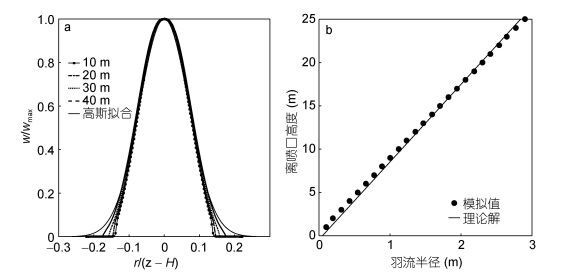 |
| 图 8 归一化垂向速度的径向分布(a)和羽流半径随高度的变化(b) Fig. 8 Normalized vertical velocity along the radial direction (a) and the plume's radius as a function of height (b) |
热液柱的体积通量、动量通量和浮力通量, 是表征其动力结果的一些重要参数, 对它们的细致研究, 有助于深入理解热液柱的动力过程。
2.4.1 体积通量体积通量Q可表示为: Q=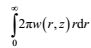
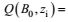
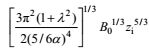
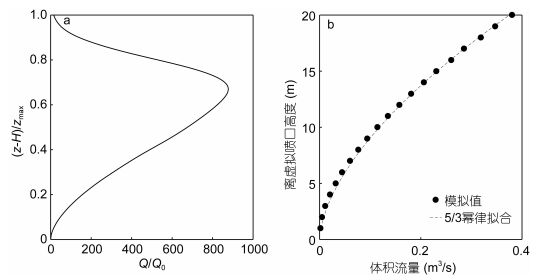 |
| 图 9 热液柱体积流量随高度的整体(a)和局部(b)变化 Fig. 9 Global (a) and local (b) variations of volume flow rate of the hydrothermal plume along vertical direction |
动量通量可表示为: M=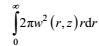
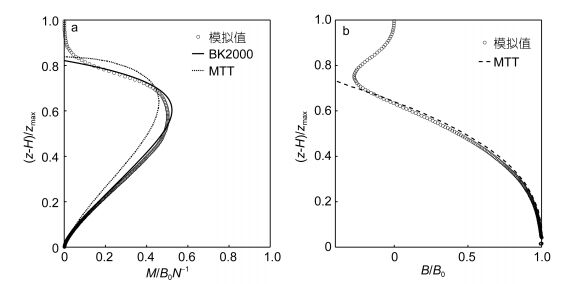 |
| 图 10 热液柱动量通量(a)和浮力通量(b)随高度的变化 Fig. 10 Vertical variations of the hydrothermal plume's momentum flux (a) and buoyancy flux (b) |
热液柱的浮力通量B可表示为: 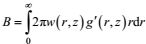
卷挟因子α是描述热液柱动力过程的关键参数, 它表征羽流在上升过程中卷挟周围海水的能力, 控制着热液喷发中的能量和物质的输运。van Reeuwijk等(2016)的数值模拟结果表明, 对于射流引起的羽流(pure jet), 其卷挟因子αj的平均值为0.067;对于热浮力引起的羽流(pure plume), 其卷挟因子αp的平均值为0.105;而对于像热液柱这种具有射流性质的热羽流(forced plume), 其卷挟因子在0.05—0.1之间变化。
热液柱的卷挟因子有多种计算方法。例如, Rona(2002)根据羽流的理论模型提出了卷挟因子的一种计算方法:首先, 利用高斯函数对羽流不同高度z处的垂向速度w进行拟合; 然后, 把速度衰减到羽流中心最大速度的37%(1/e)时的径向位置, 作为羽流的特征半径be, 进而得到be随z变化的斜率θ=dbe/dz, 其中θ又可被当作羽流的膨胀率; 最后, 利用卷挟因子α与膨胀率θ的关系式θ=1.2(6/5)α进行反推便可得到α(Xu et al, 2013)。Rona(2006)在对胡安德富卡洋脊的热液区进行观测时发现, 该方法计算的卷挟因子平均值在α=0.07左右。在考虑背景流的影响时, 热液柱将在横流作用下变得倾斜, 倾斜的羽流将有利于周围流体补充其上升过程中腾出的空隙, 卷进更多的流体, 卷挟能力因而得到提高。Rona(2002)的观测结果表明, 在热液柱倾斜角为37°的时候, α的最大值可达0.18。需注意的是, Rona(2002)的方法得到的是卷挟因子的平均值, 若要计算不同高度位置的卷挟因子, 研究卷挟因子随高度的变化规律, 则需利用另外的方法。例如, 根据羽流的数值模拟研究结果, Suzuki等(2010)提出了计算α的一种新方法:
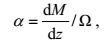 (4)
(4)式中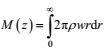

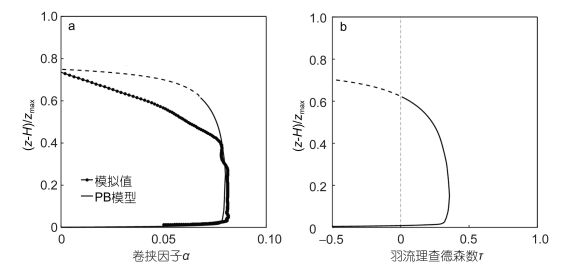 |
| 图 11 羽流的卷挟因子(a)和理查德森数(b)随高度的变化 Fig. 11 The plume's entrainment rate (a) and Richardson number (b) as a function of height |
Ezzamel等(2015)认为, 射流和热羽流具有不同的动力特性, 射流的平均卷挟因子要小于热羽流。通过定义羽流的理查德森数τ, 可以解释羽流卷挟因子的变化原因, 它与羽流局部的体积通量、动量通量以及浮力通量有关。τ具体由以下公式计算:
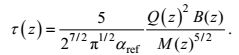 (5)
(5)上式中的Q、B、M分别为羽流的体积通量、浮力通量以及动量通量, 其中αref取0.15(Ezzamel et al, 2015)。当τ=1时, 可认为是热浮力作起的卷挟; 当τ=0时, 是射流引起的卷挟; 而当0<τ<1时的卷挟是羽流和射流两者共同作用所引起的。
从图 11(b)可知, 在z*<0.02zmax的位置(约1.3m), τ接近0, 表明热液柱对周边流体的卷挟主要具有射流的特性; 之后τ随高度迅速增加至0.35左右, 说明这时候热浮力的卷挟作用开始凸显; 在0.6zmax的位置附近, 随着浮力通量(图 10b)逐渐减小为0, τ随之也减小为0, 这说明了在靠近中性浮力面高度的地方, 热羽流的卷挟作用已很弱。
Priestley等(1955)根据射流和热羽流的不同特点, 结合羽流的理查德森数, 提出了关于计算羽流卷挟因子的Priestley-Ball(简称PB)模型:
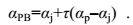 (6)
(6)结合van Reeuwijk等(2016)提供的参考值(αj= 0.067, αp=0.105), 我们利用PB模型计算了羽流的卷挟因子, 发现在0.07—0.4zmax(4.4—25.3m)的高度范围内, PB模型的计算的平均值为0.0803, 与公式(4)的计算结果一致。
由以上分析可知, 在不考虑海底背景流的情况下, Jiang等(2014)模拟的卷挟因子在0.07—0.4zmax的高度范围内的平均值为0.15, 而本文利用定义(式4)与PB模型(式6)得到的热液柱卷挟因子在平均值分别为0.0807和0.0803, 相比之下, 本文的模拟结果与Rona(2006)的观测结果(α=0.07)更为接近。
3 结论本文结合2014年冲绳热液航次的实测资料, 对冲绳海槽热液柱的动力过程进行了模拟分析, 得到以下结论:
(1) 在热液柱演化的初始时刻, 其中心的最大上升速度可达0.35m/s, 在茎部的两侧产生明显的涡旋; 在大约2000s之后, 羽流进入准稳态演化阶段, 在中性浮力面高度向四周扩散。
(2) CFD模拟的热液柱最大上升高度为63.62m, 与MTT理论模型预测的结果吻合; 利用不同层结条件下的模拟数据进行回归分析, 得到MTT模型中的经验系数为3.46, 比建议值3.76偏小8%;热液柱中性浮力面高度与最大高度之比η的平均值为0.768, 与理论模型的结果相符。
(3) 热液柱的垂向速度满足高斯分布, 半径随高度线性增加: b=0.0985(z-H); 根据半径随高度的变化规律, 发现虚拟喷口到实际喷口的距离为zi0= 0.535m。
(4) 羽流的体积通量Q与到虚拟喷口的距离zi符合5/3幂律, 体积通量的最大值为1.034m3/s, 是喷口初始体积通量的878倍; 在一定高度范围内, 动量通量与到实际喷口的距离符合4/3幂律, 比起MTT模型, BK2000模型的预测结果与CFD模拟的结果更接近; MTT模型预测的浮力通量与CFD模拟结果基本吻合, 在z*<0.63zmax的高度范围内浮力通量的变化满足二次函数关系, 在0.63zmax<z*<zmax的范围内则满足三次函数关系。
(5) 热液柱的卷挟因子α的平均值为0.0807, 与现场观测结果符合; α随高度先增加后减小, 在0.72zmax的位置开始变为负值, 羽流开始向水平方向扩散; 通过羽流理查德森数的计算, 发现羽流在离喷口较近的位置主要靠射流作用对周边流体进行卷挟, 在主体上升高度内为射流和热浮力共同卷挟, 接近中性浮力面高度时热浮力卷挟作用开始消失; PB模型计算的卷挟因子的平均值为0.0803, 与CFD模拟结果一致。
| 张巍, 赵亮, 贺治国, 等, 2016. 线性层结盐水中的羽流运动特性. 水科学进展, 27(4): 602–608 |
| 陈小丹, 梁楚进, 董昌明, 2015. 西南印度洋龙旂热液区羽流信号的检测与通量估计. 海洋学研究, 33(4): 43–52 |
| 黄丁勇, 林荣澄, 牛文涛, 等, 2011. 深海热液活动及热液生物群落研究概述. 中南大学学报(自然科学版), 42(s2): 196–203 |
| 曾志刚, 2010. 海底热液地质学. 北京: 科学出版社, 183-235 |
| 温竹青, 2011. 基于FLUENT的深海热液羽状流流动模拟. 北京: 中央民族大学硕士学位论文, 51-52 http://cdmd.cnki.com.cn/Article/CDMD-10052-1011165796.htm |
| Bloomfield L, Kerr R, 2000. A theoretical model of a turbulent fountain. Journal of Fluid Mechanics, 424: 197–216 DOI:10.1017/S0022112000001907 |
| Carazzo G, Jellinek M, 2012. A new view of the dynamics, stability and longevity of volcanic clouds. Earth and Planetary Science Letters, 325: 39–51 |
| Deveish B, Rooney G, Thomson D, 2010. Large-eddy simulation of a buoyant plume in uniform and stably stratified environments. Journal of Fluid Mechanics, 652: 75–103 DOI:10.1017/S0022112010000017 |
| Escartin J, Barreyre T, Cannat M, et al, 2015. Hydrothermal activity along the slow-spreading Lucky Strike ridge segment (Mid-Atlantic Ridge):Distribution, heatflux, and geological controls. Earth and Planetary Science Letters, 431: 173–185 DOI:10.1016/j.epsl.2015.09.025 |
| Ezzamel A, Salizzoni P, Hunt G, 2015. Dynamical variability of axisymmetric buoyant plumes. Journal of Fluid Mechanics, 765: 576–611 DOI:10.1017/jfm.2014.694 |
| Jiang H, Breier J, 2014. Physical controls on mixing and transport within rising submarine hydrothermal plumes:A numerical simulation study. Deep-Sea Research I, 92: 41–55 DOI:10.1016/j.dsr.2014.06.006 |
| Lavelle, J, 1997. Buoyancy-driven plumes in rotating, stratified cross flows:Plume dependence on rotation, turbulent mixing, and cross-flow strength. Journal of Geophysical Research:Oceans, 102(C2): 3405–3420 DOI:10.1029/96JC03601 |
| Lavelle J, Di Iorio D, Rona P, 2013. A turbulent convection model with an observational context for a deep-sea hydrothermal plume in a time-variable cross flow. Journal of Geophysical Research:Oceans, 118(11): 6145–6160 DOI:10.1002/2013JC009165 |
| Morton B, Taylor G, Turner J, 1956. Turbulent gravitational convection from maintained and instantaneous sources. Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Sciences. The Royal Society, 234(1196): 1–23 DOI:10.1098/rspa.1956.0011 |
| Priestley C, Ball F, 1955. Continuous convection from an isolated source of heat. Quarterly Journal of the Royal Meteorological Society, 81(348): 144–157 DOI:10.1002/(ISSN)1477-870X |
| Rona P, K Bemis, Silver D, et al, 2002. Acoustic imaging, visualization, and quantification of buoyant hydrothermal plumes in the ocean. Marine Geophysical Researches, 23: 147–168 DOI:10.1023/A:1022481315125 |
| Rona P, K Bemis, Jones C, et al, 2006. Entrainment and bending in a major hydrothermal plume, Main Endeavour Field, Juan de Fuca Ridge. Geophysical Research Letters, 33(19) |
| Rudnicki M, Elderfield H, 1992. Theory applied to the Mid-Atlantic Ridge hydrothermal plumes:The finite-difference approach. Journal of volcanology and geothermal research, 50(1): 161–172 |
| Speer K, P Rona, 1989. A model of an Atlantic and Pacific hydrothermal plume. Journal of Geophysical Research:Oceans, 94(C5): 6213–6220 DOI:10.1029/JC094iC05p06213 |
| Sun H, Feistel R, Koch M, et al, 2008. New equations for density, entropy, heat capacity, and potential temperature of a saline thermal fluid. Deep Sea Research Part Ⅰ:Oceanographic Research Papers, 55(10): 1304–1310 DOI:10.1016/j.dsr.2008.05.011 |
| Suzuki Y, Koyaguchi T, 2010. Numerical determination of the efficiency of entrainment in volcanic eruption columns. Geophysical Research Letters, 37(5) |
| Takai K, Mottl M J, Nielsen S H et al, 2011. Proceedings of the Integrated Ocean Drilling Program, 331 |
| Tao Y, Rosswog S, Brüggen M, 2013. A simulation modeling approach to hydrothermal plumes and its comparison to analytical models. Ocean Modelling, 61: 68–80 DOI:10.1016/j.ocemod.2012.10.001 |
| Turner J, Campbell I, 1987. Temperature, density and buoyancy fluxes in 'black smoker' plumes, and the criterion for buoyancy reversal. Earth and Planetary Science Letters, 86: 85–92 DOI:10.1016/0012-821X(87)90191-9 |
| Turner J, 1973. Buoyancy effects in fluids. UK: Cambridge University Press, |
| van Reeuwijk M, Salizzoni P, Hunt G, et al, 2016. Turbulent transport and entrainment in jets and plumes:A DNS study. Physical Review Fluids, 1(7): 074301 DOI:10.1103/PhysRevFluids.1.074301 |
| Wen H, Sano Y, Takahata N, et al, 2016. Helium and methane sources and fluxes of shallow submarine hydrothermal plumes near the Tokara Islands, Southern Japan. Scientific reports, 6: 34126 DOI:10.1038/srep34126 |
| Xu G, Jackson D R, Bemis K G, et al, 2013. Observations of the volume flux of a seafloor hydrothermal plume using an acoustic imaging sonar. Geochemistry, Geophysics, Geosystems, 14(7): 2369–2382 DOI:10.1002/ggge.20177 |
| Xu G, Jackson D, Bemis K, et al, 2014. Time-series measurements of hydrothermal heat flux at the Grotto mound, Endeavour Segment, Juan de Fuca Ridge. Earth and Planetary Science Letters, 404: 220–231 DOI:10.1016/j.epsl.2014.07.040 |
| Zhang X, Du Z, Zheng R, et al, 2017. Development of a new deep-sea hybrid Raman insertion probe and its application to the geochemistry of hydrothermal ven and cold seep fluids. Deep-Sea Research I, 123: 1–12 DOI:10.1016/j.dsr.2017.02.005 |
 2017, Vol. 48
2017, Vol. 48


