
中国海洋湖沼学会主办。
文章信息
- 杜石霞, 金宝轩, 李石华, 周峻松, 彭双云. 2018.
- DU Shi-Xia, JIN Bao-Xuan, LI Shi-Hua, ZHOU Jun-Song, PENG Shuang-Yun. 2018.
- 近40年来抚仙湖面积时空分异遥感动态监测
- THE spatiAL-temporal variation of Fuxian Lake area DURING 1974-2014 based on remote sensing
- 海洋与湖沼, 49(1): 40-51
- Oceanologia et Limnologia Sinica, 49(1): 40-51.
- http://dx.doi.org/10.11693/hyhz20170100012
-
文章历史
- 收稿日期:2017-01-13
- 收修改稿日期:2017-01-13
2. 云南省国土资源厅信息中心 昆明 650224;
3. 云南省基础地理信息中心 昆明 650034;
4. 云南师范大学旅游与地理科学学院 昆明 650500
2. Information center, Department of land resources of Yunnan Province, Kunming 650224, China;
3. Yunnan Provincial Geomatics Centre, Kunming 650034, China;
4. College of Tourism and Geographic Sciences, Yunnan Normal University, Kunming 650500, China
地球表面水资源存储的形式有冰川、积雪、河流、地下水、水库、湖泊等, 其中湖泊是最典型的陆面蓄水方式, 是生态系统的重要组成部分, 其变化直接或间接的反映了湖区气候的变化和人类的活动。而随着时间的推移, 湖泊的数量、大小的变化也会作用于人类活动和气候变化(毋亭等, 2016)。遥感技术能够实时、低成本、高效率地获取湖泊变化的动态数据, 而且受人为和自然因素影响较小, 遥感与地理信息系统的有效结合作为一种新的技术支撑着湿地研究的开展(陈晓英等, 2015)。
目前, 对于湖泊面积变化的监测是借助遥感影像来提取湖面信息进而分析湖泊的时间和空间变化特征。例如: Mujabar等(2014)、李磊等(2013)不仅讨论了岸线的定义和分类, 而且总结了岸线信息的提取技术, 展望了其发展方向及研究趋势, 给以后的岸线研究提供参考。张郝哲(2012)以1999—2009年的TM和ETM遥感影像为信息源, 对内蒙古达里诺尔湖泊的现状进行调查, 通过湖泊面积、空间分异性、岸线变化三个方面以及和其他湖泊的对比, 发现湖泊正在萎缩, 并且具有典型的代表性, 能够反映地区的气候、生态变化情况, 提出气温和降水是导致湖泊变化的主要原因, 畜牧业的过度发展也是不可避免的原因之一。刘佳丽等(2016)利用1990—2015年覆盖青藏高原的LandsatTM遥感影像对青藏高原湖泊的变迁情况进行监测, 研究表明湖泊在逐年扩张, 且气温变化、冰水容水量的增加、降水量的增多是引起湖面变化的原因。贾恪(2014)选取科尔沁沙地沙丘与草甸相间地区, 基于遥感影像提取1986—2013年湖泊个数和湖面信息, 分析其变化规律和空间分异特征, 采用偏相关分析方法对驱动因子进行分析。
从上述研究可以看出, 多数研究者在青藏高原、新疆、内蒙古以及沿海地区采用GIS和RS结合的方式提取湖面信息并分析其时间和空间变化规律, 主要基于偏相关分析、层次分析、主成分分析等方法进行驱动力研究。高原湖泊是国际湖泊研究热点, 抚仙湖地处低纬度、高海拔的云贵高原, 是独具特色的高原湖泊生态系统, 因受东亚和西南季风影响, 成为全球变化响应最为敏感的代表性湖泊之一。然而, 由于气候变暖和人类经济活动的增加, 近年来水位呈下降趋势, 水域面积逐渐缩小(Li et al, 2016)。利用遥感技术及空间分析技术对其面积变化和驱动因子分析鲜见报道。为此, 本研究开展近40年抚仙湖面积遥感动态监测, 分析其湖岸线和面积的时空变化情况、辨识其驱动因子。
1 研究区域概况抚仙湖是中国最大的深水型淡水湖泊、珠江源头第一大湖, 属南盘江水系, 位于云南省玉溪市澄江、江川、华宁三县间, 在昆明市东南方向60km处, 居滇中盆地中心, 地理位置为24°21′28″—24°38′00″N, 102°49′12″—102°57′26″E。抚仙湖湖面海拔高度为1723.35m, 湖容积为206.2亿m3, 湖水平均深度为95.2m, 最深处有158.9m。抚仙湖位于亚热带季风气候区, 属中亚热带半湿润季风气候。冬春季受印度北部次大陆干暖气流和北方南下的干冷气流控制, 夏秋季主要受印度洋西南暖湿气流和北部湾东南暖湿流影响, 形成春暖旱重、夏无酷暑、秋凉雨少、冬无严寒, 干、湿(雨)季分明的气候特征。流域常年平均气温15.5℃, 年降雨量800—1100mm, 全年80%— 90%的雨量集中在5—10月份的雨季。蒸发量一般大于降雨量, 在1200—1900mm, 日照时数为2000— 2400h。
2 数据和研究方法 2.1 数据来源和处理 2.1.1 遥感数据1974年至2015年间, 对抚仙湖面积监测主要采用了多源遥感低分辨率数据(空间分辨率为60m, 主要包括: 1974和1977年一共2期数据), 中分辨率数据(空间分辨率为30m, 主要包括: 1987、1993、1996、2000、2001、2002、2004、2005年, 一共8期数据), 高分辨率数据(彩红外航片, QuickBird数据, WorldView-2数据, 主要包括2006、2009、2012、2014、2015年一共5期数据)。影像来源:http://glovis.usgs.gov/; 云南省第二次土地调查影像; 云南省第一次全国地理国情普查影像成果(DOM); 卫星代理商购买。根据项目建设要求, 需要监测抚仙湖枯水期(3—4月份)的湖岸线的变化情况, 本研究查找了1974—2015年间监测区3—4月份的影像, 综合考虑云量等影像质量情况, 故选择了不等时间间距的15期质量较佳的影像。
2.1.2 气象、人口经济、土地利用数据包括从气象局获取的抚仙湖流域澄江县(龙街观测站、右所观测站、吉里村观测站)、江川县(雄关观测站)和华宁县(白龙河观测站、盘溪观测站、红岩观测站)各测站的年降水、月降水数据, 年蒸发、月蒸发数据, 以及气象观测资料。从水利局获取的1987—2012年的人口经济数据(流域总人口和国内生产总值)以及监测出来的1974—2014年的土地利用变化数据(1974—2014年的土地利用转移矩阵), 利用统计分析方法进行计算。
2.2 研究方法 2.2.1 湖岸线提取和湖面面积计算多源遥感影像水体信息提取采用计算机自动分类与人工判读解译结合的方式。用ERDAS图像处理软件对影像进行校正, 几何误差控制在1个像元内, 空间参考使用国家2000大地坐标系, 投影类型采用中央经线为105°E高斯-克吕格6°分带投影。
对中等分辨率遥感影像数据, 采用边缘检测法提取水体信息, 实际水位点检测辅助, 将提取的水体信息转化成矢量湖边界信息, 最后统计水体区域的像元个数, 将像元个数与影像分辨率相乘得到面积。传统的边缘检测算法在检测精度上效果不是很理想, 数学形态学作为一种新兴的图像处理技术, 它的结构元素形态、尺寸多变等特点决定了基于形态学的边缘检测方法在结构性和灵活性上强于传统边缘检测(闫海霞, 2009; 潘建平等, 2010; 李玲等, 2013)。根据使用的形态学操作的不同基于形态学的边缘检测算子可以分为膨胀型、腐蚀型、膨胀腐蚀型、开、闭及开闭型。本研究使用膨胀型和腐蚀型算子, 该方法对水体边缘细节的检测比较敏感, 算法简单, 能体现较多的图像细节, 协调检测精度与抗噪性能间的矛盾。并且相对于本文使用的60m、30m分辨率的遥感影像, 膨胀腐蚀型算子足以满足提取要求, 抚仙湖属于小面积内陆高原湖泊, 在清晰度和细节纹理提取上效果不错。
首先使用一种边缘检测算子合成边缘检测结果:
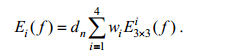
式中, wi表示第i个n维尺寸结构元素在输出结果中其方向所占的权重, dn表示n×n尺寸结构元素在输出结果中尺寸n所占的权重, 本研究采用3×3的影像尺度。
再求出腐蚀型、膨胀型算子的加权和即为膨胀腐蚀型边缘检测结果。
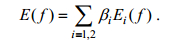
式中, βi表示使用不同边缘检测算子得到的结果Ei(f)在最终边缘检测结果中所占的权重。
借助MATLAB求出最终的水体边缘检测结果后在ERDAS中进行二值化及降噪处理, 再用掩膜工具进行掩膜处理, 得到各期湖岸线边缘检测结果。如图 1为其中2015年湖岸线提取信息, 依次提取每一期的湖岸线。
 |
| 图 1 2015年湖岸线边缘检测结果 Fig. 1 The edge detection results of shoreline in 2015 |
对于水体信息复杂的高分辨率影像和彩红外航片, 直接进行人工解译提取水体信息。对提取的湖边缘线采用矢量的方式进行湖面面积计算。高分辨率影像在提取湖岸线过程中, 误差控制在5个像元内。
2.2.2 湖岸线分形维数作为海岸线分形理论中常用的定量指数, 分形维数的大小可表达海岸线形状的复杂程度, 值越大海岸线形状越复杂(徐进勇等, 2013)。分形维数的计算方法有量规法和网格法。有研究者基于Matlab, 采用网格法计算了黄河三角洲岸线的分形维数(Jabaloy-Sánchez et al, 2014; 刘鹏等, 2015)。网格法的思想是用不同尺度的网格覆盖海岸线, 不同尺度对应不同网格总数, 取网格数的对数与网格尺度的对数的斜率的绝对值作为海岸线的分形维数(刘鹏等, 2015)。计算方法如下:
作为海岸线分形理论中常用的定量指数, 分形维数的大小可表达海岸线形状的复杂程度, 值越大海岸线形状越复杂(徐进勇等, 2013)。分形维数的计算方法有量规法和网格法。有研究者基于Matlab, 采用网格法计算了黄河三角洲岸线的分形维数(Jabaloy-Sánchez et al, 2014; 刘鹏等, 2015)。网格法的思想是用不同尺度的网格覆盖海岸线, 不同尺度对应不同网格总数, 取网格数的对数与网格尺度的对数的斜率的绝对值作为海岸线的分形维数(刘鹏等, 2015)。计算方法如下:
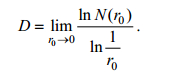
式中, D为分形维数, r0为网格的尺度, 即为网格的边长, N(r0)为网格的总数。网格的尺度根据所用影像的分辨率来决定。例如本次分析中有使用30m的, 所以最小测尺为30m, 则网格长度取30m的整数倍, 即30, 60, 90, 120, 150, 180, 210和240m。
2.2.3 灰色关联度分析为了定量的描述事物之间的关联程度, 人们提出了许多形式的相关系数, 比如典型的相关系数等等, 其原理都是以数理统计的方法为基础, 可靠性取决于是否具备大量的数据, 而无法支撑数据量少的统计研究。灰色关联度在某些程度上弥补了这种缺陷, 其分析方法是灰色系统理论的一个分支(布买日也木·买买提, 2016)。对于灰色关联分析方法, 序列曲线几何形状的相似程度决定了各因素之间的关联程度大小。曲线越接近, 关联程度就越大, 反之越小(叶绍明等, 2010; 张有利等, 2010)。灰色关联分析可以弥补传统数理统计方法的不足, 对样本量的多少和样本有无规律同样适用(段旭等, 2010; 伊丽努尔·阿力甫江等, 2015)。计算公式如下:
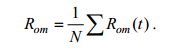
式中, Rom是子序列m与母序列o的灰色关联度, N为数据序列长度, 即数据数, 是子序列m与母序列o在t时刻的关联系数, 其计算公式为
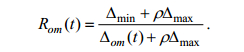
式中, Δmin和Δmsx分别表示各时刻两序列绝对差的最大值和最小值; Δom表示t时刻两序列的绝对差; ρ为分辨系数, 通常取值0.5。
2.2.4 岸线提取精度地面验证为了进一步对提取的岸线信息精度进行验证, 以2015年的影像数据提取的岸线为检核数据, 地面验证时间选择了与影像获取时间相对同步, 于2015年4月1—3日沿湖边选择30个水位点进行实测, 采用高精度双频大地型GPS接收机, 观测模式为基于云南省卫星定位连续运行基准站(YNCORS)的区域静态网观测模式, 测量水位点的2000大地坐标, 将实测的点位与采集的岸线进行叠加验证, 如图 2所示。
 |
| 图 2 实测水位点分布图 Fig. 2 The distribution of observation sites |
最大误差–9.684m, 最小误差为0m, 误差控制在较小的范围内, 精度良好, 可以确定本文所用的岸线面积提取方法具有可靠性。
3 结果与分析 3.1 湖岸线变化分析 3.1.1 长度和变化强度采用计算机自动分类与人工判读解译结合的方式, 将采用边缘检测法提取的水体信息转化成矢量湖边界信息, 通过GIS软件统计出各岸线的长度如下表 1所示。
| 年份 | 长度(km) |
| 1974 | 108.6164 |
| 1977 | 109.9151 |
| 1987 | 111.7801 |
| 1993 | 111.7771 |
| 1996 | 112.5755 |
| 2000 | 113.9115 |
| 2001 | 112.1748 |
| 2002 | 111.9112 |
| 2004 | 112.2258 |
| 2005 | 112.0167 |
| 2006 | 109.9221 |
| 2009 | 115.9048 |
| 2012 | 102.8280 |
| 2014 | 100.0881 |
| 2015 | 98.380 |
从表 1可得出, 抚仙湖岸线变化分为四个阶段。1974—2000年湖岸线持续变长, 2000年长度最长, 为113.9115km。2000—2005年间湖岸线长度在111— 113km, 变化幅度不明显。在2006—2014年间, 湖岸线变动的幅度较大, 先变长后变短, 在2009年出现自1974年以来的最长长度, 达115.9048km, 然而在2014年, 湖岸线仅为100.0881km。从数据可以看出在近几年抚仙湖湖岸线长度变化很不稳定。
为了客观地比较各时段湖岸线长度变化速度, 采用某一时间段内湖岸线长度的年均变化百分比来表示湖岸线的变化强度。根据公式(林乃峰等, 2012)分四个时段计算出了湖岸线的变化强度, 从结果中可以看出2005—2015年变化强度最大, 达到1.386%, 与湖岸线长度在此期间不稳定的变化趋势趋于一致。1974—1987年抚仙湖湖岸线以0.2241%的强度变长, 仅次于2005—2015年。1996—2005年变化强度最小, 为0.0552%。计算公式如下:

式中, LCIij为第i年至第j年海岸线长度变化强度, Lj和Lj分别为第i年和第j年海岸线长度。
3.1.2 分形维数基于网格法(Jabaloy-Sánchez et al, 2014)利用GIS软件的创建渔网功能以及最小二乘线性回归分析原理计算出各时期抚仙湖湖岸线的分型维数如下表所示(分辨系数为0.5), R2均在0.99以上, 说明分形维数可以用来表征抚仙湖湖岸线特征。
分形维数值越大形状越复杂, 计算出各时期抚仙湖湖岸线的分形维数, 如表 2所示: 2005年是一个转折点, 在2005年之前, 维数变化幅度小, 但都大于1.2, 说明相比于一般的湖泊, 抚仙湖的形状比较复杂, 而且分形维数整体属于上升的趋势。2005年以后, 分形维数值突然减小, 2012年最小, 仅为1.0181, 湖岸线分形维数呈减小的趋势, 而2014年以后又有所回升。从整体来看, 分形维数并不总是保持同一趋势, 说明近40年来抚仙湖的湖岸线变化具有一定的复杂性。
| 年份 | R2 | 分形 维数 |
| 1974 | 0.9982 | 1.2345 |
| 1977 | 0.9979 | 1.2638 |
| 1987 | 0.9983 | 1.2733 |
| 1993 | 0.9979 | 1.258 |
| 1996 | 0.9986 | 1.2495 |
| 2000 | 0.9988 | 1.2748 |
| 2001 | 0.9990 | 1.2219 |
| 2002 | 0.9984 | 1.2441 |
| 2004 | 0.9982 | 1.2666 |
| 2005 | 0.9983 | 1.2397 |
| 2006 | 0.9961 | 1.0591 |
| 2009 | 0.9969 | 1.0441 |
| 2012 | 0.9982 | 1.0181 |
| 2014 | 0.9986 | 1.0373 |
| 2015 | 0.9998 | 1.0436 |
计算面积通过统计水体区域的像元个数, 将像元个数与影像分辨率相乘得来, 1974—2014年面积计算结果统计如图 3所示。从图 3中可以看出: 1974— 2014年, 抚仙湖最小面积是211.41km2(1977年), 最大面积是216.61km2(2006年)。1974—1977年抚仙湖面积从212.25km2萎缩到211.41km2, 萎缩了0.84km2, 然而到1987年湖面面积又扩张到1974—2000年以来的最大值215.01km2, 达到了1974—2014年以来的第一个峰值。1987年之后, 抚仙湖面积进入一个萎缩、扩张又萎缩的过程, 直到2006年面积增加到216.61km2, 出现1974—2014年以来的第二个峰值, 也是40年来的最大值。2006—2015年, 面积开始小幅度回落, 到2015年, 面积减小为215.13km2。
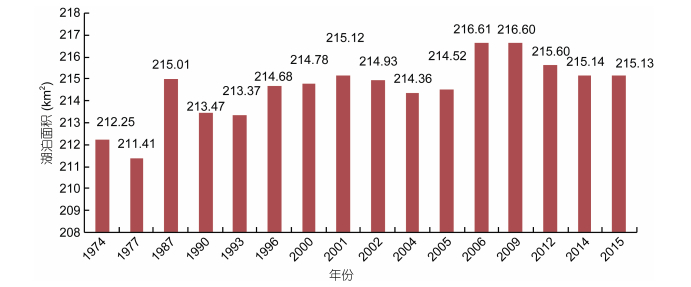 |
| 图 3 1974—2015年抚仙湖面积变化 Fig. 3 The area change of Fuxian Lake between 1974 and 2015 |
湖面面积的变化不仅体现在时间尺度上, 更体现在空间位置上。为了能更直观的体现面积的变化, 本文借鉴几何学中的象限分析方法(许宁等, 2016)。将平面分为45°的八个象限来分析湖面的空间分异特征, 即以1974年的湖面重心(102°53′10.916″E, 24°31′10.588″N)作为起点, 以东西方向为横轴, 南北方向为纵轴按照象限方位将平面划分为八个象限, 以10年为间隔计算不同时间段内的面积在每个象限内的变化量如表 3所示。
 |
一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
| 1974—1977年 | –0.1197 | –0.1736 | –0.1026 | –0.4175 | 0.0773 | 0.0330 | 0.0425 | –0.1710 |
| 1977—1987年 | 0.6363 | 0.4003 | 0.2801 | 0.5776 | 1.0768 | 0.0065 | 0.0881 | 0.6466 |
| 1987—1996年 | –0.1701 | –0.0018 | 0.0328 | 0.1732 | 0.0100 | 0.0566 | 0.0392 | –0.0535 |
| 1996—2005年 | 0.0321 | –0.0410 | –0.0934 | –0.1285 | –0.1324 | –0.0117 | –0.0244 | –0.0225 |
| 2005—2015年 | 0.2813 | 0.2442 | 0.0899 | 0.4208 | 0.1598 | 0.0014 | 0.0096 | 0.0759 |
| 总共 | 0.6599 | 0.4283 | 0.2069 | 0.6257 | 1.1915 | 0.0859 | 0.1550 | 0.4756 |
| (正值表示为面积扩张, 负值表示萎缩) | ||||||||
同时为了方便直观地展现各时段不同方位的变化差异和主导方向变化, 绘制了湖泊不同时段变化的综合玫瑰图, 如图 4所示。
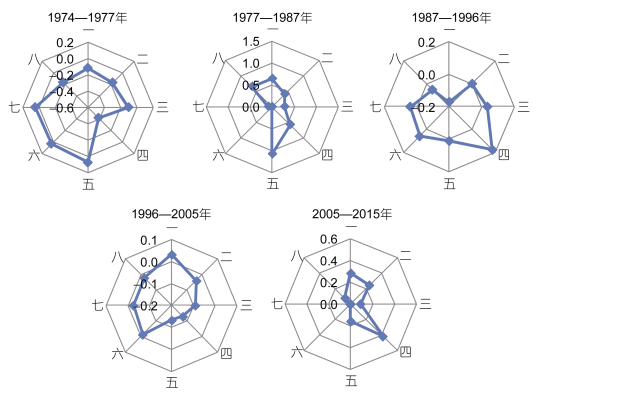 |
| 图 4 抚仙湖各时间段各方向面积变化统计图 Fig. 4 The area change of Fuxian Lake in different direction during various time periods |
湖泊重心的转移反映了湖泊面积、湖底地形、湖底沉积的动态变化(董芳, 2003)。近40年间, 由于湖泊面积在不同方向上的扩张缩小比例不均衡, 导致湖泊重心的不断转移。为了分析湖泊重心偏移情况, 以10年为间隔计算了重心经纬度(表 4), 提取了湖泊的偏移轨迹如图 5所示。
| 年份 | 经度 | 纬度 |
| 1974 | 102°53′10.92″E | 24°31′10.59″N |
| 1977 | 102°53′10.35″E | 24°31′10.92″N |
| 1987 | 102°53′10.55″E | 24°31′10.02″N |
| 1996 | 102°53′10.52″E | 24°31′9.47″N |
| 2005 | 102°53′10.48″E | 24°31′9.91″N |
| 2015 | 102°53′11″E | 24°31′9.63″N |
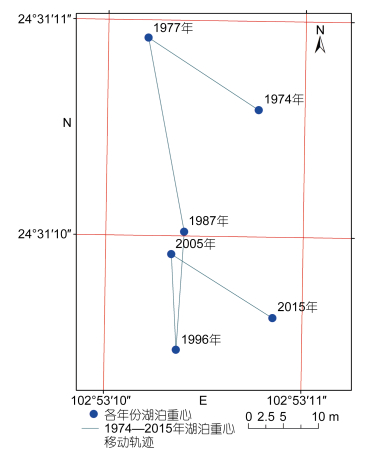 |
| 图 5 抚仙湖近40年重心移动轨迹图 Fig. 5 Moving track of barycenter of Fuxian Lake in recent 40 years |
根据表 4计算可以得出湖泊重心从1974—1977年, 仅3年时间向东南偏东偏移了18.8285m。1977— 1987年重心偏移最大, 向正南偏东方向偏移了28.1896m, 位置从(102°53′10.352″E, 24°31′10.917″)偏移到(102°53′10.548″E, 24°31′10.019″N)。1996— 2005年重心偏移最小, 偏移量仅为13.6662m。2005— 2015年, 重心向东南方向偏移了17.0742m, 位置由(102°53′10.484″E, 24°31′9.914″N)偏移到(102°53′ 11.001″E, 24°31′9.625″N)。结合表 4和图 4, 可以得出湖泊的重心偏移方向与其象限区域变化密切相关。抚仙湖的重心偏移方向与面积在各方向上的变化基本一致, 对重心偏移的分析为面积变化提供一种佐证。
4 驱动力分析 4.1 抚仙湖流域的水源和去向抚仙湖流域共有大小入湖河流103条(含季节河、农田排灌沟), 河流普遍短小, 最长的梁王河21km, 其次是东大河19.9km, 其余多在10km以下。由于抚仙湖属雨水补给型湖泊, 河道径流调节性能很差, 多为间歇性河流、暴涨暴落、汇流时间短, 并携带大量泥沙入湖。湖岸周围有地下水补给, 例如东岸老鹰地溶洞、猪嘴山溶洞群、禄充大洞、甸朵大洞, 北岸的西龙潭, 东岸的大湾、小船尖落水洞、热水塘等。海口河是抚仙湖历史上唯一的明河出水口, 从海口村起东流约14.5km入南盘江。为了更好利用河道落差的水力资源, 先后在河道上修建了海口河一级、水轮泵二级、大村三级、观音塘四级、朱家桥五级、河尾六级等水电站, 总装机容量达16410kW, 年发电量约为7700×104kWh。出流改道实施后, 隔河流向改变, 也成为抚仙湖的主要出湖河流之一, 抚仙湖水经隔河泄入星云湖。
湖面的变化可被认为是自然和人为因素共同作用的结果, 即直接因素和间接因素。本文采用土地利用、气温、降水以及蒸发量四个因素来定量的描述抚仙湖湖面变化的驱动力。
4.2 人为因素 4.2.1 土地利用因素土地利用变化是人类经济活动最直接的反映, 人类对大自然的干扰能直接体现在土地利用变化上, 而湖泊就是第一承受者。因此, 土地利用/土地覆被变化必然会影响湖泊的变化。研究通过对获取的影像采用监督分类和非监督分类结合的方式进行分类, 并进行转移矩阵计算, 提取耕地、房屋建筑(区)、林地、草地在各时期的面积以及转移面积较大的几个地类, 提取部分有用信息的转移矩阵如表 5所示:
| 单位: (km2) | ||||||
 |
耕地 | 林地 | 草地 | 房屋建筑区 | 水域 | 其他 |
| 耕地 | 4600.6 | 1022.96 | 240.92 | 700.26 | 77.94 | 914.17 |
| 林地 | 7252.81 | 18761.12 | 3410.34 | 384.87 | 103.03 | 1515.53 |
| 草地 | 1816.59 | 2611.23 | 1226.62 | 84.27 | 16.57 | 426.84 |
| 房屋建筑区 | 157.28 | 24.15 | 10.21 | 311.43 | 2.9 | 46.41 |
| 水域 | 13.19 | 53.26 | 52.07 | 5.19 | 21638.86 | 50.66 |
将土地利用的数据与岸线和面积叠加分析, 二者变化趋势高度一致(图 6—图 9)。可以将变化分为两个时段, 在2009年之前岸线长度和面积整体处于上升趋势, 之后都处于下降的趋势。耕地面积从1974年的0.76万km2增加到2009年的1.54万km2, 2009年之后岸线长度和湖泊面积同时减小。从转移矩阵可以看出变化最明显的是有7252.81km2的林地转换为耕地, 而耕地仅有2042.08km2转换为林地、草地、房屋建筑区和水域。房屋建筑区自1974年以来一直在增加, 2009年以后尽管岸线长度和湖泊面积减小, 其仍在增加, 从552.38km2增加到1465.69km2, 然而从转移矩阵中可以看出其他研究地类转换成房屋建筑区的面积并不大, 可以推断是其自身的增长。林地与岸线长度和面积呈负相关关系, 2000年以前林地面积在减少, 岸线和面积增加, 2000年以后趋势相反, 但2009年以后再次出现交点, 说明林地面积是引起岸线和面积变化的主要因素之一。结合灰色关联分析结果我们可以看到无论岸线和面积怎么变化, 草地面积都变化平稳, 其对岸线和面积的变化影响较小。
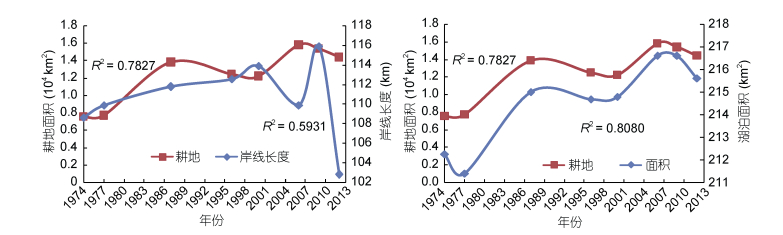 |
| 图 6 抚仙湖流域1974—2012年耕地面积和岸线长度、面积趋势对比图 Fig. 6 The trends of changes in cultivated land area and coastline length, and the total lake area of the Fuxian Lake basin from 1974 to 2012 |
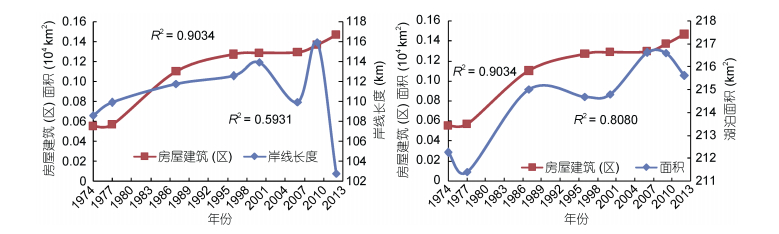 |
| 图 7 抚仙湖流域1974—2012年房屋建筑(区)面积和岸线长度、面积趋势对比图 Fig. 7 The trends of changes in house-construction area, coastline length, and the total lake area of the Fuxian Lake basin from 1974 to 2012 |
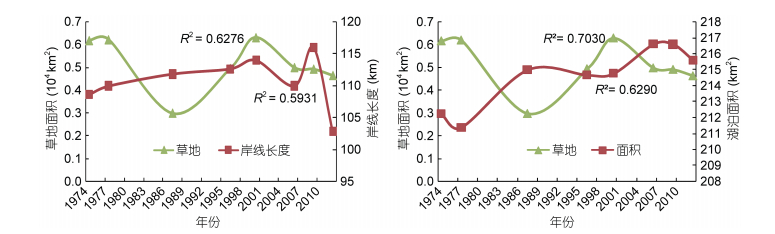 |
| 图 8 抚仙湖流域1974—2012年草地面积和岸线长度、面积趋势对比图 Fig. 8 The trends of changes in grassland area, coastline length, and the total area of the Fuxian Lake basin from 1974 to 2012 |
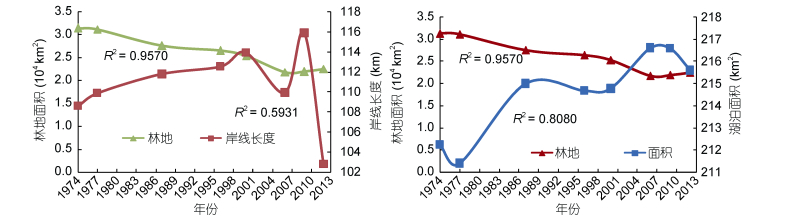 |
| 图 9 抚仙湖流域1974—2012年林地面积和岸线长度、面积趋势对比图 Fig. 9 The trends of changes in forest land area, coastline length, and the total area of the Fuxian Lake basin from 1974 to 2012 |
抚仙湖流域的经济和人口逐年增长, 流域旅游业也极大的促进了经济的增长, 必定会增加人类社会经济活动。抚仙湖流域的人口从1987年的13.9万人增加到20.9万人, 以每年0.18万人的速度增加。人口的增长导致城镇及乡村生活用水量增加, 水利工程项目增多, 高密度和高强度的人类活动对岸线造成威胁, 岸线趋于复杂、长度变长, 2009年达到最大值。分析2006年玉溪市GDP构成, 第一产业产值为45.6亿元, 占GDP总量的20.9%, 第二产业产值为62.8亿元, 占GDP总量的28.8%。GDP的增长需要水资源的支持, 第一产业用水量为5.822亿m3, 占生产用水的68.0%;第二产业用水量2.559亿m3, 占生产用水的29.9%;第三产业用水量0.1759亿m3, 占生产用水的2.1%。在2009年以后湖岸线开始变短, 面积变小。
4.3 自然因素 4.3.1 蒸发量和降水量从图 10和图 11中我们可以看出年平均降水量、蒸发量与湖岸线呈正相关关系。平均蒸发量、降水量两条曲线在1987、2001、2005、2009、2012年相继出现拐点, 而湖岸线和面积在此时也出现拐点, 充分说明它们之间的相互影响关系。
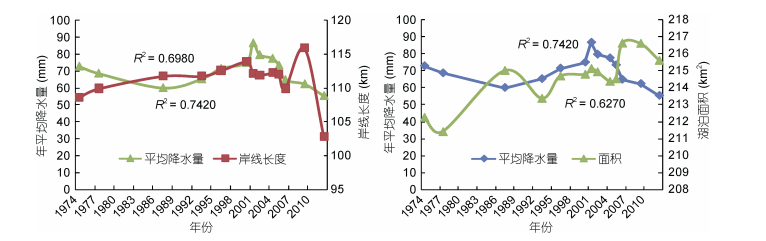 |
| 图 10 抚仙湖流域1974—2012年年平均降水量和岸线长度、面积趋势图 Fig. 10 The trends of changes in average annual precipitation, coastline length, and the total area of the Fuxian Lake basin from 1974 to 2012 |
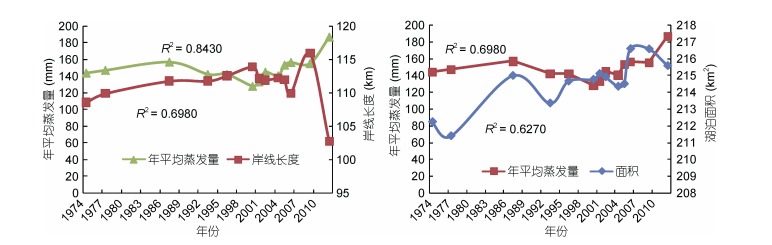 |
| 图 11 抚仙湖流域1974—2012年年平均蒸发量和岸线长度、面积趋势图 Fig. 11 The trends of changes in average annual evaporation, coastline length, and the total area of the Fuxian Lake basin from 1974 to 2012 |
抚仙湖流域的年平均蒸发量总体处于上升趋势, 2000年出现最低值, 低达128.48mm, 2000年之后增长趋势越来越大, 2012年达到最大值186.66mm, 高出平均值37.85mm, 湖岸线的长度随着年平均蒸发量的增减而减增。近40年抚仙湖流域的年平均降水量的平均值为70.39mm, 标准差最大为14.91mm。降水量的变化趋势可分为两个时间段, 2001年以前, 年平均降水量呈上升趋势, 从73mm上升到86.92mm, 同时达到1974年以来的峰值; 2001—2012年一直在下降, 以每年2.86mm的速度在减小, 2012年达到最小值55.48mm。
4.3.2 平均气温在全球气温变暖的背景下, 近40年抚仙湖流域的平均气温也呈较微弱的上升趋势, 2014年较1974年仅升高了1.97℃。除了在2006年突然有小幅度降低, 流域气温近40年一直在上升, 尽管幅度很小。气温的变化影响蒸发的过程, 温度的升高导致蒸发面饱和水汽压增大, 若其他条件稳定的情况下必定会加快蒸发, 使湖面萎缩。因此尽管抚仙湖流域气温上升缓慢仍应引起重视。从趋势图中可以看出年平均气温与岸线和面积的变化趋势一致。
4.4 灰色关联分析从上面对趋势线的分析可以确定耕地、房屋建筑区、年平均降水量、年平均蒸发量以及年平均气温都是引起抚仙湖湖面变化的因素。为了能够更准确的说明它们与湖面变化的相关性, 采用灰色关联分析法计算各因素与湖岸线和面积的灰色关联度, 结果如表 6所示。
| 年份 | 耕地 | 林地 | 草地 | 房屋建筑(区) | 年平均气温 | 年平均蒸发量 | 年平均降水量 | 流域人口 | 流域国内生产总值 | 年平均蒸发量 | |||||||||||||||||||
| 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | 岸线 | 面积 | ||||||||||
| 1974 | 1.000 | 1.000 | 0.591 | 0.590 | 0.651 | 0.645 | 1.000 | 1.000 | 0.946 | 0.997 | 0.729 | 0.648 | 0.834 | 0.950 | 0.729 | 0.648 | 0.834 | 0.950 | 0.729 | 0.648 | |||||||||
| 1977 | 0.990 | 0.989 | 0.594 | 0.592 | 0.649 | 0.643 | 0.987 | 0.983 | 0.937 | 1.000 | 0.711 | 0.673 | 0.766 | 0.935 | 0.711 | 0.673 | 0.766 | 0.935 | 0.711 | 0.673 | |||||||||
| 1987 | 0.709 | 0.707 | 0.644 | 0.643 | 1.000 | 1.000 | 0.673 | 0.639 | 0.929 | 0.990 | 0.647 | 0.714 | 0.663 | 0.887 | 0.647 | 0.714 | 0.663 | 0.887 | 0.647 | 0.714 | |||||||||
| 1993 | / | / | / | / | / | / | / | / | 0.926 | 0.994 | 0.776 | 0.633 | 0.711 | 0.913 | 0.776 | 0.633 | 0.711 | 0.913 | 0.776 | 0.633 | |||||||||
| 1996 | 0.757 | 0.755 | 0.991 | 0.991 | 0.752 | 0.747 | 0.611 | 0.573 | 0.923 | 0.991 | 0.785 | 0.626 | 0.768 | 0.933 | 0.785 | 0.626 | 0.768 | 0.933 | 0.785 | 0.626 | |||||||||
| 2000 | 0.766 | 0.764 | 1.000 | 1.000 | 0.643 | 0.636 | 0.607 | 0.569 | 0.916 | 0.991 | 1.000 | 0.557 | 0.794 | 0.948 | 1.000 | 0.557 | 0.794 | 0.948 | 1.000 | 0.557 | |||||||||
| 2001 | / | / | / | / | / | / | / | / | 0.929 | 0.991 | 0.890 | 0.579 | 1.000 | 1.000 | 0.890 | 0.579 | 1.000 | 1.000 | 0.890 | 0.579 | |||||||||
| 2002 | / | / | / | / | / | / | / | / | 0.932 | 0.992 | 0.751 | 0.639 | 0.884 | 0.968 | 0.751 | 0.639 | 0.884 | 0.968 | 0.751 | 0.639 | |||||||||
| 2004 | / | / | / | / | / | / | / | / | 0.928 | 0.993 | 0.800 | 0.618 | 0.849 | 0.961 | 0.800 | 0.618 | 0.849 | 0.961 | 0.800 | 0.618 | |||||||||
| 2005 | / | / | / | / | / | / | / | / | 0.935 | 0.996 | 0.678 | 0.692 | 0.797 | 0.942 | 0.678 | 0.692 | 0.797 | 0.942 | 0.678 | 0.692 | |||||||||
| 2006 | 0.650 | 0.648 | 0.886 | 0.886 | 0.748 | 0.744 | 0.603 | 0.567 | 0.948 | 0.988 | 0.637 | 0.700 | 0.725 | 0.899 | 0.637 | 0.700 | 0.725 | 0.899 | 0.637 | 0.700 | |||||||||
| 2009 | 0.662 | 0.660 | 0.899 | 0.898 | 0.755 | 0.750 | 0.582 | 0.543 | 0.912 | 0.989 | 0.694 | 0.691 | 0.648 | 0.889 | 0.694 | 0.691 | 0.648 | 0.889 | 0.694 | 0.691 | |||||||||
| 2012 | 0.691 | 0.689 | 0.927 | 0.927 | 0.782 | 0.778 | 0.550 | 0.515 | 1.000 | 0.993 | 0.449 | 1.000 | 0.702 | 0.867 | 0.449 | 1.000 | 0.702 | 0.867 | 0.449 | 1.000 | |||||||||
| 关联度 | 0.778 | 0.777 | 0.817 | 0.816 | 0.747 | 0.743 | 0.702 | 0.674 | 0.935 | 0.993 | 0.734 | 0.675 | 0.780 | 0.930 | 0.734 | 0.675 | 0.780 | 0.930 | 0.734 | 0.675 | |||||||||
| (表中“/”表示无原始数据无法计算出关联系数) | |||||||||||||||||||||||||||||
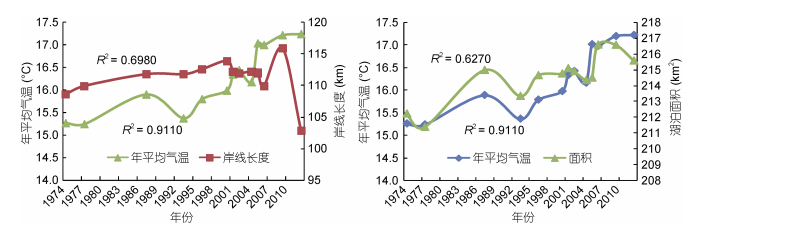 |
| 图 12 抚仙湖流域1974—2012年年平均气温和岸线长度、面积趋势图 Fig. 12 The trends of changes in average annual temperature, coastline length, and the total area of the Fuxian Lake basin from 1974 to 2012 |
将耕地面积(X1)、房屋建筑区面积(X2)、林地面积(X3)、草地面积(X4)、年平均气温(X5)、年平均蒸发量(X6)、年平均降水量(X7)、流域人口(X8)以及流域国内生产总值(X9)作为灰色关联因子计算得到的关联系数和关联度如上表所示。可以看出这些因子与岸线和面积的关联度都大于0.6, 说明相关性良好, 对湖面变化的影响都比较显著, 同时也说明选择这些因子具有科学性和合理性, 因此这9个因素完全可以作为影响湖面变化的主要因素。对于岸线(Y1)来说, 关联度排序为年平均气温 > 林地面积 > 流域人口 > 年平均降水量 > 耕地面积 > 草地面积 > 年平均蒸发量 > 房屋建筑区面积 > 流域国内生产总值。对于面积(Y2)来说, 这9个因子的关联度分别为0.777, 0.816, 0.743, 0.674, 0.993, 0.675, 0.930, 0.809, 0.672, 年平均气温影响最大, 其次是年平均降水量, 影响最小的是流域国内生产总值。从整体来说, 自然因子的影响大于人为因子。为了能够反映这些驱动因子对抚仙湖岸线和面积的综合影响程度, 借助SPSS软件构建驱动因子多元线性回归模型:
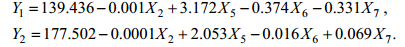
Y1、Y2模型的R分别为0.892和0.923, R2分别为0.795和0.851, 该线性模型可以解释自变量79.5%和85.1%的变差, 拟合度很好; F检验的显著性值为0.007和0.005, 都小于0.05, 通过检验, 共线性也通过检验, 模型可靠。实测与模拟对比散点图如图 13所示。
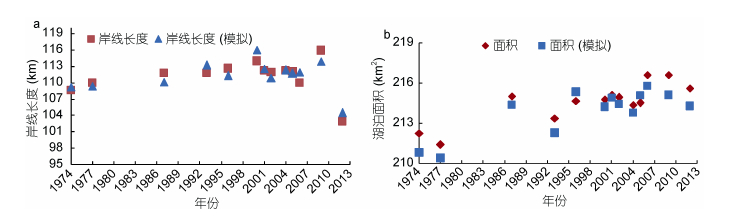 |
| 图 13 抚仙湖流域1974—2012年多元线性回归模型检验散点图 Fig. 13 The scatter plot of multivariate linear regression model for the Fuxian Lake basin from 1974 to 2012 |
(1) 近40年内, 抚仙湖的岸线长度在2009年以前都在108—114km之间波动, 分形维数无规律的变化、变化强度突然增大说明抚仙湖变化具有一定的复杂性; 面积整体在缓慢增长, 在每个方向上都有扩张萎缩, 重心偏移最大距离达到28.1896m。湖泊的岸线与其面积在2009年都达到1974年以来的峰值, 二者的时空动态变化大致可以分为两个阶段: 1974—2009年, 抚仙湖岸线与面积呈上升趋势; 2009—2015年, 抚仙湖岸线与面积呈明显下降趋势。
(2) 抚仙湖的岸线和面积变化主要受人口、经济、耕地面积、房屋建筑区面积等人为因素和气温、地面蒸发量、降水量等自然要素的驱动和制约。
(3) 抚仙湖作为云南九大高原湖泊的典型代表, 深受季风气候及城市化双重因素的影响。将GIS和RS有效结合, 准确又高效地从岸线的长度和分形维数、面积和空间分异特征定量的描述抚仙湖近40年的湖面变化及其原因分析, 能够弥补历来对抚仙湖此项研究的缺失, 也能够为抚仙湖以外的整个云贵高原地区对于湖泊变化的研究提供参考。
(4) 湖泊面积变化是各种不确定性因素共同影响下的动态过程, 驱动因素虽复杂且数量少, 符合灰色关联分析法统计过程的性质。因此文章基于此方法, 选取了几个主要的人为和自然要素与岸线和面积变化趋势开展了分析, 其变化是气候和社会经济因子共同作用的结果, 然而影响湖泊岸线和面积变化的因素具有复杂性, 为全面弄清其变化的驱动因子, 建议对抚仙湖流域进行长时间的变化监测。
| 毋亭, 侯西勇, 2016. 海岸线变化研究综述. 生态学报, 36(4): 1170–1182 |
| 布买日也木·买买提, 丁建丽, 孜比布拉·司马义, 2016. 阿克苏市城市化发展与建设用地结构变化之间的关联性研究. 冰川冻土, 38(1): 279–290 |
| 叶绍明, 温远光, 杨梅, 等, 2010. 连栽桉树人工林植物多样性与土壤理化性质的关联分析. 水土保持学报, 24(4): 246–250, 256 |
| 伊丽努尔·阿力甫江, 海米提·依米提, 麦麦提吐尔逊·艾则孜, 等, 2015. 1985-2012年博斯腾湖水位变化驱动力. 中国沙漠, 35(1): 240–247 DOI:10.7522/j.issn.1000-694X.2014.00087 |
| 刘鹏, 王庆, 战超, 等, 2015. 基于DSAS和FA的1959-2002年黄河三角洲海岸线演变规律及影响因素研究. 海洋与湖沼, 46(3): 585–594 DOI:10.11693/hyhz20141200343 |
| 刘佳丽, 刘旭, 2016. 1990-2015年青藏高原湖泊变化遥感监测分析. 科技经济导刊,(11): 102–103 |
| 闫海霞, 2009. 基于数学形态学的图像边缘检测和增强算法的研究. 长春: 吉林大学博士学位论文, 65-66 http://cdmd.cnki.com.cn/Article/CDMD-10183-2010031918.htm |
| 许宁, 高志强, 宁吉才, 2016. 基于分形维数的环渤海地区海岸线变迁及成因分析. 海洋学研究, 34(1): 45–51 |
| 李玲, 周新志, 黄君, 2013. 多结构元素组合型MODIS影像水体边缘检测. 测绘科学, 38(2): 90–92 |
| 李磊, 李艳红, 陈成贺日, 等, 2014. 1972-2011年期间艾比湖面积变化研究. 湿地科学, 12(2): 263–267 |
| 张有利, 张之一, 翟瑞常, 等, 2010. 土壤系统分类中均腐土土系质量评价——以灰色关联方法为例. 土壤通报, 41(3): 513–517 |
| 张郝哲, 2012. 基于GIS和RS的内蒙古高原封闭盐湖动态监测: 以达里诺尔湖泊为例. 北京: 中国地质大学(北京)硕士学位论文, 45-46 |
| 陈晓英, 张杰, 马毅, 等, 2015. 近40a来三门湾海岸线时空变化遥感监测与分析. 海洋科学, 39(2): 43–49 DOI:10.11759/hykx20141011004 |
| 林乃峰, 沈渭寿, 张慧, 等, 2012. 近35a西藏那曲地区湖泊动态遥感与气候因素关联度分析. 生态与农村环境学报, 28(3): 231–237 |
| 段旭, 王彦辉, 于澎涛, 等, 2010. 六盘山分水岭沟典型森林植被对大气降雨的再分配规律及其影响因子. 水土保持学报, 24(5): 120–125 |
| 贾恪, 2014. 科尔沁沙地沙丘-草甸相间地区湖泊的演变规律及其驱动力分析. 呼和浩特: 内蒙古农业大学硕士学位论文, 36-39 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2600479 |
| 徐进勇, 张增祥, 赵晓丽, 等, 2013. 2000-2012年中国北方海岸线时空变化分析. 地理学报, 68(5): 651–660 DOI:10.11821/xb201305007 |
| 董芳, 2003. 基于陆地卫星TM/ETM+和GIS的济南城区扩展动态监测研究. 泰安: 山东农业大学硕士学位论文, 33-36 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y507566 |
| 潘建平, 李治, 2010. 数学形态学多结构元素的道路提取. 计算机工程与应用, 46(11): 233–235 DOI:10.3778/j.issn.1002-8331.2010.11.071 |
| Jabaloy-Sánchez A, Lobo F J, Azor A, et al, 2014. Six thousand years of coastline evolution in the Guadalfeo deltaic system (southern Iberian Peninsula). Geomorphology, 206: 374–391 DOI:10.1016/j.geomorph.2013.08.037 |
| Mujabar P S, Chandrasekar N, 2013. Shoreline change analysis along the coast between Kanyakumari and Tuticorin of India using remote sensing and GIS. Arabian Journal of Geosciences, 6(3): 647–664 |
 2018, Vol. 49
2018, Vol. 49


