
中国海洋湖沼学会主办。
文章信息
- 冯兴如, 杨德周, 尹宝树, 李明杰. 2018.
- FENG Xing-Ru, YANG De-Zhou, YIN Bao-Shu, LI Ming-Jie. 2018.
- 中国浙江和福建海域台风浪变化特征和趋势
- THE CHANGE AND TREND OF THE TYPHOON WAVES IN ZHEJIANG AND FUJIAN COASTAL AREAS OF CHINA
- 海洋与湖沼, 49(2): 233-241
- Oceanologia et Limnologia Sinica, 49(2): 233-241.
- http://dx.doi.org/10.11693/hyhz20180200036
-
文章历史
- 收稿日期:2018-02-12
- 收修改稿日期:2018-02-17
2. 中国科学院海洋环流与波动重点实验室 青岛 266071;
3. 青岛海洋科学与技术国家实验室海洋动力过程与气候功能实验室 青岛 266237;
4. 中国科学院大学 北京 100049;
5. 国家海洋环境预报中心 北京 100081
2. Key Laboratory of Ocean Circulation and Waves, Chinese Academy of Science, Qingdao 266071, China;
3. Function Laboratory for Ocean Dynamics and Climate, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, China;
4. University of Chinese Academy of Science, Beijing 100049, China;
5. National Marine Environmental Forecasting Center, Beijing 100081, China
中国是海洋大国, 海洋灾害频发, 其中海浪是引起海洋灾害的主要原因之一。台风过境时, 风速较大, 由其造成的台风浪更容易造成较大的海洋灾害, 统计显示, 2013台风浪造成的人员伤亡78人, 经济损失6.19亿元(李硕等, 2017)。因此研究台风浪的长期变化特征和趋势对于海岸带管理、海浪的长期预测以及防灾减灾等具有重要的意义。石永芳等(2014)基于卫星高度计资料研究了1993—2011年北太平洋波浪的变化趋势; 对于中国近海, He等(2018)基于第三代海浪模式模拟了中国东海1988—2002年的波浪场, 并分析了该海域的极值波高; 李硕等(2017)研究了中国2002—2015年共15年间的海浪灾害特征, 并对台风浪灾害进行了单独分析, 发现台风浪在海浪灾害中导致的人员死亡比例呈下降趋势; 彭冀等(2013)通过分析2002—2011年近10年的海浪灾害数据发现, 浙江遭受海浪灾害最严重, 福建受海浪灾害影响增长幅度最大, 并且台风浪是造成海浪灾害损失最大的因素。因此, 本文将浙江和福建海岸带的台风浪作为研究内容, 研究该海域1997—2016年最近20年台风浪的变化特征和趋势。
研究海浪的长期变化特征和趋势需要长时间序列的海浪数据, 但是目前国内高质量的海浪连续观测数据较少, 这样海浪数值模式便成了一个重要的工具。近岸海浪受时空变化的水位和流场影响较大, 采用考虑水位和海流影响的耦合模式可以显著提高近岸海浪的模拟准确度(Huang et al, 2010; Feng et al, 2016)。此外, 福建和浙江海岸线复杂, 因此本文采用非结构网格的海浪-海流耦合模式来模拟研究海域的台风浪过程, 既可以提高准确性, 又可以很好的刻画海岸线。
本文针对浙江和福建海域建立了高分辨率的非结构计算网格, 基于海浪-海流耦合模式模拟了1997—2016年共20年间所有影响该海域台风过程期间的海浪过程, 并对模拟结果进行了充分验证。之后对模拟结果进行分析, 得出了研究海域海岸带台风浪的变化特征和趋势。该研究对于研究海域海浪的长期预测和防灾减灾具有重要意义。同时对于航运和近岸的泥沙输运研究也有一定的借鉴意义。
1 历史台风浪模拟本研究采用非结构网格的海浪-海流耦合模式, 对浙江和福建海域1997—2016年间所有影响该海域台风过程期间的海浪过程进行了模拟。模式采用的计算网格以及考虑的所有台风过程的路径分别见图 1a和图 1b。
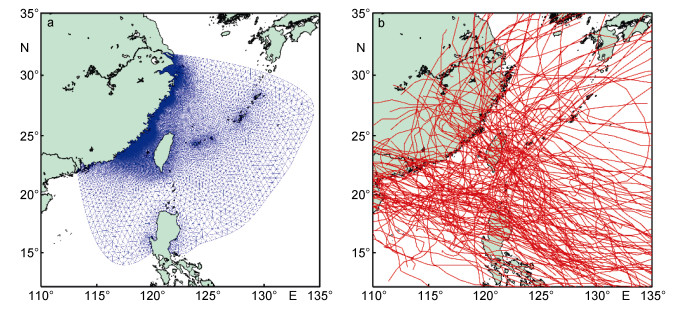 |
| 图 1 a:模式计算网格; b:1997—2016年间影响浙江和福建海域的158个台风过程 Fig. 1 a: Computational grid of the coupled model; b:Paths of the typhoons that affected sea area of Zhejiang and Fujian Provinces from 1997 to 2016. A total of 158 typhoons were selected |
本文采用的海浪-海流耦合模式为SWAN+ ADCIRC(Dietrich et al, 2011), 其中ADCIRC (Advanced Circulation Model)模式是一种非结构网格有限元水文动力模式(Westerink et al, 1991), SWAN (Simulating WAvesNearshore)模式为Zijlema(2010)在曲线正交网格模式基础上, 修改得到的基于三角形网格的海浪模式。本研究中, 耦合模式运行的物理机制为: ADCIRC将模拟得到的水位和流场提供给SWAN, 作为海浪模式的背景场; SWAN模式将计算得到的辐射应力提供给ADCIRC作为外力驱动, 同时海浪模式中的波长和周期信息用来参与ADCIRC模式的风应力计算。
其中, 对于风应力的计算, 原模式中, 风应力计算公式为Garratt(1977)公式: Cd=0.001∙(0.75+0.067W), W为风速, 模式将Cd的上限默认为0.0035。在该研究中, 风应力拖曳系数采用同时考虑依赖波龄和风速的Donelan(1993)公式:
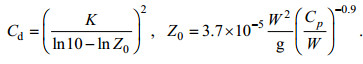 (1)
(1)其中, Cd为风应力拖曳系数, K为Karman常数, 取0.4, Z0为海表面粗糙度, Cp为海浪谱峰频率对应的波速, W为风速, Cp/W代表波龄。当风速超过33m/s时, 将风应力拖曳系数设为其上限0.0025(Donelanet al, 2004)。
1.2 模式设置耦合模式的计算网格为高分辨率的非结构网格, 见图 1a。计算区域大体位于15°—32°N, 112°—135°E这个范围内, 模式的分辨率从外海的30′逐渐过渡到近岸的100m, 一共274415个节点, 525071个三角形单元。模式采用的水深数据在近岸为分辨率为3″×3″的高分辨率地形, 外海采用ETOPO2数据, 该水深数据来自美国国家地球物理资料中心(NGDC), 其水平分辨率为2′一个格点。
对于ADCIRC模式, 初始流速和水位都为0;模式海岸边界条件取: Vn=0, 这里Vn是指固边界的法向水深平均流速。开边界上采用M2, S2, K1, O1, N2, S2, P1, Q1共8个分潮的调和常数预报的水位作为驱动, 这些调和常数来自NAO99潮汐模型(Matsumoto et al, 2000)。SWAN模式的计算网格和水深与ADCIRC模式完全一致。初始频率为0.04Hz, 频率增加因子为1.1, 频率数为41, 波浪谱方向的分辨率为10°, 模式计算的时间步长为30分钟。耦合模式在运行时, 模式间交换数据的时间间隔为30分钟。
1.3 风场模型和台风过程本研究采用的风场驱动为混合风场, 具体方法为在8倍最大风速半径内完全采用模型风场, 8倍和10倍最大风速半径内逐渐转换为背景风场, 10倍最大风速半径外, 完全采用背景风场, 本研究选取的背景风场为ECMWF(European Centre for Medium- Range Weather Forecasts, https://www.ecmwf.int/, 2018)风场。其中模型风场采用的是Jelesnianski的圆形台风模型(Jelesnianski, 1965)。该台模型对风场的计算考虑了台风的移动速度。其对风场和气压的计算公式如下:
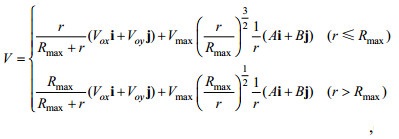 (2)
(2)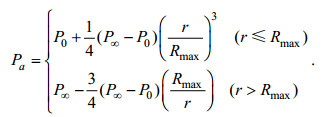 (3)
(3)其中A=-[(x-xc)sinθ+(y-yc)cosθ], B=[(x-xc)cosθ-(y-yc) sinθ], (x, y)和(xc, yc)分别代表计算点的位置和台风中心的位置; (Vox, Voy)分别为台风中心的移动速度在x和y方向的分量; Vmax为台风最大风速; Rmax为最大风速半径; r为计算点到台风中心的距离; θ为流向角, 在本研究中, 当r≤Rmax时θ=20°, r > Rmax时θ=15°; V为计算点的速度; i和j分别代表x和y方向的单位矢量; P0为台风的中心气压; P∞为台风的外围气压, 模式中设为1010hPa。
台风模型中的最大风速计算公式为:
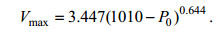 (4)
(4)Atkinson等(1977)在分析了位于西北太平洋沿岸以及一些岛屿观测站上的近28年的最大台风风速观测数据后, 提出了上述最大台风风速和台风中心气压之间的关系式。
基于耦合模式, 本研究共模拟了1997—2016年间, 所有影响浙江和福建海域的158个台风期间的海浪过程。其台风路径和强度数据均来自中国台风网的热带气旋最佳路径数据集(http://tcdata.typhoon.org.cn/) (Ying et al, 2014)。
2 模拟结果验证 2.1 1319号台风过程海浪模拟验证为了对耦合模式结果进行验证, 首先搜集了2013年1319号台风过程期间的4个站位处的海浪观测数据。2013年19号台风“天兔”于9月17号生成于西北太平洋菲律宾东部海域, 并在22号登陆广东, 造成了严重的灾害, 台风路径见图 2。模拟得到的海浪与实测结果的对比见图 3。可以看出, 耦合模式很好的模拟出了该台风过程中4个站位处的波高变化, 4个站位处有效波高极值模拟的相对误差平均为21%, 由于考虑了时空变化的流场和水位, 4个站位处的海浪的模拟结果也出现了和实测资料一致的波动信号。
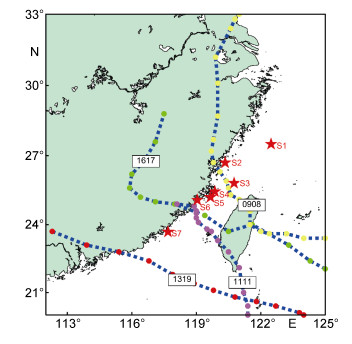 |
| 图 2 模式验证采取的4个台风过程路径及7个海浪观测站位分布 Fig. 2 Distribution of the four typhoon paths and 7wave observation stations |
 |
| 图 3 1319号台风“天兔”期间海浪有效波高模拟结果和实测结果在4个站位处的对比。a: S2;b: S4;c: S6;d: S7 Fig. 3 Simulated and observed significant wave height during typhoon "Usagi" at stations of a: S2; b: S4; c: S6; d: S7 |
为对模拟结果作进一步的验证, 将0908号、1111号、1319号和1617号台风过程中的海浪模拟结果与搜集到的对应观测资料进行了对比。这4个台风的路径以及用来验证的海洋观测站点分布如图 2所示。验证结果如图 4所示。海浪模拟结果和观测结果二者相关系数为0.79, 图 4中拟合曲线倾斜率为0.83, 并且通过了100%的显著性检验。说明海浪模拟结果和观测结果吻合较好。
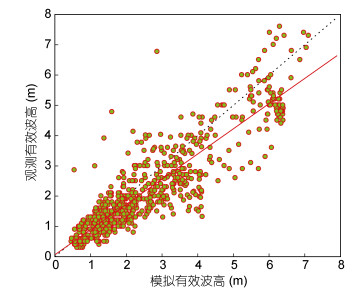 |
| 图 4 4个台风过程期间海浪有效波高模拟结果和实测结果在7个站位处的对比结果 Fig. 4 Simulated and observed significant wave height during four typhoons at seven stations |
对模拟得到的浙江福建海域1997—2016年共20年间对研究区域有影响的158个台风过程期间的海浪模拟结果进行了统计, 分析了研究海域台风浪的变化趋势及其与ENSO指数的关系。为了分析研究海域海浪的变化趋势, 特选取了研究海域岸线上的172个点位处的海浪波高序列进行分析, 这些点位的分布如图 5所示。
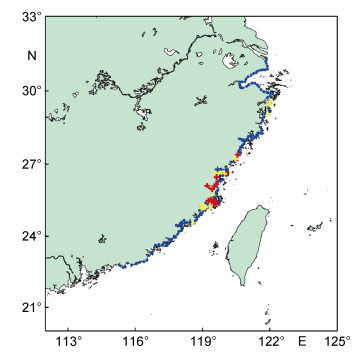 |
| 图 5 分析台风浪模拟结果所涉及的研究海域岸线上172个点位 Fig. 5 Distribution of the 172 stations, on which the wave results are analyzed along the coast of the study area 注:其中tHs > 1变化趋势通过90%显著性检验, 趋势为正显示为红色+号, 趋势为负显示为红色–号; tHs > 1变化趋势显著性检验结果位于70%至90%之间, 趋势为正显示为黄色+号, 趋势为负显示为黄色–号; 其他没有显著趋势的显示为蓝色·。(tHs > 1代表每年台风浪有效波高大于1m的持续时间) |
对1997—2016年20年间模拟得到的台风浪进行统计, 得到图 5中172个站位处的台风浪有效波高年极值序列。之后, 对每个站位处的浪高年极值进行趋势分析, 分析结果见图 6。可以看出, 台风浪高极值的最大正增长趋势值为0.05m/年, 通过了95%的显著性检验, 该值出现在26.1°N附近, 位于福建省岸线的闽江口附近海域。进一步分析可以看出, 增长趋势为正值, 且通过90%显著性检验的位置大都位于福建省岸线的中部海域, 这说明, 该海域的台风浪极值有显著增长的趋势。图 6也有增长趋势为负值的区域, 但极少有通过90%的显著性检验。对于其他海域, 台风浪极值的变化趋势大都不明显, 没有通过70%的显著性检验。总体来看, 福建北部海域岸线台风浪极值具有增长的趋势。
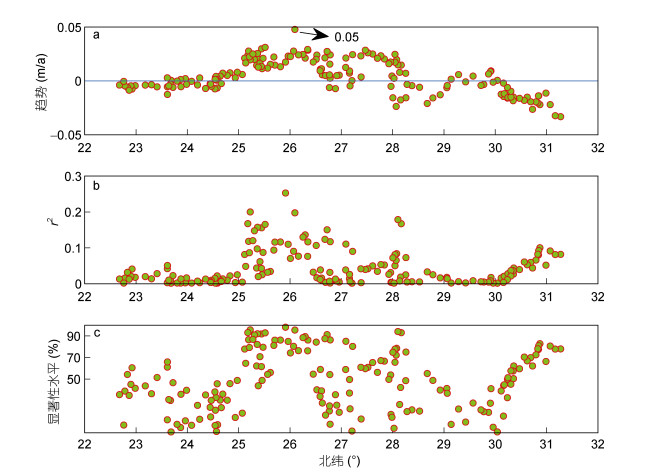 |
| 图 6 172个站位处的台风浪有效波高年极值变化趋势及其对应的显著性检验结果 Fig. 6 Trends of the extreme typhoon significant wave height and the corresponding significance test results for the 172 selected stations |
海浪浪高大于某个值的持续时间, 也是影响海浪致灾程度的一个重要因素。因此, 本研究还统计了图 5中各个站位处, 每年台风浪有效波高大于1m的时间(tHs > 1), 并做了趋势分析, 结果见图 7。为了更清晰的分析图 7的结果, 在图 5中, 本文将tHs > 1变化趋势通过90%显著性检验, 趋势为正显示为红色+号, 趋势为负显示为红色–号; tHs > 1变化趋势显著性检验结果位于70%至90%之间, 趋势为正显示为黄色+号, 趋势为负显示为黄色–号; 其他没有显著趋势的显示为蓝色·。由图 5可以看出, tHs > 1变化趋势为负的站位, 都没有通过70%的显著性检验, 变化趋势为正, 且通过90%显著性检验的站位基本都位于福建北部海域。浙江中部海域有若干站位具有显著性位于70%至90%之间的正的增长趋势。其他站位的tHs > 1没有显著性变化趋势。进一步分析图 7的结果可以发现, 通过90%显著性检验的正的增长趋势值基本位于0.54至1.72h/a之间, 主要位于纬度为25.4°—27.3°N, 该区域对应着福建北部海域, 说明该海域的海浪灾害有增加的风险。
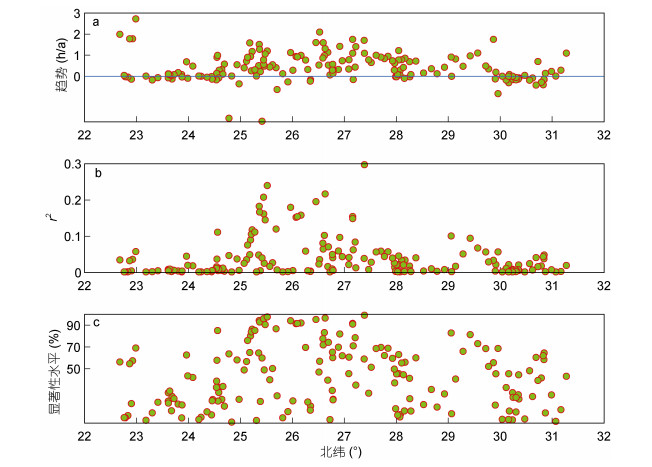 |
| 图 7 172个站位处的台风浪有效波高大于1m的持续时间(tHs > 1)年变化趋势及其对应的显著性检验结果 Fig. 7 Trends in the duration of significant wave height greater than 1m and the corresponding significance test results for the 172 selected stations |
本文还对台风浪有效波高大于1.5m的时间(tHs > 1.5)做了趋势分析, 结果见图 8。由图 8可以看出, tHs > 1.5与tHs > 1的变化趋势在空间上的分布比较相似, 变化趋势为负的站位, 都没有通过70%的显著性检验, 变化趋势为正, 且通过90%显著性检验的站位基本都位于福建北部海域。同样, 浙江中部海域也有若干站位具有显著性位于70%至90%之间的正的增长趋势。其他站位的tHs > 1.5没有显著性变化趋势。台风浪有效波高大于1.5m的时间(tHs > 1.5)通过90%显著性检验的正的增长趋势值基本位于0.19至1.50h/a之间, 要小于tHs > 1的增长趋势。
 |
| 图 8 172个站位处的台风浪有效波高大于1.5m的持续时间(tHs > 1.5)年变化趋势及其对应的显著性检验结果 Fig. 8 Trends in the duration of significant wave height greater than 1.5m and the corresponding significance test results for the 172 selected stations |
为了研究台风浪的年变化规律以及ENSO信号对台风浪的影响, 将图 5中不同站位处每年台风浪有效波高大于1m的持续时间(tHs > 1)与ENSO指数做相关性分析, 其中采用的ENSO指数为来自美国的NCEP资料(http://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php, 2018)。结果见图 9。可以看出, tHs > 1与ENSO指数的相关系数最大可达0.43, 并且通过了94%的显著性检验。这说明, ENSO信号对台风浪的影响在研究海域的某些岸段还是比较明显。图 9显示, 在纬度为23.0°—25.0°N以及29.0°—30.5°N区间内一些站位的tHs > 1与ENSO指数的相关性较显著, 这两个区域分别对应着福建省南部以及浙江省北部海域, 具体为福建省南部海域台风浪与ENSO指数有较显著的负相关, 浙江省北部海域台风浪与ENSO指数有较显著的正相关。同时, 对比图 7和图 9可以看出, 在tHs > 1的增长趋势显著的海域, tHs > 1与ENSO指数的相关性却不显著。
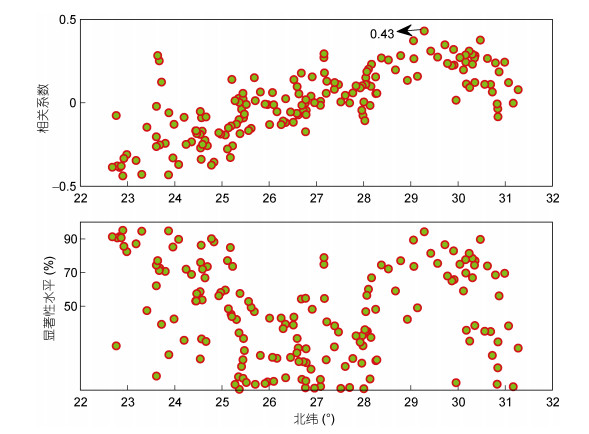 |
| 图 9 172个站位处的年台风浪有效波高大于1m的持续时间(tHs > 1)与ENSO指数之间的相关系数及其对应的显著性检验结果 Fig. 9 Correlation coefficient betweentHs > 1 (duration of significant wave height greater than 1m) and annual ENSO index, and the corresponding significance test results for the 172 selected stations |
本文基于海浪-海流耦合模式, 研究了浙江和福建海域台风浪的变化特征和趋势, 该研究对于这两个海域的台风浪长期预报以及防灾减灾具有重要的意义, 主要结论如下:
(1) 针对浙江和福建海域建立了高分辨率的海浪-海流耦合数值模式, 海浪模拟结果与实测结果对比较好, 可以用来研究该海域的台风浪变化特征和趋势。
(2) 基于该耦合模式模拟了1997—2016年20年间对研究区域有影响的158个台风过程期间的海浪过程, 并对模拟结果进行了统计, 发现福建北部海域台风浪极值和台风浪有效波高大于1m和1.5m的持续时间有增长的趋势。
(3) 分析台风浪有效波高大于1m的持续时间及其与ENSO指数的关系发现, 福建省南部海域台风浪与ENSO指数有较显著的负相关, 浙江省北部海域台风浪与ENSO指数有较显著的正相关。ENSO信号对这两个海域的台风浪有较显著的影响。
致谢 本文的数值模拟是在中国科学院海洋研究所的高性能计算平台上完成的, 特此致谢。| 李硕, 陶爱峰, 吴迪等, 2017. 近15年中国海浪灾害特性分析. 第十八届中国海洋(岸)工程学术讨论会论文集(上), 195-197 |
| 彭冀, 陶爱峰, 齐可仁等, 2013. 近十年中国海浪灾害特性分析. 第十六届中国海洋(岸)工程学术讨论会论文集(上), 805-808 |
| 石永芳, 杨永增, 吴克俭, 等, 2014. 1993-2011年北大西洋与北太平洋的波浪变化及其原因探究. 海洋与湖沼, 45(4): 685–694 DOI:10.11693/hyhz20130600077 |
| Atkinson G D, Holliday C R, 1975. Tropical Cyclone Minimum Sea Level Pressure/Maximum Sustained Wind Relationship for the Western North Pacific. Monthly Weather Review, 105(4): 25 |
| Dietrich J C, Zijlema M, Westerink J J, et al, 2011. Modeling hurricane waves and storm surge using integrally-coupled, scalable computations. Coastal Engineering, 58(1): 45–65 DOI:10.1016/j.coastaleng.2010.08.001 |
| Donelan M, Dobson F, Smith S, et al, 1993. On the Dependence of Sea Surface Roughness on Wave Development. Journal of Physical Oceanography, 23(9): 2143–2149 DOI:10.1175/1520-0485(1993)023<2143:OTDOSS>2.0.CO;2 |
| Donelan M, Haus B, Reul N, et al, 2004. . On the limiting aerodynamic roughness of the ocean in very strong winds. Geophysical Research Letters, 31(18): 355–366 |
| Feng X, Yin B, Yang D, 2016. Development of an unstructured-grid wave-current coupled model and its application. Ocean Modelling, 104: 213–225 DOI:10.1016/j.ocemod.2016.06.007 |
| Garratt J R, 1977. Review of drag coefficients over oceans and continents. Monthly Weather Review, 105(105): 915–929 |
| He H, Song J, Bai Y et al, 2018. Climate and extrema of ocean waves in the East China Sea, SCIENCE CHINA Earth Sciences, https://doi.org/10.1007/s11430-017-9156-7 |
| Huang Y, Weisberg R H, Zheng L, 2010. Coupling of surge and waves for an Ivan-like hurricane impacting the Tampa Bay, Florida region. Journal of Geophysical Research C:Oceans, 115: C12009 DOI:10.1029/2009JC006090 |
| Jelesnianski C, 1965. A numerical computation of storm tides induced by a tropical storm impinging on a continental shelf. Monthly Weather Review, 93(6): 343–358 DOI:10.1175/1520-0493(1993)093<0343:ANCOS>2.3.CO;2 |
| Matsumoto K, Takanezawa T, Ooe M, 2000. Ocean Tide Models Developed by Assimilating TOPEX/POSEIDON Altimeter Data into Hydrodynamical Model:A Global Model and a Regional Model around Japan. Journal of Oceanography, 56(5): 567–581 DOI:10.1023/A:1011157212596 |
| Westerink J J, Luettich R A, Baptista A M, et al, 1991. Tide and storm surge predictions using finite element model. Journal of Hydraulic Engineering, 118(10): 1373–1390 |
| Ying M, Zhang W, Yu H, et al, 2014. An Overview of the China Meteorological Administration Tropical Cyclone Database. Journal of Atmospheric and Oceanic Technology, 31(2): 287–301 DOI:10.1175/JTECH-D-12-00119.1 |
| Zijlema M, 2010. Computation of wind-wave spectra in coastal waters with SWAN on unstructured grids. Coastal Engineering, 57(3): 297–277 |
 2018, Vol. 49
2018, Vol. 49


