
中国海洋湖沼学会主办。
文章信息
- 孟素婧, 王辉, 卢伟, 王兆毅, 李云. 2018.
- MENG Su-Jing, WANG Hui, LU Wei, WANG Zhao-Yi, LI Yun. 2018.
- 海上无动力船舶漂移轨迹模型及其在“桑吉”油轮漂移模拟中的应用
- DRIFT TRAJECTORY MODEL OF THE UNPOWERED VESSEL ON THE SEA AND ITS APPLICATION IN THE DRIFT SIMULATION OF THE SANCHI OIL TANKER
- 海洋与湖沼, 49(2): 242-250
- Oceanologia et Limnologia Sinica, 49(2): 242-250.
- http://dx.doi.org/10.11693/hyhz20180200037
-
文章历史
- 收稿日期:2018-02-12
- 收修改稿日期:2018-03-11
2. 国家海洋环境预报中心 北京 100081
2. National Marine Environmental Forecasting Center, Beijing 100081, China
无动力或破损的船舶在海上自由漂移对海上的各项生产活动带来巨大风险。同时, 船舶携带的燃油、油气等危化品对海洋生态和环境也构成巨大的威胁(Hackett et al, 2006; 胡志武等, 2007; Breivik et al, 2011), 因此开展遇难船舶漂移预报技术的研究是非常重要的, 海上船舶漂移轨迹模型的建立可以为搜寻这些海上目标提供支持(Hackett et al, 2006; Breivik et al, 2008; Davidson et al, 2009)。海上船舶事故发生后, 准确的漂移轨迹预报不仅需要准确的现场风场、海流数据的支持, 而且需要具有理论支持的海上漂移轨迹模型及合理的海上目标漂移特征参数。不同类型的海上目标在同样的海洋环境影响下的漂移运动是不同的; 即使是同一类型, 其在海上不同的配置状态及漂移状态也会导致漂移轨迹显著不同(Allen et al, 2005)。
当前的海上船舶漂移轨迹预测主要通过建立风压模型或理论模型, 利用局地的海流、风场数据作为强迫场来进行预报。风压漂移是海上目标水面以上部分受风、浪作用而发生的相对于局地海流的运动(Breivik et al, 2013), 风压方法的研究始于Pingree (1944)关于海军救生筏的风压漂移的报告, 该方法通过开展大量的海上目标漂移试验来获取漂移观测数据, 利用经验统计方法拟合得到风压与海面风速之间的关系, 确定模型参数, 忽略波浪作用力(Breivik et al, 2008), 将尺寸小于30m的海上目标所受到的波浪作用力考虑到水面以上部分受到的风致漂移中(Breivik et al, 2012)。从20世纪60年代起, 有学者通过开展不同类型海上船舶的漂移试验, 积累了多种船舶类型的风压模型参数(Chapline, 1960; Allen, 1996; Allen et al, 1999; 李云等, 2011)。理论模型的建立通常采用半解析方法即通过受力分析在合理假定条件下简化得出, 关于船舶漂移的理论模型研究有来自挪威气象研究所针对大尺寸船舶建立的船舶漂移模型(Hackett et al, 2006), 该模型中船舶被近似为一个相近尺度的长方形盒子, 船型参数被简化为长、宽、吃水这三个参数, 建立了船型参数库, 综合考虑风、浪对漂移目标的作用力。Ni等(2010)针对船舶漂移, 通过受力分析及合理假设, 建立了船舶运动的理论模型, 得出风压角度与海上目标的外形特征无关, 在波浪振幅小于船只长度1/30时, 波浪作用可被忽略。Wang等(2014)将海上漂移物的形状特征作为一个要素考虑到了漂移模型中, 用于提高漂移平均速度模拟的准确性, 文章分析了方形和圆形两种形状漂移物的受力及漂移模拟, 引入了权重系数向量用于描述形状特征与随机运动之间的关系。胡志武等(2007)以日本海上保安厅海洋情报部开发的漂流轨迹预测系统的成果为基础, 在考虑了海流、潮流、风所引起的漂流速度的轨迹预测系统中追加了波浪所引起的漂流速度成分, 开展了遇难船舶漂流轨迹预测技术的研究, 结果显示未有改进。
风压模型在模拟船舶漂移轨迹时存在一定的局限性, 模型中已有的船舶类型参数主要适用于对应特征的海上目标类型, 对于新的船舶类型或不便于开展漂移观测试验的大尺寸船舶类型, 在使用风压模型时无法合理选择模型参数。与经验风压模型相比, 基于半解析方法建立的船舶漂移模型, 考虑船舶外形特征及海洋环境场的作用力, 模型参数少, 对于海上目标漂移试验数据不存在依赖性, 有助于从理论上了解海上船舶的漂移运动特征, 该方法被广泛应用于集装箱、海冰以及落水人员等海上目标的漂移轨迹模拟研究中(Sodhi et al, 1980; Perrie et al, 1997; Daniel et al, 2002; Kubat et al, 2005; Breivik et al, 2012; Maio et al, 2016)。
本文在常用半解析方法的基础上(Daniel et al, 2002; Ni et al, 2010), 通过对海上漂浮的船舶进行受力分析, 考虑船舶的外形特征及漂浮状态, 建立了海上船舶漂移轨迹模型, 并在如下2个方面做了改进, 1)考虑风拖曳系数的变化, 对面积比、风拖曳系数、流拖曳系数等模型参数进行了敏感性分析, 2)在“桑吉”油轮的漂移轨迹模拟中考虑科氏力的作用, 并考虑了科氏参数随纬度的变化。本文在第一部分将介绍利用半解析方法建立的海上船舶漂移轨迹模型, 第二部分将给出利用历史的海上渔船漂移试验案例进行的漂移模拟轨迹与观测轨迹的对比结果, 并将模型应用于2018年1月6日晚20时左右在我国东海海域遇难的巴拿马籍油轮“桑吉”的漂移轨迹模拟, 第三部分对影响漂移轨迹模拟的原因进行了分析讨论, 第四部分给出本文的结论与展望。
1 海上船舶漂移轨迹模型 1.1 船舶受力分析海上船舶在海面漂移时, 根据牛顿第二定律, 其动力学方程可以写为如下公式:
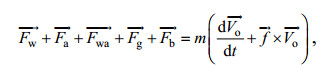 (1)
(1)式中, t是漂移时间, m是船舶的质量; 
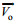
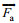
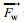
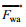
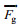
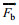
大气拖曳力:
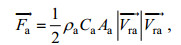 (2)
(2)式中, ρa是大气密度, 取1.29kg/m3; Ca是风拖曳系数; Aa是风作用于海面以上船舶的受力面积; 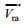
海水拖曳力:
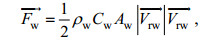 (3)
(3)式中, ρw是海水密度, 取1026kg/m3; Cw是流拖曳系数; Aw是海流作用于海面以下船舶的受力面积; 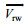
波浪辐射力:
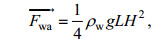 (4)
(4)式中, g是重力加速度; L是船舶长度; H是波浪振幅。由于风、浪导致的漂移过程在观测中无法准确区分, 从前人研究结果看, 考虑海浪作用力后, 海上目标漂移模拟的改善效果不一(胡志武等, 2007; 徐江玲等, 2017)。本文在模型中忽略波浪力, 在不考虑涌浪时, 可将风浪的作用力通过调高风拖曳系数的方法体现风浪对漂移的影响(Daniel et al, 2002)。
1.2 船舶漂移模型假设只考虑海上船舶的水平漂移运动, 船舶在单位时间内受力平衡, 每个时刻的物理量相互独立, 科氏力与大气拖曳力和海水拖曳力相比量级较小, 当偏小2个量级时可忽略, 假定忽略科氏力, 则运动方程简化为如下形式:
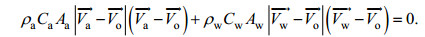 (5)
(5)则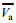
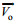
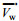
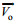
 (6)
(6)简化后的模型如下:
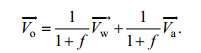 (7)
(7)从式7可以看出, 海上船舶的漂移运动速度是海流速度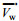
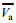
关于风拖曳系数Ca的取值, 针对集装箱取1(Smith, 1993; Daniel et al, 2002), 针对外形复杂的冰山取1.5(Sodhi et al, 1980), 本文针对海上船舶取值为0.7—1.3(洪碧光, 1991), 在对大尺寸海上船舶进行模拟时, Ca取1.5, 以此考虑风浪的作用。关于流拖曳系数Cw, 有研究的试验结果为0.8—1.2, 针对集装箱取1(Daniel et al, 2002), 本文取值为0.8—1.2。
1.3 漂移轨迹的计算漂移轨迹的计算采用拉格朗日质点追踪方法。拉格朗日方法是把海上漂浮目标看作质点, 通过对该质点的运动过程进行追踪, 来描述该质点的位置随时间变化的规律, 即漂移轨迹。质点位移计算的向量方程为:
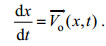 (8)
(8)对于漂移轨迹方程的求解, 本文采用欧拉法, 它是一种显式单步方法, 具有一阶精度, 是解微分方程的一种最简单和普遍的方法。用欧拉法解轨迹方程, 可以写为:
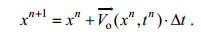 (9)
(9)式中, Δt为积分步长, n是时间指数, tn=nΔt。本文所述时间均为北京时。
1.4 无动力渔船漂移试验数据本文利用中国近海2次海上漂移试验的无动力渔船轨迹对该模型对进行了检验。海上试验的观测数据来源于2011年2月和4月在珠江口海域开展的无动力渔船漂移试验。该渔船类型为珠江口海域较为普遍的木质渔船, 长约20m, 宽6m(图 1), 渔船上装载有GPS定位系统、300kHz声学多普勒海流剖面仪(Acoustic Doppler Current Profilers, ADCP)和船舶用自动气象站。海上试验中, 渔船处于无动力漂移状态, 同步观测表层海流(海面以下5m的海流)和海面风(海面以上6—7m的风), 同时每10min记录一次渔船位置。本文所用的海流、海面风观测数据为10min平均的数据(周水华等, 2013)。
 |
| 图 1 珠江口海域常见渔船 Fig. 1 Common fishing vessel in the Pearl River Estuary |
2011年2月试验, 无动力渔船持续向西南方向漂移约17h, 试验海域以东北风为主, 风速以6—10m/s为主, 海流以西南和南向流为主, 最大流速约0.5m/s。4月试验, 无动力渔船持续漂移约73h, 试验海域海况良好, 以西南风为主, 在试验初期以东北风为主, 先后转为东南风、西南风, 风速以1—5m/s为主, 最大风速约7m/s, 最大流速约0.5m/s。
为分析该模型对渔船漂移轨迹的模拟能力, 试验现场观测的风、流数据经修订后用于模型驱动计算, 此处假设风、流场是空间均匀的。观测海面风根据式10被调整为海面以上10m高度风, 表层海流以观测到的海面以下5m的流来表示。
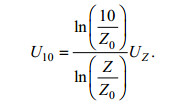 (10)
(10)式中, U10为海面以上10m高度风速, Z为观测风速的高度, UZ为观测风速, 当风速大于7m/s时, Z0=0.022, 当风速不大于7m/s时, Z0=0.023。(谢小萍等, 2014)
由于渔船在海上漂浮时的面积比没有准确的记录值, 因此考虑了在不同载重情况下的多种面积比进行渔船漂移轨迹的模拟。假定风拖曳系数Ca和流拖曳系数Cw均取1, 从结果看, 当选择合适的模型参数时, 可对该渔船的漂移轨迹进行合理模拟(图 2)。2月试验中, 面积比为1时模拟轨迹与实际轨迹基本吻合; 4月试验中, 面积比为3时模拟轨迹与观测轨迹最为接近。
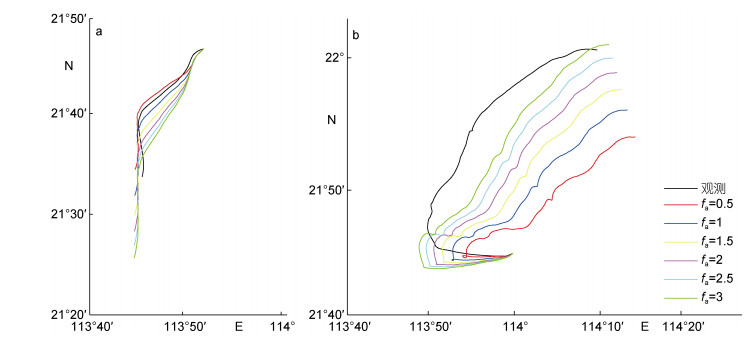 |
| 图 2 2011年2月(a)和4月(b)珠江口无动力渔船漂移模拟轨迹与观测轨迹对比图 Fig. 2 Simulated and observed drifting trajectories of the unpowered fishing vessel in the Pearl River Estuary, February, 2011 (a) and April, 2011 (b) considering different fa |
2018年1月6日20时左右, 在浙江外海(30°51′N, 124°58′E)处发生船只相撞事故, “桑吉”油轮爆燃并在燃烧状态下自由漂移, 于1月14日16时45分, 在(28°22′N, 125°55′E)处沉没, 漂移轨迹见图 3。据了解, 该油轮总长约274m, 型宽约50m, 型深约23m, 设计吃水约17m, 设计载重约16万t。
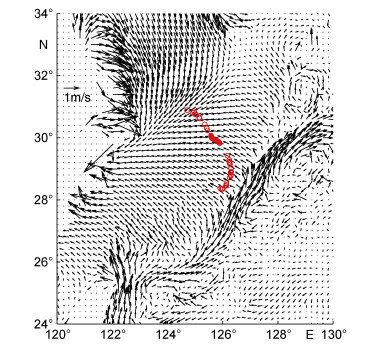 |
| 图 3 “桑吉”油轮漂移轨迹(红圆圈)及所在海域的1月6日20时表层海流分布 Fig. 3 The drifting trajectory(red circle) of the Sanchi Oil tanker and the surface current distribution from 20 hours, 6th January |
“桑吉”油轮的漂移轨迹模拟采用的表层海流数据来自国家海洋环境预报中心基于ROMS(Regional Ocean Modeling System)开发的黄东海业务化海流预报系统输出的0—17m水深垂直平均流(ROMS流场), 该预报系统的模式水平分辨率为1/30°×1/30°, 同化了海表面温度、海表面高度等观测资料, 利用GFS风场、热通量、淡水通量进行强迫, 每日20时进行起报, 做未来5天的流场大面预报。模拟采用的海面10m高度风场预报数据来自国家海洋环境预报中心基于WRF(Weather Research and Forecasting)开发的西北太平洋业务化海面风场预报系统输出的海面以上10m高度风场24h预报(WRF风场), 该预报系统的模式水平分辨率为0.2°×0.2°, 每日08时和20时进行起报, 做未来5天的海面风场预报。
利用收集的船舶信息对模型参数进行估计, 考虑到船载的凝析油在不断燃烧之后, 其载重会减少, 面积比会增大, 因此假定面积比为1.5, 同时由于油轮在自由漂移约1天之后周边海域风力增强, 风速大于10m/s, 最大风速达15m/s(图 4), 海浪对该尺寸的船只影响不可忽视, 因此通过增加风拖曳系数来考虑局地风浪对船舶漂移的作用, 假定风拖曳系数为1.5。此外, 流拖曳系数取1。
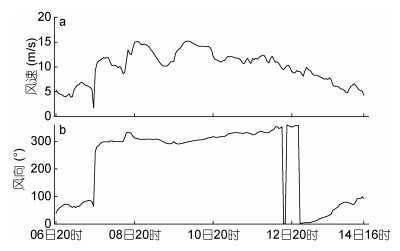 |
| 图 4 “桑吉”油轮漂移轨迹上24h预报的风速(a)和风向(b) Fig. 4 24-hour forecasted wind speed (a) and wind direction (b) on the drifting trajectory of the Sanchi Oil tanker |
利用WRF风场、ROMS流场驱动模型, 分别开展了两种漂移轨迹模拟, 即逐日模拟和全程模拟, 模型参数的设置均为fa=1.5, Cw=1, Ca=1.5。逐日模拟以当日获取的油轮位置为起点共进行了8次模拟, 第1—7天模拟时间为24h, 第8天模拟时间为29h(最后时刻为“桑吉”轮沉没时刻)。每日模拟轨迹与实际观测位置的对比结果显示第1、2天预报的油轮轨迹与实测位置比较接近, 对假定的面积比、风拖曳系数、流拖曳系数的合理性进行了初步验证, 第3天预报的漂移方向与实际漂移方向在开始比较吻合, 之后逐渐向左偏移, 预报漂移速度低于实际漂移速度, 第4—7天预报的油轮漂移速度与实际的相当, 但漂移方向均偏左, 第8天预报的油轮漂移轨迹与实测位置基本吻合(图 5a)。全程模拟是从事发时刻对全程漂移轨迹进行模拟, 结果显示在第1—4天的模拟与实际轨迹较符合, 5天之后模拟的漂移方向与实际相比偏左, 并且随着模拟时间的增加, 模拟误差得到了不断累积放大, 导致后期漂移模拟效果较差(图 5b)。
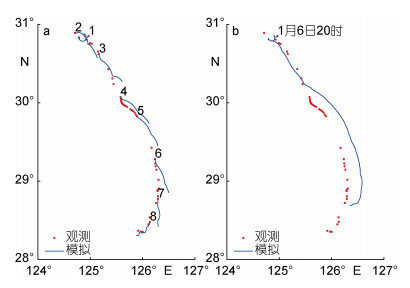 |
| 图 5 “桑吉”油轮漂移的逐日模拟轨迹(a)、全程模拟轨迹(b)与观测轨迹 Fig. 5 Daily simulated (a), wholly simulated (b) and observed drifting trajectories of the Sanchi Oil |
船舶漂移预报的准确度与模型参数的准确度有直接关系, 除了海流、风场等预报数据的误差之外, 漂移目标特征的不确定性对漂移预报有主要的影响(Breivik et al, 2008, 2011)。从2011年2月和4月珠江口渔船漂移轨迹模拟结果看, 虽然是同一类型渔船, 但模型中适用的面积比参数却不一样, 原因可能有两点。首先, 开展试验期间的渔船配置状态及漂浮状态未知, 因此可能是2次试验期间渔船的配置不一样导致的, 由于没有相关记录无法得到验证; 其次, 2次试验海域的风、流场差异较大, 风拖曳系数和流拖曳系数的取值都为1的假设不符合实际也可能会导致一定的误差, 另外, 4月试验相对2月试验漂移时间长, 渔船的漂浮姿态不断变化带来更多不确定性。
针对第二个可能的误差来源, 本文对2次试验海域的风场进行了分析比较, 2月风速大于4月风速, 2月风向稳定, 4月风向发生了明显变化, 根据洪碧光(1991)的研究结果, 船舶的风拖曳系数取值在0.7—1.3之间, 当相对风舷角为90°时, 风拖曳系数约为0.7。相对风舷角的变化与风场变化有一定关系, 当风场稳定时, 船舶在横风状态时保持平衡, 此时相对风舷角约为90°, 当风场改变时, 船舶会通过调整相对风舷角来达到新的受力平衡。利用2011年2月和4月珠江口渔船漂移轨迹的模拟, 分别对风拖曳系数、流拖曳系数进行了敏感性分析, 假设面积比fa=2。从结果看, 渔船漂移轨迹的模拟对风拖曳系数、流拖曳系数较为敏感(图 6和图 7)。在2月试验中, 当fa=2, Cw=1, Ca=0.7时, 模拟轨迹与实测轨迹基本吻合(图 6a), 17h内的漂移距离误差最大约6.6km, 但在fa=1, Cw=1, Ca=1时, 模拟轨迹与实测轨迹最吻合(图 2a), 距离误差最大约3.7km; 在4月试验中, 当fa=2, Cw=1, Ca=1.3时, 模拟轨迹与实测轨迹最接近(图 6b), 73h内的漂移距离误差最大约8.2km。以此可见, 在稳定风场的作用下, 风拖曳系数取0.7合适, 在风场变化的背景下, 风拖曳系数取1.3合适。
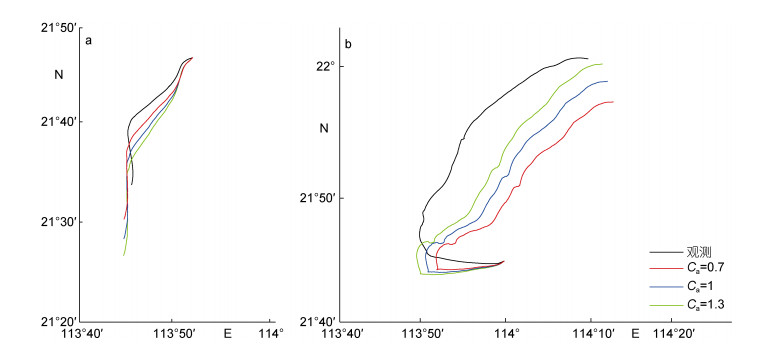 |
| 图 6 模型在设置不同风拖曳系数时的2011年2月(a)与4月(b)渔船漂移模拟轨迹与观测轨迹 Fig. 6 Simulated and observed drifting trajectories of the vessel considering different wind drag coefficient, February, 2011 (a) and April, 2011(b) |
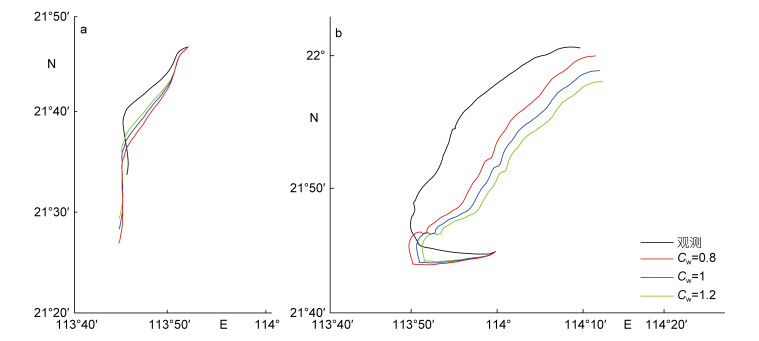 |
| 图 7 模型在设置不同流拖曳系数时的2011年2月(a)与4月(b)渔船漂移模拟轨迹与观测轨迹 Fig. 7 Simulated and observed drifting trajectories of the vessel considering different current drag coefficient, February, 2011 (a) and April, 2011 (b) |
从“桑吉”油轮的逐日漂移轨迹模拟结果看, 模拟轨迹较为合理, 对于海上搜救行动的开展及风险评估工作有一定的参考价值, 相较于第1—4天, 第5天之后, 预报轨迹出现较为明显的漂移方向误差, 误差可能来源于三个方面。首先是海洋环境场的模拟预报误差, 从“桑吉”油轮所在海域的表层海流(图 3)可以看出, 油轮漂移5天之后所在海域的海流结构比较复杂, 受复杂地形和黑潮流系的影响, 此处海流的准确预报还存在一定难度。第二个误差来源于对科氏力的忽略。第三个误差来源于对“桑吉”油轮漂移状态及模型参数的估计误差, 尤其是对面积比的估计。
针对海洋环境场模拟预报的误差, 本文分别利用附近海域定点浮标的观测数据对模拟预报结果进行了检验。表层海流的预报检验采用在“桑吉”油轮事故发生后在事故海域附近(29°59.48′N, 125°59.09′E)处布放的浮标观测数据, 以此了解该海域海流预报系统的模拟能力。从1月19日08时至1月25日08时的对比结果看(图 8), 该预报系统可以较好地对浮标位置的流速和流向进行模拟预报, 流速预报整体偏大, 流速均方根误差为0.23m/s, 流向的绝对平均误差为35°。假定该浮标处的海流误差对“桑吉”油轮漂移附近海域的海流有一定的代表性, 对海流的流速预报结果进行了订正, 订正后的预报结果较订正前有了较好的改善(图 8a), 之后的分析均采用了订正后的结果。海面风场的预报检验采用事故海域附近(29°30′N, 124°E)处的浮标观测数据, 从1月6日20时至1月14日16时的对比结果看(图 9), WRF风场可以较好地对浮标位置的风速和风向进行模拟预报, 风速均方根误差为1.4m/s, 风向的绝对平均误差为20.2°。
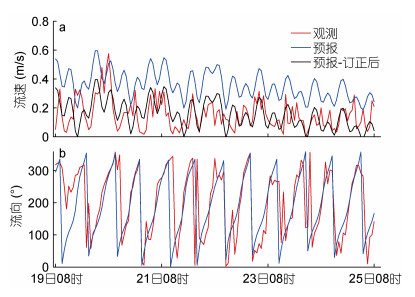 |
| 图 8 ROMS海流预报与观测随时间的对比图 Fig. 8 Comparison of forecasted surface current speed(a) and direction(b) from ROMS and observations |
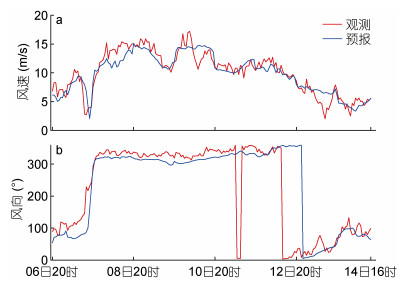 |
| 图 9 WRF风场预报与观测随时间的对比图 Fig. 9 Comparison of forecasted sea surface wind speed (a) and direction (b) from WRF and observations |
另外, 为了解海面风场、表层流场在此次“桑吉”油轮漂移过程中的贡献, 设置了2种实验, 分别用单独的WRF风场、单独的ROMS流场驱动模型, 漂移轨迹对比如下图(图 10)。由图可见海面风场在漂移过程中的贡献显著大于表层流场, 在不考虑风场的作用时, 对油轮漂移轨迹的模拟效果较差, 漂移方向与前期较为吻合, 但漂移速度却显著偏小。据此可以推断海流误差对漂移轨迹模拟误差的贡献也相对较小。
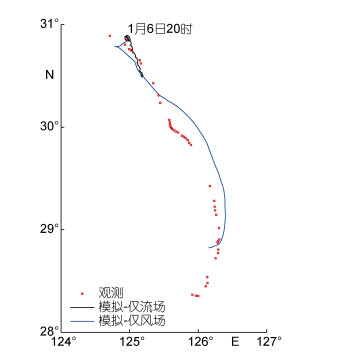 |
| 图 10 基于单独的WRF风场和单独的ROMS流场驱动模型的模拟轨迹与观测轨迹 Fig. 10 Simulated and observed drifting trajectories of the Sanchi Oil tanker with the only wind data from WRF and only current data from ROMS |
针对第二种可能的误差来源, 本文对桑吉油轮在漂移过程中的科氏力进行了计算, 对于274m的桑吉油轮, 科氏力量级为104kg∙m/s2, 风流拖曳力的量级为105kg∙m/s2, 科氏力的量级约为风流拖曳力的0.1倍, 不可忽略。从考虑了科氏力作用后的漂移轨迹模拟结果看, 逐日模拟(图 11a)、全程模拟(图 11b)的效果均得到了较好的改善。从逐日模拟的漂移轨迹来看(图 11a), 第2天的模拟误差较大, 为了消除其对全程漂移轨迹模拟的影响, 利用第3天起报时刻(即1月8日22时)的位置开始模拟至沉船时刻(阶段性模拟), 从结果看, 模拟轨迹与实际观测位置较为吻合(图 11c)。
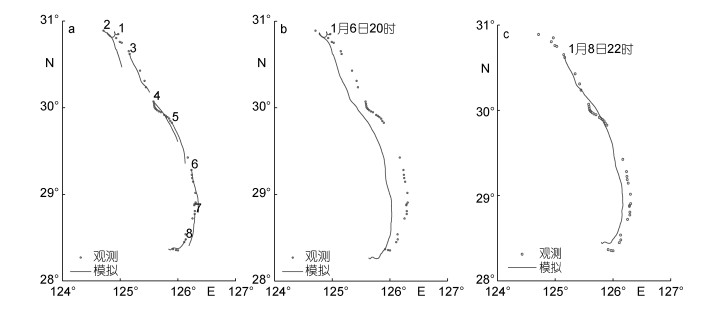 |
| 图 11 考虑科氏力作用的逐日模拟(a)、全程模拟(b)、阶段性模拟(c)的“桑吉”油轮漂移轨迹与观测轨迹 Fig. 11 Daily (a), wholly (b), phased (c) simulated and observed drifting trajectories of the Sanchi Oil tanker considering Coriolis force |
针对第三种可能的误差来源, 本文对面积比这个模型参数进行了敏感性分析。“桑吉”油轮在漂移过程中, 装载的凝析油经过燃烧之后, 载重减轻, 同时不断燃烧对船体有大的损害, 因此, 在油轮漂移轨迹的模拟中, 面积比是个不确定的参数。以第3天漂移模拟24h的结果为例, 当Cw=1, Ca=1.5时, 可以看出该模型对面积比fa敏感, 当fa=2.5时模拟轨迹与实测位置最接近(图 12), 较fa=1.5时的模拟轨迹效果好。
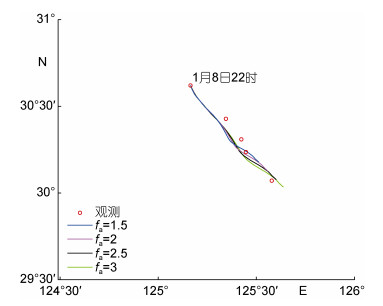 |
| 图 12 考虑科氏力之后的模型在设置不同面积比时从1月8日22时起报24h的“桑吉”油轮漂移模拟轨迹与观测轨迹 Fig. 12 24-hour simulated and observed drifting trajectories of the Sanchi Oil tanker from 22 hours, 8th January considering different fa and Coriolis force |
综上所述, 基于半解析方法建立的海上船舶漂移轨迹模型能够合理模拟中国近海渔船、“桑吉”油轮的漂移轨迹。该模型中, 海面以上与以下侧向投影面积之比是影响漂移轨迹模拟的一个重要参数, 漂移轨迹的模拟对于风拖曳系数、流拖曳系数的取值较为敏感, 在“桑吉”油轮的漂移轨迹模拟中, 考虑了吃水深度以上平均海流对船舶的作用, 海面风场的贡献远大于流场的贡献, 科氏力的作用不可忽视。对于同一类型渔船, 在不同漂浮状态、不同海况时模型参数不同, 不同风、流场对船舶漂移的影响有待进一步研究, 在实际的海上船舶搜救应急预报工作中, 需根据不断更新的实际位置对参数进行确定优化。对于大型油轮这种尺寸的海上搜寻目标, 需根据实际的目标特征对科氏力进行计算, 以决定是否对其进行考虑, 对于其他参数, 下一步可通过等比例缩小尺寸的模型或物体对其进行海上漂移试验来获取观测数据, 记录面积比这个重要参数, 对模型参数进行优化改进。
海洋环境预报场的准确度对于漂移轨迹模拟的影响非常重要, 下一步将通过提高风、流预报的准确度及精细化程度来改进漂移轨迹的预报, 对风、流误差在漂移轨迹模拟误差中的贡献开展进一步研究, 并将在模型中加入波浪作用力, 对海上无动力船舶漂移轨迹模型进行完善。
本文对于海上船舶仅开展了轨迹漂移, 而对于海洋环境预报、模型参数、海上目标特征、事发时间及位置等多种信息误差带来的不确定性考虑不够全面。下一步将把多种不确定性考虑到模型中, 为无动力或受损船舶的搜寻以及风险评估等工作提供更为合理参考。
| 李云, 刘钦政, 王旭, 2011. 海上失事目标搜救应急预报系统. 海洋预报, 28(5): 77–81 DOI:10.11737/j.issn.1003-0239.2011.05.012 |
| 胡志武, 张秋荣, 顾维国, 2007. 遇难船舶漂流轨迹技术. 航海技术, 24(3): 18–21 |
| 周水华, 杨阳, 冯伟忠, 2013. 广东海域模拟人和无动力渔船海上漂移试验研究. 热带海洋学报, 32(1): 87–94 |
| 洪碧光, 1991. 船舶风压系数计算方法. 大连海运学院学报, 17(2): 113–121 |
| 谢小萍, 魏建苏, 黄亮, 2014. ASCAT近岸风场产品与近岸浮标观测风场对比. 应用气象学报, 25(4): 445–453 DOI:10.11898/1001-7313.20140407 |
| 徐江玲, 高松, 葛勇, 等, 2017. 海浪对海上漂浮物漂移轨迹作用分析. 防灾科技学院学报, 19(2): 75–79 |
| Allen A A, 1996. The leeway of Cuban refugee rafts and a commercial fishing vessel. U. S. Coast Guard Rep. CG-D-21-96, 121 |
| Allen A A, Plourde J V, 1999. Review of leeway: Field experiments and implementation. U. S. Coast Guard Rep. CG-D-08-99, 351 |
| Allen A A, 2005. Leeway divergence. U. S. Coast Guard Rep. CG-D-05-05, 128 |
| Breivik Ø, Allen A A, 2008. An operational search and rescue model for the Norwegian Sea and the North Sea. J Mar Syst, 69(1-2): 99–113 DOI:10.1016/j.jmarsys.2007.02.010 |
| Breivik Ø, Allen A A, Maisondieu C, et al, 2011. Wind-induced drift of objects at sea:The leeway field method. Appl Ocean Res, 33: 100–109 DOI:10.1016/j.apor.2011.01.005 |
| Breivik Ø, Allen A A, Maisondieu C, et al, 2012. The leeway of shipping containers at different immersion levels. Ocean Dyn, 62(5): 741–752 DOI:10.1007/s10236-012-0522-z |
| Breivik Ø, Allen A A, Maisondieu C, et al, 2013. Advances in search and rescue at sea. Ocean Dynamics, 63(1): 83–88 DOI:10.1007/s10236-012-0581-1 |
| Chapline W E, 1960. Estimating the Drift of Distressed Small Craft. Coast Guard Alumni Association Bulletin, 22(2): 39–42 |
| Daniel P, Jan G, Cabioc'h F, et al, 2002. Drift modelling of cargo containers. Spill Science & Technology Bulletin, 7(5-6): 279–288 |
| Davidson F J, Allen A A, Brassington G B, et al, 2009. Applications of GODAE ocean current forecasts to search and rescue and ship routing. Oceanography, 22(3): 176–181 DOI:10.5670/oceanog |
| Hackett B, Breivik , Wettre C, 2006. Forecasting the drift of objects and substances in the ocean. In: EP Chassignet, J Verron (Eds. ), Ocean weather forecasting——an integrated view of oceanography. Dordrecht: Springer, 507-523 |
| Kubat I, Sayed M, Savage S B, et al, 2005. An operational model of iceberg drift. International Journal of Offshore and Polar Engineering, 15(2): 125–131 |
| Maio A D, Martin M V, Sorgente R, 2016. Evaluation of the search and rescue LEEWAY model in the Tyrrhenian Sea:a new point of view. Nat Hazards & Earth Syst Sci, 16(8): 1979–1997 |
| Ni Z, Qiu Z, Su T C, 2010. On predicting boat drift for search and rescue. Ocean Engineering, 37(13): 1169–1179 DOI:10.1016/j.oceaneng.2010.05.009 |
| Perrie W, Hu Y C, 1997. Air-ice-ocean momentum exchange. Part Ⅱ:Ice drift. Journal of Physical Oceanography, 27(9): 1976–1996 DOI:10.1175/1520-0485(1997)027<1976:AIOMEP>2.0.CO;2 |
| Pingree F, 1944. Forethoughts on rubber rafts. Technical Report Woods Hole Oceanographic Institution. |
| Smith S, 1993. Hindcasting iceberg drift using current profiles and winds. Cold Regions Sciences and Technology, 22(1): 33–45 DOI:10.1016/0165-232X(93)90044-9 |
| Sodhi D S, EI-Tahan M, 1980. Prediction of an iceberg drift trajectory during a storm. Annals of Glaciology, 1: 77–82 DOI:10.3189/S0260305500017018 |
| Wang S Z, Nie H B, Shi C J, 2014. A drifting trajectory prediction model based on object shape and stochastic motion features. Journal of Hydrodynamics, 26(6): 951–959 |
 2018, Vol. 49
2018, Vol. 49


