中国海洋湖沼学会主办。
文章信息
- 尹丽萍, 郭景松, 乔方利. 2018.
- YIN Li-Ping, GUO Jing-Song, QIAO Fang-Li. 2018.
- 地形对陆架拦截波性质及机制的影响
- IMPACT OF BOTTOM TOPOGRAPHY ON THE CHARACTER AND MECHANISM OF COASTAL TRAPPED WAVES
- 海洋与湖沼, 49(2): 263-270
- Oceanologia et Limnologia Sinica, 49(2): 263-270.
- http://dx.doi.org/10.11693/hyhz20170500140
-
文章历史
- 收稿日期:2017-05-22
- 收修改稿日期:2017-06-28
2. 青岛海洋科学与技术国家实验室区域海洋动力学与数值模拟功能实验室 青岛 266237;
3. 海洋环境科学和数值模拟国家海洋局重点实验室 青岛 266061;
4. 国家海洋局数据分析与应用重点实验室 青岛 266061
2. Laboratory for Regional Oceanography and Numerical Modeling, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, China;
3. Key Laboratory of Marine Sciences and Numerical Modeling, State Oceanic Administration, Qingdao 266061, China;
4. Key Laboratory of Data Analysis and Applications, State Oceanic Administration, Qingdao 266061, China
陆架拦截波是能量限制在陆架上的一类波动, 在陆架海域广泛存在。周期为几天到几周不等, 波长几十到几百甚至上千千米(Mysak, 1980)。波动传播方向平行于等深线, 受科氏力影响, 在南北半球波导分别在陆地的右侧和左侧。拦截波可快速的将海水的运动形态传播到远处, 改变海水本来的运动形式, 进而影响到一系列海洋现象。如影响边界流的流速及结构, 甚至会造成水体输运的反转; 影响上升流结构进而影响到上升流区的营养盐输送; 还可能会影响风暴潮、陆架中尺度涡旋、厄尔尼诺信号的传播等。
陆架拦截波的性质和陆架地形密切相关。实际上, 波动的频散关系正是由地形函数决定的, 不同海底地形确定了具有不同频散性质的陆架波系(Mysak, 1980)。近年来, 在引入了新的地形函数后, 人们发现一些新的波动频散关系(Sansón, 2011; Schulz et al, 2011; 冯立成等, 2013; Drivda et al, 2015)。然而, 即使是在相同的地形函数下, 若陆架的宽度和坡度不同, 波动性质也会不同, 形成不同的波动频散关系。一般而言, 大陆架宽度可从数十公里到数百甚至上千千米不等。可见在分析特定海区的陆架拦截波性质时, 不但要考虑海底地形, 陆架宽度也是重要的影响因素。陆架的宽度及坡度影响波长(Schumann et al, 1990)及波动的相速度(秦曾灏等, 1988); 波动在宽陆架上受幅散的影响大于在窄陆架上受到的影响; 若陆架宽度小于200km, 波动频率在一定程度上受β效应影响(秦曾灏等, 1988)。若存在底摩擦, 波动振幅在底摩擦的影响下随时间消衰。地形参数的改变, 即使波动在传播过程中有相同的底摩擦系数, 也会造成摩擦效应及波动衰减率的区别。冯士筰(1979)指出零阶陆架拦截波的阻尼衰减因子明显受陆架宽度影响, 陆架越宽即坡度越小, 湍阻尼效应越大, 而且湍阻尼效应只有在相对较宽的陆架上才显著。而秦曾灏等(1988)则认为波幅衰减率几乎完全由底阻尼系数决定而不用考虑陆架宽度影响。陆架的连续变化会引起波动能量在不同模态间的转移, 若陆架宽度在波的传播的方向上变宽, 能量会从低模态转向高模态(Wilkin, 1990), 在经过岬角、海底峡谷或者陆架变窄时能量可能丢失(Platov, 2016)。
过境的天气扰动如寒潮(李晓红等, 2011)、台风、顺岸方向周期性的风应力等都可以引起陆架拦截波。其中风引起的Ekman输运是陆架拦截波生成的主要机制(Gill et al, 1974; Brink, 1991)。不同的地形会造成不同的波动形成机制、维持波动的外力及波动形式。周期在天气尺度上的波动, 在波动形成后, 传播过程中若继续受到周期性风的影响, 很容易和当地的天气强迫发生共振, 使振幅增强(Igeta et al, 2015), 进而形成局地的强迫陆架陷波。强迫波振幅除了远处传来的波动的贡献外, 可能还会受外力如顺岸向风应力、海区上的风应力旋度和气压强迫等的影响(Gill et al, 1974)。如在美国西海岸(Mitchum et al, 1986)、中国南海(Ding et al, 2012)等陆架较窄的海区, 影响陆架拦截波的主要外力为顺岸向的风; 而在中国东海(Yin et al, 2014), 除顺岸向风应力外, 风应力旋度对陆架拦截波也有较大影响。由于陆架的宽窄、坡度不尽相同, 因此在不同类型或者同一类型不同地形参数的陆架上, 影响波动振幅的机制也不同。
近年来针对陆架陷波的研究逐渐增多, 像Noto半岛(Fukudome et al, 2016)、Alborán海(Serrano et al, 2015)、中国的东海(Yin et al, 2014)、南海(Ding et al, 2012; Zheng et al, 2014; Li et al, 2015)、挪威西海岸(Drivda et al, 2015)等研究都有新的发现。各海区的地形形态不同。如Alborán海具有双陆架, 东海陆架宽广而南海陆架相对较窄。由于陆架海区本身的地形条件以及外在强迫不同, 陆架海上波动性质, 波动的生成、传播机制, 波动生长、消亡过程都有区别, 因此需要针对不同的海区采对陆架地形和波动性质的关系做系统的定量研究。目前并未见针对陆架的宽度和坡度定量分析陆架拦截波性质的报道。本文将基于Clark和Van Gorder(Clarke et al, 1986)提出的方法, 利用Brink建立的斜压陆架拦截波模型(Brink, 2006), 分析陆架地形对于陆架拦截波频散关系、传播特性以及生成和强迫机制的影响。
1 理论基础模型海洋满足静力近似和Boussinesq近似, 包含上下Ekman边界层。在局地笛卡尔坐标系下, 规定原点位于海面边界处, x轴垂直于岸线并指向外海, y轴为岸线方向, 与波动传播方向相反, z轴垂直于海平面并竖直向上。海水受风应力和底摩擦的影响。海水运动方程如下:
 (1a)
(1a) (1b)
(1b)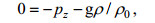 (1c)
(1c) (1d)
(1d) (1e)
(1e)其中, u, v, w 分别是x, y, z方向的扰动速度分量, g为重力加速度, ρ、ρ0分别为海水的扰动密度和平均密度, p、pa表示扰动压力和大气压力, f科氏参数, τzx为x方向的风应力, τzy包括两部分, 即海表面的顺岸向风应力以及海底的底摩擦, 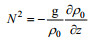
方程(1)需满足以下边界条件: (a)“连续”条件, 即在不同地形交界处压力和流速连续; (b)在远离边界处, 波动振幅为零; (c)在侧边界及底边界, 需要满足“无法向流”条件。
假设方程具有波动解:
 (2)
(2)ω表示波动频率, l为顺岸方向的波数。根据此波动解, 在不同的地形函数下, 由方程(1)得到不同的解, 由此可确定不同类型的频散关系式。但通常情况下, 除了在几种特殊的海底地形如线性、指数、多项式函数等情况下能求得解析解, 理论求解方程的频散关系非常困难。而实际海底地形复杂多样, 据此Brink(2006)提供了一个求解方程(1)在任何地形下数值解的方法, 包括求解方程的频散关系, 在长波假设下求解长波方程的相速度及其他波动参数。
本文假设海底地形由大陆架、陆架坡折、海盆区三部分构成(图 1)。为便于直观的描述陆架的宽度和坡度, 三部分的水深分别用线性表示。自由波的频散关系利用Brink(2006)的方法求得。
 |
| 图 1 陆架地形示意图 Fig. 1 Sketch of topography of a coastal ocean |
实际观测到的陆架拦截波, 波长基本和海区的长度一个量级, 属于长波。在长波假设下, 自由波的相速度不再随波长变化, 在固定的模态有固定的值。而强迫方程(1)可以由以下“函数分裂”方法求得。
假设方程(1)具有如下强迫解:
 (3)
(3)将(3)式代入(1)后利用特征函数的正交性, 化简可得,
 (4)
(4)其中,
 (5a)
(5a)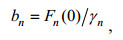 (5b)
(5b) (5c)
(5c)对应第n个模态, bn表示风耦合系数, ann为摩擦衰减常数, 其倒数为摩擦衰减距离; amn为第n个模态对第m个模态的摩擦耦合; cn为相速度。方程(4)可以用特征线方法求得。将Yn带回(3)即可得到强迫方程的压力解。方程(4)等式后的三项, 分别表示陆架边缘处顺岸向风应力、气压的时间变率在整个陆架上的积分以及风应力旋度在整个陆架上的积分。对于自由波, 此三项是波动形成的可能机制; 对于强迫波, 此三项是波动传播过程中影响波动振幅的可能因素。
以上为自由陆架拦截波和强迫陆架拦截波的理论框架, 本文将在此框架基础上, 分析陆架宽度对不同模态自由波速度的影响以及外部强迫(如底摩擦和风应力等)对强迫陆架拦截波的作用。
2 陆架地形对陆架拦截波的影响 2.1 陆架地形对自由波的影响 2.1.1 非长波假设下地形对频散关系的影响陆架拦截波的能量主要集中在陆架上浅水区, 在深水区波动的能量基本为零, 因此本文所指的“陆架宽度”均指海岸至陆架坡折处的距离。本文不讨论陆架坡折处的影响, 令坡折处高度d2均为800m, 坡折宽度L2均为60km。大陆架最大深度一般不超过200m, 分别取d1为75m, 100m, 150m, 200m。科氏参数f取为30°N处的值。
陆架宽度分别为100 -500m, 陆架最大深度d1为200m时前三个模态的频散关系如图 2所示。陆架拦截波的频率均低于惯性频率, 属于低频波。高模态的波动频率小。频散曲线顶点对应波数的值基本都在10-5/m以内, 波数小于此的波动认为是长波。陆架越宽, 长波对应波长的范围越小, 陆架宽度为100km时, 波长大于66km即可认为是长波; 而陆架宽度为500km时, 波长需要在200km以上才可以认为是长波。在长波情况下, 陆架越宽, 频散曲线的斜率越大; 而斜率表示波动的相速度, 说明陆架越宽, 相速度越大。在长波情况下, 频散曲线的斜率基本是常数。因此波动的相速度仅由地形及波动模态决定, 与波长及频率无关。而在短波情况下, 陆架宽度对波动的频散关系没有明显的影响。另外, 陆架越宽, 频散曲线的顶点越高而且“陡峭”, 说明在宽陆架上可能观测到比在窄陆架更高频率的波动, 但由于对应于高频率波动的波长范围小, 因此观测到的概率相对较小。
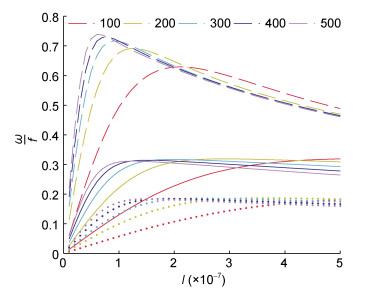 |
| 图 2 陆架宽度为100—500m时陆架拦截波前三个模态的频散关系 Fig. 2 The dispersion relation of the first three modes of the coastal trapped waves 注:虚线、实线、点线分别表示第一、第二、第三模态 |
波动的频散关系决定了特定波形波长和相速度的关系。但上文提到, 在长波假设下, 相速度不再受波长的影响。取定以上参数后, 由频散关系式(3)可求得陆架宽度从50km连续变化到500km对应的前三个模态的自由波相速度(图 3)。其中第一模态陆架拦截波相速度远大于后两个模态, 波动性质类似于Kelvin波, 因此定义第一模态波动为Kelvin波(KW)。后两个模态波动的性质和KW有不同之处, 定义为边界波SW(分别为SW1和SW2)。
 |
| 图 3 自由陆架拦截波第一(a)、第二(b)和第三(c)模态相速度随陆架宽度的变化情况 Fig. 3 The changes in the phase speed of the first three wave modes with the change of continental shelf width 注:深蓝、浅蓝、黄色、红色分别表示陆架宽度为75m, 100m, 150m, 200m时波动的相速度。实线表示方程无辐散(刚盖近似)时求得的相速度, 虚线表示有辐散(自由表面)时的结果 |
单纯的陆架宽度变化对相速度的影响较大。由图 3知KW和SW的相速度均几乎线性地随陆架变宽而变大。陆架的坡度对相速度的影响不大, 但是SW对坡度的敏感性要大于KW。另外, 比较水平辐散(虚线)和水平无辐散(实线)情况下的结果, 当陆架宽度小于200km时, 原始波动方程中水平辐散的存在与否对陆架拦截波的频散性质几乎没有影响。但陆架宽度增加后, 受辐散影响相速度变小。陆架拦截波起主要作用的是第一和第二模态(Brink, 2006), 因此在窄陆架下, 为了分析的方便可以简化原始波动方程为无辐散方程; 而在宽陆架下, 需考虑辐散对波动性质的影响。
过去针对同期不同海区上低频水位的观测研究验证了上述结论。赵保仁等(1987)利用验潮站资料, 观测到在黄海北部的波动相速度约为18-20km/h, 到东海北部沿岸逐渐增至30km/h。陈大可等(1987)利用黄东海验潮站的资料观测到的自由陆架波的传播, 其相速度在南黄海约13-15m/s, 在东海增大到14-15m/s, 在南海又逐渐减小到6m/s。另外, Yin等(2014)利用外海锚系资料观测到的南东海的波动, 靠近长江口陆架宽的区域相速度为16m/s, 而南部相对较窄的区域为14.3m/s。上述结果均表明陆架宽度越大, 相速度越大。
2.2 陆架地形对强迫波的影响 2.2.1 摩擦衰减距离实际海洋中, 波动受海底摩擦影响, 在海表则受到大气强迫以及风应力等的影响, 因此观测到的大部分波动属于强迫波, 或者有能量衰减的自由波。强迫的陆架拦截波的生成、传播机制的理论基础, 目前广泛应用的是Gill等(1974)建立的风生陆架波理论, 重点讨论风应力在陆架拦截波生成传播过程中的作用。但该理论中外强迫的适用范围, 如摩擦对波动耗散的影响、海表面强迫对波动的能量贡献等, 目前没有定量研究。
摩擦衰减距离衡量了波动在底摩擦存在下的传播范围。可以估计某一海区内的波动是自由波占主导还是强迫波占主导。若衰减距离大, 说明波动衰减率小, 传播距离远, 波动很容易受远处自由波的影响。而若衰减距离小, 说明波动耗散大, 波动基本由当地的强迫引起。
取底摩擦系数r为3×10-4m/s, 由式(5a)得各模态的摩擦衰减距离, 反映了波动在空间上的衰减率。衰减距离大说明波动的衰减率小, 即波动的传播范围广。摩擦衰减主要影响高阶模态, 对低阶模态的影响很小。图 4可知对于KW, 摩擦衰减距离几乎线性的随陆架变宽而增大, 而SW的摩擦衰减距离基本不变。因此在存在底摩擦情况下, SW波只能在一定范围内存在, 属于局地波。陆架拦截波水位的变化主要由KW决定, 因此KW的衰减距离决定了方程(4)的积分长度。对于窄陆架上的陆架拦截波, 远处波动到达计算区域时能量已几乎被耗散掉, 因此只需粗略估算出第一模态的摩擦衰减距离, 则可令积分边界为距离计算区域衰减距离处, 并令边界处的波动振幅为零。但宽陆架上的模拟, 衰减距离都在上千km以上, 计算区域的波动一般是当地强迫波和远处传播波动相互作用的结果, 需要预知边界处的运动情况。如图 4所示, 当陆架宽度大于120km时, KW的衰减距离大于1000km, 可认为计算或观测区域的陆架拦截波非局地波动。
 |
| 图 4 前三个模态陆架拦截波的摩擦衰减距离随陆架宽度的变化 Fig. 4 The frictional decay with different shelf width |
方程(4)右端项是陆架拦截波的强迫源, 分别表示沿岸风应力、大气强迫和风应力旋度。在一般风生陆架拦截波理论框架下, 沿岸风应力起绝对主导作用。现有对陆架上低频水文特征的模拟研究, 也只考虑了风应力的贡献而不考虑后两项。但是Yin等(2014)对东海陆架拦截波的研究发现, 在加入了风应力旋度项后的风生陆架拦截波模型对东海陆架拦截波的模拟能力有很大提高。适用于大部分陆架海区的窄陆架风生模型中波动只受沿岸处顺岸向风应力的影响, 与此不同的是, 东海的陆架拦截波动很大程度上依赖于风应力旋度的贡献。而从方程(4)可知, 风应力对陆架拦截波的影响只限于其在沿岸值的大小, 和陆架地形无关; 而大气强迫和风应力旋度则需要在整个陆架断面上积分, 陆架宽度直接影响到它们对陆架拦截波贡献的大小。
为分析三个强迫项在陆架拦截波机制中的作用, 分别设计了四组实验。控制实验包含所有三个强迫项, 对比实验一、二、三分别令大气强迫、风应力旋度、沿岸风应力为零。结果图 5所示。
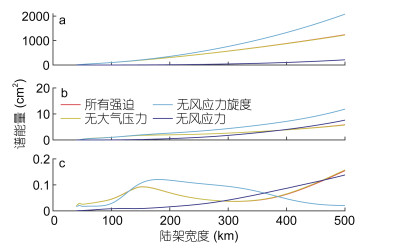 |
| 图 5 模拟前三个模态波动的总能量随陆架宽度变化 Fig. 5 The totalenergy of the first three mode with different shelf width and different forcing sources |
沿岸风应力是陆架拦截波最主要的能量来源, 特别是陆架宽度小于200km时, 表面强迫可以只考虑风应力而不考虑其他项。但若陆架宽度大于200km, 风应力旋度给予前两个模态波动的能量占总能量的比重随陆架宽度的增加而逐渐增大。在陆架宽度达到500km时, 其贡献几乎和沿岸风应力相当。风应力旋度对SW2的能量贡献没有明显规律可循, 但在整个实验的陆架宽度范围内, 风应力旋度对波动能量的贡献显著。陆架拦截波动中, KW占据了90%以上的水位变化和40%以上的顺岸流变化, SW1占据了40%以上的沿岸流变化(Mysak, 1980)。可见在宽陆架情况下, 若忽略风应力旋度对陆架拦截波生成的贡献, 势必造成对水位和顺岸流模拟的偏差。大气强迫的作用可以忽略, 在所讨论的陆架宽度范围内, 大气强迫几乎对波动能量没有贡献。
2007年1月至3月期间, 在东海进行了锚系水位观测。利用该观测数据, Yin等(2014)分析发现东海低频水位变化可用陆架波解释。求解强迫陆架波的公式(3-5), 得到模拟的低频水位变化, 结果和观测水位的低频变化吻合, 相关性可达0.8以上。本文利用此数据, 分析公式(4)中三个外力强迫对水位变化的影响。观测站位、观测数据的信息见Yin等(2014)。
模拟的时间区间为2007年1月1日至2017年3月31日。所用同期风场和大气压强从NCAR数据中心获取(https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.surfaceflux.html)。实验分别计算了所有强迫都存在、无风应力旋度、无大气压力和无顺岸向风应力情况下水位变化的时间序列。其中, 所有强迫都存在时的结果已被证实和观测结果基本一致(Yin等, 2014)。图 6显示四种情况下三个月水位时间序列的波动谱密度和波动能量密度在所有频率上的积分。冬季寒潮天气下, 天气原因引起的水位变化为低频波(周期大于一天), 能量主要集中在周期为3-5天的波动上。顺岸向风应力消失后, 从能量密度图可以看出波动能量大大减小, 顺岸向风应力是引起东海低频水位变化的主要原因。风应力旋度作用也较重要, 其消失后3-5天周期波动能量密度的减少量大约为顺岸向风应力引起水位波动的能量密度的一半。而大气压强对水位变化基本没有贡献。为分析三个月期间三种外力强迫对水位总的贡献, 对能量密度在所有频率上进行积分。图 6柱状图显示了各外力强迫下, 低频波动的总能量。图 6可以看出, 若方程(4)中不考虑风应力旋度, 两个站位水位波动总能量比所有强迫都考虑时分别减少了18%和17%;而若顺岸向风应力消失, 能量分别减少32%和33%;大气压强使得能量减少分别为4%和5%。可见在东海陆架地形下, 在冬季寒潮暴发期间, 风应力旋度引起水位的变化, 其作用可达到顺岸向风应力引起的水位变化的一半。
 |
| 图 6 包含所有外强迫力(红色)、无风应力旋度(青色)、无岸线处顺岸向风应力(黄色)以及无大气压力变化(蓝色)情况下, 由公式(3—5)模拟得到的东海JZ0604(a、c)和JZ0903(b、d)两个站点(Yin等, 2014)在2007年1月1日至3月31日期间低频水位变化的能量谱密度(a、b)和总能量(c、d) Fig. 6 The power spectral density of simulated sea level fluctuation from 1 Jan. 2007 to 31 Mar. 2007 (a, b) and the whole power spectral of all frequencies that are lower than 1 cpd (c, d). Experiments were run under the conditions of: all the forces included (red), zero wind stress curl (cyan), zero time derivative of the atmosphere pressure (yellow), and zero alongshore wind stress (blue) |
过去针对窄陆架上陆架波的研究, 几乎都认为陆架波的能量来源是顺岸向的风应力。如Brink(2006)在针对风生陆架波的综述中, 只考虑了顺岸向风应力; Jordi(2005)针对地中海东北部陆架拦截波的模拟, 同样只考虑顺岸向风应力得到了很好的结果。而在陆架宽广的东海, 顺岸向风应力和风应力旋度均对陆架拦截波的生成传播有贡献。
3 小结本文基于陆架拦截波理论, 计算了分段线性地形下陆架拦截波前三个模态的频散关系、长波假设下波动的相速度、阻尼情况下的波动耗散率以及强迫波的外力影响因子。分析了分段线性陆架地形下的陆架宽度及坡度对自由及强迫陆架拦截波性质的影响。并利用实际观测数据和模拟比较, 验证了风应力旋度在强迫波生成机制的作用。研究表明, 波动性质受陆架宽度的影响很大。
陆架宽度影响陆架拦截波的频散关系。陆架变宽, 使得波动的最高频率增大, 长波频散曲线的斜率增大。长陆架拦截波的相速度随陆架宽度的增加而增大, 而坡度对相速度的影响很小。宽陆架情况下, KW受辐散影响相速度减小, 而SW几乎不受辐散影响, 但SW对陆架坡度的敏感性大于KW。随着陆架宽度增加, KW的摩擦衰减距离增大。SW的摩擦衰减距离则不受陆架宽度的影响。对于强迫陆架拦截波, 沿岸风应力是陆架拦截波的主要能量来源。陆架宽度的增加使得风应力旋度的重要性逐渐增大, 即在宽陆架地形下, 应充分考虑风应力旋度对于低频水位变化的影响。而大气强迫对陆架拦截波的生成几乎无影响。
综上, 宽陆架上的波动特征及机制, 应区别于窄陆架。200km左右是分析陆架拦截波的一个临界宽度。小于这个宽度的陆架上, 可以近似认为波动水平无辐散, 这为理论分析提供了便利; 此宽度以下, 表面强迫可仅考虑沿岸风应力而忽略大气强迫和风应力旋度的作用, 方便数值计算。而在大于200km的陆架上, 由于必须引入幅散以及多种外界强迫的影响, 研究陆架拦截波比较复杂性。若陆架宽度窄于120km, 第一模态波动的衰减距离小于1000km, 说明波动在传播此段距离后能量衰减至零。因而在计算某处海区的波动时, 只需考虑当地的强迫作用, 不用考虑远处自由波的输入。
| 冯士筰, 1979. F-平面上的宽陆架诱导阻尼波. 海洋学报, 1(2): 177–192 |
| 冯立成, 巢纪平, 2013. 非线性陆架坡度作用下的陆架地形波. 中国科学:地球科学, 43(3): 499–502 |
| 李晓红, 董礼先, 2011. 冬季寒潮期间黄、渤海水位低频波动研究. 海洋与湖沼, 42(4): 467–473 DOI:10.11693/hyhz201104001001 |
| 陈大可, 苏纪兰, 1987. 中国沿岸陆架波的初步研究. 海洋学报, 9(1): 1–15 |
| 赵保仁, 曹德明, 1987. 冬季黄、东海中国沿岸水位的低频波动. 海洋与湖沼, 1(6): 563–574 |
| 秦曾灏, 刘秦玉, 1988. 摩擦和β效应对地形拦截波的影响. 海洋与湖沼, 19(1): 8–17 |
| Brink K H, 1991. Coastal-trapped waves and wind-driven currents over the continental shelf. Annual Review of Fluid Mechanics, 23(1): 389–412 DOI:10.1146/annurev.fl.23.010191.002133 |
| Brink K H, 2006. Coastal-trapped waves with finite bottom friction. Dynamics of Atmospheres and Oceans, 41(3-4): 172–190 DOI:10.1016/j.dynatmoce.2006.05.001 |
| Clarke A J, Van Gorder S, 1986. A method for estimating wind-driven frictional, time-dependent, stratified shelf and slope water flow. Journal of Physical Oceanography, 16(6): 1013–1028 DOI:10.1175/1520-0485(1986)016<1013:AMFEWD>2.0.CO;2 |
| Ding Y, Bao X W, Shi M C, 2012. Characteristics of coastal trapped waves along the northern coast of the South China Sea during year 1990. Ocean Dynamics, 62(9): 1259–1285 DOI:10.1007/s10236-012-0563-3 |
| Drivdal M, Weber J E H, Debernard J B, 2015. Dispersion relation for continental shelf waves when the shallow shelf part has an arbitrary width:Application to the shelf west of Norway. Journal of Physical Oceanography, 46(2): 537–549 |
| Fukudome K I, Igeta Y, Senjyu T, et al, 2016. Spatiotemporal current variation of coastal-trapped waves west of the Noto Peninsula measured by using fishing boats. Continental Shelf Research, 115: 1–13 DOI:10.1016/j.csr.2015.12.013 |
| Gill A E, Schumann E H, 1974. The generation of long shelf waves by the wind. Journal of Physical Oceanography, 4(1): 83–90 DOI:10.1175/1520-0485(1974)004<0083:TGOLSW>2.0.CO;2 |
| Igeta Y, Yamazaki K, Watanabe T, 2015. Amplification of coastal-trapped waves resonantly generated by wind around Sado Island, Japan. Journal of Oceanography, 71(1): 41–51 DOI:10.1007/s10872-014-0259-z |
| Jordi A, Orfila A, Basterretxea G, et al, 2005. Coastal trapped waves in the northwestern Mediterranean. Continental Shelf Research, 25(2): 185–196 DOI:10.1016/j.csr.2004.09.012 |
| Li J Y, Zheng Q A, Hu J Y, et al, 2015. Wavelet analysis of coastal-trapped waves along the China coast generated by winter storms in 2008. Acta Oceanologica Sinica, 34(11): 22–31 DOI:10.1007/s13131-015-0701-0 |
| Mitchum G T, Clarke A J, 1986. Evaluation of frictional, win-forced long-wave theory on the west Florida shelf. Journal of Physical Oceanography, 16(6): 1029–1037 DOI:10.1175/1520-0485(1986)016<1029:EOFWFL>2.0.CO;2 |
| Mysak L A, 1980. Recent advances in shelf wave dynamics. Reviews of Geophysics, 18(1): 211–241 DOI:10.1029/RG018i001p00211 |
| Platov G A, 2016. The influence of shelf zone topography and coastline geometry on coastal trapped waves. Numerical Analysis and Applications, 9(3): 231–245 DOI:10.1134/S1995423916030058 |
| Sansón L Z, 2011. Simple models of coastal-trapped waves based on the shape of the bottom topography. Journal of Physical Oceanography, 42(3): 420–429 |
| Schulz W J Jr, Mied R P, Snow C M, 2011. Continental shelf wave propagation in the mid-atlantic bight:a general dispersion relation. Journal of Physical Oceanography, 42(4): 558–568 |
| Schumann E H, Brink K H, 1990. Coastal-trapped waves off the coast of south Africa:generation, propagation and current structures. Journal of Physical Oceanography, 20(8): 1206–1218 DOI:10.1175/1520-0485(1990)020<1206:CTWOTC>2.0.CO;2 |
| Serrano M A, Díez-Minguito M, Ortega-Sánchez M, et al, 2015. Continental shelf waves on the Alborán sea. Continental Shelf Research, 111: 1–8 DOI:10.1016/j.csr.2015.11.004 |
| Wilkin J L, Chapman D C, 1990. Scattering of coastal-trapped waves by irregularities in coastline and topography. Journal of Physical Oceanography, 20(3): 396–422 DOI:10.1175/1520-0485(1990)020<0396:SOCTWB>2.0.CO;2 |
| Yin L P, Qiao F L, Zheng Q A, 2014. Coastal-trapped waves in the East China sea observed by a mooring array in Winter 2006. Journal of Physical Oceanography, 44(2): 576–590 DOI:10.1175/JPO-D-13-07.1 |
| Zheng Q A, Zhu B L, Li J Y, et al, 2014. Growth and dissipation of typhoon-forced solitary continental shelf waves in the northern South China Sea. Climate Dynamics, 45(3-4): 1–13 |
 2018, Vol. 49
2018, Vol. 49


