中国海洋湖沼学会主办。
文章信息
- 姜锦东, 方国洪, 滕飞, 徐晓庆. 2018.
- JIANG Jin-Dong, FANG Guo-Hong, TENG Fei, XU Xiao-Qing. 2018.
- 内潮耗散与自吸-负荷潮对南海潮波影响的数值研究
- DISSIPATION AND SELF-ATTRACTION-AND LOADING OF INTERNAL TIDES: IMPACT ON THE TIDAL WAVES IN THE SOUTH CHINA SEA
- 海洋与湖沼, 49(3): 457-470
- Oceanologia et Limnologia Sinica, 49(3): 457-470.
- http://dx.doi.org/10.11693/hyhz20171200316
-
文章历史
- 收稿日期:2017-12-17
- 收修改稿日期:2018-01-25
2. 青岛海洋科学与技术国家实验室区域海洋动力学与数值模拟功能实验室 青岛 266200
2. Laboratory for Regional Oceanography and Numerical Modeling, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266200, China
南海是位于我国大陆南端的陆缘海, 南海北部通过台湾海峡与东海相连, 东北部通过吕宋海峡与太平洋相邻, 南部通过卡里马塔海峡与爪哇海相连, 东南部通过民都洛海峡和巴拉巴克海峡与苏禄海相连, 西南部通过马六甲海峡与印度洋相通, 是沟通太平洋和印度洋的重要通道之一(图 1)。南海及其周边海域水深变化较大, 岸线曲折, 且包含的岛礁众多, 尤其是南海海域内包含了东沙群岛和台湾浅滩, 地形变化剧烈, 这些因素使得南海的潮汐潮流运动及潮汐能量的耗散十分复杂。
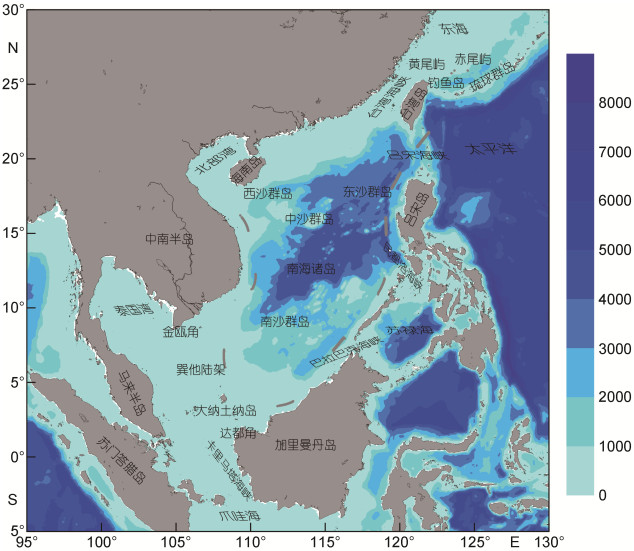 |
| 图 1 研究海域水深(单位: m) Fig. 1 Study area and the bathymetry(unit: m) |
关于南海潮汐潮流的研究, 最早是基于沿岸和岛屿上的观测资料展开的。俞慕耕(1984)利用320个验潮站的调和常数绘制了南海海域同潮图的, 较好的展现了南海潮汐分布规律。曹德明等(1997)采用200多个沿岸及岛屿的验潮站调和常数资料绘制了南沙及其西南海域M2、S2、K1、O1四个主要分潮的同潮图。随着计算机技术的进步, 数值模式计算得到蓬勃发展。Ye等(1983)首次利用数值模式模拟了南海的M2和K1分潮, 给出了同潮图及潮能通量分布图。沈育疆等(1985)计算了M2、S2、K1和O1四个主要的分潮, 给出了分潮同潮图并讨论了潮波分布。方国洪等(1994)采用二维球坐标数值模式计算了南海M1和M2分潮, 模拟效果良好, 给出了潮汐、潮流、潮余流及潮能通量分布图。Fang等(1999)进一步计算了南海M2、S2、K1和O1分潮并给出了潮汐潮流及潮能通量的分布特征。Cai等(2006)研究了不同开边界条件对模拟结果的影响。以上的南海潮波数值模拟研究都只考虑了底摩擦耗散而未考虑南海内潮耗散的影响。Egbert等(2000)的研究结果表明潮能不仅仅通过浅水区域的底摩擦进行耗散, 同样可以通过表面潮向内潮的转换的方式在深水区域发生耗散。而南海作为内潮的多发区, 内潮耗散对南海潮波系统产生的影响不容忽视。对于南海的内潮耗散前人已进行了大量的研究(例如见Gao et al, 2015; Wang et al, 2016)。此外, 自吸-负荷潮在潮汐模拟中同样十分重要(Ray, 1998)。虽然自吸-负荷潮的振幅与平衡潮的振幅相比较小, 但由于自吸-负荷潮波长短, 它所引起的水平梯度力则可能和引潮力的水平分量相近, 甚至大于引潮力的水平分量(Fang et al, 2013)。因此本研究在对南海潮汐进行模拟时, 同时考虑了引潮力和自吸-负荷潮的影响。
本文采用Chen等(2006)提出的有限体积FVCOM海洋数值模式, 并在二维潮波方程中引入参数化的内潮耗散项和自吸-负荷潮项。模式所用网格为非结构三角形网格, 可以有针对性的对南海的岛屿、海峡和大陆沿岸等地形复杂的区域进行网格加密处理, 以提高模式对于复杂地形的模拟效果。模式同时对南海M2、S2、K1和O1分潮进行模拟, 所得到的调和常数与沿岸的63个验潮站的调和常数资料进行对比验证。根据模式结果, 分析了南海及其周边海域的潮汐潮流的分布特征和潮波的传播特征及潮汐能量的耗散情况。
1 数值模式与参数设置 1.1 基本方程由于计算海域范围较大, 模拟时需考虑不同纬度所引起的科氏力变化, 采用球坐标方程, 并在动量方程中加入参数化的内潮耗散项和自吸-负荷潮项。加入参数化的内潮耗散项和自吸-负荷潮项后的方程具有如下形式:
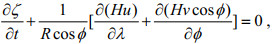 (1)
(1)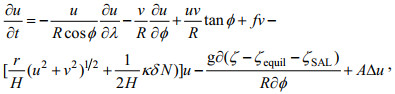 (2)
(2)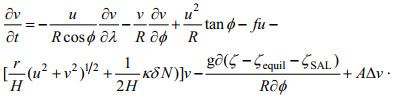 (3)
(3)式中, R为地球半径, λ和φ代表经度和纬度, H代表总水深, ζ为相对于未扰动海面的潮汐高度, t为时间, ζequil为考虑了地球体潮后的平衡潮高, ζSAL为自吸-负荷潮高, u和v分别表示东向和北向速度, f表示科氏参数, g为地球重力加速度, A表示水平涡动黏性系数。上式中平衡潮等于
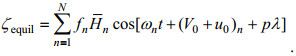 (4)
(4)其中, 对于全日潮p=1, 对于半日潮p=2, 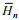
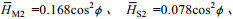
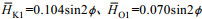
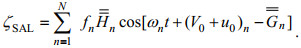 (5)
(5)式中, 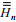
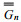
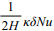
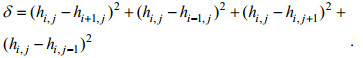 (6)
(6)式中, hi, j为第(i, j)个网格点水深。hi+1, j, hi-1, j,hi, j+1和hi, j-1分别为第(i, j)个网格点相邻的四个网格点的水深。
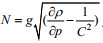
本文模拟海域范围为1°—28°N, 99°—125°E, 包含南海及其周边海域。计算所用网格在岛屿及陆地沿岸进行了加密处理。岸线及岛屿附近网格的平均分辨率为1/20度, 外海及开边界附近网格平均分辨率大约为1/3度。计算网格共包含31418个节点, 60358个三角单元(图 2)。FVCOM的二维数值格式是基于三角形网格的有限体积法, 将连续方程和动量方程在三角形单元内积分后, 通过改进的四阶龙格库塔方法求解。本计算中时间步长取6s;初始条件取海表面的扰动水位全部为0, 所有网格中心点的流速u=v=0。本模式海域共设有4个开边界, 开边界上每个点的水位考虑了M2, S2, K1和O1四个分潮, 由T-tide的预报程序给出(Pawlowicz et al, 2002), 其中的调和常数取自DTUl0数据(Cheng et al, 2011)。模式运行90d, 对后30d时间序列进行调和分析, 得到网格点上水位的调和常数和每个三角形中心点的潮流各分量的调和常数和椭圆要素。
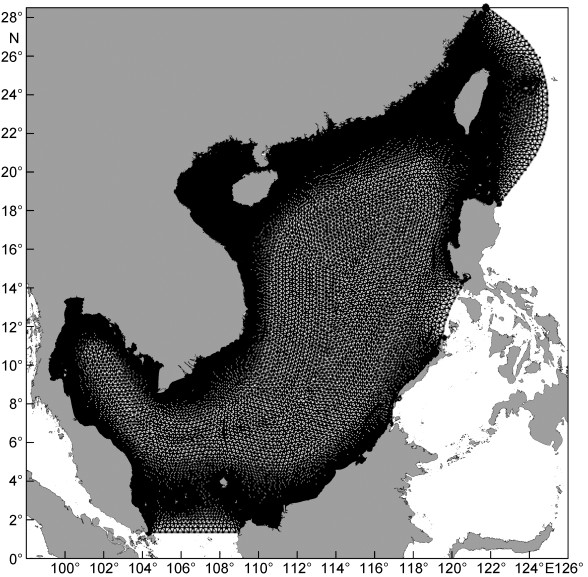 |
| 图 2 计算网格 Fig. 2 computation grids |
对于一个给定的分潮, 其模拟值与观测值之间偏差的评估有多种方式, 其中以各分潮振幅和迟角的绝均差最为直观, 具体的计算公式为:
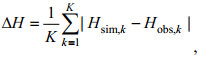 (7)
(7)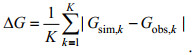 (8)
(8)式中, H为振幅, G为迟角, 下标sim和obs分别代表模拟值和观测值, K为观测站总个数。但是当振幅H值较小时, 计算和观测的迟角值都不稳定; 同时当振幅H值较小时, 迟角的误差对潮高误差的影响也较小, 不考虑振幅大小的差别而直接将迟角差进行平均存在很大的不确定性。由此我们采用模式所得调和常数和实测调和常数的向量均方根(RMS)偏差σ作为模拟结果准确度的代表量, 其计算公式如下:
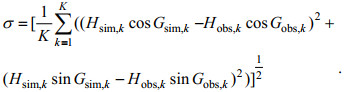 (9)
(9)由于该式σ的计算考虑了分潮振幅和相位的共同影响, 使模拟效果的评估更加合理。四个分潮总体准确度可以用各个分潮σ值的均方根σ来评价, σ值越小代表偏差越小, 模拟结果越好。
1.4 模式参数选取水深的选取对潮汐模拟十分重要。我们比较了现有的格点化水深数据ETOPO1, ETOPO5, GEBCO_08, 林美华等(1999)数据表及海图数据在南海的水深分布, 发现它们在深水区一致性较好, 但浅水区域的一致性较差。对于陆架海域, 海图水深数据的准确性一般要高于国外现有的地形数据集(吴頔等, 2015)。本文采用的水深数据主体为林美华等(1999)的南海水深数据集, 该数据集的分辨率为5′的格点化海图水深数据, 对于该数据集没有覆盖到的区域我们使用GEBCO_ 08水深数据加以补充。对于底摩擦系数和内潮耗散系数, 我们采用Teng等(2017)的方法。该方法的基本做法是选取不同的(r, κ)参数组合进行数值试验, 并比较在各种(r, κ)组合下得到的σ值, 并认为当σ达最小时对应的(r, κ)最好。在这个过程中, σ可称为成本函数。由以往的经验我们可以估计底摩擦系数r处于0.001到0.004之间, 内潮耗散系数κ在6×10-6到1.2×10–5之间(Egbert et al, 2000)。我们首先在这个范围r以0.5×10–3, κ以1×10–6为间隔进行了49组试验来初步确定r和κ的取值与σ的关系(图 3), 通过对比不同试验所得到的发现当r和κ分别为0.0025和9×10-6时σ值最小。之后我们以这个点为基准采用加密了的间隔又进行了多组试验, 发现当底摩擦系数r值为0.0024, 内潮耗散系数κ值为9.2×10–6时σ值最小而在最终的模拟中予以采用。
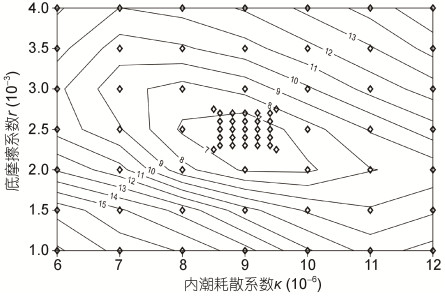 |
| 图 3 成本函数σ与参数组合(r, κ)的关系 Fig. 3 Dependence of the cost function σ on the parameter combination(r, κ) |
为了对模式模拟结果进行验证, 本文将模式结果与验潮站资料进行了比较。我们选用了计算海域内与Fang等(1999)相同的63个验潮站的调和常数, 与相应的模拟结果进行了对比(由于篇幅限制对比表从略)。表 1给出了各验潮站四个分潮调和常数观测值和模拟结果之间偏差绝对值的平均值。由表可见, M2、S2、K1和O1四个分潮的振幅和迟角绝均差分别为4.9cm, 6.2°; 2.3cm, 11.3°; 3.9cm, 6.0°和3.7cm, 6.8°。与Fang等(1999)的模拟结果相比较, 偏差总体上有明显降低(它们对应的偏差分别为6.5cm, 9.9°; 2.7cm, 17.8°; 4.6cm, 8.7°和3.0cm, 10.6°)。这说明引入内潮耗散与自吸-负荷潮并配之以较高模式分辨率可以明显改进数模结果。
| M2 | S2 | K1 | O1 | ||||||||
| 振幅(cm) | 迟角(°) | 振幅(cm) | 迟角(°) | 振幅(cm) | 迟角(°) | 振幅(cm) | 迟角(°) | ||||
| 绝均差 | 4.9 | 6.2 | 2.3 | 11.3 | 3.9 | 6.0 | 3.7 | 6.8 | |||
图 4—7分别为各个分潮的同潮图(虚线为等振幅线, 单位为cm, 实线为等迟角线, 时间采用东8时区)。由图 4可知, 南海M2分潮潮波经由吕宋海峡传入南海, 潮波的主要部分向南海内部传播, 少部分向北转入台湾海峡。M2分潮在进入台湾海峡后与来自东海方向的潮波相遇, 由于来自南海方向的分潮振幅小于东海方向的分潮振幅, 造成台湾海峡处振幅等值线非常密集, 最大振幅出现在海峡的西北部, 超过2m。第二大振幅出现在加里曼丹岛西北岸的南部, 达1.6m以上。在北部湾湾内形成一个退化的无潮点, 湾内分潮振幅较小。M2分潮在泰国湾湾口存在一个顺时针旋转的无潮点, 无潮点位置与Fang等(1999)的结果基本一致。M2分潮在金瓯角东北方沿岸有1m左右的振幅。
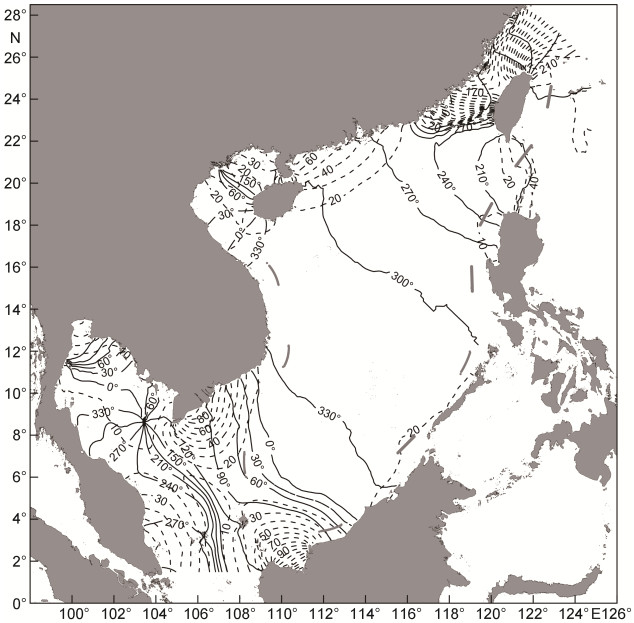 |
| 图 4 M2分潮同潮图 Fig. 4 Simulated cotidal chart for M2 |
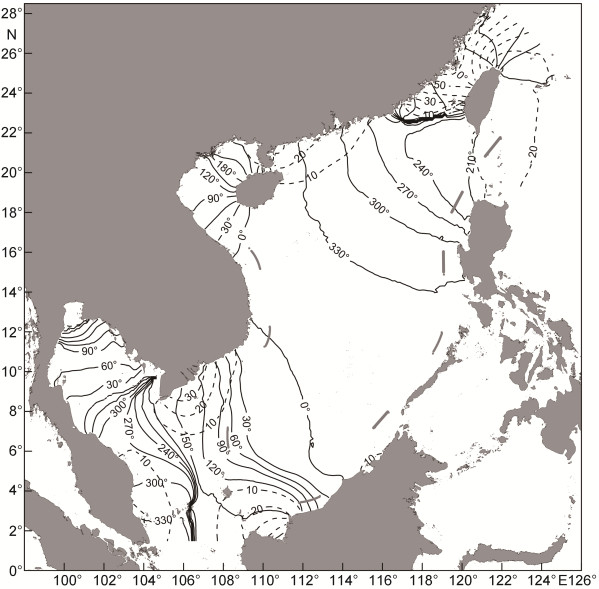 |
| 图 5 S2分潮同潮图 Fig. 5 Simulated cotidal chart for S2 |
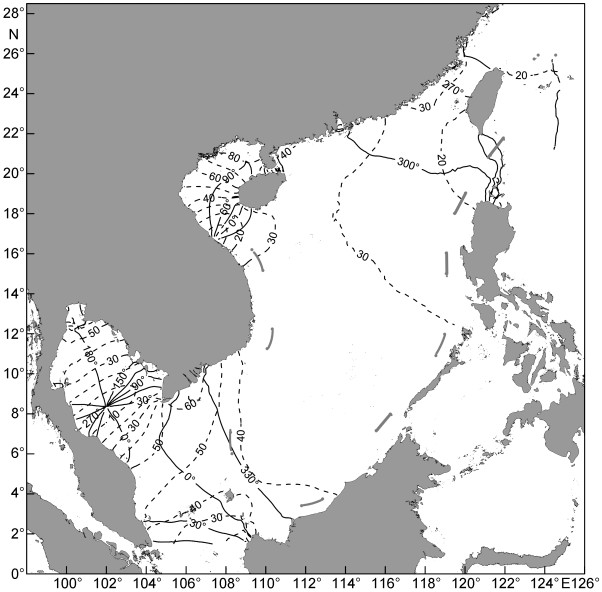 |
| 图 6 K1分潮同潮图 Fig. 6 Simulated cotidal chart for K1 |
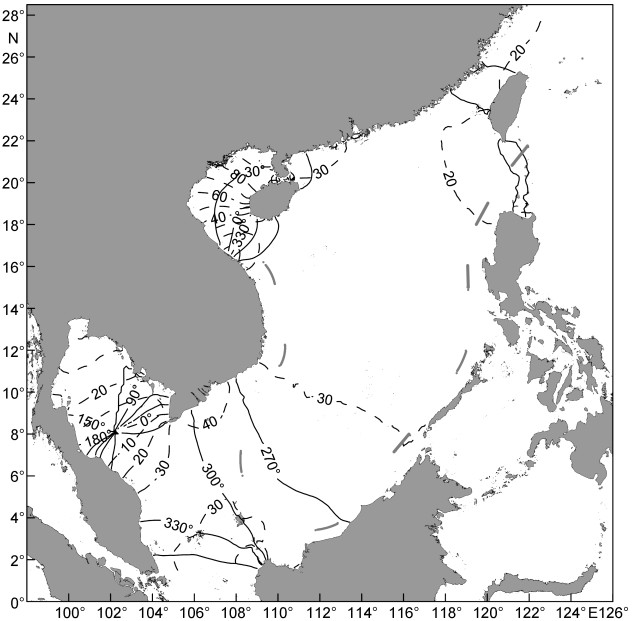 |
| 图 7 O1分潮同潮图 Fig. 7 Simulated cotidal chart for O1 |
S2分潮的分布在南海的大部分海域都与M2分潮相一致, 但是振幅相对于M2分潮来说小很多。与M2分潮相比, S2分潮在泰国湾湾口附近存在一个退化的无潮点而在大纳土纳岛西北方向没有无潮点出现, 这与Fang等(1999)的结果不同, 但和毛庆文等(2006)利用卫星高度计进行调和分析所得的结果相符合。
全日潮K1分潮和O1分潮有相似的潮波系统。与半日潮相同, 全日潮潮波同样是由吕宋海峡传入并由东北向西南方向传播, 但在台湾海峡处全日潮没有出现北向的传播。在泰国湾内K1分潮和O1分潮均有一个完整的逆时针方向旋转的潮波系统。K1分潮和O1分潮都是在北部湾湾顶位置振幅达到最大, 最大值都达到了0.8m以上, 且O1分潮振幅略大于K1。这是由于北部湾的O1分潮周期更接近于自由振荡周期, 使O1分潮潮波在北部湾产生共振, 从而使得O1分潮的振幅增强。
3.2 潮流分布图 8和图 9分别为M2和K1分潮的潮流椭圆分布。对于M2分潮, 台湾海峡、金瓯角和达都湾附近潮流较大, 南海中央深水区潮流较小。台湾海峡北部大部分区域, 金瓯角附近海域和泰国湾湾顶为逆时针旋转。
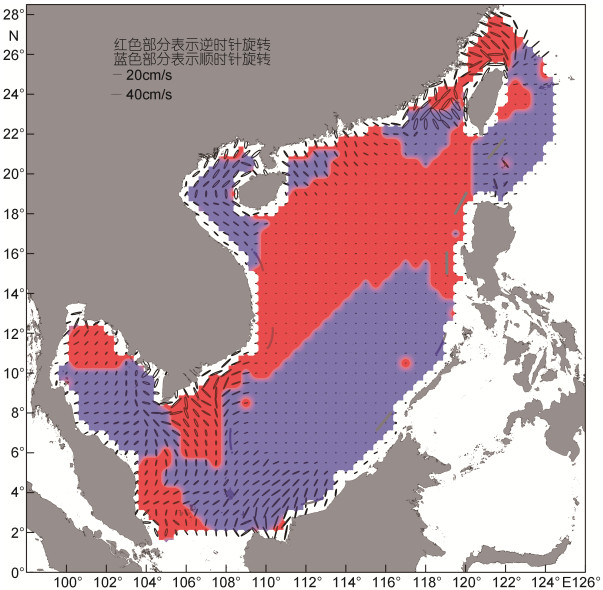 |
| 图 8 M2分潮潮流椭圆 Fig. 8 M2 current ellipses |
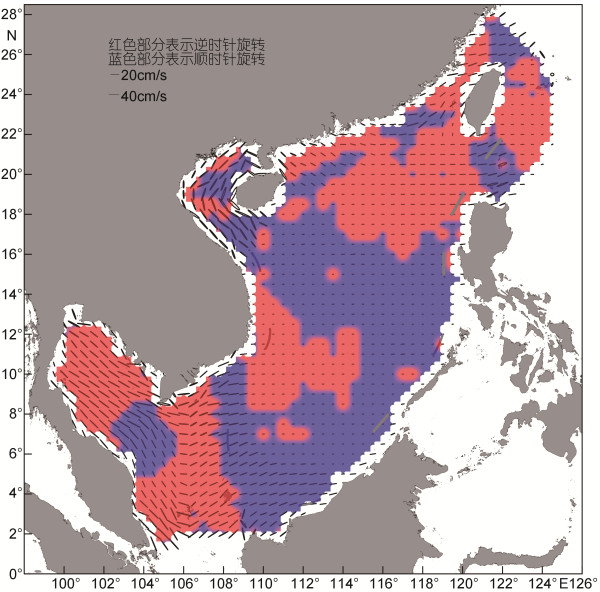 |
| 图 9 K1分潮潮流椭圆 Fig. 9 K1 current ellipses |
对于K1分潮, 在泰国湾和北部湾海域的潮流流速较大。北部湾大部分区域为顺时针旋转, 泰国湾湾口附近为顺时针旋转, 湾内为逆时针旋转。
4 潮汐能量平衡为了探究控制方程中各项的作用, 我们分析了南海的潮能平衡。对于潮汐能量前人已进行过大量的研究(Garrett, 1975; Fang et al, 1999; Zu et al, 2008; 佟景全等, 2010), 其中Fang等(1999)给出的潮能平衡方程较为完整。本文在其基础上进一步加入内潮耗散和自吸-负荷潮项, 具体方法如下。首先对方程中的各非线性项进行Fourier展开, 其展开式如下:
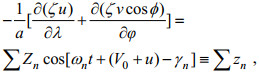 (10)
(10)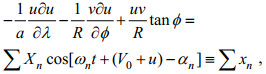 (11)
(11)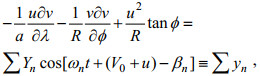 (12)
(12)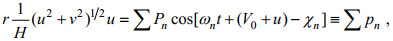 (13)
(13)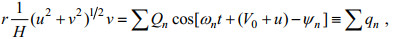 (14)
(14)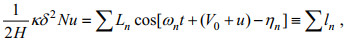 (15)
(15)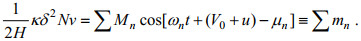 (16)
(16)从而对一特定分潮n, 二维潮波方程变为如下形式:
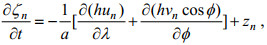 (17)
(17)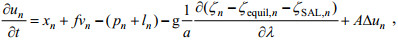 (18)
(18)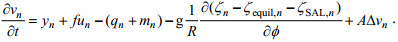 (19)
(19)上列诸式中a=Rcosϕ。对方程(17)~(19)分别乘以ρgζ, ρhu和ρhv后再相加(省略分潮符号n), 然后对其进行周期平均并在研究区域G上作积分后可得到如下等式:
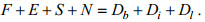 (20)
(20)式中, S和Di为本研究在Fang等(1999)基础上增加的自吸-负荷潮项和内潮耗散项。上式左边为能量输入项, 右边为消耗项, 各项的具体计算公式如下:
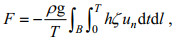 (21)
(21)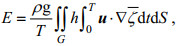 (22)
(22)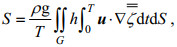 (23)
(23)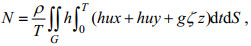 (24)
(24)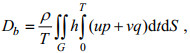 (25)
(25)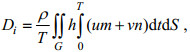 (26)
(26)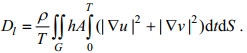 (27)
(27)其中, B为区域G的开边界, u为潮流向量, un为与边界B垂直的潮流分量。
潮能通量表示单位时间内通过单位宽度的垂直断面的能量通量, 又称能通强度或能通量密度。M2分潮与K1分潮的能通量密度如图 10和图 11所示, 其中矢量箭头为潮能通量方向, 填充色表示潮能通量的大小。计算得到的潮能通量与Fang等(1999)和Zu等(2008)的结果基本一致。从图中可以看出, M2和K1分潮的潮能通量最大值都是出现在吕宋海峡, 然后向西南方向输送, 沿途并有部分潮能分别进入北部湾和泰国湾。M2分潮在台湾海峡有较强的南向能通量, 但在台湾海峡西南部有从吕宋海峡沿台湾西南岸向北的能通量。台湾海峡中K1分潮能通量则很弱, 且不存在沿台湾西南岸向北的能通量。
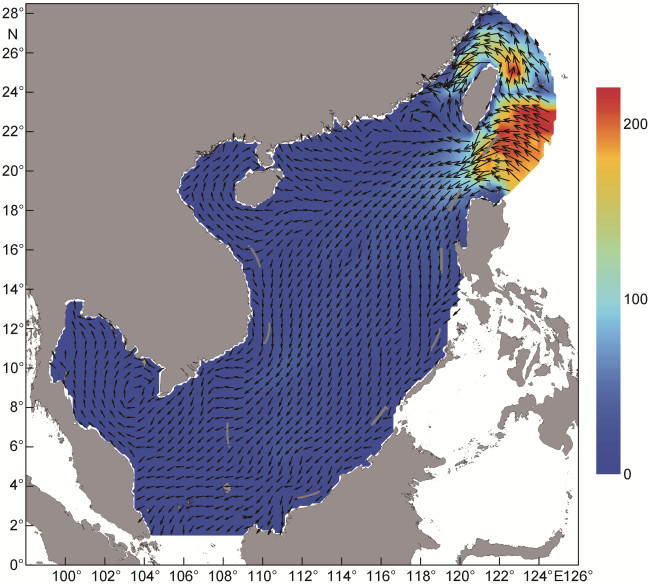 |
| 图 10 M2分潮能通量密度分布图(单位: kW/m) Fig. 10 The energy flux density vectors of tidal constituent M2 (kW/m) |
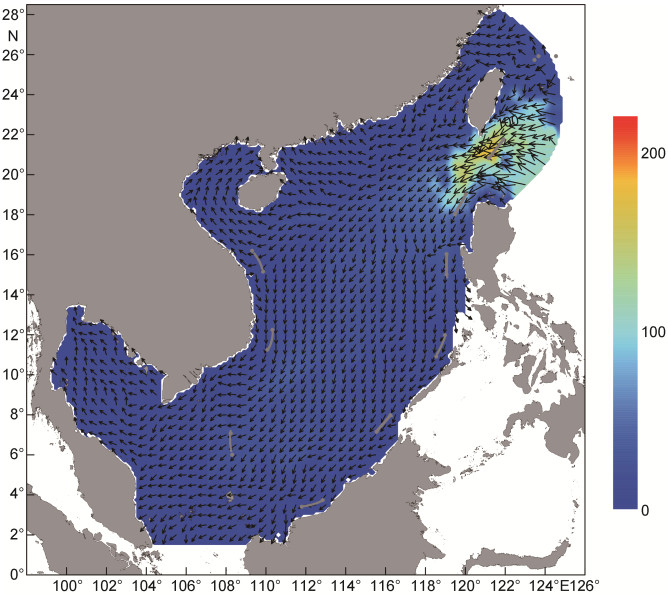 |
| 图 11 K1分潮能通量密度分布图(单位: kW/m) Fig. 11 The energy flux density vectors of tidal constituent K1(kW/m) |
为了分析南海潮汐能量收支, 我们将研究海域划分出G1—G6等6个分区(图 12), 分别代表台湾海峡、吕宋海峡西部、南海深水区、北部湾、泰国湾和位于南海之外的吕宋海峡东部。其中分区G2和G6与Zu等(2008)的关注区域(见该文图 10a)一致, 以便于比较。各分区的边界分别用B1—B15表示。
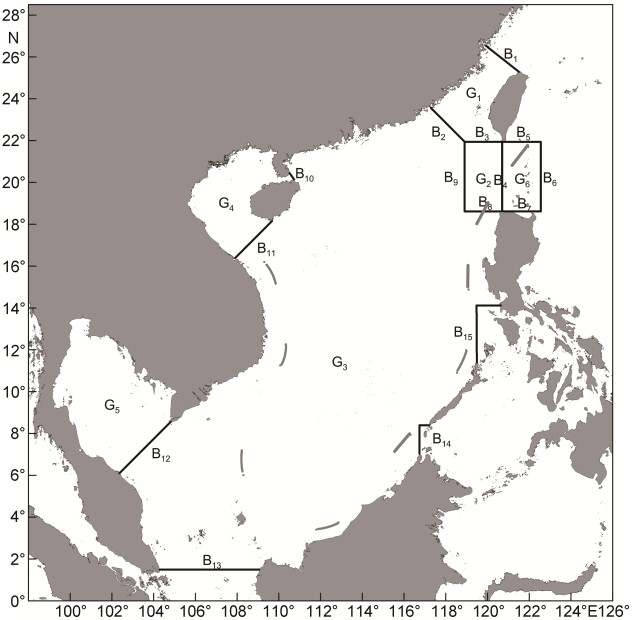 |
| 图 12 南海潮汐能量收支估算的分区图 Fig. 12 Divisions of the South China Sea in estimating tidal energy budget |
根据模式计算结果我们得到计算所得通过B1—B15边界的潮能通量如表 2所示。由表可知南海潮汐主要是由西北太平洋通过吕宋海峡传输进入的潮能通量来维持的。M2、S2、K1和O1分潮通过吕宋海峡B4断面(图 12)进入南海的能通量分别为38.1, 4.5, 29.1和22.9GW。尽管M2分潮通过B1进入台湾海峡的潮汐能量也很大, 但由B2和B3的潮能通量值可见, 它们都是流入台湾海峡而不是流出, 因此从B1输入的潮能几乎都在台湾海峡内部耗散掉。与M2分潮相比K1分潮能通量在B2处的方向与之相反而在B3处与之方向相同, 故来自东海的K1分潮能通量经过台湾海峡后有少量流入南海。
| 断面编号 | 通量正方向 | M2 | S2 | K1 | O1 | 合计 |
| B1 | 西南 | 16.59 | 1.49 | 0.67 | 0.49 | 19.24 |
| B2 | 东北 | 1.04 | 0.12 | –0.87 | –0.58 | –0.29 |
| B3 | 北 | 6.67 | 0.54 | 0.57 | 0.38 | 8.16 |
| B4 | 西 | 38.06 | 4.52 | 29.05 | 22.93 | 94.56 |
| B5 | 南 | 3.64 | 0.41 | 6.46 | 3.38 | 13.89 |
| B6 | 西 | 42.55 | 5.19 | 32.33 | 25.88 | 105.95 |
| B7 | 北 | 4.18 | 0.56 | 2.71 | 1.94 | 9.39 |
| B8 | 南 | 6.12 | 0.77 | 5.86 | 3.71 | 16.46 |
| B9 | 西 | 16.22 | 2.48 | 15.33 | 13.21 | 47.24 |
| B10 | 西南 | 0.12 | 0.04 | 0.12 | –0.13 | 0.15 |
| B11 | 西北 | 0.87 | 0.11 | 4.07 | 5.86 | 10.91 |
| B12 | 西北 | 1.26 | 0.23 | 4.42 | 1.96 | 7.87 |
| B13 | 北 | –2.36 | –0.16 | –6.26 | –5.93 | –14.71 |
| B14 | 西北 | 0.62 | 0.05 | –0.96 | –0.44 | –0.73 |
| B15 | 西北 | 0.97 | 0.11 | –1.73 | –1.22 | –1.87 |
表 3—6列出了各分区能量收支的对比。由于FVCOM模式的计算采用三角网格, 我们在计算能量平衡时要将模式输出值插值到矩形网格中, 因此计算得到的各部分能量值在方程(20)中并不能完全保持平衡。由表 3—6可以看出, 就能量输入部分而言, 能通量F无疑是最重要的构成部分, 与之相反, 非线性作用N则是可以忽略的。半日潮的引潮力能量输入E大都为负值, 而全日潮的引潮力能量输入大都为正值, 说明半日潮的引潮力减弱了南海的潮汐, 而全日潮的引潮力则加强了南海的潮汐。这与方国洪等(1994)的结论一致。自吸-负荷潮的作用S与引潮力一致, 即减弱了半日潮而加强了全日潮, 但量值上更大。就能量消耗部分而言, 侧向摩擦的作用Dl一般要比其他两项小一个量级以上; 在浅水海域(G1, G4和G5)海底摩擦Db起主要作用; 在深水海域(G2, G3和G6)则内潮消耗Di起主要作用。
| 区域编号 | F | E | S | N | Db | Di | Dl | F+E+S+N | Db+Di+Dl |
| G1 | 24.30 | 0.06 | –0.23 | 0 | 22.86 | 0.37 | 1.02 | 24.13 | 24.25 |
| G2 | 9.05 | –0.82 | –1.33 | 0 | 0.08 | 6.63 | 0 | 6.90 | 6.71 |
| G3 | 18.28 | –2.85 | –3.83 | 0.11 | 5.13 | 6.04 | 0.64 | 11.71 | 11.81 |
| G4 | 0.99 | –0.09 | 0.25 | –0.12 | 0.92 | 0.04 | 0.04 | 1.03 | 1 |
| G5 | 1.26 | –0.11 | 0.18 | 0.01 | 1.22 | 0.03 | 0.03 | 1.34 | 1.28 |
| G6 | 12.31 | –1.05 | –1.86 | 0 | 0.12 | 9.22 | 0.03 | 9.40 | 9.37 |
| G2+G3+G4+G5 | 29.58 | –3.87 | –4.73 | 0 | 7.35 | 12.74 | 0.71 | 20.98 | 20.80 |
| 区域编号 | F | E | S | N | Db | Di | Dl | F+E+S+N | Db+Di+Dl |
| G1 | 2.15 | 0.01 | 0.03 | 0 | 2.09 | 0 | 0.07 | 2.19 | 2.16 |
| G2 | 0.73 | –0.05 | 0.13 | 0 | 0 | 0.79 | 0 | 0.81 | 0.79 |
| G3 | 2.75 | –0.55 | –0.64 | 0 | 0.62 | 0.92 | 0.06 | 1.56 | 1.60 |
| G4 | 0.15 | –0.01 | 0.01 | 0 | 0.13 | 0.01 | 0.01 | 0.15 | 0.15 |
| G5 | 0.23 | –0.02 | 0.01 | 0 | 0.2 | 0 | 0 | 0.22 | 0.2 |
| G6 | 1.64 | –0.14 | 0.22 | 0 | 0.01 | 1.70 | 0 | 1.72 | 1.71 |
| G2+G3+G4+G5 | 3.86 | –0.63 | –0.49 | 0 | 0.95 | 1.72 | 0.07 | 2.74 | 2.74 |
| 区域编号 | F | E | S | N | Db | Di | Dl | F+E+S+N | Db+Di+Dl |
| G1 | 0.37 | –0.02 | 0.07 | –0.01 | 0.36 | 0.03 | 0.02 | 0.41 | 0.41 |
| G2 | 7.29 | 1.02 | 1.42 | 0 | 0.14 | 9.72 | 0 | 9.73 | 9.86 |
| G3 | 4.5 | 1.72 | 2.77 | –0.01 | 3.47 | 4.56 | 0.67 | 8.98 | 8.70 |
| G4 | 4.19 | 0.15 | 0.32 | 0.05 | 4.37 | 0.17 | 0.21 | 4.71 | 4.75 |
| G5 | 4.42 | 0.07 | 0.16 | –0.03 | 4.53 | 0.02 | 0.08 | 4.62 | 4.63 |
| G6 | 12.45 | –0.14 | 0.47 | 0 | 0.1 | 12.77 | 0.02 | 12.78 | 12.89 |
| G2+G3+G4+G5 | 20.40 | 2.96 | 4.67 | 0.01 | 12.51 | 14.47 | 0.96 | 28.04 | 27.94 |
| 区域编号 | F | E | S | N | Db | Di | Dl | F+E+S+N | Db+Di+Dl |
| G1 | 0.29 | 0.01 | 0.05 | –0.01 | 0.31 | 0.02 | 0.01 | 0.34 | 0.34 |
| G2 | 5.63 | 0.28 | 1.13 | 0 | 0.13 | 6.81 | 0 | 7.04 | 6.94 |
| G3 | 2.22 | 0.88 | 2.12 | 0 | 2.16 | 2.52 | 0.61 | 5.22 | 5.29 |
| G4 | 5.73 | 0.06 | 0.22 | 0.03 | 5.45 | 0.36 | 0.22 | 6.04 | 6.03 |
| G5 | 1.96 | 0.09 | 0.31 | –0.02 | 2.27 | 0.03 | 0.02 | 2.34 | 2.32 |
| G6 | 8.27 | 0.11 | 0.14 | 0 | 0.09 | 8.44 | 0 | 8.52 | 8.53 |
| G2+G3+G4+G5 | 15.54 | 1.31 | 3.78 | 0.01 | 10.01 | 9.72 | 0.85 | 20.64 | 20.58 |
表 3—6中最下面一行代表了南海内部能量收支情况。M2、S2、K1和O1分潮的能通量输入分别为29.6, 3.9, 20.4和15.5 GW; 引潮力能量输入分别为-3.9, -0.6, 3.0和1.3GW; 自吸-负荷潮能量输入分别为-4.7, -0.5, 4.7和3.8GW。除了S2其他各分潮的自吸-负荷潮能量输入在绝对值上都大于引潮力能量输入。M2、S2、K1和O1分潮的海底摩擦能量消耗分别为7.4, 1.0, 12.5和10.0GW; 内潮耗散分别为12.7, 1.7, 14.5和9.7GW。除了O1其他各分潮的内潮耗散均大于海底摩擦耗散。
由表 3—6还可以看出, 吕宋海峡是能量最大的输入区域同样也是最大的能量耗散区。这里潮能耗散的主要形式不同于台湾海峡等以海底摩擦为主的浅水区域, 其耗散形式主要为内潮耗散。其中位于南海之外的吕宋海峡东部(G6分区)的内潮耗散量要超过位于南海之内的吕宋海峡西部(G2分区)的内潮耗散量。Zu等(2008)曾用同化方法反推了吕宋海峡的内潮能耗。如果用该文给出的同化和非同化能耗之差作为内潮能耗值, 则吕宋海峡的M2分潮和K1分潮的内潮能耗分别为16.1和20.2GW。本文所得G2和G6分区内M2分潮和K1分潮的总的内潮耗散值分别为15.9和22.5GW, 与该文结果基本一致。
5 结论本文利用FVCOM海洋数值模式, 建立了南海及其周边海域的二维潮汐潮流数值模型, 为了研究内潮耗散、引潮力和自吸-负荷潮对南海潮汐的影响, 在二维潮波方程中加入参数化的内潮耗散项和自吸-负荷潮项。模式同时对M2、S2、K1和O1分潮进行了模拟, 并与沿岸63个验潮站资料进行对比, 得到的M2、S2、K1和O1分潮振幅和迟角绝均值分别为4.9cm, 6.2°, 2.3cm, 11.3°, 3.9cm, 6.0°, 3.7cm, 6.8°, 符合良好。与Fang等(1999)的模拟结果相比较, 偏差总体上有明显降低, 说明引入内潮耗散与自吸-负荷潮并配之以较高模式分辨率可以明显改进数模结果。
潮能收支的计算结果显示, 维持南海潮汐运动的潮能主要是由西北太平洋经吕宋海峡输入的潮能通量。南海内部获得的M2、S2、K1和O1分潮能通量分别为29.6, 3.9, 20.4和15.5 GW。半日周期的自吸-负荷潮能量输入以负值居多, 而全日周期的自吸-负荷潮能量输入以正值居多, 因而自吸-负荷潮减弱了南海的半日潮, 并加强了南海的全日潮。引潮力的作用也减弱了半日潮而加强了全日潮, 但其作用要小于自吸-负荷潮。南海内部因海底摩擦消耗的M2、S2、K1和O1分潮能量分别为7.4, 1.0, 12.5和10.0GW; 因转换为内潮而耗散的能量分别为12.7, 1.7, 14.5和9.7GW。因此, 除了O1其他各分潮的内潮耗散均大于海底摩擦耗散。
潮能耗散的分析显示底摩擦耗散在沿岸浅水区域起主导作用, 内潮耗散则主要发生在深水区域。内潮耗散的最大值出现在吕宋海峡, 且位于南海之外的海峡东部的耗散量大于位于南海之内的海峡西部的耗散量。对M2、S2、K1和O1分潮吕宋海峡的内潮耗散总值分别达到15.9, 2.5, 22.5和15.3GW。
| 毛庆文, 齐义泉, 施平, 等, 2006. 在南海南部大纳土纳岛附近存在s_2分潮的无潮点吗?. 科学通报, 51(B11): 23–26 |
| 方国洪, 曹德明, 黄企洲, 1994. 南海潮汐潮流的数值模拟. 海洋学报, 16(4): 1–12 |
| 吴頔, 方国洪, 崔欣梅, 等, 2015. 泰国湾及邻近海域潮汐潮流的数值模拟. 海洋学报, 37(1): 11–20 |
| 佟景全, 雷方辉, 毛庆文, 等, 2010. 不考虑局地引潮势的南海正压潮能通量与潮能耗散. 热带海洋学报, 29(3): 1–9 DOI:10.11978/j.issn.1009-5470.2010.03.001 |
| 沈育疆, 胡定明, 梅丽明, 等, 1985. 南海潮汐数值计算. 海洋湖沼通报,(1): 26–35 |
| 林美华, 李常珍, 方国洪, 1999. 中国海标准经纬度水深和基准面数据表. 青岛: 中国科学院海洋研究所, 1-145 |
| 俞慕耕, 1984. 南海潮汐特征的初步探讨. 海洋学报, 6(3): 293–300 |
| 曹德明, 方国洪, 黄企洲, 等, 1997. 南沙及其西南海域的潮波系统. 海洋与湖沼, 28(2): 198–208 |
| Cai S Q, Long X M, Liu H L, et al, 2006. Tide model evaluation under different conditions. Continental Shelf Research, 26(1): 104–112 DOI:10.1016/j.csr.2005.09.004 |
| Chen C S, Beardsley R C, Cowles G, 2006. An Unstructured Grid, Finite-Volume Coastal Ocean Model, FVCOM User Manual, FVCOM User Manual. 2nd ed. New Bedford, MA: SMAST/UMASSD, 1-135 |
| Cheng Y, Andersen O, 2011. Multimission empirical ocean tide modeling for shallow waters and polar seas. Journal of Geophysical Research Oceans, 116(C11): 1130–1146 |
| Egbert G D, Ray R D, 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature, 405(6788): 775–778 DOI:10.1038/35015531 |
| Fang G H, Kwok Y K, Yu K J, et al, 1999. Numerical simulation of principal tidal constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand. Continental Shelf Research, 19(7): 845–869 DOI:10.1016/S0278-4343(99)00002-3 |
| Fang G H, Xu X Q, Wei Z X, et al, 2013. Vertical displacement loading tides and self-attraction and loading tides in the Bohai, Yellow, and East China Seas. Science China Earth Sciences, 56(1): 63–70 DOI:10.1007/s11430-012-4518-9 |
| Gao X M, Wei Z X, Lv X Q, et al, 2015. Numerical study of tidal dynamics in the South China Sea with adjoint method. Ocean Modelling, 92: 101–114 DOI:10.1016/j.ocemod.2015.05.010 |
| Garrett C, 1975. Tides in gulfs. Deep Sea Research and Oceanographic Abstracts, 22(1): 23–35 DOI:10.1016/0011-7471(75)90015-7 |
| Jayne S R, St Laurent L C, 2001. Parameterizing tidal dissipation over rough topography. Geophysical Research Letters, 28(5): 811–814 DOI:10.1029/2000GL012044 |
| Locarnini R A, Mishonov A V, Antonov J I et al, 2013. World ocean atlas 2013, volume 1: Temperature. NOAA Atlas NESDIS 73, Washington, DC: NOAA, 1-40 |
| Millard R C, Owens W B, Fofonoff N P, 1990. On the calculation of the brunt-väisäla frequency. Deep Sea Research Part A. Oceanographic Research Papers, 37(1): 167–181 DOI:10.1016/0198-0149(90)90035-T |
| Pawlowicz R, Beardsley B, Lentz S, 2002. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Computers & Geosciences, 28(8): 929–937 |
| Ray R D, 1998. Ocean self-attraction and loading in numerical tidal models. Marine Geodesy, 21(3): 181–192 DOI:10.1080/01490419809388134 |
| Teng F, Fang G H, Xu X Q, 2017. Effects of internal tidal dissipation and self-attraction and loading on semidiurnal tides in the Bohai Sea, Yellow Sea and East China Sea:a numerical study. Chinese Journal of Oceanology and Limnology, 35(5): 987–1001 DOI:10.1007/s00343-017-6087-4 |
| Wahr J M, 1981. Body tides on an elliptical, rotating, elastic and oceanless earth. Geophysical Journal International, 64(3): 677–703 DOI:10.1111/gji.1981.64.issue-3 |
| Wang X W, Peng S Q, Liu Z Y, et al, 2016. Tidal mixing in the South China Sea:An estimate based on the internal tide energetics. Journal of Physical Oceanography, 46(1): 107–124 DOI:10.1175/JPO-D-15-0082.1 |
| Ye A L, Robinson I S, 1983. Tidal dynamics in the South China Sea. Geophysical Journal International, 72(3): 691–707 DOI:10.1111/j.1365-246X.1983.tb02827.x |
| Zu T T, Gan J P, Erofeeva S Y, 2008. Numerical study of the tide and tidal dynamics in the South China Sea. Deep Sea Research Part Ⅰ:Oceanographic Research Papers, 55(2): 137–154 DOI:10.1016/j.dsr.2007.10.007 |
 2018, Vol. 49
2018, Vol. 49


