中国海洋湖沼学会主办。
文章信息
- 郑堃, 林霄沛, 朱亚楠. 2018.
- ZHENG Kun, LIN Xiao-Pei, ZHU Ya-Nan. 2018.
- 南海上层中尺度涡统一三维结构
- ON UNIVERSAL 3D STRUCTURE OF MESOSCALE EDDIES IN UPPER LAYER OF SOUTH CHINA SEA
- 海洋与湖沼, 49(3): 490-496
- Oceanologia et Limnologia Sinica, 49(3): 490-496.
- http://dx.doi.org/10.11693/hyhz20170300042
-
文章历史
- 收稿日期:2017-03-01
- 收修改稿日期:2017-03-23
2. 中国海洋大学海洋与大气学院 青岛 266100
2. College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China
中尺度涡通常是指生存周期在几十到数百天, 空间尺度在几十到数百千米的长期封闭环流。中尺度涡在海洋之中无处不在, 是海洋的重要组成部分, 它蕴含巨大能量, 对全球海洋的物质和能量的输运发挥着重要作用, 同时对海洋的气象和水文环境产生重要影响(Qiu et al, 2005; Yang et al, 2015)。
南海是西北太平洋最大的边缘海, 地形非常复杂, 受东亚季风和黑潮入侵影响, 蕴含着较为复杂的多尺度海洋动力过程。卫星资料、观测资料以及海洋模式资料均显示南海涡旋活动十分活跃, 多个发生在南海的涡旋也被通过海洋观测手段捕捉发现并进行研究。高度计资料极大提高了人们对南海中尺度涡的空间分布、季节特征和运动学特征的认识, 但是由于水下观测资料获取难度较大, 因此目前对南海中尺度涡空间结构的研究成果比较少, 只有针对个别涡旋的研究。例如Li等(1998)运用CTD资料分析了1994年秋季出现在南海东北部的一个反气旋涡的空间结构, 发现涡旋能够从表层延伸到1000m的深度。Nan等(2011)利用18°N断面的CTD资料, 分析了2007年夏季吕宋岛西侧三个反气旋涡的垂直结构, 发现由涡旋引起的地转流速在900m深度能够达到5cm/s的量级。Hu等(2011)在2007年9月对越南冷涡进行了走航观测, 利用大面积CTD观测资料给出了越南冷涡由表层至500m深度的三维结构, 发现涡旋的流速随着深度的增加迅速衰减, 到300m深度基本为0, 同时冷涡的中心随着深度增加略微地向东北方向倾斜。Zhang等(2016)通过2013年10月至2014年6月期间在南海北部布放的潜标阵列获得的观测数据, 运用合成分析的方法刻画了南海北部的一对涡旋的全水深三维结构, 发现中尺度涡的信号能够从表层一直延伸到海底, 并且在海底处的流速仍然可以达到5cm/s, 同时也发现中尺度涡从表层至海底轴心逐渐往西南方向倾斜, 最大倾斜距离达到150km。除此之外, 部分学者分别运用高分辨率海洋模式对南海中尺度涡的垂向结构也进行了研究(Chen et al, 2010; Chu et al, 2014; Zhang et al, 2015), 他们指出在模式中涡旋的形状主要分为“碗状”、“棱镜状”和“锥状”三种结构, 其中“碗状”结构的中尺度涡占总数的80%。
Argo浮标的出现使得海洋学家能够获得全球范围大量的温盐剖面数据。结合卫星高度计资料, 通过合成分析方法, 前人在不同的研究海区分析了中尺度涡的结构, 如东南太平洋(Chaigneau et al, 2011)、西北太平洋(Qiu et al, 2005; Yang et al, 2013)、热带印度洋(Yang et al, 2015)、东南印度洋(Souza et al, 2011)等。Zhang等(2013)结合高度计和Argo资料, 运用合成分析的方法对大洋中尺度涡的空间结构进行了深入的研究, 发现在地转近似的条件下, 全球大洋中尺度涡的水平结构和垂直结构可以分离并且具有统一的空间结构。
综上所述, 前人通过观测资料和数值模拟研究了南海个别中尺度涡的空间结构, 也通过大量的温盐剖面数据和高度计资料研究得到了全球大洋中尺度涡统一的水平和垂直结构。但是, 南海中尺度涡是否也具有统一的空间结构, 南海中尺度涡空间结构与大洋中尺度涡空间结构有何异同等问题我们尚不清楚。由于南海Argo资料较少, 因此我们利用CTD资料和卫星高度计资料, 通过合成分析的方法得到了归一化之后南海中尺度涡统一的空间结构, 并将结果与全球大洋中尺度涡的结构特征进行对比, 从而更好地理解南海中尺度涡的结构特征。
1 数据与方法 1.1 数据资料 1.1.1 卫星高度计资料本文使用的卫星高度计资料为海表面高度异常数据(SLA), 是由法国国家空间研究中心卫星海洋学数据存档中心(AVISO)提供的延迟时间海表面高度异常格点数据(DT-MSLA), 该数据由TOPEX/Poseidon、Jason-1和ERS卫星数据融合得到, 为格点数年集。该数据采用Mercator坐标系, 时间分辨率为7天, 空间分辨率为1/4°×1/4°。本文选取的空间范围是0°—25°N, 105°—125°E。本文中使用的海表面高度异常(SLA)都是相对以七年为时间窗口的平均值计算得到的。
1.1.2 CTD数据本文采用的CTD数据是来自国际合作与交流资料、东方红2号海洋科学考察船高分辨率CTD调查资料和国内其他涉海部门1993年至2009年在南海进行的CTD调查资料, 共计1460个CTD剖面。使用的CTD型号为海鸟CTD 911(917)。图 1展示了这些CTD剖面在南海的空间分布情况, 数据主要分布在4°—25°N, 105°—125°E之间, 基本遍布南海海域。
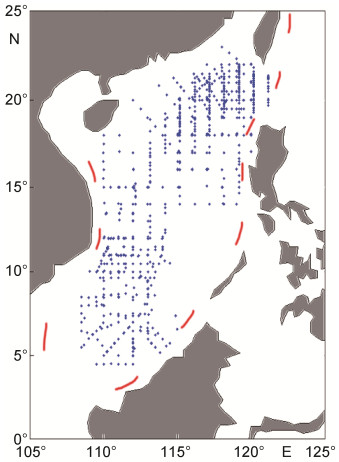 |
| 图 1 CTD剖面在南海的分布 Fig. 1 The distribution of CTD profile in SouthChina Sea(SCS) |
图 2展示了不同深度CTD观测数据的数量。由于水深大于900m之后CTD数据数量较少, 为使得我们的研究具有代表性和可信性, 只取了800m以上的CTD数据进行合成分析。
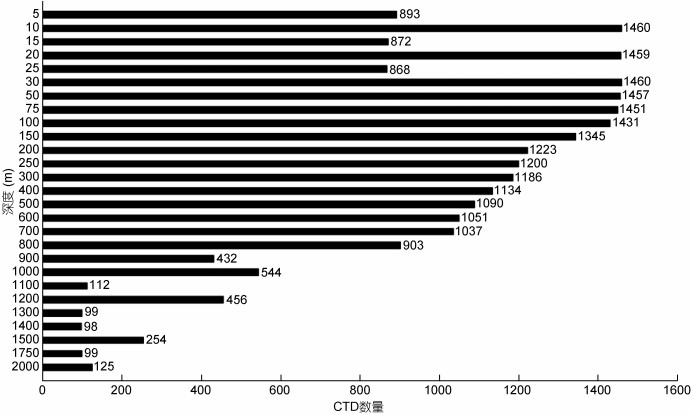 |
| 图 2 CTD数据在不同深度的分布 Fig. 2 Distribution of CTD data in different depth |
WOA09(World Ocean Atlas 09)数据是由美国国家海洋和大气管理局(NOAA)旗下的美国海洋资料研究中心(NODC)制作的世界海洋水文数据。WOA09数据空间分辨率有5°×5°和1°×1°之分, 时间分辨率有年平均数据、季平均数据和月平均数据。数据包括溶氧量、表观耗氧量、磷酸盐、硅酸盐、硝酸盐、盐度和温度等水文数据信息。年平均数据与季平均数据可选择0—5500m的深度范围, 分为33层, 月平均数据可选择0—1500m的深度范围, 分为24层。本文采用的数据范围是0°—25°N, 105°—125°E, 空间分辨率为1°×1°的月平均数据, 垂向水深取0—800m。
1.2 涡旋的归一化合成方法 1.2.1 涡旋与CTD的匹配方法我们根据CTD剖面观测时间找出时间上最接近的高度计观测数据, 然后通过Okubo-Weiss方法对中尺度涡进行识别。在这里我们将所有的海表面高度异常的局地极大值和极小值被Okubo-Weiss参数W= –2×10–12/s2 (Chaigneau et al, 2011)的闭合等值线包围的点认定为一个真实的涡旋中心。其中Okubo-Weiss参数为(Isern-Fontanetet al, 2003): W=4(ux2+vxuy), 下标x, y分别代表东西向与南北向的空间导数。然后通过地转平衡关系, 由高度计数据计算得出地转流u=-(g/f)ηy和v=-(g/f)ηx(η是海表面高度异常, g是重力加速度)。我们将W= –2×10–12/s2等值线所包围的面积A作为涡旋的面积, 将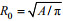
通过高度计资料得涡旋的中心和半径之后, 比较涡心与CTD剖面的距离, 选择L(L=3倍涡旋半径R)为搜索半径, 将所有落入搜索范围的涡旋与CTD剖面进行匹配。匹配的方法见图 3。
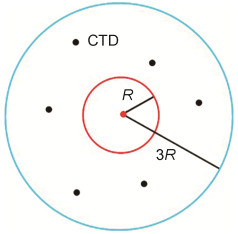 |
| 图 3 涡旋匹配方法 Fig. 3 The method of mesoscale eddiesmatching 注:红点为涡旋中心, 黑色圆点为CTD剖面的位置, 红色圆圈为涡旋半径R确定的涡旋边缘, 蓝色圆圈为搜索半径L=3R确定的搜索区域 |
在这里有必要解释一下选择3倍涡旋半径作为搜索半径的原因。如果L选取的较小, 那么落入搜索范围的CTD剖面数据数量就会减少。由于统计样本不足, 就容易造成较大的相对误差。而如果L选取过大, 则统计区域内数据不能够真实表征涡旋的信息, 从而得到错误的合成结果。我们分别尝试过L选取从R到5R, 结果证明L=3R时既能保证获得较多的统计样本, 又能保证统计区域足够小, 涵盖尽量多的涡旋信息。
根据我们采用的涡旋与CTD数据的匹配方法, 共有247个涡旋与CTD剖面匹配成功, 参与了南海中尺度涡统一三维结构的合成, 其中气旋涡116个, 反气旋涡131个。由于现场观测的不确定性, 不同涡旋匹配的CTD数目有所不同, 匹配CTD数目最多的涡旋匹配的CTD的数目为53个, 最少的仅有3个。
以1994年4月13日出现在南海北部的一个中尺度涡为例, 展示了涡旋的识别过程及涡旋与CTD的匹配情况(图 4), 匹配出的CTD的温度及盐度剖面(图 5)。
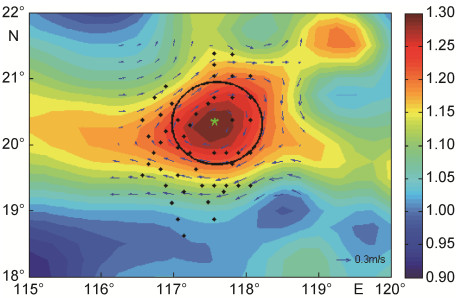 |
| 图 4 利用高度计资料识别中尺度涡 Fig. 4 Using altimeter data to identify mesoscale eddies 注:图中背景颜色代表海表面高度异常, 单位: m。绿色*标志是用Okubo-Weiss方法识别出的涡旋中心的位置, 黑色的圆圈是识别出的涡旋半径, 蓝色矢量箭头为地转流速, 黑色点为匹配出的CTD剖面 |
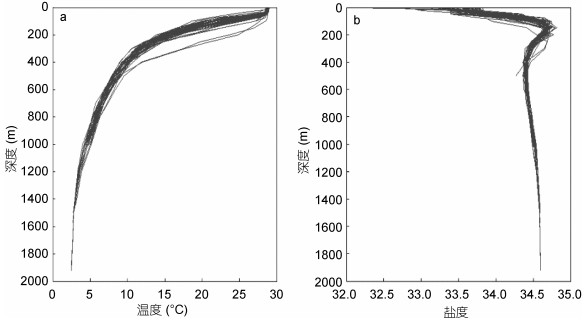 |
| 图 5 匹配出的CTD温度(a)及盐度(b)剖面 Fig. 5 Matched CTD temperature salinity profile 注:蓝色实线代表每一个CTD得到的温度剖面和盐度剖面 |
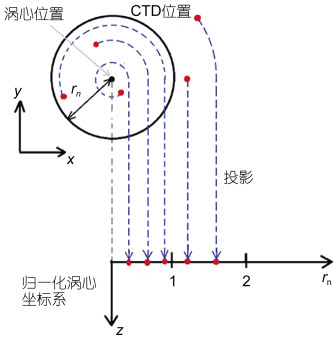
匹配完成后, 以涡旋中心为原点, 建立涡心坐标系(r, z), r是CTD剖面与涡心的距离, z是深度。为了排除中尺度涡水平尺度大小造成的影响, 我们用R0去归一化r, 得到归一化之后的距心距离rn=r/R0作为合成时使用的径向坐标。我们将大量的观测数据投射到以涡旋中心为原点的坐标系下, 从而得到一个涡旋在平均意义下的结构图像。投影方法见图 6。由于每一个CTD剖面观测到的涡旋的振幅、极性和强度存在差别, 为了排除这些因素的影响, 我们还需要对振幅和极性进行归一化, 方法就是通过涡旋在海表涡心位置的压强异常对应的CTD观测到的压强剖面进行归一化, 即:pn(rn, z)=p0-1·p'(r/R0, z)。其中压强异常p'被它在海表面涡旋中心处的观测值p0归一化, 得到归一化之后的压强异常pn; 距心距离r被涡旋半径R0归一化, 得到归一化的径向坐标rn。
中尺度涡的压强异常场p'代表了涡旋的水平地转流函数φ(φ=p'/f, f是科氏参数), 并将决定整个涡旋的动力结构。位势密度可以通过温盐剖面直接计算得到, 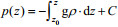
根据Zhang等(2013)的结论中尺度涡的水平结构和垂直结构是可以分离的, 即p'可以表示为p'=F1(x, y, t)·F2(z)。因此我们可以分别合成水平和垂直结构。考虑到中尺度涡通过高度计观察基本上是轴对称的(Chelton et al, 2011), 并且不同层次的中尺度涡的压强异常在结构上具有一致性(Zhang et al, 2013), 压强异常pn在各个深度上水平分布应该一致, 只是振幅不一样, pn的最大值总是出现在涡旋中心处, 因此, 我们用各个深度层次上涡旋中心处pn的值对这一深度上pn的水平分布进行振幅的归一化: pn(rn, z)/pn(0, z), 它是深度z层次上振幅归一化的压强异常的水平分布, 即代表了pn在各个深度上的水平分布的性状。对pn(rn, z)/pn(0, z)求垂向平均, 就得到R(rn)。
类似的, 对不同距心距离rn上pn的垂向分布也可以用对应距心距离海表面处的值进行振幅归一化: pn(rn, z)/pn(rn, 0), 它是距心距离rn处振幅归一化的压强异常的垂向分布, 即代表了pn在不同rn处垂直分布的形状。对pn(rn, z)/pn(rn, 0)求径向平均就得到了H(z)。
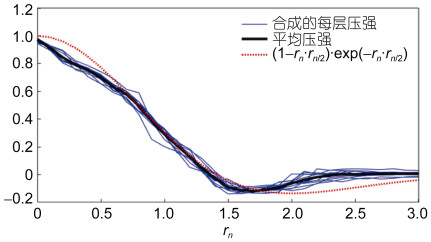
2 结果与分析 2.1 南海中尺度涡水平结构的合成结果图 7蓝色实线为南海海域不同深度(5, 10, 15, 20, 30, 50, 75, 100, 125, 150, 200, 300, 400, 500, 600, 700, 800m)归一化合成的中尺度涡压强异常的水平结构, 横坐标是归一化涡心距离rn, 黑色实线则代表了它们的平均曲线。红色虚线为全球大洋中尺度涡水平结构的解析函数曲线(Zhang et al, 2013): R(rn)=(1-rn2/2)·exp(-rn2/2)。
 |
| 图 7 南海中尺度涡统一的压强异常的水平结构 Fig. 7 The universal horizontal structure of abnormal pressure in mesoscale eddies in SCS |
由图 7我们可以看出, 不同的深度条件下, 通过对涡旋的极性、振幅和半径进行归一化之后得到的压强异常曲线十分接近, 这说明南海的中尺度涡在统计意义下具有统一的水平结构。对pn=(rn, z)/pn(0, z)求垂向平均得到R(rn), 即图 7中的黑色实线。
通过与全球大洋中尺度涡水平结构的解析函数曲线对比, 我们发现南海中尺度涡水平压强异常曲线与全球大洋中尺度涡的水平压强异常曲线的解析函数在rn<1.5区间, 两者结构比较一致, 但是在rn>1.5区间两者结构具有明显的不同。南海中尺度涡水平结构在2.5倍涡旋半径处水平结构已经收敛趋近于0, 全球大洋中尺度涡的水平结构在4倍涡旋半径处水平结构才收敛趋近于0。经测算, 在1.5倍涡旋半径之外, 前者水平结构的收敛速度约为后者的2.5倍, 前者比后者水平结构的影响范围要小约1.5倍涡旋半径。这说明南海中尺度涡的影响范围要小于全球大洋中尺度涡的影响范围, 主要是由于1.5倍涡旋半径之外的南海中尺度涡水平结构的收敛速度更快。
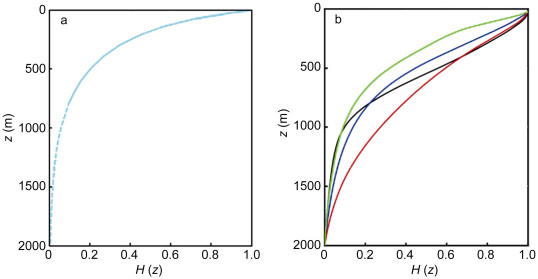
2.2 南海中尺度涡垂直结构的合成结果图 8a为南海中尺度涡垂直结构的合成结果, 图 8b为全球大洋四个代表海区中尺度涡垂直结构的合成结果。横坐标为垂直结构H(z), 纵坐标为深度z, 单位为m。
由于数据原因, 我们仅得到了0至800m水深南海中尺度涡的垂直结构, 未能体现涡旋的全水深结构。图 8a实线部分为南海归一化合成的中尺度涡的垂直结构H(z)的实际结果, 虚线部分为沿着实测结果的自然延伸, 仅作为垂直结构的参考, 并无实际意义。通过与图 8b同等深度全球大洋四个代表海区中尺度涡垂直结构的对比我们可以看出, 中尺度涡的垂直结构在不同海区均有较大差别, 并不具有统一性, 这主要是由于背景层结和科氏参数的差别所致, 符合我们的预期。南海相较于其他四个海区, 中尺度涡的垂直结构随着水深的增加, 衰减速度明显更快。800m水深处, 南海中尺度涡的垂直结构H(z)已经小于0.1, 与北太平洋副热带逆流区涡旋的垂直结构较为接近, 明显小于其他三个海区。
3 结论为了更好地理解南海中尺度涡的结构特征, 我们利用CTD资料和卫星高度计资料通过归一化合成分析的方法, 在满足静力平衡条件和地转平衡条件的假设下, 分别得到了南海中尺度涡统一的水平结构和垂直结构。得到结论如下。
(1) 从水平结构的合成结果来看, 南海的中尺度涡具有统一的水平结构特征。在0至1.5倍涡旋半径区间, 基本与解析函数R(rn)=(1-rn2/2)·exp(-rn2/2)重合, 这与Zhang等(2013)得到的全球大洋中尺度涡水平结构的合成结果一致。
(2) 在1.5倍涡旋半径以外, 南海中尺度涡的水平结构的收敛速度明显要快于全球大洋中尺度涡水平结构的收敛速度, 前者在2.5倍涡旋半径处水平结构已经收敛趋近于0, 后者在4倍涡旋半径处水平结构才收敛趋近于0。经测算, 在1.5倍涡旋半径之外, 南海中尺度涡水平结构的收敛速度约为全球大洋中尺度涡水平结构收敛速度的2.5倍, 前者比后者水平结构的影响范围要小约1.5倍涡旋半径。
(3) 从南海0至800m水深南海中尺度涡垂直结构的合成结果来看, 南海中尺度涡的垂直结构与全球大洋各海区中尺度涡的垂直结构存在明显差别。这主要是不同海区科氏参数和背景层结不同所致, 这一点符合我们的预期。但是通过对比我们可以看出, 南海中尺度涡的垂直结构随着深度的增加, 相较于其他海区衰减的速度明显更快。
综上所述, 我们通过CTD资料和卫星高度计资料得到的南海中尺度涡统一的水平结构与Zhang等(2013)得到的全球大洋中尺度涡的结果存在差异, 南海中尺度涡的水平结构明显要比全球大洋中尺度涡水平结构的收敛速度更快, 这也说明在经过归一化之后, 南海中尺度涡水平结构的影响范围要明显小于全球大洋中尺度涡水平结构的影响范围。南海中尺度涡的垂向构与全球大洋各个海区中尺度涡垂直结构相比, 其随深度的衰减速度明显更快。这两种差异究竟是由于计算和仪器的误差导致还是在海洋中真实存在, 两者之间是否有什么联系, 还需要我们下一步通过更多的观测数据来进一步验证。中尺度涡的三维空间结构在很大程度上能够影响其输运能力, 正确认识南海中尺度涡的结构特征, 有助于更好地评估南海中尺度涡对物质和能量的输运能力。
| 张正光, 2014. 中尺度涡. 青岛: 中国海洋大学博士学位论文 |
| Chaigneau A, Le Texier M, Eldin G, et al, 2011. Vertical structure of mesoscale eddies in the eastern South Pacific Ocean:a composite analysis from altimetry and Argo profiling floats. Journal of Geophysical Research:Atmospheres, 116(C11): C11025 DOI:10.1029/2011JC007134 |
| Chelton D B, Schlax M G, Samelson R M, et al, 2007. Global observations of large oceanic eddies. Geophysical Research Letters, 34(15): L15606 |
| Chelton D B, Gaube P, Schlax M G, et al, 2011. The influence of nonlinear mesoscale eddies on near-surface oceanic chlorophyll. Science, 334(6054): 328–332 DOI:10.1126/science.1208897 |
| Chen G X, Hou Y J, Chu X Q, et al, 2010. Vertical structure and evolution of the Luzon Warm Eddy. Chinese Journal of Oceanology and Limnology, 28(5): 955–961 DOI:10.1007/s00343-010-9040-3 |
| Chu X Q, Xue H J, Qi Y Q, et al, 2014. An exceptional anticyclonic eddy in the South China Sea in 2010. Journal of Geophysical Research:Oceans, 119(2): 881–897 DOI:10.1002/2013JC009314 |
| Hu J Y, Gan J P, Sun Z Y, et al, 2011. Observed three-dimensional structure of a cold eddy in the southwestern South China Sea. Journal of Geophysical Research:Oceans, 116(C5): C05016 |
| Isern-Fontanet J, Garcia-Ladona E, Font J, 2003. Identification of marine eddies from altimetric maps. Journal of Atmospheric and Oceanic Technology, 20(5): 772–778 DOI:10.1175/1520-0426(2003)20<772:IOMEFA>2.0.CO;2 |
| Li L, Nowlin W, Su J L, et al, 1998. Anticyclonic rings from the Kuroshio in the South China Sea. Deep Sea ResearchPart Ⅰ:Oceanographic Research Papers, 45(9): 1469–1482 DOI:10.1016/S0967-0637(98)00026-0 |
| Nan F, He Z G, Zhou H, et al, 2011. Three long-lived anticyclonic eddies in the northern South China Sea. Journal of Geophysical Research:Atmospheres, 116(C5): C05002 |
| Qiu B, Chen S M, 2005. Eddy-induced heat transport in the subtropical North Pacific from Argo, TMI, and altimetry measurements. Journal of Physical Oceanography, 35(4): 458–473 DOI:10.1175/JPO2696.1 |
| Souza J M A C, Montégut C D B, Cabanes C, et al, 2011. Estimation of the Agulhas ring impacts on meridional heat fluxes and transport using ARGO floats and satellite data. Geophysical Research Letters, 38(21): L21602 |
| Yang G, Wang F, Li Y L, et al, 2013. Mesoscale eddies in the northwestern subtropical Pacific Ocean:Statistical characteristics and three-dimensional structures. Journal of Geophysical Research:Oceans, 118(4): 1906–1925 DOI:10.1002/jgrc.20164 |
| Yang G, Yu W D, Yuan Y L, et al, 2015. Characteristics, vertical structures, and heat/salt transports of mesoscale eddies in the southeastern tropical Indian Ocean. Journal of Geophysical Research:Oceans, 120(10): 6733–6750 DOI:10.1002/2015JC011130 |
| Zhang W Z, Xue H J, Chai F, et al, 2015. Dynamical processes within an anticyclonic eddy revealed from Argo floats. Geophysical Research Letters, 42(7): 2342–2350 DOI:10.1002/2015GL063120 |
| Zhang Z G, Zhang Y, Wang W, et al, 2013. Universal structure of mesoscale eddies in the ocean. Geophysical Research Letters, 40(14): 3677–3681 DOI:10.1002/grl.50736 |
| Zhang Z W, Tian J W, Qiu B, et al, 2016. Observed 3D structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Scientific Reports, 6: 24349 DOI:10.1038/srep24349 |
 2018, Vol. 49
2018, Vol. 49