
中国海洋湖沼学会主办。
文章信息
- 胡冬, 陈希, 毛科峰, 滕军, 李妍, 彭旭东. 2018.
- HU Dong, CHEN Xi, MAO Ke-Feng, TENG Jun, LI Yan, PENG Xu-Dong. 2018.
- 黑潮延伸体邻近区域中尺度涡特征统计分析
- STATISTICAL CHARACTERISTICS OF MESOSCALE EDDIES NEAR THE KUROSHIO EXTENSION REGION
- 海洋与湖沼, 49(3): 497-511
- Oceanologia et Limnologia Sinica, 49(3): 497-511.
- http://dx.doi.org/10.11693/hyhz20170900232
-
文章历史
- 收稿日期:2017-09-08
- 收修改稿日期:2017-12-01
2. 国防科技大学气象海洋学院 南京 211101
2. College of Meteorology and Oceanography, National University of Defense Technology, Nanjing 211101, China
黑潮(Kuroshio)是发源于太平洋北赤道流的一支极为强烈的西边界海流, 在(35°N, 142°E)附近, 黑潮与日本海岸分离转向东流去, 这部分水体称为黑潮延伸体(Kuroshio Extension, KE), 其地理范围一般定义为(32°—38°N, 140°—180°E)(张笑等, 2013)。黑潮延伸体具有惯性射流的性质, 并呈现为“蛇曲”, 不断有涡旋脱落(Qiu et al, 2003)。
在海洋大尺度环流中存在许多中尺度现象, 包括中尺度涡、锋面、跃层等。中尺度涡是指时间尺度在几十天到数百天, 空间尺度在几千米到几百千米之间的海洋涡旋, 垂直影响深度可达几千米(Chelton et al, 2007; Adams et al, 2011), 它普遍存在于全球大洋中(Chelton et al, 2011), 在海洋动力学(Zhang et al, 2013)、热力学(Nan et al, 2011)、海气能量交换(Chelton, 2013)等过程中具有重要作用。
黑潮延伸体是中纬度海洋-大气相互作用的关键区域(张笑等, 2013), 该区域的中尺度涡数量密集(郑聪聪等, 2014), 是太平洋涡动能(Eddy Kinetic Energy; EKE)最大的区域之一(Scharffenberg, 2008)。如图 1所示, 在黑潮主轴转向处附近存在一个EKE的强值区, 这个强值区一直向东延伸, 形成一条高EKE的带状区域, 且纬向平均EKE在黑潮主轴附近(34°—35°N)达到最大(图 1b)。KE的中尺度涡对黑潮急流的形态及其时间变化起着重要的调整作用(Waterman et al, 2011), 对北太平洋副热带模态水具有重要影响作用(Xu et al, 2014), 此外, 涡旋对该区域大气边界层和海面风场的变化也有重要影响(Small et al, 2008), 甚至对北太平洋风暴轴的变化具有一定调整作用(冯劭华等, 2015)。因此, 开展该区域中尺度涡的研究具有重要意义。
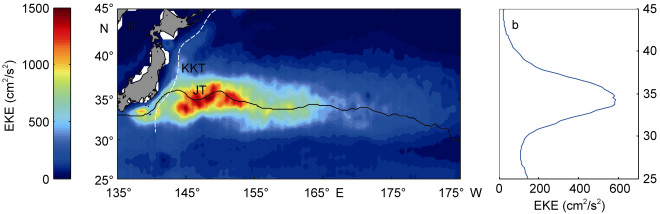 |
| 图 1 黑潮延伸体邻近海区EKE的分布 Fig. 1 Distribution of EKE (eddy kinetic energy) in the adjacent area of Kuroshio extension 注: a:基于卫星高度计观测得到的1993年1月至2012年12月共20年的海表面地转流异常数据, 进行了52周的高通滤波计算得到的EKE(单位: cm2/s2)地理分布, 黑色实线为1m等SSH线, 表示气候态下黑潮急流主轴的大致位置, 白色虚线表示Japan Trench(JT)和Kuril-Kamchatka Trench(KKT)的位置; b: EKE(单位: cm2/s2)的纬向平均(日本以东的135°E—175°W经向范围)分布 |
在卫星高度计资料出现之前, 黑潮延伸体区域中尺度涡的研究多基于个例观测。随着卫星高度计资料的广泛使用, 中尺度涡的时空分布、强度、移动等特征的研究逐渐开展。Chelton等(2007)利用连续10年的SSHA资料对全球中尺度涡(生命周期 > 4周)进行了统计研究, 结果表明黑潮延伸体区域仅存在数量较少的中尺度涡, 这些涡旋对该区域SSH变化的贡献仅为25%, 这一结论与之前调查观测结果存在很大差异。此后, Itoh等(2010a)利用融合高度计的SSHA资料, 对黑潮延伸体区域中尺度涡进行了统计分析, 结果表明, 反气旋涡(anticyclonic eddy; AE)的数量密集区位于黑潮延伸体北侧, 而气旋涡(cyclonic eddy; CE)数量的密集区主要在黑潮流轴及其南侧, 黑潮主轴的南北两侧分别是气旋涡和反气旋涡强度较大的区域。Itoh等(2010b)的研究进一步发现, 在黑潮延伸体北侧多为反气旋式暖涡, 其寿命较长, 而在南侧多为气旋式冷涡, 且强度较大。崔伟等(2017)对西北太平洋中尺度涡的统计结果显示, 30°—35°N的黑潮延伸体区域涡旋与同纬度其他区域相比半径较大, 具有明显更高的涡动能和涡振幅。
此外, 关于该区域中尺度涡的季节性变化, Mizuno等(1983)和Qiu等(1991)的研究认为, EKE季节变化可能与从黑潮上游传来的扰动有关, 这种扰动到达黑潮延伸体后继续东传, 并在夏季信号达到最大。Scharffenberg等(2008)也发现, 黑潮延伸体区域EKE存在夏季强冬季弱的现象, 并认为这种现象是由风场的季节性变化引起海洋正压响应造成的。Aoki等(1995)和Wang等(1995)的研究发现, EKE的空间分布和低频变化与底地形存在密切关系, 并认为底地形通过调制黑潮流轴的不稳定性质进而影响EKE的季节变化。
总结以上研究可以发现, 前人对黑潮延伸体区域中尺度涡的研究内容主要包括涡旋个例的观测分析、EKE的变化等。然而, EKE的强度分布和变化并不能完全代表中尺度涡的分布和变化情况, 也无法得到中尺度涡的半径、强度等特征, 尽管Itoh等(2010a)对涡旋的各类统计特征进行了较为详细的分析, 但其研究区域集中在黑潮—亲潮交汇区, 对170°E以东的黑潮延伸体区域没有进行统计, 且对涡旋的生命周期、演变特征、季节性变化等方面没有涉及, 而这些也是分析该区域中尺度涡特征十分重要的问题。因此, 本文针对以上问题开展相关研究, 研究区域的空间范围(25°—45°N, 135°E—175°W)如图 1所示, 这一范围比黑潮延伸体的定义范围(32°— 38°N, 140°—180°E)略大一些, 目的是为了将整个黑潮延伸体区域涵盖在内, 对该区域内中尺度涡进行系统全面的统计分析。
1 资料和方法 1.1 卫星高度计资料本文主要基于卫星高度计资料对中尺度涡进行统计分析, 它由法国国家空间研究中心的卫星海洋存档数据中心(AVISO)提供, 融合Jason-1、Topex/Poseidon、Envisat、GFO、ERS-1 & 2等多颗卫星的数据, 包括了全球网格化的海平面高度异常(Sea Level Anomaly, SLA)数据, 空间分辨率为1/4°×1/4°, 根据研究需要, 本文选取的资料空间范围为25°—45°N, 135°E—175°W, 时间跨度为1993年1月至2012年12月共20年。
由SLA根据地转关系可计算得到表层地转流异常:
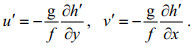
其中, u'和v'分别为地转流异常的纬向和经向分量, g为重力加速度, f为科氏参数, h'为SLA的大小。
1.2 涡旋识别和追踪方法本文采用Nencioli等(2010)提出的一种基于流场几何形态方法, 对中尺度涡进行自动识别和跟踪, 该方法在南加利福利亚海湾(Southern California Bight)的数值模式流场中, 判别效果明显好于winding- angle和Okubo-Weiss方法, 此外, 该方法还运用于其他海域的相关研究(Dong et al, 2014; 祖永灿等, 2016)。这种方法主要分为三步:
一、利用流场数据, 基于以下四个给定的约束条件确定出涡旋中心: (1)沿纬向(东西向)穿越涡中心时, 中心左右两侧的南北向流速v速度方向相反, 且离涡中心越远其值越大; (2)沿经向(南北向)穿越涡中心时, 中心上下两侧的东西向流速u方向相反, 且离涡中心越远其值越大; (3)涡中心是局部速度最小值的位置; (4)涡中心附近, 流速方向必须沿着同一方向(顺时针或逆时针)旋转, 相邻的两个速度向量必须在同一个象限或相邻的两个象限内。
二、在第一步的基础上确定出涡旋边界(将中尺度涡的边界定义为距中尺度涡中心最远的闭合流函数等值线)。
三、通过比较不同时次内的涡旋中心位置来确定出涡旋轨迹, 具体来说, 对于某一个涡旋轨迹, 若它在第t时次被检测出, 且涡旋中心位置为(x, y), 则在第t+1时次, 以点(x, y)为中心, r(r为一设定的值)为半径搜索该范围内的同类型(气旋或反气旋)涡, 在t+1时次搜索到的涡旋则与t时次的涡旋属于同一涡旋轨迹。本文研究区域内, 涡旋的典型移动速度约为1—10cm/s(Qiu et al, 2010; Chelton et al, 2011), 相邻时次的时间间隔为7d, 因此这里取搜索半径r=60km。另外, 本文仅对存活时间不短于4周的涡旋进行统计分析。
1.3 中尺度涡一些特征量的定义确定出中尺度涡的中心和边界后, 可计算出涡旋的面积S, 涡的半径R定义为具有相同面积圆的半径, 即: 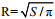
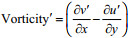
涡动能EKE的计算首先采用Liang等(2007)创建的多尺度子空间变换(Multiscale Window Transform; MWT)泛函工具, 将原始速度的时间序列正交地分解成时间平均(大尺度)和扰动(中尺度)过程, 即U=UL+US, 其中, UL和US分别表示原始速度U的低频(大尺度)和高频(中尺度)成分。在MWT框架下, 不同时间尺度的过程分别对应着两个时间采样空间的系数Ûn~L和Ûn~S, 每部分的能量正比于各自的MWT变换系数的平方, 即(Ûn~L)2和(Ûn~S)2, 其中下标n表示MWT框架下多尺度能量随时间的变化。在此基础上, 涡动能场可表示为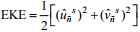
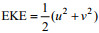
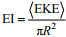
利用1.2节的涡旋自动识别方法, 在研究区域内共检测到5893个涡旋轨迹, 其中气旋涡轨迹和反气旋涡轨迹分别为3006和2887个, 气旋涡轨迹比反气旋涡轨迹多4.1%。将各个涡旋轨迹在各时次内被探测到的记录相加, 则共包含27930个气旋涡和29822个反气旋涡。
涡旋的生命周期表示一个涡旋从产生到消失所持续的时间, 图 2显示了涡旋生命周期分布情况(大于52周的记总数量)。所有涡旋的平均生命周期为10.49周, 这与西北太平洋(崔伟等, 2017)及黑潮再循环流区域(Ma等, 2014)的统计结果基本一致。涡旋生命周期众数为5周, 当周期大于5周时, 随着周期的增加, 涡旋数量近似呈指数型减小(图 2中黑色实线为函数y=2522×e–0.1978x的拟合结果)。67.4%的涡旋周期不超过10周, 约0.38%的涡旋存在时间超过了一年(即52周)。
 |
| 图 2 涡旋生命周期的数量分布图 Fig. 2 Histograms of the eddy lifespan 注:黑色实线为涡旋数量与生命周期的函数拟合结果(y=2522×e–0.1978x, R2=99.0%, rms=18.6) |
气旋涡和反气旋涡的生命周期存在较大差异:它们的平均生命周期分别为9.99周和11.00周, 反气旋涡略长; 对于周期小于16周的涡旋而言, 气旋涡比反气旋涡的数量多10.3%, 而对于周期大于16周的涡旋而言, 反气旋涡比气旋涡多出20.1%, 即短周期的涡旋以气旋涡为主, 而长周期的涡旋以反气旋涡为主。
2.2 半径本节讨论的涡旋半径是基于所有时次中被识别出来的涡旋而言, 即27930个气旋涡和29822个反气旋涡。经统计, 气旋涡和反气旋涡的平均半径分别为69.5km和71.8km。图 3为涡旋半径的概率密度分布, 该图表明, 气旋涡和反气旋涡半径的概率密度函数均呈正偏态分布, 概率密度的峰值出现在55—60km区间, 这种半径的概率密度分布特征在许多其他海域也是存在的, 如东南太平洋(Chaigneau et al, 2008)、副热带西北太平洋(Yang et al, 2013)、热带东南印度洋(Yang et al, 2015)。半径在40—90km的气旋涡和反气旋涡分别占总数的74.8%和73.7%, 大于180km的涡很少, 气旋涡和反气旋涡所占比例分别为0.67%和0.97%(图中实心圆点)。
 |
| 图 3 涡旋半径的概率密度分布 Fig. 3 Probability density function of the eddies relative to the eddy radius 注:蓝色和红色图标分别代表气旋涡和反气旋涡; 半径大于180km的涡旋概率密度以实心圆表示 |
为分析涡旋的涡度、EKE和EI随半径变化的平均情况, 我们首先将半径从小到大间隔5km划分成若干个区间, 考虑到若区间内的涡旋数量过少, 则不能反映涡旋的统计特征, 因此我们只选取涡旋数量超过总数0.1%的区间进行研究, 即15—170km的半径范围。图 4a表明, 随着半径从15km增加到50km, 气旋涡和反气旋涡的涡度(为方便比较, 已将反气旋涡的涡度取绝对值, 下文同)迅速增大至1.2×10–5/s; 而在50—100km的半径区间内, 涡度值变化较小; 随着半径继续增大至150km, 气旋涡和反气旋涡的涡度均呈增长趋势, 并在半径为150km左右时达到最大值1.5×10–5/s, 但反气旋涡的涡度增长速率明显大于气旋涡; 当半径大于150km时, 两种涡旋的涡度均呈不稳定波动变化, 但总体保持在1.3×10–5—1.5×10–5/s的水平。EKE随半径的变化如图 4b所示, 当半径为15km时, 气旋涡和反气旋涡的平均EKE分别仅为19和20cm2/s2, 随着半径增加至50km, 两种类型涡旋的EKE迅速增长到295和195cm2/s–2; 当半径继续增大时, 两种涡旋的EKE变化存在明显差异:气旋涡的EKE值缓慢增大而后趋于平稳, 最大值可达460cm2/s2, 当半径大于150km时, EKE减小; 反气旋涡的EKE随着半径的增大呈准线性增长, 并在半径为150km左右时达到最大值600cm2/s2, 而后EKE值略有下降。这种EKE与半径对应关系与其他海区, 如副热带西北太平洋(Yang et al, 2013)、东南太平洋(Chaignuea et al, 2008)EKE随半径呈准线变化的结果有所差异, 原因可能在于黑潮和涡旋之间强烈相互作用可以极大地改变涡旋结构(Zheng et al, 2011), 甚至可以造成涡旋破裂形成更小涡旋(Yang et al, 2013), 导致EKE在不同尺度涡旋间重新分配。如图 4c所示, 两种类型涡旋的EI的随半径变化的形势相似, 均为先增大后减小, 气旋(反气旋)涡EI的最大值出现在半径为50(40)km时, 最大值为3.3×10–2(2.2×10–2) cm2/(s2∙km2), 造成这种EI与半径对应关系的原因在于, 气旋(反气旋)涡半径小于50(40)km时, EKE的增加速率快于涡旋面积的增大速率, 半径大于50km时的情况正好相反, 因此EI在半径为50(40)km左右时达到极大值, 即涡旋动能最集中, 这一结果与南印度洋(胡冬等, 2017)的涡旋统计结果一致。此外, 对比气旋涡和反气旋涡的以上三种特征量与半径的关系可以发现, 对于具有相同半径的涡旋而言, 半径小于140km时, 气旋涡的平均涡度大于反气旋涡, 尤其是半径在50—100km区间时二者相差较大; 半径小于110km时, 气旋涡的EKE和EI均大于反气旋涡, 半径大于110km时, 反气旋涡的EKE明显大于气旋涡, 二者的EI则十分接近。
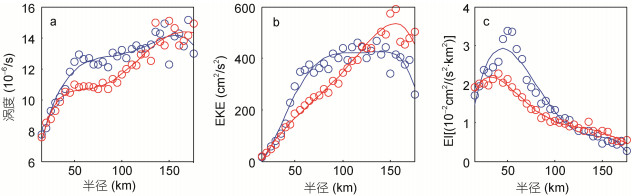 |
| 图 4 涡旋的各特征量与半径的关系 Fig. 4 Eddy parameters as a function of eddy radius 注: a:涡度(单位: 10–6/s), b: EKE(单位: cm2/s2); c: EI(单位: 10–2cm2/(s2·km2))。蓝色和红色圆圈分别表示气旋涡和反气旋涡的特征量, 实线为对应的特征量经过五次拟合后的结果 |
涡旋的出现频率(以下简称涡旋频率)表示研究区域内某点处于涡旋内的概率(Chaigneau et al, 2009), 计算公式为: F=n/N×100。其中, n是某网格点位于涡旋内的次数, N是总的观测次数。涡旋频率的空间分布如图 5a所示。整体而言, 涡旋频率的空间分布很不均匀, 沿黑潮主轴附近存在一个涡旋频率高值区, 涡旋频率值最大可达33%, 这一高值区一直延伸到175°W, 与图 1中的EKE高值区域对应较好, 表明该区域内高频率的涡旋活动对高EKE分布具有重要作用。在高值区的南北两侧, 涡旋频率较小。此外, 沿Japan Trench(JT)和Kuril-Kamchatka Trench(KT)的狭长区域涡旋频率也很大, 这Itoh等(2010a)的统计结果一致。从纬向平均上看(图 5.b), 35°N为涡旋频率的峰值区, 这一纬度大致对应黑潮主轴所在的平均纬度, 平均涡旋频率为17.6%, 35°N向南北两侧频率值逐渐减小。
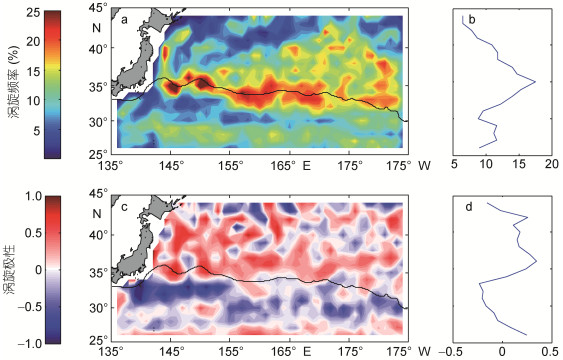 |
| 图 5 涡旋频率和极性分布 Fig. 5 Spatial distribution of eddy frequency and polarity 注: a:涡旋频率(%)的地理分布; b:涡旋频率(%)的纬向平均; c:涡旋极性的地理分布; d:涡旋极性的纬向平均。a和c采用了不同的色标, 黑色实线为黑潮主轴的大致位置 |
涡旋极性表示某一点处于气旋涡或反气旋涡内的概率(Chaigneau et al, 2009), 计算公式为: P= (FAE–FCE)/(FAE+FCE), 其中, FAE和FCE分别表示反气旋涡和气旋涡的频率。涡旋极性空间分布(图 5c)的最大特点是, 黑潮主轴的南北两侧, 极性值分别以负值和正值为主, 即分别以气旋涡和反气旋涡数量占多。极性值的正负交界区大致沿急流主轴分布, 且其两侧的极性变化迅速, 这与黑潮流轴容易在南北两侧分别脱落形成气旋涡和反气旋涡有关(Stammer et al, 1999)。这种极性分布特点在纬向平均分布图中(图 5d)也有所体现, 且与Itoh等(2010a)和郑聪聪等(2014)的结果类似。
2.4 涡旋特征量的地理分布为分析涡旋半径、EKE、EI及涡度等特征量的地理分布特征, 将研究海区划分成1°×1°网格, 并计算各网格内所有移动经过的涡旋的平均半径、EKE、EI和涡度。
如图 6a和图 6b所示, 气旋涡和反气旋涡的平均半径均呈较明显的纬向分布特征: 32°—37°N附近的平均半径较大, 明显大于南北两侧, 即涡旋平均半径从南至北呈“小-大-小”的纬向分布。涡旋的平均EKE(图 6c, d)、EI(图 6e, f)、涡度(图 6g, h)具有相对一致的分布特征, 即沿黑潮主轴附近, 存在EKE、EI和涡度的带状高值区, 尤其在144°E附近, 这些特征量值明显大于其他区域, 其中, EKE和EI比其他区域高出约2个量级, 涡度比其他区域高出约1个量级。崔伟等(2017)统计发现30°—35°N之间的黑潮延伸体区域中尺度涡具有更高的涡动能和涡振幅, 本文的涡旋强度带状高值区与其位置是基本一致的。此外, 气旋涡各要素值与反气旋涡存在明显差异:气旋涡EKE、EI和涡度的强值区主要出现在黑潮流轴的偏南侧, 而反气旋涡的强值区出现在偏北侧(Itoh et al, 2010a); 绝大部分区域, 尤其是在黑潮流轴附近区域, 气旋涡的EKE、EI和涡度均明显大于反气旋涡, 而在沿JT和KKT的狭长区域, 反气旋涡的EKE、EI和涡度值略大于气旋涡, 这一结果与Itoh等(2010a)的相关结论一致。
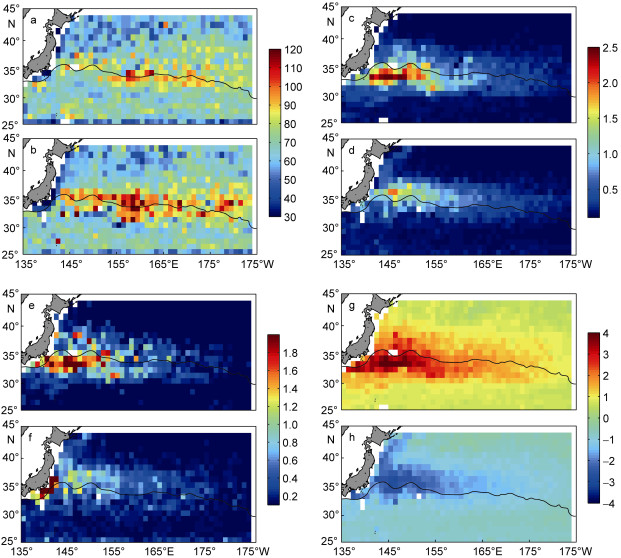 |
| 图 6 涡旋特征量的地理分布 Fig. 6 Spatial distributions of the eddy mean properties 注: a:气旋涡的半径(单位: km); c:气旋涡的EKE(单位: 103cm2/s2); e:气旋涡的EI(单位: 10–2cm2/(s2∙km2)); g:气旋涡的涡度(单位: 10–5/s); b, d, f, h分别为对应反气旋涡的EKE、EI和涡度的分布, 各子图中黑色实线为黑潮主轴的大致位置 |
为进一步分析长生命周期涡旋在生命周期内各种性质的演变特征, 我们选取生命周期不短于20周的涡旋(包括266个气旋涡轨迹, 372个反气旋涡轨迹), 将各个涡的周期在[0, 1]区间内平均分成20个时间段, 并将各涡旋的半径等参数值插值到这20个时间段内, 以分析在涡旋周期内, 各参数随时间变化的平均情况(图 7)。
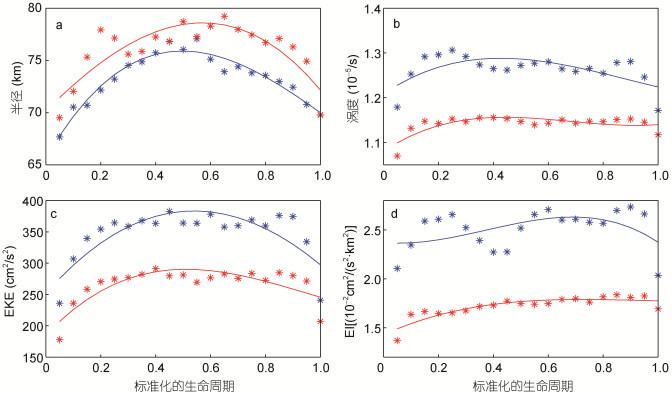 |
| 图 7 长生命周期涡旋性质的演变 Fig. 7 Evolutions of the properties of long-lived eddies 注: a:半径(单位: km); b:涡度(单位: 10-5/s); c): EKE(单位: cm2/s2); d: EI(单位: 10–2cm2/(s2∙km2)); 各子图中蓝色和红色星号分别代表气旋涡和反气旋涡, 实线是对应参数经3次拟合后结果 |
对于半径而言(图 7a), 气旋涡和反气旋涡在生成后的2/5周期内, 半径逐渐变大, 随后的2/5周期内半径出现小幅波动, 但大小基本保持不变, 在4/5周期之后半径迅速减小。
对于涡度而言(图 7b), 在整个生命周期中, 其变化较为缓慢且变化幅度很小。在前1/5周期, 气旋涡和反气旋涡的涡度均有小幅增大, 之后涡度值基本保持不变(分别为约1.28×10–5/s和1.16×10–5/s), 且反气旋涡的涡度值直至消亡时刻仍变化很小, 而气旋涡的涡度值在最后1/10周期阶段略有下降。
如图 7c所示, 气旋涡和反气旋涡EKE的变化形势较为一致, 在周期的前2/5阶段, EKE值迅速增长, 最大值分别为380cm2/s2和290cm2/s2, 比初始状态分别高出60%和58%, 随后EKE值基本不变, 但在周期的最后1/10阶段, 气旋涡和反气旋涡的EKE均出现大幅下降情况。
EI的变化情况如图 7d所示, 气旋涡呈现增大-减小的趋势, 且变化幅度较大, 而反气旋涡的EI在前2/5周期内逐渐增大后趋于平稳, 且整体变化幅度与气旋涡相比较小。
总体而言, 气旋涡和反气旋涡的半径、涡度、EKE和EI随时间的变化趋势相近, 都经历了增大而后减小的过程, 综合考虑它们的变化可以发现, 涡旋在其生命周期内大致经历了增大-基本保持不变-减小这三个阶段, 但是EKE和半径变化幅度大, 而涡度和EI的变化幅度较小。
此外, 在涡旋的整个周期中, 除了半径是反气旋涡大于气旋涡外, 涡度、EKE和EI均是气旋涡大于反气旋涡, 其中, 气旋涡的平均涡度和EKE分别比反气旋涡高出10%和30%, 而气旋涡的平均EI更是比反气旋涡高出45%。若以涡度、EKE和EI综合判断涡旋的强弱, 则长生命周期的气旋涡强度始终大于反气旋涡。
2.6 移动特征为了较为清晰地显示涡旋的移动轨迹特征, 这里作出周期大于20周的涡旋移动轨迹(如图 8), 该图表明, 较长周期的气旋涡轨迹主要分布于黑潮主轴南侧, 反气旋涡轨迹主要分布在黑潮主轴的北侧以及30°N以南区域, 而主轴以南至30°N区域长周期反气旋涡轨迹数量很少, 这种特征与胡冬等(已录用)的结果是一致的。总体而言, 黑潮主轴以南的较长周期气旋涡和反气旋涡的移动均以西向为主, 经向移动距离较小, 而在主轴以北, 涡旋移动轨迹较为零乱且经向移动距离较大。
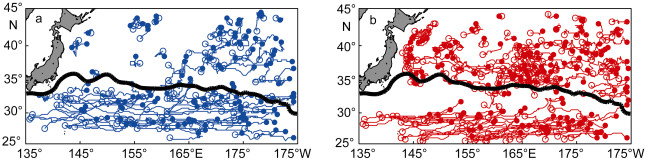 |
| 图 8 周期大于26周的涡旋移动轨迹 Fig. 8 The trajectories of the eddy tracks with a lifespan longer than 26 weeks 注: a:气旋涡; b:反气旋涡。实心点为涡旋的产生地点, 空心圈为涡旋的消失地, 黑色实线为黑潮主轴位置 |
图 9显示了所有涡旋在统一起点(0, 0)处的移动轨迹, 横轴正方向表示向西移动, 纵轴的正负方向分别表示向北(极向)和向南(赤道)移动。该图表明, 绝大多数气旋涡和反气旋涡都沿纬线向西移动, 气旋涡(反气旋涡)平均向西移动1.14(1.25)个经度, 最多的可西传32.25(18)个经度; 在经向上涡旋的移动距离较小, 且两种极性的涡旋在西向传播过程中, 都具有明显的向南(赤道)偏离趋势。Morrow等(2004)在统计全球三个典型东边界流区的中尺度涡移动轨迹时发现, 长周期反气旋涡和气旋涡分别有较小的向赤道和极地偏移趋势, Chelton等(2007)和Yang等(2013)分别基于全球和副热带逆流区中尺度涡的统计结果也发现了相似的结论。Morrow等(2004)认为这种现象与β效应有关, 一般发生在背景流较弱区域。而在其他一些海区的统计结果表明, 受β效应、背景流场、地形等共同作用, 涡旋的偏移方向与上述结论存在较大差异(Sangrà et al, 2009; Chen et al, 2011)。在本文研究区域, 仅有32.9%的气旋涡向北(极地)方向偏离趋势, 原因可能在于受黑潮急流阻挡作用, 气旋涡很难穿越主轴向北移动。
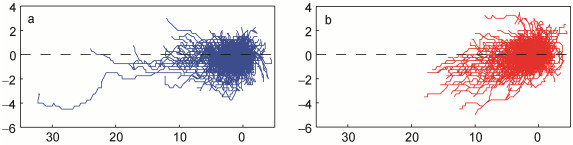 |
| 图 9 涡旋的移动路径合成图 Fig. 9 Composed trajectories of the eddy tracks 注: a:气旋涡路径; b:反气旋涡路径。横轴正方向表示向西移动的经度, 纵轴的正负方向分别表示向北(极向)和向南(赤道)移动的纬度 |
图 10为涡旋平均移动速度的分布。涡旋平均移速大小为2.8cm/s, 速度大小大致沿纬线呈带状分布, 由南向北速度大小逐渐减小。160°E以西、33°N以南区域为移速的大值区。32°N以南涡旋的移向以西向为主, 经向移动很小, 且涡旋移动速度较大; 而在32°N以北, 大部分区域涡旋的移速也以西向分量为主, 但在黑潮主轴附近以及西边界附近区域, 涡旋的平均移向变化较大、移速分布较为紊乱, 表明该区域涡旋的移动可能受黑潮流的影响很大, 这与另一个西边界流——湾流附近中尺度涡移速分布特征十分相似(洪森等, 2016)。
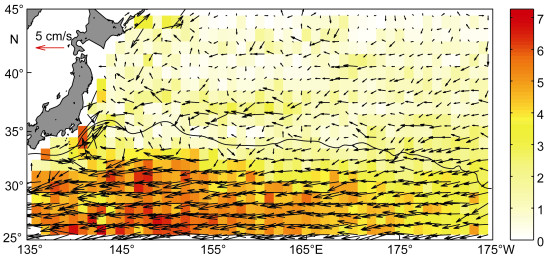 |
| 图 10 涡旋移动速度的分布图 Fig. 10 Distribution of the eddy speed 注:箭头表示在1°×1°网格内的平均移速, 色块表示速度大小(单位: cm/s), 黑色实线为黑潮主轴的大致位置 |
将所有时次的速度平均到1°间隔的纬度上, 得到平均纬向速度u和平均经向速度v随纬度的分布情况(如图 11所示)。图 11a表明, 除44°—45°N范围外, 涡旋在不同纬度上的平均纬向速度均向西, 且西向传播速度均随纬度的增加呈减小趋势, 这一变化特征与理论计算得到的一阶非线性、自由传播的斜压罗斯贝波相速度(图 11a中黑色实线)的变化特征基本一致, 但在35°N附近, 涡旋的西向移速明显小于其两侧的涡旋移速, 这可能是由于受黑潮流的影响。此外, 气旋涡的平均西向传播速度均大于反气旋涡。图 11b表明, 气旋涡和反气旋涡的经向传播速度差异不大, 除40°—45°N的部分纬度带涡旋经向速度向北外, 其余纬度范围内, 两种极性涡旋的平均经向速度都向南, 且随着纬度的减小, 平均南向移动速度呈增大趋势。
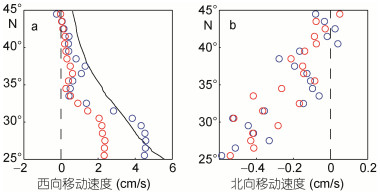 |
| 图 11 涡旋平均纬向速度和平均经向速度分布 Fig. 11 Distribution of mean zonal and meridional speed of the eddies 注: a:平均纬向传播速度(单位: cm/s), 黑线为一阶斜压罗斯贝波相速度; b:平均经向传播速度(单位: cm/s), 蓝圈和红圈分别表示气旋涡和反气旋涡的速度 |
研究区域内平均EKE的季节变化如图 12所示, 该图表明, EKE的季节性差异较大, 月平均值以8月的最大, 可达232cm2/s2, 2月最小, 仅为182cm2/s2; 季节平均值以夏季最大, 为231cm2/s2, 其次为春季和秋季, 最小值为冬季的186cm2/s2。这一结果与Scharffenberg(2008)的EKE夏季强冬季弱的观点是相同的。然而, Waterman等(2011)的计算结果表明, 涡旋引起的EKE变化在黑潮流轴两侧的总变化中所占比重仅为38%, 因此不能完全以EKE来分析中尺度涡的各类性质和季节变化。本节在上文的工作基础上, 对研究区域内中尺度涡的数量、生命周期等性质的季节变化特征进行具体研究。这里, 分别对新生成涡旋和所有时次出现的涡旋进行讨论。
 |
| 图 12 黑潮延伸体及其邻近海区平均EKE的季节变化图 Fig. 12 Seasonal variatiosn of EKE in the adjacent area of Kuroshio extension 注:黑色实线为各月的平均值, 灰色柱状图为各季节的平均值 |
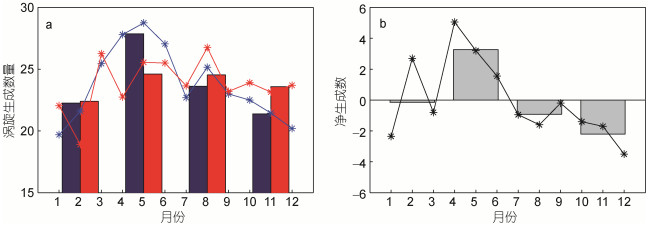
新生成涡旋数量的季节变化如图 13所示。各月新生成的涡旋平均数量(图 13a中蓝线)在19.7—28.8个, 具有明显的月变化特征, 生成数量最多和最少的月份分别为5月和1月, 从12月至5月涡旋生成数量逐渐上升, 5月至12月生成数量呈下降趋势。各季节平均生成数量(图 13a中蓝色条形图)的差异也很明显, 春季最多, 可达27.9个, 秋季最少, 仅为21.4个。涡旋的各月消亡数量(红色实线)和各季节平均消亡数(图 13a中红色条形图)差异并不十分明显, 但总体而言, 春夏季略多, 冬季最少。
 |
|
图 13 涡旋数量的季节变化 Fig. 13 Seasonal variations of eddy amount 注: a:涡旋生消数量的平均月变化和季节变化, 蓝色和红色实线分别为各月的涡旋平均生成和消亡数, 条形图为各季节(3个月)平均涡旋生成数和消亡数; b:涡旋净生成数的平均月变化和季节变化, 图中实线为各月的净生成数量, 灰色条形图为各季节(3个月)平均净生 成数 |
这里定义涡旋的“净生成数”为某一段时期内涡旋的生成数和消亡数之差。研究区域内涡旋的“净生成数”如图 13.b所示, 该图表明, 各月的涡旋净生成数差异很大:除2月、4—6月净生成数为正值外, 其他月份净生成数均为负值, 净生成数的最大值和最小值分别出现在4月和12月, 其值分别为5.1个和–3.5个, 4月—12月, 净生成数呈下降趋势, 并逐渐由正值变为负值。平均净生成数的季节变化也很明显:冬季净生成数几乎为0, 春季净生成数为正值, 且为各季的最大值, 从春季至夏季, 净生成数由正值变为负值, 最大负值出现在秋季。上述结果表明, 春季该区域内涡旋的生成数量相对于消亡数量明显占多, 夏秋季则与之相反。
新生成涡旋生命周期等要素的变化如图 14所示。生成于春夏季的涡旋生命周期明显大于生成于秋冬季的涡旋(图 14a), 即生成于春夏季的涡旋平均存活时间更长。图 14b表明, 新生成涡旋平均半径的季节性差异不大, 最大只相差1 km左右。新生成涡旋平均涡度的季节变化如图 14c所示, 该图表明, 各月的平均涡度差异十分明显, 最大值和最小值分别出现在6月和1月, 平均涡度值在春季达最大, 秋季为最小。EKE的变化(图 14d)与涡度变化有所差异, 季节平均值分别在夏季和冬季达最大和最小。EI的季节最大值同样出现在夏季, 但最小值则出现在春季(图 14e)。
 |
| 图 14 新生成涡旋各要素的平均季节变化 Fig. 14 Seasonal variations of properties of newly generated eddies 注: a:生命周期(单位:周); b:半径(单位: km); c:涡度(单位: 10–5km); d: EKE(单位: 102cm2/s2); e: EI(单位: 10–2cm2/(s2∙km2))。条形图为季节平均值, 实线为各月平均值 |
综上可知, 涡旋的生成数量在春季最多, 生成于春夏季的涡旋生命周期较长、强度较强, 生成于秋冬季的涡旋强度较弱, 这种季节性差异对于气旋涡和反气旋涡这两种不同类型的涡旋来说是相似的(图略)。
3.2 所有涡旋的季节性变化特征区域内所有涡旋的各要素季节变化如图 15所示。图 15a为涡旋总数量的季节性变化, 春夏季的涡旋数量明显多于秋冬季, 即涡旋活动更加频繁; 涡旋的半径变化幅度较小(图 15b), 各季节间的平均半径相差不到1km; 与半径的变化幅度相比, 涡旋的涡度(图 15c)、EKE(图 15d)和EI(图 15e)的季节变化较大, 其中, 涡度的季节最大值出现在春季, EKE和EI的最大值均出现在夏季, 三者的季节最小值出现在冬季。
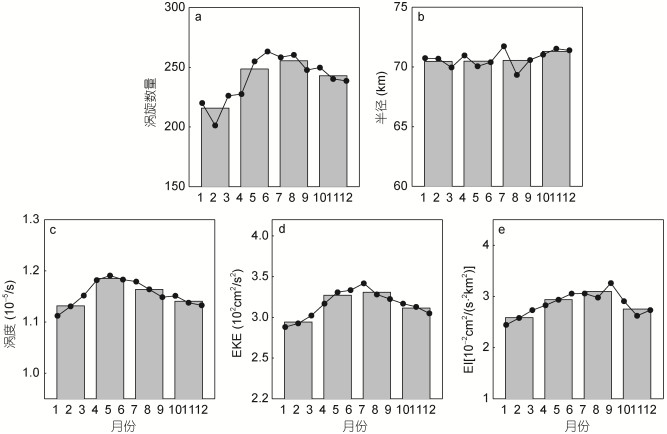 |
| 图 15 涡旋各要素的平均季节变化 Fig. 15 Seasonal variations of properties of all eddies 注: a:生命周期(单位:周); b:半径(单位: km); c:涡度(单位: 10–5/s); d: EKE(单位: 102cm2/s2); e: EI(单位: 10–2cm2/(s2∙km2))。条形图为季节平均值, 实线为各月平均值 |
对于气旋涡和反气旋涡, 涡旋数量等要素的季节变化存在一定差异。如图 16a所示, 两种类型的涡旋数量分布较为相似, 最大值和最小值均分别出现在夏季和冬季, 各月的涡旋数量变化形势较为一致, 但反气旋涡的数量始终大于气旋涡。对于半径而言(图 16b), 气旋涡和反气旋涡的季节性差异均不明显, 但各季节的反气旋涡平均半径略大于气旋涡。图 16c—e分别为两种类型涡旋的涡度、EKE、EI的季节变化, 对于气旋涡而言, 涡度、EKE、EI的最大值均出现在夏季, 最小值出现在冬季, 而反气旋涡的季节平均最大值出现在春季, 最小值出现在春季或冬季。两种类型涡旋相比, 气旋涡的变化幅度更大、强度也明显大于反气旋涡, 且这种差异性在夏季体现得最为明显, 夏季气旋涡的涡度、EKE和EI分别比反气旋涡高15%, 35%, 69%。
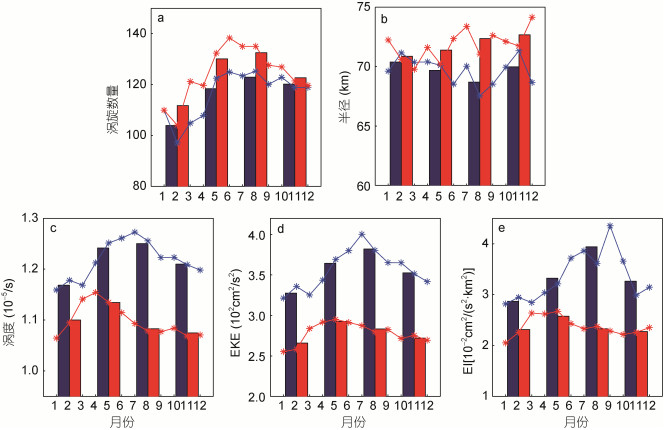 |
| 图 16 不同类型涡旋各要素的平均季节变化 Fig. 16 Seasonal variations of properties of different types of eddies 注: a:涡旋数量; b:半径(单位: km); c:涡度(单位: 10–5/s); d: EKE(单位: 102cm2/s2); e: EI(单位: 10–2cm2/(s2∙km2))。条形图为季节平均值, 实线为各月平均值, 蓝色和红色图标分别代表气旋涡和反气旋涡 |
综上分析可知, 春夏季是涡旋的多发期和活跃期, 这一时期的涡旋数量和强度均处于较高水平。前人的许多研究表明, 黑潮延伸体表层流量具有夏秋季大、冬春季小的季节性特性(Tatebe et al, 2001; 张志春等, 2015; 赵新华等, 2016)。而关于黑潮延伸体区域中尺度涡的季节特征, 前人主要从EKE的时间变化进行分析(参见本文引言部分), 并得到较为一致的“夏强冬弱”季节分布特征。本节具体从中尺度涡的涡度、EKE、EI等特征量季节变化的角度, 基本证实了这种观点。然而, 这种季节变化特征的物理机制, 以及EKE与黑潮延伸体流轴的季节变化之间是否存在关联尚不完全清楚(张笑等, 2013)。值得注意的是, 另一个西边界流延伸体区域——湾流延伸体区域的中尺度涡也在明显的“夏强冬弱”季节特征(胡冬等, 已录用), 因此我们可以推测这两个区域中尺度涡季节变化的物理机制可能是相同或相似的, 今后在研究涡旋季节变化的物理机制时可将两个区域联系起来进行分析讨论。
4 结论本文利用卫星高度计资料, 对黑潮延伸体邻近海区海洋中尺度涡的分布等统计性特征和季节变化进行了统计研究, 主要结论如下:
(1) 共识别出3006个气旋涡轨迹和2887个反气旋涡轨迹。气旋涡和反气旋涡的平均周期分别为9.99周和11.00周, 平均半径分别为69.5km和71.8km。
(2) 黑潮主轴附近是涡旋的高发区, 主轴的南北两侧, 极性值分别以负值和正值为主, 即分别以气旋涡和反气旋涡数量占多。
(3) 涡旋的平均半径从南至北呈“小-大-小”的纬向分布, 涡旋的平均EKE、EI、涡度在黑潮主轴附近存在带状高值区, 强度明显大于其他区域。
(4) 长生命周期气旋涡和反气旋涡的半径、涡度、EKE和EI随生命周期的变化趋势相近, 大致都经历了增大-基本保持不变-减小这三个阶段, 气旋涡强度始终大于反气旋涡。
(5) 绝大多数涡旋沿纬线向西移动, 经向上移动距离较小, 气旋涡和反气旋涡在西向传播过程中都具有明显的向南(赤道)偏离趋势。涡旋的平均移动速度大小大致沿纬线呈带状分布, 由南向北逐渐减小。西边界区域和黑潮主轴附近区域, 涡旋的移向移速分布较为紊乱。
(6) 涡旋的生成数量与总数量均在春夏季达到最多, 且这一时期涡旋的涡度、EKE、EI均处于较高水平。各季节中反气旋涡数量占多, 但气旋涡的涡度、EKE、EI等强度明显大于反气旋涡。
| 冯劭华, 罗德海, 钟霖浩, 2015. 黑潮延伸体中尺度涡年代际变化与北太平洋风暴轴变化之间的关系. 大气科学, 39(5): 861–874 |
| 张志春, 袁东亮, 李博, 2015. 基于Argo浮标的西北太平洋环流特征分析. 海洋科学, 39(7): 93–102 DOI:10.11759/hykx20130319001 |
| 张笑, 贾英来, 沈辉, 等, 2013. 黑潮延伸体区域海洋涡旋研究进展. 气候变化研究快报, 2(1): 1–8 |
| 郑聪聪, 杨宇星, 王法明, 2014. 北太平洋中尺度涡时空特征分析. 海洋科学, 38(10): 105–112 DOI:10.11759/hykx20130129004 |
| 赵新华, 杨俊钢, 崔伟, 2016. 基于20a卫星高度计数据的黑潮变异特征. 海洋科学, 40(1): 132–137 DOI:10.11759/hykx20150108002 |
| 胡冬, 陈希, 毛科峰, 等, 2017. 南印度洋中尺度涡统计特征及三维合成结构研究. 海洋学报, 39(9): 1–14 |
| 胡冬, 陈希, 赵艳玲, 等, 2018. 两个西边界流延伸体区域中尺度涡统计特征分析. 海洋学报(已录用), |
| 洪森, 胡冬, 陈希, 等, 2016. 湾流及其邻近海域中尺度涡统计特征分析. 解放军理工大学学报(自然科学版), 17(5): 459–466 |
| 祖永灿, 方越, 高晓倩, 等, 2016. 北太平洋中尺度涡季节和年际变化的统计分析. 海洋科学进展, 34(2): 197–206 |
| 崔伟, 王伟, 马毅, 等, 2017. 基于1993-2014年高度计数据的西北太平洋中尺度涡识别和特征分析. 海洋学报, 39(2): 16–28 |
| Adams D K, McGillicuddy Jr D J, Zamudio L, et al, 2011. Surface-generated mesoscale eddies transport deep-sea products from hydrothermal vents. Science, 332(6029): 580–583 DOI:10.1126/science.1201066 |
| Aoki S, Imawaki S, Ichikawa K, 1995. Baroclinic disturbances propagating westward in the Kuroshio Extension region as seen by a satellite altimeter and radiometers. Journal of Geophysical Research:Oceans, 100(C1): 839–855 DOI:10.1029/94JC02255 |
| Chaigneau A, Gizolme A, Grados C, 2008. Mesoscale eddies off Peru in altimeter records:Identification algorithms and eddy spatio-temporal patterns. Progress in Oceanography, 79(2-4): 106–119 DOI:10.1016/j.pocean.2008.10.013 |
| Chaigneau A, Eldin G, Dewitte B, 2009. Eddy activity in the four major upwelling systems from satellite altimetry (1992-2007). Progress in Oceanography, 83(1-4): 117–123 DOI:10.1016/j.pocean.2009.07.012 |
| Chelton D, 2013. Ocean-atmosphere coupling:Mesoscale eddy effects. Nature Geoscience, 6(8): 594–595 DOI:10.1038/ngeo1906 |
| Chelton D B, Schlax M G, Samelson R M, et al, 2007. Global observations of large oceanic eddies. Geophysical Research Letters, 34(15): L15606 |
| Chelton D B, Schlax M G, Samelson R M, 2011. Global observations of nonlinear mesoscale eddies. Progress in Oceanography, 91(2): 167–216 DOI:10.1016/j.pocean.2011.01.002 |
| Chen G X, Hou Y J, Chu X Q, 2011. Mesoscale eddies in the South China Sea:Mean properties, spatiotemporal variability, and impact on thermohaline structure. Journal of Geophysical Research:Oceans, 116(C6): C06018 |
| Dong C M, McWilliams J C, Liu Y, et al, 2014. Global heat and salt transports by eddy movement. Nature Communications, 5: 3294 DOI:10.1038/ncomms4294 |
| Itoh S, Yasuda I, 2010a. Characteristics of mesoscale eddies in the kuroshio-Oyashio extension region detected from the distribution of the sea surface height anomaly. Journal of Physical Oceanography, 40(5): 1018–1034 DOI:10.1175/2009JPO4265.1 |
| Itoh S, Yasuda I, 2010b. Water mass structure of warm and cold anticyclonic eddies in the western boundary region of the subarctic North Pacific. Journal of Physical Oceanography, 40(12): 2624–2642 DOI:10.1175/2010JPO4475.1 |
| Ma L B, Wang Q, 2014. Mean properties of mesoscale eddies in the Kuroshio recirculation region. Chinese Journal of Oceanology and Limnology, 32(3): 681–702 DOI:10.1007/s00343-014-3029-2 |
| Mizuno K, White W B, 1983. Annual and interannual variability in the Kuroshio current system. Journal of Physical Oceanography, 13(10): 1847–1867 DOI:10.1175/1520-0485(1983)013<1847:AAIVIT>2.0.CO;2 |
| Morrow R, Birol F, Griffin D, et al, 2004. Divergent pathways of cyclonic and anti-cyclonic ocean eddies. Geophysical Research Letters, 31(24): L24311 DOI:10.1029/2004GL020974 |
| Nan F, He Z G, Zhou H, et al, 2011. Three long-lived anticyclonic eddies in the northern South China Sea. Journal of Geophysical Research:Atmospheres, 116(C5): C05002 |
| Nencioli F, Dong C M, Dickey T, et al, 2010. A vector geometry-based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California bight. Journal of Atmospheric and Oceanic Technology, 27(3): 564–579 DOI:10.1175/2009JTECHO725.1 |
| Qiu B, 2003. Kuroshio extension variability and forcing of the pacific decadal oscillations:Responses and potential feedback. Journal of Physical Oceanography, 33(12): 2465–2482 DOI:10.1175/1520-0485(2003)033<2465:KEVAFO>2.0.CO;2 |
| Qiu B, Chen S M, 2010. Interannual variability of the North Pacific subtropical countercurrent and its associated mesoscale eddy field. Journal of Physical Oceanography, 40(1): 213–225 DOI:10.1175/2009JPO4285.1 |
| Qiu B, Kelly K A, Joyce T M, 1991. Mean flow and variability in the Kuroshio Extension from Geosat altimetry data. Journal of Geophysical Research:Oceans, 96(C10): 18491–18507 DOI:10.1029/91JC01834 |
| Liang X S, 2016. Canonical transfer and multiscale energetics for primitive and quasigeostrophic atmospheres. Journal of the Atmospheric Sciences, 73(11): 4439–4468 DOI:10.1175/JAS-D-16-0131.1 |
| Liang X S, Anderson D G M, 2007. Multiscale window transform. Multiscale Modeling & Simulation, 6(2): 437–467 |
| Sangrà P, Pascual A, Rodríguez-Santana Á, et al, 2009. The canary eddy corridor:A major pathway for long-lived eddies in the subtropical North Atlantic. Deep Sea Research Part Ⅰ:Oceanographic Research Papers, 56(12): 2100–2114 DOI:10.1016/j.dsr.2009.08.008 |
| Scharffenberg M, 2008. Annual variations of geostrophic currents and eddy kinetic energy inferred from TOPEX/Poseidon and Jason-1 Tandem Mission data. In: Ocean Sciences Meeting. Orlando: Ocean Sciences Meeting, 3-7 |
| Small R J, DeSzoeke S P, Xie S P, et al, 2008. Air-sea interaction over ocean fronts and eddies. Dynamics of Atmospheres and Oceans, 45(3-4): 274–319 DOI:10.1016/j.dynatmoce.2008.01.001 |
| Stammer D, Wunsch C, 1999. Temporal changes in eddy energy of the oceans. Deep Sea Research Part Ⅱ:Topical studies in Oceanography, 46(1-2): 77–108 DOI:10.1016/S0967-0645(98)00106-4 |
| Tatebe H, Yasuda I, 2001. Seasonal axis migration of the upstream Kuroshio Extension associated with standing oscillations. Journal of Geophysical Research:Oceans, 106(C8): 16685–16692 DOI:10.1029/2000JC000467 |
| Wang L P, Koblinsky C J, 1995. Low-frequency variability in regions of the Kuroshio extension and the gulf stream. Journal of Geophysical Research:Oceans, 100(C9): 18313–18331 DOI:10.1029/95JC01832 |
| Waterman S, Hogg N G, Jayne S R, 2011. Eddy-mean flow interaction in the Kuroshio extension region. Journal of Physical Oceanography, 41(6): 1182–1208 DOI:10.1175/2010JPO4564.1 |
| Xu L X, Xie S P, McClean J L, et al, 2014. Mesoscale eddy effects on the subduction of North Pacific mode waters. Journal of Geophysical Research:Oceans, 119(8): 4867–4886 DOI:10.1002/2014JC009861 |
| Yang G, Wang F, Li Y, et al, 2013. Mesoscale eddies in the northwestern subtropical Pacific Ocean:Statistical characteristics and three-dimensional structures. Journal of Geophysical Research:Oceans, 118(4): 1906–1925 DOI:10.1002/jgrc.20164 |
| Yang G, Yu W D, Yuan Y L, et al, 2015. Characteristics, vertical structures, and heat/salt transports of mesoscale eddies in the southeastern tropical Indian Ocean. Journal of Geophysical Research:Oceans, 120(10): 6733–6750 DOI:10.1002/2015JC011130 |
| Yang Y, San Liang X, 2016. The instabilities and multiscale energetics underlying the mean-interannual-eddy interactions in the Kuroshio Extension region. Journal of Physical Oceanography, 46(5): 1477–1494 DOI:10.1175/JPO-D-15-0226.1 |
| Yang Y, San Liang X, Qiu B, et al, 2017. On the decadal variability of the eddy kinetic energy in the Kuroshio Extension. Journal of Physical Oceanography, 47(5): 1169–1187 DOI:10.1175/JPO-D-16-0201.1 |
| Zhang Z W, Zhao W, Tian J W, et al, 2013. A mesoscale eddy pair southwest of Taiwan and its influence on deep circulation. Journal of Geophysical Research:Oceans, 118(12): 6479–6494 DOI:10.1002/2013JC008994 |
| Zheng Q A, Tai C K, Hu J Y, et al, 2011. Satellite altimeter observations of nonlinear Rossby eddy-Kuroshio interaction at the Luzon Strait. Journal of Oceanography, 67(4): 365–376 DOI:10.1007/s10872-011-0035-2 |
 2018, Vol. 49
2018, Vol. 49


